HIV AND POPULATION DYNAMICS: A GENERAL MODEL AND MAXIMUM-LIKELIHOOD STANDARDS FOR EAST AFRICA*

Abstract

In high-prevalence populations, the HIV epidemic undermines the validity of past empirical models and related demographic techniques. A parsimonious model of HIV and population dynamics is presented here and fit to 46,000 observations, gathered from 11 East African populations. The fitted model simulates HIV and population dynamics with standard demographic inputs and only two additional parameters for the onset and scale of the epidemic. The underestimation of the general prevalence of HIV in samples of pregnant women and the fertility impact of HIV are examples of the dynamic interactions that demographic models must reproduce and are shown here to increase over time even with constant prevalence levels. As a result, the impact of HIV on population growth appears to have been underestimated by current population projections that ignore this dynamic.

National population forecasts are essential instruments of development planning. Since the mid-1950s, nearly all national and international agencies producing such forecasts have relied on a population-dynamics model known to demographers as the cohort-component model of population projection (hereafter, CCMPP). For a number of African countries, the main challenge to demographic forecasting has been to meet even the relatively modest data requirements of this model. Toward this end, international donors sponsored the first censuses and fertility surveys in a number of countries. Concurrently, demographers developed a series of ingenious “indirect” techniques (e.g., Brass 1975; United Nations (UN) 1967, 1983) and empirical models (e.g., model life tables; Coale and Demeny 1983; UN 1982) which allowed them to extract, correct, and supplement the required information from incomplete or inaccurate data.

HIV has quickly rendered obsolete these contributions to demographic estimation and forecasting in the populations that have been the hardest hit by the epidemic. The new challenge to population forecasting for these countries is not merely the uncertainty about the future level of mortality. Because the age pattern of AIDS-related mortality is so different from the existing J-shaped model age patterns of mortality, no existing model accurately represents the age structure of mortality when AIDS accounts for a significant proportion of all deaths. The epidemic also invalidates many indirect techniques that rely on now-untenable assumptions, such as the independence of the mother’s and the child’s survival.

There is no shortage of HIV/AIDS models, but these models either exceed the availability of data in African nations or lack the basic age structure that demographic models and methods require. Because HIV and population dynamics are intertwined, the lack of demographics in these models does not merely hinder their import in the field of population studies. Just as the estimates inferred from traditional demographic techniques may be biased by the HIV epidemic, the values of epidemiological estimates are influenced by the underlying population dynamics. This mutual dependence is perhaps clearest in the relationship between fertility rates and HIV infection. On the one hand, HIV infection reduces fecundability (Carpenter et al. 1997; Fylkesnes et al. 1998; Gray et al. 1998; Kigadye et al. 1993; Kilian et al. 1998); on the other hand, the proportion of sexually active individuals is expected to be lower in the HIV-negative population. Population-based data have confirmed that age-specific fertility rates are higher among HIV-positive women at early reproductive ages, whereas the reverse occurs at older ages, when the selection effect begins to fade out. The age structure of reproductive-age women therefore contributes to the all-age prevalence level estimated from data from antenatal clinics, the backbone of many surveillance systems that are designed to monitor HIV trends over time.

Therefore, to conduct national population projections and even to estimate basic demographic indicators in countries in which the prevalence of HIV exceeds a few percentage points, demographers require models that allow for the different age-specific rates of mortality and childbearing of HIV-positive individuals. In turn, a demographically sound model may well contribute to a better monitoring of the epidemic’s dynamics. This article presents one such model that takes into account the specific scarcity of data in East African countries, which, given their adult seroprevalence levels of 20% nationally, are among the worst hit (Piot et al. 2001). The model can be described as a “minimalist” multistate extension of the CCMPP.

Taking stock of the extant epidemiological literature, this article also provides default values for all but two of the parameters added to the single-state CCMPP. The literature review led to a classification of these additional parameters into three categories. The first consists of parameters that appear similar across all populations. HIV epidemics share, for instance, a similar progression, from an early “explosive” phase to a subexponential growth and an eventual saturation, a pattern typical of individual-to-individual transmission in a risk-heterogeneous population (Chin and Lwanga 1991; Stoneburner et al. 1996). The average duration from HIV to AIDS or from AIDS to death is also similar across populations (Alcabes et al. 1993; Moss and Bacchetti 1989; Schwartländer et al. 1999). Values for the corresponding parameters, if they are not available for the population of interest, can be taken directly from the literature.

The second category, however, consists of the parameters that are entirely population specific. Even though the diffusion of the epidemic often seems to follow a similar trend over time across populations, HIV epidemics have begun in different years and appear likely to stabilize at different levels (Caraël and Holmes 2001). Hence, there appears no alternative to the selection of a specific starting date of the HIV epidemic and of at least one indicator of the specific “scale” of the epidemic for each population.

The third category consists of “intermediate” parameters that are not readily available in the literature, but if they are not available for the population of interest, can be borrowed from other East African populations with reliable data. In the past two decades, a number of population-based research projects have been conducted in the region. The data generated by these projects and published in the epidemiological literature are extensive and reliable, but they do not directly provide values of the parameters required by the multistate extension of the CCMPP.

At the core of this article is the maximum-likelihood (ML) estimation of default values for these parameters, based on model predictions for the over 46,000 sex- and age-specific “HIV-related observations” that were collected through a comprehensive review of the data reported from the region. Examples of such observations include the pregnancy or survival of an individual of a given sex, age group, and HIV-infection status during a follow-up period and the outcome of the HIV testing of an individual of a given sex and age group. The parameters for which default values are hence selected include a sex- and age-specific pattern of HIV incidence and a duration-specific pattern of fertility reduction because of HIV infection. It is certainly a bold assumption to maintain that these patterns are constant across the region, but demographers will recognize here the classical approach of constructing a model pattern from satisfactory data and using it when original data are unavailable or unreliable.

HIV AND POPULATION MODELS FOR AFRICA: A CRITICAL REVIEW

Adding HIV/AIDS to a Demographic Model: The “External” Approach

In the years following the identification of HIV in 1983–1984, HIV epidemics of an unprecedented scale were gradually recognized in areas of central, eastern, and southern Africa, where HIV began spreading extensively, perhaps as early as the late 1970s (Piot et al. 1988). Under increasing criticism for failing to account explicitly for the demographic impact of the epidemic in its projections, the UN convened a meeting in 1989 to survey the available AIDS models (Palloni and Glicklich 1991). The models that were most appealing from a modeling perspective explicitly represented the different modes of HIV infection and made specific assumptions regarding the individual behaviors that condition the risk of infection. Because of the complexity involved in representing individual-to-individual heterogeneity with respect to these behaviors, these models make demands on data that have been impossible to meet for most, if not all, African populations (Palloni and Glicklich 1991; Stoto 1993).¹

Next, in decreasing order of both appeal and complexity were models that did not attempt to represent the determinants of the HIV infection, but did account for separate modes of transmission and postulated incubation periods for each mode. Meanwhile, the HIV trends were derived by simple extrapolation, using a mathematical function whose parameter values were selected by fitting past HIV trends to the model. The UN chose to use one such model, Epimodel (Chin 1994; Chin and Lwanga 1991), to project future mortality from HIV. In Epimodel, a gamma curve serves as the parametric function representing the trend in adult infection over time. The second mode of transmission is perinatal, from mother to child.

With a virtually endless number of HIV/AIDS models now available, Epimodel continues to provide an attractive option for many African countries because it requires more easily obtainable data than biobehavioral models and presents a more satisfactory modeling alternative to other simple models. As more data accumulate, the accuracy of the gamma curve appears to be mixed (Salomon and Murray 2001). On the one hand, the curve proved to have anticipated rather well the trend of new infections from their onset to their peak. On the other hand, it clearly projected too fast a decline after the peak. In particular, the possibility that new infections would decline and then remain at an endemic level for some time now appears more likely than the foretold disappearance of new infections within two decades of the peak (UN 1999).

A more persistent difficulty, however, is that Epimodel, like other models with affordable data requirements, does not provide a demographic component that is acceptable for population forecasting. The population forecaster must therefore continue to rely on a standard CCMPP, but only after preparing external HIV/AIDS projections to adjust original mortality rates before reimporting them into the CCMPP. (See Heuveline et al. 1992; UNAIDS 2002; UN 1999 for details on the UN procedure over time and the U.S. Census Bureau 1999 on the bureau’s.) The adjustment procedure can best be conceived as the reverse of the standard derivation of an associated single-decrement life table from a multidecrement life table (e.g., Preston, Heuveline, and Guillot 2001).

Such external adjustments to the CCMPP have become increasingly unsavory over time for at least three reasons. The first relates to the necessary assumptions about population dynamics that are used in the external HIV/AIDS model or in the adjustment procedure, as well as to the lack of feedback to ensure the compatibility of those assumptions with the population dynamics that are ultimately projected. These concerns about internal consistency become more serious over time as both the epidemic and population dynamics increasingly influence each other. For example, an AIDS model may project only a total number of AIDS-related deaths in a given period and use a fixed age-pattern to break down those deaths by age. As is confirmed later, one can expect the age pattern of AIDS-related deaths to change over time as the epidemic alters the age-structural dynamics of the population.

Second, the addition of AIDS-related deaths of HIV-infected individuals accounts for only the most visible demographic consequences of AIDS. A number of other downstream effects of the epidemic are now becoming manifest: the lower fertility of HIV-infected women, the increased mortality risks of “AIDS orphans,” and the synergistic relationship between HIV and tuberculosis, to name only a few (Heuveline 1997). Additional external procedures can certainly be derived to adjust the parameters of a standard CCMPP further. Estimates of the population impact of HIV on fertility (Zaba and Gregson 1998), for instance, can be used to correct age-specific fertility rates. But it becomes less and less clear that the long-term needs of forecasting high-prevalence populations will be best served by continued ad hoc “patching” of the single-state CCMPP approach.

The third reason that argues against the external approach relates to the necessity that population projections in the absence of AIDS must first be undertaken before the results of HIV/AIDS projections are added. Although this initial, counterfactual projection was relatively easy to prepare in the early years of the epidemic, it has become increasingly difficult and untenable to estimate demographic trends without AIDS. With the current approach, what should be seen as an empirical opportunity—the increasing availability of data on the intertwined epidemic and population dynamics—becomes an inconvenience.

Modeling HIV and Population Dynamics: Challenges to an Integrated Approach

Palloni (1996) clearly exposed the challenges of jointly modeling the dynamics of HIV and its host population. Compartmentalizing the population aged a at time t into three states with respect to HIV and AIDS—uninfected individuals H(a,t), infected individuals yet to develop AIDS I(a,t), and those who have AIDS A(a,t)—Palloni (1996:626) extended to these three states the differential equations of population dynamics known to demographers as variable-r equations:

$$\{\begin{array}{c}\partial H(a+\nu ,t+\nu )∕\partial \nu =-({\mu }_1(a,t)+\lambda (a,t))H(a,t)\hfill \\ \partial I(a+\nu ,t+\nu )∕\partial \nu =-({\mu }_2(a,t)+\delta \left(a\right))I\left(a\right)+\lambda (a,t)H(a,t)\hfill \\ \partial A(a+\nu ,t+\nu )∕\partial \nu =-{\mu }_3(a,t)A(a,t)+\delta \left(a\right)I(a,t)\hfill \end{array}\phantom{\}}$$ (1)

where μ₁(a,t), μ₂(a,t), and μ₃(a,t) are the mortality rates corresponding to each of the three states; λ(a,t) is the rate of new infection or incidence rate; δ and (a,t) is the rate at which HIV-infected individuals develop AIDS.

Just as the standard CCMPP is a macro-level, time-discrete Markovian model built on the single-state variable-r equation, the model developed in this article builds on Palloni’s set of differential equations in Eq. (1). An important difficulty noted by Palloni is that the incidence rate should be endogenous to the system because the rate at which susceptible individuals become infected depends on the number and characteristics of infected individuals. Attending to this difficulty requires modeling the individual behaviors that lead to infection and the population heterogeneity with respect to that risk. The associated data requirements hindered the use of the first demographic models that incorporated an epidemiological submodel into a traditional CCMPP (e.g., Bongaarts 1989; Bulatao 1991).

Moreover, in macromodels, the grouping of individuals into behavioral groups that are assumed to be homogeneous with respect to the risk of infection fails to represent fully individual-to-individual heterogeneity. As a result, these models underestimate the “saturation” that typically occurs, even in the absence of any behavioral change, with individual-to-individual transmission. A well-known related issue is the assumption regarding sexual mixing patterns (Anderson et al. 1991; Garnett and Anderson 1993). Simulations demonstrate that the more individuals tend to choose partners similar to themselves—that is, the less “random” the mixing pattern—the more quickly the epidemic growth rate tapers off (Brookmeyer and Gail 1994). The importance of the sexual mixing patterns was also illustrated at great costs by international surveys on sexual behavior that found that, unless several other key characteristics of the network of sexual partners are accounted for, the prevalence of extramarital sex or the average number of partners in a population correlates poorly with the prevalence of HIV (e.g., Caraël, Cleland, and Ingham 1994; Morris 1997). The dimensions of endogamy in sexual choices are numerous and difficult to encompass fully with a reasonably sized model.

Palloni (1996:629) argued, then, that “to see the forest,” one must reduce this complexity and use the best possible approximation of the set of equations in Eq. (1). One of Palloni’s (1996) suggestions is to assume a constant incidence rate, which would lead to a stable state. This approach can contribute to our understanding of the impact of the epidemic in the long run (e.g., Zaba 1994), but just as in the single-state case, stable-population theory provides little insight into the transitional dynamics that matter in population forecasting. The alternative proposed later borrows the trend in new infections over time from the UN model, that is, incidence is assumed, after a period of growth from the onset of the epidemic to its saturation, to decline and level off at an endemic level. The difference with the UN approach is that instead of importing AIDS mortality into the projections, with the aforementioned problems, the proposed model simply imports the all-age adult incidence trend over time; all other quantities are then derived internally.

A few issues must still be addressed before I turn the set of equations in Eq. (1) into an operational macro-level, time-discrete Markovian model for population forecasts. First, it is problematic that in Palloni’s equations the survival of HIV-infected individuals depends on their age, whereas the time since their infection (duration) is probably more important. Representing this dependence in Palloni’s model, however, would violate the Markovian assumption itself. The model presented here overcomes the obstacle by creating four duration states (0–4, 5–9, 10–14, and 15+) instead of two (asymptomatic HIV and full-blown AIDS), which thereby allows vital rates some duration dependence.² The second problem is that the parametric incidence trend is an all-age adult trend, whereas the model requires sex- and age-specific incidence rates. This problem is addressed by applying a model sex and age pattern of incidence that can be derived from available data by ML estimation. Finally, reproduction, absent from equations in Eq. (1), must be added to account for both the lower fertility of HIV-infected women and the possibility of vertical transmission. Values for the corresponding parameters are also derived from available data by ML estimation.

DATA AND METHODS

The Model

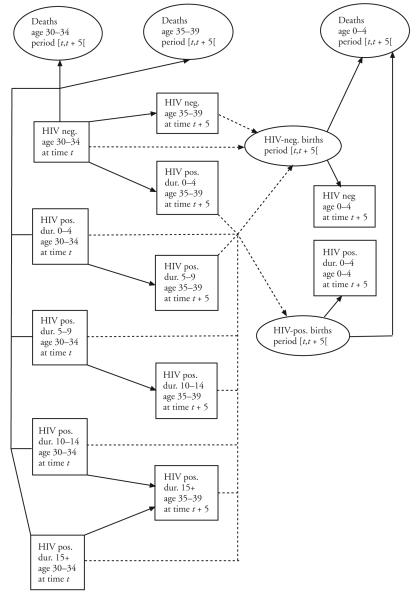
The model is a multistate extension of the CCMPP, building on Palloni’s (1996) assessment of the dynamics of HIV and its host population, along with the adjustments described earlier. The structure of the closed-population version of the model is represented in Figure 1. (Although this model excludes migration for purposes of simplicity, this factor can readily be added.) As in the single-state CCMPP, the population at the beginning of a projection interval is first divided into sex and age groups; here, however, each sex- and five-year age group is further divided into five states: the HIV-negative and the four HIV-positive duration states. Following Palloni (1996), the HIV negatives are subjected to two age-specific decrements, mortality and incidence, with the individuals “escaping” both decrements constituting the HIV negatives of the next age group at the beginning of the next projection interval. HIV positives are subjected to an age- and duration-specific mortality force, with the survivors constituting the HIV positives of the next duration state (the “open duration” state excepted), in the next age group at the beginning of the next interval. As in the single-state CCMPP, births are derived from age-specific fertility rates and the number of women of reproductive ages at the beginning and end of the projection interval. Here, different fertility rates are used for each of the five states. A vertical transmission rate is also used to separate HIV positives and HIV negatives among the babies born to HIV-positive mothers.

Figure 1.

Model Structure: Illustration for 30- to 34-Year-Old Women at the Beginning of the Projection Interval

The passage from continuous mathematical representations of individual chances of survival and reproduction to a discrete model involves a few approximations, generally acceptable for short projection intervals and small age groups. For instance, the single-state CCMPP represents the k-year survival of a k-year age group as follows:

$$W(a,k,t)=S(a,t,k)\times W(a-k,k,t-k),$$ (2)

where W(a,k,t) is the number of women aged a to a + k at time t. As discussed in the Appendix, there is no approximation involved in Eq. (2) because S(a,t,k) can be defined as the quantity that satisfies Eq. (2). An approximation is introduced in the single state of the CCMPP by ignoring that S(a,t,k) should depend on the exact age distribution between age x − k and x at time t – k, whereas its value is often estimated as the survivorship ratio from age group [a − k,a[ to age group [a,a + k[ in a life table that is believed to represent the mortality of the period t − k to t. This approximation, in effect, removes the dependence on the exact age distribution at time t – k; it would be exact if the age distribution of the population were that of the stationary population associated with the life table, but it is also acceptable, numerically speaking, when the age groups are small enough. Five-year age groups are often used in population projections because (1) mortality does not change rapidly with age except at the youngest and oldest ages and (2) within five-year age groups, age distributions vary little across most populations.

As is described in the Appendix, the decision, based on similar logic, to ignore within-group heterogeneity guided the derivation of the model’s equations from the underlying fertility, mortality, and incidence processes represented as continuous functions of age, time, and duration since infection. For instance, assuming that within-age-group heterogeneity is unimportant in respect to incidence, which is typically done in regard to mortality alone, the decline in the size of noninfected cohorts can be represented by two similar ratios:

$$W^0(a,5,t)=S^0(a,t,5)\times (1-I(a,t,5))\times W^0(a-5,5,t-5),$$ (3)

where W ⁰(a,5,t) is the number of HIV-negative women aged a to a + 5 at time t, S ⁰(a,t,5) is the survivorship ratio representing the survival to time t of HIV-negative women aged a – 5 to a at time t – 5, and I(a,t,5) represents the ratio of women aged a – 5 to a at time t – 5 who would be HIV positive at time t if they were to survive the risk of death between time t – 5 and time t.

Conversely, the survival of individuals who are HIV positive at the beginning of the projection period is represented as a function of the underlying duration-independent age-specific mortality risk, summarized by the same survival ratio as before, and an additional risk captured by a second age- and duration-dependent ratio. Denoted W ¹(a,d,5,t), the number of women aged a to a + 5 and infected for d to d + 5 years at time t is

$$W^1(a,d,5,t)=S^0(a,t,5)\times S^1(a,d,t,5)\times W^1(a-5,d-5,5,t-5),$$ (4)

where S ¹(a,d,t,5) is now the survivorship ratio that corresponds to additional mortality between time t – 5 and t of women aged a to a + 5 and infected for d to d + 5 years (at time t). These ratios can also be used to represent the infection and subsequent survival of individuals who become infected during the projection interval:

$$W^1(a,0,5,t)=S^0(a,t,5)\times S^1(a,0,t,5)\times I(a,t,5)\times W^0(a-5,5,t-5).$$ (5)

The number of births between time t – 5 and t from HIV-negative mothers and mothers who have been HIV positive for d to d + 5 years at the time of birth, respectively, B⁰(t – 5,5) and B¹(d,t – 5,5), are also estimated as in the single-state CCMPP, that is, by applying their respective period age-specific fertility rates to the average number of women in a given age group and state at the beginning and end of the projection interval. But births from HIV-positive women require further distribution between HIV-negative and HIV-positive births, which is accomplished here through the application of a duration-specific vertical transmission rate, V(d,t – 5,5) to B¹(d,t – 5,5). Finally, the proportion of births that survive to time t is estimated separately for each sex, using, as in the single-state CCMPP, a fixed sex ratio at birth s and a survivorship ratio from birth to age group [0,5[, though with different ratios for the two categories of HIV status at birth. For women, the size of the first age group of those who are HIV negative is therefore represented as

$$W^0(0,5,t)=\left(\frac{1}{1+s}\right)\times S^0(0,t,5)\times \left(B^0(t-5,5)+\sum _{d=0,5}(1-V(d,-5,5))\times B^1(d,t-5,5)\right),$$ (6)

whereas the size of the first age group in the first HIV-duration state is represented by

$$W^1(0,0,5,t)=\left(\frac{1}{1+s}\right)\times S^0(0,t,5)\times S^1(0,0,t,5)\times \sum _{d=0,5}V(d,t-5,5)\times B^1(d,t-5,5).$$ (7)

Empirical Regularities and Model Reduction

The foregoing multistate model improves on the single-state CCMPP’s representation of population dynamics in high HIV-prevalence populations, and entirely specified by Eqs. (3) to (7), the model is the least expansion of the CCMPP that provides for sex-, age-, and HIV-duration variations in survival and fertility. Such an improvement obviously comes at the expense of additional parameters to be estimated, and a model is more attractive for practical applications only insofar as reliable estimates of these parameters are available. In addition to the single-state model parameters, this model requires estimates of age-specific incidence ratios, I(a,t,5); age- and duration-specific survival ratios, S¹(a,d,t,5); age- and duration-specific female fertility rates, F¹(a,d,t,5); and duration-specific vertical transmission rates, V(d,t,5). Even these limited data requirements are not easily met for many of the world’s highest-prevalence populations, which are located in sub-Saharan Africa.

One of the classic demographic approaches to such data limitations has been to derive from the empirical regularities observed in populations with reliable data a model representation that could be substituted for missing, incomplete, or inaccurate data in other populations. This time-honored tradition is followed here to provide guidance in the choice of the parameters of the foregoing model when some parameters cannot be estimated reliably from available data. An examination of the epidemiological literature suggests that a few features of the HIV epidemic should apply to most populations. Survival from HIV infection has, for example, been studied across many populations, and the distributions of the progression time from HIV infection to AIDS and from AIDS to death appeared roughly similar until the introduction of highly active antiretroviral therapies (HAART). The median time from HIV infection to AIDS was consistently estimated at slightly under 10 years, and the median survival time to AIDS, at about 1 year (Alcabes et al. 1993; Anzala et al. 1995; Morgan et al. 2002; Moss and Bacchetti 1989; Schwartländer et al. 1999). Several studies have reported shorter survival times to HIV infection in African populations (Nunn et al. 1997; Sewankambo et al. 1994), but unless higher mortality from other causes is properly accounted for, these shorter survival times cannot be clearly attributed to a faster progression of the infection. There do not appear to be gender differences in survival to infection once age at the time of infection, the demographic factor best shown to affect survival, is adjusted for (Gregson and Garnett 2000).

The values of the age- and duration-specific survival ratios, S¹(a,d,t,5), can be calculated from the distribution of survival time after infection as the ratio of the person-years expected to be lived between duration d and d + 5 to the person-years expected to be lived between duration d – 5 and d according to that distribution (see the Appendix for more details). Default values, identical for both sexes, were so estimated from distributions with median survival times ranging from 8 to 12 years for adults, depending on the age at infection (combined with other causes of death, the median survival time after HIV infection is shorter). For HIV-positive births, the default survival ratios to age groups 0–4 and 5–9 correspond to a median survival time of just over 3 years (Chin 1994).

The choice of sex- and age-specific incidence ratios is more complex, foremost because incidence rates, rarely measured directly, are most often estimated from routinely collected prevalence data and “back calculation” methods (Brookmeyer and Gail 1994). The sex and age patterns of the prevalence of HIV display much regularity, at least across sub-Saharan African populations, typically peaking in the late 20s for females and late 30s for males. Insofar as the survival time following infection is relatively invariant, it is reasonable to assume that sex and age patterns of HIV incidence also share similarities across these populations. The level of incidence, however, can vary abruptly from one population to the next, even within short distances. Variations are due, in part, to differences in timing. As I discussed earlier, the early trends in the incidence of HIV appear to follow a reasonably similar pace over time when heterosexual intercourse is the dominant mode of HIV transmission (Stoneburner et al. 1996). In neighboring populations, too, incidence levels can be different when the epidemic is still at its onset in a given population, while it has already “matured” in another. But differences in timing do not tell the whole story. For reasons that are not yet fully understood, the epidemic appears to approach saturation at widely different prevalence levels across populations (Caraël and Holmes 2001).

To account for these interpopulation differences and similarities, the age- and time dependence of sex-specific incidence ratios can be separated as follows:

$$I(a,t,5)=\Gamma (t-t_0,5)\times H\times J(a,5),$$ (8)

where Γ(t – t₀,5) is the trend in the HIV epidemic as a function of time since the onset of the epidemic (time t₀, hence, Γ(t – t₀,5) = 0 when t ≤ t₀), H is a scale factor of the HIV epidemic in this particular population, and J(a,5) is the sex- and age-specific scaling factor of incidence for women aged a to a + 5 relative to women aged 25 to 29 at time t (thereafter female age-specific relative incidence ratio). Male incidence ratios can be similarly decomposed with the same values of Γ(t − t₀,5) and H, but with different values of J(a,5). To avoid overdetermination, J(25,5) for women must be a given constant value, thereafter equal to 1.

This decomposition of the incidence ratio brings forth three different types of parameters. First, when data on incidence trends over time are unavailable from the population of interest, a population-invariant timing function can be used as a default, Γ(t − t₀,5), which requires only an estimate of t₀. Past experience suggests that from the onset of the epidemic to its peak, the gamma curve is an appealingly simple possibility. Second, no such default values are available from the literature for the sex and age patterns of incidence. A few studies have produced estimates of incidence by age (e.g., Boerma et al. 1999; Kamali et al. 2000; Kengeya-Kayondo et al. 1996; Wawer et al. 1994), but these estimates are derived from a small number of seroconversions. A more robust pattern is estimated next by pooling a large number of observations from different East African populations that are related to age-specific incidence. When specific data are unavailable for the population of interest, using the pattern estimated from these pooled observations appears preferable to “borrowing” the data from a single one of the aforementioned studies. Third, the estimates of t₀ and of H must also be estimated, but here specific estimates are needed for each population.

Turning to perinatal infections, vertical transmission rates have been found to vary across regions (European Collaborative Study 1999; Gibb and Tess 1999; Leroy et al. 2001), which probably reflects differences in birth delivery environments. As for fertility rates, the crossover of age-specific fertility rates for HIV-positive and HIV-negative women (discussed earlier) can be accounted for with the following decomposition:

$$F^1(a,d,t-5,5)=E(a,5)\times F^0(a,t-5,5)\times G(d,5),$$ (9)

where F¹(a,d,t – 5,5) is the period fertility rate of women aged a to a + 5 and HIV-positive for d to d + 5 years; F ⁰(a,t – 5,5) is the fertility rate of the HIV-negative women of the same age, both between time t – 5 and t; G(d,5) is an age-independent, duration-specific fertility impairment coefficient; and E(a,5) is an early-selection fertility coefficient accounting for the sexual activity and related higher fertility of the 15- to 19-year-old HIV positives (equal to 1 except when a is equal to 15, fertility being assumed to be null below age 15). Even if we assume that the effects of HIV infection on fecundability, like its effect on survival, are likely to be similar across populations, the same does not hold for the impact of HIV on fertility rates in that fecundability is only one of the determinants of fertility. The effects on fertility can be expected to be similar only across populations that are comparable with respect to the other determinants of fertility, foremost, marriage and contraception. Likewise, significant differences in the onset patterns of reproductive behavior across populations would likely invalidate the assumption that the selection effect for women under age 20 is similar across these populations.

ML Estimation

From the foregoing review, standard patterns for the J(a,5), V(d,5), E(a,5), and G(d,5) parameters appear plausible for sub-Saharan African populations that are not too heterogeneous with respect to marriage, contraception, and the onset of reproductive behavior. The corresponding values are not directly available in the literature, however. The derivation of these standards builds on the approach developed by Ewbank’s (2002) study of Alzheimer’s disease. Central to this modeling approach is the representation of the dynamics of disease and host populations, which allows the model to predict population-based values reported in the literature, with the predicted values related to the parameters of interest. The most common data, for instance, are the number of HIV-positive and HIV-negative persons in a tested population. Starting with a given set of parameter values, the model predicts these numbers in the population and estimates the likelihood of finding the observed number of HIV-positive persons among those tested. If π(a,5,t) is the proportion of HIV-positive among the age group a to a + 5 at time t, the likelihood of finding P(a,5,t) positives among N(a,5,t) those aged a to a + 5 tested at time t is estimated with a binomial distribution:

$$\left(\begin{array}{c}\hfill P(a,5,t)\hfill \\ \hfill N(a,5,t)\hfill \end{array}\right){\left(\Pi (a,5,t)\right)}^{P(a,5,t)}{(1-\Pi (a,5,t))}^{N(a,5,t)-P(a,5,t)}.$$ (10)

Other usable proportions reported in the literature include HIV-positive babies among all babies tested after birth to HIV-positive mothers, HIV-positive women among pregnant women tested, seroconversion during a follow-up of HIV-negative people, and deaths during a follow-up of HIV-positive people.

The empirical database was constituted through a review of the available data from East Africa. To sustain the assumption of a common “standard,” the geographic scope of the review was limited to countries stretching eastward and southward from Uganda and Kenya to Zimbabwe. Although South Africa, Botswana, and Namibia now exhibit some of the highest prevalence rates in the world, these countries were not included because their levels and age patterns of fertility differ substantially from those of East Africa, suggesting a different onset of reproductive behavior that would lead to a different age pattern of HIV incidence. Also implicit in the derivation of standard patterns is an assumption of relatively stable reproductive behaviors over time, which seems acceptable, to date, for most populations in the region (e.g., Kamali et al. 2000). Rwanda and Mozambique were excluded, however, because periods of war in these two countries do not appear compatible with the foregoing assumption.

The best empirical data are typically provided by relatively small, not necessarily nationally representative, population-based studies. Eleven such populations were identified within the aforementioned geographic restrictions (Table 1), together providing over 46,000 outcomes: HIV-test result, seroconversion, and death. From any initial set of parameter values, all the π(a,5,t) proportions corresponding to these 46,000 outcomes can be estimated; the logarithms of the likelihood from all the different population/age group/quantity can then be added to compute the total log-likelihood corresponding to the initial values. In each of the 11 populations, the vital rates of the HIV-negative individuals and the onset year of the epidemic are estimated from ancillary data (UN 1998, 1999) and treated as fixed. The varying parameters are the J(a,5), V(d,5), E(a,5), and G(d,5) patterns and one specific value of H per population. Their values are modified by iteration to select the set that maximizes the all-population likelihood.

Table 1.

Data Sources for the Maximuim-Likelihood Estimation, by Type and Populatioin of Origin

Data Type	Fort Portal, Uganda	Gulu, Uganda	Masaka, Uganda	Rakai, Uganda	Mara, Tanzania	Mwanza, Tanzania	Bujumbura, Burundi	Mangochi, Malawi	Lusaka, Zambia	Mposhi, Zambia	Mutasa, Zimbabwe
HIV Test Results in a  General-Population  Sample	Killian et al. (1998)	Fabiani et al. (2001)	Nunn et al. (1997)	Wawer et al. (1991); Serwadda et al. (1992)	Shao et al. (1994)	Gross-kurth et al. (1995)	Saidel et al. (1996)		Fylkesnes et al. (1998)	Fylkesnes et al. (1998)	Gregson and Garnett (2000)
HIV Test Results  in an ANC-Patient  Sample	Killian et al. (1998)						Sokal et al. (1993)	Slutsker et al. (1994)
HIV Test Results in  All or a Sample of  Births From HIV-  Positive Mothers			Carpenter et al. (1997)	Gray et al. (1998)					Hira et al. (1989)
HIV Test Results During  a Follow-up of an  HIV-Negative Sample			Kengeya- Kayondo et al. (1996)	Wawer et al. (1994)			Saidel et al. (1996)
Survival During a  Follow-up of HFV-  Positive Individuals			Nunn et al. (1997)	Sewankambo et al. (1994)		Todd et al. (1997)

Tests of significance were conducted to check whether all parameters contributed to improve the model’s fitness. The model failed to be significantly improved by, for instance, the distinction of differential fertility impairment for 10 to 15 years’ duration and for the duration of 15 years and over, and the number of G(d,5) factors was reduced from four to three. The model with four duration-dependent vertical transmission rates, V(d,5), did not significantly outperform a model with a single vertical transmission rate. Although duration-dependence is likely, this effect is difficult to isolate from data reported to date. Finally, too few data from these populations are available to estimate age-specific relative incidence ratios beyond age 60. Ultimately, ML estimation yields one value of the HIV-scale parameter H for each of the eight populations, and one standard value for each of 22 epidemiological parameters, including 17 sex- and age-specific relative incidence ratios, J(a,5), for five-year male and female age groups 15–19 to 55–59. The ratios for the 60- to 64 year olds are assumed to be half the ratios for the 55- to 59 year olds, and no incidence is modeled after age 65. The other five standard values so selected are those of the three duration-specific fertility impairment coefficients, G(d,5); the early-selection fertility co-efficient, E(15,5); and a single vertical transmission rate, V.

RESULTS

ML Estimates

The ML estimation of the 22-parameter values that optimize the fitness of the model are shown in Table 2, with their respective confidence intervals (CI). The ML estimates of the female age-specific relative incidence ratio display the expected single-peak pattern of HIV infection (see Figure 2). The confidence intervals around the estimates of J(a,5) are relatively narrow at young ages but become broader at older ages because fewer people are tested at these ages. The female age-specific relative incidence ratio peaks among the 20- to 24 year olds at the end of the five-year interval during which infection occurs, suggesting that HIV incidence peaks early, around age 20 for women, in these populations. The male age pattern peaks 5 to 10 years later than the female age pattern and does not taper off as quickly as the female pattern. As a result, from age 25 to age 50, male age-specific relative incidence ratios are higher or equal to same-age female ratios, while female ratios are higher at younger ages.³

Table 2.

Initial and Final Sets of Maximum-Likelihood Estimates for 22 Epidemiological Parameters, With 95% Confidence Interval

Parameters	Starting Values	Ending Values	Confidence Interval
Vertical Transmission Rate (%)	38.5	38.5	29.7	47.8
Early-Selection Fertility  Coefficient	1.226	1.672	1.492	1.865
Duration-Specific Fertility  Impairment Coefficients
0–4	0.646	0.848	0.798	0.909
5–9	0.646	0.357	0.276	0.450
10 and above	0.646	0.293	0.078	0.607
Female Age-Specific Relative  Incidence Ratio
15–19	0.393	0.594	0.545	0.650
20–24	0.864	1.325	1.239	1.412
25–29	1.000	1.000	—	—
30–34	0.795	0.752	0.647	0.886
35–39	0.580	0.635	0.482	0.762
40–44	0.365	0.551	0.409	0.795
45–49	0.317	0.356	0.159	0.544
50–54	0.269	0.295	0.095	0.679
55–59	0.134	0.246	0.087	0.627
Male Age-Specific Relative  Incidence Ratio
15–19	0.126	0.059	0.024	0.109
20–24	0.498	0.583	0.483	0.684
25–29	0.914	1.149	0.986	1.285
30–34	1.000	0.963	0.773	1.130
35–39	0.965	0.759	0.573	0.944
40–44	0.929	0.769	0.554	1.007
45–49	0.754	0.622	0.409	0.879
50–54	0.578	0.417	0.120	0.773
55–59	0.289	0.168	0.001	0.445

Notes: Starting values are set by finding the prediction a given parameter affects most and maximizing the likelihood function on the single population that, among the 11 populations, provides most of the data on the corresponding prediction. When a prediction depends on one parameter only and all corresponding data originate from a single population, the initial value does not change in the all-population maximization of the likelihood function.

Figure 2.

HIV-Incidence Ratio Relative to 25- to 29-Year-Old Women, by Sex and Age Group

The vertical transmission rate is estimated from only a small number of observations from these populations. The CI is thus large (29.7% to 47.8%), but the ML estimate (38.5%) is within the 25%–40% range typically reported in African populations (Working Group on Mother-To-Child Transmission 1995). The ML estimates also confirm the higher fertility of HIV-positive females before age 20. Among the 15- the to 19 year olds, the fertility rate of the HIV positives would be 67.2% higher than that of the HIV negatives if HIV infection had no impact on fertility (CI: 49.2% to 86.5%). Because the fertility impairment for females who are infected for fewer than five years is estimated as 15.2% (CI: 9.1% to 20.2%), the overall fertility estimate is 41.8% higher for the 15- to 19-year-old HIV positives than for same-age HIV negatives. Fertility impairment increases significantly 5–9 years after infection (64.3%, CI: 55.0% to 72.4%) and appears to increase further 10 years or more after infection (79.7%, CI: 39.3% to 92.2%), but the difference between the last two parameters is statistically insignificant. The drastic impairment 5 or more years after infection is likely a result of more than the biological impact of infection on fecundability and reflects the increasing morbidity of HIV-positive women and the increasing proportions of widows among them inasmuch as many were infected by their husbands.

Sensitivity Analyses

The confidence intervals reported in Table 2 underestimate the actual uncertainty sur-rounding the ML estimates. The reason is that some parameters of the model are obtained from ancillary data and treated as fixed, that is, estimated without uncertainty, whereas no underlying value can be known exactly. Treating all parameters as unknown and to be determined by ML estimation is an unattractive alternative, however, because some of the information regarding the estimates cannot be entirely incorporated into the empirical database of ML procedure (e.g., the typical J-pattern of age-specific mortality among HIV-negative individuals). To the extent that some estimation power would then be diverted to estimate parameters that are better known that we can specify empirically, this alternative approach would yield unnecessarily large CIs for the parameters of interest.

Assigning values from ancillary data to the parameters for which the relevant information cannot be comprehensively specified and holding them constant in the ML procedure is perhaps most problematic with regard to incidence trends over time. Clearly, these trends are not known exactly in all populations (for an ML approach to estimate these trends, see Salomon and Murray 2001). Although one might want to treat these trends as part of the unknown features of the model, the functional space within which to maximize the likelihood of the curve can hardly be specified.⁴ For the purposes of this population-dynamics model, however, the incidence trends per se are not needed; rather what needs to be estimated is the duration distribution of HIV infection within sex and age groups. The faster the epidemic is growing, the “younger” the duration distribution, and because the impacts of both mortality and fertility increase with the duration of infection, the lesser the mortality and fertility differences between the HIV-negative and HIV-positive populations. Although the exact shape of the incidence trends over time in all the populations considered here may be unknown, what is known is that incidence was growing from the onset of the epidemic to at least the early 1990s, but at a subexponential rate. Up to a few years past the incidence peak, the duration distribution can hence be described as intermediate between the distributions that would be yielded by two extreme cases: constant incidence rates (uniform distribution) and exponentially growing incidence rates.

Table 3 compares the ML estimates obtained when the incidence curve is assumed to follow a time-invariant, a gamma, or an exponential curve (values outside the CIs obtained with the gamma curve are shaded.) As expected, the duration-specific fertility impairment coefficients are strongly dependent on the assumed shape of the incidence curve, whereas the ML estimate of the vertical transmission rate, assumed to be duration independent, is unchanged. Under the assumption of an exponential growth in incidence, the model yields lower estimates for the fertility impairment coefficients, that is, a stronger effect of infection on fertility. Because the exponential curve implies a shorter duration, on average, than does the gamma curve and because fertility impairment increases with duration, the model estimates stronger effects of infection on fertility to match the reduced fertility observed among the HIV-positive population.

Table 3.

Sets of Maximum-Likelihood (ML) Estimates for 22 Epidemiological Parameters, With a Time-Invariant, a Gamma, or an Exponential Incidence Curve

Parameters	Time Invariant	Gamma	Exponential
Vertical Transmission Rate (%)	38.5	38.5	38.5
Early-Selection Fertility  Coefficient	1.431	1.672	1.707
Duration-Specific Fertility  Impairment Coefficients
0–4	1.000	0.848	0.758
5–9	0.478	0.357	0.303
10 and above	0.332	0.293	0.238
Female Age-Specific Relative  Incidence Ratio
15–19	0.789	0.594	0.480
20–24	1.486	1.325	1.114
25–29	1.000	1.000	1.000
30–34	0.744	0.752	0.718
35–39	0.617	0.635	0.534
40–44	0.684	0.551	0.549
45–49	0.272	0.356	0.266
50–54	0.323	0.295	0.375
55–59	0.275	0.246	0.314
Male Age-Specific Relative  Incidence Ratio
15–19	0.075	0.059	0.054
20–24	0.735	0.583	0.499
25–29	1.318	1.149	0.975
30–34	1.077	0.963	0.983
35–39	0.731	0.759	0.682
40–44	0.678	0.769	0.619
45–49	0.733	0.622	0.558
50–54	0.437	0.417	0.468
55–59	0.152	0.168	0.168
Number of Observations	46,387	46,387	46,387
Log-Likelihood	‒587.2	‒566.8	‒675.8
Degrees of Freedom	33	33	33

Note: Figures that are shaded are those outside the confidence interval for the ML estimates when the gamma curve is used. In addition to the 22 parameters shown in the table, the degrees of freedom include 11 parameters for the scale of the epidemic in each of the 11 populations.

Similarly, because point prevalence in the 15–19 age group depends only on incidence in the previous five years, but depends on incidence trends stretching 10 more years backward in the 25–29 age group, the ML estimates of age-specific relative incidence ratios decrease for the youngest age groups when incidence is assumed to grow exponentially. Point prevalence estimates at older ages being composites of past incidence over a longer period, the estimates of the relative incidence ratios become less affected by the assumed shape of the incidence curve with age. Perhaps less intuitive is the increase of the estimated early-selection fertility coefficient with the exponential, rather than gamma, curve. This increase can likely be related to the lower estimates of the relative incidence ratios for the 15- to 19-year-old females, suggesting the later onset of sexual activity, on average, and hence a stronger difference in sexual behavior between HIV-positive and HIV-negative women in that age group. Although the CIs corresponding to the uniform and exponential distribution can be estimated, they are not useful in quantifying the total variance of the model (i.e., including the uncertainty about the exact shape of the incidence curve) because they correspond to two extreme cases that do not actually represent incidence trends in any actual population. Without being more specific, one can simply conclude from these simulations that the CIs reported in Table 2 are too narrow mostly for the fertility coefficients and the relative incidence ratios of the youngest age groups.

Another aspect of the model variance not incorporated into the CIs of Table 2 relates to the assumed homogeneity of the selected populations with respect to the behaviors that affect the model parameters, foremost, sexual behavior. To study the model’s sensitivity to this restriction, the ML estimates derived from the 11 populations selected here were compared with those derived after excluding the data from Zimbabwe (where the prevalence of contraceptive use is higher) and three more urban populations (Bujumbura, Fort Portal, and Lusaka), hence leaving a smaller, presumably more homogeneous, set of 7 populations (full results not shown). The only ML estimates from the reduced set that are not within the confidence interval of the ML estimates from the full set are the relative incidence ratio of the 15- to 19-year-old females (.690 in the smaller sample vs. CI: .545 to .650 in the full sample) and the early-selection fertility coefficient (1.263 in the smaller sample vs. CI: 1.492 to 1.865 in the full sample). (The estimate for 15- to 19-year-old males is also reduced but not significantly so.) The direction of the change suggests that, on average, early sexual behavior would be less common—or prophylactics more commonly used— in Zimbabwe and the three urban centers, and again, the early-selection effect varies in the opposite direction. Differences in the ML estimates derived from the two sets of populations confirm that some population heterogeneity remains in spite of the geographic restriction imposed to select the 11 populations. The size of those differences suggests, however, that this heterogeneity constitutes a relatively small, if unaccounted for, component of the model’s overall variance.

Simulations of Epidemic and Population Dynamics

With the ML estimates from Table 2 taken as default parameter values, model simulations of the interactions of the epidemic and population dynamics require only the standard demographic input of single-state CCMPP and two-point estimates of adult prevalence (or an estimated onset date of the epidemic and a single-point prevalence estimate).⁵ A simulation for a typical East African population (demographic data taken from the East Africa totals in UN 1999) reaching exactly 20% adult seroprevalence 15 years after the onset of the epidemic illustrates the dynamic nature of the relationship between HIV and the host population.⁶

First, the simulation shows the changing age pattern of mortality as AIDS-related deaths account for gradually increasing proportions of all deaths. Although the HIV epidemic clearly reduces life expectancy at birth, the mortality impact remains concentrated in selected age groups. For males (see Figure 3a), age-specific mortality rates begin to increase substantially 10 years into the epidemic, mostly for ages 30 to 60. The changes are even more spectacular for females (see Figure 3b), for 10 or more years into the epidemic, they produce an unusual pattern of mortality between ages 20 and 50. The impact of the epidemic on females is more visible than it is on males because female mortality from other causes is lower than it is for males. First, the incidence of HIV for females peaks at younger ages than it does for males when other-cause mortality is lower; moreover, past this peak, the incidence for females declines more rapidly with age than it does for males. None of the existing model age patterns of mortality can capture the changes illustrated in Figure 3, especially for females. These results are consistent with earlier estimates of changes in mortality during the 1980s derived from national-level data by Timæus (1998).⁷ Timæus reported a two- to threefold increase in adult mortality rates, similar to what can be found by comparing the periods 5–10 years after onset and 15–20 years after onset in Figure 3. The changes in the age patterns and the gender differences that Timæus (1998:S22, figure 2) estimated for Zambia are also qualitatively similar to those reported here.

Figure 3.

Male and Female Age Patterns of Mortality With HIV Diffusion

This simulation also illustrates the epidemic’s impact on fertility because of the reduced fertility of HIV-infected individuals. The ML estimations reported earlier reveal the strong duration-dependence of the fertility impact of infection, suggesting that the population-attributable change (PAC) in fertility should accentuate as the epidemic ages, even with stable prevalence levels. The results of the simulation, shown in Table 4, confirm this expectation. The estimated PAC 20 years after the onset of the epidemic (–0.408) is extremely close to Zaba and Gregson’s (1998) earlier estimate of –0.4 times HIV prevalence among adults, which they derived from data from the early 1990s. The simulation shows, however, that the PAC keeps increasing to –0.459 times prevalence five years later.

Table 4.

HIV Population-Attributable Change in Fertility

Fertility Indicators	Year 10	Year 15	Year 20	Year 25
Total Fertility Rate, HIV Negatives	6.86	6.68	6.21	5.79
Total Fertility Rate, All Women	6.78	6.35	5.60	5.23
Fertility Reduction (%)	1.2	5.0	9.8	9.6
Adult Female Prevalence, 15–50 (%)	12.5	22.6	24.0	21.0
Ratio of Total Fertility Change to Adult  Female Prevalence	0.096	0.220	0.408	0.459

Notes: These values result from a simulation of HIV and population dynamics in which the epidemic is assumed to have started in 1975 (year 0). Average values for East Africa (1) from 1975 to 2000 were selected for all demographic variables. The scale of the epidemic were adjusted so that with the maximum-likelihood values of all parameters shown in Table 2, seroprevalence reached exactly 20% of the adult population (aged 15–50, both sexes) in 1990.

The dynamics of HIV and its host population also have consequences for monitoring prevalence trends in the general population from the most common convenience sample used for this purpose: pregnant women attending antenatal care clinics (ANC). Existing adjustments of ANC-based data rest on static or stable population models (e.g., Nicoll et al. 1998; Zaba et al. 2000), but the results of the simulation illustrate how the bias can be expected to change over time (see Table 5). ANC-based data slightly underestimate the prevalence of HIV in the adult female population during the first 15 years. ANC-based estimates are initially close to the both-sexes adult prevalence, however, because male adult prevalence is lower than female adult prevalence in this simulation. As is shown in Figure 2, male and female age patterns of incidence cross over in the mid-20s, and the all-adult age-sex ratio depends on the exact population dynamics. For the first 25 years of the epidemic, this simulation yields sex ratios that decline to about 1.3 females per male among 15- to 50-year-old HIV positives, values close to the median of those reported in populations across the region (Gregson and Garnett 2000).

Table 5.

Prevalence of HIV Over Time Among Different Groups

Prevalence	Year 10	Year 15	Year 20	Year 25
Adult Male Prevalence, 15–50 (%)	9.8	17.4	17.9	15.3
Adult Female Prevalence, 15–50 (%)	12.5	22.6	24.0	21.0
Sex Ratio Among HIV Positives	0.79	0.77	0.75	0.73
Prevalence Among ANC Patients (%)	12.7	20.3	18.4	14.4
ANC/Adult Female Ratio	1.02	0.90	0.77	0.69

Note: These values are the result of the same simulation of HIV and population dynamics as in Table 3.

Beyond the first 15 years, the prevalence from ANC data becomes seriously biased downward and even lower than the prevalence among adult males. After 25 years, the prevalence among ANC patients is 30% lower than among women aged 15 to 50. The increasing bias over time has less to do with changes in seroprevalence, which remains here at similar levels 15 to 25 years after the onset, than with the increasing average duration of the infected population and the increase in fertility impairment with duration. The simulation demonstrates the dynamic interactions of HIV and its host population, underscoring the need to take into account the timing of the epidemic to estimate demographic or epidemiological measures correctly.

CONCLUSIONS

Taking into account the special needs and data limitations in many of the populations that are the most affected by the HIV epidemic, the model developed here provides a parsimonious representation of HIV and population dynamics that focuses on the sex, age, and HIV-duration variations in survival and fertility. The representation of HIV and population dynamics constitutes a clear improvement over existing models that incorporate the demographic impact of HIV/AIDS by adjusting externally the vital rates required in standard demographic projections. The “internalization” of HIV infection in a demographic model solves a number of extant limitations with external procedures, but also provides tools to make the best use of the data that are becoming available from some nonrepresentative samples, such as ANC patients. This advantage was illustrated here by an ML procedure that fit the model to over 46,000 observations reported from various samples of general populations in East Africa.

One immediate benefit of the ML estimation is to provide default values for all but two of the parameters that this model adds to the input requirements of a standard, single-state CCMPP. In some populations, estimates of the parameter values may be available to replace the ML standards as default values. In any population that is demographically comparable to the populations used in the ML estimation, a preferable approach would be to combine the available data and the ML estimates, using the latter as a prior set in empirical Bayes methods (Stolzenberg and Melles 1989). For instance, if test results were available by age and sex for a random sample of the population, the model could be used to predict the age and sex pattern of prevalence, given the overall prevalence among adults. Although the exact age pattern obtained from that population is subjected to sample variability, empirical Bayes methods with the model prediction as a prior yields improved estimates (greatly reducing standard errors, though at the possible cost of introducing a small bias) under the simple condition of exchangeability (Greenland 2000).

For populations in the region that fall into the least-favorable data situations, full demographic projections by sex, age group, and duration of HIV can be prepared using the ML estimates as the default, the standard demographic inputs of the CCMPP, an estimated onset date of the epidemic, and a later prevalence point estimate (or two point estimates).⁸ This parsimony is clearly achieved by a high model aggregation. Although the model could readily be expanded, the added complexity would provide no benefit as long as the empirical record does not allow for estimation of the additional parameters. One example provided here is that a certain number of parameters (e.g., the duration-specific vertical transmission rate) had to be lumped together for lack of statistical power to distinguish among them from the available data. Another example is the desirability of breaking age, time, and duration intervals into single years, which is not possible at the moment with study results typically reported in five-or, more rarely, three-year intervals.

Even given the limited input demands of the present model of HIV and population dynamics, using this model for demographic forecasting has several difficulties. The first concerns the uncertainty about the temporal trends of the epidemic, G(t,5). Although the gamma curve fits past data reasonably well, given its simple parametric form, much less is known about the future pattern of the epidemic (see UNAIDS 2002, for a more recent approach to forecasting HIV trends). A second uncertainty concerns the future availability to these populations of therapies that would affect other parameters in the mid- to long term, such as the vertical transmission rate, V(d); the impact of infection on fertility, G(d,5); and most important, survival to HIV infection, S¹(a,d,t,5).

Another important uncertainty concerns age- or sex-specific changes in sexual behavior that may, in turn, modify the age-and-sex pattern of incidence and the possible heterogeneity of behavior across populations that may limit the estimates’ relevance to other populations. The assumption of relative stability appears reasonable in respect to the past couple of decades (Kamali et al. 2000), but becomes problematic when it is extended into the future (Fylkesnes et al. 2001). Reports that the epidemic induced faster behavioral changes among the youngest cohorts and delayed the onset of sexual activity would imply, as shown in the Sensitivity Analysis section, that the risk of incidence of those under age 20 may decline relative to the 20- to 24 year olds and that the early-selection effect on fertility may increase over time.

In high-fertility populations, fertility levels constitute the main determinant of future population dynamics, and the main uncertainty here is the independent impact that the epidemic may have on future fertility levels. If fertility levels were unchanged by the HIV epidemic, these populations would have continued to grow even under different mortality and prevalence conditions (Bongaarts 1996). But fertility is clearly affected by the HIV epidemic, given that HIV-positive women have significantly lower fertility rates than do their HIV-negative counterparts. The simulation presented here suggests that 25 years into the epidemic, a 21% adult female prevalence can reduce total fertility by nearly 10% through the reduced fertility of HIV-positive women alone. This seemingly small impact on fertility has been shown to outweigh the mortality impact of the epidemic on future growth (Heuveline 1997). Moreover, the impact of the epidemic on the majority of people of reproductive ages who remain HIV negative is still largely unknown. As yet, there are few data, although there is reason enough to suspect that the strains imposed on the noninfected population in high-prevalence areas (care of sick family members, fostering of orphaned relatives) may depress their own fertility (Ainsworth, Filmer, and Semali 1997; Gregson 1994; Grieser et al. 2001; Heuveline 1997). If this is so, the empirical model provided here confirms that contrary to current official projections that account only for the mortality impact of the epidemic, population decline within a couple of decades is a real possibility.

APPENDIX

If mortality is represented as depending only on exact age, the size of an age group at time t is simply a function of the size and exact age distribution of a younger age group at time t − k (for all ages above age k at time t − k):

$$W(a,k,t)={\int }_a^{a+k}w(x-k,t-k)\times \exp \left(-{\int }_0^k\mu (x+y-k,t+y-k)dy\right)dx,$$ (1a)

where W(a,k,t) is the number of women aged a to a + k at time t, w(x − k,t − k) is the number of women of exact age x − k at time t − k, and μ(x + y – k,t + y – k) is the instantaneous female mortality rate at age x + y – k and time t + y – k.

The single-state formulation of CCMPP simulates survival during a k-year projection interval [t − k,t[ separately for each sex and each k-year age group by applying survival ratios, S(a,t,k), to the number of women aged [a – k,a[ at time t − k:

$$W(a,k,t)=S(a,t,k)\times W(a-k,k,t-k).$$ (2)

Estimating W(a,k,t) as the simple product in Eq. (2), rather than the integral sum of products in (1a), in effect ignores the within-age-group distribution.

In its usual “female-dominant” form, the CCMPP then derives the number of births in each projection interval [t − k,t[ from female period fertility rates specific to each age group [a,a + k[, F(a,t − k,k). The size of the youngest male and female age groups (under age k at time t) is estimated by applying to the number of births since time t − k, a maternal-age- and time-invariant sex ratio at birth s and another survival ratio from birth to time t, S(0,t,k):

$$W(0,k,t)=S(0,t,k)\times \frac{B(t-k,k)}{(1+s)},$$ (2a)

where B(t − k,k) is the number of births between time t − k and time t. Estimating W(0,k,t) as the simple product in Eq. (2a) now ignores the actual distribution of births over time. The size of the age group would again be more accurately described as an integral sum of products because it should depend on the exact birth distribution:

$$W_{0,k,t}={\int }_{t-k}^t\frac{b\left(u\right)}{(1+s)}\times \exp \left(-{\int }_0^{t-u}\mu (y,u+y)dy\right)du,$$ (2b)

where b(u) is the number of births at time u. The number of births B(t − k,k) is generally obtained by adding the number of births produced by each maternal age group in the period. It requires estimating the size of each female age group throughout the period, which can be approximated from the size of the age group at time t − k and at time t (survivors from the k-year-younger age group at time t − k):

$$\begin{array}{cc}\hfill B(a,t-k,k)& =F(a,t-k,k)\times {\int }_0^{k}W(a,k,t+u-k)du\hfill \\ \hfill & =\left(\frac{k\times F(a,t-k,k)}{2}\right)\times [W(a,k,t-k)+(S(a,t,k)\times W(a-k,k,t-k))],\hfill \end{array}$$ (2c)

where F(a,t − k,k) is the fertility rate of women aged a to a + k in the period t − k to t, and B(a,t − k,k) is the number of their births between time t − k and time t. The approximation would be exact only if the size of each age group changed linearly within the time interval and is numerically acceptable in most typical patterns of population change. Migration can readily be added to the closed-population formulation.

To derive the basic equations of the five-state model, it is again useful to start from the continuous representation of HIV incidence as a function of exact age, and mortality and fertility as two functions of exact age and duration since infection. In this representation, the number of HIV-negative women aged a to a + 5 at time t, W ⁰(a,5,t), depends on both survival and HIV incidence:

$$W^0(a,5,t)={\int }_a^{a+5}{w}^0(x-5,t-5)\times \exp \left(-{\int }_0^{5}i(x+y-5,t+y-5)dy\right)\times \exp \left(-{\int }_0^5{\mu }^0(x+y-5,t+y-5)dy\right)dx,$$ (2d)

where w⁰(x – 5,t – 5) is the number of HIV-negative women aged x – 5 at time t – 5, and μ⁰(x + y – 5,t + y – 5) is the mortality rate and i(x + y – 5,t + y – 5) is the incidence rate that these women face at age x + y – 5 and time t + y – 5. Eq. (2d) is similar to Eq. (1a) except that the distribution of women at time t – 5 is now modified by another exponential function. Because the CCMPP assumes that the exact within-age-group distribution is negligible numerically, the survival of each five-year cohort of HIV negatives can still be summarized by a simple survivorship ratio, S ⁰(a,t,5):

$$W^0(a,5,t)=S^0(a,t,5)\times {\int }_a^{a+5}{w}^0(x-5,t-5)\times \exp \left(-{\int }_0^{5}i(x+y-5,t+y-5)dy\right)dx.$$ (2e)

Moreover, if the within-age-group heterogeneity can be assumed to be unimportant with respect to incidence, as well as to mortality, the decline in the cohort size that is due to HIV incidence can be represented by a similar ratio:

$$W^0(a,5,t)=S^0(a,t,5)\times (1-I(a,t,5))\times W^0(a-5,5,t-5),$$ (3)

where I(a,t,5) represents the ratio of women aged a – 5 to a at time t – 5 who would be HIV positive at time t if they were to survive the risk of death between time t – 5 and time t.

The additional mortality rate of HIV negatives is simulated here as a function of exact duration z, but also as a stepwise function of age x (a ::: x < a + 5) at time t, denoted μ¹(a,5,z,t). The number of women aged a to a + 5 and who are infected for d to d + 5 years at time t, W¹(a,d,5,t), thus depends on the number of women who are infected at time t – 5 and on their survival in spite of both risks of mortality:

$$W^1(a,d,5,t)={\int }_a^{a+5}{\int }_d^{d+5}{w}^1(x-5,z-5,t-5)\times \exp \left(-{\int }_0^5{\mu }^0(x+y-5,t+y-5)dy\right)\times \exp \left(-{\int }_0^5{\mu }^1(a,5,z+y,t+y-5)dy\right)dzdx,$$ (3a)

where w¹(x – 5,z – 5,t – 5) is the number of women aged exactly x – 5 and infected for z – 5 years at time t – 5. (In Eqs. (9)–(11), d can take the values 5, 10, and 15 with the convention that when it is equal to 15, the group is open-ended with respect to duration.)

Because μ⁰ does not depend on duration, the impact of mortality unrelated to infection can be isolated and with the CCMPP assumption that the exact within-age-group distribution is negligible numerically, summarized by the same survival ratio as before:

$$\begin{array}{cc}\hfill W^1(a,d,5,t)& ={\int }_a^{a+5}\exp \left(-{\int }_0^5{\mu }^0(x+y-5,t+y-5)dy\right)\times \left[{\int }_d^{d+5}{w}^1(x-5,z-5,t-5)\times \exp \left(-{\int }_0^5{\mu }^1(a,5,z+y,t+y-5)dy\right)dz\right]dx\hfill \\ \hfill & =S^0(a,t,5)\times \left[{\int }_a^{a+5}{\int }_d^{d+5}{w}^1(x-5,z-5,t-5)\times \exp \left(-{\int }_0^5{\mu }^1(a,5,z+y,t+y-5)dy\right)dzdx\right].\hfill \end{array}$$ (3b)

Similarly, because the additional risk does not vary with age within the cohort, its impact can be represented by another multiplier:

$$\begin{array}{cc}\hfill W^1(a,d,5,t)& =S^0(a,t,5)\times {\int }_d^{d+5}\exp \left(-{\int }_0^5{\mu }^1(a,5,z+y,t+y)dy\right)\times \left({\int }_a^{a+5}{w}^1(x-5,z-5,t-5)dx\right)dz\hfill \\ \hfill & =S^0(a,t,5)\times S^1(a,d,t,5)\times W^1(a-5,d-5,5,t-5),\hfill \end{array}$$ (4)

where S¹(a,d,t,5) is now the survivorship ratio corresponding to additional mortality between time t – 5 and t of women aged a to a + 5 and infected for d to d + 5 years (at time t). While the ratio should depend on the actual duration distribution of women aged a – 5 to a at time t – 5, the within-duration-state distribution is again assumed to be numerically unimportant and, therefore, the ratio can be estimated from the age- and duration-specific mortality rates alone.

The size of an age group in the first duration state (infected in the past five years) at time t depends on the number of infections between time t – 5 and time t and on their survival to time t:

$$W^1(a,0,5,t)={\int }_a^{a+5}{\int }_{t-5}^t{w}^1(x+u-t,0,u)\times \exp \left(-{\int }_0^{t-u}{\mu }^0(x+u+y-t,u+y)dy\right)\times \exp \left(-{\int }_0^{t-u}{\mu }^1(a-5,5,y,u+y)dy\right)dudx={\int }_{t-5}^t{\int }_a^{a+5}{w}^0(x-5,t-5)\times i(x+u-t,u)\times \exp \left(-{\int }_0^5{\mu }^0(x+y-5,t+y-5)dy\right)\times \exp \left(-{\int }_0^{t-u}{\mu }^1(a-5,5,y,u+y)\right)dxdu.$$ (4a)

As with Eq. (3b), Eq. (4a) can be simplified because of the stepwise formulation of the age dependence of the additional mortality:

$$W^1(a,0,5,t)={\int }_{t-5}^t\left({\int }_a^{a+5}{w}^{\ast }(x,t-u,t)dx\right)\times \exp \left(-{\int }_0^{t-u}{\mu }^1(a,5,y,u+y)dy\right)du,$$ (4b)

where w^*(x,t – u,t) is the number of women who would be aged x and infected for t – u years at time t had they faced the same mortality as the HIV-negative population. Eq. (4b) is similar to Eq. (2b), which represents the survival of births in the single-state model, and can be simplified by a similar relationship:

$$\begin{array}{cc}\hfill W^{+}(a,0,5,t)& =S^{+}(a,0,t,5)\times {\int }_{t-5}^t\left({\int }_a^{a+5}{w}^{\ast }(x,u,t)dx\right)du\hfill \\ \hfill & =S^{+}(a,0,t,5)\times W^{\ast }(a,0,5,t-5),\hfill \end{array}$$ (4c)

where W^*(a,0,5,t) is the number of women aged a to a + 5 and infected for 0 to 5 years who would be alive at time t had they faced the same mortality rates as HIV-negative women during the past five years. Again, S¹(a,0,5,t) should depend on the exact distribution over time of new infections (adjusted for survival to non-HIV-related mortality), but when those are uniformly distributed over time, it depends only on the duration-specific survival ratios of that age group. W^*(a,0,5,t) is readily obtained by comparing Eqs. (2) and (3):

$$W^{\ast }(a,0,5,t)=S^0(a,t,5)\times I(a,t,5)\times W^0(a-5,5,t-5).$$ (4d)

The size of an age group in the first duration HIV-positive state can thus also be estimated as a simple product of ratios:

$$W^1(a,0,5,t)=S^0(a,t,5)\times S^1(a,0,t,5)\times I(a,t,5)\times W^0(a-5,5,t-5).$$ (5)

The number of births between time t – 5 and t, B⁰(t – 5,5) and B¹(d,t – 5,5) from, respectively, HIV-negative mothers and HIV-positive mothers for d to d + 5 years, are estimated, as in the single-state model, by applying their respective period age-specific fertility rates to the average number of women in a given age group and infection status at the beginning and end of the projection interval. Births from HIV-positive women must be distributed between HIV-negative and HIV-positive births by applying a duration-specific vertical transmission rate, V(d,t – 5,5) to B¹(d,t – 5,5). Finally, the proportion of births surviving to time t is estimated separately for each sex, as in the single-state model, but also for each HIV status at birth. For females, the size of the first age group of HIV negatives is:

$$W^0(0,5,t)=\left(\frac{1}{1+s}\right)\times S^0(0,t,5)\times \left(B^0(t-5,5)+\sum _{d=0,5}(1-V(d,t-5,5))\times B^1(d,t-5,5)\right),$$ (6)

whereas the size of the first age group in the first HIV-duration state is

$$W^1(0,0,5,t)=\left(\frac{1}{1+s}\right)\times S^0(0,t,5)\times S^1(0,0,t,5)\times \sum _{d=0.5}V(d,t-5,5)\times B^1(d,t-5,5).$$ (7)