Significance
The social cost of carbon—the cost to society of an additional ton of CO2 emissions—is a crucial measure of the desirable intensity of climate policy. The models economists use to calculate it, however, are highly sensitive to the choice of discount rate, which measures our concern for the well-being of future generations. Different economists favor different values, and this leads to radically different policy prescriptions. We present a method for combining a diverse set of discount rates into a single “representative” rate and apply it to the analysis of the social cost of carbon performed by the US government. This approach may help resolve ethical conflicts and, hence, lead to consensus policy recommendations.
Abstract
Disagreements about the value of the utility discount rate—the rate at which our concern for the welfare of future people declines with their distance from us in time—are at the heart of the debate about the appropriate intensity of climate policy. Seemingly small differences in the discount rate yield very different policy prescriptions, and no consensus “correct” value has been identified. We argue that the choice of discount rate is an ethical primitive: there are many different legitimate opinions as to its value, and none should receive a privileged place in economic analysis of climate policy. Rather, we advocate a social choice-based approach in which a diverse set of individual discount rates is aggregated into a “representative” rate. We show that performing this aggregation efficiently leads to a time-dependent discount rate that declines monotonically to the lowest rate in the population. We apply this discounting scheme to calculations of the social cost of carbon recently performed by the US government and show that it provides an attractive compromise between competing ethical positions, and thus provides a possible resolution to the ethical impasse in climate change economics.
A central feature of the economic analysis of climate change policy is that it requires us to weigh costs and benefits that are distributed across very long time horizons. Most of the benefits of policies that aim to reduce greenhouse gas emissions will be realized only by future generations, whereas their costs must be borne by us today. Any sensible climate policy thus needs to trade off future benefits against current costs.
Economists who study climate change have a standard tool for aggregating consequences that are distributed across time. They make use of dynamic social welfare functions of the discounted utilitarian type. Let 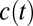 be a measure of the set of goods and services we consume at time t. Then under discounted utilitarianism, a policy that gives rise to a sequence of consumption
be a measure of the set of goods and services we consume at time t. Then under discounted utilitarianism, a policy that gives rise to a sequence of consumption 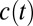 is preferred over a policy that gives rise to the sequence
is preferred over a policy that gives rise to the sequence 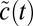 if and only if
if and only if
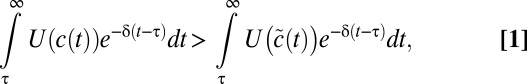 |
where τ is the current time, 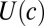 is a utility function assumed to be increasing and concave
is a utility function assumed to be increasing and concave 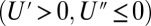 , and
, and 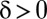 is the utility discount rate, also known as the pure rate of time preference. This approach aggregates future utilities additively, but down-weights welfare consequences that are distant in time by an exponentially declining discount factor
is the utility discount rate, also known as the pure rate of time preference. This approach aggregates future utilities additively, but down-weights welfare consequences that are distant in time by an exponentially declining discount factor 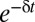 . The larger the discount factor δ, the more this welfare function favors policies that benefit the present rather than the future.
. The larger the discount factor δ, the more this welfare function favors policies that benefit the present rather than the future.
The normative justification for using the exponentially discounted utility model for dynamic welfare analysis was laid out forcefully in the axiomatic work of Koopmans (1). This model respects two attractive properties of dynamic choice (independence and stationarity; see e.g., ref. 2) and gives rise to optimal plans that are time-consistent—the mere passage of time does not cause us to alter the plans we made in the past. It thus has become the standard method for policy choice and evaluation in dynamic contexts, including climate change.
Whose Discount Rate?
Although there is a near-unanimous adherence to the social welfare function defined in Eq. 1 in climate economics, there are substantial and persistent disagreements about the appropriate value of the discount rate δ. These disagreements are encapsulated by a long-standing debate between two of the most well-known proponents of the field—Nicholas Stern and William Nordhaus—who recommend values for δ of 0.1% per year and 1.5% per year, respectively. Although a 1.4% difference in δ may not seem like much, it has an enormous effect on policy recommendations. Stern (3) recommends aggressive mitigation investments, whereas Nordhaus’s analysis (4) argues for a much less intensive climate policy. This is reflected in the fact that the value of the social cost of carbon (SCC; the estimated welfare cost of emitting one additional ton of CO2) obtained by Stern is more than 10 times Nordhaus’s value. The cause of these widely different policy recommendations may be traced largely to the different discount rates the two authors assume in their analysis (4).† Other commentators have argued for their own preferred values of δ, with no convergence to a single unanimously agreed upon value in sight. Given the important effect δ has on policy prescriptions, this disagreement has led to an uncomfortable stalemate in climate change economics, which has led some to question the value of economic models of the issue (5).
Our view is that the choice of δ represents a primitive ethical judgment—it captures how much one cares about the welfare of future generations. As such, it is a parameter that is unique to each person; much like the moral legitimacy of the death penalty or abortion rights, it is the kind of thing reasonable people may reasonably disagree about.‡ Once we adopt this position, it becomes clear that the economist’s role is not to impose his or her own preferences on society, but rather to adopt a welfare framework that aims to represent the distribution of ethical views. There are no objectively “correct” values of δ, only different ethical positions, and each should be given some weight in policy prescriptions. The analysis of climate policy thus becomes an exercise in social choice—we need to aggregate the diverse preferences of individuals into a representative discount rate and use this to evaluate policy options.
Discounting Under Disagreement
Individuals with different discount rates have different preferences regarding the timing of consumption. Those with high discount rates will have stronger preferences for immediate consumption, whereas those with low discount rates will be more willing to defer consumption into the future. Given a set of policy choices (e.g., global mitigation effort and savings rates), the total quantity of global consumption is determined by technological and climatic factors. To assign a value to this consumption path, we need a rule for allocating global consumption between individuals with different discount rates. It is natural to require that such an allocation be efficient. An allocation is efficient if it cannot be altered to make one person better off without making someone else worse off.
Efficient consumption allocations may be determined through the follow procedure. Let global consumption per capita at time t be 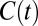 . Suppose a planner allocates consumption
. Suppose a planner allocates consumption 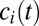 to individual i with discount rate
to individual i with discount rate 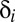 according to
according to
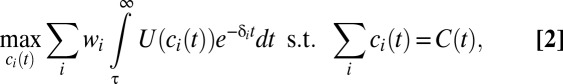 |
where 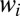 is a set of positive Pareto weights, with
is a set of positive Pareto weights, with 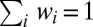 . It is well know that allocations
. It is well know that allocations 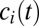 chosen in this manner will be efficient. To ensure equal treatment, we further assume that
chosen in this manner will be efficient. To ensure equal treatment, we further assume that 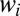 is chosen to coincide with the proportion of individuals in the population with discount rate
is chosen to coincide with the proportion of individuals in the population with discount rate 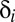 .
.
Given this allocation rule, which discount rate should we use to evaluate global consumption streams 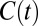 ? To answer this question, we need to find a representative agent whose preferences over global consumption streams will be derived endogenously from the efficient sharing rule defined in Eq. 2. This approach was pioneered by ref. 7 and was generalized by us in ref. 8. Formally, we solve for the efficient allocations
? To answer this question, we need to find a representative agent whose preferences over global consumption streams will be derived endogenously from the efficient sharing rule defined in Eq. 2. This approach was pioneered by ref. 7 and was generalized by us in ref. 8. Formally, we solve for the efficient allocations 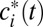 that solve the optimization problem in Eq. 2. These solutions will depend on the global consumption stream
that solve the optimization problem in Eq. 2. These solutions will depend on the global consumption stream 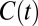 and on time, i.e.,
and on time, i.e., 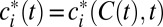 . We then can define the group’s instantaneous welfare from global per capita consumption
. We then can define the group’s instantaneous welfare from global per capita consumption 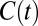 through
through
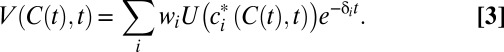 |
This function captures the group’s preferences over global consumption streams 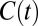 . The utility discount rate of the representative agent is then given by minus the elasticity of marginal welfare with respect to time:
. The utility discount rate of the representative agent is then given by minus the elasticity of marginal welfare with respect to time:
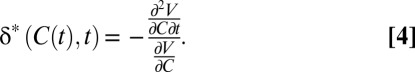 |
To simplify the analysis,§ assume that agents’ utility functions 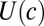 take the widely used isoelastic form
take the widely used isoelastic form
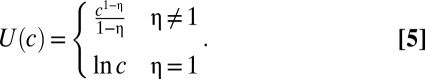 |
Here 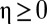 is the elasticity of marginal utility, which measures aversion to consumption inequality. To understand its interpretation, imagine that a rich person with consumption c donates $1 to a contemporaneous poor person who has consumption
is the elasticity of marginal utility, which measures aversion to consumption inequality. To understand its interpretation, imagine that a rich person with consumption c donates $1 to a contemporaneous poor person who has consumption 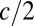 , but that only a fraction x of this transfer arrives in the poor person’s pocket. With utility function 5, this transfer is socially desirable if
, but that only a fraction x of this transfer arrives in the poor person’s pocket. With utility function 5, this transfer is socially desirable if 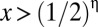 . Thus, for
. Thus, for 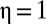 , half of this “leaky” transfer needs to reach the poor person for it to be socially beneficial, but for
, half of this “leaky” transfer needs to reach the poor person for it to be socially beneficial, but for 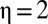 , only a quarter of the transfer needs to arrive. In general, the larger η is, the more averse we are to consumption inequality and the more we are willing to pay to decrease inequality. We will discuss estimated values for η below.
, only a quarter of the transfer needs to arrive. In general, the larger η is, the more averse we are to consumption inequality and the more we are willing to pay to decrease inequality. We will discuss estimated values for η below.
With the isoelastic utility function 5, the group’s discount rate in Eq. 4 reduces to (see derivation in Appendix)
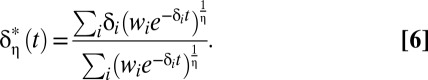 |
For this utility function, the group’s discount rate does not depend on 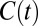 . It is simply a weighted sum of the individuals’ discount rates, with time-dependent weights
. It is simply a weighted sum of the individuals’ discount rates, with time-dependent weights 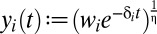 .
.
Defining the expectation operator 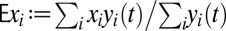 and differentiating Eq. 6 with respect to time, we find
and differentiating Eq. 6 with respect to time, we find
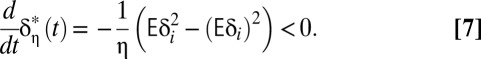 |
Also, letting 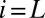 index the agent with the lowest discount rate, we have
index the agent with the lowest discount rate, we have
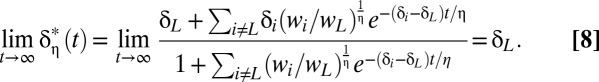 |
Thus, although each member of the group has a constant discount rate 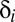 , the efficient discount rate for the group as a whole is time dependent and declines monotonically to the lowest rate in the population.
, the efficient discount rate for the group as a whole is time dependent and declines monotonically to the lowest rate in the population.
Disagreement and the Social Cost of Carbon
In this section, we demonstrate how the theory of discounting under disagreement may be applied to the analysis of climate policy. We focus on the effects of discounting on estimates of the SCC, perhaps the most important summary statistic in climate change economics. As mentioned above, the SCC measures the welfare cost of an additional unit of CO2 emissions to current and future generations. In a “first-best” world, it coincides with the optimal tax rate on CO2 emissions. The SCC has been the subject of several studies commissioned by national governments, including a recent one by an Interagency Working Group (IWG) in the United States (9, 10), which we will use as a point of comparison in our analysis.
To estimate the SCC, we need an integrated model of the climate–economy system that captures how the trajectory of future global temperatures change in response to an additional unit of CO2 emissions, how these climatic changes affect the global economy over time, and finally, how these impacts alter global consumption and welfare. We will make use of a version of the well-known Dynamic Integrated Climate Economy (DICE) model (4). To make our analysis directly comparable with the IWG's, our version of DICE makes use of the same socioeconomic scenarios and model parameterization as their study,¶ with one important difference. The IWG used constant values of the consumption discount rate in its analysis. For deterministic consumption streams and isoelastic utility, the consumption discount rate 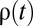 is related to the utility discount rate δ through
is related to the utility discount rate δ through
where 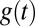 is the mean consumption growth rate up to time t (see e.g., ref. 2). This is the rate used to discount changes in consumption
is the mean consumption growth rate up to time t (see e.g., ref. 2). This is the rate used to discount changes in consumption 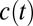 rather than changes in utility
rather than changes in utility 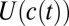 , which are discounted at the rate δ. Because
, which are discounted at the rate δ. Because 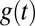 is generally nonconstant in the DICE model, even if δ is a constant, as is conventionally assumed, the consumption discount rate cannot be constant. Our analysis thus will make use of formula 9, in which the consumption discount rate is derived from explicit welfare assumptions and the rate of consumption growth that emerges endogenously from the DICE model, rather than assuming an ad hoc constant rate.
is generally nonconstant in the DICE model, even if δ is a constant, as is conventionally assumed, the consumption discount rate cannot be constant. Our analysis thus will make use of formula 9, in which the consumption discount rate is derived from explicit welfare assumptions and the rate of consumption growth that emerges endogenously from the DICE model, rather than assuming an ad hoc constant rate.
To operationalize discounting formula 9, we need to specify values for δ and η. We consider three different schemes for δ: First, we use Stern’s value of 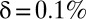 , then Nordhaus’s value of
, then Nordhaus’s value of 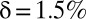 ; finally, we consider the efficient discount rate under disagreement
; finally, we consider the efficient discount rate under disagreement 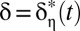 from Eq. 6, where we assume equal weights on the Stern and Nordhaus values of δ. The value of η can be estimated from a variety of empirical sources, including income tax schedules (12), asset markets (13), and behavioral surveys (14). Although the empirical literature is not without its problems,
from Eq. 6, where we assume equal weights on the Stern and Nordhaus values of δ. The value of η can be estimated from a variety of empirical sources, including income tax schedules (12), asset markets (13), and behavioral surveys (14). Although the empirical literature is not without its problems, 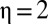 is often taken as a reasonable starting point (15), with values between 1 and 3 recommended for sensitivity analysis (16). We adopt this approach and compute the SCC for
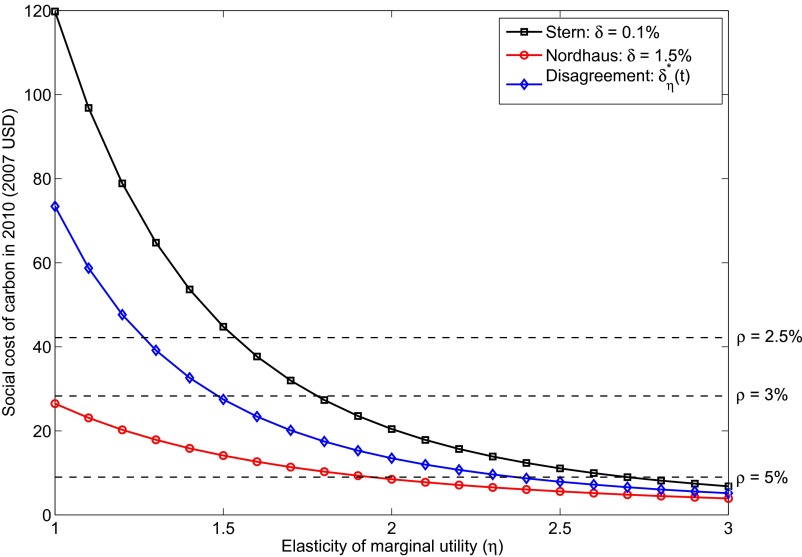
is often taken as a reasonable starting point (15), with values between 1 and 3 recommended for sensitivity analysis (16). We adopt this approach and compute the SCC for 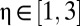 for each of our three choices for δ using the IWG's version of the DICE model. Our results are displayed in Fig. 1. For reference, we also plot the value of the SCC for the three constant consumption discount rate scenarios used by the IWG:
for each of our three choices for δ using the IWG's version of the DICE model. Our results are displayed in Fig. 1. For reference, we also plot the value of the SCC for the three constant consumption discount rate scenarios used by the IWG: 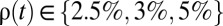 .
.
Fig. 1.
The SCC as a function of η for two constant utility discount rates [Stern (black), 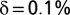 ; Nordhaus (red),
; Nordhaus (red), 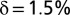 ] and for the efficient discount rate under disagreement (blue) given by
] and for the efficient discount rate under disagreement (blue) given by 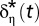 in Eq. 6. The values of the SCC under the three constant consumption discount rate scenarios used by the IWG are indicated by the dashed lines.
in Eq. 6. The values of the SCC under the three constant consumption discount rate scenarios used by the IWG are indicated by the dashed lines.
As the figure makes clear, the values of the SCC computed with the efficient discount rate 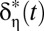 lie between those computed with the Stern and Nordhaus values of δ for each value of η. The SCC values under disagreement are derived from a procedure that is both equitable and efficient; thus, they achieve a successful compromise between opposing viewpoints.
lie between those computed with the Stern and Nordhaus values of δ for each value of η. The SCC values under disagreement are derived from a procedure that is both equitable and efficient; thus, they achieve a successful compromise between opposing viewpoints.
The SCC is a declining function of η in our simulations, with differences in the value of δ having a large effect for small values of η, and a smaller effect for larger values of η. This can be understood by examining the formula for the consumption discount rate in Eq. 9.‖ Because 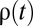 is increasing in η, climate damages that are distant in time are discounted heavily for large values of η. This gives rise to low values of the SCC. For large enough η, the weight placed on future climate damages is already small for
is increasing in η, climate damages that are distant in time are discounted heavily for large values of η. This gives rise to low values of the SCC. For large enough η, the weight placed on future climate damages is already small for 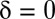 , so changing the value of δ has a comparatively small absolute effect on the SCC, as this modifies an already small quantity. The relative effect of a change in δ on the SCC, however, is still significant for large η, with the Stern value 74% larger than the Nordhaus value, even for
, so changing the value of δ has a comparatively small absolute effect on the SCC, as this modifies an already small quantity. The relative effect of a change in δ on the SCC, however, is still significant for large η, with the Stern value 74% larger than the Nordhaus value, even for 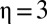 . Regardless of the exact value of η, the efficient discount rate under disagreement thus may be used to resolve empirically meaningful disputes about the value of δ.
. Regardless of the exact value of η, the efficient discount rate under disagreement thus may be used to resolve empirically meaningful disputes about the value of δ.
Conclusions
As many economists have emphasized (e.g., refs. 16, 19), ethical judgments are intrinsic to climate change policy, and nowhere do they play a greater role than in the question of how to discount the far future. As with all ethical judgments, there is a plurality of legitimate viewpoints about the appropriate value for the utility discount rate. Although public reasoning and debate may help us refine our positions, the outcome of this process is unlikely to result in a unique consensus. As Amartya Sen (20) noted, “Even the most vigorous critical examination can still leave conflicting arguments that are not eliminated by impartial scrutiny.” How can rational policy recommendations be made in an environment characterized by such persistent and quantitatively important disagreements?
We have argued for a social choice-based approach to climate policy that reflects the diversity of opinion on ethical matters. This has both pragmatic and philosophical advantages. Pragmatically, our approach provides a formal mechanism for avoiding impasses caused by ethical disagreements. Everyone’s opinion counts, and no one can claim that policy recommendations are derived from morally high-handed modeling assumptions. Philosophically, our method draws on a long democratic tradition in social choice theory that assigns each preference an equal weight in public decision making to arrive at a consensus acceptable to all.
We hope the techniques we have identified will help resolve debates about “the” appropriate value of the discount rate and allow research attention to focus instead on empirical questions such as the specification of the damage function in integrated assessment models, as well as comprehensive quantifications of the uncertainty in the technological and climatic components of these models (21). Although ethical assumptions are important drivers of the policy recommendations from integrated assessment models, this should not be seen as a strike against them. Ethical positions will always be irreducibly diverse, but we may nevertheless respectfully agree to disagree.
Appendix
We can solve the maximization problem in Eq. 2 by the method of Lagrange multipliers. The Lagrangian is
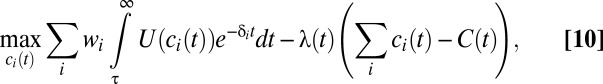 |
where 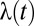 is a sequence of Lagrange multipliers. The first-order conditions for the efficient allocations
is a sequence of Lagrange multipliers. The first-order conditions for the efficient allocations 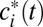 yield
yield
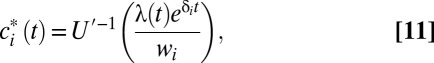 |
and the constraint 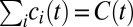 implies that
implies that
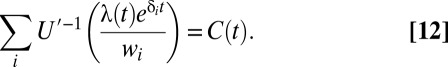 |
Now assume that 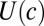 is an isoelastic utility function, as in Eq. 5. Then,
is an isoelastic utility function, as in Eq. 5. Then, 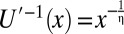 . Substituting this relationship into Eq. 12 allows us to solve for
. Substituting this relationship into Eq. 12 allows us to solve for 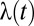 in terms of
in terms of 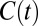 . This expression for
. This expression for 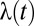 in turn may be substituted into Eq. 11 to find
in turn may be substituted into Eq. 11 to find
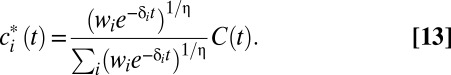 |
Substituting this expression into Eq. 3, we find that the group’s instantaneous welfare at the optimal allocation may be written as
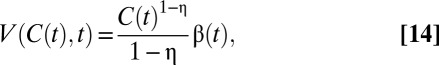 |
where the group’s effective discount factor 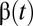 is given by
is given by
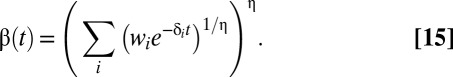 |
The group’s discount rate 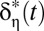 then is determined by Eq. 4, which reduces to
then is determined by Eq. 4, which reduces to
 |
Straightforward algebra then yields the expression for 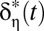 in Eq. 6.
in Eq. 6.
Acknowledgments
A.M. acknowledges support from the Economic and Social Research Council and the Grantham Research Institute on Climate Change and the Environment.
Footnotes
The authors declare no conflict of interest.
*This Direct Submission article had a prearranged editor.
†The Stern review also initially chose a low value of the elasticity of marginal utility (i.e., η = 1, where η is defined in Eq. 5 below), thus compounding the differences between its analysis and that of Nordhaus (who uses 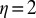 ). The postscript to the review, however, contains a sensitivity analysis over η. Arguably, η has more of a positive flavor than δ, as it measures aversion to inequality, including contemporaneous inequality, and thus may be estimated empirically, as we discuss below. There is no conceptual difficulty in accounting for heterogeneous utility functions too (see e.g., refs. 7, 8), but analytic solutions for the representative discount rate are not possible in this case. We keep to the case of common utility functions to simplify the exposition.
). The postscript to the review, however, contains a sensitivity analysis over η. Arguably, η has more of a positive flavor than δ, as it measures aversion to inequality, including contemporaneous inequality, and thus may be estimated empirically, as we discuss below. There is no conceptual difficulty in accounting for heterogeneous utility functions too (see e.g., refs. 7, 8), but analytic solutions for the representative discount rate are not possible in this case. We keep to the case of common utility functions to simplify the exposition.
‡Remarkably, both Stern and Nordhaus enunciate this position in their writings. Stern (6): “Value judgements are, of course, precisely that and there will be many different positions.” Nordhaus (4): “It should be clear that alternative ethical perspectives are possible…[and] provide vastly different prescriptions about desirable climate change policies.” Both authors nevertheless perform their analysis with a single preferred value of δ.
§See refs. 7 and 8 for a general analysis with arbitrary, possibly heterogeneous, utility functions.
¶The version of DICE used by the IWG makes use of five socioeconomic scenarios and a large Monte Carlo sample from the probability distribution for the climate sensitivity parameter derived in ref. 11. The final SCC values reported are averages over all scenarios and Monte Carlo samples for a given value of the consumption discount rate. Our analysis uses an identical methodology. Note, however, that the final summary values of the SCC adopted by the IWG average estimates from DICE and two other integrated assessment models. We use just the DICE model, as it is freely available and easy to implement. SCC estimates from the DICE model fall between those from the other two models.
‖Technically, because our computation of the SCC averages over many scenarios for global consumption, we should examine the certainty equivalent consumption discount rate 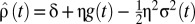 , where
, where 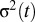 is the variance in consumption growth at time t (see e.g., ref. 15). In practice, the variance term is much smaller than the other two terms in the standard parameterization of the DICE model, and can be neglected for qualitative purposes. This, however, is not a generic result, and it relies largely on the assumed functional form for the DICE damage function at large temperatures. See ref. 17 for a discussion of the effect of the choice of damage function on the variance term in the discounting formula. The literature contains an extensive analysis of how uncertainty in the consumption growth rate also may give rise to a consumption discount rate
is the variance in consumption growth at time t (see e.g., ref. 15). In practice, the variance term is much smaller than the other two terms in the standard parameterization of the DICE model, and can be neglected for qualitative purposes. This, however, is not a generic result, and it relies largely on the assumed functional form for the DICE damage function at large temperatures. See ref. 17 for a discussion of the effect of the choice of damage function on the variance term in the discounting formula. The literature contains an extensive analysis of how uncertainty in the consumption growth rate also may give rise to a consumption discount rate 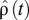 that declines with time (15, 18).
that declines with time (15, 18).
References
- 1.Koopmans TC. Stationary ordinal utility and impatience. Econometrica. 1960;28(2):287–309. [Google Scholar]
- 2.Heal G. Intertemporal welfare economics and the environment. In: Mäler K-G, Vincent JR, editors. Handbook of Environmental Economics. Vol 3. Amsterdam: Elsevier; 2005. pp. 1105–1145. [Google Scholar]
- 3.Stern N. The Economics of Climate Change: The Stern Review. Cambridge, UK: Cambridge Univ Press; 2007. [Google Scholar]
- 4.Nordhaus WD. A Question of Balance. New Haven, CT: Yale Univ Press; 2008. [Google Scholar]
- 5.Pindyck RS. Climate change policy: What do the models tell us? J Econ Lit. 2013;51(3):860–872. [Google Scholar]
- 6.Stern N. The economics of climate change. Am Econ Rev. 2008;98(2):1–37. [Google Scholar]
- 7.Gollier C, Zeckhauser R. Aggregation of heterogeneous time preferences. J Polit Econ. 2005;113(4):878–896. [Google Scholar]
- 8.Heal G, Millner A. 2013. Discounting Under Disagreement. (Natl Bureau Economic Res, Cambridge, MA), NBER Working Paper No 18999.
- 9.Interagency Working Group on the Social Cost of Carbon . Technical Support Document: Social Cost of Carbon for Regulatory Impact Analysis—Under Executive Order 12866. Washington, DC: US Government; 2010. [Google Scholar]
- 10.Greenstone M, Kopits E, Wolverton A. Developing a social cost of carbon for US regulatory analysis: A methodology and interpretation. Rev Environ Econ Policy. 2013;7(1):23–46. [Google Scholar]
- 11.Roe GH, Baker MB. Why is climate sensitivity so unpredictable? Science. 2007;318(5850):629–632. doi: 10.1126/science.1144735. [DOI] [PubMed] [Google Scholar]
- 12.Stern N. The marginal valuation of income. In: Artis M, Nobay A, editors. Studies in Modern Economic Analysis. Oxford: Blackwell; 1977. [Google Scholar]
- 13.Epstein LG, Zin SE. Substitution, risk aversion, and the temporal behavior of consumption and asset returns: An empirical analysis. J Polit Econ. 1991;99(2):263–286. [Google Scholar]
- 14.Barsky RB, Juster FT, Kimball MS, Shapiro MD. Preference parameters and behavioral heterogeneity: An experimental approach in the health and retirement study. Q J Econ. 1997;112(2):537–579. [Google Scholar]
- 15.Gollier C. Pricing the Planet’s Future: The Economics of Discounting in an Uncertain World. Princeton: Princeton Univ Press; 2012. [Google Scholar]
- 16.Dasgupta P. Time and the generations. In: Hahn RW, Ulph A, editors. Climate Change and Common Sense: Essays in Honour of Tom Schelling. New York: Oxford Univ Press; 2012. [Google Scholar]
- 17.Millner A, Dietz S, Heal G. Scientific ambiguity and climate policy. Environ Resour Econ. 2013;55(1):21–46. [Google Scholar]
- 18.Arrow K, et al. Environmental economics. Determining benefits and costs for future generations. Science. 2013;341(6144):349–350. doi: 10.1126/science.1235665. [DOI] [PubMed] [Google Scholar]
- 19.Arrow KJ. Discounting, morality, and gaming. In: Portney PR, Weyant JP, editors. Discounting and Intergenerational Equity. Washington, DC: Resources for the Future; 1999. [Google Scholar]
- 20.Sen A. The Idea of Justice. London: Penguin; 2010. [Google Scholar]
- 21.Heal G, Millner A. Uncertainty and decision making in climate change economics. Rev Environ Econ Policy. 2014;8(1):120–137. [Google Scholar]