The ecology in the hematopoietic stem cell niche determines the clinical outcome in chronic myeloid leukemia

Significance

Three contrasting models of the ecological interactions in the hematopoietic stem cell niche explain clinical progression of chronic myeloid leukemia equally well, but do so in different ways. We identify key differences between models and find that we can conclusively rule out those that fail to take competition between healthy and leukemic lineages explicitly into account. Detailed analysis of population dynamics within the bone marrow niche allows us to ascribe mechanisms to distinct disease outcomes and suggests experiments to distinguish between these mechanisms.

Abstract

Chronic myeloid leukemia (CML) is a blood disease that disrupts normal function of the hematopoietic system. Despite the great progress made in terms of molecular therapies for CML, there remain large gaps in our understanding. By comparing mathematical models that describe CML progression and etiology we sought to identify those models that provide the best description of disease dynamics and their underlying mechanisms. Data for two clinical outcomes—disease remission or relapse—are considered, and we investigate these using Bayesian inference techniques throughout. We find that it is not possible to choose between the models based on fits to the data alone; however, by studying model predictions we can discard models that fail to take niche effects into account. More detailed analysis of the remaining models reveals mechanistic differences: for one model, leukemia stem cell dynamics determine the disease outcome; and for the other model disease progression is determined at the stage of progenitor cells, in particular by differences in progenitor death rates. This analysis also reveals distinct transient dynamics that will be experimentally accessible, but are currently at the limits of what is possible to measure. To resolve these differences we need to be able to probe the hematopoietic stem cell niche directly. Our analysis highlights the importance of further mapping of the bone marrow hematopoietic niche microenvironment as the “ecological” interactions between cells in this niche appear to be intricately linked to disease outcome.

Hematopoiesis is the intricate process that provides the vast diversity of cells found in the blood and immune system of vertebrate organisms. To generate great numbers of very different cells—ranging from erythrocytes to highly specialized lymphocytes—a delicate balance of activity of transcriptional programs and hematopoietic growth factors is required (1). Within this system, hematopoietic stem cells (HSCs) give rise to (lymphoid and myeloid) progenitors, which in turn through further differentiation steps yield the panoply of cells found in the blood (2). Given the complexity of the hematopoietic system it is remarkable how robustly this process works in general.

The cellular and molecular processes involved in healthy hematopoiesis must be disrupted in disease (3). There is however solid evidence that disease processes operate in parallel to the normal hematopoietic system. Thus, a branch of the hematopoietic system will propagate deficient cells and generate the ensuing pathology, but other cells of the system will continue to operate alongside (4–7). This is, of course, akin to problems encountered in ecology. Based on this analogy we here attempt to understand the interplay between the healthy and chronic myeloid leukemia (CML) systems. This is a particularly helpful perspective if interactions between healthy and diseased cell types can affect the disease progression, as is now widely believed.

Interactions will include shared reliance on nutrients, cofactors, and physiological conditions required to maintain stem cell properties. These factors can be subsumed under the umbrella of the stem cell niche, first introduced in ref. 8. In adult mammals the bone marrow is the site of hematopoiesis and contains the HSC niche. Although much has been learnt about the HSC niche in the last decade, which particular elements constitute the niche continues to be debated (9–14). The dynamics in the niche impact the abundance and maintenance of stem cells, so in the case of cancer arising in the niche, stem cell dynamics will certainly be affected. The ensuing interactions between healthy and cancer stem cells can be considered as competitive interactions, given that they must share the influence of niche constituents (15).

Here we investigate models of hematopoiesis that describe both healthy and leukemic-related hematopoietic systems derived from leukemia stem cells (LSCs) in light of data for the changing levels of leukemia in patients over time. These models differ quite profoundly in the manner in which they consider interactions (or competition) between different cell types.

The level of leukemia in patients is quantified by measuring the proportion of differentiated leukemic cells in blood. The patients are receiving tyrosine kinase inhibitor (TKI) therapy (16), and our data fall into two different categories: data for patients that go into remission, and data for patients exhibiting relapse. We consider these cases separately to identify possible functional differences that give rise to—or at least are correlated with—the different clinical outcomes. We use a Bayesian computation framework throughout to calibrate models against data and compare the performance of the different models.

We will show that detailed analysis of the models allows us to reject those models that fail to account for niche dynamics explicitly and from the outset. Furthermore we can show that the available data suggest strongly an important role of the HSC niche dynamics for CML disease progression and outcome. We find evidence for the niche effects extending beyond the HSC/LSC level and also affecting the dynamics of progenitor and quite possible other cell types in the hematopoietic hierarchy.

Models for CML Dynamics

Three models for CML progression are studied. Each describes the dynamics of healthy and leukemic stem cell lineages and accounts for the impact of the niche in different ways.

Model M1—Niche Competition.

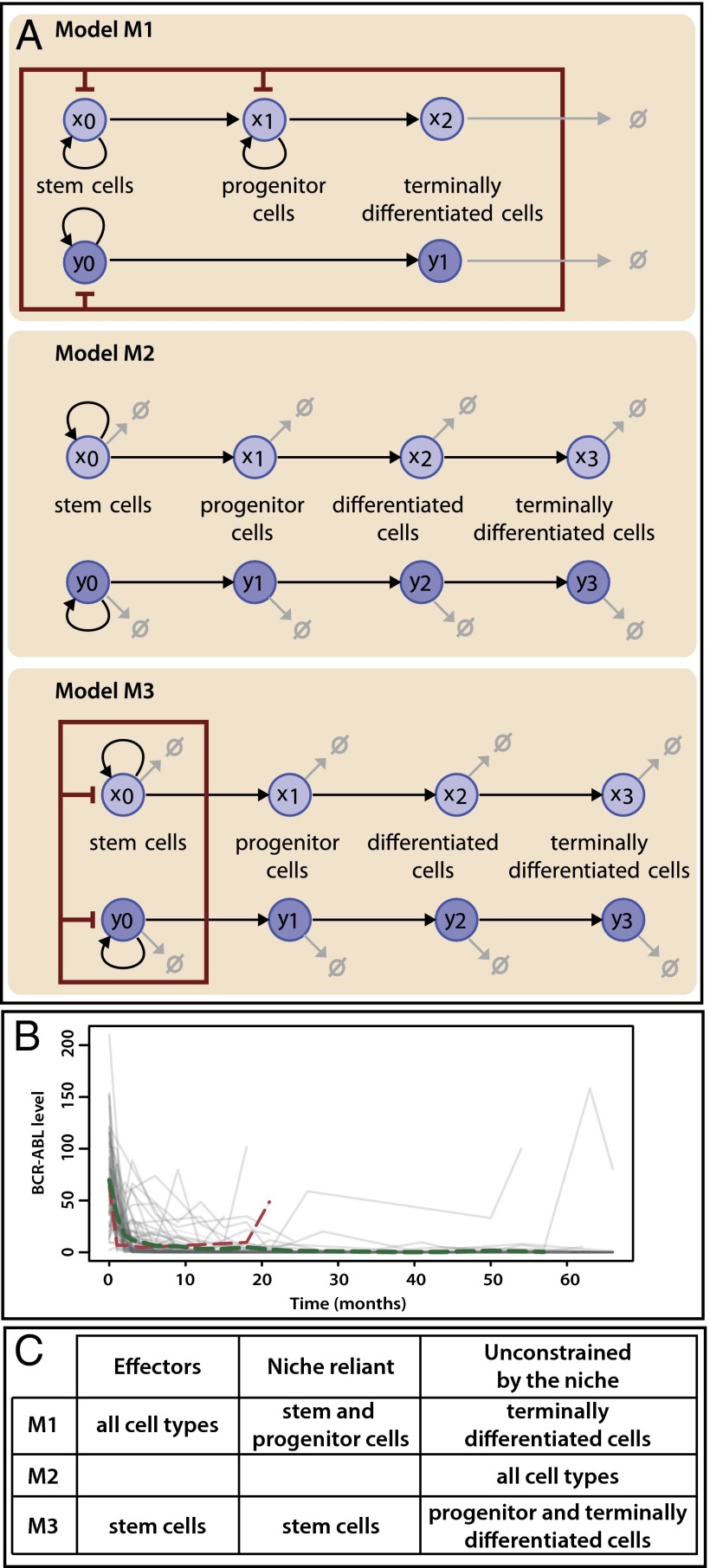
The first model describes the dynamics of five species of interacting cell populations (17): HSCs 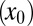, healthy progenitor 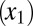and differentiated cells 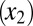, LSCs 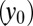, and differentiated leukemia cells 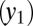(Fig. 1A). The dynamics are given by:

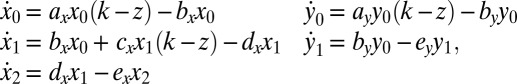where the parameters 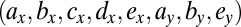that characterize the phenotypes of the cells are described in Table 1. Here, k represents the so-called carrying capacity, i.e., the total number of cells that can exist within the bone marrow; in this analysis we use 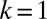so population sizes are given as concentrations. Here z represents the total size of the niche, i.e., 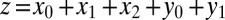, thus occupation of the niche is not limited to the stem cell species, but extends to progenitor and differentiated cells.

Fig. 1.

Mechanistic models for hematopoiesis in CML and experimental measurements of leukemia progression in patients. (A) Graphical description of models M1, M2, and M3. The hematopoietic niche is represented by a red rectangle: every species inside the rectangle influences the niche, whereas only species marked by red inhibitory arrows are affected by it. Cell death is illustrated by light gray arrows. (B) The change in the BCR-ABL level over time (in months) is represented by gray lines for each of the 69 patients under CML treatment. The average change over all patients is illustrated by a dashed green line; the change in the BCR-ABL level for a patient who exhibits disease relapse is illustrated by a dashed red line. Our model comparison analysis is based on these two trajectories. (C) Description of how niche competition is treated by each model. Each species can impact the niche (effector), be affected by the niche (niche reliant), and/or be fully unconstrained by the niche.

Table 1.

Model parameters

Model	Symbol	Definition
M1	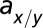*	Self-renewal rate of stem cells
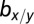		Production rate of progenitor cells
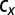		Self-renewal rate of healthy progenitor cells
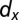		Production rate of healthy differentiated cells
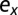		Death rate of healthy differentiated cells
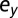		Death rate of leukemic differentiated cells
M3	κ	Carrying capacity of the niche
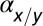	*	Production rate of progenitor cells
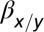	*	Production rate of differentiated cells
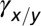	*	Production rate of fully differentiated cells
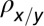	*	Growth rate of HSCs/LSCs (rescaled)
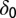		Death rate of stem cells†
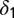		Death rate of progenitor cells†
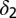		Death rate of differentiated cells†
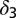		Death rate of fully differentiated cells†

^*x denotes healthy lineage; y denotes leukemic lineage.

^†Death rates for model M3 are shared between healthy and leukemic lineages.

Model M2—Niche Independence.

This model was developed to describe the dynamics of HSCs and LSCs and their temporal evolution under TKI therapy and contains eight species: HSCs with three progenitor populations, and LSCs and their corresponding three leukemic progenitor populations (18). The model is depicted in Fig. 1A and the equations that specify it are:

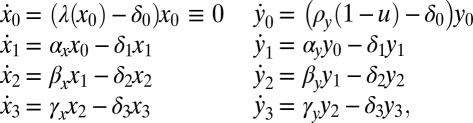where 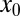are HSCs, 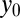are LSCs, and the 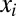, 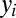for 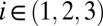are progeny of the two stem cell populations, respectively. Also, 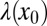describes a homeostatic function defined such that 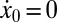; the HSC population in this case is constant over time. Here, u is the number of resistance mutations, which is assumed to be 0 (a version of the model that did include resistance mutations was briefly considered, but mechanistically it offers no more than the form presented here, because there are no additional interactions between species). Note that the 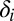, which are referred to as death rates in the succeeding analysis, subsume the processes of differentiation and migration out of the niche; these are shared between healthy and leukemic lineages. The parameters that are shared by model M3 are described in Table 1.

Model M3—Partial Niche Dependence.

Model M2 does not allow for competition between HSCs and LSCs, and in ref. 19 a model is introduced that describes the dynamics of the same eight species as in M2, but where the growth of stem cells is affected by the population size of HSCs and LSCs. We have rescaled model M3 compared with ref. 19 to allow for comparison of the three models considered here:

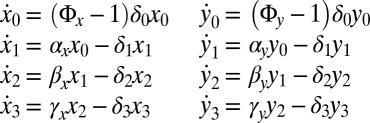and

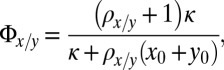where the species 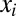, , 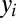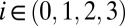are the same as for M2. The parameters that specify this model are described in Table 1. We have also considered reduced forms of model M3—containing two or three species per lineage instead of four—to investigate the properties of the model’s intermediate species. We perform a similar analysis on these reduced models as the analysis of M3 (Supporting Information).

In summary, these three models can be split according to whether they assume complete independence between lineages (M2) or assume that the evolution of one lineage has an impact on the evolution of the other (M1 and M3). In model M1, all species (z) have an influence on the dynamics of healthy and leukemic stem and progenitor cells, thus all species are effectors of the niche, and stem and progenitor cells are affected by the niche (Fig. 1C). In model M3, the niche is only composed of stem cells; explicit interactions occur only between these two species. All others (progenitor and differentiated and terminally differentiated cells) are not directly constrained by the niche although their evolution does have niche dependence through the stem cell species that produced them.

In addition to these three models, we have studied one further established model that describes interactions between HSCs and LSCs, including competition, presented in ref. 20. Here similar cellular processes are modeled but using an agent-based modeling approach. The large computational cost of simulating this model, however, precludes the Bayesian analysis attempted here.

Results and Discussion

We study how well each model can explain the CML outcomes of disease remission or disease relapse (Fig. 1B). Behavior is classified as remission when the level of CML in the blood is decreasing over time. This is the case for the majority of patient trajectories, therefore we used the mean over 69 patients (averaged at each time point where there were at least 20 measurements taken) to represent remission behavior. Behavior is classified as relapse if an initial decrease in CML is followed by a pronounced and continuing increase in CML levels. Due to variability among patients in the time at which relapse occurs, each relapse patient should be considered independently. We base the subsequent analysis on a single relapse patient trajectory. We performed similar analyses on other relapse patients and found qualitatively similar behavior. We compare how each model explains the data, and from this we are able to draw conclusions about mechanisms of the dynamics of the disease.

Models Cannot be Distinguished Based on Fit to the Data Alone.

We use Bayesian parameter inference and model selection algorithms to determine which of the three models best captures the two observed clinical progressions, remission and relapse, as measured by the levels of the BCR-ABL tyrosine kinase—the product of the BCR-ABL gene fusion that is a hallmark of CML—in CML patients being treated with TKIs.

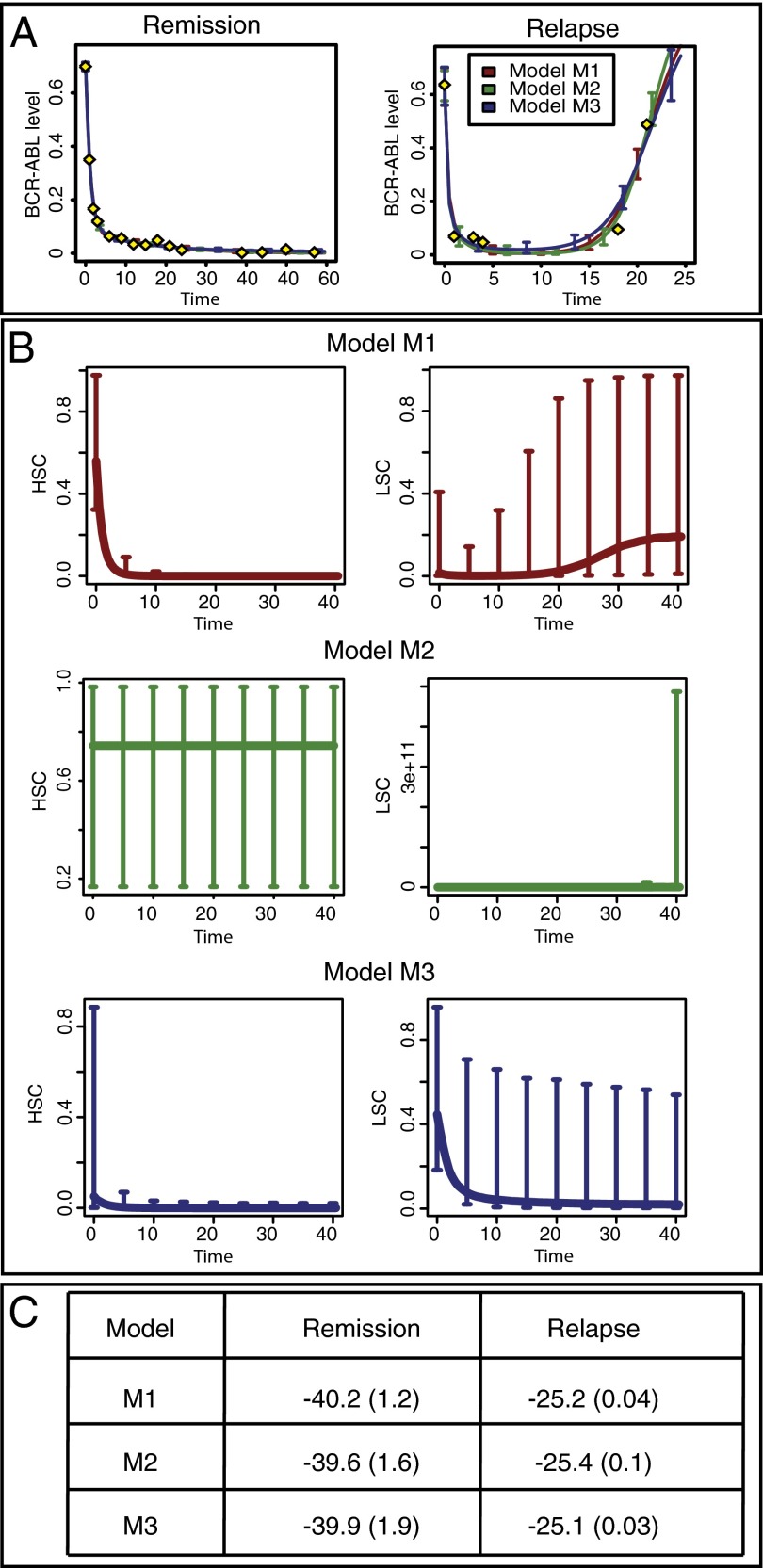
We first use likelihood-free sequential Monte Carlo (SMC) Bayesian inference (21) to perform parameter inference independently for the three models. As shown in Fig. 2A, the simulated behaviors obtained for each of the three models and two outcomes are very similar to the observed behaviors. The acceptance threshold between simulated and observed data was chosen so that the final Euclidian distance between the two was lower than 4.0 in the case of remission and 15.0 for relapse. From the similarity of the fits, we conclude that all three models are able to explain these outcomes, over some range of parameters.

Fig. 2.

Model comparison based on the fit to the data and the importance of niche competition. (A) Fits to the data (yellow diamonds) for the three models and the two outcomes. All three models are able to explain the observed disease progression for both outcomes. (B) Predicted trajectories for stem cell species for each model. The lines represent the median of the evolution and the error bars designate the 5% and 95% percentiles for a set of 1,000 parameters sampled from the posterior distribution. For model M2, LSCs exhibit unbounded exponential growth for all sampled parameter values. (C) Models are ranked by the probability of each to explain the observed datasets. For each model and each outcome, the logarithm of the model probability is computed using a SMC sampler; the average over 10 independent runs is displayed and the number in brackets is the SD.

To further compare the models, we use a likelihood-based Bayesian SMC sampler (22) assuming additive Gaussian measurement noise and again find no evidence in favor of any one of the three models. The model probability (log likelihood of the model given the data) for each case is shown in Fig. 2C, and there is no statistically significant difference between them (23). It should be noted that the data measure the ratio of leukemic and healthy terminally differentiated cells, and given information about the unobserved (stem and progenitor) species, the model probabilities could change dramatically. As the available data alone does not allow us to discriminate between the three models considered here, we need to consider other properties of these models coupled with biological reasoning to elucidate the mechanisms underlying CML etiology and progression.

Model Checking—The Importance of Competition.

The posterior distributions obtained from Bayesian parameter inference allow us to predict cell-type behavior: trajectories of individual species are simulated using parameter values sampled from the posterior. In Fig. 2B, the trajectories for HSCs and LSCs are plotted for each model in the case of relapse. Whereas for models M1 and M3 both stem cell species reach finite and biological plausible steady states, in the case of model M2 we find that LSCs and their progeny species grow exponentially. Thus, this model cannot represent the underlying biological mechanisms and cannot describe the dynamics of the hematopoietic system. Because our goal is to explain mechanisms of leukemia growth and decline, we cannot hope to gain much insight out of a model with such drastically implausible growth kinetics. In light of the behavior found we can reject model M2 and focus our further attention on the models M1 and M3: a model with two independent stem cell lineages fails to describe the dynamics of CML. This rejection suggests that interactions between the two lineages are important. The models considered here (M1 and M3) describe these interactions as competition between species within a niche; other models may explain the same behavior in different ways.

Model Comparison—M1 and M3 Offer Contrasting Mechanisms for CML Progression.

To compare the two mechanistic models, we exploit the posterior distributions obtained from the parameter inference. It is difficult to directly identify differences between models from these distributions because none of the model parameters are tightly constrained by the data, and most of the parameters are highly correlated (see Supporting Information); although this may be seen as failure of the inference, it is in fact, a reflection of the data (their nature, quality, and quantity) and is itself informative. More crucially, perhaps, it highlights the importance of assessing the uncertainty of estimates instead of merely obtaining “optimal estimates” of parameter values. In the Bayesian framework we can still derive useful insights by making the posterior distribution the center of the analysis and using it to predict the behavior of the different cell types over time. The corresponding predicted trajectories for each outcome are shown in Fig. 3.

Fig. 3.

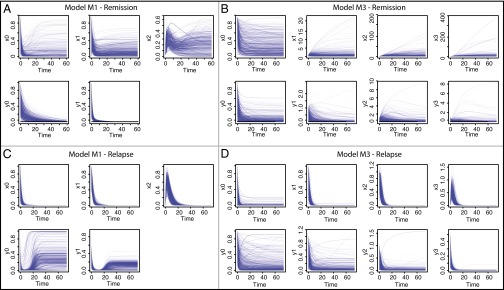
The predicted change over time of each species for a timespan of 6 y (the total period of the trial), for (A and C) model M1 and (B and D) model M3 and (A and B) remission and (C and D) relapse. For each model and each outcome, 1,000 parameter sets were sampled from the posterior distribution and each line corresponds to the simulated trajectory for one of these parameter sets.

We first focus on the mechanisms leading to remission under both models. For model M1, the level of leukemic species declines over time, with differentiated leukemia cell levels being tightly constrained (Fig. 3A). In the healthy lineage, the HSC population initially decreases, leading to an initial peak in the level of healthy progenitor and (with greater variance and delay) differentiated cells. After this peak the behavior for all healthy species is unconstrained. Therefore, model M1 explains disease remission by suppression of leukemic species and expansion of the healthy differentiated cell populations through transient progenitor growth. This prediction would be directly testable by studying healthy blood progenitor abundances over the course of CML treatment to determine whether a growth peak occurs after initial administration of TKIs. In contrast to model M1, model M3 permits a large variety of behaviors and high species’ concentrations 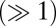, shown in Fig. 3B; this makes its behavior harder to understand and interpret. Similarly to model M1, the level of healthy cells is higher than their leukemic counterparts, which leads to the outcome of remission. It is interesting to note that the level of LSCs permitted at steady state can constitute a substantial proportion of the niche. This is surprising to see under remission (in contrast with M1) and could be tested by directly measuring species’ abundances in the niche.

For CML relapse, the species’ behaviors are more constrained than for remission—even though the posterior distributions are still broad. We observe similarities between the two models, in particular for the behavior of the healthy species (Fig. 3 C and D): both models require low levels of healthy differentiated cells at steady state as well as an initial peak in the level of healthy progenitor and differentiated cells, explaining the temporary suppression of leukemia.

We also find significant differences between the two models under relapse: for model M3, leukemic stem and progenitor cells can exhibit wide-ranging behaviors, whereas, for M1, leukemic stem and differentiated cells always initially decrease before increasing to fill (at least a proportion of) the niche. This transient behavior of leukemia suppression before a return of the disease is in agreement with the literature on recurrence of CML (24). The variety of species’ behaviors we see for HSCs (which can occupy up to 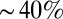of niche space) and leukemic stem and progenitor cells under model M3 could be due to the number of layers in the hierarchy of M3 and the fact that we only measure fully differentiated cells. As a result, effects originating at the stem cell level are dampened in successive progenitor populations. For model M3, the differentiated leukemic cells decrease to a low steady state, similarly to the differentiated healthy cells, and the inferred rates of death/differentiation (coupled between healthy and leukemic lineages) are all high. Thus, we suggest that an explanation for the CML relapse could be that healthy and leukemia cells are pushed toward differentiation, with the leukemia lineage slightly ahead. This high rate of differentiation (or progression through the hematopoietic hierarchy) should be measurable in principle if it does indeed exist. It is intriguing that both models predict that relapse is linked to very low levels (also in the periphery) of lymphocytes, as measured in ref. 25; this should also be measurable.

Model Comparison—Disease Outcome Is Controlled by Either LSC Growth Rate (for M1) or Progenitor Death Rate (for M3).

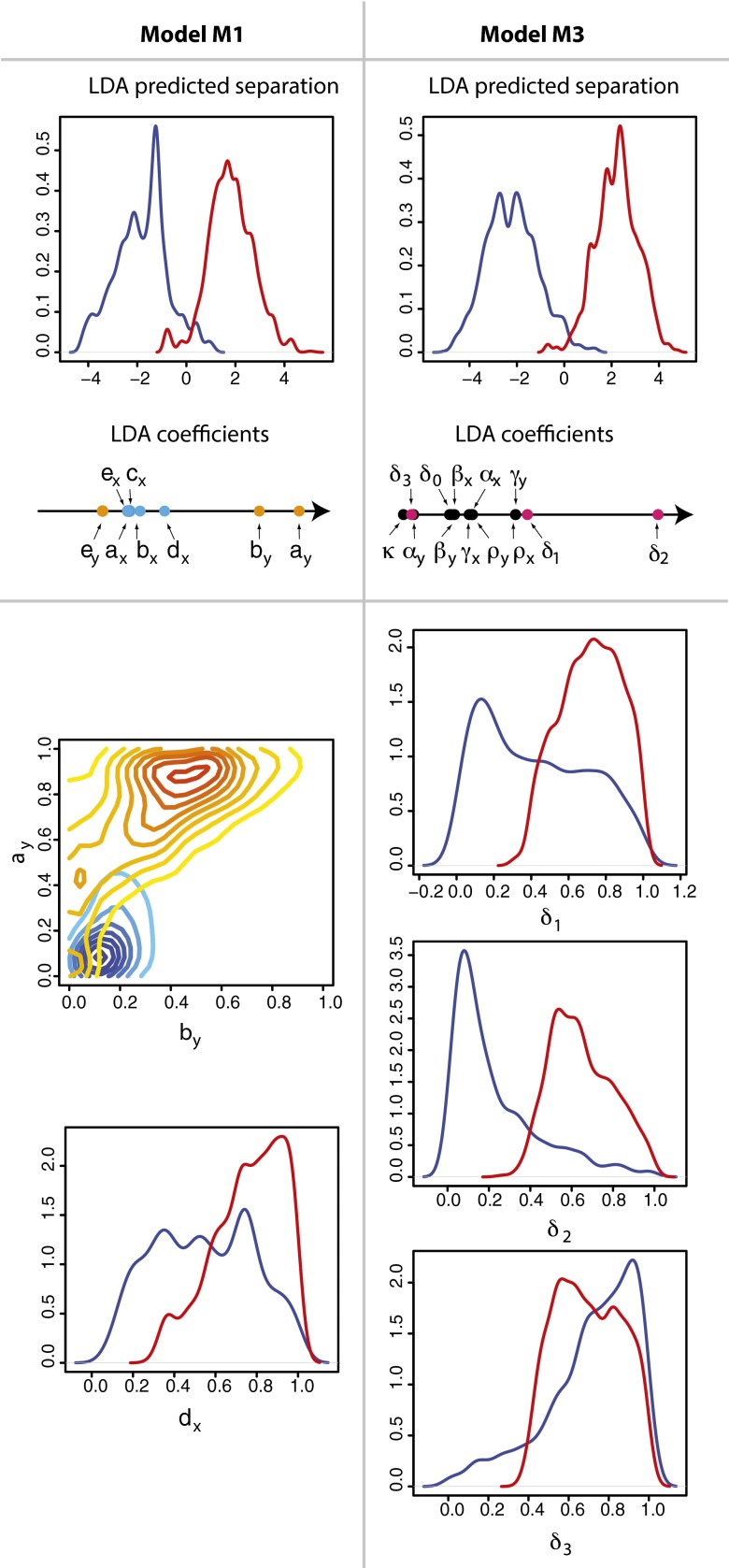
We next determine which combinations of parameters best explain the differences between remission and relapse. For each model we compare the posterior parameter distributions associated to each outcome to determine the parameter combination that best separates the two clinical outcomes. Linear discriminant analysis provides a convenient way to do this; the results of this analysis are summarized in Fig. 4. For both models M1 and M3 a clear separation was found despite the fact that the individual posterior distributions were broad.

Fig. 4.

Linear discriminant analysis was used to predict the key differences between remission and relapse. For (Left) model M1 and (Right) model M3, clear separation between disease outcomes can be made (Upper). The parameter contributions (coefficients) to the linear discriminant are shown on a horizontal axis. For model M1, the healthy parameters are represented by blue dots and the leukemic parameters by orange dots; for model M3, the pink dots designate the death rates. (Lower) Shown for model M1 is a density plot of 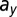against 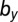with the location of remission outcomes marked in blue and the relapse outcomes in red: using only these two parameters a good separation is already achieved. We also show the posterior density distribution of parameter 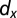alone in case of remission (blue) and relapse (red)—moderate separability is observed. For M3 we show the posterior density distribution for each of the death rates and we see that for 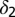, remission (blue) and relapse (red) can be well distinguished.

For M1 we find that parameters 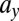, , 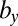and 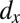explain most of the differences seen between clinical outcomes. The pair of parameters contributing most to the linear discriminant, 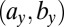, describe growth and differentiation of LSCs. In the case of remission both parameters have to be low for leukemic cell production to be kept in check, whereas for relapse 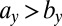is required, which maintains growth of the LSC pool. Parameter 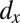, although not constrained for remission, should be relatively high for relapse; this is required to produce the sharp peak in healthy differentiated cells. Overall, for M1, controlling leukemia species is more important than controlling healthy species in determining clinical outcome.

This leads us to predict that disease outcome could be controlled by variation only in parameters related to LSC function. To test this we simulate model M1 under relapse conditions until the onset of disease relapse, and study the effect of varying 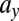. We see that by decreasing 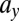while keeping all other parameters constant, we can stop relapse from occurring and the patient goes back into remission (see Supporting Information). This intervention—selectively suppressing the growth of LSCs—thus seems promising, but is probably not yet possible to achieve clinically.

For M3 we find that a single parameter, 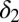, explains most of the variation between outcomes (Fig. 4). Relapse requires all of the differentiation/death rates to be high to produce the desired peak in healthy differentiated cells from peaks in the progenitor cell species; for remission, 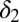, should be moderate or low. We observe that finite populations of partially differentiated cells 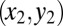must be maintained (explaining the low value of 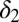) so that fully differentiated cells 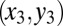can be produced. Given the relative importance of 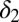, we perform a similar in silico treatment analysis as that above and test how M3 responds to a change in 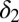at the point of relapse. We observe that although the rate of relapse is slowed, disease eventually returns and the patient does not recover (see Supporting Information). As a possible explanation for this, we note that for M3 at the point of relapse, the levels of all cell species (healthy and leukemic) are very low; at this point a return to healthy conditions might not be possible. This also suggests that there are intricate dependencies between the parameters of M3, requiring more subtle interventions to reverse clinical outcome.

Conclusion

CML has been studied in great detail and a number of models describing different aspects of disease progression have been developed in the past decade (17–20, 25–28). However, there remains uncertainty about the cellular processes that control disease etiology and outcome. Here we have approached this question by comparing three models of CML dynamics and their ability to explain clinical data on CML progression.

With our Bayesian framework we found that all of the models can be fitted to data for both remission and relapse and receive the same level of statistical support. Because of the limitations of the data we thus have to adopt more detailed model analysis and model-checking tools to discriminate between these different mechanistic hypotheses.

Model M2, for example, can be ruled out as it requires sustained exponential growth of LSCs to explain the data. The key difference between this and the other two models is that M2 does not allow for interactions in the stem cell niche; instead all cell types evolve independently. This suggests that cellular competition is an important and perhaps crucial aspect of a model seeking to describe the ecology of hematopoietic and leukemic cells inside CML patients.

Despite the limited nature of the data, our Bayesian framework allowed us to analyze the remaining models in more detail, and we used posterior simulations to explore the behavior of the different models in patients exhibiting relapse and remission. Posterior distributions, even though frequently broad, can nevertheless give rise to constrained behavior of the cell types modeled here. Crucially, our analysis has allowed us to show the effects that the niche can exert on disease progression: as more cell types—HSCs and LSCs reside necessarily inside the niche microenvironment—are exposed or contribute to the cell population dynamics inside the niche, model M3’s behavior increasingly resembles that of M1. If the niche does indeed extend its influence also over progenitor cells, then our analysis suggests that clinical outcome is primarily determined by how effectively TKI therapy targets LSCs. In M3, by contrast, we found that the differences between patients showing remission or relapse are less pronounced, with the death rate of progenitor cells being the parameter exerting most influence over a patient’s prognosis.

Despite the large body of knowledge gathered, and despite the successful treatments for CML, there remain large gaps in our understanding of the cellular processes that underpin this disease. Here we have identified mechanistic differences at the cellular level between different mechanistic hypotheses of CML progression that we hope will become experimentally testable as methods for probing the HSC niche advance. The ability to map the hematopoietic system and its dynamics in vivo will almost certainly also benefit our understanding of other hematological disorders.

Materials and Methods

Experimental Data.

In the dataset used for analysis, CML levels are assayed through measurements of transcript levels of the BCR-ABL protein in the blood (Fig. 1), which is a proven marker for CML. Each of the 69 patients in the study is being treated with tyrosine kinase inhibitors that selectively bind to the BCR-ABL protein present on CML cells (16). Blood samples are taken every few months although not always at the same time points across all patients.

Bayesian Parameter Inference and Model Comparison.

We use a sequential approximate Bayesian computation (ABC) algorithm (21) to infer the model parameters and the initial conditions for each species. ABC approaches use systematic comparison between simulated trajectories and the observed data to identify parameters associated with simulated trajectories that are closest to the observed data. Here, the time series for BCR-ABL (described above) is compared (using Euclidian distance) to the ratio 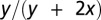, where y is the number of leukemic differentiated cells and x is the number of healthy differentiated cells (20). We use the package, which provides a python implementation of this algorithm with graphical processing unit (GPU) support (29).

Use of a likelihood-based SMC sampler (22) enables us to compute the model evidence, which is the probability to observe a dataset under a given model. We used our own implementation of the SMC sampler algorithm in python as well as an interface to simulate the models in a computationally efficient manner using a GPU accelerated ordinary differential equation solver (30).