Abstract
We introduce an regularized reconstruction scheme to recover dynamic imaging datasets with significant inter frame motion from undersampled Fourier data. The proposed non-local regularization penalty is an unweighted sum of distances between image patch pairs in the 3-D dataset. We use robust distance metrics to compute the distance between image patches; these metrics encourage the smoothing between similar patches, while discouraging the averaging of dissimilar patches. Hence, this algorithm is capable of exploiting the similarities between patch pairs in adjacent frames even when they are well separated due to motion, eventhough it does not perform explicit motion estimation. Unlike current non-local regularization schemes, the proposed penalty does not need good initial guesses to estimate the weights. Hence, this approach is readily applicable to accelerated dynamic imaging problems, where good initial guesses are challenging to obtain. The validation of the proposed scheme on numerical phantoms and dynamic MRI datasets demonstrate the superior performance of the proposed scheme over current dynamic imaging schemes.
1. INTRODUCTION
The imaging of time varying phenomenon is a key application in several imaging modalities (eg. cardiac MRI, in-vivo microscopy). It is often difficult to simultaneously achieve high spatial and temporal resolutions in dynamic imaging, especially when there is significant inter frame motion (e.g.. free breathing cardiac perfusion MRI). Several dynamic MRI schemes that share data between adjacent frames (e.g. sliding window and temporal smoothing schemes) were introduced to reduce the data demand [1, 2]. However, effectiveness of these data-sharing methods degrade considerably with inter frame motion, since the local similarity (similarity between corresponding pixels in adjacent frames) will be lost. However, note that there is still considerable similarity between adjacent image frames, since we are imaging a specific object or objects that are evolving in time. To exploit this redundancy, several researchers have recently introduced algorithms based on motion estimation and motion compensation (ME-MC) methods [3, 4]. These algorithms explicitly model the deformation field between adjacent frames. They alternate between motion estimation and motion compensated reconstruction steps to simultaneously recover the dynamic imaging dataset and the motion model. The main challenge associated with these approaches is the lack of a unified energy minimization framework for the entire setup; since the ME and MC steps are decoupled, it is often difficult to monitor the convergence of the entire scheme. Moreover, the final results are often heavily dependent on the frequency of the updates and complexity of the motion and signal models.
We introduce an energy minimization framework to recover the dynamic imaging dataset from very few samples. Unlike ME-MC methods, the proposed scheme does not explicitly model and estimate the deformation field. The central idea of the proposed scheme is illustrated in Fig. 1. We pose the recovery as a regularized reconstruction scheme, where the non-local regularization penalty is an unweighted sum of distances between image patch pairs in the 3-D dataset. For each patch in a specified frame, the summation includes distances between itself and the patches in a cube shaped neighborhood around it. We use robust distance metrics to compute the distance between image patches; these metrics encourage the smoothing between similar patches, while discouraging the averaging of dissimilar patches. If the image region corresponding to the specified patch has moved to another region within the search window, the algorithm is able to capitalize on the redundancy between these patches to significantly decrease the aliasing artifacts. In contrast, local smoothing schemes only involve differences between the intensities of the adjacent pixels in the dataset and is not capable of exploiting this redundancy.
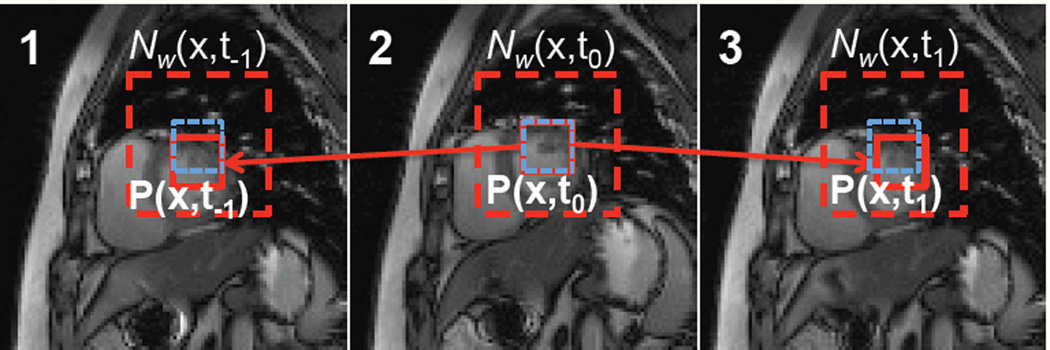
Fig. 1.
Illustration of the proposed dynamic imaging penalty: The penalty is an unweighted sum of distances between patch pairs in the 3-D dataset. For a specified image patch, the penalty involves the distances between itself and other patches in its cube shaped neighborhood. The robust distance metric ϕ is capable of exploiting the redundancy between similar patches, while excluding the dissimilar patches from averaging. Hence, the algorithm can capitalize on the similarity between the corresponding patches, even if they have moved to another location. The blue squares indicate the location of the square in frame 2, while the red squares are the ones with the highest similarity with the red square in frame 2.
This work is built upon the unified non-local image regularization scheme introduced in our earlier work [5], which is also similar to [6]. The main difference of the framework in [5] with classical non-local schemes is the independence of the penalty on pre-specified weights. Classical non-local schemes estimate the inter-patch weights from an initial guess [7]. Since the proposed penalty is independent of predetermined weights, it is readily applicable to heavily under-sampled dynamic imaging problems, even when good initial guesses to estimate the weights are not available. We have shown that the first iteration of the proposed scheme to be similar to classical non-local schemes; since the proposed scheme is iterative, it is capable of further improving the performance. The proposed dynamic imaging algorithm have some similarity to the non-local scheme of Adluru et al., who used a combination of two non-local penalties: the first 2-D penalty exploits the similarity of patches within the same frame, while the second 1-D non-local penalty exploits the similarity of the intensities of a specific voxel along time. Since the temporal non-local term is 1-D in nature, this approach is not capable of exploiting the similarities between image regions in adjacent frames, especially when large motion is present. Since we use a fully 3-D non-local scheme, our algorithm is capable of fully exploiting the redundancy between adjacent frames (see Fig. 1). We demonstrate the utility of this scheme in the context of free breathing CINE MRI data. The comparisons demonstrate that the proposed scheme is capable of achieving high accelerations with minimal blurring, when the local TV method results in considerable blurring.
2. ROBUST NON-LOCAL REGULARIZATION OF DYNAMIC IMAGING PROBLEMS
We pose the nonlocal regularized reconstruction of the dynamic dataset f(x, t) from its sparse Fourier measurements b = 𝒜f as the optimization problem:
| (1) |
Here, x is the spatial variable and t denotes the temporal variable. We assume (x, t) ∈ Ω, where Ω = [0, Nx] × [0, Ny] × [0, T]. The regularization penalty in (1) is specified by
| (2) |
Here, ϕ is an appropriately chosen robust distance metric (see Fig. 2). The term P(x, t) (f) denotes a patch of the 3-D volume, which is centered at the point (x, t). We denote the size of the patch as Np,x × Np,y × Np,t. The pixel locations of this patch are indicated by ℬx, t. The size of the patch is smaller than the of the search window 𝒩(x, t), whose dimensions are indicated by Nw = Nw,x × Nw,y × Nw,t (see Fig. 1). Note that the nonlocal penalty 𝒢(f) is not dependent on any apriori selected weight function. Hence, the new framework can be readily applied to under-sampled dynamic imaging problems, where good initial guesses are difficult to derive.
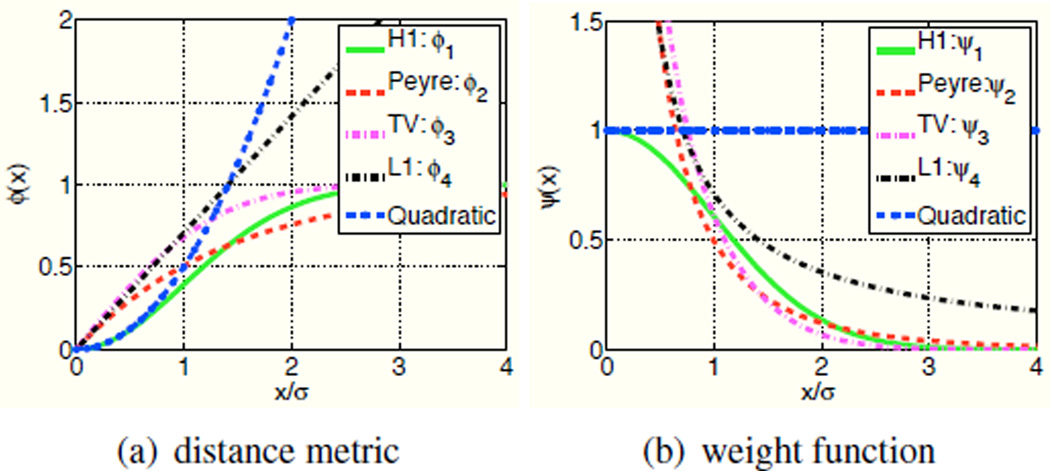
Fig. 2.
Comparison of the distance metrics ϕ and corresponding weight functions ψ (a) and (b). We compute these distance functions such that the first iteration of the proposed scheme matches the current non-local algorithms (eg. NLTV, NLH1, Peyre’s method). Note that these distance functions saturate with Euclidean inter-patch distance, thus preventing the averaging of dissimilar patches. Our experiments show that these non-convex schemes provide good reconstructions, if appropriate continuation schemes are used.
2.1. Relation to current non-local schemes
We majorize the proposed penalty term 𝒢(f) by a simpler quadratic surrogate functional:
| (3) |
where wf (x, y) is specified by
| (4) |
where ψ(x) = ϕ′(x)/2x. Ignoring the constant b in (3) for simplicity, the quadratic surrogate functional that majorize the actual penalty becomes
| (5) |
where the weights γf are specified by
| (6) |
Note that the expression of the surrogate criterion 𝒢w in (5) is very similar to classical non-local penalties. We have shown in [5] that most of the current non-local schemes can be interpreted as the first iteration of the proposed scheme, if the penalty functions (ϕ) can be chosen appropriately to match the expression for the weights. The distance metrics and the corresponding weight functions, corresponding to current non-local schemes, are plotted in Fig. 2.
2.2. Majorize minimize (MM) algorithm
We use the majorization of the regularization penalty, introduced in Section 2.1, to develop a two-step alternating algorithm. The algorithm alternates between the solution of the quadratic surrogate problem:
| (7) |
and the estimation of the weights from the current iterate as wfn(x, y) = ψ (‖Px(fn) − Py(fn)‖η). Here, f is the vectorized image, A is the matrix operator corresponding to the forward model, and Γn is the sparse matrix with the entries: Γn(x, y) = γfn(x, y). Here, γfn(x, y) is the sum of similarity measures w(x, y) using (6). Note that the optimization criterion in (7) is a quadratic. We solve this using conjugate gradients optimization.
Different majorizations of the criterion in (1) may be considered to obtain alternate MM algorithms, similar to shrinkage based algorithms in compressive sensing. For example, the data consistency term can be majorized to decouple the problem into a steepest descend update, followed by a non-local smoothing. The non-local smoothing can be performed iteratively using fixed point iterations [6]. Another option is to majorize both the data and penalty terms. The resulting algorithm involves one steepest descend update, followed by one fixed point step as in [8]. However, both of these schemes will involve at least one evaluation of weights per steepest-descend step. The computation of the weights in non-local algorithm involves the evaluation of the distances between all patch pairs. In contrast, each of the CG steps involves three FFTs (in Fourier inversion and deblurring applications) and a weighted linear combination of pixel values (evaluation of Γnf ) per iteration, which are relatively inexpensive. Since the proposed scheme relies on one weight computation, followed by several CG updates, we observe this algorithm to be more computationally efficient than other methods. The comparison of the algorithms demonstrate that the proposed scheme provides a 10 fold reduction in computation time, compared to the alternate majorizations. These gains are especially relevant in the context of reconstruction of 3-D datasets. Our MATLAB implementation takes 7–10 minutes to recover the 3-D dataset in perfusion experiment (90×90×40 matrix). We expect to further accelerate the algorithm by exploiting the parallelism and customizing the code for graphical processing units.
3. RESULTS
We now demonstrate the utility of the 3-D non-local algorithms in dynamic imaging applications. We compare this scheme with classical local smoothing methods and 2-D non-local schemes. We consider the recovery of the NCAT phantom with both respiration and cardiac motion from 12 radial lines per frame; the acceleration factor is approximately 9.25. The trajectory is rotated from frame to frame to guarantee incoherence between the acquisitions. A single frame of the reconstructed dataset is shown in Fig. 3. We choose a patch size of 3×3 and a search volume of 5×5×5 for 3D NLM. In 2D NLM, we recover each frame independently, where we choose the patch size and search window to be 3×3 and 5×5, respectively. To ensure fair comparisons, we choose the regularization parameter that provides the best reconstructions for all methods. The experiments demonstrate that the proposed non-local scheme provides good reconstructions with minor artifacts. In contrast, the 3-D local TV reconstructions are significantly blurred due to the significant inter frame motion. Note the non-local reconstructions are crisp, but exhibit significant distortions. Since the 3-D NL scheme can average across time frames, it can exploit the redundancies between the different frames and the incoherence in sampling patterns to reduce the artifacts. We observe a 5–7 dB improvement over the competing methods. These results clearly show the benefit in using the proposed scheme for dynamic MRI. We use the same algorithm to accelerate free breathing cardiac CINE MRI data in Fig. 4. The motion between adjacent frames is high in this dataset, in addition to the images possessing significant detail. Most of the current algorithms fail in this case. We compare the utility of the local TV algorithm with the 3-D nonlocal scheme in accelerating this dataset. Here, we randomly sample the free breathing dynamic MRI data to achieve an acceleration factor of 3. Similar to the NCAT comparisons, the local TV reconstructions show significant blurring. In contrast, the 3-D non-local scheme provide good quality reconstructions with minor temporal blurring and preservation of small image features. It also provides an SNR improvement of approximately 4 dB.
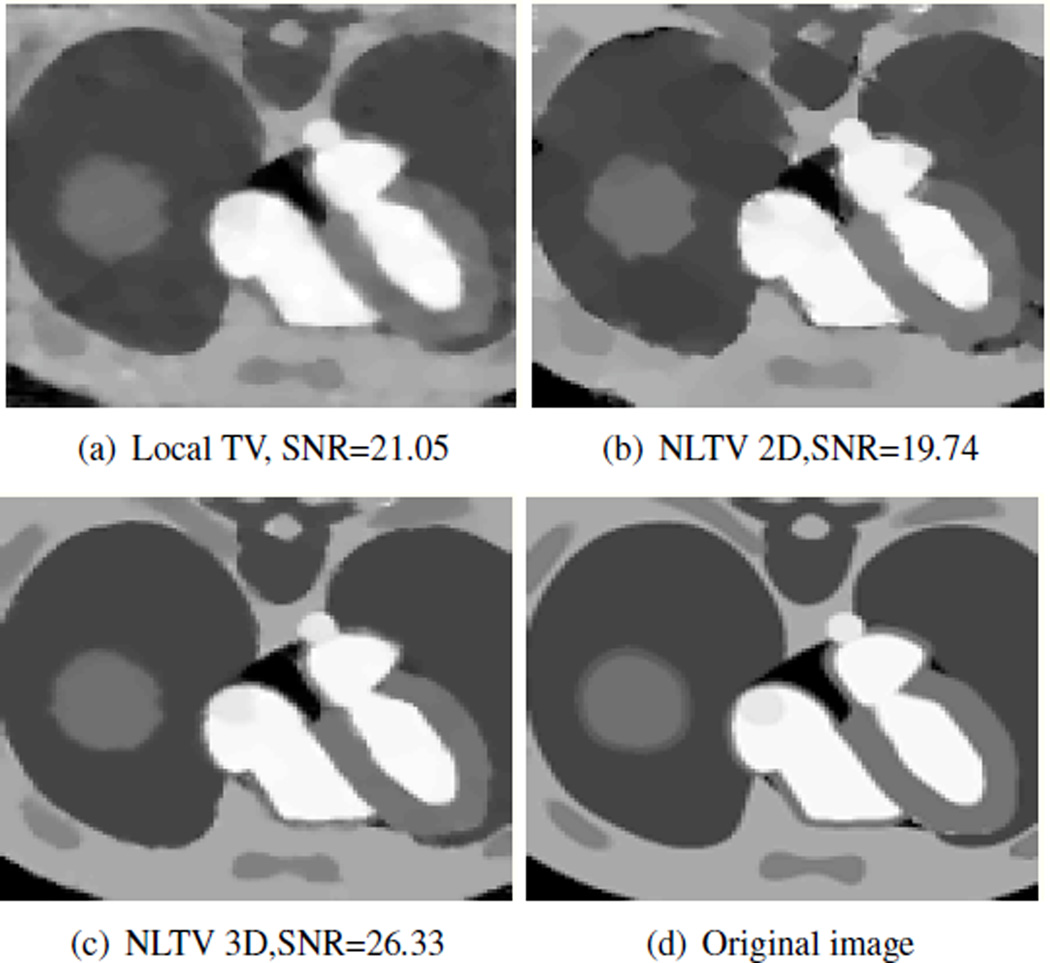
Fig. 3.
We reconstructed the breathing NCAT phantom images from 9.25 times undersampled k-space data using 12 lines in polar trajectories. The figure shows reconstructed images of the 10th frames by local TV Fig.(a), nonlocal 2D Fig.(b), nonlocal 3D Fig.(c). Comparing with the original image Fig.(d), the nonlocal algorithms preserve more details while standard TV introduces patchy artifacts.
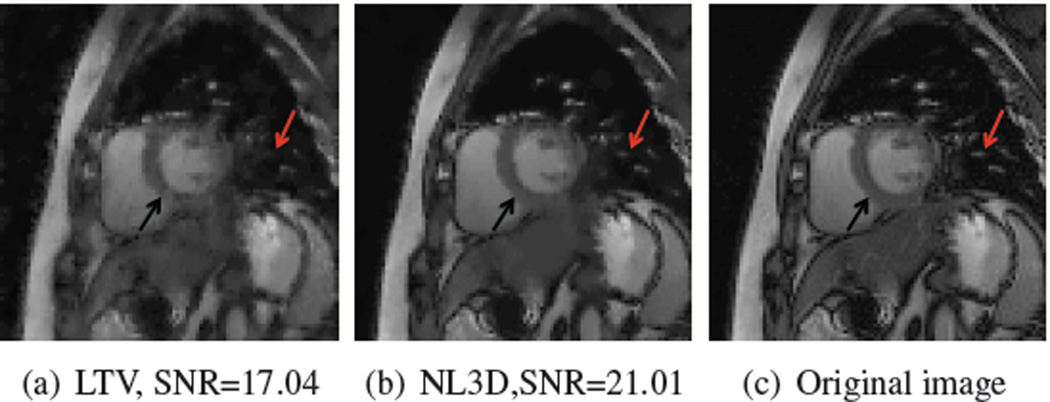
Fig. 4.
We apply the proposed nonlocal algorithms to free breathing MRI data set, which is undersampled randomly the acceleration factor of 3. Noticeably, there is some residual artifacts left in the reconstructed image by local TV Fig.(a), pointed by the black arrow, while the nonlocal H1 Fig.(b), nonlocal TV Fig.(c) show a better performance in reducing the undersampling artifacts and preserving the small structure, notified by the red arrow.
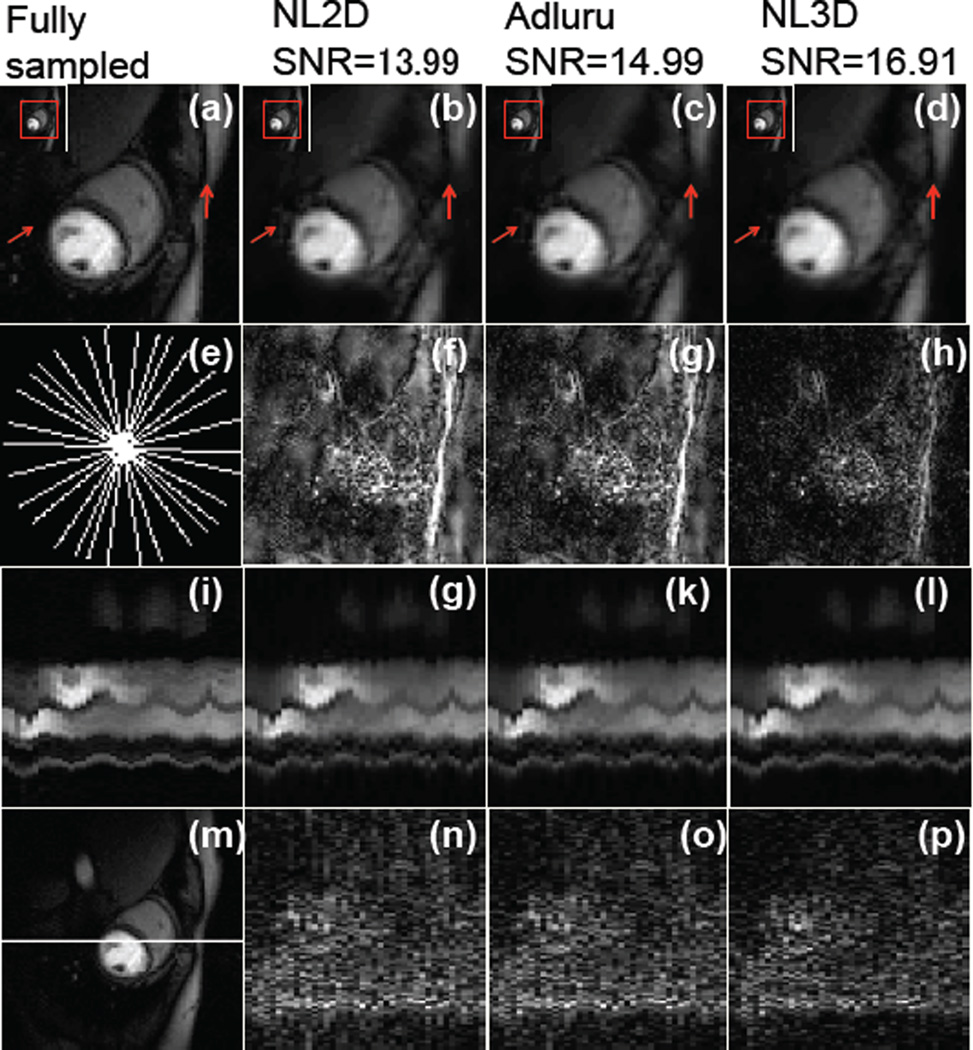
Finally, we apply our 3D nonlocal algorithm to free breathing perfusion MRI data with a matrix size of 90 × 90×40. The results are shown in Fig. 5. We downsample the k-space data using golden ratio polar trajectory with 15 lines per frame, corresponding to a 6.7 fold acceleration. There is considerable motion in this dataset, mainly due to respiration (see third row of Fig. 5). We compare the proposed algorithm with 2D non-local schemes and the method of Adluru et al. [8], which uses a combination of 2D spatial and 1-D temporal non-local penalties. We observe that the proposed scheme to improve the SNR by approximately 3dB. Since this is a preliminary experiment and the tuning of parameters is complex due to the run time of the algorithm, we expect to considerably improve the gains in the future.
Fig. 5.
We retrospectively downsample the k-space data of a 90×90×40 perfusion MRI data set with a golden ratio radial trajectory with 15 lines; the trajectory is shown in Fig.(f). The columns represent different reconstruction algorithms. The first and second rows show the 14th frame and the corresponding spatial error image. The third row illustrates the time profile through the line in Fig.(p), while the fourth row shows the error in time profiles. The ripples in the time profiles are due to respiratory motion.
4. CONCLUSION
We introduced a robust spatio-temporal nonlocal regularization algorithm for the dynamic MRI reconstruction. The non-local penalty is an unweighted sum of robust distances between non-local patch pairs in the 3-D dataset. Hence, this algorithm is capable of exploiting the similarities between patch pairs in adjacent frames even when they are well separated due to motion. The validation of the proposed scheme on numerical phantoms and dynamic MRI datasets demonstrate the superior performance of the proposed scheme over current dynamic imaging schemes.
Acknowledgments
This work is supported by NSF awards CCF-0844812 and CCF-1116067.
REFERENCES
- 1.d’Arcy J, Collins D, Rowland I, Padhani A, Leach M. Applications of sliding window reconstruction. NMR in Biomedicine. 2002;vol. 15(no. 2):174–183. doi: 10.1002/nbm.755. [DOI] [PubMed] [Google Scholar]
- 2.Adluru G, Whitaker R, DiBella E. IEEE ISBI. IEEE; 2007. Spatio-temporal constrained reconstruction of sparse dynamic contrast enhanced radial mri data; pp. 109–112. [Google Scholar]
- 3.Lingala S, Nadar M, Chefd’hotel C, Zhang L, Jacob M. IEEE ISBI. IEEE; 2011. Unified reconstruction and motion estimation in cardiac perfusion mri; pp. 65–68. [Google Scholar]
- 4.Jung H, Ye J. Motion estimated and compensated compressed sensing dynamic magnetic resonance imaging. International Journal of Imaging Systems and Technology. 2010;vol. 20(no. 2):81–98. [Google Scholar]
- 5.Yang Z, Jacob M. IEEE ISBI. 2011. A unified energy minimization framework for nonlocal regularization. [Google Scholar]
- 6.Wang G, Qi J. IEEE ISBI. 2011. Patch-based regularization for iterative pet image reconstruction. [Google Scholar]
- 7.Lou Y, Zhang X, Osher S, Bertozzi A. Image recovery via nonlocal operators. Journal of Scientific Computing. 2010;vol. 42(no. 2):185–197. [Google Scholar]
- 8.Adluru G, Tasdizen T, Whitaker R, DiBella E. Improving undersampled mri reconstruction using non-local means. MRM. 2010 [Google Scholar]