Discriminative motif analysis of high-throughput dataset

Abstract

Motivation: High-throughput ChIP-seq studies typically identify thousands of peaks for a single transcription factor (TF). It is common for traditional motif discovery tools to predict motifs that are statistically significant against a naïve background distribution but are of questionable biological relevance.

Results: We describe a simple yet effective algorithm for discovering differential motifs between two sequence datasets that is effective in eliminating systematic biases and scalable to large datasets. Tested on 207 ENCODE ChIP-seq datasets, our method identifies correct motifs in 78% of the datasets with known motifs, demonstrating improvement in both accuracy and efficiency compared with DREME, another state-of-art discriminative motif discovery tool. More interestingly, on the remaining more challenging datasets, we identify common technical or biological factors that compromise the motif search results and use advanced features of our tool to control for these factors. We also present case studies demonstrating the ability of our method to detect single base pair differences in DNA specificity of two similar TFs. Lastly, we demonstrate discovery of key TF motifs involved in tissue specification by examination of high-throughput DNase accessibility data.

Availability: The motifRG package is publically available via the bioconductor repository.

Contact: yzizhen@fhcrc.org

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

The emergence of high-throughput sequencing technology for genome-wide profiling of transcription factor binding sites (TFBS) has made precise categorization of their DNA motifs possible. Harnessing the power of large quantities of data generated by this technology presents many computational challenges. Motif discovery is a classical bioinformatics problem and has been an active area of research for decades. Existing tools can be roughly classified as profile-based, such as MEME (Bailey and Elkan, 1995), or pattern-based like CONSENSUS (Hertz and Stormo, 1999) [see (Tompa et al., 2005) for a review and performance study of popular motif discovery tools]. Most of these tools, however, do not easily scale to large datasets. Users typically limit the motif search to top ranking peaks, thus sacrifice the power of the data, which may be critical for accurate modeling of the TFBS and for identification of cofactors. Large amounts of data also increase the power to detect various non-random signals, many of which may not be directly related to the problem of interest. The new challenge is to understand the nature of motif signals and determine the relevant ones. We propose to test the motif enrichment in a foreground dataset against an explicitly stated background dataset, rather against a non-informative null distribution. The background dataset should be carefully selected to represent the systematic biases present in the foreground.

Discriminative motif discovery is not a new approach. Pioneering work includes, but is not limited to, DME (Smith et al., 2006), DIPS (Sinha, 2006) and DEME (Redhead and Bailey, 2007). These methods find a discriminative position weight matrix (PWM) to optimize an objective function, which for the case of DEME and DME, is the likelihood of the data given the model and sequence class. However, the optimization procedures of many of these methods are computationally expensive, making them unsuitable for large datasets. Recent works designed for high-throughput datasets use more simplified statistical models. For example, DREME [MEME suite (Bailey, 2011)] and oligo-diff [RSAT suite (Thomas-Chollier et al., 2012)] use Fisher’s exact test and PeakRegressor (Pessiot et al., 2010) applies a linear regression model to fit peak scores by motif counts.

In this study, we propose a new discriminative motif discovery algorithm motifRG that distinguishes two sequence datasets. We measure the discriminative power of a motif by a logistic regression model, which shows some similarity to DREME and PeakRegressor, but offers a better combination of robustness and flexibility. We also provide an effective and efficient iterative process for motif refinement and extension and apply a bootstrap robustness test to avoid over-fitting in the optimization process. The logistic regression framework offers direct measurement of statistical significance, and we demonstrate by permutation tests that the associated z statistics reflect the probability of occurrence by chance. This framework also provides flexibility to handle existing bias between the two datasets, and to weight the sequences according to their importance, both important features when dealing with some challenging datasets (see Section 3 for details). The method is implemented in R (R Development Core Team, 2010) Bioconductor Core Team, and is publicly available via the Bioconductor (Gentleman et al., 2004) repository.

We applied this method in a comprehensive motif study of 207 ENCODE ChIP-seq datasets for TFBS. Under the default setting, motifRG successfully discovered accurate motifs in 78% of the datasets with known motifs, demonstrating its flexibility in handling diverse applications. In many cases, biologically plausible cofactor motifs are also discovered. Compared with DREME, motifRG had comparable performance at identifying the core motif, and generally ran about 40% faster. Its advantages over DREME in terms of both accuracy and efficiency are more obvious for longer motifs and motifs with degenerate flanking sequences, probably due to a more effective refinement procedure. By exploring the cases where we fail to detect known motifs, we identify several common factors likely to compromise the motif search results and propose strategies that exploit the flexibility of motifRG to deal with these challenges. Using one in-depth case study, we demonstrate the power of discriminative motif analysis for the study of DNA binding specificity of similar members of one protein family. We also show that this tool can be applied to DNaseI accessibility datasets to identify TFBS that are enriched at cell type specific accessible sites, which may act as key regulators of cell lineage specific chromatin remodeling.

Our method, and discriminative motif discovery in general, represents powerful tools to exploit various types of high-throughput datasets to answer many fundamental biological questions.

2 METHODS

2.1 Logistic regression modeling of motifs

We cast the problem of discriminative motif discovery in the framework of logistic regression. For a given motif, let 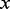be the motif count in each sequence. The basic assumption of logistic regression is that sequences with equal motif counts have equal probabilities P of containing binding sites, and that the logarithm of the odds ratio is linearly related to the count:

More generally, we fit

where w represents ≥1 optional terms reflecting other biases such as GC content. Model parameters (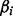) are estimated by the principle of maximum likelihood. The statistical significance of each coefficient 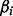is estimated by a Wald test, which calculates Z-statistics: 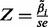, where 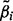is the maximum likelihood estimate of 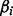and se the estimated standard error of 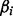. The z value is then squared, yielding a Wald statistic with a chi-square distribution (Hosmer and Lemeshow, 2000; Sinha, 2006). Our motif search optimization goal is to find a motif representation with maximum absolute z-value. As motif counts have few unique values, we tabulate the all values of 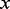and fit the model with only the unique values, weighting each unique value by its count. For applications in which the sequences are weighted, the weight for each unique value is the sum of all weights of the sequences with the given value. This reduced representation speeds up the logistic regression model significantly for large datasets.

Regression was introduced to motif search by pioneering work of Bussemaker et al. (2001), which models the correlation of motif occurrences and gene expression by linear regression. A similar model was adopted by PeakRegressor for applications for ChIP-Seq datasets, which uses peak scores as response. A potential pitfall of this model is sensitivity to outliers. PeakRegressor tried to avoid the problem of outliers by using different regularization techniques such as L1-norm, ridge regression and so forth, which involve additional parameterization. Recent study suggests that other factors such as chromatin accessibility (John et al., 2011; Neph et al., 2012) are likely to have greater effect on intensities of ChIP-Seq signal than motif counts. We believe logistic regression is an appropriate choice for this application because it offers a good combination of flexibility and robustness.

2.2 Search strategy

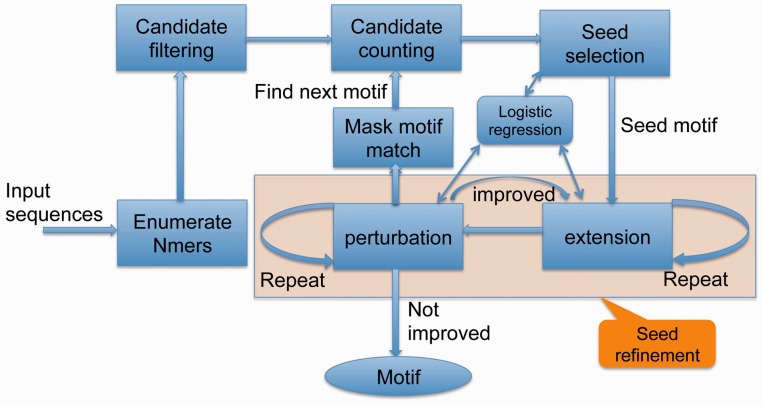
We start by enumerating all nmers with a given width n, fitting the above regression model and sorting the nmers by the absolute z-value. The most significant nmer is chosen as the seed motif. To address the concern that candidates with small enrichment can be highly statistical significant in large datasets, we set an enrichment ratio threshold for the seed motif to ensure that the enrichment is biologically meaningful. We further refine the seed motif by extension and small perturbations by testing all variants with Hamming distance of one over the full IUPAC nucleotide alphabet. The general flow chart of this method is shown in Figure 1.

Fig. 1.

motifRG method outline (see also Supplementary Fig. S1)

To extend the seed, we append a given number f of Ns at both sides of the motif and enumerate all replacements of one N letter by a more specific letter in the IUPAC alphabet. We choose the one with maximum absolute z-value, which becomes the new motif if it improves the z-value, and repeat this process. If no further improvement can be made at the current motif length, append additional Ns to both ends so that each side still has f Ns. If no replacement of Ns yields a better motif, terminate and trim all flanking Ns. This process is illustrated in Supplementary Figure S1B.

Next, we try to refine the motif by small perturbations. We enumerate all candidates with Hamming distance of one that are compatible with the seed and not previously tested. We then choose the candidate with the most improved z-value as the new motif. Repeat this process until no improvement can be made. This process is illustrated in Supplementary Figure S1C.

If there are any changes made to the seed at extension or permutation steps, the whole refinement process is repeated. Conceptually, we can examine all extension and perturbation candidates at the same time. We find that separating the two steps yields better performance and cuts down memory usage by decreasing the search space. We perform the extension step first, as we think it is more important to determine the full-length signature of the motif. 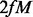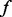In the extension step, the maximum number of candidates tested is where is the number of flanking Ns on each side, and 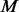the size of IUPAC alphabet. In the perturbation step, the maximum number is 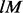, where 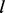is the length of the pattern. The perturbed patterns must be compatible with the initial seed motif, and we filter the candidates by requiring either an increase of total foreground counts or a decrease of total background counts, so the number of allowed candidates is a lot smaller. Using this strategy we can afford to extend the motif as long as needed.

The refinement step can be subject to over-fitting, as a small z-value improvement may not be meaningful. To improve robustness, we perform the following bootstrap test to determine the significance of the improvement: randomly sample the whole sequence dataset (including positive and negative sequences) with replacement for a few times (default 5 times), calculate the z-values for the new and the original motif for each sampling and compute the P-value by applying t-tests on two sets of z-values. Accept the new motif if the P-value is under a given threshold. Although the number of bootstraps we performed is small, we found the variance estimate is reasonably accurate and informative to guide refinement to be more aggressive or conservative (see Section 3 for details).

Candidate enumeration, evaluation and bootstrap validation can be performed in parallel in each iteration, and parallelization is implemented by the ‘parallel’ package of Bioconductor. After refining the top motif, we mask all of its occurrences and repeat the process to find the next motif.

3 RESULTS

3.1 motifRG accurately predicted annotated motifs

To assess the performance of our method for de novo motif discovery in a real world application under different conditions, we tested it on 207 ENCODE ChIP-seq datasets collected from two groups, HAIB_TFBS by HudsonAlpha and SYDH_TFBS by Yale and UCD (see Supplementary Table S1 for the complete list). This dataset covers 82 unique TFs and 25 cell types with different characteristics: the number of peaks varies from a few hundreds to hundreds of thousands, the average GC content ranges from 0.40 to 0.66 and median peak width varies from 100 to 1000 nucleotides (Supplementary Fig. S2). We made a number of decisions to standardize/simplify the analysis and believe they have no real effect on the outcome. If the number of peaks exceeded 50K, we randomly sampled 50K peaks. This approach was further justified by the analysis presented below in section ‘Motif significance and sample size’, which examines the effect of number of peaks on motif prediction. For each peak in each dataset, we first chose one corresponding background sequence from the flanking regions, randomly chosen from either side 0–200 nt from the edge of the peak, and with the same width as the peak. We then predicted up to five enriched motifs. Our software also identifies depleted motifs, but they were ignored here. To find the annotated motif of the ChIP-ed TF, we matched TF names/aliases with the motif names in the motif databases Jaspar (Bryne et al., 2008; Redhead and Bailey, 2007) and Uniprobe (Newburger and Bulyk, 2009). If no exact matches were found, we used the motif of a homolog; e.g. we annotated Atf3 using the Atf1 motif. We then compared the PWMs derived from the top five predicted motifs against the motif database using Tomtom (Tanaka et al., 2011) with default settings. We claimed success in finding the annotated motif if it was among the Tomtom reported matches. We compared our results to DREME, which was run on the same sets of foreground and background sequences under the default setting with maximum of five output motifs.

Among 148 ENCODE datasets with annotated motifs for the TF, motifRG identifies a match to the annotated motif in 115 and does not identify a match in 33. By this criterion, we succeeded in finding the right motifs in 78% of datasets. In comparison, DREME found annotated motif in 116 datasets, almost the same set as ours.

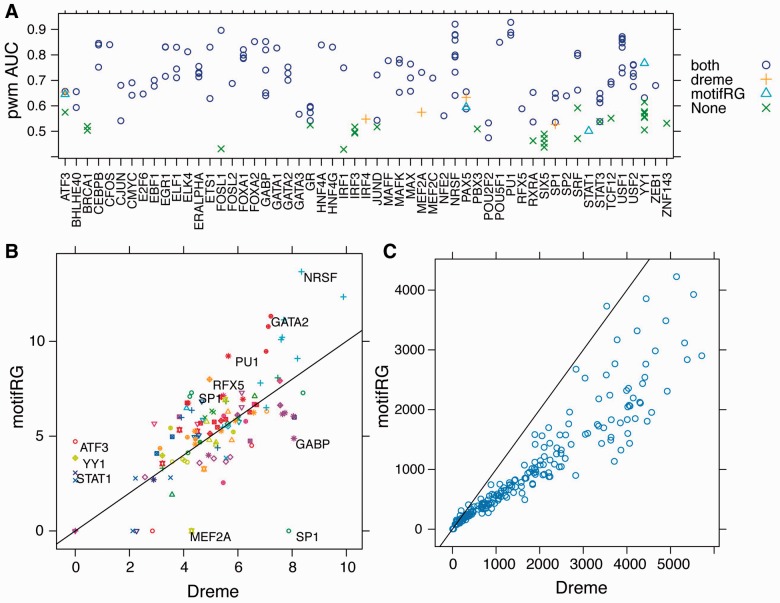
We hypothesized that the annotated motifs are not enriched significantly in the datasets where motifRG and/or DREME failed. To test this hypothesis, we scanned for the best PWM match of the annotated motif in each sequence in both the foreground and the corresponding background datasets, and computed AUC (the area under the receiver operating characteristic curve) (Brown, 2006) by varying the PWM threshold to discriminate foreground from background. The datasets for which we failed to find the motifs generally have low AUC, which suggest low enrichment of the annotated motif relative to the control (Fig. 2A). Therefore, we believe that failure to discover the annotated motifs was likely due to the lack of the TF motif enrichment in the datasets, rather than to the failure of the algorithms. We plot the P-values inferred by Tomtom for motifs predicted by motifRG and DREME against each other in Figure 2B. The two methods predict similar motifs most of the time (Supplementary Table S2), whereas motifRG tends to infer more information in the flanking regions of core motifs, manifested by overall better P-values. To examine whether the differences were due to the fact that DREME uses maximum motif width of 8 under default setting, we also ran DREME with maximum motif width of 12 (referred to as DREME12). However, DREME12 did not demonstrate significant improvement, and in some cases, it terminated without predicting any motifs (Supplementary Fig. S3A). Next we examined two examples in which DREME succeeded, whereas motifRG failed. For the case of SP1 in HepG2, the top motifs predicted by both DREME and motifRG were motifs for cell type-specific master regulators FOX and HNF4. MotifRG predict additional variants of FOX, HNF4 and motif for ETS. When configured to predict more motifs, motifRG discovers an SP1 motif among the top eight motifs. For the case of MEF2A in GM12878, motifRG predicted a more degenerate variant of MEF2A, which was not detected by TOMTOM as matching the MEF2A motif.

Fig. 2.

Performance evaluation of motifRG and DREME. (A) AUC scores for datasets with known motifs. The ROC curve is calculated using the best PWM scores of each sequence based on the annotated motif and measuring the discrimination between foreground and background as the PWM score threshold is varied. The datasets in which both motifRG and DREME found motifs matching to the database are marked by circle, DREME only by plus, motifRG only by triangle and neither by cross. (B) Accuracy for matches of predicted motifs to annotated motifs based on P-values inferred by Tomtom in–log10 transformation. Datasets corresponding to the same TF are marked by the same colors and symbols. The TFs of datasets in which motifRG and DREME performed significantly differently are shown. (C) Comparison of running time (in seconds) for motifRG and DREME

The running time of motifRG grows linearly with size of input (Supplementary Fig. S3B), and runs ∼40% faster than DREME (Fig. 2C), although such a difference can be easily affected by implementation details and subject to change. DREME can be configured to run with python package psyco for 2- to 3-fold speedup, which we did not use due to lack of support by psyco for 64-bit systems. Our method supports a parallel mode for further speed-up, which we did not use for fair comparison. DREME12 runs ∼3–4 times slower than DREME under default settings (Supplementary Fig. S3C), which suggests significant overhead for learning longer motifs, which is not the case for our motif extension procedure. MotifRG uses a lot more memory than DREME, as it is implemented in a high-level programming language that exploits many third party functionalities. We performed memory profiling of motifRG to examine the relationship between memory usage and input size (Supplementary Fig. S3D), which suggested that memory usage grows linearly with input size. Memory usage does not appear to be a bottleneck for most applications, so we did not seek further optimization at this point.

Next, we investigate the cases in which we failed to identify the annotated motifs. The main compromising factors that we identified include significant GC bias, noisy/indirect binding sites inferred by ChIP-Seq or overshadowing cofactors motifs. Many TFBS lie in GC-rich regions (including CpG islands) at both the promoter or enhancer regions. Although we tried to select background sequences with similar genomic context, the GC content variation can be local, so it is still likely for foreground sequences to have higher GC content, resulting in prediction of generic GC-rich motifs. One can control for GC bias by using shuffled sequences of the foreground that maintain the same nucleotide or di-nucleotide composition as control. But, this may not be sufficient for adjusting other biases. Many TFs interact indirectly with the DNA sequences through mechanisms such as tethering. Indirect binding sites tend to have lower ChIP-seq signals compared with directly bound sites and lower the motif enrichment for the direct sites. We also note that many TFBS samples in the same cell type are enriched for the same sets of motifs corresponding to the master regulators in that cell type. For example, most ChIP-Seq samples in GM12878 (a lymphoblastoid cell line) have motif enrichment of RUNX, which is a key TF required for lymphocyte differentiation (Wong et al., 2011). Although this is an interesting phenomenon by itself, these motifs probably serve a generic functional role in the given cell type rather than acting as specific cofactor motifs for the ChIPped TF.

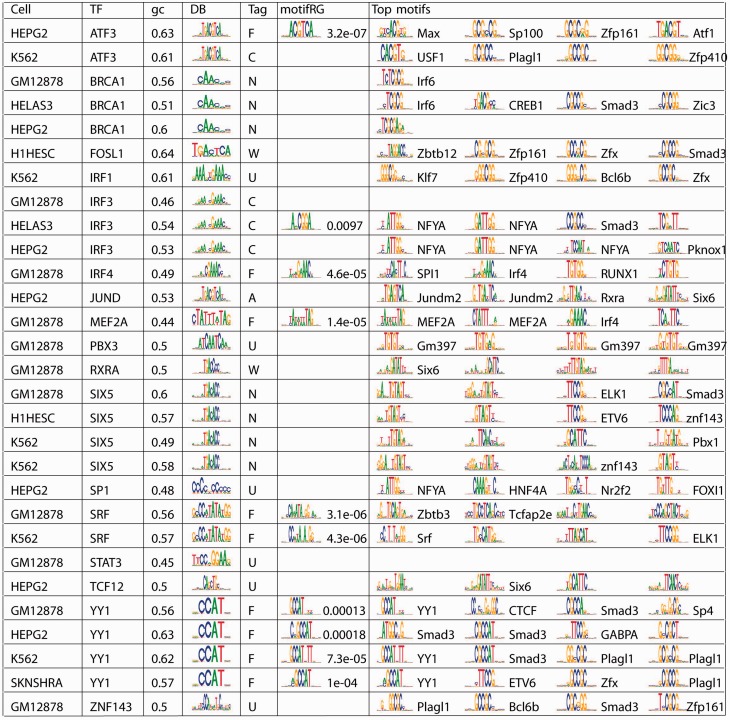
We designed the following strategy to cope with the above issues: we used discretized (for efficiency) GC content as covariant in the regression model, weighted the sequences based on ChIP-seq signals that were then normalized by peak width and chose background as accessible regions without ChIP-seq peaks. Recent study suggests that most TFBS occur in the accessible regions profiled by a DNaseI assay (Neph et al., 2012). By using accessible regions without peaks as background, we hope to eliminate common motifs for all accessible regions and highlight the ones that are specific for the ChIPped TF. Many other methods can be used to adjust for discussed biases, such as using only the top ranking peaks, using shuffled sequences as control and so forth. But our approach provides enough flexibility to addresses multiple issues while keeping the power of large datasets. We applied this strategy to 29 of 33 cases where we previously failed, selected based on availability of appropriate DNaseI data (Fig. 3). We predicted annotated motifs in 9 cases, where we previously failed. For 7 of 20 remaining cases, we identified the same novel motif for the same TF (Brca1 and Six5, respectively) across multiple cell types, whereas annotated motifs have low enrichment across all cell types, suggesting that predicted motifs are likely to be true motifs that are previously unknown. We also found motifs for NFYA, a known cofactor (Li-Weber et al., 1994) interacting with IRF homologs, to be strongly enriched in two IRF3 samples, suggesting IRF3 is likely to bind predominantly indirectly at its targets. The strongest predicted motif for JUND in HEPG2 corresponds to a known secondary motif for JUND. For RXRA in GM12878 and FOSL1 in H1hesc cell, it was puzzling why we failed in these cases, whereas succeeded in the RXRA and FOSL1 ChIP-Seq samples generated by the same laboratory using the same antibody for the other cell lines. After closer examination, we found evidence suggesting that the protein or the protein complex interacting with DNA may be present at low abundance in the given cell type (Supplementary Fig. S4), leading to poor ChIP-seq results. We have remaining 6 cases that are unaccounted for, which may be subject to other issues such as antibody specificity, PCR bias and so forth, and require further biological and technical examination. Overall, we found our refined strategy to be flexible and effective at addressing more challenging datasets.

Fig. 3.

MotifRG failure cases under default settings. Using a modified approach, we recover known motifs in many datasets. These datasets are categorized as F (found), N (novel), C (interacting cofactor), A (secondary motif), W (weakly expressed ChIPped TF) and U (unknown). Columns are cell type (Cell), TF, average GC content of the peak (gc), annotated motif (DB), categories (Tag), motifRG motifs that match the annotation and corresponding P-values (motifRG) and the top four predicted motifs (Top motifs)

Finally, we present the motifs predicted for proteins with no annotated motifs in the database in Supplementary Table S3. Although not annotated in the databases, numerous motifs have been reported in the literature to bind the given TF or its cofactors. For example, RAD21, a component of the cohesin complex, is involved in chromosome cohesion, DNA repair and apoptosis. We identified CTCF as its top motif, known for recruitment of cohesin genome wide (Parelho et al., 2008). Our method can be a powerful tool for curation of novel motifs into motif datasets.

3.2 Application to sequence specificity of homologous TFs

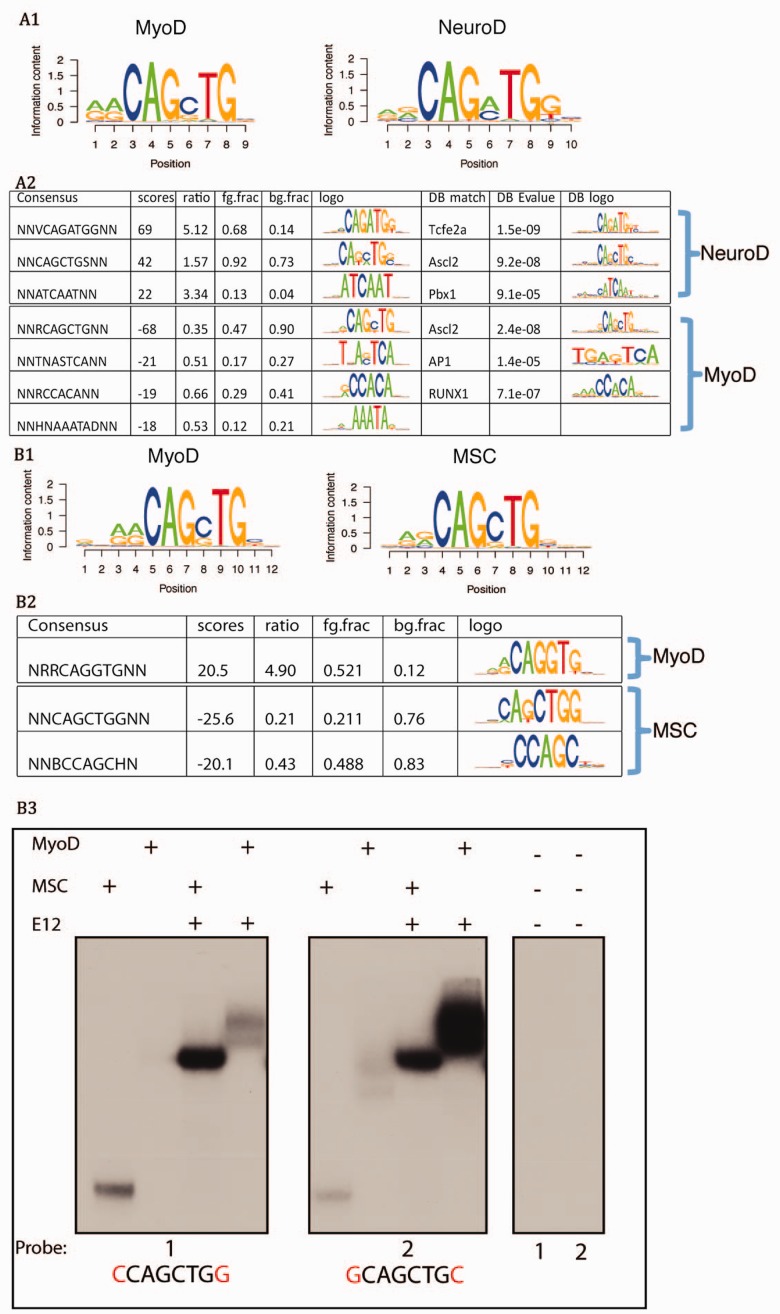
The greatest advantage of discriminative motif discovery tools over traditional methods is to facilitate direct comparison of two similar datasets. Here we demonstrate this in a case study to assess DNA binding specificity for two similar TFs. MYOD and NEUROD2 are both bHLH TFs that form heterodimers with an E-protein and regulate myogenesis and neurogenesis, respectively. Both bind a CANNTG E-box motif. A motif search in MYOD ChIP or NEUROD2 ChIP sequences against flanking background revealed RRCAGSTG as the MYOD motif and RRCAGMTGG as the NEUROD2 motif (Fig. 4, A1). Direct comparison of MYOD specific sites with NEUROD2 specific sites (Fig. 4, A2) identified CAGGTG as a MyoD private E-box and CAGATG as a NEUROD2 private E-box, whereas the sites bound by both factors were enriched in the CAGCTG E-box (Fong et al., 2012). The motif analysis results were confirmed by gel shift and competition assays (Fong et al., 2012).

Fig. 4.

Predicting the specificity of similar bHLH TFs. (A1) Predicted PWMs for MyoD (left) and NeuroD2 (right), (A2) Discriminative motifs based on direct comparison of MyoD sites (foreground) with NeuroD2 sites (background), suggesting MyoD and NeuroD2 preferred ebox and cofactor motifs. (B1 and B2) Comparison of MyoD and MSC. Similar to A1 and A2. (B3) Gel shift demonstrating that MSC/E12 heterodimer binds strongly at CCAGCTGG and MyoD/E12 binds weakly, whereas GCAGCTGC binds strongly to both MyoD/E12 and MSC/E12. MSC homodimer also binds stronger at CCAGCTGG than GCAGCTGC

We performed a similar comparison of MYOD and MSC in Rhabdomyosarcoma. MSC is a bHLH protein that also forms heterodimers with E-proteins and binds E-boxes and acts as an inhibitor of muscle differentiation. We compared the binding profiles of MYOD and MSC in the Rhabdomyosarcoma cell line RD. The PWMs of the top motifs for both factors were similar (Fig. 4, B1). Discriminative motif analysis by direct comparison of MYOD specific binding sites versus MSC specific binding sites indicated that MYOD has more CAGGTG binding sites (Fig. 4, B2), and MSC has more CAGCTGG sites. Electrophoretic mobility shift assays confirmed the predicted flanking preference of CAGCTG E-box of these factors (Fig. 4 B3).

3.3 Application to cell type specific accessible sites

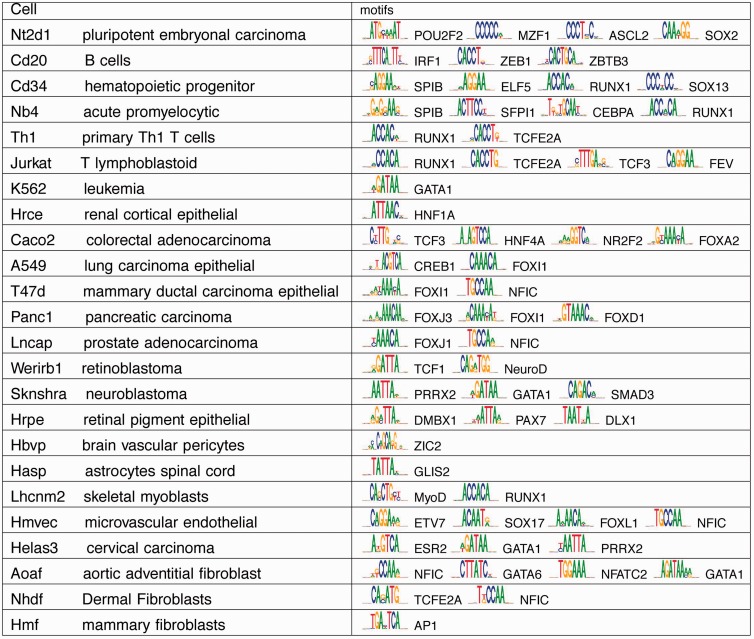
Discriminative motif analysis can be applied to any high-throughput sequence datasets besides ChIP-Seq data. We used this method to identify key TFs that are involved in regulation of cell type-specific chromatin remodeling using DNaseI hypersensitivity data. We collected 211 DNaseI hypersensitivity datasets from the ENCODE Web site. Combining highly similar ones yielded 77 profiles. We defined cell type-specific accessible sites as the sites that are shared by ≤5 profiles. To predict motifs in each set of cell type specific sites, we chose background as the random sampling of the cell type-specific sites in all cell types that do not overlap with the foreground. The predicted motifs for a set of well-studied cell types are shown in Figure 5 (full results in Supplementary Table S4). We found many key TFs that are known to regulate the given cell type. For example, we found motifs for Oct4 (annotated as Pou2f2), Sox2 and GC-rich motifs that mimic KLF4 (annotated as MZF1 and ASCL2) in Nt2d1, an embryonic cell line. All these factors are well known to be markers of cell pluripotency. We found motifs for IRF1 in B cells, a key factor for immune response. In various lymphocyte cells, we found motifs for E2A (annotated as TCFE2A), Runx and ETS family TFs (annotated as SPIB, ELF5, SFPI1), all of which are critical immune system regulators. For various differential epithelial cells in kidney, colon, lung, breast, pancrease and prostate, FOX family motifs are dominant and motifs for HNF family are enriched in kidney and colon. Similarly, we found significant enrichment of various Homeobox, NeuroD and Zic2 motifs in nervous system and MyoD motifs in skeletal muscle. A recent ENCODE study (Neph et al., 2012) used motifs in curated databases or de novo predicted motifs to scan accessible regions and compute enrichment in the given cell type. We offer a more direct alternative by combining motif prediction and discriminative analysis. The predicted motifs are consequently optimized to highlight the distinction between foreground and background, thus likely to be more informative in this setting.

Fig. 5.

Predicted motifs for cell type specific accessible sites. The full list is included as Supplementary Table S4

3.4 Motif significance and sample size

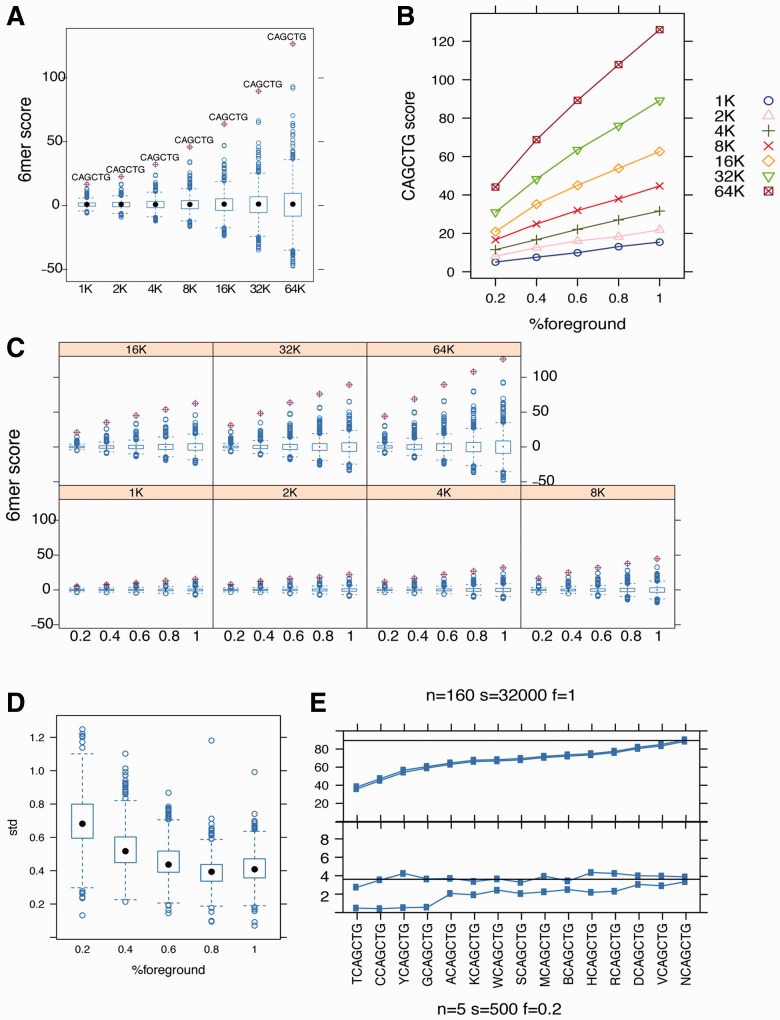
We have shown that our method can discover biologically relevant motifs in a wide range of biological samples and application settings. Here, we also give evidence that the z-value calculated by our software is a true indication of a motif’s statistical significance, and that the method is robust to variation in sample size and motif enrichment level. To quantify motif significance, we use the z-value statistic from the logistic regression model as the ‘motif score.’ To test its validity, we performed the following experiment on the MyoD ChIP-seq dataset: we randomly sampled 1–64K sequences from the combined foreground and background datasets and then randomly permuted the class labels within each sample. We repeated the permutation 5 times. The z-values for all enumerated 6mers in each permutation are approximately normally distributed, as shown by quantile–quantile plots (Supplementary Fig. S5A), indicating an accurate reflection of true statistical significance.

To determine how the z-scores of enriched motifs change with sample size, we plotted the distribution of z-values for all 6mers using samples from 1 to 64K, and highlight CAGCTG, which is identified as the most significant 6mer using all the data. CAGCTG is consistently the most significant motif for each sample size (Fig. 6A), and the motif score is linear with the square root of the sample size (Supplementary Fig. S5B), in accord with the central limit theorem. We also tested how the motif scores correlate with motif enrichment level. For each sampling with size from 1 to 64K, we randomly kept 20, 40 to 100% of the original foreground samples and replaced the remaining foreground sequences with background sequences while keeping the original class labels. CAGCTG remains the strongest 6mer, even at low foreground proportion and small sample size (Fig. 6B) and the motif score is roughly linear to the true foreground proportion (Fig. 6C). Therefore, this method can robustly detect a motif present in a small subset of foreground sequences.

Fig. 6.

Motif significance with respect to sample size and enrichment. (A) Score distribution of for all 6mers. CAGCTG ebox, marked by ‘+’, is the most significant 6mer for all sample sizes. X-axis: dataset sample size. Y-axis: motif scores. (B). Correlation between motif scores (Y-axis) against true foreground proportion (X-axis). Curves with different symbols correspond to different sample sizes. (C) Distribution of all 6mers with varying sample size and proportion of true foreground; CAGCTG is highlighted by ‘+’. X-axis: the proportion of true foreground in shuffled foreground, Y-axis: motif scores. Panels correspond to different sample sizes. (D) The standard deviation of motif scores for all CAGCTG −1 extensions based on bootstraps decreases with the proportion of true foreground. Y-axis: the standard deviation. X-axis: the proportion of true foreground. (E) When motif enrichment is low, motif scores are more variable. X-axis: all −1 extensions of CAGCTG. Y-axis: motif scores. The 95% confidence intervals are plotted based on bootstrapping mean and variance. Upper panel: 160 bootstrap iterations, total sample size 32 000 and 100% of true foreground; lower panel: using 5 bootstrap iterations, total sample size 500 and only 20% of true foreground

Next, we examined the effects of peak width on motif prediction. Besides the MyoD dataset, we also studied YY1 ChIP-Seq in H1-hESC, using YY1 as an example of degenerate motifs, which are likely to be more sensitive to the choice of peak widths. In each case, we started from the peak summits and extended the peak to width ranging between 25 and 1600 bases. For the case of YY1, we did not have peak summits information, so we assumed that peak summits were in the middle of the peaks. This seems to be a reasonable approximation because the peaks were called by MACS, which assumes a symmetric distribution of reads at both sides of the binding sites. The best matching motifs in each test are shown in Supplementary Supplementary Figure S5C. For MyoD, the best matching motif has maximum score at peak width of 200, which achieves the best discrimination between foreground and background. At peak width of 25, about half of peaks do not contain a consensus motif because peak summits do not always indicates presence of binding sites precisely. At peak width of 100, ∼90% of peaks contain a consensus motif. We also noticed that when peak width increases from 25, 50 to 100, the motif PWM becomes more informative, gaining specficity at the ebox flanking region. This is probably because wider peaks increase the motif occurences by chance. The method consequently fine tuned the motif model to increase discrimination against background. For the case of MyoD case, the method suceeded to find the motif in peaks as wide as 1600 bp. For the case of YY1, we predicted YY1 motif at peak width of 25 to 400, and the motif lost discriminative power at peak width 800 and 1600 due to increasing chance of random occurrence. The percent of peaks with the motif ranges from ∼10% at peak width of 25, and 58% at peak width of 400, whereas relative enrichment stabilizes between 2- and 3-fold. Assuming uniform nucleotide distribution of the genome, a 5mer motif occurs once approximately every 1Kb, which explains why we lost discriminative power at peak width of 800. In summary, informative motifs can be predicted in wide peaks, but keeping peaks with reasonable width is important for prediction of degenerate motifs.

Finally, we want to address the issue whether bootstrapping in our refinement step usefully combats over-fitting. We used the CAGCTG example shown earlier in text and tested all extension variants at position −1 using different numbers of bootstrap replicates, sample sizes and motif enrichment levels. We computed the standard deviation of scores for each variant based on bootstraps. The distribution of standard deviation does not change significantly with number of bootstraps performed or with the sample size (Supplementary Fig. S5D and E), but correlate strongly with the motif enrichment level (Fig. 6D). When enrichment level is low, the scores of better candidates (based on datasets with the biggest sample size and highest enrichment level) tend to be within confidence interval of worse candidates (Fig. 6E), in which case, based on t-test results, we terminate the refinement process early. Therefore, the bootstrapping technique guides motif refinement to be more aggressive when motif signal is strong, but conservative when motif signal is low, effectively avoiding over-fitting at reasonable cost.

4 DISCUSSION

The main challenge of traditional motif discovery is to increase signal to noise ratio due to lack of power from small input datasets. High-throughput datasets present different challenges: besides scalability concerns, they are likely to produce large numbers of statistically significant motifs due to the power of the large sample size, many of which are hard to interpret. To effectively use the motif prediction results to guide further study, it is important to understand the nature of these motifs and why they are enriched. It is well understood that genomes are far from random, which presents complicated higher order structure such as dinucleotide sequence preference, repetitive sequences, nucleosome positioning signals and so forth. Genomic sequences in promoters, which usually show enrichment of TFBS, also contain different characteristics from other parts of genome such as enrichment of CpG islands, common motifs for housekeeping TFs and so forth. These factors can all cause certain sequence patterns to be enriched in a given dataset. In addition, many ChIP-Seq and DNaseI hypersensitivity studies suggest that TFs tend to colocalize on a common set of accessible regions. It is unclear if these TFs collectively determine the accessibility of the given sites or some bind non-specifically at the accessible sites. Discriminative motif analysis is a powerful tool to address whether the predicted motifs are truly involved in the biological problem under study by use of a rigorous control group, a methodology frequently used in experimental design. The key to success for this method is proper choice of background, which might not be clear until we have a better understanding of factors that affects binding of TFs. By examination of a large set of ChIP-Seq profiles, we identified some common motifs for TFs in a certain category. For example, TFs that bind predominantly in promoter regions are likely to be associated with ETS, SP1 and other GC-rich motifs, and TFs with most of sites in distal regions tend to have enrichment of AP1 sites. To determine if the associated motifs are truly specific to the given TFs, we can iteratively test for potential biases as we find them, each time making the background as similar to the foreground as possible except for the defined difference under study. As accessible regions in the given cell type can be viewed as the union of all TFBS that are associated with active chromatin in that cell type, they present some generic features common to most TFBS and can serve as a good background for comparison with adjustment to other bias. Further, downstream analysis can be used to validate predicted motifs. For example, direct TFBS should contain a clear DNaseI digital footprinting signature (Neph et al., 2012) and be close to the centers of ChIP-Seq peaks (Bailey and Machanick, 2012).

We noticed that stronger peaks tend to be associated with stronger motifs, as measured by the PWM scores, particularly for TFs with long motifs, which is consistent with the theory that PWM scores roughly reflect the DNA/protein binding affinities in vitro (Stormo and Fields, 1998). In such cases, including weaker peaks usually results in more permissive motifs, lacking the full DNA specificity for the strong peaks. However, recent work suggests that weak sites can be functionally important, e.g. Prep1 regulates temporal expression of Pax6 via a pair of low affinity DNA binding sites during lens formation (Rowan et al., 2010). Our previous work also suggests that although strong peaks are more likely to be associated with gene regulation, the peak strength is not deterministic of function (Cao et al., 2010). Several rank-based motif prediction methods designed for protein binding microarrays used the binding affinities measured by probe intensities (Berger and Bulyk, 2009; Chen et al., 2007). Our method provides support for sequence weighting, with which the users have the flexibility to put more focus on a subset of sequences. These methods including our own, however, still build a single PWM motif to represent all binding sites, whereas some weaker sites are functionally more important than others with similar PWM scores. We think a mixture or higher order model may be more appropriate, a direction for our future investigations.

One key feature of our method and other discriminative motif discovery tools is the support for comparison of two similar profiles. By comparison of NeuroD and MyoD, two similar bHLH proteins, we have shown that although shared core eboxes are involved in activation of chromatin, specific eboxes are more directly involved in activation of differentiation programs in neurogenesis and myogenesis, respectively (Fong et al., 2012). Similar studies can be performed systematically to identify delicate specificity for members of other protein families that share almost identical motifs, such as the ETS and FOXO families. Such studies may shed more light of their functional roles and evolution of protein families in general. We have also demonstrated its application to DNaseI hypersensitivity data to identify key regulators involved in cell type-specific chromatin reprogramming. We can further zoom in to compare more similar samples, such as two different differentiated epithelial cells, or, before and after a certain treatment. By applying this approach systematically, we can gain deeper understanding about cell lineage restriction and differentiation program.