Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 Mar 18;4:4399. doi: 10.1038/srep04399

Theoretical modeling of relative humidity on contact electrification of sand particles

XiaoJing Zheng 1,2, Rui Zhang 2, HaoJie Huang 2,a
PMCID: PMC3957149  PMID: 24637964

Abstract

Contact electrification of identical insulating particles has crucial significance for industrial and environmental science, especially in wind-blown granular systems. At the same time, the experimental phenomena of charge transfer first increased and then decreased with the increase of relative humidity has attracted the interest of many researchers. Humidity can affect the charge transfer has been early observed in the experiment, but the reason always puzzles researchers. In this study, based on trapped high-energy electron transfer mechanism, we introduce the effect of the water film in the charge transfer model and consider the actual situations of the sand particles in the collision process. Furthermore, charge transfer between sand particles in a single collision under different humidity conditions is investigated. The predicted results agree well with the law obtained in existing experiments qualitatively and thereby a possible explanation why humidity can affect the charge transfer is given.

The electrification of sand is a natural phenomenon in wind-blown granular systems, e.g., dust devil, sand/dust storm and wind-blown saltation. The earliest observation on electrification of sand can be traced back to 1914 conducted by British physicist Rudge1 who performed a measurement experiment of the electric field in the sand dust storm. This contact electrification of identical materials phenomenon also exists in other granular systems, including fluidized beds2, powder handling3,4, volcanic eruptions5,6, wind-blown snow7. In wind-blown granular systems, both the measurements and the theoretical predictions of the polarity of charged sand particles indicate that smaller particles generally charge negatively, while larger particles charge positively8,9,10,11,12. Although existing theoretical models can explain the contact electrification of identical materials of part phenomenon observed in experiments to some extent, it's still not perfect. And we know little about the microscopic mechanism of how humidity can affect the charge transfer.

Humidity can affect the charge transfer has been observed in many experiments. The electric field changes with the relative humidity had been early observed by Lowell and Truscott13 and Pence et al.14. Guardiola et al.15 adopted a fluidized bed of glass beads experiment to investigate the influence of humidity on the degree of electrification and indicated that the variance of the charge with humidity existing five regions, and first increase then decrease to zero with the humidity. The wind tunnel experiment of Qu et al.16 indicated that moisture content could influent the electric field. In the experiment, the electric field intensity increases with moisture content in the region of 0.5% ~ 1.0%, but when it increases to 2%, electric field intensity decreases, which suggests that humidity can influent the charge transfer. Ducati et al.17 found that the change of environment humidity can make the insulator surface charge easily. The wind tunnel experiment of Xie and Han18 showed that aeolian electrical field intensity linearly increases when the relative humidity is less than critical relative humidity, but exponentially decreases when the relative humidity is higher than the critical value. And the critical relative humidity is affected by the wind speed. Giffin and Mehrani19 measured the net charge of three regions of the fluidized bed at two fluidization gas velocities and different relative humidities, and they directed that humidity can affect the charge in all regions and the variations of charge with humidity are not unique.

Although the above experimental results have proven that water plays a significant role in contact electrification process of identical insulators, how humidity can affect the charge transfer so far still has not obtained a good explanation within the theoretical simulation. The insulator contact electrification mechanism mainly has two viewpoints, one is based on the mechanism of ion transfer, and another is based on the mechanism of electrons or holes transfer.

The representative work for the ion transfer is completed by Latham et al.20. They regarded that there exists a temperature contrast, between the sand particles during the collision due to the difference of the sand surface area. This temperature contrast leads to the certain ions (H+ or OH−) transfer along the direction of the temperature gradient and then sand particles charge. Subsequently, other scholars17,21,22,23 carried out the further researches based on the ion transfer. However, it is difficult to measure the temperature contrast and the charge between two sand particles of different diameters during the collision. Therefore, it is hard to be proved from the experiment. And researches have shown that the identical insulator surface can be charged even in the condition of absence of water13. Thus, the ion transfer model cannot describe the contact electrification phenomenon in a dry environment.

Lowell and Truscott24 suggested the asymmetric contact electrification theory of identical insulators based on high energy trapped electrons. And many scholars25,26,27,28,29 expanded and optimized this theory to further explain the causes of contact electrification and processes of sand particles or other insulating particles in the last five years. Lacks and Levandosky26 proposed a simple charge model to explain the tendency of smaller particles charge negatively while larger particles charge positively based on the explanation of Lowell and Truskott24. Kok28 further simplified the trapped high-energy electrons transfer rule and assumed that electrons on the surface of particles can be in either a low-energy or high-energy state and electrons can be only released from high-energy states to low-energy states. Besides, he assumed that the amount of high-energy electrons transfer depend on particle diameters because of the existence of maximum distance that an electron can tunnel during a collision. Hu30 considered different contact areas using the elastic-plastic contact theory instead of the point contact in Kok's model28 and thought that holes release lead to the insulator charging. However, electrons or holes transfer mechanism also cannot explain how humidity can affect the charge transfer.

Generally speaking, the mechanism of ion transfer is based on the temperature contrast which is hard to be measured between two different diameter sand particles during the collision. And although the model of Hu30 is more close to the actual situation which considered the plastic deformation, when adding the water film, using this model will increase the difficulty and complexity, besides, the cracking of water film is not considered, which means the surface of particles do not contacted in the collision process. Therefore, in this paper, the electron transfer model of Kok28 is adopted to discuss the effect of the water film. The nanoscale pores of the sand surfaces31 and extrusion deformation of the water film are considered in our model.

We introduce the physical model which considers the thickness of the water film, see Fig. 1. Then we can get the radius of the sand particle i and j which covered the water film:

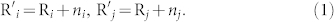graphic file with name srep04399-m1.jpg

Kok28 assumed that electrons on the surface of particles can be in either a low-energy or a high-energy state. The numbers of high and low energy electrons on particle i and j at time t are represented as niH(t), niL(t), njH(t), njL(t). The density of high-energy surface states are both represented as ρ32,33. Then the initial numbers of high-energy states can be obtained:

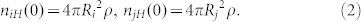graphic file with name srep04399-m2.jpg

Kok28 also assumed that electrons can only release from high-energy states to low-energy states and cannot release to its own. For particle i, the net charge after one collision at time t is

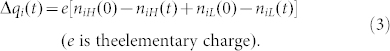graphic file with name srep04399-m3.jpg

And we can know that the numbers of high-energy state electrons of particle i release to low-energy states of particle j are accordant with the numbers of low-energy states of particle j obtain from high-energy states of particle i, i.e.,

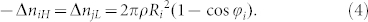graphic file with name srep04399-m4.jpg

In our model, we can get the following algebraic relations:

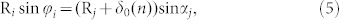graphic file with name srep04399-m5.jpg
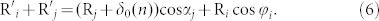graphic file with name srep04399-m6.jpg

From equation (5) and (6), we can derive the following relation:

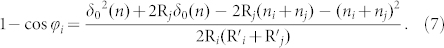graphic file with name srep04399-m7.jpg

Then we can rewrite equation (4):

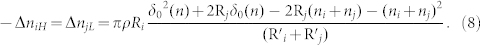graphic file with name srep04399-m8.jpg

As symmetry,

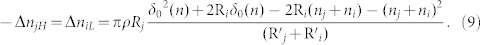graphic file with name srep04399-m9.jpg

Finally, the relationship of charge transfer can be described as:

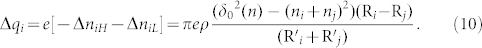graphic file with name srep04399-m10.jpg

Compared with the results of Kok28, our theoretical equation (10) cannot only reflect the tendency of smaller particles charge negatively while larger particles charge positively but can also take the effect of the thickness of water film into account. Because ni and nj are too small comparing with grain radius Ri and Rj, so their effects on the R'i and R'j can be neglected. We all know that the thickness of a water molecule is about 0.4 nm. And the maximum distance δ0(n) is also in the nanometer magnitude28. Then we will analyze the maximum distance δ0(n) quantitatively.

Figure 1. Schematic of the charge transfer occurring during a collision between two different diameter sand particles which are covered by the water film.

Figure 1

Open in a new tab

Ri and Rj are the radius of sand particle i and j, ni and nj are the water film thickness of sand particle i and j (ni = nj in the simulation), and δ0(n) is the maximum distance that an electron can tunnel between two sand particles.

The existing literature shows that, at the temperature of T = 23°C, the surface conductivity σ increases with the increase of the water film layers absorbed on the surface of quartz34 (the most components of sand particles), and satisfies the following relations:

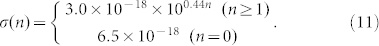graphic file with name srep04399-m11.jpg

Where n is the absorbed water film layer. The relationship between surface conductivity σ and energy barrier Eb described as follows35:

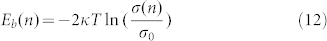graphic file with name srep04399-m12.jpg

Where k is the Boltzmann constant, T is thermodynamic temperature. We can see that the increase of the surface conductivity makes electrons through the energy barrier easier. The relation between energy barrier Eb and the maximum distance δ0(n) can be described as36

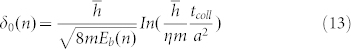graphic file with name srep04399-m13.jpg

Where 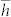Inline graphic is the reduced Planck constant, a is the radius of the well corresponding to the electron trap, tcoll is the time scale of the collision, m is the electron mass, and 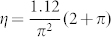Inline graphic. Thus we can obtain the relational expression between the maximum distance δ0(n) and the absorbed water film layers:

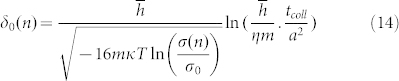graphic file with name srep04399-m14.jpg

In the equation (14), the maximum distance δ0(n) increased with the increase of the absorbed water film layers. Here, we notice that the item 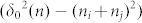Inline graphic in the equation (10) will become interesting and may get the results that we want.

Results

It is worth mentioning that we also consider the actual situations of the sand particles in the collision process. (i) The nanoscale pores exist in the sand particle surface31 and can absorb water molecules in the air. Based on this, when particle begin to absorb some layers of water molecules, water molecules do not immediately cover the sand particle surface to form the water film but exist in the nanoscale pores. It does not increase the collision distance but increase the conductivity until the water molecules fill the nanoscale pores. After that, the water film will be formed on the sand particle surface. And then this part (ni + nj)2 will be calculated by the equation (10). (ii) The thickness of the water film is not invariant during the collision. Because of the extrusion during the collisions, the thickness of water film will be compressed. Here, we define a compression ratio as

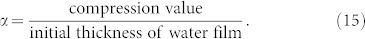graphic file with name srep04399-m15.jpg

Summer and Pitts37 gave the relationship between absorbed water film layers on the glass surface and the relative humidity. Their results showed that the absorbed water film layers increase with the increase of the relative humidity. It is very difficult to directly measure the thickness of the water film on a tiny sand particle surface. So in our simulation, we use the data of glass which the compositions close to the sand. In order to be more intuitive and easy to compare, we use the relative humidity to replace the absorbed water film layers in our results, and the corresponding relations shown in table 1.

Table 1. the relationship between relative humidity and absorbed water film layers.

Water film layers 0 1 2 3 4 5 6 7 8 9 10 11 12
Relative humidity(%) 0 4 8.5 20.9 31.5 37.3 43.7 48.5 53 56.9 60.1 64.1 68.1
Open in a new tab

First, we consider the existence of the nanoscale pores on the surface31 to investigate the effect of the thickness of water film on charge transfer. And we study whether the water film can be formed when the sand particle absorbs Nab = 1 ~ 5 layers of water molecules. Here, we adopt the energy barrier is 4.5 ev28 when there is no water, for the given physical model, only the item of 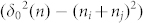Inline graphic changes in the equation (10), so we discuss the change of this item to reflect the influence of humidity on the charge transfer. And when the value of 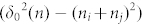Inline graphic is negative, it means an electron is no longer able to tunnel during the collision rather than transfer reversely.

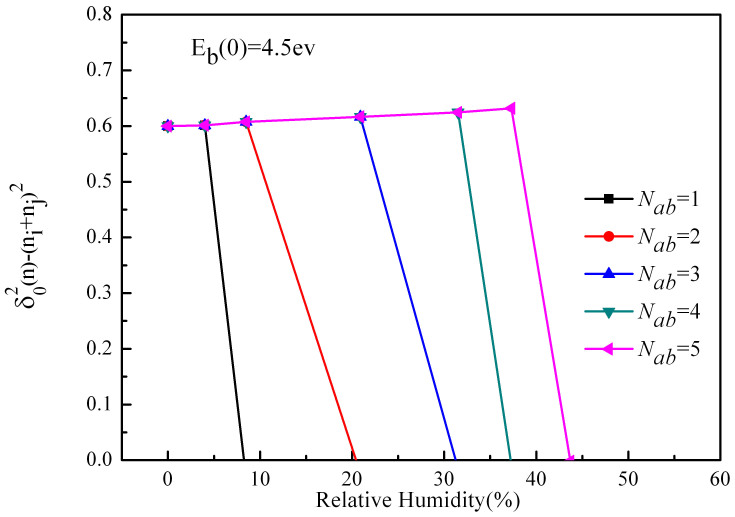
Fig. 2 shows the variation of this item with humidity at different absorbed water layers in a single collision. We can see that when the more absorbed water molecules needed to form the water film, the larger the critical humidity of charge transfers. As we can see, in Nab = 5 case, the critical humidity of charge transfer is about 43.7%, and the charge transfer first increases then decreases to zero, which is accordant with the experimental results of Guardiola et al.15. In spite that the measurement results of Guardiola et al.15 are macroscopical quantities and particles average, while our results just show the charge transfer between two sand particles, but our results also can reflect the rules from a certain extent. In addition, in the results of Guardiola et al.15, we can see the influence of the relative humidity on the charge is considerable, especially the increment at the peak is obvious (the minimum increment of the given data is 21%), but in this model, it is small.

Figure 2. The effect of humidity on charge transfer after absorbing Nab = 1 ~ 5 water layers.

Figure 2

Open in a new tab

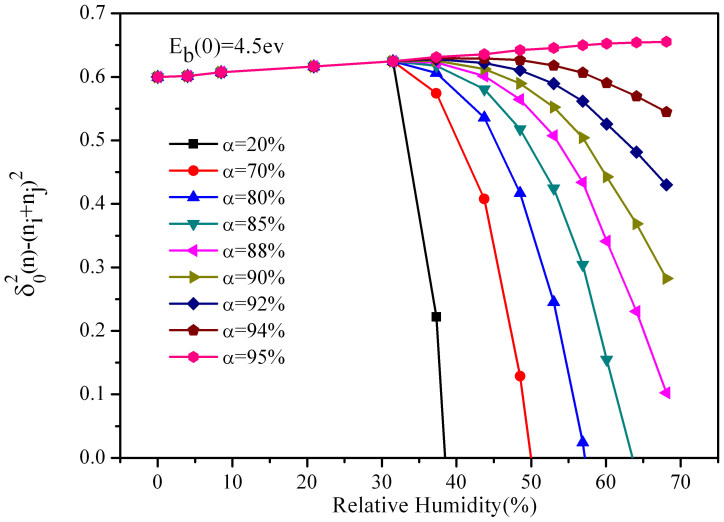
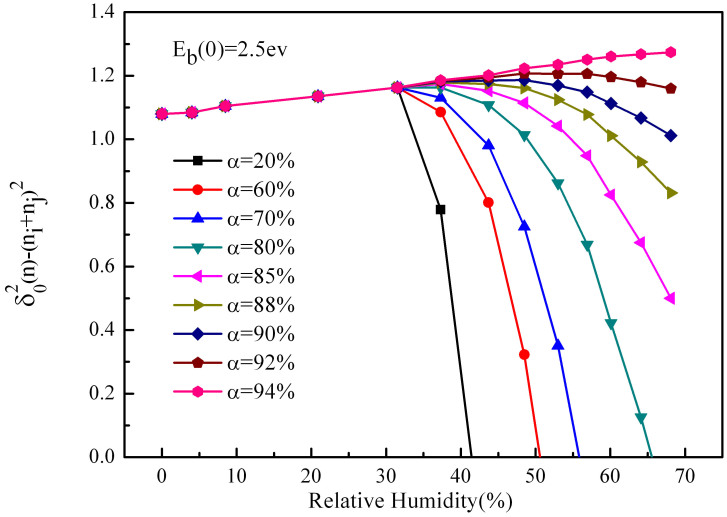
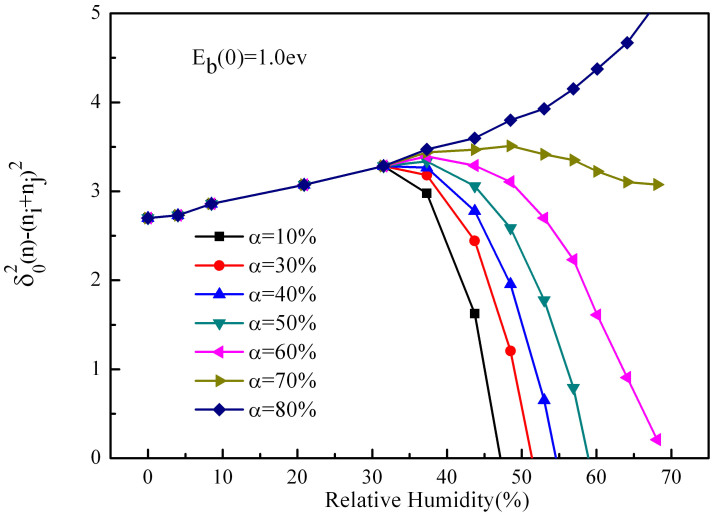
Hence, in order to keep accordant with the actual situation, we improve our model by considering the compression of the water film. Reference on the former step, we assume that the sand particle becomes to form the film when it absorbs 4 layers of water molecules. Fig. 3, Fig. 4 and Fig. 5 shows the variation of charge transfer with relative humidity in a single collision when the energy barrier are 4.5, 2.5, 1.0 ev respectively (The different components of the sand particles may result in the energy barrier variation). We can see that in the three cases, along with the increase of compression, the charge transfer experience three situations (a)first increase then decrease sharply, (b)first increase then decrease slowly, (c)only increase. From Fig. 3, when analyze the data at the compression of 88%, we find that the peak of the charge is at 35% humidity, and when the humidity is at 70%, the charge transfer tends towards zero, which agree with the results of Guardiola et al.15. Compare Fig. 3, Fig. 4 and Fig. 5, we can find that reducing the energy barrier can effectively increase the charge transfer, and make the peak increments increase significantly. From Fig. 5, when analysis the data at the compression of 60%, we find that the peak of the charge is at 40% humidity, and the peak increment is 26% (compare to the humidity is zero). Besides, we find that the increment is much more obvious after considering the compression, and the tendencies of most curves are accordant with Guardiola et al.15, only a fraction of curves consistently increase with relative humidity. While Giffin and Mehrani19 indicated that the variations of net charge with humidity obey different rules for different measurement locations in their fluidized bed experiment. One of his data attracts our attention, which showed that at a large fluidization gas velocity, the charge constantly increases with humidity, and it is accordant with part of our results. Our results are derived at large compression, and Giffin19 is derived at large fluidization gas velocity, so the coincidence can be explained as: when the velocity of the sand particle is large, the contact is more violent, and compression of the water film is much larger. The law of the experiment of Giffin19 is accordance with Guardiola et al.15 at small velocity, which is embodied in our simulation. At the same time, we note that the corresponding relative humidity at the peak of charge increases with the fluidized bed velocity of Guardiola et al.15, which is the same with our results.

Figure 3. Charge transfer varies with relative humidity at different compressions when the energy barrier is 4.5 ev.

Figure 3

Open in a new tab

Figure 4. Charge transfer varies with relative humidity at different compressions when the energy barrier is 2.5 ev.

Figure 4

Open in a new tab

Figure 5. Charge transfer varies with relative humidity at different compressions when the energy barrier is 1.0 ev.

Figure 5

Open in a new tab

Discussion

In summary, based on trapped high-energy electrons transfer theory, considering the actual situations of the sand particles in collision process, a possible theoretical model is proposed. We establish the relationship between relative humidity and charge transfer and simulate the effects qualitatively. The results show that our simulation results are accordant with the universal experimental results of the charge transfer first increased and then decreased with the increase in relative humidity. Our analyses also suggest that the surface conductivity increases with the relative humidity increasing. Thus, the trapped high-energy electrons can tunnel easier at first, then harder and decrease to zero after the relative humidity reaches a critical humidity. In particular, when the water film is not cracking, we can speculate that if the velocity of sand grain increases, the compression of the water film will become much severer accordingly. However, the water film may rupture at a critical velocity, and then the charge transfer decreases with this part of surface conductivity decreasing. It may be a reason why the effect of wind velocity is the same as humidity on the aeolian electric fields.

In actual industrial production, the contact electrification of identical insulating particles is a common problem. Through above researches, we can control not only the humidity but also the dimension, surface condition and velocity to strengthen or weaken the charge transfer.

Methods

We establish a charge transfer physical model when the sand particle surface is covered with the water films. Then we consider the actual situations of the sand particles in the collision process and parameterize the assumptions. Finally, we carry out a numerical simulation of different hypothetical cases and compare with the existing experimental results.

Author Contributions

H.H. introduced the model and in writing the manuscript. R.Z. prepared figures 1–5. X.Z. participated in the analysis and in writing the manuscript. All authors reviewed the manuscript.

Acknowledgments

This research was supported by a grant from the National Natural Science Foundation of China (No. 11072097, No. 11232006, No. 11202088, No. 10972164, No. 11121202), National Key Technology R&D Program (2013BAC07B01), the Science Foundation of Ministry of Education of China (No. 308022), Fundamental Research Funds for the Central Universities (lzujbky-2009-k01) and the Project of the Ministry of Science and Technology of China (No. 2009CB421304). The authors express their sincere appreciation to the supports.

References

  1. Rudge W. D. On the electrification produced during the raising of a cloud of dust. Proc. R. Soc. Lond. A 90, 256–272 (1914). [Google Scholar]
  2. Forward K. M., Lacks D. J. & Sankaran R. M. Charge Segregation Depends on Particle Size in Triboelectrically Charged Granular Materials. Phys. Rev. Lett. 102, 028001 (2009). [DOI] [PubMed] [Google Scholar]
  3. Inculet I. I., Peter Castle G. S. & Aartsen G. Generation of bipolar electric fields during industrial handling of powders. Chem. Eng. Sci 61, 2249–2253 (2006). [Google Scholar]
  4. Mehrotra A., Muzzio F. J. & Shinbrot T. Spontaneous Separation of Charged Grains. Phys. Rev. Lett. 99, 058001 (2007). [DOI] [PubMed] [Google Scholar]
  5. Miura T., Koyaguchi T. & Tanaka Y. Measurements of electric charge distribution in volcanic plumes at Sakurajima Volcano, Japan. B. Volcanol 64, 75–93 (2002). [Google Scholar]
  6. James M. R. et al. Electrical Charging of Volcanic Plumes. Space Sci. Rev. 137, 399–418 (2008). [Google Scholar]
  7. Schmidt D. S., Schmidt R. A. & Dent J. D. Electrostatic Force in Blowing Snow. Bound-Lay Meteorol 93, 29–45 (1999). [Google Scholar]
  8. Freier G. D. The electric field of a large dust devil. J. Geophys. Res. 65, 3504–3504 (1960). [Google Scholar]
  9. Zheng X. J., Huang N. & Zhou Y. H. Laboratory measurement of electrification of wind-blown sands and simulation of its effect on sand saltation movement. J. Geophys. Res. 108, 4322 (2003). [Google Scholar]
  10. Shinbrot T. & Herrmann H. J. Granular matter: Static in motion. Nature 451, 773–774 (2008). [DOI] [PubMed] [Google Scholar]
  11. Forward K. M., Lacks D. J. & Sankaran R. M. Particle-size dependent bipolar charging of Martian regolith simulant. Geophys. Res. Lett. 36, L13201 (2009). [Google Scholar]
  12. Sow M., Crase E., Rajot J. L., Sankaran R. M. & Lacks D. J. Electrification of particles in duststorms: Field measurements during the monsoon period in Niger. Atmos. Res 102, 343–350 (2011). [Google Scholar]
  13. Lowell J. & Truscott W. S. Triboelectrification of identical insulators. I. An experimental investigation. J. Phys. D. Appl. Phys 19, 1273 (1986). [Google Scholar]
  14. Pence S., Novotny V. J. & Diaz A. F. Effect of Surface Moisture on Contact Charge of Polymers Containing Ions. Langmuir 10, 592–596 (1994). [Google Scholar]
  15. Guardiola J., Rojo V. & Ramos G. Influence of particle size, fluidization velocity and relative humidity on fluidized bed electrostatics. J. Electrostat 37, 1–20 (1996). [Google Scholar]
  16. Jianjun Q. et al. Wind tunnel simulation experiment and investigation on the electrification of sandstorms. Sci. China Ser. D-Earth Sci. 47, 529–539 (2004). [Google Scholar]
  17. Ducati T. R. D., Simões L. s. H. & Galembeck F. Charge Partitioning at Gas−Solid Interfaces: Humidity Causes Electricity Buildup on Metals. Langmuir 26, 13763–13766 (2010). [DOI] [PubMed] [Google Scholar]
  18. Xie L. & Han K. Influence of relative humidity on the aeolian electric field. Aeolian. Res 7, 45–50 (2012). [Google Scholar]
  19. Giffin A. & Mehrani P. Effect of gas relative humidity on reactor wall fouling generated due to bed electrification in gas-solid fluidized beds. Powder. Technol 235, 368–375 (2013). [Google Scholar]
  20. Latham J. The electrification of snowstorms and sandstorms. Q. J. Roy. Meteor. Soc 90, 91–95 (1964). [Google Scholar]
  21. Hogue M. D. et al. Insulator–insulator contact charging and its relationship to atmospheric pressure. J. Electrostat 61, 259–268 (2004). [Google Scholar]
  22. Hogue M. D., Mucciolo E. R., Calle C. I. & Buhler C. R. Two-phase equilibrium model of insulator–insulator contact charging with electrostatic potential. J. Electrostat 63, 179–188 (2005). [Google Scholar]
  23. Gu Z., Wei W., Su J. & Yu C. W. The role of water content in triboelectric charging of wind-blown sand. Sci. Rep. 3, (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Lowell J. & Truscott W. S. Triboelectrification of identical insulators. II. Theory and further experiments. J. Phys. D. Appl. Phys 19, 1281 (1986). [Google Scholar]
  25. Farrell W. M., Delory G. T., Cummer S. A. & Marshall J. R. A simple electrodynamic model of a dust devil. Geophys. Res. Lett. 30, 2050 (2003). [Google Scholar]
  26. Lacks D. J. & Levandovsky A. Effect of particle size distribution on the polarity of triboelectric charging in granular insulator systems. J. Electrostat 65, 107–112 (2007). [Google Scholar]
  27. Kok J. F. & Renno N. O. Electrostatics in Wind-Blown Sand. Phys. Rev. Lett. 100, 014501 (2008). [DOI] [PubMed] [Google Scholar]
  28. Kok J. F. & Lacks D. J. Electrification of granular systems of identical insulators. Phys. Rev. E 79, 051304 (2009). [DOI] [PubMed] [Google Scholar]
  29. Pahtz T., Herrmann H. J. & Shinbrot T. Why do particle clouds generate electric charges? Nat. Phys 6, 364–368 (2010). [Google Scholar]
  30. Hu W., Xie L. & Zheng X. Contact charging of silica glass particles in a single collision. Appl. Phys. Lett 101, 114107–114105 (2012). [Google Scholar]
  31. Alcañiz-Monge J., Linares-Solano A. & Rand B. Mechanism of Adsorption of Water in Carbon Micropores As Revealed by a Study of Activated Carbon Fibers. J. Phys. Chem. Lett. B 106, 3209–3216 (2002). [Google Scholar]
  32. Duff N. & Lacks D. J. Particle dynamics simulations of triboelectric charging in granular insulator systems. J. Electrostat 66, 51–57 (2008). [Google Scholar]
  33. Lacks D. J., Duff N. & Kumar S. K. Nonequilibrium Accumulation of Surface Species and Triboelectric Charging in Single Component Particulate Systems. Phys. Rev. Lett. 100, 188305 (2008). [DOI] [PubMed] [Google Scholar]
  34. Awakuni Y. & Calderwood J. H. Water vapour adsorption and surface conductivity in solids. J. Phys. D. Appl. Phys 5, 1038 (1972). [Google Scholar]
  35. Guan D., Zhang T. & Jiao J. Physical properties of inorganic materials.Tsinghua University Press, Beijing, 240–241 (1992).
  36. Lowell J. Tunnelling between metals and insulators and its role in contact electrification. J. Phys. D. Appl. Phys 12, 1541 (1979). [Google Scholar]
  37. Sumner A. L., Irvine C. & Finlayson-Pitts B. Steps towards understanding heterogeneous chemistry in the troposphere water uptake on environmental relevant surfaces. 5th Conference on Atmospheric Chemistry. Paper No. 1.4 (2003). [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES