A New Approach for Resolution of Complex Tissue Impedance Spectra in Hearts

Abstract

This study was designed to test the feasibility of using sinusoidal approximation in combination with a new instrumentation approach to resolve complex impedance (uCI) spectra from heart preparations. To assess that feasibility, we applied stimuli in the 10–4000 Hz range and recorded potential differences (uPDs) in a four-electrode configuration that allowed identification of probe constants (Kp) during calibration that were in turn used to measure total tissue resistivity ρ_t from rabbit ventricular epicardium. Simultaneous acquisition of a signal proportional to the supplied current (Vstim) with uPD allowed identification of the V –I ratio needed for ρ_t measurement, as well as the phase shift from Vstim to uPD needed for uCI spectra resolution. Performance with components integrated to reduce noise in cardiac electrophysiologic experiments, in particular, and provide accurate electrometer-based measurements, in general, was first characterized in tests using passive loads. Load tests showed accurate uCI recovery with mean uPD SNRs between 10¹ and 10³ measured with supplied currents as low as 10 nA. Comparable performance characteristics were identified during calibration of nine arrays built with 250 µm Ag/AgCl electrodes, with uCIs that matched analytic predictions and no apparent effect of frequency (F = 0.12, P = 0.99). The potential ability of parasitic capacitance in the presence of the electrode–electrolyte interface associated with the small sensors to influence the uCI spectra was therefore limited by the instrumentation. Resolution of uCI spectra in rabbit ventricle allowed measurement of ρ_t = 134 ± 53 Ω·cm. The rapid identification available with this strategy provides an opportunity for new interpretations of the uCI spectra to improve quantification of disease-, region-, tissue-, and species-dependent intercellular uncoupling in hearts.

I. Introduction

In a traditional four-electrode configuration, information regarding total tissue resistivity ρ_t can be obtained from heart preparations more readily than with two- or three-electrode configurations because the delivery of supplied current and the sensing of the resulting voltages are performed with separate pairs of electrodes. In theory, this improvement results from the elimination of the need to account for any contribution of the electrode–electrolyte interface for the individual sensors. Electrodes are arranged in a line such that two outer stimulating electrodes are considered point sources (or sinks) and two inner noncurrent-carrying voltage electrodes provide information on the potential field established by the stimulating pair. Because ρ_t measurement assumes, incorrectly, that tissue located between the stimulating electrodes is a uniform and isotropic monodomain, an analytic framework to derive that resistivity given the separation between electrodes, the amplitude of the central potential difference, and the amplitude of the total supplied current is available [1]. A common practical step in ρ_t measurements is to identify the ratio between the voltage and current during calibration in conducting solution with known resistivity ρ_c in advance of heart experiments to derive a “probe constant” [2]. Ratios obtained during subsequent electrophysiological study are then scaled by the probe constant to provide ρ_t. Such measurements have been used in experiments involving myocardial ischemia, where an initial rise in ρ_t is related to increased resistance in the interstitial compartment that accompanies loss of perfusion and a later rise in ρ_t that is related to gap junction uncoupling [3]–[7].

While experiments involving ischemia development typically use dc stimulation or ac stimulation at a single frequency, some investigations in which the tissue’s electrical properties are presumed to be more stable have used more than one frequency [1], [8]–[11]. With stimulation at multiple frequencies, changes in the voltage to current ratio can develop such that the relationship must be considered as a complex composite impedance (uCI). The uCI amplitude and phase depend upon membrane capacitance and resistance as well as on the electrical properties of the interstitial and intracellular compartments. Resolution of uCI spectra may therefore prove valuable, as interpretation of uCIs at different frequencies that incorporate more comprehensive structural frameworks than an isotropic monodomain may improve the quantification of intercellular coupling. As one example of this possibility, we note that Cooklin et al. [12] compared spectra identified in two-electrode experiments with superfused guinea pig trabeculae to spectra derived from different circuit representations to quantify elevated gap junction resistance with hypertrophy development.

Practical limitations pose the main obstacles to more widespread resolution of uCI spectra in cardiac electrophysiology experiments. The detection of any phase shift between the current and voltage using lock-in amplifiers [3], [7], [9], [10], phase-to-voltage converters [11], or sample-and-hold thresholding [1] requires access to or development of analog-based phase detection schemes that must be integrated into the overall hardware. As described by Tsai et al. [2], noise limitations can preclude accurate phase identification with such schemes, which in turn complicates rapid resolution of uCI spectra. Noise is typically more pronounced with the small electrodes desirable for cardiac electrophysiologic studies, which is one possible reason that quantitative measurements using sensors smaller than 250 µm with heart preparations have not previously been reported. The presence of an electrode–electrolyte interface at each sensor is important in this regard, as electrode impedance generally increases as available sensor surface area decreases. Amplifier inputs for the voltage sensing may not function as open circuits when small electrodes are used because each electrode-amplifier interconnection has the potential to establish a capacitive shunt to system ground that depends upon the electrode impedance [13]. This can lead to probe constants during calibration that vary over the frequency range of interest, complicating segmentation of the instrumentation’s influence on the uCI spectra from the tissue’s influence on the uCI spectra. Furthermore, use of small electrodes necessitates use of low amplitude supplied currents to limit possible alteration of electrode impedance over the time course of an experiment. This suggests advantages to lowering the 10–50 µA currents that have provided robust SNRs in previous investigations to preserve stability of small electroplated sensors.

This paper documents a new approach to resolve uCI spectra with small electrodes.We use digital acquisition to archive uPD simultaneously with a sinusoidal voltage signal (Vstim) that is directly related to the supplied current. Acquisition is rapid. Samples from each signal are then systematically compared to samples from a unit sinusoid at each prescribed stimulation frequency to approximate uPD and Vstim, allowing straightforward expression of uCI spectra without the need for analog phase detection. Signal generation for supplied current, voltage recording at the four sensors, amplification for uPD, and signal combination for Vstim are performed with dedicated stages whose interconnections were designed to limit the impact of parasitic capacitance in the presence of an electrode–electrolyte interface at each sensor. Following initial tests in which expected uCIs were measured with passive loads, favorable uPD SNRs were identified at supplied currents over the 10 nA to 1 mA range, and the ability to resolve phase shift was demonstrated, we analyzed performance in a ρ_t experiment. Arrays were assembled with 250 µm sensors that were comparable in size to sensors used by van Oosterom et al. [1] and smaller than those used by other investigations in which ρ_t was quantified in hearts [1], [3]–[11], [14], [15]. Probe constants had no frequency dependence in the 10–4000 Hz range analyzed by van Oosterom et al. [1] using supplied currents of ≈1 µA, and ρ_t identified from rabbit ventricular epicardium was comparable to ρ_t measured in a wide range of reports. These initial findings suggest routine implementation as a part of cardiac electrophysiologic study is practical and support a transition to use of even smaller electrodes. We believe this will allow development of more complete frameworks for interpretation of uCI spectra.

II. Signal Processing

A. Data Acquisition

All signals were archived to an IOTech DaqBoard/2005 (Measurement Computing, Norton, MA, USA) data acquisition card residing in a PC running Linux (RedHat, Durham, NC, USA). We used two channels. The signal on each channel was digitized to 12 bits at a 100 000 samples per second (sps) rate and stored in 1 s epochs.

B. Sinusoidal Approximation

Sets of samples for unit sine and cosine waves at a specified frequency (f) were first generated for direct comparison with acquired samples (sig(i)) in a given epoch. The phase shift ψ for sig(i) on each channel was identified from

$$\psi ={\tan }^{-1}\frac{-{\sum }_{i=1}^N\text{sig}(i)*\text{sin}\left(\frac{2\pi f}{sps}i\right)}{{\sum }_{i=1}^N\text{sig}(i)*\text{cos}\left(\frac{2\pi f}{sps}i\right)}$$ (1)

$$A=\sqrt{\frac{2}{N}({(\sum _{i=1}^N\text{sig}(i)*\text{sin}(\frac{2\pi f}{sps}i\left)\right)}^2+{(\sum _{i=1}^N\text{sig}(i)*\text{cos}(\frac{2\pi f}{sps}i\left)\right)}^2)}$$ (2)

the amplitude A for the approximation to sig(i) on each channel was identified from (2), as shown at the bottom of the page, and a SNR between each sig(i) and its approximation was quantified from

$$\mathrm{S}\mathrm{N}\mathrm{R}=A/\sqrt{\frac{1}{N}\sum _{i=1}^N{(\text{sig}(i)-A*\text{cos}(\psi +\frac{2\pi f}{sps}i\left)\right)}^2}.$$ (3)

Such representation ensured each epoch was parameterized as A∠ψ, with SNR quantifying the extent to which sinusoidal approximation was effective. Here, care was taken to sum the signals over an integral number of cycles, which was straightforward to achieve through the selection of stimulation frequencies and the high sampling rate. This insured orthogonality of sine and cosine functions when integrated over time. Transfer from channel 1 to channel 2 at any given frequency was expressed as A₂/A₁∠(ψ₁ − ψ₂).

C. Control Recordings

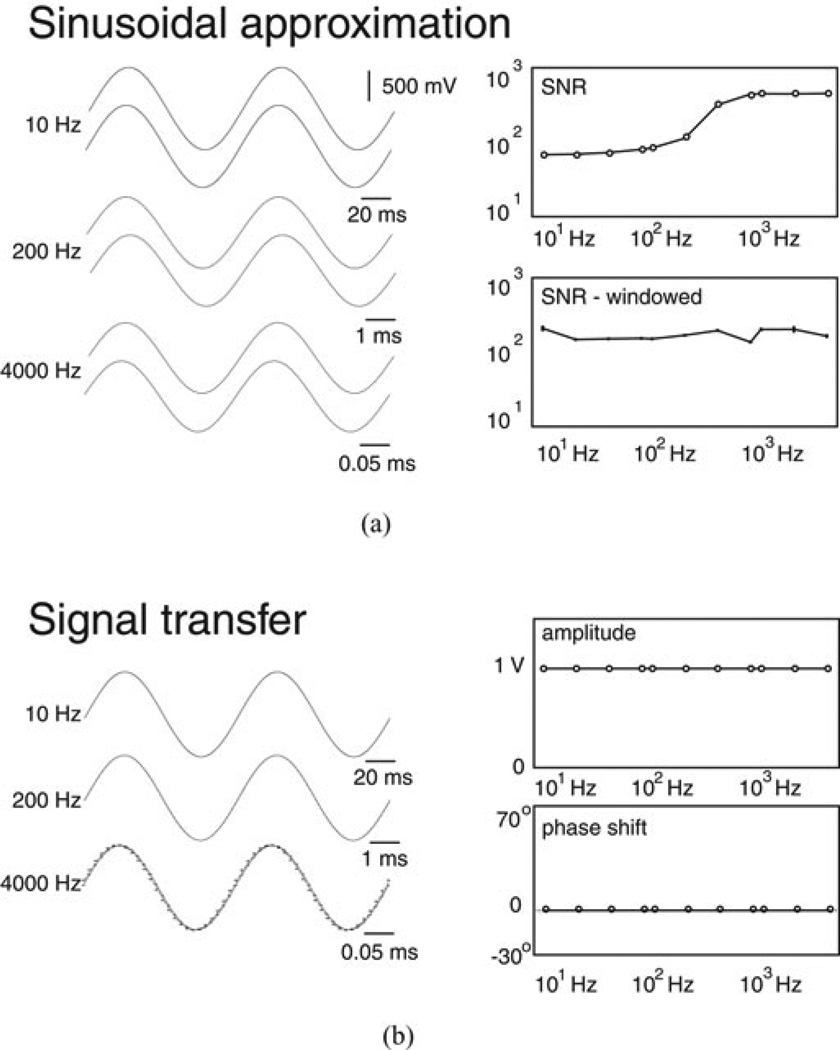
To demonstrate signal processing, we acquired an ≈1 V peak-to-peak signal on both channels during frequency adjustment from 10–20, 40, 80, 100, 200, 400, 800, 1000, 2000, and 4000 Hz. Signals acquired at these 11 frequencies were grouped to form “acquisition intervals.” Fig. 1(a) (left side) shows the original signals acquired on channel 1 above a set of samples generated by sinusoidal approximation with the 10 (top), 200 (middle), and 4000 Hz (bottom) records. The time scale for the display of each record was adjusted to limit each display to two total cycles. Fig. 1(a) (right side, top) shows the SNRs calculated using (3) for all signals acquired during the acquisition interval. SNRs near 10² supported effective approximation, which was preserved when 100 ms windowed segments from the original signals were analyzed. Fig. 1(a) (right side, bottom) shows mean ± SD from ten separate SNRs calculated from windowed segments of the original signals. Amplitudes and phase shifts during windowing (not shown) were comparable to those from the full epoch. Fig. 1(b) (left side) shows the signals acquired on channels 1 and 2 at 10 (top), 200 (middle), and 4000 Hz (bottom). At 10 and 200 Hz, we measured A₂/A₁ = 1.0 and ψ₁ − ψ₂ ≤ 0.3°. At 4000 Hz, however, we measured ψ₁ − ψ₂ = 7.2°. We note that phase shift matched the (4000 Hz/100 000 sps)180° = 7.2° shift predicted by a one-sample delay associated with switching between channels 1 and 2. All uCI phase shifts measured in our subsequent analyses were therefore corrected to account for this acquisition-based one sample shift. Fig. 1(b) (right side) shows A₂/A₁ =1.0 above the corrected ψ₁ − ψ₂ for all frequencies.

Figure 1.

(a) Control records obtained on one channel showing the original and approximated signal at different frequencies (left side) alongside the frequency-dependent SNR (right side) available with approximation. (b) Records obtained on two channels (left side) alongside frequency spectra (right side) for the transfer from channel 1 to channel 2 during control recording.

III. Instrumentation Development

A. Frequency Control

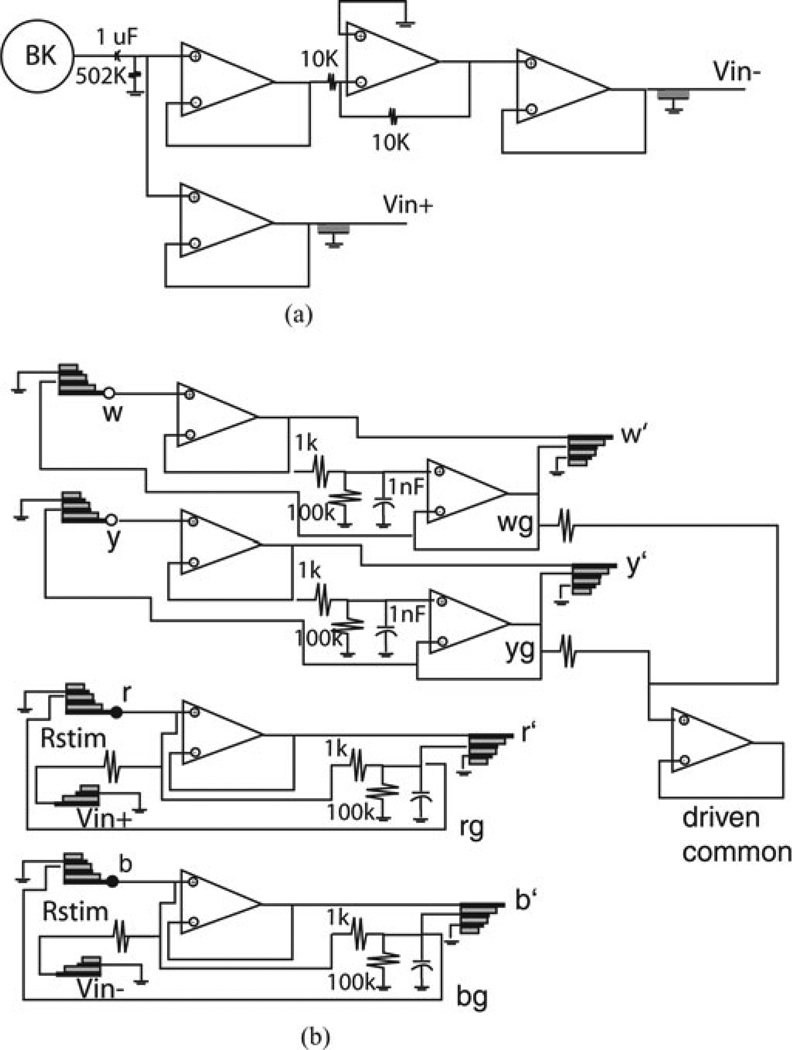
To ensure stimulation at precise frequencies, we used a handheld function generator (B&K Precision, Yorba Linda, CA, USA) accurate to 0.1 Hz as the input to a signal generation stage that supplied sinusoidal voltages for stimulation. Signals generated by this stage included high (Vin⁺) and low (Vin⁺) side sinusoids centered on 0 V that were 180° out of phase. Fig. 2(a) shows a schematic diagram of the stage, which eliminated dc offset in the signal provided by the BK unit before buffering to generate Vin⁺. Quad TLC2274 (Texas Instruments, Dallas, TX, USA) operational amplifier packages with input resistance of 10¹² Ω, input capacitance of 10 pF, and closed loop output impedance of 130 Ω were used for this and other stages. Vin⁻ was generated using the buffer-inverter-buffer combination shown in the upper part of Fig. 2(a). Coaxial connections between the signal generation stage and other amplifier stages were used to limit the development of parasitic capacitance associated with interstage connections. Similarly, lines between the signal generation and other stages were kept under 6 inches.

Figure 2.

Schematic diagrams of the (a) signal generation and (b) head stages.

B. Head Stage

To limit the development of parasitic capacitance associated with the interconnections between the electrodes and amplifiers for voltage sensing, we designed a head stage that established high- and low-side voltages for the stimulating pair of electrodes and buffered the voltages needed for uPD and Vstim identification. Fig. 2(b) shows a schematic diagram of this stage. Stages were physically assembled using printed circuit boards with 1.75 × 1.75 in² footprints that facilitated close placement during measurements. By convention, we labeled the high-side stimulus location r, the high-side voltage sensing location w, the low-side voltage sensing location y, and the low-side stimulating location b. The Vin⁺ signal was routed into a resistor (Rstim) whose selection allowed coarse adjustment of supplied current. The voltage at r was buffered to establish an output rb used to assemble Vstim and was also routed into a filter stage that established a guard signal rg. As described by Metting van Rijn et al. [16], selection of filter components to establish a signal with amplitude ≈99% of the amplitude for r and r′ allowed rg to be routed on an outer conductor in a coaxial arrangement and limit line capacitance through active shielding. Full triaxial shielding was employed on the r interconnection to sensor tips and on the r′ interconnection to the amplifiers that generated Vstim, with system ground routed on a conductor that surrounded the coaxial line to limit interference with rg. Triaxial lines were made by hand using fine coaxial wire (World Precision Instruments, Sarasota, FL, USA) encased in Teflon tubing that was in turn wrapped in 3/32″ inner diameter sections of braid shielding (Digikey, Thief River Falls, MN, USA). The same approach was used for low-side shielding of b and b′. On the voltage sensing lines, the y and w signals were buffered before filtering to establish wg and yg. The wg and yg signals were also averaged to generate a driven common signal [17]. One advantage to our use of a driven common is that it obviated the need to locate a reference in solution when measurements were made with electrodes. This limited one potential source for capacitive shunting to system ground under experimental conditions. Triaxial lines from r,w, y, and b on the head stage connected to electrodes.

C. uPD and Vstim

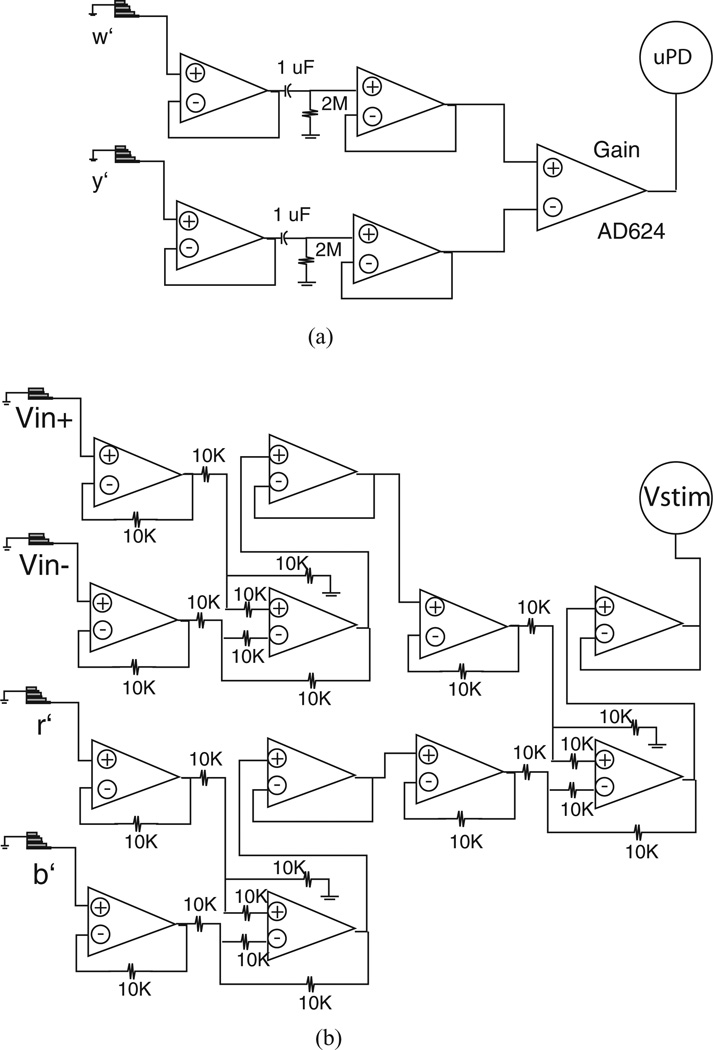
Voltages r′,w′, y′, and b′ sensed on the head stage were routed to uPD and Vstim stages that generated the signals archived for uCI identification. The stage shown schematically in Fig. 3(a) generated uPD = w′ −y′, using an AD624 low-noise instrumentation amplifier (Analog Devices, Norwood, MA, USA) as a difference amplifier. This model was selected because it allowed preset gains of 1, 100, 200, and 500 that were straightforward to modify as supplied currents were adjusted by changing Rstim on the head stage. Measurement of supplied current (Istim) was achieved through combination of unity gain difference amplifiers that generated

$$\text{Vstim}=\mathrm{V}\mathrm{i}{\mathrm{n}}^{+}-\mathrm{V}\mathrm{i}{\mathrm{n}}^{-}-r\prime +b\prime$$ (4)

as shown schematically in Fig. 3(b). While we expected contributions from r′ and b′ to Vstim would be small in most tests, inclusion was necessary here for tests with Rstim close to load resistors. Furthermore, we recognized that under conditions where an imbalance between the electrode–electrolyte impedances at the stimulus locations developed experimentally, including contributions from r′ and b′ would be advantageous to resolve any influence on Istim. Archival of uPD and Vstim was sufficient to identify uCI as (Rstim·A_uPD/AV_stim)∠(ψ_Vstim − ψ_uPD)).

Figure 3.

Schematic diagrams of the (a) uPD and (b) Vstim recording stages.

D. Test Loads

To establish performance characteristics, we first identified uCIs with different resistive loads in 44 separate acquisition intervals. Our rationale for completing these tests was to identify any deviations from expected responses in the absence of any electrode–electrolyte interface. Matched resistors (Ra) were placed in series on a breadboard measuring 2 × 3 in². One Ra was positioned between the r and w connections. Two separate resistors were placed between w and y. One Ra was positioned between y and b. To limit the contributions of the interconnections between these loads and the head stage to overall parasitic capacitance, 3-inch semirigid triaxial lines attached to the (r,w, y, b) points on the head stage were mated with 2-inch flexible triaxial lines attached to sensor locations on the bread-boards. Each breadboard was completely covered in aluminum foil coupled to system ground.

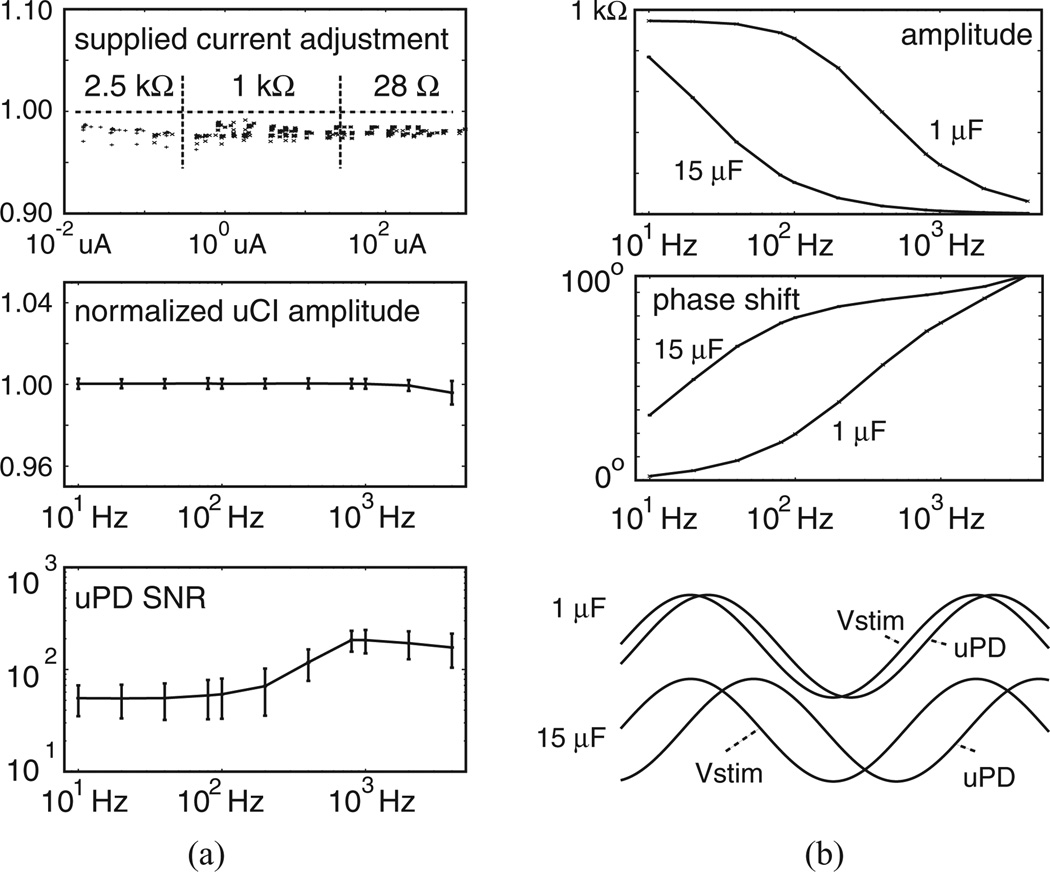
Fig. 4(a) summarizes performance characteristics with test loads including Ra = 28 Ω (20 acquisition intervals), Ra = 1 kΩ (20 acquisition intervals), and Ra = 2.5 kΩ (four acquisition intervals). Here, the lower bound Ra was selected because we expected measurement of uCIs lower than this size in our tests with the assembled electrode arrays would be unlikely because of the electrode separation. Similarly, the upper bound of 2.5 kΩ was selected as one much larger than any we anticipated. For these tests, we used different Rstim to provide coarse adjustment of supplied current and altered BK signal amplitude to provide fine adjustment of supplied current in different acquisition intervals. Because these test loads included no capacitors, we expected measured uCIs would be equivalent to the total resistance between the w and y circuit nodes and therefore normalized responses as |uCI|/2Ra. This allowed identification of the extent to which Istim influenced uCI identification over a 10 nA to 1 mA range. Fig. 4(a) (top) shows the normalized responses, which included minimal difference over the wide range of Istims tested. Fig. 4(a) (middle) shows mean ± SD for normalized uCI amplitudes from all 44 acquisition intervals with the three test loads. As expected, normalized amplitudes remained near 1.0. Fig. 4(a) (bottom) shows mean±SD for uPD SNRs.Variability resulted, primarily, from use of uPD recording gains that ranged from 1 to 500 in different acquisition intervals. However, mean uPD SNRs were comparable to those identified in our control recordings suggesting effective instrumentation development.

Figure 4.

Performance characteristics using (a) different resistive loads and (b) capacitance introduced to establish uCI phase shift.

To demonstrate the ability of our approach to detect phase shifts from Vstim to uPD, we then placed 1 or 15 µF capacitors in parallel with the Ra = 1 kΩ resistors positioned between w and y. Fig. 4(b) (top) shows the expected reduction in uCI amplitude with increasing frequency that resulted from the introduction of known capacitance to the load. That impact wasmore pronounced with 15 µF than with 1 µF at the lower frequencies. Fig. 4(b) (middle) shows the accompanying phase shifts, while Fig. 4(c) (bottom) includes normalized Vstim and uPD records.

IV. Calibration for Probe Constant Determination

A. Electrode Array Assembly

After establishing effective performance with test loads, we next sought to compare the characteristics to those identified in tests in which an electrode–electrolyte interface was present. We therefore assembled electrode arrays and used those arrays to resolve uCI spectra and recover probe constants during stimulation and recording with a calibrated solution. Arrays were built using 250 µm silver wires separated by 2 mm. To limit possible development of parasitic capacitance within arrays themselves, individual wires on which (r,w, y, b) were sensed were encased in teflon tubing and wrapped in a single layer of aluminum foil tape that carried the (rg, wg, yg, bg) signals. At the proximal end of each array, exposed silver wires were pulled through small transparency paper strips on which 250 µm circles were generated to serve as templates for holes spaced 2 mm apart. Wires were fixed in place with polyurethane. At the distal end, exposed silver wires were soldered into small (1.2 × 1.5 cm²) printed circuit boards (PCBs) in which (r,w, y, b) connections were standard through holes spaced 2.5 mm apart. Connections for (rg, wg, yg, bg) were made through similar holes located 3 mm proximal to the (r,w, y, b) connections using fine wire looped around each sensor and soldered into the PCB. These solder holes routed to a distal pair through which male hookup pins were soldered for mating with the semirigid triaxial lines emanating from the head stage. Successive coats of polyurethane were then used to fix the sensors to the PCB and provide top side insulation. Solder joints on the bottom side were carefully sanded and insulated using polyamide tape. Full assemblies were then wrapped in aluminum foil tape that was connected to system ground. To limit the likelihood that this layer contacted conducting solution, successive coats of liquid rubber were brushed onto the sensors and the arrays were inspected under a dissecting microscope until no ground layer could be seen through the rubber at the proximal end. Silver wires were then cut flush to the transparency paper strip, the strip was trimmed to approximately 0.5 cm² × 1 cm² and each wire was lightly sanded to ensure the electrode tip was parallel with the transparency paper. All electrodes were chloridized before use to establish aAg/AgCl interface and lower electrode–electrolyte impedance from that with bare wire.

B. Stimulation and Recording Protocol

We used a 0.15% sodium chloride solution as described by van Oosterom et al. [1]. For tests, a syringe filled with that solution was attached to an opening in the bottom of a cylindrical chamber of ≈1 in diameter and ≈1 in depth onto which a chloridized silver wire was looped around the inner wall near the chamber bottom. The driven common signal generated by the head stage was routed to this wire via a coaxial line. During tests, the head stage was positioned next to the chamber and individual arrays were mated to the semirigid triaxial lines such that the sensor tips were located centrally within the chamber near the chamber’s top. Separation between the sensors and the head stage amplifiers was ≈4 in. The syringe was then used to fill the chamber, slowly, as uPD and Vstim signals were monitored on an oscilloscope. When the calibration solution just touched the electrode surface, a marked change in uPD was observed. Stimulation was initiated after uPDs settled using nine different arrays. Tests were performed at room temperature. We measured ρ_c ≈ 345 Ω·cm before and after tests with a handheld conductivity meter.

C. Performance Characteristics

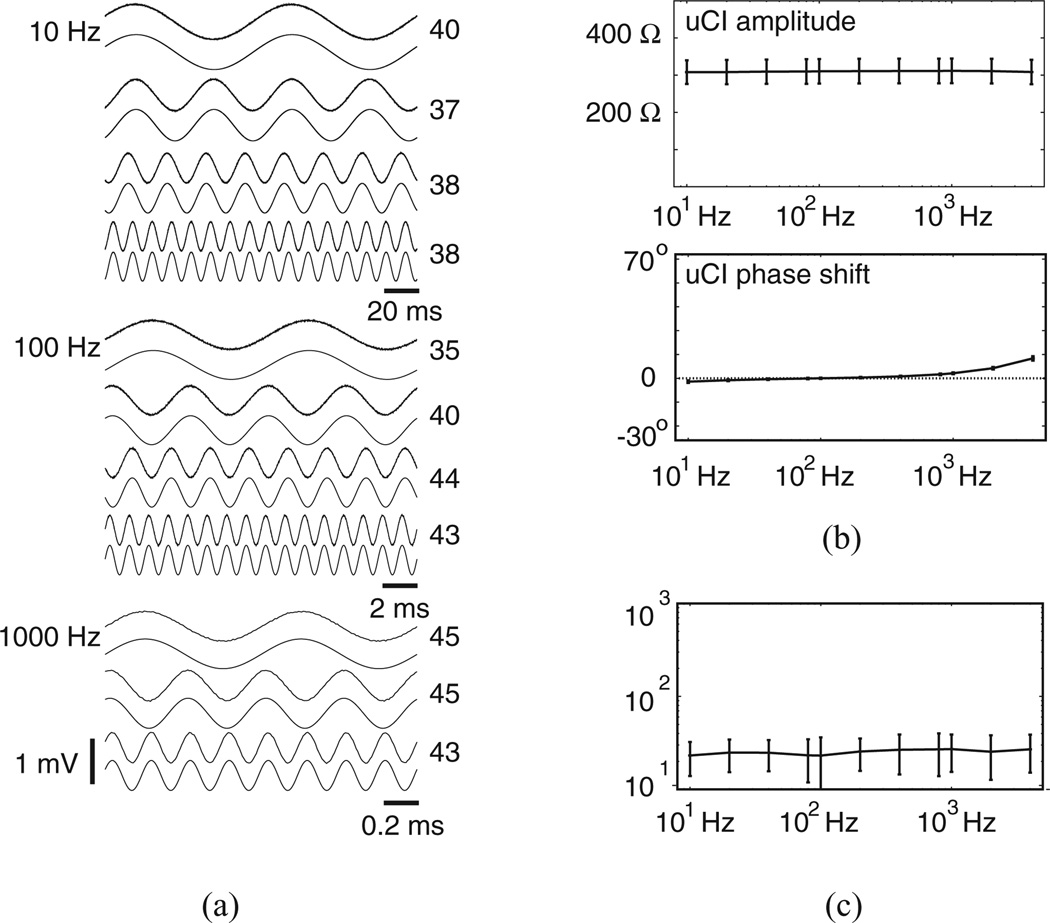
The favorable characteristics identified with test loads were largely preserved during calibration. Fig. 5(a) shows uPDs recorded from all frequencies drawn just above the sinusoidal approximations used for uCI identification at frequencies between 10 and 80 Hz (top), 100 and 800 Hz (middle), and 1000 and 4000 Hz (bottom) during one acquisition interval. All records were obtained with Istim at 1.6–1.9 µA such that peak-to-peak uPD amplitudes were between 0.5 and 1.0 mV. Individual records from this acquisition interval showed effective sinusoidal approximation, as uPD SNRs presented on the right edge of each trace ranged from a low of 35 to a high of 45. Fig. 5(b) (top) shows mean ± SD for uCI amplitudes from all acquisition intervals. Those means only varied between 308 and 311 Ω, with the flat frequency response suggesting minimal influence of parasitic capacitance. SDs varied from 32 to 33 Ω with that variability being primarily related to uCIs identified with different arrays as opposed to uCIs identified across different frequencies. In fact, one-way ANOVA test of the uCI spectra using frequency and array as separate groups showed no statistically significant impact of frequency on uCI (F = 0.11, p = 0.99). This observation was consistent with the mean ± SD for the phase shift as shown in Fig. 5(b) (bottom). From Fig. 5(c), mean ± SD for uPD SNRs were slightly lower than those measured with test loads.

Figure 5.

Performance characteristics in tests with calibration solution. (a) Recorded uPDs atop approximations from one acquisition interval. Number to the right of each pair of traces is uPD SNR. (b) uCI frequency spectra and (c) uPD SNRs.

D. Analytic Framework

The predicted uCI for a four-electrode configuration with sensors denoted (r,w, y, b) for an array placed on the surface of a large isotropic volume conductor is given by,

$$\mathrm{u}\mathrm{C}\mathrm{I}=\frac{{\rho }_c}{2\pi }(\frac{1}{|r-w|}+\frac{1}{|b-y|}-\frac{1}{|b-w|}-\frac{1}{|r-y|}).$$ (5)

Equation (5) is adapted from van Oosterom et al. [1], who considered calibration of intramural needle electrode arrays placed within a large isotropic volume conductor. Here, |r − w| is the separation between electrodes r and w, |b − y| is the separation between electrodes b and y, |b − w| is the separation between electrodes b and w, and |r − y| is the separation between electrodes r and y. Predicted uCI for our calibration tests measured 275 Ω assuming center-to-center separations (2 mm, 4 mm) between electrodes and 335 Ω assuming edge-to-edge separations (1.75 mm, 3.75 mm) between electrodes. Mean uCIs measured in our tests were therefore very close to analytic predictions.

E. Probe Constants

Mean ± SD for probe constants (Kp = ρ_c/uCI) using uCIs at all frequencies from the acquisition intervals for each array are summarized in Table I. Mean values ranged from 0.99 to 1.39 cm. Variability related to use of uCIs from all frequencies was limited, as SDs were 0.01 cm or lower.

TABLE I.

Probe Constants

array	Kp (cm)
1	1.08±0.00
2	1.16±0.00
3	1.27±0.01
4	1.07±0.01
5	0.99±0.00
6	1.08±0.01
7	0.99±0.01
8	1.39±0.01
9	1.09±0.01

Cardiac tissue is anisotropic, so the probe constant measured for an isotropic medium might be different when measuring in anisotropic media.

V. Total Tissue Resistivities

A. Rabbit Ventricular Epicardium

We used seven of the arrays for stimulation and recording of rabbit ventricular epicardium. One New Zealand white rabbit (3–5 kg) was anesthetized with intramuscular ketamine (44 mg/kg) and xylazine (20 mg/kg), followed by intravenous heparin (2.0 ml) during isoflurane inhalation (0.3%). The heart was rapidly excised after a medial sternotomy and retrogradely perfused through the aorta with 3–4 L of recirculating, oxygenated (95% O₂–5% CO₂) normal solution containing (in g/L) 7.36 NaCl, 3.96 glucose, 0.2 MgCl₂, 2.5 taurine 0.65 creatine, 0.55 sodium pyruvate, 0.14 NaH2PO₄, 3 NaHCO₃, and 0.12 CaCl₂. Temperature was maintained at 36 ± 1 °C and pH was fixed at 7.3 to 7.4. Shortly after perfusion was established, a 1 × 1 in² rubber strip with a rectangular window was carefully glued to the epicardium near the region of the left anterior descending (LAD) artery such that the long axis of the window was oriented parallel to and just below the LAD to insure all four sensors were positioned on muscle. For each sequence of measurements, an array was attached to semirigid lines emanating from the head stage and positioned near the epicardial window. A micromanipulator then advanced the array and held the tip against muscle in the window. Two successive acquisition intervals were archived before a switch to a different array.

B. Performance Characteristics

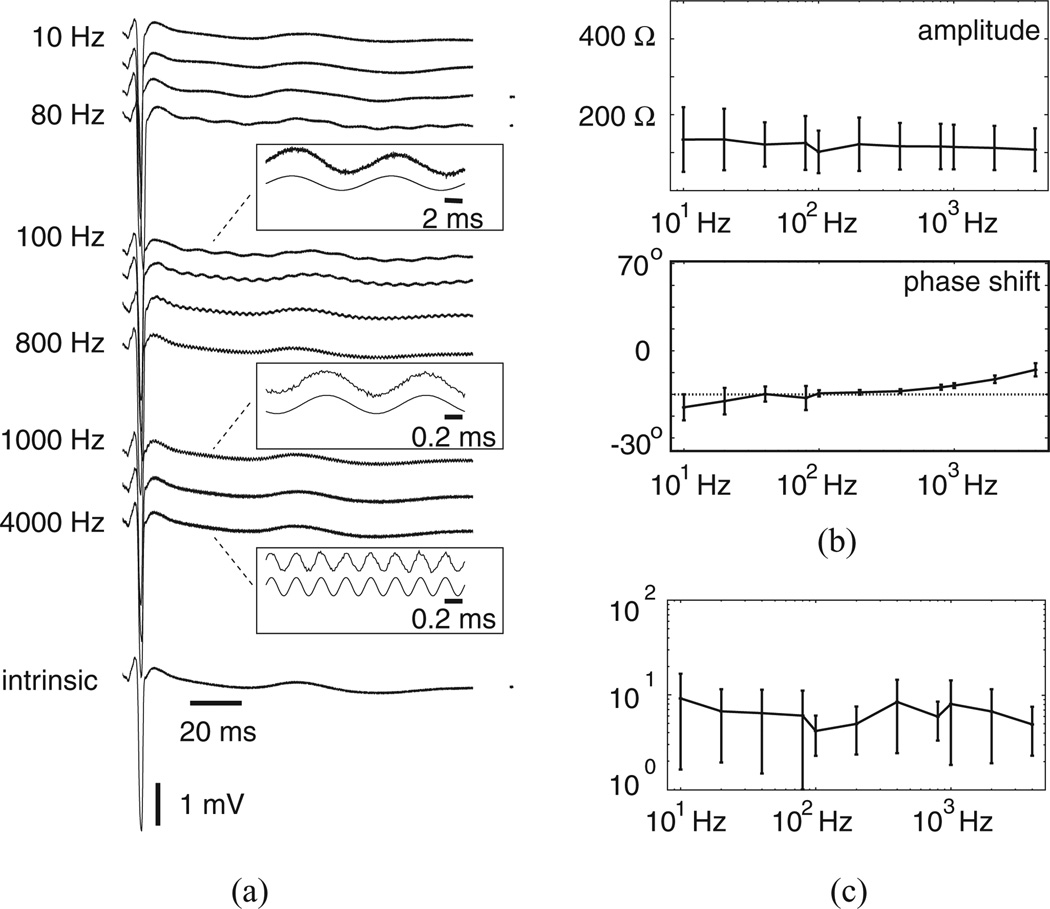
Characteristics were comparable to those identified with test loads and calibrated solution. Fig. 6(a) shows uPDs recorded at all frequencies during an acquisition interval with Istim at 1.4 to 1.7 µA. The waveform drawn just below the recorded uPDs is the intrinsic recording archived during an interval with no stimulation. All uPD recordings were aligned to the QRS complex of the intrinsic waveform to highlight the marked difference between signal associated with rhythmic activation of tissue in the measurement region and the signal resulting from frequency-dependent stimulation. Examples with limited cycles acquired during 100, 1000, and 4000 Hz stimulation are shown as insets near the recorded uPDs, with acquired samples drawn directly above those identified with sinusoidal approximation. Approximation appeared to be effective. Fig. 6(b) shows mean ± SD for uCI spectra determined from all acquisition intervals. For these analyses, we used 100 ms segments windowed from signal regions 5–10 ms after the development of the QRS complex to limit contributions from intrinsic activity during sinusoidal approximation. Mean amplitudes fell from 135 Ω at 10 Hz to 108 Ω at 4000 Hz with SDs that varied more widely than during calibration. However, one-way ANOVA showed no statistically significant evidence of an effect of frequency (F = 0.33, p = 0.97). Phase shifts also showed more variability than during calibration, with mean shift measuring 12.6° at 4000 Hz. From Fig. 6(c), mean uPD SNRs were lower than SNRs identified with test loads and during calibration. Although windowing limited contributions of the differences between the sinusoidal approximations and the recorded uPDs in the identified SNRs, supplied currents of ≈1 µA generated peak-to-peak uPDs that consistently fell below 200 µV. Accurate resolution of these small signals was achieved, in large part, because of the instrumentation steps designed to limit the impact of parasitic capacitance on recorded uPDs.

Figure 6.

Performance characteristics from rabbit experiment. (a) uPDs from one acquisition interval with examples cycles at 100, 1000, and 4000 Hz includes as insets in which recorded uPDs were drawn atop approximations. (b) uCI frequency spectra and (c) uPD SNRs.

C. Total Tissue Resistivities

Table II summarizes total tissue resistivities ρ_t derived from the probe constants and mean ± SD for uCIs at all frequencies and acquisition intervals with each array used in the rabbit experiments. Mean ρ_t ranged from 65 to 193 Ω·cm, so there was wider variability across the different arrays tested than in the meanK_p values identified during calibration. Similarly, uCI variability with frequency in different acquisition intervals was more pronounced, as SDs range from 9 to 35 Ω·cm. Pooling all ρ_t resulted in 134 ± 53 Ω·cm.

TABLE II.

Total Tissue Resistivities

array	ρt (Ω-cm)
1	177±29
2	67±12
3	152±29
5	65±9
7	160±24
8	122±35
9	193±20
pooled	134±53

VI. Discussion

The goal of this study was to document performance characteristics of a new approach for uCI spectra resolution suitable for use with smaller electrodes than those generally employed for ρ_t measurements in heart preparations. The main challenges for using smaller electrodes involve: 1) limiting the impact of noise on the voltages sensed in a four-electrode configuration, which complicates accurate identification of uCI amplitude and phase, 2) limiting possible influences of parasitic capacitance in the presence of an electrode–electrolyte interface, which complicates segmentation of the instrumentation’s influence on the uCI spectra from the tissue’s influence on the uCI spectra, and 3) the need to lower supplied current and limit alteration of the electrode–electrolyte interface during stimulation and recording, which complicates accurate uCI identification by reducing signal in the presence of noise. After identifying performance characteristics in load tests that confirmed the approach was stable with supplied currents as low as 10 nA, we showed those characteristics were largely preserved with electrode arrays placed in calibrated solution and on rabbit epicardium. Implementation here allowed ρ_t identification in a way that could be used routinely to monitor intercellular coupling strength.

A. Importance of Calibration

To appreciate the integration of the approximation strategy with the instrumentation design as a way to achieve routine implementation, we note that four-electrode measurements require careful calibration because errors can develop in a number of ways. This issue was systematically addressed by Tsai et al. [2], [8] in their in vivo resistivity measurements in pig. Those investigators used arrays built from 27G stainless steel hypodermic needles embedded in epoxy. Using our nomenclature, they attached the r electrode to a computer-controlled function generator that served as a current source, the w and y electrodes to the inputs of a differential amplifier, and the b electrode to a I–V converter. Two channels of a digital oscilloscope recorded the amplifier and converter outputs. With this arrangement, errors measured in different steps were used as corrections for the identified ρ_t. For example, an oscilloscope constant that accounted for any disparities between the two channels was initially identified using reference resistors between electrode connections. Saline resistivities for a number of different calibration solutions were measured independently with a separate system to identify temperature effects as a separate source for error. Probe constants were measured at different frequencies with each of the calibration solutions to account for subtle differences in electrode positions and electrode impedances with individual arrays. Since each potential error source necessarily influenced derivation of ρ_t from uCIs measured at different ventricular sites, step-by-step corrections were employed. One reason corrections were needed was that parasitic capacitance was initially estimated at ≈250 pF, despite the use of lead lines that were shorter than 6 in. Although we made no attempt to estimate parasitic capacitance in the absence or presence of the active shielding incorporated into out instrumentation design, such shielding is known to reduce line capacitance markedly. We view that shielding in combination with the overall component layout as the main reason we found flat uCI amplitudes and minimal phase shifts in the frequency responses from calibration solution with nine different arrays.

B. Small Electrodes

The use of small electrodes complicates the issues identified by Tsai et al. [8] further because of the accompanying increase in electrode impedance. This is likely one reason that investigations in heart with smaller electrodes than 250 µm have focused attention on relative changes in uCI to provide a qualitative index for intercellular coupling as opposed to ρ_t measurements. For example, Owens et al. [6] used 7 µmelectrodes with stimulating electrodes separated by a 3 mm span in their studies of ischemia development in blood-perfused rabbit hearts. Relative changes from preischemic uCI amplitudes allowed identification of the onset of gap junction uncoupling. Comparison of that onset with changes in a number of other parameters therefore provided insight into the intricacies associated with the transition to the phase Ib ischemia interval when arrhythmia development becomes pronounced. Similarly, Hund et al. [18] used 38 µm sensors (10 mm span) to document relative uCI amplitude changes and identify the onset of gap junction uncoupling in wild-type and protein kinase C epsilon knockout mouse hearts subjected to ischemic preconditioning. Their approach led to demonstration that protein kinase C epsilon participates in preservation of C × 43 signaling.

C. Measured ρ_t Comparison

We view our quantitative identification of ρ_t at 135±53Ω·cm as valuable, in its own right, because that ρ_t was comparable to values reported in a range of heart studies in which electrodes of 250 µm diameter or larger were employed. Our ρ_t is slightly lower than values identified in experiments with dog, pig, and sheep ventricle. In dog, Steendijk et al. [9] (400 µm electrodes, 3 mm span) reported 212 ± 32 and 313 ± 49 Ω·cm for ρ_t identified along and across epicardial fibers over the 5 Hz to 60 kHz range, Cinca et al. [3] (400 µm electrodes, 7.5 mm span) reported 237 ± 41 Ω·cm for preischemic epicardial ρ_t at 7 kHz and van Oosterom et al. [1] (250 µm electrodes, 3 mm span) reported intramural ρ_t at 410 Ω·cm over the 10 Hz to 5 kHz range. In pig, Smith et al. [4] (250 µm electrodes, 10 mm span) reported preischemic epicardial ρ_t of 187 ± 120 Ω·cm, deGroot et al. [5], (700 µm electrodes, 6 mm span) reported preischemic epicardial ρ_t of 332 ± 13 Ω·cm, Salazar et al. [10] (400 µm electrodes, 7.5 mm span) reported epicardial and intramural ρ_t at 1 kHz of 254 ± 52 and 279 ± 81 Ω·cm, respectively, and Tsai et al. [8] (410 µm electrodes, 4.5 mm span) reported subepicardial ρ_t at 1 Hz and 1 MHz of 319 ± 60 and 166 ± 15 Ω·cm, respectively. In sheep, Fallert et al. [11] (325 µm electrodes, 9 mm span) reported epicardial ρ_t at 1 and 5 kHz of 165 ± 28 and 200 ± 37 Ω·cm, respectively. Our ρ_t were also slightly lower than values identified in rabbit ventricle. Baynham and Knisley [14] (1 mm electrodes, 10 mm span) reported ρ_t that ranged from 184 ± 100 to 191 ± 98 Ω·cm along and across epicardial fibers, respectively, and Dumas et al. [15] (280 µ electrodes, 12 mm span) reported ρ_t of 194 ± 42 Ω·cm.

D. Core-Conductor ρ_t Comparison

Studies with quantitative measurements that matched ours most closely were, for the most part, completed using perfused rabbit papillary muscles. Although Rodriguez-Sinovas et al. [7] (400 µm electrodes, 7.5 mm span) reported ρ_t of 122 ± 13 Ω·cm for rat epicardium at 7 kHz in four-electrode experiments, a number of different papillary muscle investigations reported values that ranged from 105 ± 3 [19] to 116 ± 7 Ω·cm [20], 126 ± 11 Ω·cm [21], 144 ± 8 Ω·cm [22], and 151 ± 16 Ω·cm [22]. We view these latter matches as especially intriguing because the technical approach as initially described by Kleber and Rieger [20] is much more challenging than the approach we employed. For their preparations, hearts were excised and dissected to remove the great arteries, the atria, and the left ventricular free wall before the remaining septal tissue was mounted in a chamber. Subsequent cannulation of the septal artery maintained perfusion of right ventricular papillary muscles, with current supplied between plates positioned near the apex and base of the muscle and a bipolar extracellular electrogram placed centrally on the muscle resolving a potential gradient from which ρ_t was derived assuming core-conductor conditions. With this preparation, simultaneous monitoring of transmembrane potential via a floating glass microelectrode allows further segmentation of ρ_t into intracellular and extracellular components following Weidmann [23].

E. Implications for Multisite Stimulation

We appreciate such segmentation requires a more detailed framework for interpretation of uCIs than the framework we considered, and view such development as a unique opportunity provided by successful demonstration of feasibility here. As highlighted in our recent modeling report [24], use of a linear set of eight electrodes spaced center-to-center at 25 µm steps such that stimulation between pairs separated by 75, 125, or 175 µm available is sufficient, in theory, to allow the measurement of directional interstitial (Rox, Roy, Roz) and intracellular (Rix,Riy,Riz) microimpedances. During interstitial stimulation at frequencies below 100 Hz, we identified uCIs that provided sufficient data to measure (Rox, Roy, Roz). This occurred because the supplied current remained primarily interstitial on such a fine size scale, so a structural framework in which intracellular and membrane contributions were included was unnecessary to interpret the uCIs.With (Rox, Roy, Roz) available, uCIs recorded at frequencies between 200 and 4000 Hz were then sufficient to measure (Rix, Riy, Riz). This occurred because membrane capacitance provided a pathway for supplied current to redistribute from the interstitial to the intracellular compartment by an amount that depended upon the frequency. Here, we emphasize that the method requires no intracellular access and as such may prove superior to isolated cell pair and perfused papillary muscle experiments that are more technically challenging to implement. While interpretation of uCIs within structural frameworks that are more involved than for ρ_t is required, the main issue for accurate experimental recovery involves uCI spectra resolution.

F. Reduced Electrode Separation

We view this development as a necessary step toward implementation of multisite stimulation with such fine electrode separation and anticipate its use will be important to quantify disease-, region-, tissue-, and species-dependent cellular uncoupling. That view is supported by the elegant work of Gielen et al. [25], who completed four-electrode experiments in skeletal muscle preparations with 70 µm sensors separated from one another by 500 µm (1.5 mm span) and stimulated those preparations at 3 Hz to 1 MHz. With this separation, derived conductivities (inverse of resistivities) along (σ_L) and across (σ_T) fibers showed changes that included: 1) increasing σ_L above 100 Hz, 2) decreasing σT between 1 and 10 kHz, and 3) phase shifts that ranged from ≈−20° to ≈+50° for specific frequencies and electrode orientations over the full range. Accompanying experiments with larger electrodes separated from one another by 3 mm showed more modest frequency dependence, with σ_L and σ_T changes limited primarily to frequencies between 100 kHz and 1 MHz. The frequency response with finer electrode separation allowed those investigators to speculate on likely directional conductivities for the interstitial and intracellular compartments and conclude skeletal muscle has unequal anisotropy ratios (L/T) with an interstitial ratio of 2.13 and an intracellular ratio of 0.83. While careful calibration related to the electrodes and instrumentation was necessary to identify these characteristics, they also noted the importance of maintaining temperature, saturating muscles with water vapor, avoiding tissue damage by limiting protocols to 1.5 h, and conditioning of the muscle surface and its surroundings to avoid short circuiting of the electrodes by electrolytes on that surface. In our experiments, use of Langendorrf perfusion maintained temperature and ensured saturation, while rapid completion of individual acquisition intervals (1 to 1.5 min) limited preparation rundown while allowing data collection with multiple different arrays. We also believe the method of array assembly with wires fixed to the surface of an insulating layer that measured ≈0.5 × 1.0 cm² in combination with the approach to positioning in which each array was held flush to epicardial muscle within a rubber window limited the ability of surface perfusate to act as a short circuit. However, this last assumption was not rigorously tested and we recognize this as a potential limitation with respect to our quantitative findings.

Biographies

Andrew E. Pollard (M’89) is currently a Professor of biomedical engineering at the University of Alabama at Birmingham, Birmingham, AL, USA. His primary research interests include the study of cardiac arrhythmias, with particular emphasis on numerical modeling and experimental mapping.

Roger C. Barr (F’06) is currently Anderson-Rupp Professor of biomedical engineering and an Associate Professor of Pediatrics at Duke University, Durham, NC, USA, where he served as the Chair of the BME Department from 1995 to 2000. His research interests include electrophysiology and electrochemotherapy.

He was the President of the IEEE/EMBS in 2004 and received the EMBS Career Achievement Award in 2008.