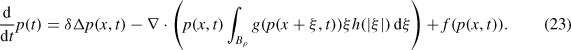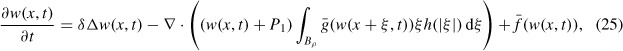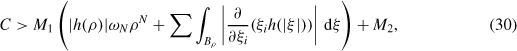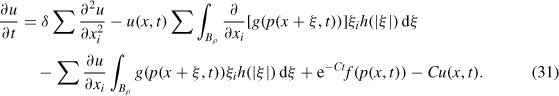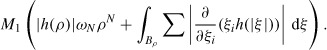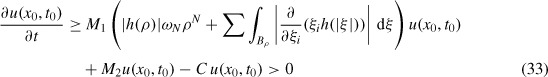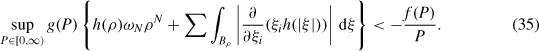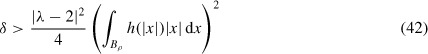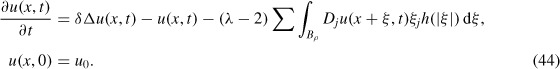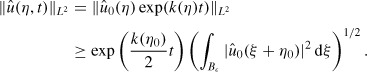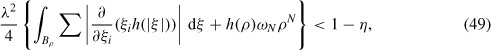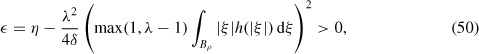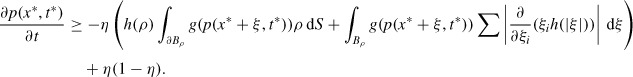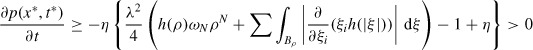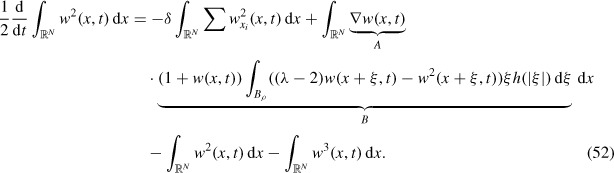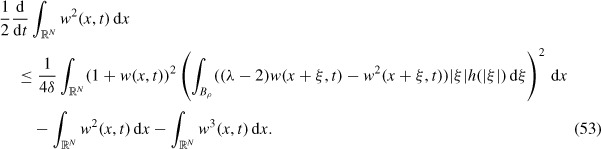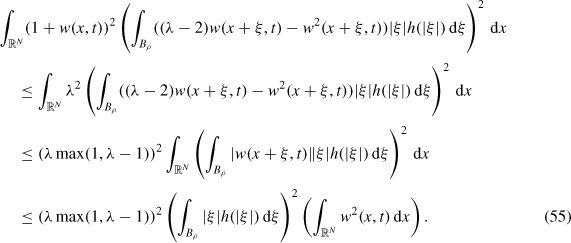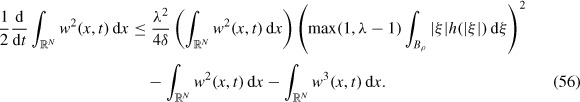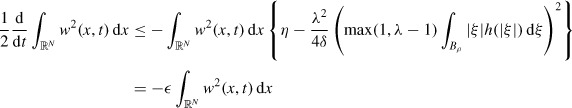A non-local evolution equation model of cell–cell adhesion in higher dimensional space

Abstract

A model for cell–cell adhesion, based on an equation originally proposed by Armstrong et al. [A continuum approach to modelling cell–cell adhesion, J. Theor. Biol. 243 (2006), pp. 98–113], is considered. The model consists of a nonlinear partial differential equation for the cell density in an N-dimensional infinite domain. It has a non-local flux term which models the component of cell motion attributable to cells having formed bonds with other nearby cells. Using the theory of fractional powers of analytic semigroup generators and working in spaces with bounded uniformly continuous derivatives, the local existence of classical solutions is proved. Positivity and boundedness of solutions is then established, leading to global existence of solutions. Finally, the asymptotic behaviour of solutions about the spatially uniform state is considered. The model is illustrated by simulations that can be applied to in vitro wound closure experiments.

AMS Classifications: 35A01; 35B09; 35B40; 35K57; 92C17

1. Introduction

Cell invasion is important in many biological processes, particularly in the invasive stage of cancer and in embryonic development [23, 32]. There has recently been some interest in how to mathematically model cell–cell and cell–extracellular matrix adhesions in the context of cancer invasion, since the latter is believed to be characterized by a number of processes that include loss of cell–cell adhesion and enhanced cell–matrix adhesion in addition to active migration, cell proliferation and the secretion of matrix degrading enzymes [15]. Accurate modelling of cell adhesion is, therefore, important, but it is challenging to do so using continuous mathematical models because in such an approach one uses continuous variables for cell densities. Individual cells are not recognized as such and, therefore, there is no representation of cell boundaries.

A modelling approach that aims to address these difficulties was proposed by Armstrong et al. [2]. The ideas have been taken further and applied to various contexts by, for example, [3, 12, 15, 23, 31]. For a cell density p(x, t) the basic model in one spatial dimension is

for x ∊ (−∞, ∞), t > 0 with initial condition p(x, 0) = ϕ₀(x). Equation (1) incorporates a direct representation of cell-cell contact via a non-local flux term, the integral term in Equation (1). Spatially structured models of tumour invasion that incorporate other aspects such as haptotaxis and age structure were considered in [9–11]; see also [34, 35].

The purpose of the present paper is to formulate and analyse an extension of Equation (1) to the case of N spatial dimensions, considering only cell-cell adhesion. Again letting p(x, t) denote the cell density at (x, t), but now with x ∊ ℝ^N, t > 0 and B_ρ denoting the N-dimensional ball centred at 0 and of radius ρ, we propose the equation

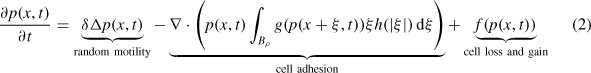with initial condition

The function f(p) models cell loss and gain, and for biological reasons we assume that f(0) = 0 and that there is a number P₁ > 0 such that f(p) > 0 for p ∊ (0, P₁), and f(p) < 0 for p > P₁. These assumptions imply that at lower densities, there is cell gain, but at large enough densities cell loss occurs more rapidly than the generation of new cells via division, due to the effects of crowding.

Equation (2) admits the possibility of two components to cell motion. Motion of cells is assumed to be partly due to Fickian diffusion, which gives rise to the Laplacian term. The need for a Fickian term is debatable, and Painter et al. [23] note from simulations of their more complex cell–matrix model that, in the absence of a Fickian term, and unusually for a continuous model, non-invasive growth is possible for some parameter regimes while invasive growth takes place in others. The other component to cell motion is the movement of cells due to adhesion as modelled by the cell adhesion term in Equation (2). It is an advective flux term and models motion of cells that is caused by mechanical forces attributable to adhesive bonds that cells have formed with their closer neighbours. Cells are able to sense their surroundings over some radius ρ, which is believed to be of the order of several cell diameters [23], due to their ability to deform and extend protrusions [8]. These protrusions cause adhesive bonds to form with other cells, and the resulting forces cause cell movement. In fact, the cell adhesion term in Equation (2) is an advective flux term of the form −▽ · (p(x, t)U(x, t)), where U(x, t) is the velocity of the cells at x ∊ ℝ^N at time t. If we imagine the cells as tiny spheres moving through a viscous fluid, then Stokes' law leads us to suppose that they are subject to a resistive force which is directly proportional to the velocity. This analogy leads us to suppose that the velocity of a cell is proportional to the net adhesive force on it due to the bonds formed with nearby cells. So, the velocity U(x, t) can effectively also be thought of as the adhesive force on a cell due to bonds with these other nearby cells within the sensing radius ρ (the range over which a cell can detect its surroundings). This force is taken to be of the form

We think of expression (4) as a force, but it is really a velocity. Expression (4) is assumed to contain dimensional constants such as the viscosity of the medium (perhaps embodied within the functions g and h), to ensure that it has the units of velocity. Viewing expression (4) as a force, we are asserting that the total force on a cell at position x is the sum, over all cells within the sensing radius ρ, of the local forces attributable to bonds formed with the cells at the nearby points x + ξ, ξ ∊ B_ρ. The function h : ℝ → ℝ describes how the magnitude of the force depends on |ξ|, and is a positive function since adhesive forces are always directed towards cell centres. The vector ξ in front of h(|ξ|), which is not present in Equation (1), gives direction to the force on cells at x due to bonds with cells at x + ξ. Another formulation would be to make this direction vector a unit vector and write (ξ/|ξ|)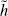(|ξ|) rather than ξh(|ξ|), as some other authors have done, see for example Painter et al. [23]. There is no real distinction; we are simply taking h(|ξ|) = 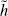(|ξ|)/|ξ|.

The magnitude of the adhesive forces from cells at the nearby location x + ξ will depend on the number of adhesive attachments made by cells at x + ξ to a cell at x, and hence on the cell density at x + ξ. This explains the term g(p(x + ξ, t)) in the integrand of expression (4), and the function g(p) describes how the forces depend on the local cell density. We anticipate that g(p) should increase linearly with p if cell density is not too great, because in this situation a doubling of the number of cells at x + ξ should roughly double the number of adhesive attachments made to cells at x. However, at higher densities, particularly as close cell packing is approached, the tendency to form attachments drops off and so g(p) in fact decreases once p has risen above a certain threshold, and is zero for all p above a critical cell density P₂ > 0 corresponding to close cell packing. The shift in balance between cell division and cell loss should occur at an achievable cell density. Thus, for biological realism, P₁ < P₂.

There is unquestionably a need for analytic study of equations of the form (2) in spatial domains of dimension N ≥ 2. Recent interest in this kind of equation has been largely in the areas of cancer cell invasion and wound healing. Gerisch and Chaplain [15] and Painter et al. [23] both consider systems containing a term of the same form as the non-local term in Equation (2), and with the same interpretation – cell velocity due to adhesive bonds with other cells – with an emphasis on two dimensions so that B_ρ becomes a disk of radius ρ. These studies have been largely numerical, which is time-consuming in the 2D case. In addition to their numerical simulations, Gerisch and Chaplain [15] examine the possibility of expanding the non-local term, using Taylor series in the case when ρ is small. This analytical approach does yield some useful insight, although the approximated equations can allow unrealistic phenomena such as blow up. Two- and three-dimensional studies are extremely important in the cancer modelling context because of the manner in which cancer cells invade tissue and the possibility of phenomena such as fingering at the invasive front (see Figure 5 in [23]). The shape of a tumour-host boundary is an important diagnostic indicator ([23], and the references therein). Straight and/or sharp boundaries tend to imply non-invasive tumours, whereas if a tumour has a diffuse and/or wavy boundary it is likely to be invasive.

Another important reason for considering equations of the form (2) in higher space dimensions is that the inclusion of another space dimension can be an important test of the stability and robustness of a one-dimensional pattern, and therefore of the plausibility of a type of mathematical model in a situation where many details are unknown. This was an important issue in Armstrong et al. [3] who considered a system with the same type of adhesive flux term as in Equation (2) as a model for somite formation. Segmentation in a number of organisms proceeds through the formation of somites, which will eventually become repeated structures such as the vertebrae. Somitogenesis is, therefore, seen as a one-dimensional process (along the anterior-posterior axis of the presomitic mesoderm) and an important step in the model validation process can be to include a second spatial dimension and investigate whether the model is still capable of forming somites, as was done in [3].

Using fractional powers of the diffusion operator, we establish results about the existence and uniqueness of solutions and their positivity and boundedness in spaces of uniformly continuous functions. We also look at solutions in L^p spaces and show that under suitable conditions the non-zero uniform state is asymptotically stable in L² and that under more stringent conditions all solutions converge to this uniform state. Finally, we look at simulations which apply to wound closure experiments.

2. Preliminaries

Initially, we will work in the spaces

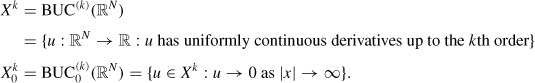In either case, take the norm ||u||_k = Σ_|Λ|≤k ||D^Λu||∞, where for i = 1, …, N, D_i : 𝒟(D_i)

so D_i is a closed linear operator. Set D = (D₁, …, D_N), with domain 𝒟(D) = 𝒟(D₁) × … × 𝒟(D_N). If Λ = (Λ₁, …, Λ_N), D^Λ = D₁^Λ₁ … D_N^Λ_N. We define |Λ| = Λ₁ + … + Λ_N and say Λ ≤ μ for N-tuples Λ and μ if the inequality holds component-wise. Note that from [22] page 33, u ∊ BUC₀^(k)(ℝ^N) implies that, for |Λ| ≤ k, D^Λu → 0 as |x| → ∞.

We write 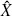^k when results apply to either X^k or X₀^k and set X = X⁰.

We define à : 𝒟(Ã) ⊂ X → X, by

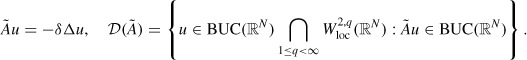For ω > 0 set A = Ã + ωI, 𝒟(A) = 𝒟(Ã) so that the spectrum of A is contained in the open right half plane.

We rewrite the problem (2)–(3) abstractly as

where p(t) : [0, ∞) → X, t ≥ 0, f : ℝ → ℝ, g : ℝ → ℝ, and

with ith component K_i(ϕ)(x).

Let T(t) be the analytic semigroup in X generated by −Ã, so

and T(t) : X₀ → X₀. Let T_k(t) be the analytic semigroup which is T(t) restricted to the space 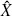^k (k an integer); the corresponding generators −Ã_k are given by the operator −Â but restricted to different domains [22].

It is easy to see that for ϕ ∊ X^k, k > 0, |Λ| ≤ k

so we also have T(t) : X^k → X^k,

and

Set A_k = Ã_k + ω. We will use the fractional powers A_k^α of A_k, and exploit the result that, for suitable α, the operator D_iA_k^−α : X^k → X^k is bounded, see [24]. We will write 𝒟^α,k = 𝒟(A_k^α) in X^k, 𝒟₀^α,k = 𝒟(A_k^α) in the space X₀^k and 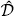^α,k = 𝒟(A_k^α) in the space 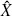^k. We give these spaces the graph norm.

Thus the mild form of (2)–(3) in X^k is

where

Observe that for ϕ ∊ 𝒟(D), g ∊ C¹(ℝ), h ∊ L¹(0, ρ), we have K(ϕ) ∊ 𝒟(𝒟),

and

Note that in our proofs of existence, we will take f, g : ℝ → ℝ but we will then prove that if ϕ₀ ≥ 0 then p(t) ≥ 0. Thus, provided there is enough smoothness at 0 it is only the properties of f and g on [0, ∞) that are relevant as we can then define f and g appropriately for p < 0.

We also have [17, 18, 22, 24]

• (i)if α > 0, then for every t > 0 the operator A_k^αT_k(t) is a bounded linear operator in 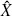^k and for any 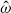> 0 there exists C₁ > 0 such that
  
• (ii)if 0 ≤ α ≤ 1, then A_k^−α : 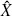^k → ^k 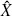is a bounded linear operator so there exists a constant C₂ ≥ 1 such that for all u ∊ X^k,
  
• (iii)if ½ < α < 1, then DiA_k^–α : 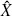^k → ^k 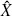is a bounded linear operator so there exists a constant C₃ ≥ 1 such that for all u ∊ X^k,
  

The following lemma is proved in very much the same way as Lemma 1 in [12]

Lemma 1

Suppose that for some k ≥ 0, f ∊ C^k+1(ℝ), g ∊ C^k+2(ℝ) and h ∊ L¹(0, ρ), ½ < α < 1 and f(0) = 0. Then G : ^k → ^k and

• (a)if ||A_k^–αϕ||_k ≤ R₁ there exists a constant K₁(R₁) such that
  
• (b)if ||ϕ_i||_k ≤ R₂, i = 1, 2, then there exists a constant K₂(R₂) such that
  
• (c)if k ≥ 2, and ||ϕ||_k–2 ≤ R₃
  

3. Existence, positivity and boundedness

We can now prove local existence, and regularity, as in Theorem 1 [12]. The continuous dependence on the initial data follows immediately from [17] Theorem 3.4.1.

Theorem 1

Suppose that for some k ≥ 0, f ∊ C^k+1(ℝ), g ∊ C^k+2(ℝ), f(0) = 0, that h ∊ L¹(0, ρ), and that ϕ₀ − Q ∊ 𝒟₀^α,k, where ½ < α < 1, and either Q = 0 or there exists P₁ > 0 such that f(P₁) = 0 and Q = P₁. Then the problem (2) and (3) has a unique mild solution p(t) such that p(t) − Q ∊ C([0, T₀]; 𝒟₀^α,k), for T₀ > 0 small enough.

In addition p(t) is the classical solution on [0, T₀] of the problem (2) and (3) in the sense that

and for 0 < t ≤ T₀, p(t) ∊ 𝒟(A_k), and

Also, under the above conditions, if k ≥ 2m,

In particular if k = 2, p(t) − Q ∊ C¹([0, T₀]; X₀) and Equation (23) also holds at t = 0.

Furthermore, there is continuous dependence on the initial data. Let [0, ₀) be the maximal interval of existence of the solution p(t). Now let p_n(t) be the solution of Equation (2) with initial data p_n(x, 0) = ϕ_n(x) where ϕ_n − Q ∊ 𝒟₀^α,k. Suppose that ||A_k^α(ϕ_n − ϕ₀)||_k → 0 as n → ∞. Then, given any t₁ ∊ [0, ₀), p_n(t) is defined on [0, t₁] for large enough n and ||A_k^α(p_n(t) − p(t))||_k → 0 as n → ∞, uniformly on [0, t₁].

Remark

To deal with the case Q = P₁ we set p(x, t) = w(x, t) + P₁ in Equations (2) and (3) to get

where f(w) = f(w + P₁), and g(w) = g(w + P₁). If we set

the abstract form of Equation (25) is

If G(ϕ) = D · ((A^−αϕ + P₁)K(A^−αϕ)) − f(A^−αϕ), then it is easy to see that G satisfies Lemma 1 and we can apply the same methods to the resulting equation in w.

We can now obtain positivity and boundedness.

Proposition 1

Suppose that h ∊ C¹ [0, ρ], f ∊ C³(ℝ), g ∊ C⁴(ℝ), f(0) = 0, and that ϕ₀ − Q ∊ D₀^α,2, where ½ < α < 1 and Q = 0 or Q = P₁ > 0 where f(P₁) = 0. Let ϕ₀(x) ≥ 0 for all x ∊ ℝ^N. If p(t) is the unique classical solution of Equations (2) and (3) on [0, T₀], then p(x, t) ≥ 0 for all 0 ≤ t ≤ T₀, x ∊ ℝ^N.

Proof Take M₁ > 0 and M₂ ≥ 0 such that

and, using the mean value theorem,

Choose C sufficiently large that

where ω_N is the surface area of ∂B₁, and define u(x, t) = p(x, t) e^−Ct, so

We now prove that p(x, t) ≥ 0 on ℝ^N × [0, T₀]. Suppose not, then u(x, t) will be strictly negative somewhere in this set and hence attains a global minimum at some (x₀, t₀) ∊ ℝ^N × (0, T₀]. Thus for all i

In the ith integral in the second term in the right-hand side of Equation (31), we may replace ∂/∂x_i by ∂/∂ξ_i and therefore an integration by parts shows that the sum at the point (x₀, t₀) equals

The above quantity is bounded in absolute value by

Evaluating Equation (31) at (x₀, t₀), and making use of (32) and the above bound, we obtain

using inequality (29), the fact that u(x₀, t₀) < 0 and that C satisfies inequality (30). This is a contradiction, hence p(t) ≥ 0.

The following two results are proved using similar arguments to that used above. (See [12] for the proof when N = 1.)

Proposition 2

Suppose that h ∊ C¹[0, ρ], h ≥ 0, f ∊ C³(ℝ),g ∊ C⁴(ℝ), f(0) = 0 and that ϕ₀ − Q ∊ D₀^α,2 where ½ < α < 1, and Q = 0 or Q = P₁ > 0 where f(P₁) = 0. Suppose there exists P₂ > P₁ such that g(P) ≥ 0 for P ∊ [0, P₂], f(P₂) < 0 and that

Let 0 ≤ ϕ₀(x) ≤ P₂ for all x ∊ ℝ^N. If p(t) is the unique classical solution of Equations (2) and (3) on [0, T₀], then 0 ≤ p(x, t) ≤ P₂ for all x ∊ ℝ^N, 0 ≤ t ≤ T₀.

Proposition 3

Suppose that h ∊ C¹ [0, ρ], h ≥ 0, g bounded, f ∊ C³(ℝ), g ∊ C⁴(ℝ), f(0) = 0, and that ϕ₀ − Q ∊ 𝒟₀^α,2 where ½ < α < 1, and Q = 0 or Q = P₁ > 0 where f(P₁) = 0. Suppose there exists P₃ > P₁ such that for P > P₃, f(P) < 0 and

Let 0 ≤ ϕ₀(x) ≤ P₃ for all x ∊ ℝ^N. If p(t) is the unique classical solution of Equations (2) and (3) on [0, T₀], then 0 ≤ p(x, t) ≤ P₃ for all x ∊ ℝ^N, 0 ≤ t ≤ T₀.

The following global existence result is proved similarly to Theorem 2 in [12]. The basic idea runs as follows. There will be global existence if ||A₂^αp(t)||₂ is bounded on bounded intervals of time. The method uses Proposition 2 or 3 to show first that p(t) is bounded on bounded intervals of time. Thus by Lemma 1(a) ||G(A^αp(t))||_∞ is bounded linearly, so we can use the Gronwall-type inequality in [17] 1.2.1 to show that ||A^αp(t)||_∞ is suitably bounded. Then we can use Lemma 1(c) to get a linear bound on ||G(A₂^αp(t))||₂, so, using the Gronwall-type inequality again, ||A₂^αp(t))||₂ is also bounded as required

Theorem 2

Suppose that h ∊ C¹[0, ρ], h ≥ 0, f ∊ C³(ℝ), g ∊ C⁴(ℝ). Let ϕ₀ − Q ∊ 𝒟₀^α,2 where ½ < α < 1, and Q = 0 or Q = P₁ > 0 where f(P₁) = 0 and ϕ₀(x) ≥ 0 for all x ∊ ℝ^N. Suppose that either

• (a)There exists P₂ > P₁ such that ϕ₀(x) ≤ P₂ for all x ∊ ℝ^N, g(P) ≥ 0 for P ∊ [0, P₂], f(P₂) < 0 and inequality (34) holds. Or
• (b)g is bounded and there exists P₃ > P₁ such that ϕ₀(x) ≤ P₃ for all x ∊ ℝ^N, and for P > P₃, f(P) < 0 and inequality (35) holds.

Then the solution p(t) in Theorem 1 is global.

4. Initial data in L^p(ℝ^N)

We can also set the problem in L^p(ℝ^N). For any 1 < p < ∞ define the operator, Ã_L^p : 𝒟(Ã_L^p) ⊂ L^p(ℝ^N) → L^p(ℝ) by

Similarly, we can also define Ã_L¹ : 𝒟(Ã_L¹) ⊂ L¹(ℝ^N) → L¹(ℝ^N), for a suitable domain 𝒟(Ã_L1) [16]. For 1 ≤ p < ∞, ω > 0, set A_L^p = Ã_L^p + ωI, 𝒟(A_L^p) = 𝒟(Ã_L^p). It is well known [19] that −Ã_L^p generates a positive analytic semigroup {T_L^p(t)}_t≥0, with ||T_L^p(t)|| ≤ 1. Thus inequalities (16) and (17) hold also in L^p(ℝ^N). Further, in the case 1 < p < ∞, from [20] Propositions 4.1.7 and 1.1.4 and Example 1.3.9, if ½ < β < α < 1,

Thus, if we define D_i : 𝒟(D_i) ∊ L^p(ℝ^N) → L^p(ℝ^N),

then inequality (18) holds in Lp(ℝ). To show that inequality (18) also holds in L1(ℝN), it is sufficient to show that 𝒟(AL1α) ↪ W1,1(ℝN). To do this note first that it follows from [20] Example 1.3.9, Example 1.3.11 and Remark 1.3.7 that if 1 < s < 2 and 0 < β < α < 1, then

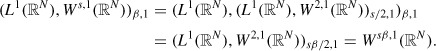Now, by [20] Proposition 4.1.7, [16] Theorem 1.7 and Prop 4.8, and [20] Prop 1.1.4, for 1 < s < 2

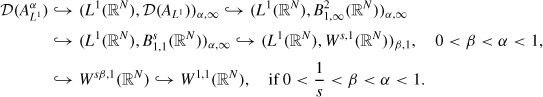(The definition and properties of the Besov spaces B^s_p,q, and their relationship to the Sobolev-Slobodeckii spaces W^s,p, can be found in [1, 16, 20].)

As before, from [19], T_L^p(t) satisfies Equation (8), hence if ϕ ∊ X^k ∩ L^p(ℝ^N), T_L^p(t)ϕ = T_k(t)ϕ. Equally ϕ ∊ 𝒟(A_L^p) ∩ 𝒟(A_L^p) implies A_L^pϕ = A_kϕ.

We now have the following local existence theorem in L²(ℝ^N):

Theorem 3

Suppose that f ∊ C1(ℝ), g ∊ C2(ℝ), that h ∊ L1(0, ρ), f(0) = 0 and that ϕ0 − Q ∊ 𝒟(AL2α), where ¾ < α < 1, and either Q = 0 or there exists P1 > 0 such that f(P1) = 0 and Q = P1. Then, for N ≤ 3, the problem (2) and (3) has a unique mild solution p(t) such that p(t) − Q ∊ C([0, T0]; 𝒟(AL2α)), for T0 > 0 small enough.

In addition p(t) is the classical solution on [0, T₀] of the problem (2) and (3) in the sense that

and for 0 < t ≤ T₀, p(t) ∊ 𝒟(A_L²), and

Also there is continuous dependence on the initial data. Let [0, 0) be the maximal interval of existence of the solution p(t). Now let pn(t) be the solution of Equation (2) with initial data pn(x, 0) = ϕn(x) where ϕn − Q ∊ 𝒟(AL2α). Suppose that ||AL2α(ϕn − ϕ0)||L2 → 0 as n → ∞. Then, given any t1 ∊ [0, 0), pn(t) is defined on [0, t1] for large enough n and ||AL2α(pn(t) − p(t))||L2 → 0 as n → ∞, uniformly on [0, t1].

Finally, if in addition ϕ0 − Q ∊ 𝒟(AL1α), then also p(t) − Q ∊ C([0, T0]; 𝒟(AL1α)).

Proof

The proof of the first part follows from Theorems 3.3.3 and 3.4.1 in [17] provided we can show that G : L²(ℝ^N) → L²(ℝ^N) and G : L²(ℝ^N) → L²(ℝ^N) are locally Lipschitz.

If we consider G then it consists of a sum of products. Each product has just one term of the form DiAL2−αϕ. The rest are functions of AL2−αϕ ∊ D(AL2α). But, for ¾ < α < β < 1, and N ≤ 3

(see [1] 7.34) and the local Lipschitzness follows. Similarly for G.

Note further that, also using inequality (18) in L1 (ℝN), G, G : L1 (ℝN) ∩ L2(ℝN) → L1 (ℝN) ∩ L2(ℝN) and are locally Lipschitz continuous in L1(ℝN). For ϕ0 ∊ 𝒟(AL1α) ∩ 𝒟(AL2−α), we set up the iteration: ν0 = AL1α ϕ0,

then the iteration converges in L¹(ℝ^N) and L²(ℝ^N) and by considering the restrictions to bounded subsets of ℝ^N, it can be seen that the limits are equal almost everywhere. Similarly for G, and the required invariance follows.

5. Stability of the uniform state

We now consider the local asymptotic stability of the uniform state p = P₁. For simplicity, we will consider the case where f and g are logistic. Each of f and g in Equation (2) can be of the form rp(1 − p/K) with different r and K. After suitable non-dimensionalization, without loss of generality, they can be taken as f(p) = p(1 − p) and g(p) = p(Λ − p), with Λ > 1. The uniform steady state is then p = 1. To examine its stability, set p = w + 1, ϕ₀ = w₀ + 1 to obtain the following equation for w:

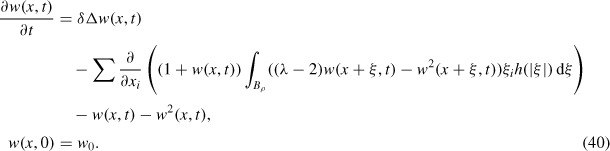Theorem 4

Take N ≤ 3. Suppose that h ∊ L2(0, ρ), and that ϕ0 − 1 ∊ 𝒟(AL2α), where ¾ < α < 1. For η ∊ ℝN define

Then if k(η) < 0 for all η ∊ ℝN the zero solution of Equation (40) is uniformly asymptotically stable in 𝒟(AL2α). Precisely, if γ > 0 is such that k(η) < −γ for all η ∊ ℝN, then there exist ζ > 0, M ≥ 1 such that if ||AL2αw0||L2 ≤ ζ, then

Moreover, k(η) < 0 for all η ∊ ℝ^N holds if

or

Conversely if there exists η₀ such that k(η₀) > 0, then the stationary solution is unstable.

Proof

We apply the results of [17] Section 5.1. The linearization of Equation (40) is

Define the bounded linear operator B : 𝒟(AL2α) → L2(ℝN), such that

and the operator H : L2(ℝN) → L2(ℝN) such that H(ϕ) = G(ϕ) − BAL2−αϕ.

Using the same reasoning as in Theorem 3 it can be seen that if ||ϕ||_L² ≤ R, then there exist constants K(R) and K(R) such that

In the case of stability, we note that this implies that H(ϕ) = o(||ϕ||L²) as ||ϕ||L² → 0. We have already seen that G : L²(ℝ^N) → L²(ℝ^N) is locally Lipschitz continuous. Thus Theorem 5.1.1 of [17] holds so that if the solutions of the linearized problem are uniformly asymptotically stable then so too are those of the nonlinear problem.

The right-hand side of Equation (44) is linear and generates an analytic semigroup R(t), say. So, for all u₀ ∊ L²(ℝ^N), Equation (44) has a global classical solution u(t) = R(t)u₀. First take u₀ ∊ L¹(ℝ^N) ∩ L²(ℝ^N), so that, as in Theorem 3, u(t) ∊ L¹(ℝ^N) ∩ L²(ℝ^N), and we may take Fourier transforms. If we denote the Fourier transform of u by

then

so

Thus, using the Plancherel identity,

as required. Thus by density ||R(t)u₀||_L² ≤ ||u₀||L₂ exp(−γt) for all u₀ ∊ L²(ℝ^N), and the result follows. The inequality (42) follows from completing the square in k(η), while inequality (43) follows from the fact that |sin(η · x)| ≤ |η · x| ≤ |η||x|.

For instability, we apply Corollary 5.1.6 of [17]. From inequality (45) H(ϕ) = O(||ϕ||²_L²) as ||ϕ||_L² → 0, so now we require that there exists Λ in the spectrum of the generator of R(t) such that Re Λ > 0. Suppose not, so that there exists M such that, for all ϕ ∊ L²(ℝ^N),

But, using the expression for û(η, t) in (46), there exists ∊ > 0 such that

If we now choose u₀ such that ∫_B∊|û₀(ξ + η₀)|² dξ > 0, then using the Plancherel identity gives a contradiction to inequality (47).

6. Convergence to the uniform state

The next result follows in a similar fashion to Theorem 3 and [12] Theorem 3.

Theorem 5

Suppose that f ∊ C3(ℝ), g ∊ C4(ℝ), h ∊ C1[0, ρ]. Let ϕ0 − Q ∊ 𝒟0α,2, where ½ < α < 1, and either Q = 0 or Q = P1 > 0 with f(P1) = 0. Suppose also that the hypotheses of Proposition 1 and of either Proposition 2 or Proposition 3 on f, g, h, and ϕ0 hold. Take also ϕ0 − Q ∊ 𝒟(AL2α). Let p(t) with p(t) − Q ∊ C([0, ∞); 𝒟0α,2) be the unique classical solution of Equations (2) and (3). Then, for each t ≥ 0, p(t) − Q ∊ 𝒟 (AL2) = W2,2(ℝN). Furthermore p(t) − Q ∊ C1((0, ∞); L2(ℝN)).

This is enough to justify calculations in the proof of the following theorem.

Theorem 6

Let h ∊ C1[0, ρ] be such that h ≥ 0, and let f(p) = p(1 − p) and g(p) = p(Λ − p) with Λ > 1. Let ϕ0 − 1 ∊ 𝒟0α,2 ∩ 𝒟(AL2α(ℝN)), where ½ < α < 1, and let p(x, t) be the solution of the problem (2) and (3).

• (a)If 0 ≤ ϕ₀(x) ≤ Λ for all x ∊ ℝ^N, where Λ satisfies
  

  then 0 ≤ p(x, t) ≤ Λ for all x ∊ ℝ^N, t ≥ 0.

• (b)If η ≤ ϕ₀(x) ≤ Λ for all x ∊ ℝ^N, where 0 < η < Λ, Λ satisfies inequality (48), and
  

  then η ≤ p(x, t) ≤ Λ for all x ∊ ℝ^N, t ≥ 0.

• (c)If η ≤ ϕ₀(x) < Λ for all x ∊ ℝ^N, where η > 0, Λ satisfies inequalities (48), (49), and
  

  then p(x, t) → 1 exponentially as t → ∞ in the sense that for all t > 0

  

Proof

First, to prove (a), note that inequality (48) implies inequality (34) with P₂ = Λ, f(P) = P(1 − P), g(P) = P(Λ − P), and thus, solutions remain in the closed interval [0, Λ] for all positive times.

Next, to prove (b), suppose that there exists t* > 0 and a corresponding x* with p(x*, t*) = η, ∂p(x*, t*)/∂x_i = 0, ∂²p(x*, t*)/∂x_i² ≥ 0, then

Note that 0 ≤ g(p) ≤ Λ²/4 when p ∊ [0, Λ]. Therefore

by inequality (49). Hence p(x, t) ≥ η for t > 0 and (b) is proved.

Last, to prove (c), define w(x, t) by p(x, t) = 1 + w(x, t), so that w(x, t) satisfies Equation (40) and η − 1 ≤ w ≤ Λ − 1. Multiplying Equation (40) by w(x, t) and integrating with respect to x over ℝ^N, and then integrating by parts on the Laplacian term and the ∂/∂x_i term (this is justified by Theorem 5),

The integrand of the middle term in the right-hand side will now be estimated by using the inequality A · B ≤ δ|A|² + |B|²/4δ with A and B identified by the underbraces. This bounds the integral by a sum of two integrals, one of which cancels with the first term on the right-hand side to give

Since Λ > 1, it is easy to show that

Recalling that 0 ≤ 1 + w(x, t) ≤ Λ, so using inequality (54) and Theorem IV.15 from [4],

Therefore inequality (53) becomes

Note that −w³(x, t) ≤ (1 − η)w²(x, t), so that inequality (56) becomes

and (c) follows from inequality (50).

7. Simulations

We illustrate in Figures 1–4 the results of the previous two sections with simulations that can be applied to in vitro wound closure experiments. In these experiments, cell cultures are scored in a thin line that closes as the cell population proliferates. A review of mathematical models of wound healing is given in [30] and other references are found in [5–7, 13, 14, 21, 25–29, 33, 36]. In previous work [12], we modelled in vitro wound healing experiments for the model (2) with N = 1, and examined the dependence of solutions on the diffusion parameter δ and the sensing radius ρ. In [12] numerical simulations demonstrated that for larger values of the diffusion parameter δ and smaller values of the sensing radius ρ the wound closed completely across the wound opening, but for smaller values of δ and larger values of ρ complex patterns arose across the wound opening with incomplete closing. Either of the alternative conditions (42) or (43) is sufficient for the stability of the uniform steady state p = 1, and note that both of these conditions are largeness conditions on δ and smallness conditions on both h(·) and on the sensing radius ρ. Similarly conditions (48), (49) and (50) are sufficient for convergence to the uniform steady state and conditions (48) and (49) are smallness conditions on h(·) and ρ while (50) is in addition a largeness condition on δ. In our simulations here, we examine the dependence of the wound healing model with respect to the parameter Λ, which is the non-dimensionalized cell density corresponding to close cell packing, in Equation (2) with g(p) = p(Λ − p).

Figure 1.

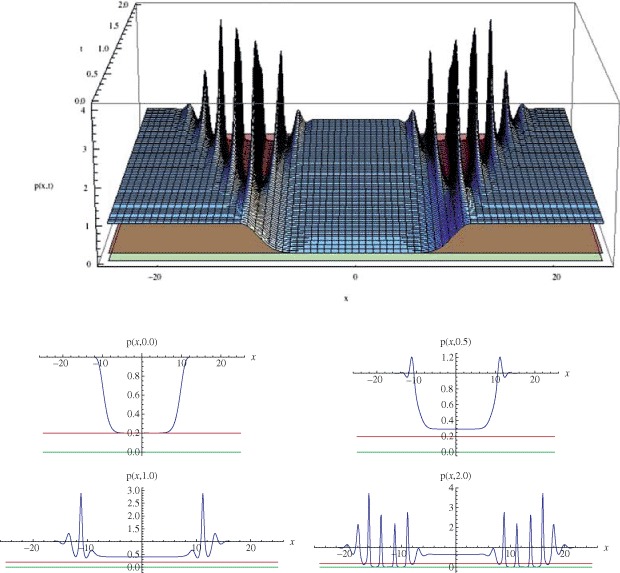
Simulation with ρ = 1.0, Λ = 19.0, δ = 0.1, η = 0.2, f(p) = p(1.0 − p), g(p) = p(Λ − p), h(x) = arctan (100.0x)/(10.0x arctan 100.0) and initial data ϕ₀(x) = 1.0 − 0.8 exp(−(0.1x)¹⁰). The red plane and lines correspond to η = 0.2 and the green plane and lines correspond to 0.0. (a) Graph of p(x, t), 0 ≤ t < 2.0. The wound does not close, and instead the solution exhibits an evolving pattern of peaks and valleys which do not converge to 1.0. (b) Graphs of p(x, .0), p(x, .5), p(x, 1.0), p(x, 2.0). The solution stays above 0.0, but not above η = 0.2.

Figure 4.

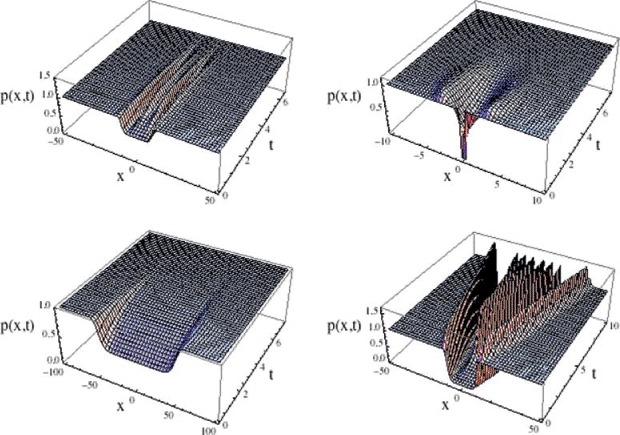
Wound healing simulations with parameters Λ = 2.0, δ = 1.0, ρ = 3.0, f(p) = p(1.0 − p), g(p) = p(Λ − p), h(x) = 9.0 arctan(100.0x)/(4.0x arctan 100.0), and initial data ϕ₀(x) = 1.0 − 0.4 exp(−(0.1x)¹⁰) (top left), ϕ₀(x) = 1.0 − 0.95 exp(−(3x)¹²) (top right), ϕ₀(x) = 1.0 − 0.5 exp(−(0.2x)¹²) (bottom left) and ϕ₀(x) = 1.0 − 0.95 exp(−(0.1x)¹⁰) (bottom right). The wounds top left and top right both close but the wound bottom right which has the same width as the first and the same depth as the second fails to close. The widest wound, bottom left, also closes.

In Figure 1, N = 1, f(p) = p(1.0 − p), g(p) = p(Λ − p), δ = 0.1, η = 0.2, ρ = 1.0, h(x) = arctan(100.0x)/(10.0x arctan 100.0), and ϕ₀(x) = 1.0 − 0.8 exp(−(0.1x)¹⁰). In this case, Theorem 6 (48) is satisfied if Λ < 18.94, (49) is satisfied if Λ < 1.457, and (50) is satisfied if Λ < 2.823. We take Λ = 19.0, so that none of the conditions (48), (49), (50) of Theorem 6 are satisfied. The simulation in Figure 1 shows that for this value of Λ, the solution does not remain bounded below by η and does not converge to the equilibrium 1.0. On the other hand, if condition (48) were satisfied, then the solution p would be bounded (0 ≤ p ≤ Λ), and Theorem 2 would give global existence of the solution. Indeed, if we take Λ = 18, then condition (48) holds, and we find that the solution behaves qualitatively the same as in Figure 1. This provides an example where the theory gives global existence of the solution, but the solution does not converge to the equilibrium but instead forms a series of peaks.

In Figures 2 and 3, N = 1, f(p) = p(1.0 − p), g(p) = p(Λ − p), δ = 1.0, η = 0.2, h(x) = arctan(100.0x)/(9.0x arctan 100.0), and ϕ₀(x) = 1.0 − 0.8 exp(−(0.1x)¹⁰). We consider different values of Λ to illustrate the sensitivity of this parameter for the convergence of the solutions to the equilibrium ≡ 1.0. The hypotheses of Theorem 6 require that Λ < 16.94 (48), Λ < 2.683 (49), and Λ < 2.597 (50). For Λ < 2.597 all three conditions are satisfied, and Theorem 6 implies the solution remains in the interval [0.2, Λ] and converges to 1.0 for all initial data such that 0.2 ≤ ϕ₀(x) ≤ Λ. On the other hand if one looks at the stability condition from Theorem 4, then the equilibrium ≡ 1.0 is asymptotically stable for Λ < 17.62 with instability if Λ > 17.62. In Figure 2 (a) Λ = 1.5 and there is convergence to 1.0 (the solution appears to converge monotonically to 1.0 from below, never rising above 1.0). In Figure 2(b)–(d) Λ = 17.0, 18.0, 19.0, respectively, and the solutions develop a series of peaks, symmetric to the right and left of 0.0, and rising above and falling below 1.0. Further examination of this wave behaviour is given in Figure 3 for the cases Λ = 17.0 (a), Λ = 18.0 (b), and Λ = 19.0 (c). For Λ = 17, the amplitude of the waves decreases as t increases and the solution appears to converge slowly to 1.0. For Λ = 18 and Λ = 19, the wave propagates with amplitude dependent on Λ (the greater the value of Λ, the greater the amplitude). In general, for the roles of the model parameters, we postulate that cells concentrate in interior and exterior regions of the wound in a regular pattern depending on the strength of adhesion Λ, the sensing radius ρ, and the diffusion coefficient δ.

Figure 2.

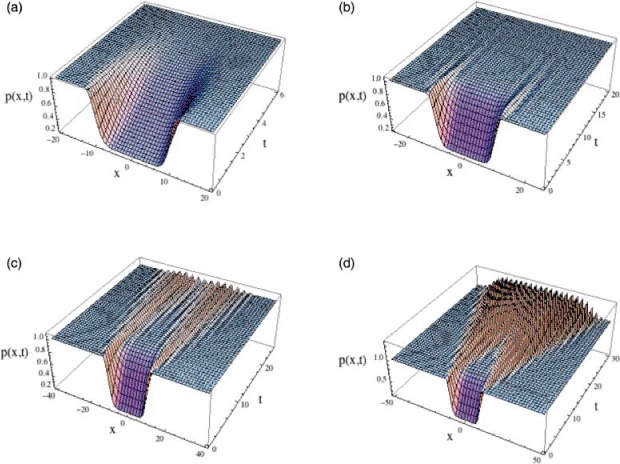
Simulation with ρ = 1.0, Λ = 1.5 (a), Λ = 17.0 (b), Λ = 18.0 (c), Λ = 19.0 (d), δ = 1.0, η = 0.2, f(p) = p(1.0 − p), g(p) = p(Λ − p), h(x) = arctan(100.0x)/(9.0xarctan 100.0), and initial data ϕ₀(x) = 1.0 − 0.8 exp(−(0.1x)¹⁰). For the higher values of Λ, complex patterns of oscillations develop across the wound.

Figure 3.

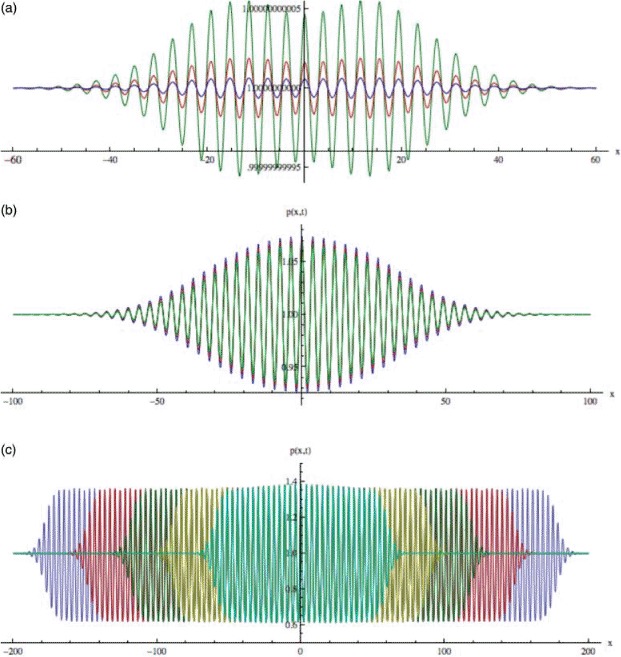
The wound healing simulation wave patterns as in Figure 2 with adhesion strength parameters (a) Λ = 17.0, (b) Λ = 18.0, and (c) Λ = 19.0. For Λ = 17.0, the solution is shown at times t = 100.0 (blue), t = 95.0 (red) and t = 90.0 (green). The amplitude envelope of the oscillation packet decreases to a minute value for the times shown. For Λ = 18.0 the solution is shown at times t = 200.0 (blue), t = 150.0 (red) and t = 100.0 (green). The envelope increases minutely for the times shown. For Λ = 19.0, the solution is shown at times t = 150.0 (blue), t = 125.0 (red), t = 100.0 (green), t = 75.0 (yellow) and t = 50.0 (cyan). The envelope widens uniformly for the times shown. The simulations indicate convergence to the uniform equilibrium ≡ 1.0 in (a) Λ < 17.62, but not in (b) and (c), Λ > 17.62.

In Figure 4, we show that the convergence to the equilibrium ≡ 1.0 corresponding to the healed wound depends on the initial conditions. In these simulations, the parameters are Λ = 2.0, δ = 1.0, ρ = 3.0, f(p) = p(1.0 − p), g(p) = p(Λ − p), and h(x) = 9.0 arctan(100.0x)/(4.0x arctan 100.0). In this figure, the only change in the simulations is the initial data – the parameters are the same for all. For initial conditions corresponding to a shallow, wide wound, and to a narrow, deep wound, closure occurs, but for an initial condition corresponding to a wound with the same width as the first and the same depth as the second, closure does not occur. A wider, shallow wound also closes. In general, the behaviour of the solutions is highly sensitive to initial conditions. We note that the function k(η) defined in Equation (41) is negative for all η ∊ ℝ, which by Theorem 4 implies that the equilibrium ≡ 1.0 is stable in this example.

We have chosen to illustrate the behaviour of solutions for the model using the simple case of an equilibrium corresponding to wound healing experiments, in which wound closure corresponds to convergence to a constant function in the x-direction, perpendicular to the direction of the scoring. Numerical simulations corresponding to higher dimensional cases will be conducted in future work.