Skip to main content
PMC home page
Genome Biology logoLink to Genome Biology
. 2004 Feb 16;5(3):R20. doi: 10.1186/gb-2004-5-3-r20

Visualization of the phylogenetic content of five genomes using dekapentagonal maps

Olga Zhaxybayeva 1, Lutz Hamel 2, Jason Raymond 3, J Peter Gogarten 1,✉
PMCID: PMC395770  PMID: 15003123

Short abstract

Dekapentagonal maps depict phylogenetic information for orthologous genes present in five genomes, and provide a pre-screen for putatively horizontally transferred genes.

Abstract

The methods presented here summarize phylogenetic relationships of genomes in visually appealing and informative figures. Dekapentagonal maps depict phylogenetic information for orthologous genes present in five genomes, and provide a pre-screen for putatively horizontally transferred genes. If the majority of individual gene phylogenies are unresolved, bipartition histograms provide a means of uncovering and analyzing the plurality consensus. Analyses of genomes representing five photosynthetic bacterial phyla and of the prokaryotic contributions to the eukaryotic cell illustrate the utility of the methods.

Background

Transfer of genetic information between divergent organisms has turned the tree of life into a net or web [1], and genomes into mosaics. Different parts of genomes have different histories; therefore representing the history of genome evolution as a single tree appears inconsistent with the data. Nevertheless, the assumption of a tree-like process still underlies many approaches. Recently, we developed a tool that provides an assessment and graphic illustration of the mosaic nature of microbial genomes [2]. The tool is based on maximum likelihood (ML) mapping developed by Korbinian Strimmer and Arndt von Haeseler [3]. They utilized Bayesian posterior probabilities to assess the phylogenetic information contained in an alignment of four homologous sequences. With four sequences there are only three possible tree topologies, and thus the three posterior probabilities corresponding to these three trees must sum to one. Utilizing a barycentric coordinate system, the resulting probability vector is represented as a point in an equilateral triangle, where the distances of the point to the three sides represent the three probabilities. Strimmer and von Haeseler applied this approach to depict the phylogenetic information content present in a multiple sequence alignment. We adapted this approach to represent the phylogenetic information content present in four completely sequenced genomes (for details and methodology see [2]; for an extension that improves taxon sampling and uses bootstrap support values see [4]). Unfortunately, this approach is limited to the analysis of only four genomes at a time. In many instances, it is interesting to compare more than four genomes simultaneously (for example [5]). The number of possible tree topologies for N taxa is (2N - 5)!/ [2N-3(N - 2)!] [6], and therefore rises dramatically as N increases. There are 15 possible unrooted tree topologies for five taxa, 105 for six taxa, and so on. Creating a visually appealing graphic representation poses a difficult challenge.

Here we report a new mapping approach to visualize data from the analyses of five genomes. The utility of this approach is illustrated by applying it to the evolution of photosynthetic bacteria and by dissecting the eukaryotic genome with respect to different prokaryotic contributions. Where the majority of the individual gene phylogenies are unresolved, a histogram giving the frequency of well-supported bipartitions provides a useful complement to the support-value maps.

Results and discussion

Using the same dataflow as described in [2], we detect sets of orthologous proteins for five genomes (quintets of orthologous proteins, or QuintOPs), and for each QuintOP we obtain posterior probabilities for each of the possible 15 tree topologies. By analogy with barycentric coordinates in ML mapping, the tree topologies are placed into vertices of a dekapentagon (that is, a polygon with 15 vertices corresponding to the 15 possible unrooted tree topologies), and each probability vector for a dataset corresponds to the point inside the dekapentagon: the vector is defined as the gravicenter of a dekapentagon where the posterior probabilities are considered as weights attached to the dekapentagon's vertices. If the distribution of topologies to the corners of the polygon is given, each probability vector unambiguously maps to a point inside the polygon (see Figure 1). However, the position of a probability vector crucially depends on the arrangement of topologies at the polygon vertices. We consider an arrangement of topologies optimal, if for a genome the probability vectors for all sets of orthologous genes map as closely to the periphery as possible. The optimal dekapentagonal map is only one of many possible projections of the 15-dimensional support-value vectors to two-dimensional space. The tree space containing all possible five taxon trees cannot be embedded into three-dimensional space [7]. The projection of tree space represented in the dekapentagonal maps highlights the ambiguities of phylogenetic reconstruction and repeated patterns of inconsistency; thus the major evolutionary histories represented by different parts of the genomes are most easily recognized.

Figure 1.

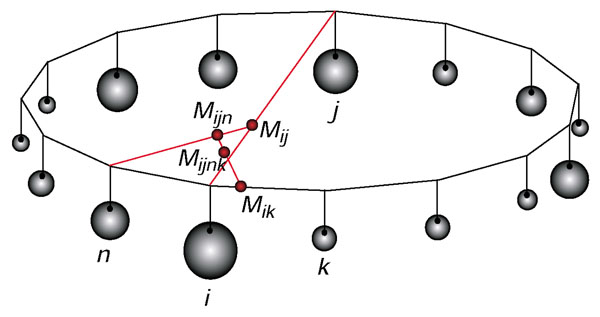
Figure 1

Open in a new tab

Schematic presentation of calculating and plotting probability vectors into a dekapentagon. Posterior probabilities associated with each vertex are represented as weights attached to the vertices. Points M indicate locations of center of gravities of vertices that are mentioned in the index associated with each point M. See Materials and methods for details of the calculation of the coordinates.

It is worth noting that while every probability vector maps to a unique place in the optimized dekapentagonal map, the reverse is not true. A single point inside the dekapentagonal map corresponds to infinitely many probability vectors. For example, a point in the center just indicates that the probabilities for topologies on opposing sites of the dekapentagon cancel each other out, but it does not indicate the identities of these topologies. Also, some points might be located close to one vertex only because the probability vector equally supports the topologies located on both neighboring vertices of the vertex. However, these points are only 'misplaced' because of the fact that the corresponding datasets do not strongly favor one or other topology; that is, these vectors represent unresolved relationships.

We use a genetic algorithm to find the optimal arrangement of the topologies at the polygon vertices. The optimality criterion is to minimize the sum of shortest distances for each mapped probability vector to the polygon's circumference. We found that the algorithm quickly converges towards solutions that are related to one another by rotation; that is, the neighborhood relations between the different topologies are the same. As our genetic optimization algorithm is a stochastic process, we measure its success on the basis of the probability of convergence. Our confidence that the algorithm did indeed find an optimal solution rises with the probability that on subsequent runs the algorithm can reproduce the same solution and that other solutions found are always inferior to the one deemed optimal. We consistently obtained a convergence rate in the range of 66% to 100%: from 50 independent runs, 33 in one case and 50 in the other converged on the same arrangement, while 17 arrangements in the former case were suboptimal. This suggests that our genetic optimization algorithm does indeed converge on the optimal arrangement.

Comparative studies have shown that bootstrap values are more conservative measures of support than Bayesian posterior probabilities [2,4,8,9], and therefore they provide a more realistic assessment of the support that the different topologies receive. Also, simulation studies have shown that increase of the size of a dataset by introducing additional homologous sequences improves the accuracy of the reconstruction [10] (see [11] and [12] for recent discussion). Therefore, in addition to plotting posterior probabilities, we also calculated and mapped bootstrap support values for each QuintOP from extended datasets - that is, the datasets containing additional homologous sequences (see [4] for details on the calculation of bootstrap support values from extended datasets).

We applied both probability mapping according to [3] and bootstrap support-value mapping to two different genome quintets. The first is the case of five bacterial genomes representing the five phyla that contain organisms with chlorophyll-based photosynthesis. The other is an interdomain genome quintet consisting of representatives of all three domains of life.

Analysis of five photosynthetic bacterial genomes

For the genome quintet of photosynthetic organisms that we initially analyzed in [5], both the posterior probability map and the bootstrap support map show that a plurality of datasets support three tree topologies: numbers 5, 10, and 15 (see Figures 2 and 3). The extended datasets (Figure 3) provide a more realistic illustration of the reliability of the individual analyses than the map based on the ML-mapping approach (Figure 2). While the plurality consensus is still discernable in Figure 3, many datasets do not map close to any of the vertices, suggesting that these sets of orthologous proteins cannot discriminate between at least some of the possible phylogenies. One might be tempted to conclude that not much phylogenetic information survived and that the apparent conflicts [5] were due to a lack of resolution only [13]. However, each five-taxon tree has two internal branches, that is, two bipartitions that contain phylogenetic information. The smallest quantum of phylogenetic information is the individual bipartition, not the resolved tree topology. In the five-taxon case a bipartition can be viewed as a partially unresolved tree where two taxa are grouped together, while the relationship among the other three taxa remains unresolved. An analysis of the possible bipartitions is a better way to gauge the extent of surviving phylogenetic information and the conflict between the individual datasets than dekapentagonal maps. We summarize the support for the 10 possible bipartitions in the form of a histogram (Figure 4). The bipartition corresponding to the plurality consensus signal for trees 5, 10 and 15 is labeled as bipartition A. This bipartition has plurality support. Xiong et al.[14] reported that enzymes involved in (bacterio)chlorophyll biosynthesis are supporting the topology that in the dekapentagonal map is labeled as topology 13. Topology 13 corresponds to two bipartitions labeled as E and G in Figure 4. In our set of 188 QuintOPs, only a few members of the chlorophyll biosynthesis pathway are present: bchB/chlB, bchL/chlL and chlM. The other members of the chlorophyll biosynthesis pathway were not picked up because of the strict requirements imposed on the QuintOP assembly, that is, the requirement that the open reading frames (ORFs) that form a QuintOP mutually pick up each other in all five genomes as top-scoring BLAST hits. The reason that some members of the chlorophyll biosynthetic pathways are not assembled into QuintOPs is that there are multiple paralogous genes present in some of those genomes (especially in the Chlorobium and Chloroflexus genomes), and these prevent proper QuintOPs from being formed. We manually compiled the extended datasets for bchH/chlH, bchI/chlI, bchD/chlD, bchN/chlN genes and calculated the bootstrap support values for bipartitions A, E and G with different phylogenetic methods (Figure 5). In all cases the members of the photosynthetic pathway do not support the plurality bipartition, but significantly support the bipartitions reported by Xiong et al. [14]. This suggests that the genes from the chlorophyll biosynthetic pathway have a phylogenetic history different from the apparent plurality consensus.

Figure 2.

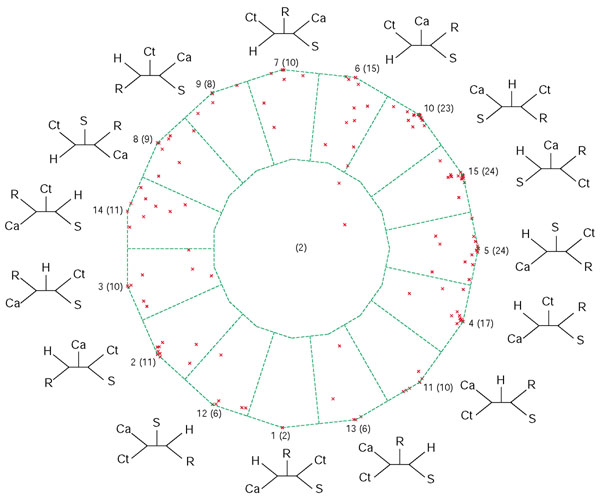
Figure 2

Open in a new tab

Posterior probability map for the analyses of five photosynthetic genomes: Synechocystis sp., Chloroflexus aurantiacus, Chlorobium tepidum, Rhodobacter capsulatus and Heliobacillus mobilis. Each QuintOP is represented by a point inside the dekapentagon (there are a total of 188 points for 188 sets of orthologs common to the five genomes [5]). The dekapentagon is divided into zones of proximity to topologies: points that fall into one of the 15 zones that correspond to the 15 tree topologies favor either that topology most or several neighboring topologies, and points that fall into the single central zone represent unresolved relationships. The tree topology number (1 to 15) is given first, followed by the number of points per zone in parentheses. Tree topology numbers correspond to the abbreviations described in [5]. Abbreviations: Ca, Chloroflexus aurantiacus; Ct, Chlorobium tepidum; H, Heliobacillus mobilis; R, Rhodobacter capsulatus.

Figure 3.

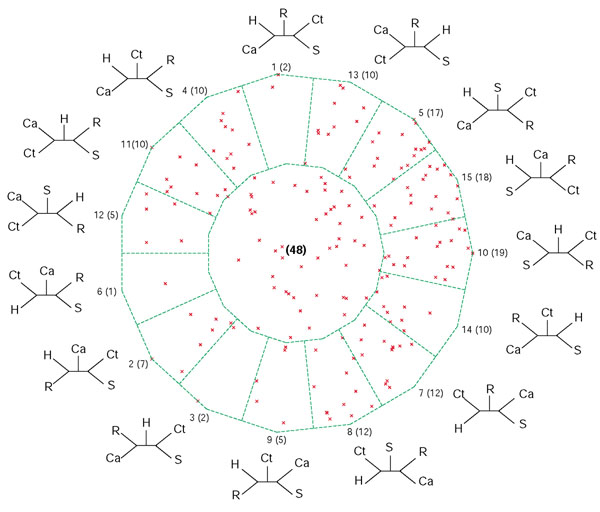
Figure 3

Open in a new tab

Bootstrap support map from extended QuintOPs of five photosynthetic genomes. For notations see legend to Figure 2.

Figure 4.

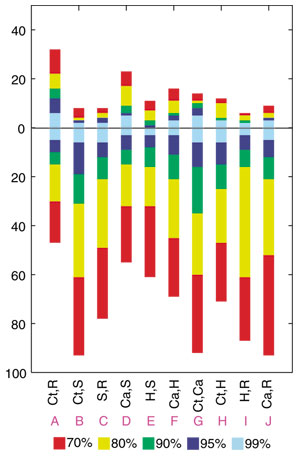
Figure 4

Open in a new tab

Modified Lento-plot for a genome quintet with five photosynthetic bacteria. We summarized the results for 15 trees into 10 possible bipartitions. Each bipartition is labeled on the modified Lento plot [29] by the two taxa that group together (the other three taxa are in an unresolved trifurcation), and by a letter A through J. For each bipartition, the bar above the x-axis gives the number of datasets that support the bipartition and the bar below the x-axis indicates the number of datasets that conflict with this bipartition. This conflict value is calculated as the sum of support for all conflicting bipartitions. The levels of support are color coded. Every bipartition is represented by at least several datasets with significant support. The plurality bipartition (grouping Chlorobium with Rhodobacter) is supported by 32 datasets with bootstrap support 70% or better. However, even more datasets support its conflicting bipartitions, and therefore appear in conflict with the plurality topology. Abbreviations as in Figure 2.

Figure 5.

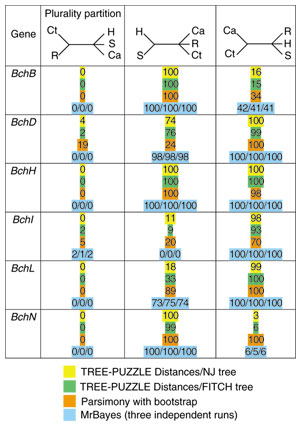
Figure 5

Open in a new tab

Summary of phylogenetic analyses of photosynthetic genes with different tree-reconstruction methods. For each gene (indicated in the first column) sequences from the genome quintet were supplemented with homologous sequences from other photosynthetic bacteria (see Materials and methods for details). Support is shown for the plurality consensus bipartition (compare Figure 4), and for the two bipartitions that correspond to the tree for photosynthetic genes reported in [14]. Support values for the different methods of phylogenetic reconstruction are color coded.

Contributions to a eukaryotic genome during its evolution

Genes in eukaryotes are proposed to represent different contributions from different organisms (Figure 6). If appropriate representatives of the bacterial and archaeal domains are chosen, the genes that were acquired from different putative contributors to the eukaryotic lineage can be differentiated through different tree topologies. Here we attempt to partition a eukaryotic genome with respect to the different contributions. We selected the genome quintet containing one well-annotated eukaryote (Saccharomyces cerevisiae), two archaea representing two archaeal kingdoms (the euryarchaeote Archaeoglobus fulgidus and the crenarchaeote Sulfolobus solfataricus), and two bacteria (the alpha-proteobacterium Rhodobacter capsulatus and the Gram-positive bacterium Bacillus subtilis).

Figure 6.

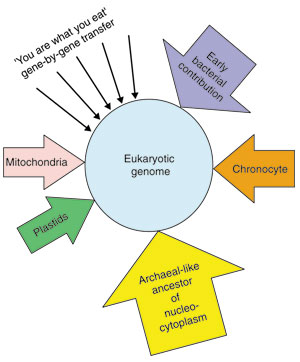
Figure 6

Open in a new tab

Schematic diagram of established and proposed contributions to the eukaryotic genome. The eukaryotic genome is proposed to contain genes from many different sources. The nucleocytoplasm was proposed to have evolved from an archaeal-like ancestor [47,48]. This archaeal ancestor was either an organism that branched off before the most recent common ancestor of the today's archaea (as in the traditional rRNA-based tree of life that contains a monophyletic archaeal clade [15]), or it might have been more specifically related to the crenarchaeota (as in the eocyte proposal [16], which results in the archaea being a paraphyletic grouping). Other well-corroborated contributions are the mitochondria and chloroplasts [49], which evolved from bacterial endosymbionts, and which contributed many genes to the nuclear genome [50]. Additional contributions were proposed to have originated from now-extinct organisms [26,27], such as the 'chronocyte', and through many single-gene transfers from many different sources that might have been ingested as food by early eukaryotes [25].

For the interdomain genome quintet (Figures 7, 8) most support-value vectors map close to four vertices: topology 11 (corresponding to the traditional ribosomal RNA tree as described by [15]), topology 12 (supporting the eocyte hypothesis, [16]), topology 9 (predicted for the genes of mitochondrial origin) and topology 4 (eukaryotic homolog with other bacteria). Notably, there are some datasets that support other topologies (see Table 1): the large subunit of carbamoyl-phosphate synthase supports topology 2, which groups a euryarchaeote within the Bacteria, and ribosomal protein S3 homologs support topology 15, which groups yeast with Archaeoglobus. The large subunit of carbamoyl-phosphate synthase contains an internal duplication ([17-19], and A. Lazcano, personal communication) and its phylogeny was described as being consistent with an interdomain horizontal gene transfer from the bacteria to the ancestor of the euryarchaeota [20-22]. Topologies 4 and 12 might represent different prokaryotic contributions to the yeast genome, transfers between the two prokaryotic domains, or a single bacterial contribution to the eukaryotic cell [23,24]. In all those datasets that group the eukaryotic homolog with bacterial sequences we were not able to detect any consistent phylogenetic signature. This finding is in agreement with the 'you are what you eat' hypothesis [25], but it also could be due to limited phylogenetic information surviving in the individual datasets.

Figure 7.

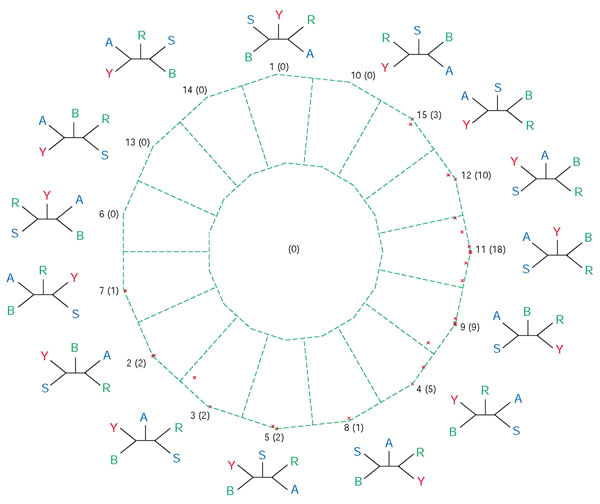
Figure 7

Open in a new tab

Posterior probability map of QuintOPs from an interdomain genome quintet. The quintet consists of genomes of yeast Saccharomyces cerevisiae (Y, red), the alpha-proteobacterium Rhodobacter capsulatus (R, green), the Gram-positive bacterium Bacillus subtilis (B, green), the euryarchaeote Archaeoglobus fulgidus (A, blue) and the crenarchaeote Sulfolobus solfataricus (S, blue). There are 53 QuintOPs in this genome quintet. For notations see legend for Figure 2.

Figure 8.

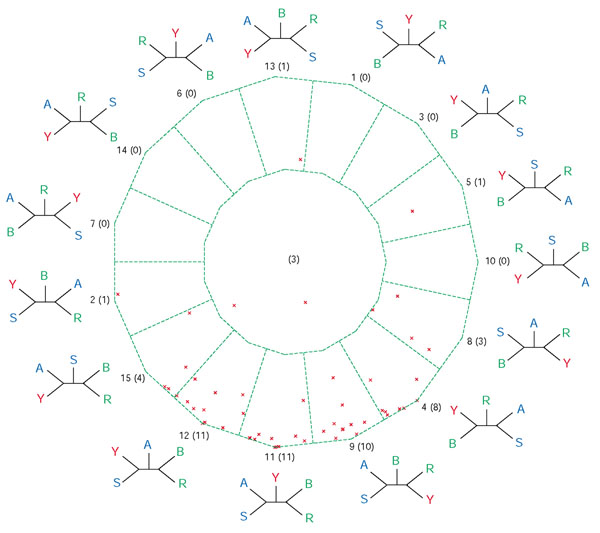
Figure 8

Open in a new tab

Bootstrap support map from extended QuintOPs for an interdomain quintet. For notations see legends for Figures 2 and 7.

Table 1.

List of QuintOPs that support the indicated tree topology with bootstrap support above 65%

Function Supporting hypothesis Bootstrap support
Undecaprenyl diphosphate synthase homologs Tree 11 [15] 81
Seryl-tRNA synthetase Tree 11 [15] 100
Arginyl-tRNA synthetase homologs Tree 11 [15] 67
Succinyl-CoA synthetase, beta subunit Tree 11 [15] 96
Signal recognition particle, subunit SRP54 Tree 11 [15] 68
Nicotinate-nucleotide pyrophosphorylase Tree 11 [15] 77
Anthranilate phosphoribosyltransferase Tree 11 [15] 70
Glu-tRNA amidotransferase, subunit A homologs Tree 11 [15] 69
Phenylalanyl-tRNA synthetase alpha subunit Tree 11 [15] 99
Adenylosuccinate lyase Tree 11 [15] 75
Aspartate aminotransferase Tree 12 [16] 92
Carbamoyl-phosphate synthase, small subunit Tree 12 [16] 83
Ketol-acid reductoisomerase homologs Tree 12 [16] 72
Dihydroxy-acid dehydratase Tree 12 [16] 100
Homoserine dehydrogenase Tree 12 [16] 82
Histidinol-phosphate aminotransferase Tree 12 [16] 66
NH3-dependent NAD+ synthetase Tree 9: genes of mitochondrial origin 67
Argininosuccinate synthetase Tree 9: genes of mitochondrial origin 95
Carbamoyl-phosphate synthase large subunit Tree 2 [20] 91
Phosphoglycerate kinase Tree 4 79
Hypothetical protein Tree 4 100
Translation initiation factor eIF-2B homologs Tree 4 67
Argininosuccinate lyase Tree 4 75
Glutamate synthase Tree 4 80
Phosphoribosylformylglycinamidine synthase Tree 15 73
Ribosomal protein S3 homologs Tree 15 71
Open in a new tab

Tree numbers correspond to the designations in used in Figures 7 and 8.

The dekapentagonal maps depicted in Figures 7 and 8 emphasize the mosaicism of the eukaryotic genome of yeast, and delineate different contributions to the yeast genome that have occurred over the course of evolution. The map reveals that individual datasets support different, in some instances conflicting, hypotheses proposed to explain the origin of eukaryotes. While the resulting maps illustrate the mosaic nature of the eukaryotic genome, their discriminatory power regarding different proposed contributions is limited. For example, the datasets that support the traditional topology (number 11) are equally compatible with genes that were contributed to the eukaryotic cell via the chronocyte [26]. Because our approach only considers unrooted trees, the two scenarios result in identical topologies, with only the branch lengths differing under the two scenarios, that is, the genes contributed by the chronocyte are expected to have the eukaryotic genes on very long branches [27]. Another shortcoming is that the map includes only two bacterial taxa. Without inspecting the phylogenies inferred from the extended datasets (see above) it is impossible to decide if many genes were contributed from a single bacterium, as assumed in hypotheses proposed in [23,24,28], or were acquired through many independent transfers [25].

Conclusions

Dekapentagonal mapping provides a useful extension to the earlier developed ML-, posterior probability, and bootstrap support-values mapping for four genomes described in [2] and [4]. For the analyses of four genomes the mapping of the support values to the two-dimensional space is unique; for analyses of five genomes we had to select one out of the many possible projections of the 15-dimensional support-value vectors to two-dimensional space. We used an optimality criterion to perform a heuristic search for a map that would emphasize genome mosaicism and frequently unresolved bifurcations. Support-value mapping using an optimized barycentric coordinate system allows us to dissect genomes into parts that have different evolutionary histories, and to focus attention on genes that contain atypical phylogenetic information.

If most of the individual molecular phylogenies are unresolved, analysis of individual bipartitions provides a means to assess a plurality phylogenetic signal. The modified Lento plot [29] applied to extended datasets provides both the bipartitions supported by the plurality of genes, and the number of genes that significantly disagree with these bipartitions.

Materials and methods

Genome quintets

The first genome quintet consists of five photosynthetic bacteria from five bacterial phyla: Rhodobacter capsulatus, Chlorobium tepidum, Chloroflexus aurantiacus, Heliobacillus mobilis and Synechocystis sp. PCC 6803.

The second genome quintet consists of genomes representing all three domains of life: the yeast genome of Saccharomyces cerevisiae, the alpha-proteobacterium Rhodobacter capsulatus, the Gram-positive bacterium Bacillus subtilis, the euryarchaeote Archaeoglobus fulgidus and the crenarchaeote Sulfolobus solfataricus.

The Rhodobacter capsulatus and Heliobacillus mobilis genome data were obtained from Integrated Genomics [30]. Genome sequence for Chlorobium tepidum was downloaded from The Institute for Genomic Research (TIGR) [31]. The Rhodopseudomonas palustris genome was downloaded from the DOE Joint Genome Institute [32]. Other genomes for the genome quintets were downloaded from the National Center for Biotechnology Information (NCBI) [33].

Assembly of quintets of orthologous proteins (QuintOPs)

Detection of QuintOPs was analogous to detection of quartets of orthologous proteins [2]. In brief, for each genome in a genome quintet, BLAST [34] searches of every ORF in one genome against the other three genomes were performed using the blastp program. The E-value cutoff for the BLAST searches was set to 10-4. We defined QuintOPs as those sets of genes that mutually pick each other as the top-scoring hit in all pairwise genome BLAST comparisons. The amino-acid sequences for each QuintOP were retrieved and the datasets were aligned with ClustalW [35]. Maximum likelihoods for 15 tree topologies for each QuintOP were calculated using TREE-PUZZLE version 5.1 [36] under the auto-detected substitution model. Posterior probability vectors were calculated from ML values.

Assembly of extended datasets for the QuintOPs

For each sequence in a QuintOP we detect the top-scoring BLAST [34] hit with an E-value above 10-8 in each of 60 completely sequenced archaeal and bacterial reference genomes (Aeropyrum pernix, Archaeoglobus fulgidus, Anabaena sp., Aquifex aeolicus, Agrobacterium tumefaciens, Borrelia burgdorferi, Bradyrhizobium japonicum, Bifidobacterium longum, Bacillus subtilis, Brucella suis, Buchnera sp., Clostridium acetobutylicum, Caulobacter crescentus, Corynebacterium glutamicum, Campylobacter jejuni, Clamydophila pneumoniae, Deinococcus radiodurans, Escherichia coli K12, Fusobacterium nucleatum, Halobacterium sp., Haemophilus influenzae, Helicobacter pylori, Leptospira interrogans, Lactococcus lactis, Listeria monocytogenes, Lactobacillus plantarum, Mycoplasma genitalium, Methanococcus jannaschii, Methanopyrus kandleri, Mezorhizobium loti, Methanosarcina mazei, Methanobacterium thermoautotrophicum, Mycobacterium tuberculosis, Neisseria meningitides, Oceanobacillus iheyensis, Pseudomonas aeruginosa, Pyrobaculum aerophilum, Pyrococcus horikoshii, Pasteurella multocida, Rickettsia conorii, Ralstonia solanacearum, Staphylococcus aureus, Streptomyces coelicolor, Sinorhizobium meliloti, Shewanella oneidensis, Sulfolobus solfataricus, Salmonella typhi, Synechocystis sp., Thermoplasma acidophilum, Thermosynechococcus elongates, Thermotoga maritime, Treponema pallidum, Thermoanaerobacter tengcongensis, Tropheryma whipplei, Ureaplasma urealyticum, Vibrio cholerae, Wigglesworthia brevipalpis, Xanthomonas campestris, Xylella fastidiosa, Yersinia pestis). These genomes were downloaded from the NCBI [33]. The resulting sequences were added to the QuintOP dataset and duplicated sequences were eliminated. The datasets were aligned with ClustalW [35], and 100 bootstrap samples were generated using the SEQBOOT program from the PHYLIP package version 3.6a2.1 [37]. The distances were generated using TREE-PUZZLE version 5.1 [36] under the auto-detected substitution model. Neighbor-joining trees were calculated from these distances using NEIGHBOR from the PHYLIP package version 3.6a2.1 [37]. The resulting trees were parsed with respect to which of the 15 five-taxon subtrees they contain.

Calculation of posterior probability vector locations for individual QuintOPs

The dekapentagon was placed into the Cartesian coordinate system with its center coinciding with the origin of the coordinate system. Then the coordinates (xi, yi) of a vertex i are xi = R*cos(i*360/15), yi = R*sin(i*360/15), where R is the distance from origin to the vertex (equal for all the vertices due to the location of the origin of the coordinate system), and 1 ≤ i ≤ 15. For each pair of vertices i and j the coordinates of the center of gravity Mij (xM, yM) are calculated according to the law of the lever: xM = xi + (xj - xi)*pj/(pi + pj), yM = yi + (yj - yi)*pj/(pi + pj), where pi and pj are the posterior probabilities of vertices i and j. The process is repeated for all pairs of vertices, and then iteratively for all 'intermediate' centers of gravities until only one pair of coordinates remains, which gives the center of gravity of the dekapentagon that is equivalent to the location of probability vector. The resulting coordinates of the dekapentagon's center of gravity do not depend on the order in which the masses are combined.

Finding of optimal arrangement and testing it for reproducibility

There are (15 - 1)!/2 = 14!/2 ≈ 4*1010 possible arrangements of topologies on dekapentagon's vertices (only free circular permutations [38] are counted, and the arrangements that become equivalent by rotation of dekapentagon or flipping the dekapentagon over are considered as the same arrangements). The arrangement was considered optimal when the topologies arranged at the polygon vertices in such way that maximizes the sum of all distances of the barycentric points from the center of the polygon. There are too many arrangements of topologies around the dekapentagon to search for the optimal arrangement exhaustively. Therefore, we used a heuristic search for optimal solutions based on a hybrid genetic algorithm [39]. Each tree topology was assigned a numerical identifier (1 through 15), and the arrangements of topologies around the dekapentagon's vertices were encoded as arrays of the tree topology identifiers where each position in the array represents a position on the polygon circumference. The genetic algorithm applies mutation and cross-over operations to each successive generation of arrangements until the optimal solution is obtained [40]. Each generation consisted of a population of 300 individuals. In order to preserve diversity among the individuals as much as possible and prevent premature convergence of the algorithm the population was divided into 10 demes (subpopulations) each with 30 individuals and with controlled migration between demes.

We hybridized the genetic algorithm by equipping the algorithm with a local search heuristic in addition to the global search strategy based on the genetic operators to explore better the space of possible arrangements. A manuscript reporting details on the algorithm for finding the optimal arrangements is in preparation (L.H., O.Z. and J.P.G., unpublished work). The program calculating the optimal arrangement of topologies is available on request.

To test the reproducibility, the search for the optimal arrangement was repeated independently 50 times with different starting seeds.

Plotting

The resulting posterior probability and bootstrap support vectors were plotted into dekapentagonal maps using GNUPLOT version 3.7 [41].

Analyses of genes from the chlorophyll biosynthesis pathway

Sequences from the genome quintet were supplemented with homologous sequences from other photosynthetic bacteria to improve taxon sampling, aligned with ClustalW [35], and phylogenetic trees were reconstructed. For distance and parsimony analyses, 100 bootstrap samples were generated with SEQBOOT [37]. Distances were calculated in TREE-PUZZLE v. 5.1 [36] with among-site rate variation taken into account. Neighbor-joining trees were calculated with NEIGHBOR [37], Fitch-Margoliash trees with FITCH [37], protein parsimony trees with PROTPARS [37]. MrBayes version 3.0B4 [42] analyses were run three times independently for 500,000 generations per run (100,000 of which were burned in), under the JTT substitution model [43], and with an exponential prior set for branch length.

Software packages used

Scripts for data manipulation were written in Perl and used many of the SEALS package subroutines [44]. Tree-parsing programs were written in Java utilizing PAL library classes [45]. The genetic algorithm was written in C++ and is based on the genetic algorithm library GALIB version 2.4.5 [46].

Additional data files

Additional data file 1 contains accession numbers for the datasets in two genome quintets analyzed in this article.

Supplementary Material

Additional data file 1

Accession numbers for the datasets in two genome quintets analyzed

Click here for additional data file (85.9KB, pdf)

Acknowledgments

Acknowledgements

We thank Korbinian Strimmer for useful comments on the manuscript. This work was supported through the NASA Astrobiology Institute at Arizona State University, the NASA Exobiology Program, and in part through the NSF Microbial Genetics Program.

References

  1. Gogarten JP. The early evolution of cellular life. Trends Ecol Evol. 1995;10:147–151. doi: 10.1016/S0169-5347(00)89024-2. [DOI] [PubMed] [Google Scholar]
  2. Zhaxybayeva O, Gogarten JP. Bootstrap, Bayesian probability and maximum likelihood mapping: Exploring new tools for comparative genome analyses. BMC Genomics. 2002;3:4. doi: 10.1186/1471-2164-3-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Strimmer K, von Haeseler A. Likelihood-mapping: a simple method to visualize phylogenetic content of a sequence alignment. Proc Natl Acad Sci USA. 1997;94:6815–6819. doi: 10.1073/pnas.94.13.6815. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Zhaxybayeva O, Gogarten JP. An improved probability mapping approach to assess genome mosaicism. BMC Genomics. 2003;4:37. doi: 10.1186/1471-2164-4-37. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Raymond J, Zhaxybayeva O, Gogarten JP, Gerdes SY, Blankenship RE. Whole-genome analysis of photosynthetic prokaryotes. Science. 2002;298:1616–1620. doi: 10.1126/science.1075558. [DOI] [PubMed] [Google Scholar]
  6. Li W-H. Molecular Evolution. Sunderland, MA: Sinauer Associates; 1997. [Google Scholar]
  7. Billera LJ, Holmes SP, Vogtmann K. Geometry of the space of phylogenetic trees. Adv Appl Math. 2001;27:733–767. doi: 10.1006/aama.2001.0759. [DOI] [Google Scholar]
  8. Douady CJ, Delsuc F, Boucher Y, Doolittle WF, Douzery EJ. Comparison of bayesian and maximum likelihood bootstrap measures of phylogenetic reliability. Mol Biol Evol. 2003;20:248–254. doi: 10.1093/molbev/msg042. [DOI] [PubMed] [Google Scholar]
  9. Alfaro ME, Zoller S, Lutzoni F. Bayes or bootstrap? A simulation study comparing the performance of bayesian markov chain monte carlo sampling and bootstrapping in assessing phylogenetic confidence. Mol Biol Evol. 2003;20:255–266. doi: 10.1093/molbev/msg028. [DOI] [PubMed] [Google Scholar]
  10. Graybeal A. Is it better to add taxa or characters to a difficult phylogenetic problem? Syst Biol. 1998;47:9–17. doi: 10.1080/106351598260996. [DOI] [PubMed] [Google Scholar]
  11. Hillis DM, Pollock DD, McGuire JA, Zwickl DJ. Is sparse taxon sampling a problem for phylogenetic inference? Syst Biol. 2003;52:124–126. doi: 10.1080/10635150309356. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Rosenberg MS, Kumar S. Taxon sampling, bioinformatics, and phylogenomics. Syst Biol. 2003;52:119–124. doi: 10.1080/10635150309344. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Daubin V, Moran NA, Ochman H. Phylogenetics and the cohesion of bacterial genomes. Science. 2003;301:829–832. doi: 10.1126/science.1086568. [DOI] [PubMed] [Google Scholar]
  14. Xiong J, Fischer WM, Inoue K, Nakahara M, Bauer CE. Molecular evidence for the early evolution of photosynthesis. Science. 2000;289:1724–1730. doi: 10.1126/science.289.5485.1724. [DOI] [PubMed] [Google Scholar]
  15. Woese CR, Kandler O, Wheelis ML. Towards a natural system of organisms: proposal for the domains Archaea, Bacteria, and Eucarya. Proc Natl Acad Sci USA. 1990;87:4576–4579. doi: 10.1073/pnas.87.12.4576. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Lake JA. Origin of the eukaryotic nucleus determined by rate-invariant analysis of rRNA sequences. Nature. 1988;331:184–186. doi: 10.1038/331184a0. [DOI] [PubMed] [Google Scholar]
  17. Lawson FS, Charlebois RL, Dillon JA. Phylogenetic analysis of carbamoylphosphate synthetase genes: complex evolutionary history includes an internal duplication within a gene which can root the tree of life. Mol Biol Evol. 1996;13:970–977. doi: 10.1093/oxfordjournals.molbev.a025665. [DOI] [PubMed] [Google Scholar]
  18. Schofield JP. Molecular studies on an ancient gene encoding for carbamoyl-phosphate synthetase. Clin Sci (Lond) 1993;84:119–128. doi: 10.1042/cs0840119. [DOI] [PubMed] [Google Scholar]
  19. van den Hoff MJ, Jonker A, Beintema JJ, Lamers WH. Evolutionary relationships of the carbamoylphosphate synthetase genes. J Mol Evol. 1995;41:813–832. doi: 10.1007/BF00173161. [DOI] [PubMed] [Google Scholar]
  20. Olendzenski L, Gogarten JP. Deciphering the molecular record for the early evolution of life: Gene duplication and horizontal gene transfer. In: Wiegel J, Adams MWW, editor. Thermophiles: The Keys to Molecular Evolution and the Origin of Life? Philadelphia: Taylor & Francis; 1998. pp. 165–176. [Google Scholar]
  21. Olendzenski L, Hilario E, Gogarten JP. Horizontal gene transfer and fusing lines of descent: the archaebacteria - a chimera? In: Syvanen M, Kado C, editor. Horizontal Gene Transfer. 1. London: Chapman and Hall; 1998. pp. 349–362. [Google Scholar]
  22. Cammarano P, Gribaldo S, Johann A. Updating carbamoylphosphate synthase (CPS) phylogenies: occurrence and phylogenetic identity of archaeal CPS genes. J Mol Evol. 2002;55:153–160. doi: 10.1007/s00239-002-2312-6. [DOI] [PubMed] [Google Scholar]
  23. Zillig W, Palm P, Klenk H-P. A model of the early evolution of organisms: the arisal of the three domains of life from the common ancestor. In: Hartman H, Matsuno K, editor. The Origin and Evolution of the Cell. Singapore: World Scientific Publishing; 1992. pp. 163–182. [Google Scholar]
  24. Gupta RS, Golding GB. Evolution of HSP70 gene and its implications regarding relationships between archaebacteria, eubacteria, and eukaryotes. J Mol Evol. 1993;37:573–582. doi: 10.1007/BF00182743. [DOI] [PubMed] [Google Scholar]
  25. Doolittle WF. You are what you eat: a gene transfer ratchet could account for bacterial genes in eukaryotic nuclear genomes. Trends Genet. 1998;14:307–311. doi: 10.1016/S0168-9525(98)01494-2. [DOI] [PubMed] [Google Scholar]
  26. Hartman H. The origin of the eukaryotic cell. Speculations Sci Technol. 1984;7:77–81. [PubMed] [Google Scholar]
  27. Sogin ML. Early evolution and the origin of eukaryotes. Curr Opin Genet Dev. 1991;1:457–463. doi: 10.1016/s0959-437x(05)80192-3. [DOI] [PubMed] [Google Scholar]
  28. Lake JA, Rivera MC. Was the nucleus the first endosymbiont? Proc Natl Acad Sci USA. 1994;91:2880–2881. doi: 10.1073/pnas.91.8.2880. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Lento GM, Hickson RE, Chambers GK, Penny D. Use of spectral analysis to test hypotheses on the origin of pinnipeds. Mol Biol Evol. 1995;12:28–52. doi: 10.1093/oxfordjournals.molbev.a040189. [DOI] [PubMed] [Google Scholar]
  30. Integrated Genomics http://www.integratedgenomics.com
  31. The Institute for Genomic Research http://www.tigr.org
  32. DOE Joint Genome Institute http://www.jgi.doe.gov/JGI_microbial/html/index.html
  33. National Center for Biotechnology Information http://www.ncbi.nlm.nih.gov
  34. Altschul SF, Madden TL, Schaffer AA, Zhang J, Zhang Z, Miller W, Lipman DJ. Gapped BLAST and PSI-BLAST: a new generation of protein database search programs. Nucleic Acids Res. 1997;25:3389–3402. doi: 10.1093/nar/25.17.3389. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Thompson JD, Higgins DG, Gibson TJ. CLUSTAL W: improving the sensitivity of progressive multiple sequence alignment through sequence weighting, position-specific gap penalties and weight matrix choice. Nucleic Acids Res. 1994;22:4673–4680. doi: 10.1093/nar/22.22.4673. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Schmidt HA, Strimmer K, Vingron M, von Haeseler A. TREE-PUZZLE: maximum likelihood phylogenetic analysis using quartets and parallel computing. Bioinformatics. 2002;18:502–504. doi: 10.1093/bioinformatics/18.3.502. [DOI] [PubMed] [Google Scholar]
  37. Felsenstein J. PHYLIP (Phylogeny Inference Package) version 3.6. Distributed by the author: Department of Genetics, University of Washington, Seattle. 1993.
  38. MathWord: circular permutations http://mathworld.wolfram.com/CircularPermutation.html
  39. Goldberg DE. Genetic Algorithms in Search, Optimization and Machine Learning. Boston, MA: Addison-Wesley; 1989. [Google Scholar]
  40. Holland JH. Adaptation in Natural and Artificial Systems. Ann Arbor: University of Michigan Press; 1975. [Google Scholar]
  41. GNUPLOT central http://www.gnuplot.info
  42. Huelsenbeck JP, Ronquist F. MRBAYES: Bayesian inference of phylogenetic trees. Bioinformatics. 2001;17:754–755. doi: 10.1093/bioinformatics/17.8.754. [DOI] [PubMed] [Google Scholar]
  43. Jones DT, Taylor WR, Thornton JM. The rapid generation of mutation data matrices from protein sequences. Comput Appl Biosci. 1992;8:275–282. doi: 10.1093/bioinformatics/8.3.275. [DOI] [PubMed] [Google Scholar]
  44. Walker DR, Koonin EV. SEALS: a system for easy analysis of lots of sequences. Proc Int Conf Intell Syst Mol Biol. 1997;5:333–339. [PubMed] [Google Scholar]
  45. Drummond A, Strimmer K. PAL: an object-oriented programming library for molecular evolution and phylogenetics. Bioinformatics. 2001;17:662–663. doi: 10.1093/bioinformatics/17.7.662. [DOI] [PubMed] [Google Scholar]
  46. Wall M. GALIB: A C++ library of genetic algorithm components http://lancet.mit.edu/ga
  47. Gogarten JP, Kibak H. The bioenergetics of the last common ancestor and the origin of the eukaryotic endomembrane systems. In: Hartman H, Matsuno K, editor. The Origin and Evolution of the Cell. Singapore: World Scientific Publishing; 1992. pp. 131–154. [Google Scholar]
  48. Cavalier-Smith T. Origin of the cytoskeleton. In: Hartman H, Matsuno K, editor. The Origin and Evolution of the Cell. Singapore: World Scientific Publishing; 1992. pp. 79–106. [Google Scholar]
  49. Sagan L. On the origin of mitosing cells. J Theor Biol. 1967;14(3):255–274. doi: 10.1016/0022-5193(67)90079-3. [DOI] [PubMed] [Google Scholar]
  50. Martin W. Gene transfer from organelles to the nucleus: Frequent and in big chunks. Proc Natl Acad Sci USA. 2003;100:8612–8614. doi: 10.1073/pnas.1633606100. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Additional data file 1

Accession numbers for the datasets in two genome quintets analyzed

Click here for additional data file (85.9KB, pdf)

Articles from Genome Biology are provided here courtesy of BMC

RESOURCES