Short abstract
This study presents an algorithm to infer direct regulatory relationships using gene expression profiles from cells in which individual genes are deleted or overexpressed.
Abstract
Here we build on a previously proposed algorithm to infer direct regulatory relationships using gene-expression profiles from cells in which individual genes are deleted or overexpressed. The updated algorithm can process networks containing feedback loops, incorporate positive and negative regulatory relationships during network reconstruction, and utilize data from double mutants to resolve ambiguous regulatory relationships. When applied to experimental data the reconstruction procedure preferentially retains direct transcription factor-target relationships.
Background
Gene-expression studies, using cDNA or oligonucleotide arrays, hold promise for elucidating the structure of genetic regulatory networks. A wealth of computational techniques have been proposed for extracting regulatory relationships from these data, many of which rely on correlated expression patterns to identify temporally co-regulated genes (reviewed in [1,2]). While these methods often detect important patterns, they cannot definitively identify the targets of transcriptional regulators.
Another approach to identifying regulatory targets involves perturbing gene activity by deleting or overexpressing a transcription factor, and analyzing the effects on the gene-expression profile. However, transcripts affected in such experiments include those of both direct and indirect targets of the perturbed gene, and in some cases the latter may dominate. Various methods have been used to identify the direct targets among the affected genes, including promoter sequence examination and/or genome-wide location analysis [3,4]. In an earlier article, one of us proposed pooling data from a complete set of single-mutant gene-expression profiles to reconstruct a tentative network, then enriching for direct targets by paring the network down to the simplest acyclic directed graph (digraph) consistent with the available data [5].
Acyclic networks, by definition, lack feedback pathways through which genes can regulate their own activity. As feedback pathways are known to exist in regulatory networks, the previously proposed algorithm also included a procedure by which it could be applied to any network, even one with cycles. This procedure transforms the network into an equivalent acyclic digraph, called a condensation, before reconstruction. The algorithm thus bypasses the cyclic components and reconstructs the acyclic portion of the network. The structure of the feedback pathways themselves, however, cannot be determined from steady-state single-mutant data [5].
To improve the ability of our algorithm to reconstruct all types of regulatory pathway, we drew from the traditional genetic approach of epistasis analysis. 'Epistasis' describes a phenomenon in which an allele of one gene can influence the phenotypic expression of an allele of another gene [6]. For example, an altered allele of a downstream gene in a biological pathway may block the effects of a mutation further upstream, thereby changing the outcome of a biological process. Such epistatic relationships can therefore be used to determine the order of gene function, or ascertain that two gene products act in parallel, independent pathways [7,8]. In epistasis analysis, genes involved in the process of interest are systematically perturbed; phenotypes of double mutants, with two genes perturbed, are compared to those of single mutants with only one perturbed gene. If the phenotype of a double mutant is different from either of the related single mutants, the two genes are presumed to act independently of each other. However, if the double mutant resembles one or the other single mutant, the genes are likely to participate in an ordered pathway and the gene whose mutant phenotype dominates is placed downstream of the other. This type of analysis has proved highly informative in the study of genetic, metabolic and signaling networks, suggesting that the inclusion of double-mutant data in genetic network analysis could greatly improve the accuracy of the network reconstruction.
Here we extend the capabilities of a genetic network reconstruction algorithm [5] to improve its performance and broaden its applicability. First, we implement a preprocessing step to accommodate feedback loops. Second, we modify the algorithm to consider positive and negative regulatory relationships when generating the reconstruction. Third, we utilize data from double mutants to resolve cyclical structures and to identify nontranscriptional or redundant regulatory relationships. The performance of these modified versions of the algorithm is then tested in multiple ways. We use synthetic networks to assess the ability of the cycle-accommodating algorithm to tolerate incomplete or noisy data, and to examine the potential improvement achieved by the incorporation of double-mutant data. Finally, we test the improved algorithm on published expression data from the budding yeast Saccharomyces cerevisiae and compare our results with transcription factor binding profiles.
Results
Graph theoretical framework
In this work we represent the genetic regulatory network as a directed graph or digraph, G, and all discussion of graphs here refers to digraphs. A digraph consists of nodes, which in this case correspond to genes, and directed edges, which in our model point from regulator to target. A graph can be represented by a diagram (Figure 1a) of nodes and edges. An alternative representation that fully defines the graph is the adjacency list, Adj(G), in which each node is listed along with the nodes to which it is connected by a directed edge (Figure 1b). In the context of a genetic regulatory network, the adjacency list of a gene includes all the genes it directly influences: for example, the genes whose promoters are bound by a transcription factor. The accessibility list, Acc(G), of the digraph lists each node along with all nodes that can be reached along a directed path of any length from that node (Figure 1c). For a genetic regulatory network, the accessibility list includes all genes whose transcription can be influenced by a gene, directly or indirectly. (For a more thorough discussion of digraphs, see [9].)
Figure 1.

Graphical representation of genetic regulatory networks. (a) A sample regulatory network; (b) its adjacency list; (c) its accessibility list; and (d) its condensation. (e) The reconstruction of this network, mapped onto the original nodes. Circles represent nodes, or genes, and arrows represent edges.
The genes whose transcript levels change when a gene is deleted or perturbed constitute an accessibility list for that gene. Reconstructing a genetic regulatory network from gene-expression data, therefore, is equivalent to determining an adjacency list based on an accessibility list [5]. Because an accessibility list does not define a unique graph, the algorithm seeks the minimum equivalent (or most parsimonious) graph, in which the number of edges is minimized. A unique most parsimonious graph, which provides a core set of edges that are present in all graphs sharing the accessibility list, exists by definition for an acyclic graph [5,10]. The algorithm obtains the simplest network that can explain the observations by a process that initially connects each perturbed gene to all genes affected by its perturbation then prunes away edges, called shortcuts, which connect one node with another node already accessible via a directed path.
Cycles present a special problem for the reconstruction algorithm in that a graph with cycles does not possess a unique minimum equivalent graph. A cycle is a closed path in a digraph that begins and ends on the same node and crosses at least one other node (for example, Figure 1a, nodes 7, 8, and 9). It is impossible to reconstruct the edges in a cycle on the basis of single-mutant data: all genes in a cycle have identical accessibility lists, so they are effectively equivalent. Such a group of nodes, in which each node can be reached from every other node, is called a strong component. A multinode strong component may contain one or many cycles, whereas each node not contained within a cycle is a strong component unto itself. Every graph has an equivalent acyclic graph [10], or condensation [9], in which each strong component is represented by a single node (Figure 1d). By mapping the tentative network onto this acyclic equivalent, the algorithm circumvents the problem of cycles [10]. This mapping is achieved by examining each perturbed gene and scanning its accessibility list for any reciprocally regulating genes, which are then assigned to the same component.
Extensions of the algorithm
While the previous paper [5] presented a basic procedure for reconstructing a network, several factors limit its applicability to gene-expression data. Here we address these shortcomings with a number of extensions. These modifications accommodate cycles in such a way that the error tolerance of the algorithm can be assessed, they distinguish between positive and negative regulation, and they incorporate information from double-mutant gene-expression profiles into the final reconstruction.
Accommodating cycles
In the previous paper, the error tolerance of the algorithm when reconstructing networks containing cycles was not examined. To compare graphs with different numbers of strong components, we devised a method of generating a reconstruction in which each node again represents one gene. In the reconstruction, any mutually regulating pairs of genes in the network are mapped onto the same strong component [5]. We have added a step to expand each strong component into its constituent genes by adding direct connections from each node in the component to all other nodes in the component, and between each node in the component and all nodes adjacent to the component (Figure 1e). This maps the reconstruction back onto the original set of nodes and allows it to be compared, edge by edge, to the original network. We chose to treat the components in this way because alternative approaches result in the undesirable situation of a single network having multiple possible reconstructions [10,11]. While our method can result in a number of extra edges in the reconstruction that are not part of the real network (false-positive edges), it does result in a unique reconstruction that minimizes the number of correct relationships missed (false-negative edges).
Positive and negative regulation
The original algorithm represents the regulatory network as a simple directed graph, in which the edges have neither magnitude nor sign. However, real genetic regulatory relationships can be either activating or repressing, and can vary in strength; failure to take this information into account could result in erroneous reconstruction. Although the strength of an interaction is difficult to determine from microarray data, it is simple to assess whether a regulatory influence is activating or repressing. Moreover, it is straightforward to incorporate this information into the reconstruction algorithm.
Mutant gene-expression data can be represented by an M × N accessibility matrix P(G), where M is the number of genes perturbed and N is the number of genes in the network. Each matrix element pij = 1 if there is an edge from node i to node j, and pij = 0 if no edge is present [5,9]. We modified this matrix such that pij = +1 if there is a positive regulatory relationship, and pij = -1 if there is a negative regulatory relationship. Thus, if the transcript level of gene j goes up when gene i is deleted, then gene i negatively regulates gene j and the matrix element pij = -1. Inspection reveals that any indirect regulatory pathway will have a value equal to the product of the intermediate edges, so the extended algorithm only prunes an edge, by converting the matrix element to zero, if this condition is met (Figure 2a, lines 15-19). For example, if the two intermediate edges both have a positive sign, the original algorithm will remove the shortcut regardless of its sign (Figure 2b), but the extended algorithm will only prune the edge if it is also positive (Figure 2c). Furthermore, an edge will not be pruned if the mediating node is a multigene strong component that contains some edges with negative sign, because edges to and from these components have ambiguous values.
Figure 2.
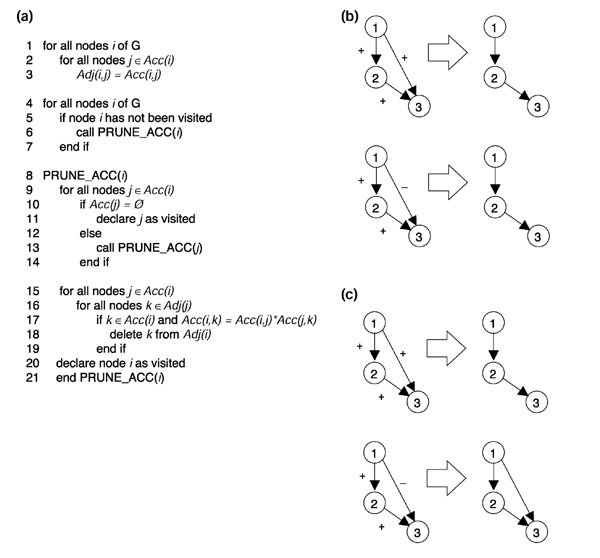
Edge-removal criteria. (a) Pseudocode of the algorithm including positive and negative regulation. Acc(i) and Adj(i) indicate the accessibility and adjacency lists for gene i, respectively, and Acc(i,j) indicates the value (+1 or -1) of the edge from i to j. (b) The original algorithm will pare away any edge connecting two nodes that already have a pathway between them. (c) Algorithm taking positive and negative regulation into account will only pare away an edge if its sign is equal to the product of the signs of the remaining edges in the pathway.
Double-mutant data
Reconstructions generated by the algorithm using data from single mutants may contain a number of unresolved strong components. Double-mutant data, from strains in which two genes have been perturbed, should allow the reconstruction of edges within these strong components. We therefore developed an algorithm (Figure 3a) that uses double-mutant data to refine the reconstruction generated with single-mutant data.
Figure 3.

Refining network structure with double-mutant data. (a) Pseudocode of the extension utilizing double-mutant data. Acc-j(i) indicates the accessibility list of gene i in the absence of gene j. i, j, k, and l are arbitrary indices for genes in the network. (b) An example of a three-gene cycle (top), its single-mutant accessibility lists (bottom left) and a reconstruction based on that data (bottom right). (c) The double-mutant accessibility lists for the cycle in (b) and the reconstruction process. For each set of double-mutant data (left), edges revealed to be indirect are removed from the reconstruction (right). The notation [1] 2 > indicates the accessibility list of gene 2 in a strain in which gene 1 is already perturbed. (d) A network in which genes 1 and 2 redundantly regulate gene 3 (right), and single-mutant and double-mutant accessibility lists for the network (left). (e) A network in which gene 1 regulates the activity of gene 3 indirectly by modifying the activity of a direct regulator, gene 2 (right); single- and double-mutant accessibility lists (left).
New accessibility lists for genes in a double mutant are generated by comparing the gene-expression profile of the double mutant to that of each single mutant. For example, in a simple three-gene cycle (Figure 3b), comparing the expression profile of a double mutant in which two genes have been deleted to that of a single mutant can reveal indirect relationships (Figure 3c). To incorporate this information, a reconstruction is first generated based on the single-mutant data alone (Figure 3b, bottom right), in which strong components are fully connected as described earlier. Information from the double mutants is then used to remove connections that are not supported by the data. If, in the reconstruction, a gene k is a member of the adjacency list of gene i, Adj(i), but not in the accessibility list of gene i in the presence of a mutation in gene j, Acc-j(i), then the connection from gene i to gene k is probably indirect. It is removed from the reconstruction as long as k is a member of Acc(j), meaning that gene j could be mediating the interaction (Figure 3a, lines 5-7). In this manner, data from each of the double mutants are used successively to refine the reconstruction (Figure 3c). To fully resolve the structure of cycles that are subcomponents of a larger graph, double-mutant data for all pairs of genes in, or immediately adjacent to, each multinode strong component are needed. This procedure is successful as long as there are not multiple cycles within the component. If there is more than one redundant, but indirect, pathway from one gene to another, the two genes will appear to be directly connected in this analysis.
Double-mutant data can similarly be used to identify redundant or nontranscriptional regulatory relationships [7], and we have extended the algorithm to reconstruct these types of relationships (Figure 3a,d,e). If two genes, i and j, have redundant or overlapping regulatory effects on a third gene, k, the transcript level of k may be unchanged in each of the single mutants but altered in the double mutant. This type of relationship can be inferred when Acc-j(i) contains members that are absent from the single-mutant accessibility list Acc(i) (Figure 3d). In such a case, the algorithm adds connections from both gene i and gene j to gene k (Figure 3a, lines 12-15). This could represent a case, for example, where either of two transcription factors can bind the same site in the promoter and activate transcription. While a reconstruction based on the single-mutant data would be incomplete, the refinement utilizing the double-mutant data adds the appropriate edges (Figure 3d).
Proteins other than transcription factors often indirectly influence gene expression. For example, a signaling kinase could phosphorylate and activate a transcription factor, initiating expression of its target genes. This type of relationship is indistinguishable from direct regulation on the basis of single-mutant data alone. Double-mutant data, however, can reveal that the action of the kinase is dependent on the presence of the transcription factor; this phenomenon is the foundation of epistasis analysis. If gene i influences gene k in a wild-type background, but not when gene j is deleted, this suggests that the effect of gene i on gene k is not direct (Figure 3e), and that it is in fact mediated by gene j. The extended algorithm will therefore remove the connection from gene i to gene k as long as k is also accessible from j (Figure 3a, lines 5-7). These observations also imply that gene i must somehow affect the activity of gene j; therefore, if gene j is not already accessible from gene i in the reconstruction, an edge is added from gene i to gene j (Figure 3a, lines 8-9; Figure 3e).
Prevalence of cycles in genetic regulatory networks
We anticipated that the ability to accurately reconstruct, or at least accommodate, cycles would be critical to the success of a reconstruction algorithm. Cycles may be positively selected for in biological networks because feedback loops can potentially provide stability and/or amplification to biological systems [12,13]. Indeed, in both yeast and Escherichia coli, autoregulatory pathways in which transcription factors regulate their own expression are common [14,15]. Multigene feedback circuits, on the other hand, are rare in E. coli [14] but possibly more common in S. cerevisiae [16]. Such multigene cycles are of concern in reconstruction because they lead to ambiguities in network structure (see Figure 1). Single-gene 'self-loops,' by contrast, are not readily evident in gene-expression data, as manipulation of a gene's activity will, in most cases, affect the level of its RNA message even in the absence of autoregulation. We exclude self-loops from our network models, as have others [10], to avoid complications they can cause in the reconstruction process.
To estimate the prevalence of cycles in real biological networks we examined the yeast dataset of Hughes et al. [17] for evidence of feedback loops. We generated accessibility lists for each of the perturbed genes, using the authors' criteria for statistically significant changes in gene expression. Any mutually regulating genes (where perturbing i affects j and perturbing j affects i) were assigned to the same strong component. Among the 260 single-gene perturbations examined, four multigene components, containing a total of 11 genes, are apparent. Two of these involve genes with closely related functions and known feedback regulation (Figure 4): one contains the genes ERG2, ERG3, ERG11, ERG28 and TUP1, whereas the other contains ADE2 and HPT1. All four ERG genes in the first group are involved in ergosterol biosynthesis and their transcription is coordinately controlled by a negative feedback pathway [18-20]. This gene set is believed to be controlled in part by the transcriptional repressors Rox1 and Mot3, which act by recruiting the co-repressor complex Ssn6/Tup1 [21-23]; this may explain the participation of TUP1 in the component. ADE2 and HPT1 are both involved in purine biosynthesis, and deletion of HPT1 is known to activate ADE2 transcription via a feedback pathway dependent on an adenine metabolite [24,25].
Figure 4.

Feedback loops in the yeast network: one controlling ergosterol biosynthesis (left) and another controlling purine biosynthesis (right). Pointed arrows indicate positive regulation while blunt-ended arrows indicate negative regulation; only statistically significant relationships are shown.
The other two multigene components, by contrast, are likely to be artifacts. One contains two open reading frames (ORFs), YML034W and YML033W, which have since been shown to be exons of a single gene, SRC1 [26]. The other contains two adjacent ORFs, RTS1 (YOR014W) and YOR015W, whose effects on each other are likely to be mediated in cis rather than in trans. We conclude that among these 260 genes, there are at least 7 genes (2.7%) that participate in cycles, demonstrating the importance of considering this type of structure when reconstructing networks. A precise determination of the prevalence of cycles will await more extensive experimental data.
Error tolerance of the algorithm
To evaluate the usefulness of the algorithm in reconstructing regulatory networks, we would like to know how errors in the data affect the final reconstruction. Previous work suggested that the accuracy of a reconstruction scaled more or less linearly with the amount of data available; however, this work was based on simulations with acyclic networks only [5]. To determine the impact of cycles on the accuracy of reconstruction, we assessed the accuracy of the reconstruction under three conditions: when data for only a subset of genes is available; where some accessibility data is missing; and where some of the accessibility data is erroneous. All of these problems are likely to present themselves to some extent in real biological data.
The ability of the algorithm to tolerate inaccuracies in the data was assessed with random 500-gene networks with varying numbers of edges (see Appendix 1 in Additional data file 1, and Materials and methods for information on the generation of these networks). For each network, accessibility lists were generated, and then altered to simulate experimental error. An initial reconstruction, based on the unaltered data, was used as the standard to which all other reconstructions were compared.
Real experimental data may not include perturbations of all genes, and not all expression changes may be detected. We investigated the impact of each type of missing data on the accuracy of reconstructions. When perturbation data is absent for up to 50% of the genes in a network, the fraction of correct edges declines roughly linearly with the number of unperturbed genes, with a slope slightly steeper than -1 (Figure 5a). Performance is somewhat more compromised by random loss of accessibility information (Figure 5b), but an informative reconstruction can still be generated from incomplete data. For example, when 10% of the accessibilities are removed, roughly 70% of the reconstructed edges are correct (Figure 5b). The impact of missing data is relatively unaffected by the density of edges in the network, at least within the tested range (1.0-1.2 edges per node).
Figure 5.
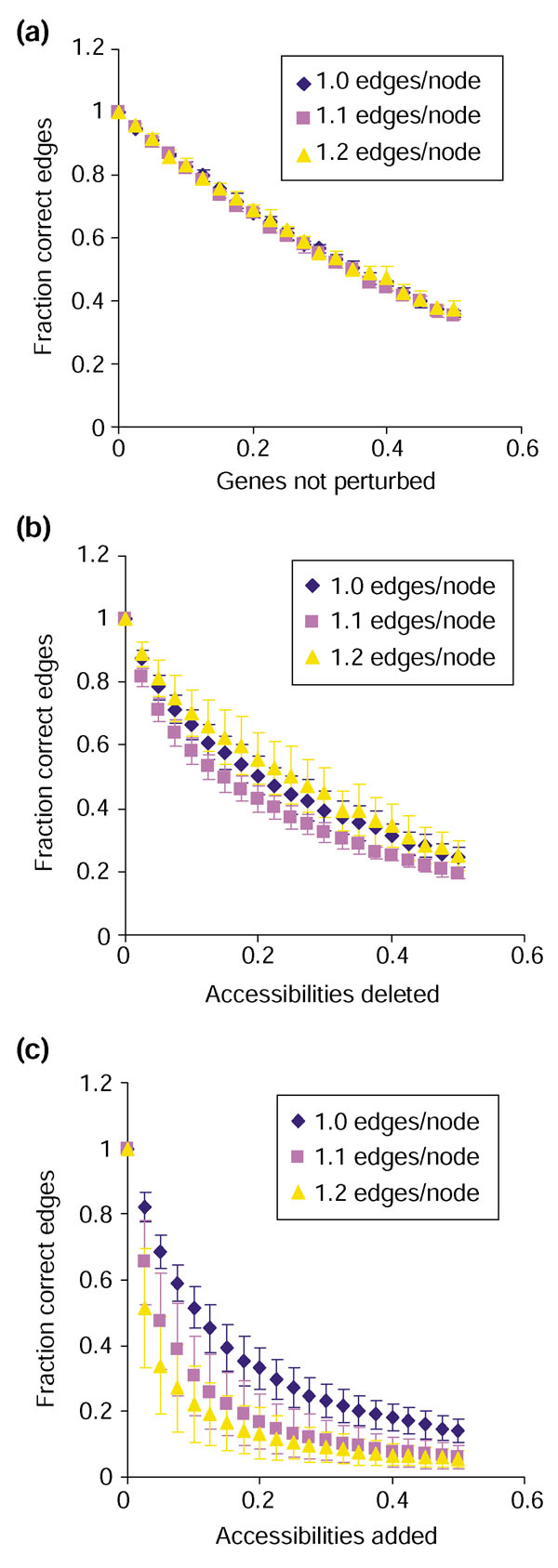
Sensitivity of the algorithm to incomplete or noisy data. On the y-axis of each graph is the fraction correct edges, (E - fn)/(E + fp), where E is the number of edges in the correct graph, and fn and fp are the number of false-negative and false-positive edges in the reconstruction. On the x-axis is (a) fraction of genes for which no accessibility information is available, (b) fraction of false-negative accessibilities, or (c) fraction of false-positive accessibilities. All data is for synthetic 500-gene networks with 500, 550, or 600 edges and edge distribution as described in Materials and methods. Each data point represents the average ± standard deviation of 10 repetitions for each of six independent networks.
To assess the effect of noise in the data, 'regulator' and 'target' genes were chosen at random, checked to make sure that no path already existed between the two, and added to the accessibility lists. Such erroneous data severely reduces the accuracy of the reconstruction (Figure 5c). For example, 10% false-positive data results in a reconstruction with only 50% or 20% correct edges for networks with 500 or 600 edges, respectively. This poor outcome results from the addition of incorrect edges to the reconstruction, some of which create circular pathways by erroneously connecting a gene to one of its upstream regulators. These 'pseudocycles' interfere with the search phase of the algorithm (Figure 2a, lines 4-14) and often result in reconstructions of poor quality. The relative sensitivity of the reconstruction algorithm to false-positive data as opposed to false-negative suggests that statistically conservative criteria should be used to define accessibility.
Improved resolution with double-mutant data
As described above, our extension to the algorithm uses double-mutant data to resolve local structures of multigene strong components. We tested the ability of this extension to improve on the reconstruction after a network is generated from single-mutant data. Because we wished to examine the ability of the algorithm to reconstruct all the edges in a network, including those within cycles, we compared each reconstruction, edge for edge, to the original synthetic network. For each of four synthetic networks of a given edge density we assessed the accuracy of the reconstruction based on the single-mutant data alone as well as the reconstruction including data for all relevant double mutants of genes within cycles and their neighbors (Figure 6a). As expected, the accuracy of the reconstruction based on single-mutant data alone declines as edge density increases, as a result of an increased number of genes in unresolved cycles. Incorporating data from double mutants substantially improves the quality of reconstructions for more highly connected networks. For example, the edges in reconstructions based on single-mutant data are only 62% correct for networks with 1.1 edges per node while they are 93% correct when double-mutant data is incorporated (Figure 6a). The improved reconstructions are not 100% correct because the synthetic random networks contain some redundant pathways that are pared away in the reconstruction process, which seeks the most parsimonious graph.
Figure 6.
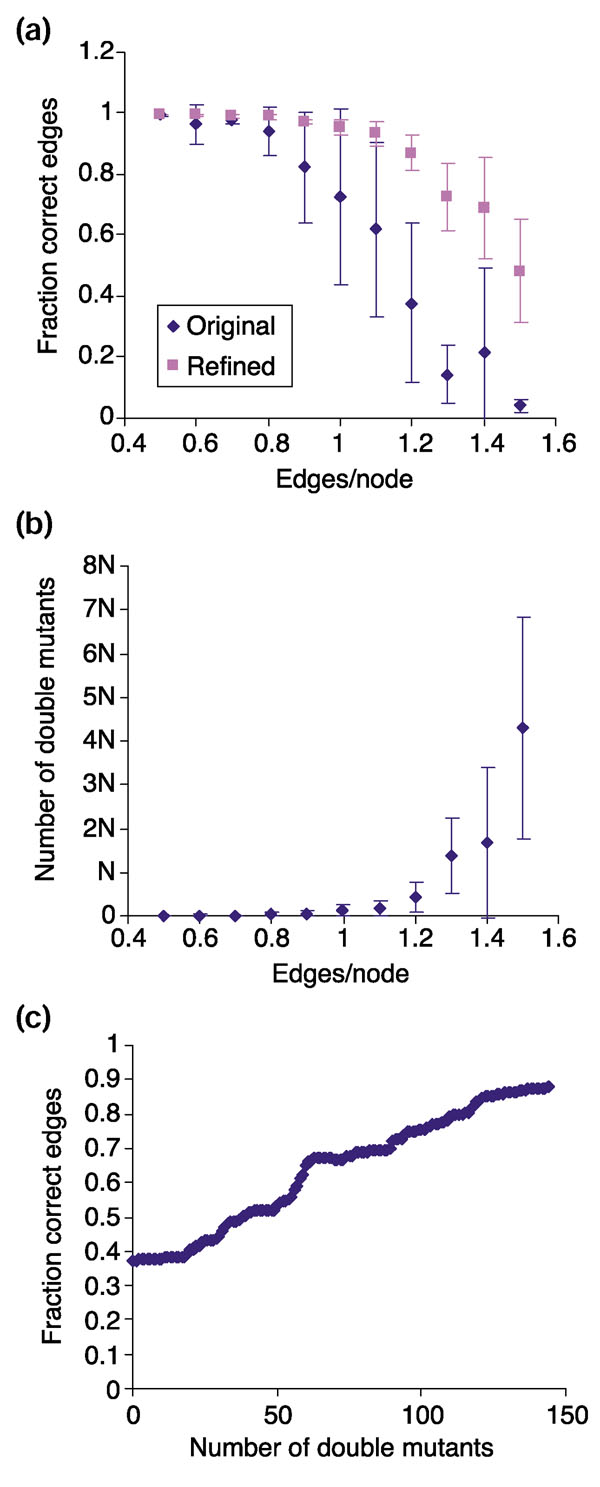
Quality of reconstruction using double-mutant data. (a) Fraction of correct edges in reconstruction (including cycles) versus edge density using single-mutant data only (original) or including double-mutant data (refined). (b) Number of double mutants needed for accurate reconstruction of networks with different numbers of edges, as compared to the number of genes in the network, N. (c) Improvement of reconstruction as double-mutant data is added for a network with 1.2 edges per node. All synthetic networks had 500 genes and the indicated number of edges. Data in (c) is for one of the four independent networks analyzed in (a) and (b), where each data point represents the average ± standard deviation for four independent networks.
Of particular note is the number of double mutants needed for this gain in accuracy (Figure 6b). For networks of 1.1-1.2 edges per node, the number of double mutants necessary is in the vicinity of 100-200 (17-33% of the number of genes in the network). Even for networks of 1.3-1.4 edges per node, the number of double-mutant profiles needed is on the order of N, the number of genes in the network, and not N2, the total number of possible double mutants (Figure 6b).
We also examined the progressive increase in accuracy as double-mutant data is incorporated into the reconstruction of an individual network (Figure 6c). For this analysis, individual pairs of genes contained in or adjacent to multigene components were chosen at random, their double-mutant gene-expression profiles analyzed, and the resulting reconstruction compared to the true network before repeating the process with another pair of genes. The reconstructions consistently improve as double-mutant data is added (Figure 6c). Thus, any available double-mutant data can be used to aid the reconstruction even if not all the relevant double mutants have been generated.
Partial reconstructions from microarray data
To test the performance of the algorithm on real data and to assess the impact of our extensions, we applied the reconstruction algorithm to the above-mentioned set of gene-expression profiles [17]. Using the authors' error model, we identified 16,133 potential targets of 260 perturbed genes. When this accessibility information is fed into the reconstruction algorithm, four multigene strong components (Figure 4c) are identified as described and collapsed into single nodes in a condensation graph. The basic algorithm then identifies 5,770 connections that are potentially indirect and prunes them from the network. However, when positive and negative regulation are taken into account, only 1,779 of these turn out to be consistent with indirect regulation by the mediating edges. This suggests that antagonistic feed-forward pathways ("incoherent feedforward loops" in the terminology of Shen-Orr et al. [27]) (Figure 2b, bottom) are common in real biological regulatory networks. Interestingly, 65% of the regulatory relationships identified in these data are apparently repressive and most of the incoherent pathways consist of three negative regulatory connections.
These results imply that it is important to take positive and negative regulatory relationships into account, as the algorithm may otherwise prune genuine direct connections from the network. But are the 1,779 connections pruned by the improved algorithm really indirect? To test this, we took advantage of a dataset containing promoter-binding information for the majority of transcription factors in yeast [16]. If a gene's promoter is bound by a transcription factor, and its transcript abundance changes upon deletion of that factor, we consider it to be a direct target of that transcription factor [4,28]. There are 17 transcription factors for which both single-mutant gene-expression profiles and chromatin-binding patterns are available in the datasets examined. Of these, one (RGT1) does not affect the transcription of any genes, and two (YAP3 and YAP7) do not bind any promoters, according to the respective authors' criteria for statistical significance, and were therefore not examined. For the remaining 14 transcription factors, anywhere from 0% (RTG1) to 100% (MBP1) of the 'expression targets' are direct as assessed by chromatin binding. Overall, of the 1,016 transcripts whose levels are affected by deletion of one of these genes, 81 (7.97%) are genuinely bound by the relevant transcription factor (Table 1, and Appendix 2 in Additional data file 1). After application of the algorithm, 835 of these connections are retained in the reconstructed network, including 78 (9.34%) that are directly bound. Of the 181 eliminated targets, only 3 (1.66%, p < 0.001) are true positives according to the binding data (Table 1). Thus using only a small dataset of expression profiles from single mutants, the algorithm prunes indirect edges more frequently than direct edges, resulting in enrichment for direct connections in the reconstruction. This enrichment, considered in the context of our simulation results (Figure 5a), suggests that when provided with more data the algorithm will successfully eliminate many indirect connections.
Table 1.
Fraction of direct targets before and after reconstruction
| Total targets* | Bound targets† | Percent bound‡ | |
| Expression data | 1,016 | 81 | 8.0 |
| Reconstruction | 835 | 78 | 9.34 |
| Eliminated targets | 181 | 3 | 1.66 |
*Total number of transcribed genes affected by transcription factor deletions. †Number of gene targets bound by relevant transcription factor. ‡Percentage of gene targets bound by relevant transcription factor.
The three 'true positives' incorrectly pruned, all putative Swi4 targets, are BAT2, SNA2 and EXG1. Interestingly, both BAT2 and SNA2 levels increase upon SWI4 deletion, suggesting negative regulation. By contrast, 18 of the other 19 'true targets' of Swi4 are reduced in a swi4Δ mutant, consistent with Swi4's known behavior as a transcriptional activator [29]. Thus, even these two may in fact be indirect expression targets, or exhibit atypical regulation by Swi4.
We also utilized the gene-expression dataset to test the extension utilizing double-mutant data, as it includes transcription profiles for several double-mutant yeast strains [17]. To use this data for epistasis analysis, one must compare it to the single-mutant expression profiles so that the effects of each individual perturbation can be discerned. These data are available for two of the double mutants: dig1Δdig2Δ and isw1Δisw2Δ, both of which bear deletions in pairs of genes believed to have redundant functions. DIG1 and DIG2, also known as RST1 and RST2, encode proteins that inhibit the Ste12 transcription factor [30]. ISW1 and ISW2 encode ATP-dependent chromatin-remodeling enzymes with partially overlapping functions [31]. Both of these pairs of genes, therefore, could be expected to exhibit parallel, redundant regulation of some transcripts.
We generated new accessibility lists from these mutant expression profiles and used this information to refine the reconstruction; specifically, edges were added from each of the mutant genes to any new genes on the double-mutant accessibility lists (Figure 3a, lines 12-15). This process resulted in quite a few genes being added to the adjacency lists of DIG1, DIG2, ISW1 and ISW2. Genome-wide binding data is available for just one of these genes, DIG1 [16]. Of the 228 'new' DIG1 targets, 18 (7.9%) are directly bound by the Dig1 protein. These relationships were absent in the original reconstruction from single-mutant data, demonstrating that double-mutant data can be of use in identifying regulatory relationships. However, significantly more double-mutant data would be required to achieve a significant improvement in the overall quality of the reconstruction. Genome-wide binding profiles are not available for Dig2, Isw1 or Isw2. However, for both DIG1 and DIG2, the new targets included several known targets of the Ste12 protein such as ERG24, PCL2, and STE12 [4], consistent with their role as regulators of Ste12p activity. Furthermore, at least one gene known to be directly regulated by both Isw1 and Isw2, FIG1 [31], is recognized as an Isw2 protein target only in the refined reconstruction.
Discussion
In this study we have extended a previously described algorithm [5] that uses information on the system-wide transcriptional effects of single-gene perturbations to reconstruct a tentative regulatory network. Several extensions presented here address weaknesses in the original algorithm and make it more effective on real biological data. One concern was that the effect of cycles in the network on the accuracy of the reconstruction was not previously assessed. We have now devised a method to compare reconstructions with different numbers of strong components and demonstrate that our method can generate a network enriched for direct regulatory relationships even when there are feedback loops in the network. The cycle-accommodating extension does not substantially change the impact of missing data observed previously [5]. However, it is sensitive to false-positive data, implying that statistically conservative criteria should be used for identifying potential regulatory targets. Another shortcoming of the original algorithm was that it did not distinguish between positive and negative regulation, an important feature of biological networks that could influence the reconstruction process. We show here by application to published data of a modified algorithm that considers both activation and repression that this inclusion is critical to proper characterization of network structure. Finally, the original algorithm had no mechanism by which to use double-mutant data, which is historically proven to be of great value in pathway interpretation. The ability to incorporate data from double mutants, in the manner of traditional epistasis analysis, considerably increases the potential power of the algorithm. We have focused here on transcriptional regulation, but our approach could easily be extended to other types of data, such as protein levels or posttranslational modifications, as they become available.
A great deal of effort has been applied to the task of extracting regulatory relationships from microarray data [1,2]. A smaller, but still substantial, set of techniques addresses the specific question of deriving genetic regulatory networks from perturbed gene-expression profiles [32-36]. Early efforts focused on Boolean network models [32,34] and made a number of interesting observations about the amount and types of data necessary to characterize a network. Evidence suggests, however, that significant information is lost in Boolean models by the discretization of data into arbitrary 'on' and 'off' categories, and that simple logical gates are unlikely to encompass combinatorial regulatory interactions [1,33]. A graph-theoretic approach, as used in our study, has the advantage of accepting continuous-valued data and placing no constraints on the number of inputs or their interactions with each other [33]. Some groups have also taken a probabilistic approach to the problem using Bayesian networks [35,36]. However, despite making biologically relevant predictions, this approach has not thus far been successful in identifying target genes of transcription factors [35,36] and is very sensitive to model parameters [37].
The starting point for our analysis is a parsimony approach analogous to that used in phylogeny. A large number of network structures could potentially explain the experimental observations, so the algorithm seeks the simplest network consistent with available data. Similar approaches have been proposed by others [11,33], who also represent gene-perturbation data in the form of an accessibility or interaction matrix. The graph implied by this matrix is then reduced to a most parsimonious graph by pruning either all redundant pathways in the graph [5,11] or only those consistent with activation and repression data ([33] and this study). Our algorithm differs from that of Kyoda and colleagues [33] in that it cannot be directly applied to networks with cycles. However, the method proposed here for processing these networks avoids the problem of arbitrary gene order within cycles [33] and the higher computational cost of the alternative algorithm (O(n3)) [33]. When we carried out the same microarray and binding-data analysis described herein, using the Kyoda et al. algorithm, the results were very similar: 168 connections were pruned, of which three (the same three as in our analysis) were direct. Essentially equivalent results (183 connections pruned, three direct) could be achieved with a minor improvement that allowed pruned edges to mediate accessibility (data not shown). Two additional indirect edges, contained within cycles, were pruned in this analysis; however, the pruning process took approximately 418 central-processing-unit (CPU) seconds as opposed to around 1 CPU second for our algorithm. While neither processing time was prohibitive in this case, for larger datasets the computation cost could become a serious concern.
The AIGNET (Algorithms for Inference of Genetic Networks) method [11] groups nodes into 'equivalence sets,' identical to strong components, before pruning indirect connections from the network. Relationships within these equivalence sets are then resolved and the network structure fine-tuned using time-course data and a dynamic S-system model [11]. How this method fares in practice, and how it compares to the double-mutant approach described here, has yet to be tested. It may well prove complementary to the analysis of steady-state double-mutant profiles, particularly in cases where a double mutation is lethal. It is clear, however, that the straightforward Boolean approach suggested by Maki et al. [11] for the creation of the 'skeleton network' will erroneously sever direct connections as a consequence of failing to consider positive and negative regulation. In our analysis, 11 additional direct connections (14 total, as compared to 3; Table 1) were incorrectly pruned when repression and activation were not treated separately.
A unique aspect of our algorithm is the manner in which double-mutant data is used. Other proposed methods have used double-mutant data, but as a means of fully exploring the logical states of a Boolean network [34] or expanding the range of perturbations to the system [35]. We have used double-mutant data here both to resolve the order of genes within feedback loops (cycles), and to detect nontranscriptional or redundant regulatory pathways. To our knowledge, no previous computational work has addressed the question of resolving feedback loop structure with double-mutant data. Classical genetic pathway analysis, however, has been automated in the program GenePath [38], which constructs acyclic genetic regulatory networks governing specific biological processes on the basis of phenotypic data from single and double mutants. The basic logic underlying the analysis performed by GenePath [38] is very similar to that described here.
The power of double-mutant analysis is evident in its extensive application in classical genetics [7,8]. These applications include the study of signaling pathways involved in transcriptional regulation, for example the repression of SUC2 by glucose [39,40]. As the number of experiments required for this method scales with the square of the number of genes under investigation, epistasis analysis cannot be easily applied on a genome-wide level. However, our algorithm generates a tentative reconstruction based on single-mutant data that can then be refined with targeted double-mutant data, bringing the number of experiments into a manageable range. The type of data required by our algorithm is rapidly becoming available through gene-deletion projects and new methods, such as RNA interference, to perturb the activity of selected genes [41-43]. For the budding yeast S. cerevisiae, a complete library of single-gene deletion mutants is available and double mutants have been created by automated high-throughput mating of these strains [44-46].
Conclusions
Application of our reconstruction algorithm to published gene-expression data from a number of S. cerevisiae mutants led to several interesting observations. The first is that 'incoherent' feedforward pathways, in which the edges are arranged such that they act antagonistically, seem to be common in the yeast regulatory network. This is in contrast to E. coli, where most (34 of 40) known feedforward motifs in transcriptional regulation are coherent [27]. In S. cerevisiae an overrepresentation of the feedforward motif, in which one gene regulates another through both direct and indirect pathways, has recently been observed in regulatory pathways documented in the literature [47]; consistent with our observations, a relatively large proportion of these (21 of 47) are incoherent. An overrepresentation of feedforward pathways has also been reported in yeast chromatin-binding data [16]; however, whether these parallel pathways act antagonistically or synergistically is unknown because the data does not indicate whether regulation is positive or negative. Our findings suggest that synergy is not necessarily the rule in the yeast network, though most of the incoherent pathways we observed are likely to be indirect at the transcriptional level.
The second important observation is that the parsimony approach embodied by this algorithm can successfully identify and prune indirect connections from a regulatory network when provided with single-mutant data alone. Although only approximately 4% of the genes in S. cerevisiae were perturbed in the dataset examined [17], a substantial number of possible connections could be pruned from the network while maintaining all regulatory relationships observed. Comparison with DNA-binding data for a small set of transcription factors suggested that these pruned connections are much more likely to be indirect than the edges retained in the reconstruction.
Finally, analysis of experimental yeast double-mutant data revealed that expression data for strains in which two genes with potentially redundant functions are both deleted can aid in the identification of true target genes. Thus, utilization of double-mutant data is likely to improve the reconstruction generated by the algorithm. Furthermore, analysis of synthetic networks suggests that data from a relatively small number of double mutants, on the order of the size of the network, N, could substantially improve the quality of the reconstruction.
In sum, we have shown that the assumption of parsimony is a reasonable one in the context of regulatory networks and is supported by available data. We have developed a method to automate this approach that can utilize single-mutant data to generate a tentative reconstruction and double-mutant data to improve its accuracy. We anticipate that application of this algorithm will greatly simplify interpretation of experimental gene perturbation data as more mutant gene-expression profiles become available for a number of organisms.
Materials and methods
Synthetic networks
We generated synthetic networks (Figures 4, 5, 6) using an adaptation of methods described in [48]. Outgoing edges were distributed according to a power law with an exponential cutoff such that the probability of a node having k_out edges, p(k_out), is proportional to (k_out)-τe-k_out/κ, where the constants τ and κ equal 0.7 and 1,000 respectively. Incoming edges were assigned according to an exponential distribution, where p(k_in) ~ e-βk_in and the constant β = 0.5. This model was based on previous analyses of regulatory networks in E. coli and S. cerevisiae (see Appendix 1 in Additional data file 1).
To create the outgoing edge distribution, each gene was assigned outgoing edge 'stubs' by the following procedure [48]. First, an edge number k_out with a distribution e-k_out/κ was generated with the transformation k_out = 1 + int(-κ ln(1 - r)) where r is a random real number uniformly distributed in the range 0 ≤ r < 1 and int(x) indicates the largest integer smaller than x. This number k_out was then accepted with probability (k_out)-τ as long as k_out was less than the total number of nodes in the network; if k_out was not accepted, the process was repeated. Each gene was then similarly assigned an incoming edge number generated with the transformation k_in = 1 + int(-(1/β)ln(1 - r)) where r is another random real number uniformly distributed in the range 0 ≤ r < 1. This number was accepted as long as k_in was less than one-quarter the total number of nodes in the network. These outgoing and incoming stubs were then joined to form edges until the desired number of edges was reached. Edge distributions of graphs generated in this manner were checked by eye to confirm that they displayed the desired behavior.
Accessibility lists for these graphs were generated by a depth-first search [49]. Double-mutant accessibility lists were created by eliminating all incoming or outgoing edges for one gene, then generating accessibility lists for all remaining genes in the network.
Error analysis
To examine the effect of not having all gene perturbations available, we deleted all accessibilities for nodes chosen at random, without replacement, in 500 gene synthetic networks. For each network, the number of nodes treated in this way ranged from 2.5% (12) to 50% (250) of the total, in 2.5% increments. We then used this limited data as input to the reconstruction algorithm, and the resulting network was compared to the initial reconstruction. Similarly, to examine the effect of incomplete data (false-negative accessibilities), we calculated the total number of accessibilities in the network, and deleted a number of accessibilities ranging from 2.5% to 50% of the total number before reconstruction. To simulate false-positive accessibilities, we added up to 50% more accessibilities to the data. In all of these cases we repeated the process 10 times for each increment. We carried out the entire analysis of the effects of incomplete, false-negative and false-positive data on the same six independent networks of each edge density.
To assess the accuracy of reconstructions from incomplete or noisy data, we compared each pair of vertices in the network to the 'correct' graph with regard to the presence of an edge. We then tallied the number of edges missing in the reconstruction (false negative, fn) or erroneously present in the reconstruction (false positive, fp) and calculated the 'fraction correct edges' (E - fn)/(E + fp), where E is the number of edges in the correct graph. In Figure 5, the standard of comparison is the reconstruction generated from the correct accessibility list, while in Figure 6, the standard of comparison is the original graph.
The addition or deletion of accessibilities during the error analysis resulted at times in the creation of 'pseudocycles,' circular pathways in the network that are not identified as cycles in the condensation step. Such pathways are also encountered in experimental data (data not shown) and the algorithm can get caught in these loops during the search phase (Figure 2a, lines 4-14). A simple modification that keeps track of the number of times the algorithm has 'stopped' at a given node during the search prevents this from happening. If the same node is encountered more than twice, an alternative search path is chosen.
Yeast datasets
The dataset examined contains 300 S. cerevisiae expression profiles, including 276 deletion mutants, 11 tetracycline-regulatable alleles of essential genes, and 13 drug treatments [17]. Of the deletion mutants, 7 are double mutants, and 20 are aneuploid. We excluded data from double-mutant and aneuploid strains but included data from the tetracycline-regulated alleles when initially generating accessibility lists, for a total of 260 expression profiles. Accessibility was defined solely by p value according to the error model of Hughes et al.: if the transcript level of a gene changed with p < 0.01, it was considered accessible from the gene mutated or perturbed in the experiment. We considered the regulation positive if the level went down and negative if it went up, as all of these experiments involved gene inactivation and not overexpression. Accessibility lists for double mutants dig1Δdig2Δ and isw1Δisw2Δ were based on two criteria: a p value less than 0.01 (relative to wild type) and a fold expression change of at least 1.8 between the single mutant and double mutant.
To test the ability of the algorithm to distinguish direct from indirect regulation, we utilized the chromatin binding data of Lee et al. [16], in which the promoter-binding profiles of 106 transcription factors in S. cerevisiae were determined by genome-wide location analysis. We used the same statistical significance threshold, p < 0.001, chosen by the authors to identify true binding targets. There are 17 transcription factors in this dataset with corresponding deletion-mutant expression profiles [17]: ARG80, CIN5, DIG1, GCN4, GLN3, HIR2, MAC1, MBP1, RGT1, RTG1, STE12, SWI4, SWI5, SWI6, YAP1, YAP3, and YAP7 [16,17]. For each of these transcription factors there is a number of genes, E, whose expression is significantly affected by deletion of the factor and which we refer to as expression targets. There is also a number of genes, B, whose promoters are bound by the transcription factor and which we refer to as binding targets. We consider the intersection of these two sets to represent the T 'true targets' (listed in Appendix 2 in Additional data file 1). The fractional overlap between the two sets (f = ΣT/(ΣE + ΣB)) was tested within the range of p < 0.001 to p < 0.01 as defined by the error models of the respective authors for each dataset. It was maximized when expression targets were defined with a p < 0.01 threshold [17] and binding targets were defined with a p < 0.001 threshold [16], in agreement with the authors' own choices. Additional criteria such as requiring a certain magnitude of expression change or magnitude of binding enrichment either did not improve or only minimally improved the overlap. A χ2 test was used to assess the statistical significance of the results.
Additional data files
The following additional data are available with the online version of this paper: a PDF file (Additional data file 1) containing four appendices; Appendix 1 is a detailed discussion of the parameters of the synthetic networks used in simulations in the paper and the rationale behind their choice; Appendix 2 lists the transcription factors and targets identified as described in the main text; Appendix 3 gives the Perl code for the algorithm described in the paper; Appendix 4 is a sample text input file for the algorithm.
Supplementary Material
A PDF file containing four appendices including a detailed discussion of the parameters of the synthetic networks used in simulations, the transcription factors and targets identified as described in the main text, the Perl code for the algorithm described in the paper and a sample text input file for the algorithm
Acknowledgments
Acknowledgements
We thank E. Bedrick for assistance with statistical analysis, J. Blanchard, M. Fuller and M. Gilchrist for critical reading of the manuscript, and P. Renaud for hosting S.L.G. in his lab during part of this project. This work was supported by the W. M. Keck Foundation.
References
- D'Haeseleer P, Liang S, Somogyi R. Genetic network inference: from co-expression clustering to reverse engineering. Bioinformatics. 2000;16:707–726. doi: 10.1093/bioinformatics/16.8.707. [DOI] [PubMed] [Google Scholar]
- de Jong H. Modeling and simulation of genetic regulatory systems: a literature review. J Comput Biol. 2002;9:67–103. doi: 10.1089/10665270252833208. [DOI] [PubMed] [Google Scholar]
- Lyons TJ, Gasch AP, Gaither LA, Botstein D, Brown PO, Eide DJ. Genome-wide characterization of the Zap1p zinc-responsive regulon in yeast. Proc Natl Acad Sci USA. 2000;97:7957–7962. doi: 10.1073/pnas.97.14.7957. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ren B, Robert F, Wyrick JJ, Aparicio O, Jennings EG, Simon I, Zeitlinger J, Schreiber J, Hannett N, Kanin E, et al. Genome-wide location and function of DNA binding proteins. Science. 2000;290:2306–2309. doi: 10.1126/science.290.5500.2306. [DOI] [PubMed] [Google Scholar]
- Wagner A. How to reconstruct a large genetic network from n gene perturbations in fewer than n(2) easy steps. Bioinformatics. 2001;17:1183–1197. doi: 10.1093/bioinformatics/17.12.1183. [DOI] [PubMed] [Google Scholar]
- Griffiths AJF, Gelbart WM, Miller JH, Lewontin RC. Modern Genetic Analysis. New York: WH Freeman; 1999. [Google Scholar]
- Avery L, Wasserman S. Ordering gene function: the interpretation of epistasis in regulatory hierarchies. Trends Genet. 1992;8:312–316. doi: 10.1016/0168-9525(92)90263-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jarvik J, Botstein D. A genetic method for determining the order of events in a biological pathway. Proc Natl Acad Sci USA. 1973;70:2046–2050. doi: 10.1073/pnas.70.7.2046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harary F. Graph Theory. Reading, MA: Perseus Books; 1969. [Google Scholar]
- Aho AV, Garey MR, Ullman JD. The transitive reduction of a directed graph. SIAM J Comput. 1972;1:131–137. [Google Scholar]
- Maki Y, Tominaga D, Okamoto M, Watanabe S, Eguchi Y. Development of a system for the inference of large scale genetic networks. Pac Symp Biocomput. 2001:446–458. doi: 10.1142/9789814447362_0044. [DOI] [PubMed] [Google Scholar]
- Becskei A, Serrano L. Engineering stability in gene networks by autoregulation. Nature. 2000;405:590–593. doi: 10.1038/35014651. [DOI] [PubMed] [Google Scholar]
- Rosenfeld N, Elowitz MB, Alon U. Negative autoregulation speeds the response times of transcription networks. J Mol Biol. 2002;323:785–793. doi: 10.1016/S0022-2836(02)00994-4. [DOI] [PubMed] [Google Scholar]
- Thieffry D, Huerta AM, Perez-Rueda E, Collado-Vides J. From specific gene regulation to genomic networks: a global analysis of transcriptional regulation in Escherichia coli. BioEssays. 1998;20:433–440. doi: 10.1002/(SICI)1521-1878(199805)20:5<433::AID-BIES10>3.0.CO;2-2. [DOI] [PubMed] [Google Scholar]
- Guelzim N, Bottani S, Bourgine P, Kepes F. Topological and causal structure of the yeast transcriptional regulatory network. Nat Genet. 2002;31:60–63. doi: 10.1038/ng873. [DOI] [PubMed] [Google Scholar]
- Lee TI, Rinaldi NJ, Robert F, Odom DT, Bar-Joseph Z, Gerber GK, Hannett NM, Harbison CT, Thompson CM, Simon I, et al. Transcriptional regulatory networks in Saccharomyces cerevisiae. Science. 2002;298:799–804. doi: 10.1126/science.1075090. [DOI] [PubMed] [Google Scholar]
- Hughes TR, Marton MJ, Jones AR, Roberts CJ, Stoughton R, Armour CD, Bennett HA, Coffey E, Dai H, He YD, et al. Functional discovery via a compendium of expression profiles. Cell. 2000;102:109–126. doi: 10.1016/s0092-8674(00)00015-5. [DOI] [PubMed] [Google Scholar]
- Arthington-Skaggs BA, Crowell DN, Yang H, Sturley SL, Bard M. Positive and negative regulation of a sterol biosynthetic gene (ERG3) in the post-squalene portion of the yeast ergosterol pathway. FEBS Lett. 1996;392:161–165. doi: 10.1016/0014-5793(96)00807-1. [DOI] [PubMed] [Google Scholar]
- Smith SJ, Crowley JH, Parks LW. Transcriptional regulation by ergosterol in the yeast Saccharomyces cerevisiae. Mol Cell Biol. 1996;16:5427–5432. doi: 10.1128/mcb.16.10.5427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vik A, Rine J. Upc2p and Ecm22p, dual regulators of sterol biosynthesis in Saccharomyces cerevisiae. Mol Cell Biol. 2001;21:6395–6405. doi: 10.1128/MCB.21.19.6395-6405.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deckert J, Torres AM, Hwang SM, Kastaniotis AJ, Zitomer RS. The anatomy of a hypoxic operator in Saccharomyces cerevisiae. Genetics. 1998;150:1429–1441. doi: 10.1093/genetics/150.4.1429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hongay C, Jia N, Bard M, Winston F. Mot3 is a transcriptional repressor of ergosterol biosynthetic genes and is required for normal vacuolar function in Saccharomyces cerevisiae. EMBO J. 2002;21:4114–4124. doi: 10.1093/emboj/cdf415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henry KW, Nickels JT, Edlind TD. ROX1 and ERG regulation in Saccharomyces cerevisiae: implications for antifungal susceptibility. Eukaryot Cell. 2002;1:1041–1044. doi: 10.1128/EC.1.6.1041-1044.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guetsova ML, Lecoq K, Daignan-Fornier B. The isolation and characterization of Saccharomyces cerevisiae mutants that constitutively express purine biosynthetic genes. Genetics. 1997;147:383–397. doi: 10.1093/genetics/147.2.383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rebora K, Desmoucelles C, Borne F, Pinson B, Daignan-Fornier B. Yeast AMP pathway genes respond to adenine through regulated synthesis of a metabolic intermediate. Mol Cell Biol. 2001;21:7901–7912. doi: 10.1128/MCB.21.23.7901-7912.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rodriguez-Navarro S, Igual JC, Perez-Ortin JE. SRC1: an intron-containing yeast gene involved in sister chromatid segregation. Yeast. 2002;19:43–54. doi: 10.1002/yea.803. [DOI] [PubMed] [Google Scholar]
- Shen-Orr SS, Milo R, Mangan S, Alon U. Network motifs in the transcriptional regulation network of Escherichia coli. Nat Genet. 2002;31:64–68. doi: 10.1038/ng881. [DOI] [PubMed] [Google Scholar]
- Simon I, Barnett J, Hannett N, Harbison CT, Rinaldi NJ, Volkert TL, Wyrick JJ, Zeitlinger J, Gifford DK, Jaakkola TS, et al. Serial regulation of transcriptional regulators in the yeast cell cycle. Cell. 2001;106:697–708. doi: 10.1016/s0092-8674(01)00494-9. [DOI] [PubMed] [Google Scholar]
- Aalfs JD, Kingston RE. What does 'chromatin remodeling' mean? Trends Biochem Sci. 2000;25:548–555. doi: 10.1016/S0968-0004(00)01689-3. [DOI] [PubMed] [Google Scholar]
- Olson KA, Nelson C, Tai G, Hung W, Yong C, Astell C, Sadowski I. Two regulators of Ste12p inhibit pheromone-responsive transcription by separate mechanisms. Mol Cell Biol. 2000;20:4199–4209. doi: 10.1128/MCB.20.12.4199-4209.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kent NA, Karabetsou N, Politis PK, Mellor J. In vivo chromatin remodeling by yeast ISWI homologs Isw1p and Isw2p. Genes Dev. 2001;15:619–626. doi: 10.1101/gad.190301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Akutsu T, Kuhara S, Maruyama O, Miyano S. A system for identifying genetic networks from gene expression patterns produced by gene disruptions and overexpressions. Genome Inform Ser Workshop Genome Inform. 1998;9:151–160. [PubMed] [Google Scholar]
- Kyoda KM, Morohashi M, Onami S, Kitano H. A gene network inference method from continuous-value gene expression data of wild-type and mutants. Genome Inform Ser Workshop Genome Inform. 2000;11:196–204. [PubMed] [Google Scholar]
- Ideker TE, Thorsson V, Karp RM. Discovery of regulatory interactions through perturbation: inference and experimental design. Pac Symp Biocomput. 2000;5:305–316. doi: 10.1142/9789814447331_0029. [DOI] [PubMed] [Google Scholar]
- Pe'er D, Regev A, Elidan G, Friedman N. Inferring subnetworks from perturbed expression profiles. Bioinformatics. 2001;17:S215–S224. doi: 10.1093/bioinformatics/17.suppl_1.s215. [DOI] [PubMed] [Google Scholar]
- Yoo C, Thorsson V, Cooper GF. Discovery of causal relationships in a gene-regulation pathway from a mixture of experimental and observational DNA microarray data. Pac Symp Biocomput. 2002:498–509. doi: 10.1142/9789812799623_0046. [DOI] [PubMed] [Google Scholar]
- Friedman N, Linial M, Nachman I, Pe'er D. Using Bayesian networks to analyze expression data. J Comput Biol. 2000;7:601–620. doi: 10.1089/106652700750050961. [DOI] [PubMed] [Google Scholar]
- Zupan B, Demsar J, Bratko I, Juvan P, Halter JA, Kuspa A, Shaulsky G. GenePath: a system for automated construction of genetic networks from mutant data. Bioinformatics. 2003;19:383–389. doi: 10.1093/bioinformatics/btf871. [DOI] [PubMed] [Google Scholar]
- Neigeborn L, Carlson M. Mutations causing constitutive invertase synthesis in yeast: genetic interactions with snf mutations. Genetics. 1987;115:247–253. doi: 10.1093/genetics/115.2.247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trumbly RJ. Glucose repression in the yeast Saccharomyces cerevisiae. Mol Microbiol. 1992;6:15–21. doi: 10.1111/j.1365-2958.1992.tb00832.x. [DOI] [PubMed] [Google Scholar]
- Kamath RS, Fraser AG, Dong Y, Poulin G, Durbin R, Gotta M, Kanapin A, Le Bot N, Moreno S, Sohrmann M, et al. Systematic functional analysis of the Caenorhabditis elegans genome using RNAi. Nature. 2003;421:231–237. doi: 10.1038/nature01278. [DOI] [PubMed] [Google Scholar]
- Chory J, Ecker JR, Briggs S, Caboche M, Coruzzi GM, Cook D, Dangl J, Grant S, Guerinot ML, Henikoff S, et al. National Science Foundation-Sponsored Workshop Report: "The 2010 Project" functional genomics and the virtual plant. A blueprint for understanding how plants are built and how to improve them. Plant Physiol. 2000;123:423–426. doi: 10.1104/pp.123.2.423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spradling AC, Stern D, Beaton A, Rhem EJ, Laverty T, Mozden N, Misra S, Rubin GM. The Berkeley Drosophila Genome Project gene disruption project: single P-element insertions mutating 25% of vital Drosophila genes. Genetics. 1999;153:135–177. doi: 10.1093/genetics/153.1.135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giaever G, Chu AM, Ni L, Connelly C, Riles L, Veronneau S, Dow S, Lucau-Danila A, Anderson K, Andre B, et al. Functional profiling of the Saccharomyces cerevisiae genome. Nature. 2002;418:387–391. doi: 10.1038/nature00935. [DOI] [PubMed] [Google Scholar]
- Winzeler EA, Shoemaker DD, Astromoff A, Liang H, Anderson K, Andre B, Bangham R, Benito R, Boeke JD, Bussey H, et al. Functional characterization of the S. cerevisiae genome by gene deletion and parallel analysis. Science. 1999;285:901–906. doi: 10.1126/science.285.5429.901. [DOI] [PubMed] [Google Scholar]
- Tong AH, Evangelista M, Parsons AB, Xu H, Bader GD, Page N, Robinson M, Raghibizadeh S, Hogue CW, Bussey H, et al. Systematic genetic analysis with ordered arrays of yeast deletion mutants. Science. 2001;294:2364–2368. doi: 10.1126/science.1065810. [DOI] [PubMed] [Google Scholar]
- Mangan S, Alon U. Structure and function of the feed-forward loop network motif. Proc Natl Acad Sci USA. 2003;100:11980–11985. doi: 10.1073/pnas.2133841100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Newman ME, Strogatz SH, Watts DJ. Random graphs with arbitrary degree distributions and their applications. Phys Rev E Stat Nonlin Soft Matter Phys. 2001;64:026118. doi: 10.1103/PhysRevE.64.026118. [DOI] [PubMed] [Google Scholar]
- West DB. Introduction to Graph Theory. Upper Saddle River, NJ: Prentice Hall; 2001. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
A PDF file containing four appendices including a detailed discussion of the parameters of the synthetic networks used in simulations, the transcription factors and targets identified as described in the main text, the Perl code for the algorithm described in the paper and a sample text input file for the algorithm


