Comparison of different segmentation approaches without using gold standard. Application to the estimation of the left ventricle ejection fraction from cardiac cine MRI sequences

Abstract

A statistical method is proposed to compare several estimates of a relevant clinical parameter when no gold standard is available. The method is illustrated by considering the left ventricle ejection fraction derived from cardiac magnetic resonance images and computed using seven approaches with different degrees of automation. The proposed method did not use any a priori regarding with the reliability of each method and its degree of automation. The results showed that the most accurate estimates of the ejection fraction were obtained using manual segmentations, followed by the semi-automatic methods, while the methods with the least user input yielded the least accurate ejection fraction estimates. These results were consistent with the expected performance of the estimation methods, suggesting that the proposed statistical approach might be helpful to assess the performance of estimation methods on clinical data for which no gold standard is available.

I. INTRODUCTION

The comparison of segmentation algorithms on clinical data is extremely challenging. Initial evaluation is often performed visually by superimposing contours provided by each segmentation method on the images to be studied. To overcome drawbacks inherent to visual inspection, a quantitative assessment is preferable and most approaches consider a ground truth to evaluate the different methods to be compared. A single manual contour delineated by an expert or a representative shape based on several manual segmentations provided by different experts is commonly used as a gold standard [1]. Several criteria measuring the overlap between the segmented region and the gold standard region, like the Dice coefficient [2], are then computed to assess the quality of the segmentation to be evaluated given the reference delineation. Since obtaining such references can be difficult, we proposed in this paper, a method based on the ”Regression Without Truth” approach (RWT) [3,4] to classify different segmentation approaches with different degrees of automation. The comparison of methods is based on the computation of a figure of merit. A second figure of merit, introduced in [5], was also considered here to carry out the classification. To get a robust comparison, a bootstrap analysis [6] was performed on top of the RWT approach followed by a rank analysis. The method is illustrated here in the framework of the study of the left ventricle ejection fraction estimated using seven segmentation approaches of the endocardium based on cardiac cine magnetic resonance (MR) images. This work was performed in the context of the French MedIEval (Medical Image segmentation Evaluation) working group.

II. MATERIALS

A. Database

Our method was applied to the datasets provided to the participants in the MICCAI 2009 Grand Challenge, by Sunnybrook Health Sciences Center [7]. The database consisted of 30 subjects from the testing and the on-line contest datasets, including 6 healthy individuals and 24 patients with different cardiac pathologies. For each patient, about ten cine steady state free precession MR short axis slices were acquired with 20 cardiac phases over the heart cycle, and scanned from the end-diastolic phase. Further details regarding the datasets and image acquisition protocol can be found in [7].

The ejection fraction is the biomarker conventionally defined as the ratio of the difference between end-diastolic and end-systolic volumes (volume of blood ejected within each beat) by the end-diastolic volume. It ranges from 0 to 1. To estimate ejection fraction, the MR slices corresponding to the end-systolic and end-diastolic phases were given to the participants to the Challenge, so as to avoid any variability only due to the choice of these time points.

B. Segmentation approaches to be evaluated

For this project, 7 segmentation methods were proposed by 5 different research teams to provide 7 independent estimates of the left ventricle ejection fraction.

Methods M1 and M7 were entirely manual and performed by two experts from two different laboratories. Semiautomated methods M2, M5 and M6, described in [8,9,10] respectively, involved an interactive definition of an initial shape or a modification of the parameters by the operators during the process. Method M2 was modified to yield a fully-automated method (M3) [11]. Method M5 was also revised to require only a very limited interaction from the operator, yielding method M4.

Fig. 1 illustrates endocardial contours obtained by a manual approach (M1) and an automated method (M3) superimposed on MRI telediastolic slices of the database.

Fig. 1.

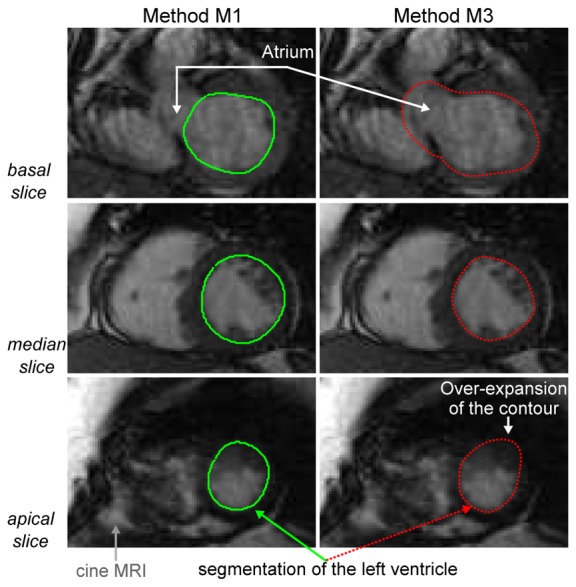
Superimposition of contours of the left ventricle provided by a manual segmentation method (M1, solid green line) and an automated approach (M3, dashed red line) on MRI slices of the database.

III. METHODS

A. Regression Without Truth approach (RWT)

1. Theory

The RWT approach is detailed in [3,4]. Here is a brief summary.

Let us consider the database containing P samples (indexed by p, ranging from 1 to P) and M segmentation methods (indexed by m, ranging from 1 to M). Each segmentation method m yields an estimate θ_pm of the biomarker of interest on sample p. The true value Θ_p of this biomarker is unknown.

The RWT approach assumes a parametric relationship between the true value Θ_p and its estimate θ_pm according to the three following hypotheses:

• H1: the distribution of the biomarker Θ for the database has a finite support.

• H2: each method m provides an estimate θ_pm of Θ_p through the linear expression (1) where ε_pm is normally distributed with zero mean and standard deviation σ_m, and where the parameters a_m and b_m are specific to method m and independent of sample p:

  $${\theta }_{pm}=a_m{\mathrm{\Theta }}_p+b_m+{\epsilon }_{pm}.$$ (1)

• H3: the error terms of each method are independent.

Given the above assumptions, the probability of the estimated values given the linear model and the true value is described through (2):

$$Pr(\{{\theta }_{pm}\}\mid \{a_m,b_m,{\sigma }_m\},{\mathrm{\Theta }}_p)=\prod _{m=1}^M\frac{1}{\sqrt{2\pi {\sigma }_m^2}}\mathit{exp}\left(-\frac{1}{2{\sigma }_m^2}{({\theta }_{pm}-a_m{\mathrm{\Theta }}_p-b_m)}^2\right).$$ (2)

Let us then consider the P samples of the database; the log-likelihood can be written as a function of a_m, b_m and σ_m and the parameters of the distribution describing the biomarker Θ [3]. The maximization of this expression leads to the estimation of the above-cited parameters for each method.

2. Application

The objective of our study was to compare the different methods of segmentation (M = 7) applied to the dataset described in II-A (P = 30). According to [4], the beta distribution, defined by two parameters (μ and ν), is a good finite support function to describe the distribution of the biomarker Θ, i.e. the ejection fraction of the left ventricle. In our study, we also chose this distribution and empirically set the parameters of the beta distribution based on 2 observations: 1) since there were more pathological patients than controls, including 16 patients with a reduced ejection fraction (≤0.45), the distribution was centered at a value slightly below 0.5; 2) since most ejection fractions ranged from 0.05 to 0.85, μ and ν were chosen so that the probability density function of the beta distribution was close to zero outside this range.

The estimation of the maximum-log-likelihood was performed by optimizing a constrained nonlinear multivariable function implemented in MATLAB (R2009a). Estimates of the parameters of the linear model (a_m, b_m and σ_m) were returned for each segmentation approach.

B. Figures of merit as comparison criteria

The figure of merit proposed in [3,4] to compare the different methods was the ratio between σ_m and a_m. We define it as F₁ hereafter.

Another figure of merit called F₂ was proposed in [5]. It was defined as the mean squared difference between the value of the parameter and the estimated value: E[Θ − a_mΘ − b_m − ε_m)²]. Considering H3 given in III-A.1 and the 1^st and 2^nd moments of a beta distribution, we computed F₂ using (3):

$$F_2={(a_m-1)}^2\frac{\mu (\mu +1)}{(\mu +\nu )(\mu +\nu +1)}+2(a_m-1)b_m\frac{\mu }{\mu +\nu }+b_m^2+{\sigma }_m^2.$$ (3)

The smaller the figures of merit, the better the estimate. The classifications of the segmentation methods based on F₁ and F₂ were compared.

Final classifications were also compared to visual inspections of the superimposition of different contours on MRI slices (see Fig. 1).

C. Bootstrap process and rank analysis

To get robust estimates of F₁ and F₂ from the small database involved in our study, a bootstrap approach was used. This statistical process is extensively described in [6]. It is useful to overcome robustness issues due to low sample size. The principle consists in drawing randomly with replacement n samples of equal size as the initial available sample, from this initial sample.

For the present work, n = 1000 different random drawings were performed from the P = 30 initial samples $\left\{\overrightarrow{{\theta }_{p_1}},\overrightarrow{{\theta }_{p_2}},\dots ,\overrightarrow{{\theta }_{p_P}}\right\}$, with $\overrightarrow{{\theta }_{p_i}}$ an array containing the M values θ_pim estimated from the p_i dataset. A Kruskal-Wallis test was then performed based on F₁ or F₂ to determine whether the figure of merit was equal among segmentation methods. When the null hypothesis was rejected, the methods were compared two by two, using a Bonferroni correction, to classify the segmentation methods (with a Type I error equal to 5%).

IV. RESULTS

A. Visual comparison of segmentation approaches

Displays such as Fig. 1 allowed us to visually compare the segmentation approaches to be evaluated. We observed that automated methods (like M3) tended to fail in segmenting the left ventricle when the intensity of the neighboring structures, like the atrium seen on basal slices, was similar to the intensity of the region to be segmented. Trained experts were able to better differentiate poorly contrasted structures hence to provide better segmentation than automated methods.

B. Estimation of the RWT parameters

Tests were carried out to experimentally determine the μ and ν parameters of the beta distribution representative of our database. According to visual inspections, the parameters were set to 4 and 5 respectively. A representation of the probability distribution function of such a beta distribution is in the upper left corner of Fig. 2.

Fig. 2.

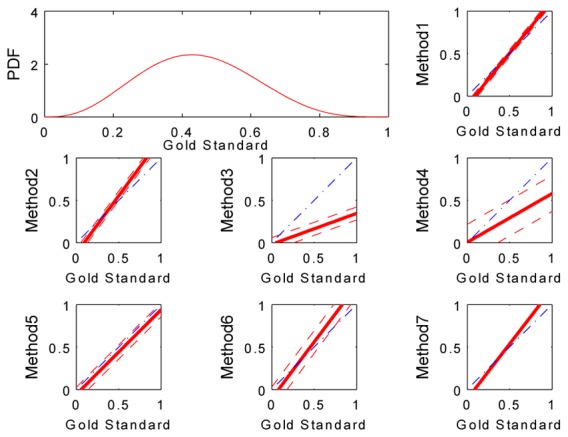
Upper left corner: Probability distribution function (PDF) of a beta distribution describing the ejection fractions of the database (μ = 4, ν= 5). The other plots in the figure show estimates of the biomarker for each method (solid red line) with their associated standard deviation (dashed red lines) superimposed on the ideal estimation (dash-dotted blue line).

Table I displays the parameters of the linear model (a_m, b_m and σ_m) estimated for each method using the RWT approach. To visually compare these parameters, estimates of the biomarker defined by such parameters were plotted against a gold standard of the ejection fraction ranging from 0 to 1 (see Fig. 2). A plot of an ”ideal” estimation (identity between the estimated values and the gold standard) was superimposed to these graphs to observe the gap between both lines. The smaller this gap, the better the estimate. Chart and figure attest that estimates of the biomarker provided by methods M1 and M7 were the most accurate, with small standard deviations, whereas results obtained from methods M3 and M4 were the least reliable, with a large underestimation of ejection fraction. We also note an important standard deviation of the M4 estimates in comparison with other results.

TABLE I.

Estimation of the RWT parameters and figures of merit for each method

Method	am	bm	σm	F1	F2
M1	1.2380	−0.1143	0.0401	0.0324	0.0031
M2	1.3573	−0.1244	0.0544	0.0401	0.0073
M3	0.3632	−0.0176	0.0767	0.2112	0.1062
M4	0.5745	0.0051	0.2122	0.3693	0.0833
M5	0.9976	−0.0568	0.0830	0.0832	0.0102
M6	1.3306	−0.1060	0.1337	0.1005	0.0222
M7	1.2982	−0.1138	0.0034	0.0026	0.0026

Table I presents the figures of merit for each method computed from the above regressions. This table shows that F₁ and F₂ led to a similar classification of the segmentation approaches except for M3 and M4: according to F₁, M3 appeared more accurate than M4 to estimate the ejection fraction whereas an analysis based on F₂ yielded the opposite conclusion. However in both cases, M3 and M4 were found to be the least accurate.

C. Rank analysis performed after the bootstrap process

The rank analysis performed after the application of the bootstrap procedure was repeated on the two figures of merit.

Fig. 3 illustrates the repartition of F₂ computed for each segmentation approach after the bootstrap process. According to this figure, results obtained from M3 and M4 are very variable and those based on M1, M2 and M7 are the most reproducible. Similar observations were made from the boxplot figure displaying the repartition of F₁ computed for each method (not shown).

Fig. 3.

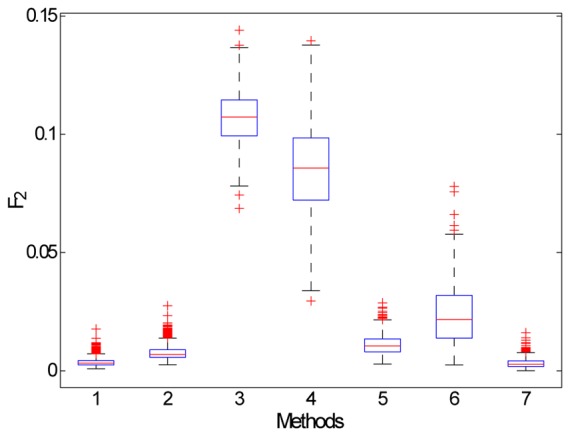
Boxplot of the distribution of F₂ computed after the bootstrap process for each method: the median value is represented by the red horizontal segment, the interquartile range by the blue rectangle, adjacent values inferior to 1.5 times the interquartile range by the dashed black line and outliers by red crosses.

Results of the rank analysis based on the second figure of merit are shown in Fig. 4. According to this figure, 6 different groups of methods can be distinguished and classified in ascending order of accuracy: M1-M7, M2, M5, M6, M4 and M3. The rank analysis based on F₁ (not shown in this paper) also distinguished 6 groups of methods as fellows (in ascending order of accuracy): M1, M7, M2, M5-M6, M3 and M4.

Fig. 4.

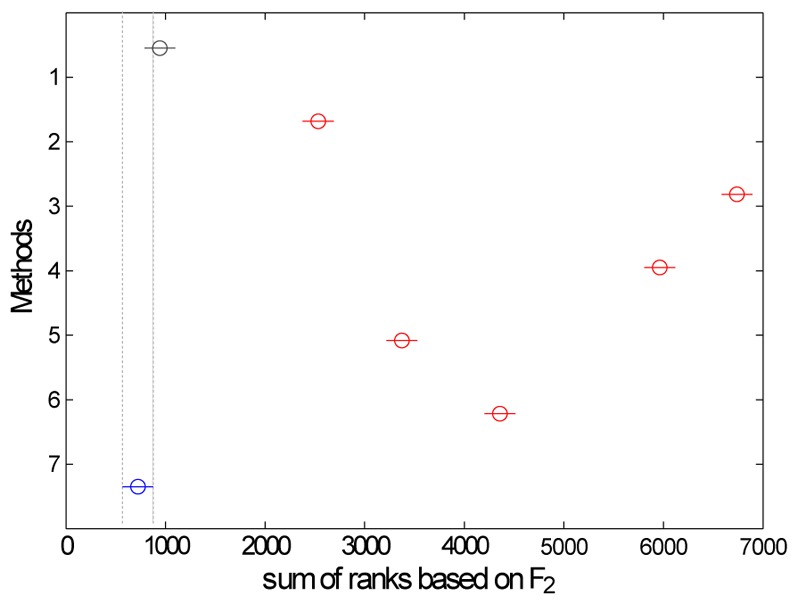
Rank analysis based on F₂ performed after the bootstrap process. The vertical dashed lines indicate the confidence interval of method M7 (blue) that includes method M1 (gray): the two methods do no yield significant different results.

V. DISCUSSION AND CONCLUSION

Seven segmentation approaches with different degrees of automation were compared using an RWT-based method to assess the ejection fraction of the left ventricle. Two figures of merit were computed to evaluate the classification: the first one was commonly used in an RWT approach [3,4] and the second one was more recently introduced in a previous work described in [5]. Both criteria produced similar assessment of the segmentation approaches: the manual delineations (M1 and M7) appeared to give the most accurate estimate of the ejection fraction and the most automated methods (M3 and M4) yielded the least accurate estimates. This quantitative evaluation was consistent with the visual assessment of the contours estimated by the segmentation methods when superimposed with the MR slices (see Fig. 1). Thus, the RWT method, only based on hypotheses described in III-A.1 and using no a priori concerning the automation of the method, seems to be relevant to compare different segmentation approaches used to subsequently derive the ejection fraction.

Other biomarkers, like the diastolic and systolic volumes or the myocardial mass, will soon be evaluated using the same proposed method to validate the classification of segmentation approaches. Additional tests will also be carried out by modifying the parameters of the beta distribution and by removing some evaluated segmentation approaches (like the manual segmentations) to compare the classification results based on the remaining methods to the initial classification results. Finally, the results of the classification method proposed in this paper will be compared to those obtained in comparing segmentations to a representative shape created either from the STAPLE algorithm [1] or from a new approach maximizing the mutual information between segmentations [12].