Nanohydrodynamics simulations: An atomistic view of the Rayleigh–Taylor instability

Abstract

Nanohydrodynamics simulations, hydrodynamics on the nanometer and nanosecond scale by molecular dynamics simulations for up to 100 million particles, are performed on the latest generation of supercomputers. Such simulations exhibit Rayleigh–Taylor instability, the mixing of a heavy fluid on top of a light in the presence of a gravitational field, initiated by thermal fluctuations at the interface, leading to the chaotic regime in the long-time evolution of the mixing process. The early-time behavior is in general agreement with linear analysis of continuum theory (Navier–Stokes), and the late-time behavior agrees quantitatively with experimental observations. Nanohydrodynamics provides insights into the turbulent mixing process that are inaccessible to either continuum calculations or to experiment.

In this article it is shown that one can make quantitative investigations of complex chaotic hydrodynamic flows, starting at the most fundamental level of atomic motion by using the latest generation of supercomputers. To do so requires solving the simultaneous Newtonian equations of motion for an enormous number of classical particles, large-scale molecular dynamics (MD), which in effect solves the Liouville equation. Such hydrodynamical simulations by MD are limited to less than a billion atoms for a nanosecond, which means systems in three dimensions are, at most, 1,000 particles wide (hundreds of nanometers); hence, one can characterize hydrodynamic flows at these time and distance scales as “nanohydrodynamics.” Recent history in the development of massively parallel computers suggests that MD will not reach the scale of micrometers and microseconds in the foreseeable future (1).

Rayleigh–Taylor (RT) Instability

The RT instability occurs when a heavy fluid lies on top of a light fluid in the attendance of a gravitational field g; the fluids will subsequently mix in a more-or-less turbulent process. The RT process is the classical example of turbulence and was first investigated by Lord Rayleigh in 1883 (2) and later theoretically investigated by Taylor (3). Its relevance ranges from astrophysical supernova explosions to geophysical formations like salt domes and volcanic islands (4, 5), all the way down to inertial confinement fusion (6) and to the general turbulent mixing of fluids.

For these purposes MD simulations have been performed on the well studied RT instability (7) as an example and validation of nanohydrodynamics. RT simulations require a large number of particles in an MD calculation (Fig. 1) to resolve fluid structures at late times and the imposition of an enormous gravitational field to reduce the most unstable wavelength to the nanoscale and to mix the fluids on the nanosecond timescale. This most unstable mode of wavelength λ (wavenumber, k = 2π/λ) must be several times smaller than the width of the simulation cell to develop several bubbles and spikes. From linear stability analysis, the most unstable wavelength decreases with increasing g (8), and thus a value of g ≈ 1 × 10¹⁰ g_Earth is required. Whether such a large g value distorts the instability process depends on whether g is a scalable variable up to that magnitude, which can be validated by comparison with experimental and continuum descriptions of the hydrodynamical problem as described by the Navier–Stokes (NS) equations, which assume scalability (4, 6, 8–14). Furthermore, supernovae explosions with g » g_Earth suggest scalability, and although most simulations were performed with that large value of g, an order of magnitude smaller value did not change the results within statistical fluctuations. The large influence of fluctuations, which have been minimized in the initial conditions by using an atomically flat interface, might lead to different results when compared with continuum descriptions where they are ignored. Here, the results of these nanohydrodynamical calculations compare quantitatively with macroscopic experiments (5, 15), and we compare them with theoretical continuum approaches.

Fig. 1.

RT mixing of 100,589,840 atoms by MD of a heavy fluid (red/yellow spheres) on top and a light fluid (blue/gray spheres) below, under the influence of a gravitational field. The predicted most unstable mode emerges quickly for an interface initially perturbed only by thermal fluctuations (Upper, time = 18t₀). Spikes and bubbles grow mushroom caps and start to interact with each other (Lower, time = 24 t₀). Only atoms at the interface of the two fluids are shown (yellow/gray); red and blue atoms mark the boundaries of the simulation box.

Atomistic Simulations

From the fundamental Liouville equation (16) that governs the evolution of an ensemble of a conservative Hamiltonian system, one can derive the usual hydrodynamic NS equations by neglecting physical nonlinearities and thermal fluctuations. Solving the Liouville equation by MD has a further advantage over solving the continuum NS equations, because one can impose much more realistic boundary conditions, as in the onset of the RT instability (2, 3), from a surface roughness generated by natural thermal fluctuations. Moreover, in MD simulations, one can control the interactions between atoms, for example, making fluids perfectly miscible or immiscible at the flick of a switch. Numerically, the advantages of MD are also significant, because MD is a gridless method that is unconditionally stable, with no continuum interface-tracking algorithms and their attendant approximations, for example. The disadvantage of MD is that it is computer-intensive, but that disadvantage is mitigated because the number of continuum grid points required to spatially resolve complex hydrodynamic flows is similar to the number of atoms required to express the structural features of the flow.

MD has played an exceptionally important role in the history of our understanding of fundamental issues in statistical mechanics, both equilibrium and nonequilibrium. First, in the early 1950s, MD helped establish the fact that to reach the thermodynamic limit was not at all the “astronomical number” (10²⁴ particles) that had been assumed for more than a century; indeed, no more than 100 particles was necessary to evaluate equilibrium averages (17). Second, in the late 1960s, MD simulations demonstrated that fluctuations in an equilibrium fluid decay quantitatively by hydrodynamic modes, at a scale of 10 nm and a few picoseconds, resulting in a surprising hydrodynamical enhancement of the memory of a particle's velocity that was not foreseen by Boltzmann in his assumption of molecular chaos (18). Third, in the early 1970s, nonequilibrium MD simulations of simple steady-state flows of mass, momentum, and energy were evaluated as responses to external driving forces, similar to those carried out in real laboratory experiments (19), except that the forces were 6 orders of magnitude larger for the measured signal to overcome the noise caused by atomistic thermal fluctuations. Nevertheless, extrapolation of nonequilibrium MD-shearing experiments to zero shear rate, even in the shear-thinning regime, gave quantitative agreement with the equilibrium fluctuation–dissipation MD results for shear viscosity (20). Thus, the danger facing nonequilibrium MD simulations is that, for driving forces that are too large, the physics can change, such as in shear thinning at extremely high rates. One must assess the characteristics of the flow in response to the large gradients imposed to be sure that unwanted transitions have not occurred. However, nonequilibrium MD simulations of strong shock waves in fluids do not depart far from the NS description (21) even though such strong shocks exhibit significant departures from local thermodynamic equilibrium caused by steep gradients in the hydrodynamic fields. All these findings encourage an effort to extend MD from simple steady-state flows to violent chaotic flows. Previous nanohydrodynamics simulations for Rayleigh–Benard and Taylor–Couette flow (22, 23) have been restricted to linear stability analysis that is rigorously valid at short times, but they have not pursued the long-time behavior into the fully chaotic regime.

Methods

Atomic Interactions and Reduced Units. The atoms within each fluid interact by means of the intermediate-range cubic spline Lennard–Jones (LJ) potential (24): φ^LJ(r) = ε[(r₀/r)¹² – 2(r₀/r)⁶], for an r less than the inflection point; for a larger r, the potential is a cubic spline with a finite range. The interactions between the two fluids was either the same potential in the miscible case or purely repulsive in the immiscible case: φ^rep = φ^LJ(r) + ε, for r < r₀, and 0 otherwise. We use reduced LJ units: bond energy, ε; bond length, r₀; and the mass of the light fluid, m₁ (except for the largest density ratio where we set m₁ = 0.25). The mass of the heavy fluid was adjusted to give the desired A. If the light fluid is methanol (m₁ = 32 atomic mass unit, ε/k_B = 507 K, r₀ = 0.402 nm, k_B is Boltzmann's constant), the units for the time, t₀ = r₀(m/ε)^1/2, and acceleration, , become 1.11 ps and 3.26 × 10¹⁴ m/s² = 3.3 × 10¹³ g_Earth, respectively.

Simulation Setup. As the initial condition we set up a mechanically stable compressed fluid at temperature T = 1.3 ε/k_B under the influence of a gravitational field g. Starting with a given pressure P₀ on top of the sample, we integrate the equation dP = –ρ(h)gdh numerically from the top to the bottom along the height h, filling up the space with a uniaxially compressed face-centered cubic (fcc) lattice. The atomic volume V is determined from an approximation of the isothermal equation of state, P(V,T = 1.3 ε/k_B). The quality of the approximation of the equation of state is not important for the results presented here. To speed up the melting of the fcc lattice, the positions were then randomized such that the closest possible atomic distance is no closer than 99% of the LJ potential minimum. Gravity ranged from 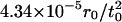to 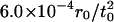and gave, for a typical system height of 612.5 r₀, pressures on top from 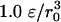to 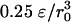and at the bottom from 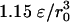to 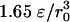. A further increase of g would reduce the wavelength of the most unstable mode and therefore the computational costs; however, this increase leads also to a solidification of the liquid near the bottom due to high pressures.

Linear Stability Analysis. A linear stability analysis of the hydrodynamic equations of a heavy fluid on top of a light fluid in the presence of a gravitational field was first presented by Harrison (25) in 1908, and later derived in a more general context by Chandrasekhar (ref. 8, see p.442, equation 113). To compare this linear stability analysis to atomistic simulations we used the surface tension and the viscosities (26) for the densities at the interfaces and solved the implicit expression derived by Harrison and Chandrasekhar numerically. [We calculated the surface tension (27) γ as a function of the pressure-volume PV at , 1.2 ε < PV < 1.7 ε.] This calculation gives the growth rate n as a function of k (Fig. 2), from which one can determine the mode of maximum growth.

Fig. 2.

The early exponential growth n of a single RT mode by MD simulations (circles) compared with linear stability analysis (line) for two fluids with an interfacial surface tension, 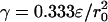, and kinematic viscosities, and 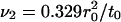at Atwood number A = 0.867. For large wavenumber k, the solution of the linear stability analysis predicts an oscillatory movement of the interface, which is confirmed by MD (circles at n = 0). Deviations between theory and simulations can be qualitatively explained due to an initially large amplitude of the single modes in simulations, which are required to overcome inherent thermal fluctuations. The gravity is 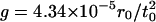and, depending on the wavelength of the perturbation, the samples contain between 376,920 and 4,357,800 atoms.

Reynolds Number. The Reynolds number 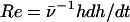, where h is the height of the mixing zone and 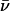is the mass-averaged shear viscosity of the two fluids (A. W. Cook, private communication) does not exceed 1,500 in the simulations, whereas experiments range from 3,700 to 10⁵ when spikes reach the bottom. Assuming h ∝ gt² provides and shows that to increase Re, either g or the system height H (which limits the possible fall height h) has to be increased. However, increasing g or h increases the pressure near the bottom such that solidification can occur. To increase the range of Re in atomistic simulations, g has to be decreased and the sample has to be widened (since the most unstable wavelength increases). Thus, the sample can be higher because the increase of pressure along the height is reduced.

Modeling. The scalable parallel short-range MD code (refs. 28 and 29; http://bifrost.lanl.gov/MD/MD.html) with pairwise additive LJ interatomic interactions was used in the simulations. The particles in each of the two fluids interact with the same potential, except that one is more massive than the other. Particles in the two different fluids either interact with the same potential for the miscible case, where the surface tension is zero, or with only the purely repulsive part of the LJ potential in the immiscible case. The heavy fluid with density ρ₂ and kinematic viscosity ν₂ is initially placed on top of the light fluid of density ρ₁ and kinematic viscosity ν₁ under the influence of the gravitational field g. The density ratio is characterized by the Atwood number, A = (ρ₂ – ρ₁)/(ρ₂ + ρ₁). The initial conditions were set up such that the system was as close as possible, given the equation of state, to a mechanically stable compressed fluid under the influence of the gravitational field. The interface roughness was then due only to atomic-scale thermal fluctuations. Most runs used a thin-slab geometry (1,400 r₀ width, 612.5 r₀ height, 5.25 r₀ thickness, with the bond length r₀) containing 3 million particles, small enough and thus short enough runs (≈12 h on 200 processors of a Linux cluster) to investigate a wide range of parameter space. However, a few runs were also performed in a fully 3D geometry; an example containing 100,589,840 atoms (544.25 r₀ × 525 r₀ × 544.25 r₀) is given in Figs. 1 and 5, which is published as supporting information on the PNAS web site.

Computing Resources. Using 1,600 central processing units (CPUs) of the ASCI Q computer system (Compaq) at Los Alamos, we simulated 100,589,840 atoms for 250,000 integration time steps (δt = 0.01t₀) (400,000 CPU hours). Smaller simulations were performed on the ASCI QSC computer system (1,024 CPUs) and the 256-CPU Linux cluster Grendels (Intel Xeon CPUs) at Los Alamos. The simulations presented here needed an estimated total of 600,000 CPU hours. Accounting for different processor speed on the used systems this is more than a week on all 4,096 CPUs of the ASCI Q computer system.

Results and Discussion

Early-Time Mixing. To demonstrate the quantitative validity of the MD approach, the early-time growth of an imposed single sinusoidal mode perturbation of the interface with wavelength λ was compared with analytical results of linear stability analysis based on continuum hydrodynamics (8, 25). The amplitude of the disturbance grows as e^nt (Fig. 6, which is published as supporting information on the PNAS web site), where the growth rate n depends on g, the surface tension, and the viscosities of the two fluids and is a function of the imposed wavenumber. This dependence on k reaches a maximum k_max, which is the fastest growing or most unstable mode, as shown in Fig. 2. It is important for quantitative purposes to solve the linear stability equation numerically rather than to depend on inaccurate analytic approximations (8). The MD simulations require an initial mode with an amplitude of 0.057λ to override the fluctuations always present in MD. The growth of the interface has been fit from t/δt = 120,000 to t/δt = 300,000 time steps (δt = 0.01 t₀), and the amplitude grows as much as 0.15λ at k_max. At earlier times the interface exhibits rather strong fluctuations, as it equilibrates from the artificial initial condition. The comparison between linear stability analysis of continuum theory and atomistic simulations in Fig. 2 shows good agreement with the value of the most unstable mode and deviations in the growth rate, which can be qualitatively explained by the nonlinearity introduced by the large initial amplitude. A numerical solution of the continuum equations for the immiscible but inviscid case (hence, no maximum) shows that an initial amplitude of 0.10(0.15)λ lowers the growth at k_max by 11(27)% (A. W. Cook, private communication). This figure also shows that fluctuations become more pronounced the smaller the structures are (i.e., the larger the k becomes). Here, thermal fluctuations have a larger influence on the growth than for the larger structures.

The growth from an interface perturbed only by fluctuations was found to be dominated quickly by the wavenumber corresponding to k_max, which then determines the initial number of bubbles and spikes. For example, the fully 3D system should, according to k_max, have 3.5 spikes along the edge of the simulation cell, whereas four were actually observed at early times (see Fig. 1). In some cases the deviations from the theoretically most unstable mode predictions were larger because the presence of multiple modes and the finite edge length.

Late-Time Mixing. At later times the spikes and bubbles develop mushrooms at their tips, which eventually interact and merge in a process that can be described as turbulent (Movie 1, which is published as supporting information on the PNAS web site). The penetration distance h of the spikes and bubbles is characterized at long times by the only relevant distance scale applicable, namely, gt² multiplied by the coefficient αA, so that h = αAgt², where h is determined at the position where the fluid concentration has changed by 95% (see Fig. 3). The fact that rise and fall of bubbles and spikes in the RT scenario has a constant acceleration rather than a constant velocity v (which is expected for a fall of an isolated droplet) can be explained by assuming the Newton friction force (–Cv²) rather than Stokes friction (–Cv), in addition to a constant buoyancy and inertia in the equation of motion for a bubble or spike. The friction coefficient C reduces with the fall, h, as C ∝ 1/h, since the structures become thinner during the fall (30). The long-time growth of the bubbles and spikes, as characterized by α, is thus determined from the slopes of the evolution of the boundaries shown in Fig. 3. Somewhat surprisingly, no statistically significant difference occurred between the average value of α, as determined from the large number of simulations done with the slab geometry at A = 0.867, and a single fully 3D system.

Fig. 3.

Penetration h of bubbles (open symbols) into the heavy fluid and spikes (closed symbols) into the light fluid as a function of the square of the time at Atwood number A = 0.867 and gravity 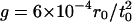. The long-time slope of the growth rate α (solid lines) of the thin slab (A, black squares) and the fully 3D MD simulation (B, red triangles) are, to within statistical error, the same. An initial single-mode perturbation with wavelength λ = 70r₀ and amplitude δh = 0.02λ (C, blue diamonds) does not change the long-term slope. However, when λ is not small compared with the system height H = 612.5r₀ (and thus the fall height of spikes and bubbles), the mixing can be enhanced (not shown).

The growth of the bubbles and spikes, as given by the value of α determined by the simulations, were found to agree with experiment (5, 15) and Youngs' theoretical model (30) (see Fig. 4). This remarkable quantitative agreement with experiment at late times and in three dimensions in the turbulent regime is a significant validation of nanohydrodynamics. At the longest time of penetration of the spikes in the simulations, the depth reached 30% of the experimental value (5), measured in terms of the most unstable wavelength. However, the Reynolds number in the simulation reached only 1,500, compared with experimental values ranging from 3,700 to 10⁵; NS calculations reached Reynolds numbers of 5,500 (6). Different continuum hydrodynamic calculations show a range of α values for bubbles between 0.03 and 0.08, compared with an experimental range of 0.05 to 0.08 (13, 14). Recently, it was suggested that the relatively large NS variation in α is due to the different initial perturbations along the interface (31, 32). Also, one should emphasize that most NS calculations use lower Atwood numbers than presented here. For spikes, α is not independent of A, as it is for bubbles, but tends toward the free fall limit at A = 1 of 0.5 (30). In this limit, the spikes are not hindered by any friction, whereas for bubbles, the dynamics is determined by a balance between friction and buoyancy.

Fig. 4.

The α values for various Atwood numbers A from MD simulations compared with experimental data (5, 15), and Youngs' model with C = 3.67 (30) (dashed lines). For large A, α approaches the free-fall value of 0.5 at A = 1. At A = 0.867, 3 miscible and 19 immiscible simulations were made, and the error bars indicate the standard deviation rather than the smaller confidence interval.

Dependence on Initial Conditions. With MD simulation it is possible to quantitatively determine how α depends on initial conditions, such as the surface tension and imposed disturbances. It was found that the α values of the spikes in the miscible case were reduced compared with the immiscible case at a high Atwood number. In the miscible case, the interface gets blurred by diffusion. This result can be interpreted as a reduction of the effective Atwood number, leading to a reduction in the α of the spikes but not bubbles, since their α value is nearly independent of A. It was also found that an initial single-mode perturbation of the interface enhances the mixing process at short times, an effect also observed experimentally (5). However, at distances large when compared with the initial perturbing mode, the effect is washed out, and α is similar to the value from a fluctuation-perturbed interface (Fig. 3). This result suggests a memory loss about the initial perturbations in time in the atomistic simulations due to the chaotic nature of the underlying equations of motions. However, continuum descriptions seem to depend on the initial perturbations on the α values (31, 32).

In any case, it is questionable whether α alone characterizes the long-time behavior (33). For example, from experiments (5) and the simulations presented in Fig. 3, oscillations in the bubble growth about the limiting slope are observed. These oscillations might have to do with the compressibility of the fluid, sometimes ignored in continuum calculations, coupled with viscous effects that have a major influence on bubble dynamics. Even more substantive are the observations of spikes in a slab that were five times higher than reported so far (3062.5 r₀). The purpose of that run (Movie 1) was to reach longer times, since in previous runs the spikes reached the bottom of the simulation cell. This simulation showed αAgt² behavior in the first half of the run but, after that, behaved dramatically differently: the mushrooms at the tips of the spikes broke off and formed droplets, an artifact that could either be due to an insufficient number of particles in the simulation or to the large value of g.∥ But it could also be real, when the thickness of the structures reach the nanoscale, since thinning of the spikes as they advance was observed experimentally (30). Furthermore, thinning and breakup of nanojets has been observed theoretically by including fluctuations, either by a full atomistic approach or by an additional stochastic term in the continuum equations (34).

Conclusions

The large-scale atomistic simulations of the RT mixing process presented here have tested and quantitatively validated long-standing efforts in complex hydrodynamical flows by a completely different approach. Our simulations compare favorably with experimental observations and can help to interpret experimental results. Furthermore, these atomistic simulations pave the way to a detailed fundamental insight into turbulent flows in general, because they can capture the smallest physical scale, the atomistic scale. Initial perturbations arising from thermal fluctuations, which are unattainable by either NS calculations or experiments, can be studied by the nanohydrodynamics approach we have reported here. A detailed comparison with continuum calculations should be undertaken to see if hydrodynamic averaging over atomistic behavior introduces any significant differences into the description of the turbulent mixing process.