Towards Effcient Label Fusion by Pre-Alignment of Training Data

Abstract

Label fusion is a multi-atlas segmentation approach that explicitly maintains and exploits the entire training dataset, rather than a parametric summary of it. Recent empirical evidence suggests that label fusion can achieve significantly better segmentation accuracy over classical parametric atlas methods that utilize a single coordinate frame. However, this performance gain typically comes at an increased computational cost due to the many pairwise registrations between the novel image and training images. In this work, we present a modified label fusion method that approximates these pairwise warps by first pre-registering the training images via a diffeomorphic groupwise registration algorithm. The novel image is then only registered once, to the template image that represents the average training subject. The pairwise spatial correspondences between the novel image and training images are then computed via concatenation of appropriate transformations. Our experiments on cardiac MR data suggest that this strategy for nonparametric segmentation dramatically improves computational efficiency, while producing segmentation results that are statistically indistinguishable from those obtained with regular label fusion. These results suggest that the key benefit of label fusion approaches is the underlying nonparametric inference algorithm, and not the multiple pairwise registrations.

1 Introduction

Image segmentation is a fundamental problem in medical image analysis. Automatic segmentation methods often require a priori knowledge in the form of training images that have been manually segmented by an expert. A classical strategy is to summarize the training data in a probabilistic atlas [1–6], which is used as a prior model in subsequent segmentation.

An alternative approach, called label fusion, manipulates the training dataset in its entirety [7–9]: each manual label map is transferred over to the novel subject’s coordinates via pairwise registrations between the novel image and training images. These propagated labels are then fused into a single segmentation estimate – a step that can be viewed as probabilistic inference based on a nonparametric model of anatomical variability [10]. Several studies have demonstrated that label fusion outperforms the single-atlas approach when the anatomical variability is too high to be accurately captured by mean statistics [10–12]. Two possible causes for performance differences between the two methods are commonly hypothesized. First, the nonparametric model captures inter-subject variability more accurately. Second, the multiple pairwise registrations provide robustness against inevitable small registration errors. This performance improvement however comes at a significant computational cost. In contrast, a single registration step is required to align a parametric atlas to a novel image.

In this paper, we present a modified label fusion method that co-registers the training images into an unbiased coordinate frame using a diffeomorphic transformation model. To segment a novel image, a single pairwise registration is performed with the template that represents the average training subject. This transformation is then concatenated with the individual transforms of the training subjects to the average space obtained in the groupwise registration to compute pairwise warps between each training image and the novel image. By performing a priori groupwise registration, the proposed approach dramatically reduces the computational burden compared to a typical label fusion implementation that requires many individual pairwise registrations during the segmentation phase.

Groupwise registration has previously been used in the context of label fusion [13, 14] to reduce the size of the employed training set by identifying training images most similar to the novel scan. In contrast, we propose to use the entire training set but reduce computational burden by relying on a single coordinate system. Using cardiac MR data, we demonstrate that the proposed method achieves comparable segmentation accuracy at a fraction of the computational cost of regular label fusion. Our experiments further suggest that when state-of-the-art registration procedures are used, the nonparametric inference approach, and not the multiple pairwise registrations, is at the core of the superior performance of label fusion algorithms.

The paper is structured as follows. We begin by discussing label fusion segmentation methods in Section 2. We continue by describing the registration approaches we employ in this work in Section 3, in particular the algorithm we use to perform groupwise registration of the training images to an average space. We then present our results in Section 4 and conclude with a discussion of their implications in Section 5.

2 Label Fusion

Label fusion can be interpreted as an inference algorithm based on a nonparametric probabilistic model [10]. In this framework, the spatial transformations that map training image coordinates to the test image are assumed to be known. Here, we use a variant of label fusion, called local label fusion, that combines the propagated labels, encoded as probabilistic priors, in a weighted fashion. The weights vary spatially and depend on the local intensity differences between the novel image and corresponding training image.

Let {I_n, L_n} denote the set of N training images and corresponding label maps, i.e., manual segmentations (n = 1, … , N). Let I denote the novel image to be segmented and ${\Psi }_n:{\mathbb{R}}^3\mapsto {\mathbb{R}}^3$ denote the spatial transformation that maps the coordinates of the novel image to the n^th training image frame. Once the transformations {ψ_n} are computed, segmentation reduces to voxel-level averaging:

$$\widehat{L}\left(x\right)=\underset{l}{\mathrm{argmax}}\sum _{n=1}^{N}p\left(L\right(x)=l;L_n,{\Psi }_n)w\left(I\right(x),I_n({\Psi }_n\left(x\right)\left)\right).$$ (1)

Similar to [10], the weight term $w\left(I_1\right(x),I_2(x\left)\right)=\exp \left\{\frac{{-\left(I_1\right(x)-I_2(x\left)\right)}^2}{2{\sigma }^2}\right\}$ encodes the local intensity similarity between the two images and the vote term $p\left(L\right(x)=l;L_n,{\Psi }_n)\infty \exp \left\{\rho D_n^l\right({\Psi }_n\left(x\right)\left)\right\}$, where $D_n^l\left({\Psi }_n\right(\cdot \left)\right)$ denotes the signed Euclidean distance transform of the warped label map, represents the propagated label prior from the n^th training subject.

A special case of this model that can be derived with σ → ∞ is “majority voting”, where the segmentation at each voxel is simply the most frequent training label [7, 9]. Since this approach ignores local intensity information, it effectively thresholds the probabilistic atlas computed from propagated label maps.

3 Registration

Any label fusion segmentation scheme relies on the spatial transformations {ψ_n} that map the novel image coordinates to each training image. In this work, we compare two different methods to estimate these transformations.

Pairwise registration

The standard approach is to apply pairwise registration between each training image and the novel image. We employ an efficient, Demons-based diffeomorphic method to perform pairwise registration [15]. The algorithm parametrizes the spatial diffeomorphism with a stationary velocity field $\upsilon :{\mathbb{R}}^3\mapsto {\mathbb{R}}^3$, via a temporal differential equation ∂φ(x, t)/∂t = v(φ(x, t)) with φ(x, 0) = x. The registration warp φ(x) is the solution of the PDE at t = 1; φ(x, 1) = exp(v)(x). Given the velocity field v, the corresponding φ can be efficiently computed via the scaling and squaring method, and the inverse can be obtained as φ⁻¹ = exp(−v) [15]. The algorithm efficiently seeks a spatially smooth transformation that minimizes the mean squared error between the two images.

Groupwise registration

The alternative strategy we explore here involves performing groupwise registration on the training data. Similar to prior work [16, 17], we build on a pairwise registration tool, namely the diffeomorphic Demons algorithm, to perform groupwise alignment. The algorithm iterates between computing the template T, which represents the average image, and performing pairwise registrations between the template and the individual training images.

To perform groupwise registration, it is necessary to define a constraint to avoid drift of the average template and guarantee an unbiased average coordinate system. When working with the stationary velocity field parametrization, one way to achieve this goal is to constrain the average velocity field at each voxel to be zero:

$$\frac{1}{N}\sum _{n=1}^N{\upsilon }_n\left(x\right)=0\forall x.$$ (2)

At each iteration of our implementation, we first register the current template to each of the training images, which produces a velocity field v_n for each training image I_n. We then adjust each velocity field

$${\upsilon }_n\leftarrow {\upsilon }_n-\overline{u},$$ (3)

where $\overline{u}=\frac{1}{N}{\sum }_{n=1}^N{\upsilon }_n$ is the common component of the velocity fields.

This guarantees that the average velocity field across the training images is zero. Furthermore, since exp(v – u) ≈ exp(v ○ exp(−u) for a small u and any v [20], the overall correspondences across the images remain approximately intact after the normalization of Eq. (3).

Once all images have been registered to the current estimate of the template, we update the template as a weighted average of the warped images [16, 21]:

$$T\left(x\right)=\frac{\sum _{n=1}^N\mid \nabla {\Phi }_n^1\left(x\right)\mid I_n\left({\Phi }_n^{-1}\right(x\left)\right)}{\sum _{n=1}^N\mid \nabla {\Phi }_n^{-1}\left(x\right)\mid },$$ (4)

where ∣ · ∣ denotes the matrix determinant, ▽ denotes the Jacobian matrix with respect to the spatial coordinates, and ${\Phi }_n^{-1}\left(x\right)=\exp (-{\upsilon }_n)\left(x\right)$. The Jacobian terms ensure a probabilistically consistent model [21, 22].

To summarize, each iteration of the groupwise registration algorithm consists of the following three steps:

1. Pairwise registrations between the current template T and individual images I_n using the diffeomorphic Demons registration algorithm [15].

2. Normalization of each resulting velocity field as in Eq. (3).

3. Update of the template as in Eq. (4).

To initialize the template image, we perform affine registration between all pairs of images. We then choose the image that has the smallest average deformation magnitude, meaning it is the least biased, as the initial template. To make sure the initial template is truly unbiased, i.e., its coordinate frame satisfies Eq. (2), we apply the inverse of the average velocity field to the “least biased” image. This warped image is then used as the template T in the first iteration.

During segmentation, we align a novel image with the group of co-registered training images by simply performing a pairwise registration with the final template T. This yields a spatial correspondence to all the individual training images via the atlas coordinate system. The spatial mapping ψ_n from the novel image coordinates to the n^th training image can therefore be obtained by concatenating the inverse of the transformation from the atlas to the novel image with the transformation from the atlas to the n^th training image.

4 Experiments

To evaluate the proposed method, we automatically segment the left atrium of the heart in magnetic resonance angiography (MRA) images. This is a particularly challenging segmentation problem because of the high anatomical variability of the left atrium across subjects. We used a set of 16 electro-cardiogram gated (0.2 mmol/kg) Gadolinium-DTPA contrast-enhanced cardiac MRA images (CIDA sequence, TR=4.3ms, TE=2.0ms, θ=40°, in-plane resolution varying from 0.51mm to 0.68mm, slice thickness varying from 1.2mm to 1.7mm, ±80 kHz bandwidth, atrial diastolic ECG timing to counteract considerable volume changes of the left atrium). The left atrium was manually segmented in each image by an expert.

We implemented label fusion using two registration strategies: (1) computing individual pairwise registrations between all training images and the test subject (“pairwise” registration), and (2) obtaining these transformations via groupwise pre-registration of the training set (“groupwise” registration), as described in the previous section. For each of these methods, we segmented the left atrium using both local label fusion (LF) and majority voting (MV) algorithms. In addition, we implemented the standard parametric EM-segmentation algorithm (EM) [5, 6] as a benchmark. The EM algorithm used the groupwise registered training data to compute a probabilistic spatial prior in the atlas coordinates.

In our experiments, we varied the number of training subjects from 1 to 13, and for each such number we sampled 10 different training sets from the full image set. In each case, we randomly chose 3 test subjects that were not part of the training set, yielding 30 segmentations per number of training subjects. We used the Dice score [23] and the mean Hausdorff distance [24], to quantify the agreement between an automatic and corresponding manual segmentation. The Dice score ranges from 0 to 1 and measures volumetric overlap, while the Hausdorff distance is a measure of the average physical distance between the boundaries of two regions.

Fig. 1 shows the average Dice and Hausdorff measures obtained with all five methods for different sizes of the training set. Unsurprisingly, all methods tend to benefit from a larger training set, yet with diminishing returns for higher numbers. We further observe that local label fusion consistently outperforms both majority voting and the traditional parametric EM-segmentation approach. Moreover, the “groupwise” and “pairwise” registration strategies yield comparable accuracy for local label fusion. In the case of majority voting, the segmentation quality using the “pairwise” strategy yields only slightly better results. Fig. 2 provides a direct comparison between “groupwise” and “pairwise” variants of each metod, by reporting the average of the difference between the individual-level Dice and Hausdorff measures computed for each test subject. These results suggest that computing all the pairwise registrations between the training images and the test image offers little, if any, improvement in segmentation accuracy over using the groupwise pre-registration approach. Fig. 3 shows example segmentation results on an image slice to illustrate the qualitative differences between the methods.

Fig. 1.

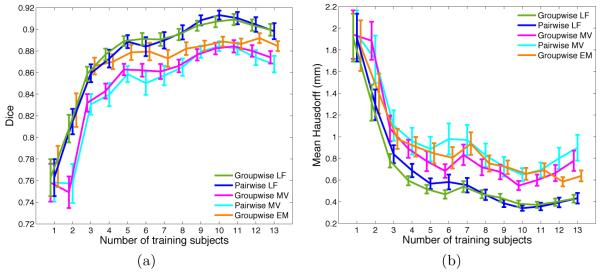
Comparison of left atrium segmentation results for different methods showing (a) average Dice overlap scores and (b) mean Hausdorff distances between automatic and expert manual segmentations for increasing numbers of training subjects.

Fig. 2.

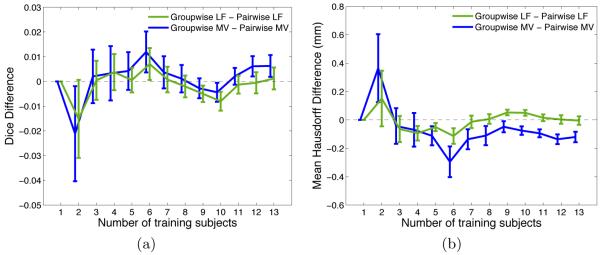
Average matched pairwise differences between (a) Dice overlap scores and (b) mean Hausdorff distances resulting from different methods.

Fig. 3.

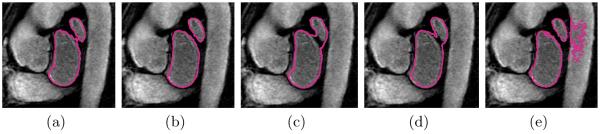
Example segmentation results for one image slice: (a) groupwise and (b) pairwise local label fusion, (c) groupwise and (d) pairwise majority voting, and (e) parametric EM-segmentation.

The computation times for each approach on a modern 12-core machine are shown in Table 1. Each iteration of the construction of the groupwise atlas involves N non-rigid registrations (6 min. each), normalizing the velocity fields (7 min.) and computing the updated average template (2.5 min.). We observed that the algorithm converged to a stable template image after 4 such iterations. Although these computations are expensive, they are done offline, prior to the segmentation of a new subject. Local label fusion that uses the groupwise atlas requires bringing the atlas to the coordinate frame of the test subject via a single registration (6 min.). Finally, in local label fusion using pairwise registrations, the subject-specific nonparametric atlas is built for each new test subject by performing N registrations (6 min. each).

Table 1.

Computation times per test subject for N training subjects (in minutes).

Method	Atlas Construction	Registration to Test Subject	Segmentation
Groupwise LF / MV	(6N + 7 + 2.5) × 4	6	1
Pairwise LF / MV	0	6N	1
Groupwise EM	(6N + 7 + 2.5) × 4	6	6

5 Conclusion

We presented a novel strategy that dramatically improves the computational efficiency of label fusion, while having minimal effect on segmentation quality. In this approach, the training data is pre-registered into a common coordinate system, similar to single-atlas segmentation methods. The novel image is then aligned to this space, which enables the computation of pairwise warps between each training image and the novel image via concatenation of individual transformations. The training images and label maps are then propagated to the coordinates of the new subject to perform nonparametric label fusion segmentation. Our experimental results also provide insight into these segmentation methods by suggesting that, when a sufficiently accurate diffeomorphic registration procedure is used, the improved segmentation quality of label fusion is likely due to the nonparametric inference strategy and not to multiple pairwise registrations between the training data and novel image.

Performing label fusion segmentation by pre-registering the training data removes a layer of robustness since the result hinges on a single registration between the average atlas template and the new subject. In practice, catastrophic failures in this registration should be easy to detect and recover from automatically, for instance by choosing a different initialization. We also found that these occur in only approximately 1% of the cases in our data. Further investigation of this question, along with experiments on larger and more varied datasets are interesting future directions of research.