Skip to main content
NCBI home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2014 Jun 1.
Published in final edited form as: Nat Neurosci. 2013 Nov 3;16(12):1812–1820. doi: 10.1038/nn.3562

Temporal synchrony and gamma to theta power conversion in the dendrites of CA1 pyramidal neurons

Sachin P Vaidya 1,2, Daniel Johnston 2
PMCID: PMC3958963  NIHMSID: NIHMS560017  PMID: 24185428

Abstract

Timing is a crucial aspect of synaptic integration. For pyramidal neurons that integrate thousands of synaptic inputs spread across hundreds of microns, it is thus a challenge to maintain the timing of incoming inputs at the axo-somatic integration site. Here we show that pyramidal neurons in the rodent hippocampus use a gradient of inductance in the form of HCN channels as an active mechanism to counteract location-dependent temporal differences of dendritic inputs at the soma. Using simultaneous multi-site whole cell recordings complemented by computational modeling, we find that this intrinsic biophysical mechanism produces temporal synchrony of rhythmic inputs in the theta and gamma frequency ranges across wide regions of the dendritic tree. While gamma and theta oscillations are known to synchronize activity across space in neuronal networks, our results identify a novel mechanism by which this synchrony extends to activity within single pyramidal neurons with complex dendritic arbors.

Keywords: HCN, synchrony, theta, gamma

Introduction

In neural systems, network oscillations synchronize neural activity within and across brain regions1–3. The rodent hippocampus is a well-studied system in this regard, where the high frequency ‘gamma’ oscillations (40–150 Hz) and the slower ‘theta’ oscillations (4–10 Hz), route information and synchronize neural activity during hippocampus-dependent behaviors4–7. These oscillations also form a basis for a temporal code where the relative timing of neuronal firing carries valuable information8,9. Interpreting the timing of these inputs, however, can be an intricate task for pyramidal neurons with extended morphologies. For example, a single CA1 neuron from the rat hippocampus is innervated by approximately 30,000 synapses spread up to 1000 μm from the axo-somatic integration site10,11. Capacitive filtering during dendritic propagation would thus result in location-dependent distortion of the timing for these inputs12. In this study, we ask whether CA1 pyramidal neurons have a mechanism that corrects for this temporal distortion.

Our results reveal that CA1 neurons have an intrinsic biophysical mechanism in the form of a gradient of inductance that compensates for capacitive location-dependent temporal delays. In a linear electrical system, capacitors and inductors are both energy storage elements that have opposing influences on the temporal relationship between current and voltage for oscillatory inputs. Capacitive elements typically cause phase delays where the voltage lags the current while inductive elements cause phase advances where the voltage leads the current13. In biological systems, the lipid bilayer imparts capacitance to the membrane. Another source of capacitance or even inductance is the gating of ion-channels depending on whether they amplify or restore changes in the membrane potential, respectively14. This type of ‘reactance’ is termed ‘phenomenological’ or ‘anomalous’ since it is unconventionally generated by the time-variant resistive properties of ion-channels14–16. In CA1 neurons, the hyperpolarization-activated cation nonselective (HCN) channels impart a strong phenomenological inductance to the membrane electrical properties17,18. This inductance leads to amplitude resonance in the theta frequency range and phase advance of the voltage relative to the current at low frequencies19–23. Both these attributes increase with distance from the soma and are accentuated in the distal dendrites due to the underlying increase in the local HCN channel density17,23,24. While the implications of this inductance gradient on the amplitude of incoming inputs is band-pass filtering of dendritic signals in the theta frequency range, its influence on the capacitive delay associated with propagation has remained unexplored25–27.

In this study, we show that the HCN gradient of inductive reactance actively compensates for distance-dependent capacitive delay of distal dendritic inputs ensuring that in spite of variable propagative distances, spatially dispersed synchronous inputs are co-incident at the axo-somatic integration zone. Using multi-site whole cell recordings and computational modeling, we show that this response synchrony at the soma is optimum for inputs in the theta frequency range. Finally, using the dynamic clamp technique to simulate synaptic events, we show that gamma and theta frequency synaptic inputs are especially well suited to take advantage of these dendritic filtering mechanisms. We find that synaptic mechanisms convert high frequency gamma power into theta power thereby facilitating the transfer of high frequency information from distal sites to the soma.

Results

Theta-frequency oscillatory synchrony at the soma

Theoretical predictions suggest that capacitive filtering in dendrites during passive propagation of electrical signals leads to location-dependent temporal differences at the soma12. For oscillatory inputs, these temporal differences would be manifested as a distinct phase delay of the distal input compared to the proximal input, when measured at the soma. We explored these location-dependent temporal differences in CA1 neurons using dual whole-cell current clamp recordings between the soma and approximately 300 μm along the apical dendrite. Surprisingly, for a sinusoidal current input of 7 Hz, the voltage response at the soma for the distal dendritic input was synchronous with that of the proximal somatic input indicating that the phase or latency of voltage response at the soma was independent of input location along the apical dendrite (Fig. 1a, b).

Figure 1. Theta frequency oscillatory synchrony in CA1 neurons.

Figure 1

Open in a new tab

(a) The somatic voltage response (normalized for amplitude) to a sinusoidal current of 7 Hz/100 pA (---) into the dendrite at 300 μm ( Inline graphic) and at the soma (black). Note both responses are measured at the soma. The responses overlap in control conditions suggesting synchrony of oscillatory response at the soma. This synchrony is disturbed by HCN blocker ZD7288; (b) Summary data for experiments described in (a) with response latency defined as the difference in time between current injection at input site and voltage response at soma (in ms). [Control: Soma 9.73±1.19 and Dendrite 9.77±1.36 (n=8; N.S., p=0.93, paired t-test); ZD7288: Soma 16.50±1.23 and Dendrite 21.51±0.90 (n=6; ***,p=0.00047, power(1–β)=0.98, paired t-test)]. (c) Impedance phase profile at soma (ZPPsoma) measured by 2s/100pA sinusoids of varying frequency when injected in the dendrite at 300μm ( Inline graphic) and at the soma (black). Note the intersection point (arrow), which suggests synchrony of response; (d) same as (c) but with ZD7288. Note the absence of synchrony; (e) Summary data for experiments in (c, d) but described as difference in phase between the dendritic response and somatic response. Positive values suggest dendritic input precedes the somatic input at the soma and vice-versa. Scale bars: 10 ms. Dendritic recording locations: 291± 11 μm (Control); 288±8 μm (ZD7288). Error bars indicate s.e.m.

The impedance phase profile at the soma (ZPPsoma) describes the phase relationship between current input at a given location and its somatic voltage response across all measured frequencies. When the ZPPsoma was compared between distal and proximal inputs, the observations were similar for all measured neurons. At lower frequencies (0–4Hz), the response to the distal input unexpectedly appeared before that of the local input at the soma. This phase advance of the distal input disappeared around 7 Hz (7.04 ± 0.44 Hz; n= 8), where the distal and the local somatic responses were synchronous. At higher frequencies (>10 Hz), the response to the distal input showed an increasing phase lag (Fig. 1c, e). This oscillatory synchrony of voltage response was dependent on the direction of propagation. When the same inputs were observed in the dendrites, the voltage response to the local dendritic input always occurred before that of the distal somatic input at all measured frequencies (Supplementary Fig. 1).

Positive impedance phase (Phase advance of voltage to current) observed at lower frequencies is a hallmark of an inductive component in a linear system. As HCN channels are known to impart membrane inductance in CA1 neurons, we tested for oscillatory synchrony with the HCN blocker ZD728823. Addition of ZD7288 abolished oscillatory synchrony at 7 Hz and led to distinct location-dependent differences across all measured frequencies (Fig. 1a, b, d, e). Thus, HCN channels play a crucial role in synchronizing the response of distal and proximal inputs at the soma in the theta frequency range.

Next, we tested whether oscillatory inputs across the entire apical dendrite are synchronized at the same frequency using two parallel approaches. Employing a computational approach, we simulated the soma and apical dendrite of a CA1 neuron using a simple “ball-and-stick” model. This model had comparable dimensions and passive membrane parameters to those experimentally measured in CA1 neurons28. The proximal and distal ZPPsoma in this model was similar to that experimentally observed during dual whole-cell recordings with HCN channels blocked (Supplementary Fig. 2). In this passive model, we then introduced HCN conductance with voltage dependence, activation/deactivation kinetics, reversal potential, and spatial distribution of conductance density similar to that reported from cell-attached recordings in CA1 neurons17. Addition of HCN conductance with these constrained parameters generated an active model that satisfactorily reproduced proximal and distal ZPPsoma observed experimentally in CA1 neurons (Supplementary Fig. 2). We then used this active model to see if oscillatory inputs across the apical dendrite are synchronized at the same frequency.

The local impedance phase profile (ZPPlocal) describes the local current-voltage phase relationship across the frequency range. The ZPPlocal showed a uniform phase advance across the frequency range with increasing distance from the soma (Fig. 2a). This suggests that for simultaneous inputs, the voltage response is earlier in the dendrites than at the soma across all frequencies23. This phase advance of the dendritic response was however neutralized at the soma. The ZPPsoma for inputs across the apical dendrite showed relatively no location-dependent differences. This was especially true at a single frequency, where inputs across the apical dendrite had a synchronous somatic response (Fig. 2b). We term this frequency ‘Synchronization Frequency (SyncFreq)’ of the neuron.

Figure 2. Inputs across the apical dendrite are synchronized at the same frequency.

Figure 2

Open in a new tab

Panels with Inline graphic indicate modeling data (a, b, f) while those in Inline graphic indicate experimental data (c, d, e) (a),(c) The latency of local voltage response to a current input reduces with distance from the soma across the frequency range. This is depicted by phase advance (upward shift) of the ZPPlocal with distance from the soma. (b),(d) Subsequently, the voltage response at the soma is relatively independent of the location of current input in the dendrites. This is seen in the close overlay of ZPPsoma for various distances along the dendrite. Note all ZPPsoma have a single intersection point, the SyncFreq, where the response latency/phase at the soma is independent of input location along the dendrite. The blue arrow and the red electrode depict a distance of 300 μm from the soma in the model and whole-cell recording respectively. (e) SyncFreq was independent of distance from the soma when sampled by dual-whole cell recordings between the soma and varying distance along the dendrite. The data suggested a slightly positive trend which was statistically not significant (n=12; r=0.563±0.26; N.S., p=0.056, power(1–β)=0.47, linear correlation test (pearson)). (f) Exponential increase in maximum HCN conductance leads to a linear increase in the SyncFreq within the neuron.

Our second approach was experimental in which we recorded simultaneously from the soma, 150 μm and 300 μm along the apical dendrite. Experimental measurements of ZPPlocal and ZPPsoma at multiple locations supported the model predictions of a local phase advance with increasing distance from the soma and the subsequent emergence of a single SyncFreq for the entire apical dendrite (Fig. 2c, d). Dual whole cell recordings at the soma and varying distance along the apical dendrite showed no significant correlation between SyncFreq and distance from the soma, further confirming that SyncFreq is uniform along the apical dendrite (Fig. 2e). Thus, using experimental and modeling approaches, we find that the presence of HCN channels synchronizes the somatic response for oscillatory inputs across the entire apical dendrite at a single frequency.

To understand the emergence of SyncFreq, we altered the maximum HCN conductance density in the model neuron and observed that SyncFreq increased linearly with an exponential increase in HCN conductance (Fig. 2f). Thus, the HCN conductance density has to be maintained in a given range for SyncFreq of the neuron to be in the theta frequency range.

We then compared the influence of a pure leak conductance with that of HCN conductance on location-dependent phase differences to understand the importance of inductance to oscillatory synchrony. This comparison showed that the gradient of inductance (HCN channels) was not only more efficient at reducing location-dependent phase differences as compared to a pure leak conductance, but it did so along with significantly less amplitude attenuation of dendritic signals (Supplementary Fig. 3). This highlights the two-fold significance of the inductive HCN gradient in reducing both, location-dependent temporal differences and amplitude attenuation associated with dendritic propagation.

Synchonization Frequency is optimally propagated to soma

Transfer Resonance Frequency (TRF) refers to the frequency at which a unit current in the dendrite has maximum voltage amplitude at the soma and refers broadly to a frequency band that is selectively filtered from the dendrite to the soma26. Comparison of SyncFreq and TRF in the models with varying density of HCN conductance showed that the SyncFreq was almost always close to the TRF (Fig. 3a). This suggests that oscillatory signals that are synchronized across the apical dendrite are also most efficiently and selectively propagated to the soma. This was supported by our experimental data from dual recordings where SyncFreq and TRF showed a strong positive correlation with the slope of the regression line statistically not different from 1 (Fig. 3b).

Figure 3. Synchronization Frequency is optimally propagated to the soma and the influence of M-channels on oscillatory synchrony.

Figure 3

Open in a new tab

(a) suggests that the transfer impedance to the soma is almost always maximum (denoted by transfer resonance frequency) at the SyncFreq. Data points reflect variations in maximum HCN conductance density in the computational model. (b) Experimental data from dual recordings at soma and approximately 300 μm along the apical dendrite confirming the modeling predictions of (a) in CA1 neurons. Slope was not statistically different from 1, regression reflected through origin. (n=8; r2=0.968±065; N.S., p=0.459, Linear Regression Test). (c) shows the transfer impedance amplitude profiles for dendritic inputs at the soma from 300 μm for the three spatial distributions of HCN conductance (inset). Note synchronization frequencies are marked on the Impedance amplitude profiles. (d) describes the somatic resonance across a voltage range for models with only HCN conductance, with HCN and M-conductances and with only M-conductance. Independent markers depict the experimentally measured resonance values in rat CA1 neurons (Ref 24; Fig. S4). (e) shows that inclusion of M-conductance has negligible, if any, effect on oscillatory synchrony. Note that oscillatory synchrony does not exist with M-conductance alone. (f) &(g) are analogous to (d) & (e) but with M-conductance enhanced 5-fold with HCN conductance being kept constant.

To understand the basis for this relationship between TRF and SyncFreq, one of the parameters that we altered was the spatial distribution of HCN conductance in the model neuron and observed that oscillatory synchrony could be achieved by a sigmoidal, linear or even an uniform distribution of HCN conductance (Supplementary Fig. 4). However, the crucial relationship between TRF and SyncFreq, which would lead to the selective propagation of signals around the SyncFreq could only be achieved by a distribution with an increasing HCN conductance (linear or sigmoidal) (Fig. 3c). Thus, the spatial distribution of HCN conductance is an important factor in selective propagation of synchronized frequencies across the apical dendrite.

We also explored the role of HCN channel parameters by altering the voltage dependence and kinetics of HCN channels. While changes in V1/2 had a predictable effect on SyncFreq similar to the increase in maximum HCN conductance, altering the kinetics of HCN channels had a relatively smaller effect on oscillatory synchrony (Supplementary Fig. 5). Our simulations also suggest that oscillatory synchrony is restricted to the sub-threshold voltage range and has a voltage-dependence that is influenced by the conductance density of HCN channels within the neuron (Supplementary Fig. 6).

Another source of inductance in CA1 neurons is the M-conductance, a non-inactivating potassium conductance that is predominantly peri-somatic in distribution and active at depolarized voltage ranges22. The presence of M-channels leads to theta-frequency resonance and phase advance of lower frequencies, analogous to HCN channels, but at depolarized potentials. We thus included M-conductance in our model neuron to assess its influence on oscillatory synchrony. Inclusion of M-conductance at conductance densities that imparted realistic resonance values at depolarized voltages had negligible influence on oscillatory synchrony, which was restricted to sub-threshold voltages (Fig. 3d, e). Furthermore, simulations with a 5–fold increase in M-conductance (while keeping the HCN conductance constant) still failed to influence oscillatory synchrony (Fig. 3f, g). We thus conclude that M-conductance has negligible effect, if any, on oscillatory synchrony.

Oscillatory synchrony in the oblique dendrites

Our experimental and modeling results describe the synchronization of inputs that are primarily on the apical dendrite of the CA1 neuron. The majority of synaptic inputs in these neurons are, however, on the oblique branches extending from the primary dendrite10. Since it is technically challenging to experimentally observe whether oscillatory synchrony extends to these inputs on oblique dendrites, we used a realistic morphological model of a CA1 neuron to address this question. It should be noted, however, that since the ion-channel densities in these oblique branches remain unexplored, we made the assumption that the HCN conductance density in these obliques is similar to that in the apical, when described as a function of distance from the soma.

Our simulations suggest that in spite of complex morphology, oscillatory synchrony extends to the synaptic inputs on oblique dendrites (Fig. 4a–d). Moreover, we also observe the logarithmic relationship between SyncFreq and HCN conductance density, and the correlation between SyncFreq and TRF that was predicted by the simple “ball-and-stick” model (Fig. 4e, f). Predictably, the transfer impedance from the proximal oblique inputs is slightly higher than those from the apical inputs as would be expected with the smaller dendritic diameter (Fig. 4g). These results suggest that oscillatory synchrony and its ancillary filtering principles most likely extend to the majority of the synaptic inputs in CA1 neurons.

Figure 4. Oscillatory synchrony extends to oblique dendrites.

Figure 4

Open in a new tab

(a) & (b) represent ZPPsoma for inputs along the apical trunk and in the oblique dendrites, respectively, in a passive morphologically realistic CA1 neuron model. (b) & (d) represent ZPPsoma for the same inputs after inclusion of HCN conductance in a sigmoidal distribution with maximum conductance density of 10−3 S/cm2. The ZPPsoma in (a)-(d) for different locations are similar to those observed in the ball-and-stick model in Fig. 2a, b. (e) The logarithmic relationship between HCN conductance density and SyncFreq observed in Fig. 2f is also observed in the morphologically realistic model.(f) shows that the correlation between SyncFreq and TRF observed in Fig. 3a also extends to the morphologically realistic model. (g) depicts the transfer impedance to the soma for the different locations marked on the morphological model (inset). Note that apart from slight increase in transfer impedance for proximal oblique locations, the morphologically realistic model suggests that inputs from the oblique branches undergo similar temporal processing as observed for the inputs from the apical trunk

Location-independence of synaptic waveforms

Our observations suggest that the gradient distribution of HCN channels in CA1 neurons ensures the selective transfer of synchronous frequencies with a high gain from dendrite to the soma. A corollary to this principle is that synaptic inputs measured at the soma would be dominated by frequency components that are synchronous irrespective of the synaptic firing pattern. This would result in similar voltage waveform at the soma for a given synaptic firing pattern irrespective of the synapse location along the dendritic arbor.

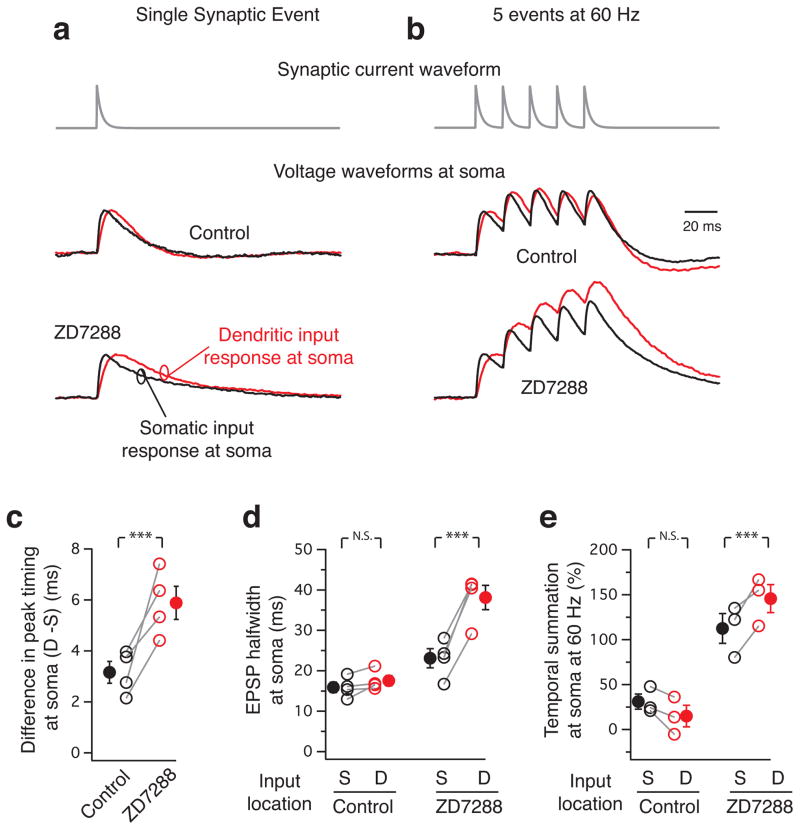
We tested this hypothesis by simulating different patterns of synaptic inputs 300 μm along the apical dendrite and at the soma using the dynamic-clamp method to simulate realistic synaptic currents (Methods) and simultaneously recording the voltage-waveform at the soma during dual whole-cell recordings. When we compared the voltage waveforms for a single synaptic event or a burst of 5 events at 60 Hz, the waveform at the soma was identical irrespective of the input location (Fig. 5a, b). Addition of ZD7288 (20 μM) to block HCN channels led to location-dependent differences in the somatic voltage waveform for the single event with increase in the latency of peak and half-width for distal inputs (Fig. 5c, d). Temporal summation, which compares the amplitude of the last EPSP to the first EPSP in a burst of synaptic inputs, also increased depicting distinct location-dependent differences in the burst waveform at the soma (Fig. 5e).

Figure 5. Synaptic inputs across the apical dendrite have similar voltage waveform at the soma.

Figure 5

Open in a new tab

(a) & (b) The somatic voltage waveform is compared for synaptic currents (gray) injected at 300 μm ( Inline graphic) or at the soma (black). (a) represents a single synaptic event, while (b) a burst of 5 events (60 Hz). Note that the waveforms are similar in control and altered after addition of ZD7288. All traces are normalized in amplitude for the first EPSP (approximately 2 mV in each case except for the dendritic burst in ZD which was 1 mV to prevent neuronal firing). (c),(d),(e) summarize the difference in voltage waveforms at soma before and after ZD7288. (c) describes the difference in timing of the EPSP peak at the soma [Control 3.16±0.43; ZD7288 5.88±0.65 (n=4; ***, p=0.0268, power(1–β)=0.95, paired t-test)]. (d) compares the EPSP half width [Control: Soma 15.9±1.3; Dendrite 17.6±1.2 (n=4; N.S., p=0.111, paired t-test); ZD7288: Soma 23.1±2.4; Dendrite 38.1±3.0 (n=4; ***, p=0.00147, power(1–β)=0.98, paired t-test)]. (e) depicts the temporal summation at soma [in %, Control: Soma 31.1±8.5 and Dendrite 14.9±12 (n=3; N.S., p=0.084, paired t-test); ZD7288: Soma 112.6±16.6 and Dendrite 145.7±15.6 (n=3; ***, p=0.043, power(1–β)=0.303, paired t-test)]. Error bars indicate s.e.m.

This location-independence of the waveform at the soma for a single synaptic event or a burst input has been observed empirically as a HCN channel dependent phenomenon in the pyramidal neurons of the hippocampus and the cortex29–31. However, understanding this phenomenon in the light of underlying frequency components uncovers the role of oscillatory synchrony during integration of synaptic inputs at the soma.

When we analyzed the frequency components that make up the synaptic input current for a single event or a burst of 5 events at 60 Hz (Fig. 6a, b), both the patterns of synaptic input differed significantly in their frequency content. While the single event had a stronger high frequency component (40–100 Hz), the synaptic burst had a distinct 60 Hz component, as expected, along with a strong low frequency component (0–10 Hz), presumably due to the envelope of depolarizing current (Fig. 6c, d). However, when the voltage waveform of these inputs was analyzed at the soma, there was an obvious similarity in their frequency content. Irrespective of the nature of their input frequencies, the voltage waveform at the soma was composed exclusively of low-frequency components, especially the ones at which oscillatory synchrony is predominant (Fig. 6e, f; Fig. 1c). This was not necessarily a surprising result, considering HCN inductance has been associated with band-pass filtering of theta-frequency (4–12 Hz) signals26,27. However, taken together with our findings of oscillatory synchrony in the same frequency range due to the characteristic distribution of HCN channels, we describe an important biophysical mechanism in CA1 neurons that counteracts location-dependent temporal differences of synaptic inputs associated with capacitive filtering. Application of ZD7288 abolished this frequency selectivity and disrupted oscillatory synchrony leading to location-dependent differences in voltage waveform at the soma further supporting this hypothesis. (Supplementary Fig. 7).

Figure 6. The voltage waveform at soma is composed exclusively of synchronous frequencies.

Figure 6

Open in a new tab

(a) & (b) describe the synaptic current injected by the dynamic clamp system at 300 μm to simulate a single synaptic event in (a) and a burst of 5 events at 60 Hz in (b), along with the corresponding voltage waveform recorded at soma in 4 different cells. (c),(d),(e) & (f) analyze the frequency components in the corresponding dendritic currents or somatic voltage waveforms for traces depicted in (a) and (b). Note that although the frequency components in the synaptic current input are different for a single synaptic event or a burst, the voltage waveform at the soma, in both the cases, is exclusively composed of low frequency components, especially the ones that are synchronous at the soma.

Gamma-frequency inputs maximize oscillatory synchrony

As the voltage waveform at the soma appears to be exclusively comprised of theta frequency components (Fig. 6e, f)26, it could be argued that temporal patterns of synaptic events that generate a strong theta-frequency component in the input current are more efficient at exploiting the biophysical filtering properties of the apical dendrite. For example, when the input current generated by a single synaptic event was compared to that generated by a burst of 5 events at 60 Hz, the burst current input had a significantly stronger (>10 fold) theta-frequency component suggesting that it is more efficient for propagation to the soma than a single synaptic event (Fig. 6c, d). This is confirmed when the voltage responses at the soma are analyzed for both these inputs (Fig. 6e, f).

To identify the temporal patterns of synaptic inputs that maximize oscillatory synchrony, we started with the burst input and altered the frequency of the synaptic events within the burst (Fig. 7a). We then analyzed the slow-frequency components in the dendritic current input that constitute the majority of the voltage output at the soma (Fig. 7b, c). Our results show that burst frequencies in the gamma frequency range (40–140 Hz) generate a slow input current component that peaks in the theta frequency range (4–10 Hz) (Fig. 7d). Additional experiments suggest that this relationship, though dependent on the burst size, holds true for synaptic bursts consisting of 3–9 impulses (Fig. 7e). Assuming gamma bursts occur on either the peak or valley of a 7 Hz theta cycle32, this range of impulses per synaptic burst would be relevant for the entire range of gamma frequencies between 40 and 120 Hz.

Figure 7. Gamma frequency synaptic bursts generate theta-frequency components important for oscillatory synchrony.

Figure 7

Open in a new tab

(a) describes the synaptic current input at 300 μm and the corresponding voltage output at the soma for bursts of increasing frequencies. (b) &(c) depict the frequency components for the current input and voltage output in (a) respectively. Note that all the high frequency components are filtered out and only the slow frequency components make up the voltage waveform at the soma. (d) describes the peak of the low frequency current component in the dendrite which determines the voltage waveform at the soma for increasing burst frequencies from 20 Hz to 180 Hz. Note that the peak component of burst frequencies from 50 – 140 Hz corresponds with the theta frequency range for bursts with 5 synaptic inputs. (e) Same as (d) but with the number of impulses per burst changing from 2–10 (f) represents the impedance measured at the peak slow frequency component for increasing burst frequency. (gray) lines represent individual cells while red solid line represents the average and s.e.m for the 4 cells. Note that the maximum impedance is for gamma frequency bursts as would be predicted from (d). Error bars indicate s.e.m.

The gamma-theta correlation of input current suggests that gamma-frequency synaptic bursts would maximize oscillatory synchrony and signal transfer to the soma. We directly confirmed this proposed efficiency of signal transfer by measuring the transfer impedance at the peak input current frequency using the simultaneously recorded voltage output at the soma (Fig. 7f). Our results confirmed that gamma frequency burst inputs maximize the gain of signal transfer to the soma. In the hippocampus, gamma oscillations synchronize distributed cell assemblies between the CA1 region and its input areas, the CA3 or the entorhinal cortex4,5. Our results suggesting that gamma frequency synaptic inputs maximize oscillatory synchrony and signal transfer within the neuron thus illustrate how signal integration within CA1 neurons is tuned to the oscillatory nature of the hippocampal network. It should also be noted that this gamma-theta correlation of synaptic currents observed in single CA1 neurons is distinct from the phenomenon of cross-frequency phase coupling observed at the network level5,33.

Oscillatory synchrony during rhythmic synaptic bursts

During the active state of the hippocampal network, gamma oscillations are modulated by the overarching theta oscillations5. From the cellular perspective, synaptic integration during these network oscillations involves rhythmic excitation and inhibition contributed by a multitude of synapses34. So is oscillatory synchrony relevant when multiple synaptic conductances, excitatory and inhibitory, influence membrane potential in a rhythmic manner? To answer this question, we used the dynamic clamp system to simulate dendritic excitation and somatic inhibition from a multitude of synapses simultaneously. Although it is not currently possible to simulate the spatio-temporal nature of in vivo-like conductances in vitro, the aim of this experiment was to identify the frequency components generated during rhythmic synaptic burst firing and assess their relevance to oscillatory synchrony. To this effect, each synapse provided stochastic burst inputs in the gamma frequency range (~90 Hz), which was modulated at a theta frequency (7 Hz) to provide rhythmic excitation and inhibition (Fig. 8a). We used this experimental paradigm 1) to test whether oscillatory synchrony can be achieved by rhythmic synaptic inputs and 2) to assess the influence of inhibition in the process.

Figure 8. Oscillatory synchrony in CA1 neurons during the active ‘theta’ state of the hippocampal network.

Figure 8

Open in a new tab

(a) (Top) illustrates the experimental paradigm of rhythmic synaptic excitation in the dendrite from 4 excitatory synapses ( Inline graphic) and alternative inhibition from 2 somatic synapses (black) at 7 Hz to mimic alternate dendritic excitation and somatic inhibition in CA1 neurons. (middle) shows the synaptic currents generated and (bottom) shows the voltage outcome at the soma. (b) describes the frequency component in the synaptic currents measured at the two electrodes in (a), while (c) describes the frequency components of the voltage output at the soma. (d) compares the voltage waveform in (a) to an alternative paradigm where excitation was injected at the soma as well keeping everything else the same. Note that the voltage waveform at the soma is synchronized irrespective of the excitation input location.

Although the inhibitory synapses had a higher synaptic conductance and slower time constant than the excitatory synapses (Methods), they generated negligible currents confirming to the role of inhibition as primarily a shunting mechanism (Fig. 8a). The input currents generated were predominantly from dendritic excitation and were dominated by the rhythmic nature of synaptic bursts. This was apparent in the strong theta frequency component observed in the input currents (Fig. 8b). In keeping with the selective filtering properties of the apical dendrite observed with oscillations or burst inputs, the voltage outcome at the soma was composed exclusively of the same theta-frequency component. The voltage waveform thus approached a pure sinusoid similar to that observed during intracellular recordings of CA1 neurons during active behavior (Fig. 8a, c)34,35. Since oscillatory synchrony is optimum in this theta-frequency range, we predicted that the somatic voltage response to rhythmic excitation would be similar irrespective of whether the excitation was in the dendrites or at the soma. Our experimental observations supported this outcome when the somatic voltage waveform was compared for rhythmic excitation in the dendrites or alternatively at the soma keeping all other conditions the same (Fig. 8d). This underscores the functional relevance of oscillatory synchrony to synaptic integration in CA1 neurons during rhythmic synaptic burst firing.

Discussion

In this study we show that the distribution of HCN channels in CA1 neurons provides a gradient of inductance that compensates for the location-dependent capacitive delay of dendritic inputs at the axo-somatic integration site. Using an experimental approach complemented by theoretical simulations, we show that the gradient of increasing inductance is an efficient strategy not only for synchronization of inputs but also for the selective and efficient transfer of particular frequency components to the soma. An outcome of these filtering properties is that the voltage waveform at the soma is less sensitive to the input location of the synapse in the dendrites of CA1 neurons. Using the dynamic clamp method to mimic temporal patterns of synaptic input, we show that these filtering properties are best harnessed by gamma frequency synaptic bursts or rhythmic burst inputs in the theta frequency range, both of which are observed during the active state of the hippocampal network.

In CA1 neurons, the conductance density of synaptic AMPA receptors increases with distance from the soma. The higher amplitude synaptic response in the dendrites compensates for voltage attenuation resulting in uniform voltage amplitude at the soma for synaptic inputs across the apical dendrite36. Our results here describe a complementary biophysical mechanism that counteracts location dependent temporal differences at the soma. Taken together, these observations suggest that CA1 neurons utilize sub-cellular gradients of active conductances to ensure that each synaptic input carries equal weight, in amplitude and timing, during subthreshold integration at the soma. The experimental evidence for this democracy of synapses is, however, limited to the Schaffer collateral pathway in CA1 neurons.

The normalization of voltage waveform at the soma for synaptic inputs at varying dendritic locations has been empirically observed as a HCN channel dependent phenomenon in CA1 neurons of the hippocampus, L5 pyramidal neurons of the somatosensory cortex and cerebellar purkinje cells29–31. To our knowledge, however, this study is the first to provide a mechanistic understanding of this phenomenon in explicit signal processing terms. The insight provided by this approach helps us appreciate subtle nuances that optimize this process, like the contribution of the spatial distribution of HCN channels, which were suggested to be inconsequential by previous studies31.

The signal processing approach also highlights that gamma frequency synaptic inputs in the dendrites of CA1 neurons undergo filtering during sub-threshold transmission to the soma such that it is not the high frequency components but the slower theta component of high-frequency bursts that actually transmits information from the dendrite to the soma. While this finding supports the efficiency of gamma-frequency inputs in distal signaling, it presents a conundrum for the notion that high frequency inputs from the CA3 region or the direct entorhinal input can entrain high frequency CA1 output4. While in vitro studies of gamma oscillations suggest that the timing of synaptic excitation and inhibition has influence on the timing of action potential generation in hippocampal pyramidal neurons37, our results suggest it is unlikely that distal high frequency inputs can entrain the axo-somatic output at high frequencies. Our results, however, do not exclude the plausibility of dendritic nonlinearities, like dendritic spikes or calcium plateau potentials in the s.l.m., to be involved during direct entrainment of high frequency dendritic inputs38,39.

We should also stress the distinction between the gamma-theta correlation of synaptic currents observed within a single CA1 neuron and the phenomenon of gamma-theta cross-frequency coupling observed at the network level5. Our results are limited to the transformation of pre-synaptic input patterns into the spectral content of the post-synaptic currents. We do not claim that this observed correlation is the basis for, or contributes to, the cross-frequency coupling between gamma and theta oscillations that plays an important role in the co-ordination of activity within neural networks33.

One of the interesting observations from this study is that every CA1 neuron has a set latency of somatic response for sub-threhsold integration across its dendritic arbor. Since this latency is dependent on HCN conductance, it can be argued that synaptic plasticity, which is accompanied by bidirectional changes in HCN conductance, could potentially alter the response latency or phase of CA1 neuronal output23,24,40,41. In fact, a similar outcome where Hebbian plasticity is used as a mechanism to alter the timing of neuronal output has been described in the insect olfactory system42. Within the hippocampus, where the timing or phase of the neuronal output carries valuable information regarding the output of the network, oscillatory synchrony and its plasticity provide a new biophysical mechanism for computation within the hippocampal network 8,9.

In a wide variety of biological networks, information is represented by transiently active neuronal ensembles or cell assemblies6,43–45. In the rodent hippocampus, such cell assemblies have been experimentally identified and are considered to be essential for information processing during spatial navigation or memory encoding/recall6,46,47. Since synchronous activity is the only hallmark for a downstream neuron to identify an upstream cell assembly, our study identifies a key adaptation in pyramidal neurons to detect meaningful signals from upstream neural layers.

In conclusion, it is perhaps a paradox that while gamma and theta oscillations are considered as network mechanisms to synchronize neuronal output, they are equally important to synchronize neuronal inputs during synaptic integration within a single neuron 1–3.

Supplementary Material

1

Supplementary Figure 1. Theta frequency oscillatory synchrony is observed only at the soma

10

Supplementary Figure 2. ZPPsoma comparison between CA1 Neuron, the ball-and-stick model and morphologically realistic model

11
12
2

Supplementary Figure 3. Gradient of inductance achieves oscillatory synchrony with less voltage attenuation

3

Supplementary Figure 4. The spatial distribution of HCN channels achieves maximum transfer at synchronization frequency

4

Supplementary Figure 5. Dependence of oscillatory synchrony on the voltage dependence of activation and kinetics of HCN channels

5

Supplementary Figure 6. Voltage dependence of Synchronization Frequency

6

Supplementary Figure 7. Addition of ZD7288 alters the band-pass filtering of synchronous frequencies

7

Supplementary Figure 8. Accuracy of Dynamic clamp over Current clamp for high frequency synaptic inputs

8

Supplementary Figure 9. Measurement of Impedance Phase Profile (ZPP) by chirp vs sinusoids

9

Supplementary Figure 10. Time-Frequency Analysis using Continuous Wavelet Transform

Acknowledgments

We thank Drs. Raymond Chitwood, Nikolai Dembrow, Richard Gray & Rishikesh Narayanan for helpful discussions during the course of this study. We also thank members of the Johnston Lab and Dr. Laura L. Colgin for helpful comments on earlier versions of this manuscript. This work was supported by grant MH 048432 from US National Institute of Health to D.J.

Footnotes

Contributions: SV & DJ designed the experiments, interpreted the results and wrote the manuscript. SV performed the experiments, computer simulations and analysis of data.

References

  • 1.Singer W, Gray CM. Visual feature integration and the temporal correlation hypothesis. Annu Rev Neurosci. 1995;18:555–586. doi: 10.1146/annurev.ne.18.030195.003011. [DOI] [PubMed] [Google Scholar]
  • 2.Engel AK, Fries P, Singer W. Dynamic predictions: oscillations and synchrony in top-down processing. Nat Rev Neurosci. 2001;2:704–716. doi: 10.1038/35094565. [DOI] [PubMed] [Google Scholar]
  • 3.Buzsáki G. Rhythms of the Brain. Oxford University Press; USA: 2011. [Google Scholar]
  • 4.Colgin LL, et al. Frequency of gamma oscillations routes flow of information in the hippocampus. Nature. 2009;462:353–357. doi: 10.1038/nature08573. [DOI] [PubMed] [Google Scholar]
  • 5.Bragin A, et al. Gamma (40–100 Hz) oscillation in the hippocampus of the behaving rat. J Neurosci. 1995;15:47–60. doi: 10.1523/JNEUROSCI.15-01-00047.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Harris KD, Csicsvari J, Hirase H, Dragoi G, Buzsáki G. Organization of cell assemblies in the hippocampus. Nature. 2003;424:552–556. doi: 10.1038/nature01834. [DOI] [PubMed] [Google Scholar]
  • 7.Chrobak J, Lorincz A, Buzsaki G. Physiological patterns in the hippocampo-entorhinal cortex system. Hippocampus. 2000 doi: 10.1002/1098-1063(2000)10:4<457::AID-HIPO12>3.0.CO;2-Z. [DOI] [PubMed] [Google Scholar]
  • 8.O’Keefe J, Recce ML. Phase relationship between hippocampal place units and the EEG theta rhythm. Hippocampus. 1993;3(3):317–30. doi: 10.1002/hipo.450030307. [DOI] [PubMed] [Google Scholar]
  • 9.Skaggs WE, McNaughton BL, Wilson MA, Barnes CA. Theta phase precession in hippocampal neuronal populations and the compression of temporal sequences. Hippocampus. 1996;6:149–172. doi: 10.1002/(SICI)1098-1063(1996)6:2<149::AID-HIPO6>3.0.CO;2-K. [DOI] [PubMed] [Google Scholar]
  • 10.Megías M, Emri Z, Freund TF, Gulyás AI. Total number and distribution of inhibitory and excitatory synapses on hippocampal CA1 pyramidal cells. Neuroscience. 2001;102:527–540. doi: 10.1016/s0306-4522(00)00496-6. [DOI] [PubMed] [Google Scholar]
  • 11.Dougherty KA, Islam T, Johnston D. Intrinsic excitability of CA1 pyramidal neurones from the rat dorsal and ventral hippocampus. J Physiol (Lond) 2012 doi: 10.1113/jphysiol.2012.242693. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Rall W. Distinguishing theoretical synaptic potentials computed for different soma-dendritic distributions of synaptic input. J Neurophysiol. 1967;30:1138–1168. doi: 10.1152/jn.1967.30.5.1138. [DOI] [PubMed] [Google Scholar]
  • 13.Alexander C. Fundamentals of Electric Circuits. 2. McGraw Hill Inc; 2004. [Google Scholar]
  • 14.Mauro A. Anomalous impedance, a phenomenological property of time-variant resistance. An analytical review. Biophy J. 1:353–72. doi: 10.1016/s0006-3495(61)86894-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Cole KS. Transverse impedance of the squid giant axon during current flow. J Gen Physiol. 1941;24:535–49. doi: 10.1085/jgp.24.4.535. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Cole KS. Membranes, Ions and Impulses. University of California Press; 1968. [Google Scholar]
  • 17.Magee JC. Dendritic hyperpolarization-activated currents modify the integrative properties of hippocampal CA1 pyramidal neurons. J Neurosci. 1998;18:7613–7624. doi: 10.1523/JNEUROSCI.18-19-07613.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Robinson RB, Siegelbaum SA. Hyperpolarization-activated cation currents: from molecules to physiological function. Annu Rev Physiol. 2003;65:453–480. doi: 10.1146/annurev.physiol.65.092101.142734. [DOI] [PubMed] [Google Scholar]
  • 19.Hutcheon B, Yarom Y. Resonance, oscillation and the intrinsic frequency preferences of neurons. Trends Neurosci. 2000 doi: 10.1016/s0166-2236(00)01547-2. [DOI] [PubMed] [Google Scholar]
  • 20.Leung LS, Yim CY. Intracellular records of theta rhythm in hippocampal CA1 cells of the rat. Brain Res. 1986;367:323–327. doi: 10.1016/0006-8993(86)91611-2. [DOI] [PubMed] [Google Scholar]
  • 21.Pike FG, et al. Distinct frequency preferences of different types of rat hippocampal neurones in response to oscillatory input currents. J Physiol (Lond) 2000;529(Pt 1):205–213. doi: 10.1111/j.1469-7793.2000.00205.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Hu H, Vervaeke K, Storm JF. Two forms of electrical resonance at theta frequencies, generated by M-current, h-current and persistent Na+ current in rat hippocampal pyramidal cells. J Physiol (Lond) 2002;545:783–805. doi: 10.1113/jphysiol.2002.029249. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Narayanan R, Johnston D. The h channel mediates location dependence and plasticity of intrinsic phase response in rat hippocampal neurons. J Neurosci. 2008;28:5846–5860. doi: 10.1523/JNEUROSCI.0835-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24.Narayanan R, Johnston D. Long-term potentiation in rat hippocampal neurons is accompanied by spatially widespread changes in intrinsic oscillatory dynamics and excitability. Neuron. 2007;56:1061–1075. doi: 10.1016/j.neuron.2007.10.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25.Ulrich D. Dendritic resonance in rat neocortical pyramidal cells. J Neurophysiol. 2002;87:2753–2759. doi: 10.1152/jn.2002.87.6.2753. [DOI] [PubMed] [Google Scholar]
  • 26.Cook E, Guest J, Liang Y, Masse N, Colbert C. Dendrite-to-Soma Input/Output Function of Continuous Time-Varying Signals in Hippocampal CA1 …. J Neurophysiol. 2007 doi: 10.1152/jn.00414.2007. [DOI] [PubMed] [Google Scholar]
  • 27.Hu H, Vervaeke K, Graham LJ, Storm JF. Complementary theta resonance filtering by two spatially segregated mechanisms in CA1 hippocampal pyramidal neurons. J Neurosci. 2009;29:14472–14483. doi: 10.1523/JNEUROSCI.0187-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 28.Golding NL. Factors mediating powerful voltage attenuation along CA1 pyramidal neuron dendrites. J Physiol (Lond) 2005;568:69–82. doi: 10.1113/jphysiol.2005.086793. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Magee J. Dendritic Ih normalizes temporal summation in hippocampal CA1 neurons. Nat Neurosci. 1999;2:848. doi: 10.1038/12229. [DOI] [PubMed] [Google Scholar]
  • 30.Williams SR, Stuart GJ. Site independence of EPSP time course is mediated by dendritic I(h) in neocortical pyramidal neurons. J Neurophysiol. 2000;83:3177–3182. doi: 10.1152/jn.2000.83.5.3177. [DOI] [PubMed] [Google Scholar]
  • 31.Angelo K, London M, Christensen SR, Häusser M. Local and global effects of I(h) distribution in dendrites of mammalian neurons. Journal of Neuroscience. 2007;27:8643–8653. doi: 10.1523/JNEUROSCI.5284-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32.Colgin LL, Moser EI. Gamma oscillations in the hippocampus. Physiology(Bethesda) 2010;25:319–329. doi: 10.1152/physiol.00021.2010. [DOI] [PubMed] [Google Scholar]
  • 33.Jensen O, Colgin LL. Cross-frequency coupling between neuronal oscillations. Trends Cogn Sci. 2007;7:267–269. doi: 10.1016/j.tics.2007.05.003. [DOI] [PubMed] [Google Scholar]
  • 34.Kamondi A, Acsady L, Wang XJ, Buzsaki G. Theta oscillations in somata and dendrites of hippocampal pyramidal cells in vivo: activity-dependent phase-precesssion of action potentials. Hippocampus. 1998;8:244–261. doi: 10.1002/(SICI)1098-1063(1998)8:3<244::AID-HIPO7>3.0.CO;2-J. [DOI] [PubMed] [Google Scholar]
  • 35.Harvey CD, Collman F, Dombeck DA, Tank DW. Intracellular dynamics of hippocampal place cells during virtual navigation. Nature. 2009;461:941–946. doi: 10.1038/nature08499. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 36.Magee JC, Cook EP. Somatic EPSP amplitude is independent of synapse location in hippocampal pyramidal neurons. Nat Neurosci. 2000;3:895–903. doi: 10.1038/78800. [DOI] [PubMed] [Google Scholar]
  • 37.Oren I, Mann EO, Paulsen O, Hajos N. Synaptic currents in anatomically identified CA3 neurons during hippocampal gamma oscillations in vitro. J Neurosci. 2006;26:9923–9934. doi: 10.1523/JNEUROSCI.1580-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 38.Gasparini S, Magee JC. State-dependent dendritic computation in hippocampal CA1 pyramidal neurons. J Neurosci. 2006;26:2088–2100. doi: 10.1523/JNEUROSCI.4428-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 39.Takahashi H, Magee JC. Pathway interactions and synaptic plasticity in the dendritic tuft regions of CA1 pyramidal neurons. Neuron. 2009;62:102–111. doi: 10.1016/j.neuron.2009.03.007. [DOI] [PubMed] [Google Scholar]
  • 40.Fan Y, et al. Activity-dependent decrease of excitability in rat hippocampal neurons through increases in I(h) Nat Neurosci. 2005;8:1542–1551. doi: 10.1038/nn1568. [DOI] [PubMed] [Google Scholar]
  • 41.Brager DH, Johnston D. Plasticity of intrinsic excitability during long-term depression is mediated through mGluR-dependent changes in I(h) in hippocampal CA1 pyramidal neurons. J Neurosci. 2007;27:13926–13937. doi: 10.1523/JNEUROSCI.3520-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 42.Cassenaer S, Laurent G. Hebbian STDP in mushroom bodies facilitates the synchronous flow of olfactory information in locusts. Nature. 2007;448:709–713. doi: 10.1038/nature05973. [DOI] [PubMed] [Google Scholar]
  • 43.Wehr M, Laurent G. Odour encoding by temporal sequences of firing in oscillating neural assemblies. Nature. 1996;384:162–166. doi: 10.1038/384162a0. [DOI] [PubMed] [Google Scholar]
  • 44.Hahnloser RHR, Kozhevnikov AA, Fee MS. An ultra-sparse code underlies the generation of neural sequences in a songbird. Nature. 2002;419:65–70. doi: 10.1038/nature00974. [DOI] [PubMed] [Google Scholar]
  • 45.Buzsáki G. Neural syntax: cell assemblies, synapsembles, and readers. Neuron. 2010;68:362–385. doi: 10.1016/j.neuron.2010.09.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 46.Buzsáki G. Theta rhythm of navigation: link between path integration and landmark navigation, episodic and semantic memory. Hippocampus. 2005;15:827–840. doi: 10.1002/hipo.20113. [DOI] [PubMed] [Google Scholar]
  • 47.Buzsáki G, Moser EI. Memory, navigation and theta rhythm in the hippocampal-entorhinal system. Nat Neurosci. 2013;16:130–138. doi: 10.1038/nn.3304. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

1

Supplementary Figure 1. Theta frequency oscillatory synchrony is observed only at the soma

NIHMS560017-supplement-1.jpg (664.5KB, jpg)
10

Supplementary Figure 2. ZPPsoma comparison between CA1 Neuron, the ball-and-stick model and morphologically realistic model

NIHMS560017-supplement-10.jpg (653.3KB, jpg)
11
NIHMS560017-supplement-11.pdf (3.4MB, pdf)
12
NIHMS560017-supplement-12.pdf (135.9KB, pdf)
2

Supplementary Figure 3. Gradient of inductance achieves oscillatory synchrony with less voltage attenuation

NIHMS560017-supplement-2.jpg (298.1KB, jpg)
3

Supplementary Figure 4. The spatial distribution of HCN channels achieves maximum transfer at synchronization frequency

NIHMS560017-supplement-3.jpg (692.9KB, jpg)
4

Supplementary Figure 5. Dependence of oscillatory synchrony on the voltage dependence of activation and kinetics of HCN channels

NIHMS560017-supplement-4.jpg (924.7KB, jpg)
5

Supplementary Figure 6. Voltage dependence of Synchronization Frequency

NIHMS560017-supplement-5.jpg (574.5KB, jpg)
6

Supplementary Figure 7. Addition of ZD7288 alters the band-pass filtering of synchronous frequencies

NIHMS560017-supplement-6.jpg (513KB, jpg)
7

Supplementary Figure 8. Accuracy of Dynamic clamp over Current clamp for high frequency synaptic inputs

NIHMS560017-supplement-7.jpg (802.5KB, jpg)
8

Supplementary Figure 9. Measurement of Impedance Phase Profile (ZPP) by chirp vs sinusoids

NIHMS560017-supplement-8.jpg (126.6KB, jpg)
9

Supplementary Figure 10. Time-Frequency Analysis using Continuous Wavelet Transform

NIHMS560017-supplement-9.jpg (477.1KB, jpg)

RESOURCES