Statistical approaches to analyzing HIV-1 neutralizing antibody assay data

Summary

Neutralizing antibody assays are widely used in research toward development of a preventive HIV-1 vaccine. Currently, the neutralization potency of an antibody is typically quantified by the inhibitory concentration (IC) values (e.g., IC50), and the neutralization breadth is estimated by the empirical method. In this paper, we propose the AUC and pAUC measures for summarizing the titration curve, which complement the commonly used IC measure. We present multiple advantages of AUC over IC50, which include no complications due to censoring, the capability to explore low-level neutralization, and improved coverage probabilities and efficiency of estimators. We also propose statistical methods for determining positive neutralization and for estimating the neutralization breadth. The simulation results suggest that the AUC measure is preferable in particular as IC50s get closer to the highest concentration of antibodies tested. For the majority of the assay data, the AUC method is more powerful than the IC50 method. However, since these methods test different hypotheses, it is not unexpected that some virus-antibody combinations are AUC positive but IC50 negative or vice versa.

1. Introduction

After decades of searching for preventive HIV-1 vaccines, it is widely believed that vaccines inducing both neutralizing antibody and T cell-mediated immune responses will be required for preventing HIV-1 infection (Pantaleo and Koup, 2004; Flynn et al., 2005; Karnasuta et al., 2005; Pitisuttithum et al., 2006). The design and evaluation of vaccine candidates that are capable of inducing broad neutralization against multiple HIV-1 virus strains has been particularly challenging and is an area of intense research (Mascola et al., 2005). Neutralization can be assessed by a variety of assays, of which one widely used assay is based on measurement of luciferase activity in the TZM-bl target cells (Montefiori, 2004; Fenyö et al., 2009). In the TZM-bl assay, the luciferase expression is directly proportional to the number of infected cells and can be quantified as relative luminescence units (RLU). The magnitude of neutralization is quantified as the inhibition of viral replication in test wells relative to non-neutralized virus control. Specifically, neutralization (y) is calculated as follows

$$y=1-\frac{{\mathrm{RLU}}_t-{\mathrm{RLU}}_c}{{\mathrm{RLU}}_v-{\mathrm{RLU}}_c},$$

where RLU_t, RLU_c and RLU_v denote RLU for test (cells + virus + antibody), cell control (cells only) and virus control (virus + cells but no antibody sample) wells, respectively. We would expect that y ranges from 0 to 1 representing no to full inhibition, respectively. However y can be negative which might reflect either statistical variation around “zero” inhibition or true biological enhancement in which certain factors in the specimens being tested increase virus infectivity.

The dose-response relationship is typically captured by a titration experiment in which neutralization responses are measured at serial dilutions of an antibody sample. For each virus-antibody combination, a titration curve can be estimated to show the relationship between neutralization responses and antibody concentrations. Because the dilution factor (titer) and concentration are inversely related, titration curves are generally decreasing or increasing depending on whether the x-axis is the titer or concentration. We focus on the case where the x-axis is a concentration. The arguments for the case that the x-axis is a titer can be derived similarly.

Given a titration curve, potency of an antibody is typically quantified as the inhibitory concentration (IC), defined as the antibody concentration at which the viral replication has been reduced by 50% (IC50) or 80% (IC80) relative to the absence of the antibody. However, it is difficult to estimate the IC50 if the titration curve does not cross the 50% inhibition within the range of concentrations, because it would require extrapolation into concentration regions where there are no data. We refer to this case as the “censored IC50 case”. In some studies, the percentage of censored IC50 cases can be quite large (e.g., Fenyö et al., 2009) and these censored cases pose challenges for further down-stream analysis (Huang et al., 2009). The current standard approach for dealing with the censored IC50 case is to estimate the IC50 with some arbitrary value, for example, with either the lowest or highest concentration depending on the censoring direction. One can simply ignore the censoring issue and use the estimated values as they are. However, this approach can under-estimate statistical uncertainty in the data particularly when the censoring rate is high and, if the analytic goal is to explore patterns of low-level neutralization, this approach is wholly unsuitable as it completely obscures such patterns. Here we propose two alternative measures, area under the curve (AUC) and the partial area under the curve (pAUC), to quantify neutralization potency. AUC and pAUC offer two advantages over IC50. Unlike IC50, estimation of AUC and pAUC is free from censoring issues and AUC summarizes the neutralization responses across the entire concentration range without requiring assumptions about the shape of the titration curve. In contrast, IC50 measures the neutralization activity at a single point and is easily interpretable only when titration curves are sigmoidal shaped within the concentration range, which are often not the case.

Given a panel of viruses, breadth of neutralization is defined as the percentage (or number) of viruses that are “positively neutralized”, where the positive neutralization must be carefully defined. Currently, a commonly used definition of positive neutralization is that neutralization is positive if at least 50% inhibition of infection is recorded at the highest concentration (Binley et al., 2004; Sather et al., 2009). We refer to this as the empirical method hereafter. Though this method is reasonable and appealing in its simplicity, it does not provide rigorous statistical evidences for true neutralization above control. Lack of controlling false positive rate makes it difficult to justify whether the method is too liberal or conservative as the assay variation varies across runs and laboratories. In addition, the empirical method does not adjust for multiple comparisons which occur when each antibody is tested against multiple viruses. For one antibody, the probability of falsely declaring a positive neutralization against any virus increases with the total number of viruses tested if no adjustment is made for multiple comparisons. This indicates that the breadth estimated by the empirical method might be overestimated because the overall false positive rate might be higher for the empirical method than the approach with multiple comparison adjustment. This motivates the second topic of this paper, which is to develop statistical methods for alternative positive criteria that control the false positive rate for estimation of breadth.

2. Methods

2.1 Curve fitting models

For one virus-antibody combination, let y_jk(j = 1,..., n, k = 1,..., r_j) be one of r_j replicate neutralization responses at the jth concentration denoted as x_j, where n is the number of concentrations. Let $N={\sum }_{j=1}^n{r}_j$. A general model for assay responses is

$$y_{jk}=f(x_j,\beta )+\sigma {∊}_{jk},$$ (1)

where f is a regression function depending on β, a vector of regression parameters; ε_jk are independent random errors with mean zero and variance 1; and σ² is the variance of y_jk. The model fitting is generally done using the ordinary least squares method. Though a heteroscedastic regression model is widely used in immunoassay data, such as enzyme-linked immunosorbent assay (ELISA), to account for the heterogeneity of variance in assay responses (Carroll and Ruppert, 1988; Belanger et al., 1996; Zeng and Davidian, 1997), it is reasonable to assume equal variance and use a ordinary regression model for the neutralization data. This is because the number of concentrations is usually not large; for a typical run, N=16 or less is common, with r_j = 2. Estimation of a variance function with 16 or fewer data points is likely to be unreliable (Zeng and Davidian, 1997). Most importantly, residuals from the ordinary regression model appear to support the equal variance assumption.

Various models have been proposed for f. The polynomial model (Ruppert et al., 2003) and five-parameter logistic model (5PL) (Gottschalk and Dunn, 2005) appear suitable for the neutralization data and will be considered throughout the paper. The polynomial model with a quadratic term is

$$f(x,\beta )={\beta }_1+{\beta }_{2}x+{\beta }_3{x}^2.$$ (2)

One parameterization for the 5PL model is

$$f(x,\beta )={\beta }_2+\frac{({\beta }_1-{\beta }_2)}{{\{1+{(x∕{\beta }_3)}^{{\beta }_4}\}}^{{\beta }_5}}.$$ (3)

Unlike the simple polynomial model, parameters in the 5PL model can have meaningful biological interpretations. When β₄ < 0, β₁ and β₂ are the assay responses at infinite and zero concentrations, respectively. When β₄ > 0, β₁ and β₂ exchange the roles. β₅ is the asymmetry factor, and the curve becomes symmetrical when β₅ = 1. β₃ is the concentration level at which the assay response is equal to β₂ + (β₁ – β₂)/2^β₅. For a symmetrical curve, β₃ is simply the mid-range concentration at which the assay response is the middle point of the two asymptotes, i.e., (β₁+β₂)/2. β₄ affects the slope of the curve at β₃. Precisely, (β₂–β₁)β₄ is proportional to the slope of the curve at β₃ and the sign of (β₂ – β₁)β₄ determines whether the curve is monotonically increasing or decreasing.

2.2 Summary measures of the curve

2.2.1 IC50 and AUC

Once the titration curve has been estimated using either the polynomial or 5PL model, it is often important to have summary measures of the curve to reduce the dimension and to convey the information of the curve. The summary measures of the curve provide the basis for comparing and further analysis of neutralization responses.

The most widely used summary measure is IC50, which is defined as x₀ = h(y₀, β) with y₀ = 0.50, where h(y, β) denotes the inverse function of f. The estimate of IC50 is ${\widehat{x}}_0=h(0.50,\widehat{\beta })$. In the case of the polynomial model (2),

$$h(y,\beta )=\frac{-{\beta }_2\pm \sqrt{{\beta }_2^2-4{\beta }_3}({\beta }_1-y)}{2{\beta }_3}.$$

Only the inverse function which has x̂₀ within the concentration range (x₁, x_n) is relevant for the estimation of IC50s. For the 5PL model as in (3),

$$h(y,\beta )={\beta }_3{\left\{{\left(\frac{{\beta }_1-{\beta }_2}{y-{\beta }_2}\right)}^{1∕{\beta }_5}-1\right\}}^{1∕{\beta }_4}.$$

For those x̂₀ that are undefined or outside the concentration range (x₁, x_n), the estimated IC50 is < x₁ or > x_n.

To get around the censoring issue, we propose an alternative summary measure, the area under the curve (AUC), defined as

$$\mathrm{AUC}=\frac{1}{x_n-x_1}{\int }_{x_1}^{x_n}f(x,\beta )dx.$$

For the polynomial model as in (2), the AUC can be estimated in a closed form

$$\widehat{\mathrm{AUC}}={\widehat{\beta }}_1+\frac{{\widehat{\beta }}_2}{2}(x_1+x_n)+\frac{{\widehat{\beta }}_3}{3}(x_1^2+x_1{x}_n+x_n^2)\equiv X_c^T\widehat{\beta },$$

where $\widehat{\beta }={({\widehat{\beta }}_1,{\widehat{\beta }}_2,{\widehat{\beta }}_3)}^T$, $X_c^T=(1,(x_1+x_n)∕2,(x_1^2+x_1{x}_n+x_n^2)∕3)$. For the 5PL model, the AUC has to be estimated using numerical integration.

The AUC can be interpreted as the average neutralization within the range of x₁ and x_n. Consider a simple ideal situation where the neutralization ranges from 0 to 1 with no negative values, then AUC ranges from 0 to 1 with 1 for the most potent antibodies and 0 for negative antibodies.

Often instead of looking at the full concentration range, it might be of interest to restrict attention to the partial range; for example, to assess the neutralization at a relatively high or low concentration range. The partial area under the curve (pAUC) is defined as

$$\mathrm{pAUC}(x_i,x_j)=\frac{1}{x_j-x_i}{\int }_{x_i}^{x_j}f(x,\beta )dx,$$

where x₁ ≤ x_i < x_j ≤ x_n. One major application of the pAUC is meta-analysis, wherein different studies use different concentration ranges; and the pAUC is computed on a partial range common to the studies.

2.2.2 Inference for IC50 and AUC

In addition to point estimates of IC50 and AUC, it is also desirable to assess the precision of these point estimates, and often this becomes essential when IC50 or AUC are used to evaluate neutralization positivity. Two common ways of constructing confidence intervals are the delta method and the bootstrap method. The former relies on the large-sample approximation; therefore the confidence intervals might fail to achieve the nominal coverage probability when the sample size is not large enough (Belanger et al., 1996; Zeng and Davidian, 1997). Alternatively, a bootstrap resampling approach is commonly used. However, the number of bootstrap replications might be quite large in order to achieve reasonable accuracy.

By the delta method, the variance of x̂₀, the estimated IC50, is

$$\mathrm{Var}\left({\widehat{x}}_0\right)=h_{\beta }^T(y_0,\beta )V{h}_{\beta }(y_0,\beta ),$$

where h_β is the derivative of h with respect to β and V is the asymptotic variance-covariance matrix of β. It can be estimated by

$$\widehat{\mathrm{Var}}\left({\widehat{x}}_0\right)=h_{\beta }^T(y_0,\widehat{\beta })\widehat{V}{h}_{\beta }(y_0,\widehat{\beta }),$$

where V̂ is an estimated V based on the information matrix.

Similarly, the variance of the estimated AUC is

$$\mathrm{Var}\left(\widehat{\mathrm{AUC}}\right)=D_{\beta }^{T}V{D}_{\beta },$$

where D_β is the derivative of AUC with respect to β. For the polynomial model (2), the variance of $\widehat{\mathrm{AUC}}$ can be estimated in a closed form

$$\widehat{\mathrm{Var}}\left(\widehat{\mathrm{AUC}}\right)={\widehat{\alpha }}^2{X}_c^T{\left(X^{T}X\right)}^{-1}{X}_c,$$

where ${\widehat{\sigma }}^2={\sum }_{j=1}^n{\sum }_{k=1}^{r_j}{(y_{ik}-f(x_j,\widehat{\beta }))}^2∕(N-3)$ and X is the design matrix. For the 5PL model (3), the variance of $\widehat{\mathrm{AUC}}$ can be estimated by

$$\widehat{\mathrm{Var}}\left(\widehat{\mathrm{AUC}}\right)=D_{\widehat{\beta }}^T\widehat{V}{D}_{\widehat{\beta }}.$$

There is no closed form for $D_{\widehat{\beta }}$, therefore numerical differentiation is needed to compute $D_{\widehat{\beta }}$.

With the IC50 and AUC estimates and their variances, one can obtain approximate 100(1 – α)% confidence intervals (CI) based on the large-sample theory, referred to as Wald intervals hereafter:

$${\widehat{x}}_0+z_{\alpha ∕2}\sqrt{\widehat{\mathrm{Var}}\left({\widehat{x}}_0\right)},{\widehat{x}}_0+z_{1-\alpha ∕2}\sqrt{\widehat{\mathrm{Var}}\left({\widehat{x}}_0\right)},$$ (4)

$$\widehat{\mathrm{AUC}}+z_{\alpha ∕2}\sqrt{\widehat{\mathrm{Var}}\left(\widehat{\mathrm{AUC}}\right)},\widehat{\mathrm{AUC}}+z_{1-\alpha ∕2}\sqrt{\widehat{\mathrm{Var}}\left(\widehat{\mathrm{AUC}}\right)},$$ (5)

where z_a is the 100ath percentile of the standard normal distribution.

Alternatively, a non-parametric bootstrap method can be used to construct variance estimates and confidence intervals. The algorithm is described as follows:

1. Fit the titration curve model as in (1) and obtain $\widehat{\beta }$, $\widehat{\sigma }$.

2. Obtain the bth bootstrap sample, $y_{jk,b}^{\ast }=f(x_j,\widehat{\beta })+\widehat{\sigma }{∊}_{jk,b}^{\ast }$, where ${∊}_{jk,b}^{\ast }$ is a random sample drawn from $\widehat{∊}$ with replacement.

3. Estimate the IC50 and AUC for the bth bootstrap sample as described in Section 2.2.1 and denote these estimates as ${\widehat{x}}_{0,b}^{\ast }$ and ${\widehat{\mathrm{AUC}}}_b^{\ast }$.

4. Repeat steps 2 and 3 B times, and retain all ${\widehat{x}}_{0,b}^{\ast }$ and ${\widehat{\mathrm{AUC}}}_b^{\ast },b=1,\dots ,B$.

5. Variances of x̂₀ and $\widehat{\mathrm{AUC}}$ are estimated using sample variances of bootstrap replicates.

6. Form the 100(1 – α)% bootstrap interval using the bias-corrected and accelerated (BCa) method based on the empirical distribution of ${\widehat{x}}_{0,b}^{\ast }$ and ${\widehat{\mathrm{AUC}}}_b^{\ast }$ (Efron and Tibshirani, 1993).

Note that the variance estimator of x̂₀, and hence also the CI, is undefined when x̂₀ < x₁ or x̂₀ > x_n.

In practice, it would be natural to model titration curves using a logarithm of titer or concentration due to the fact that neutralization assays are usually conducted in a serial dilution fashion. With this transformation, the polynomial model (2) becomes

$$f(x,\beta )={\beta }_1+{\beta }_2\log x+{\beta }_3{\left(\log x\right)}^2,$$ (6)

and the 5PL model (3) is re-parameterized to

$$f(x,\beta )={\beta }_2+\frac{({\beta }_1-{\beta }_2)}{{\{1+{\left(e^{\log x-\log {\beta }_3}\right)}^{{\beta }_4}\}}^{{\beta }_5}}.$$

Consequently, the AUC becomes a integration of f over log x.

2.3 Positivity criteria and breadth

In this section, we describe several statistical criteria for positive neutralization that can be used to estimate the breadth.

2.3.1 Single virus case

First we consider a simplest case with a single virus. We want to test the null hypothesis

$$H^0:IC50\ge c_1,\text{versus}{H}^a:IC50<c_1,$$

or the null hypothesis

$$H^0:AUC\le c_2,\text{versus}{H}^a:AUC>c_2.$$

A Wald test statistic can be formed using either IC50 or AUC as follows:

$$Z_1=\frac{\widehat{IC50}-c_1}{\sqrt{\widehat{\mathrm{Var}}\left(\widehat{IC50}\right)}},Z_2=\frac{\widehat{AUC}-c_2}{\sqrt{\widehat{\mathrm{Var}}\left(\widehat{AUC}\right)}}.$$ (7)

Asymptotically, Z₁ and Z₂ follow the standard normal distribution under the null. All the tests are one-sided; therefore, the p-values for IC50 and AUC are estimated as Φ(Z₁) and 1 – Φ(Z₂) , respectively, where Φ is the standard normal cumulative distribution function. Alternatively, the p-values can be estimated using the non-parametric bootstrap as described in Section 2.2.2.

The specification of c₁ and c₂ is more of a biological question than a statistical question. For IC50, c₁ is usually chosen to be the highest concentration in the range as in the empirical method. However, it is not as clear which c₂ is biologically appropriate for the AUC test statistic. Though it is natural to choose c₂ to be the AUC from the negative control antibody against the same virus and conduct a two-sample test, one may want to choose non-zero null hypotheses to avoid statistically significant but biologically meaningless positive results. For example, monoclonal antibody (mAb) 1418 is specific for an irrelevant virus and displays no cross-reactivity against HIV-1 viruses and is therefore commonly used as a negative control. The titration curves of mAb1418 typically fluctuate around zero and some of the AUCs are even less than zero. Therefore, it makes no sense to test AUC against a negative or zero AUC from mAb1418. One solution for this is to test against non-zero null hypotheses with c₂ chosen based on the distribution of AUC from mAb1418 against a panel of viruses. For example, c₂ could be the mean plus two standard deviations (sd) of AUCs from mAb1418 against a panel of viruses. Alternatively, c₂ could be specified based on biological knowledge. For example, if it is believed that the AUC must be at least 25% to be biological meaningful, one can choose c₂ = 0.25.

2.3.2 Multiple viruses case

In evaluating antibodies for the capability of broad neutralization against multiple HIV-1 strains, neutralization responses are often dichotomized into positive or negative to determine the breadth of neutralization.

Suppose a panel of m viruses is tested against a given antibody. Denote the m p-values by p₁, p₂, . . . , p_m for the antibody. Formally we can define the breadth, B, as the number of null hypotheses that are false. So the breadth can be estimated by

$${\widehat{B}}_{m_0}=m-{\widehat{m}}_0,$$

where m₀ is the number of true nulls. However it is difficult to estimate m₀ because we do not know the distribution of truly significant p-values. Alternatively, when m̂₀ is not available, it becomes natural to estimate the breadth by the number of rejected nulls, denoted as B̂_V+T.

There are many methods for controlling the type I error rate in a multiple testing setting. We refer to Ge et al. (2003) and Dudoit et al. (2008) for a comprehensive review of this topic. Although controlling the family wise error rate (FWER) is an attractive method and commonly used for multiple testing correction, we will focus on controlling the false discovery rate (FDR), which is defined as the expected proportion of false positives among the rejected hypotheses (Benjamini and Hochberg, 1995), for three reasons. First, generally speaking, controlling the FDR can be more powerful than controlling the FWER (Ge et al., 2003). Second, controlling FDR seems more scientifically appropriate than controlling FWER when estimation of breadth is of interest. Lastly, FDR-based methods provide a way to estimate the number of true nulls m₀ that is the key parameter for estimation of breadth.

We consider two FDR-based approaches, adaptive step-up method proposed by Benjamini and Hochberg (2000) (referred to as ABH) and the q-value method proposed in Storey and Tibshirani (2003) and Storey et al. (2004). These methods both provide estimates of m₀. The q-value method uses a tuning parameter λ that can be automatically chosen using the R package qvalue. Storey et al. (2004) showed that the q-value method provides control of the FDR for large number of hypotheses m and weak dependence structure. We refer interested readers to the original references for more details about the ABH and q-value methods. It is worth noting that the ABH and q-value methods provide an inconsistent estimator of m₀ that overestimates m₀ to ensure control of the FDR.

2.4 Simulation study

To evaluate the performance of the proposed methods for finite samples, we conduct two sets of simulation studies. The first assesses the point estimators and confidence intervals of IC50 and AUC, as described in Section 2.2, for a single virus case. The second compares different FDR-based methods and the empirical method in a multiple viruses setting. Throughout the simulation study, the FDR level is 0.10 and the titration curves are fitted using the polynomial model with logarithm transformed concentrations (6).

2.4.1 Single virus case

We generated f(x, β) according to (6) with four sets of β chosen from real neutralization curves: β = (0.4014, 0.5978, –0.1530) for case 1, β = (0.2256, 0.2104, 0.0160) for case 2, β = (0.1519, 0.0881, 0.0841) for case 3 and β = (0.1610, 0.0977, 0.0662) for case 4. The standard concentrations x_j were set to be {0.390625, 0.78125, 1.5625, 3.125, 6.25, 12.5, 25, 50}, then we generated duplicate (r_j = 2) responses y according to (1), where the errors ε_jk ~ N(0, 1) and σ = 0.05.

We generated 1000 realizations of neutralization curves. For each realization, we fit the titration curve by ordinary least squares, and calculated both asymptotic variances and Wald intervals (4) and (5) for IC50 and AUC, respectively. Realizations with estimated IC50s outside the concentration range are excluded. For each realization, we also generated B = 10, 000 bootstrap samples and formed the bootstrap intervals using the algorithm described in Section 2.2.2. For both Wald and bootstrap intervals, the α level is 0.05.

2.4.2 Multiple viruses case

We conducted another simulation study to assess the performance of several methods for making positivity calls and for estimating the breadth. The methods include the empirical method, the ABH method, and the q-value method using either the natural cubic spline smoother or the bootstrap for choosing λ. All the methods are assessed in a broad range of scenarios by varying the following parameters:

• Number of tests: m = 30.

• Number of false nulls: m₁ = 0, 10.

• σ: 0.01, 0.02, 0.03, 0.04, 0.05, 0.075, 0.10, 0.15, 0.20.

To make the simulation more realistic, all the true titration curves f were chosen based on fitted curves from a typical TZM-bl assay. The standard concentrations were the same as in single virus case. We generated duplicate responses y according to (1), where the errors ε_jk ~ N(0, 1). The estimated σs from typical TZM-bl assay data range from 0.001 to 0.147 with an average of 0.062, so we considered different σs ranging from 0.01 to 0.20 in the simulation study.

We considered three cases and chose c₁ = 50μg/ml and c₂ = 0.25 for each case:

• Case 1 (complete null): m₁ = 0, all 30 virus-antibody combinations have no positive responses with all IC50s greater than 50μg/ml and AUC less than 0.25 ranging from −0.16 to 0.24 with a median of 0.10.

• Case 2 (weak positive responses): m₁ = 10, 10 of 30 virus-antibody combinations have positive responses with IC50 less than 50μg/ml and AUC greater than 0.25, and the other 20 viruses remained the same as in Case 1. All IC50s range from 47.51 to 2.35 with a median of 40.02 and AUCs range from 0.27 to 0.59 with a median of 0.29.

• Case 3 (strong positive responses): m₁ = 10, 10 of 30 virus-antibody combinations have positive responses with IC50 less than 50μg/ml and AUC greater than 0.25, and the other 20 viruses remained the same as in Case 1. All IC50s range from 43.38 to 0.78 with a median of 1.70 and AUCs range from 0.31 to 0.71 with a median of 0.63.

We simulated S = 1000 data sets. For each simulated data set, the number of false positives (V) and number of true positives (T) are computed for each method. Then the FDR, average power and breadth are estimated. Specifically, the FDR is estimated as

$$\widehat{FDR}=\frac{1}{S}\sum _1^S\frac{V}{max\{V+T,1\}}.$$

We adopted the concept of average power defined in Dudoit et al. (2008). The average power (AP) is defined as the expected proportion of correctly rejected hypotheses,

$$AP=\frac{E\left(T\right)}{m_1}.$$

If m₁ = 0, i.e., complete null, then the average power is undefined as for the power in the classical single hypothesis testing. The average power can be estimated by

$$\widehat{AP}=\frac{1}{m_{1}S}\sum _1^{S}T$$

For the empirical method, the breadth is estimated as the number of viruses with IC50s less than the highest concentration. Since the ABH and q-value methods provide the estimates of m₀, the breadth can be estimated by two approaches: B̂_m0 and the number of rejected nulls, B̂_V+T = V+T.

3. Results

3.1 Simulation study

3.1.1 Single virus case

Table 1 shows the simulation results for a single virus case at σ = 0.05. Overall, there are three interesting points. Firstly, the Wald interval has a better coverage probability than the bootstrap interval except for the IC50 when the censoring rate is high (cases 3 and 4). The asymptotic standard errors (SE) are almost identical to the empirical SE when N = 16 except for the IC50 when the censoring rate is high. This suggests that the large sample approximation is reasonable when N = 16, which is typical in neutralization assay data. Secondly, IC50 estimates become more biased and less precise as the IC50 gets closer to the highest concentration while AUC estimates are unbiased and equally precise for all four cases regardless of overall response levels. For case 3, although 6.5% of estimated IC50s that are outside the concentration range are excluded from the analysis, which leads to a smaller empirical SE, the IC50 is still slightly overestimated with 1.6% bias. When σ is increased to 0.10 (results not shown), the censoring rate increases more than three-fold to 22.7% and the bias in IC50 increases to 2.2%. Lastly, AUC methods perform better than IC50 methods in terms of coverage probability in Wald intervals. This phenomenon is consistent with what we will demonstrate in the next simulation study.

Table 1.

Simulation results for estimates of IC50 and AUC and of Wald intervals and bootstrap intervals. Point and confidence limit estimates are computed as averages over the 1000 simulated data sets. The nominal level of coverage is 0.95. SE stands for standard error. Censoring rate is the proportion of 1000 estimated IC50s outside the concentration range.

	Case 1	Case 2	Case 3	Case 4
	IC50
True	1.49	15.69	37.76	43.88
Bias	0	0.09	0.59	−0.69
Asymptotic SE	0.10	2.51	6.03	7.42
Empirical SE	0.11	2.49	5.88	5.89
Censoring rate	0	0	0.065	0.264
Wald interval
Endpoints	(1.29, 1.69)	(10.89, 20.69)	(25.71, 49.37)	(26.22, 55.29)
Coverage	0.910	0.936	0.921	0.882
Bootstrap interval
Endpoints	(1.32, 1.69)	(11.91,21.66)	(29.69, 47.18)	(31.77, 49.20)
Coverage	0.901	0.909	0.926	0.940
	AUC
True	0.667	0.374	0.275	0.276
Bias	−0.001	0.000	0.000	0.000
Asymptotic SE	0.012	0.013	0.013	0.013
Empirical SE	0.013	0.013	0.013	0.013
Wald interval
Endpoints	(0.642, 0.690)	(0.349, 0.399)	(0.250, 0.300)	(0.251, 0.301)
Coverage	0.931	0.930	0.931	0.931
Bootstrap interval
Endpoints	(0.644, 0.688)	(0.352, 0.397)	(0.252, 0.298)	(0.254, 0.299)
Coverage	0.904	0.911	0.911	0.911

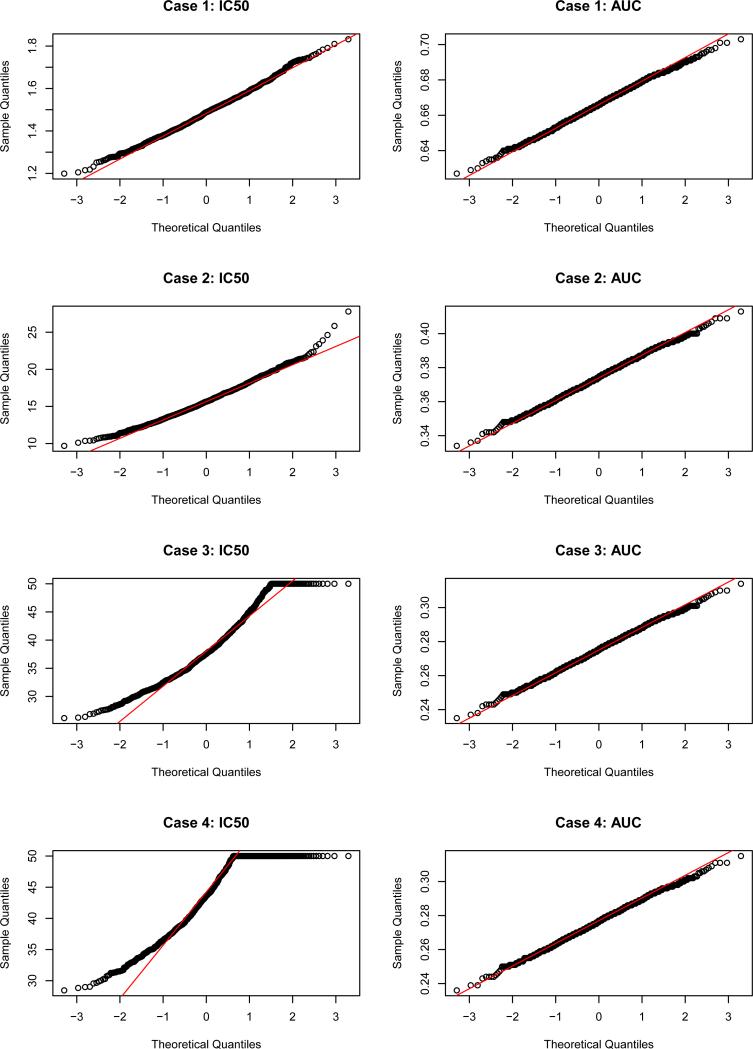
To understand why Wald intervals have worse coverage for IC50 at cases 3 and 4 but slightly better coverage for all other cases relative to bootstrap intervals, the Q-Q plots of 10, 000 bootstrap replicates of IC50 and AUC estimates are plotted in figure 1. As we expected, the estimated IC50 is approximately normally distributed for cases 1 and 2 but not normally distributed for cases 3 and 4 due to censoring. The estimated AUC is normally distributed for all four cases regardless of overall response levels. Note that the bootstrap intervals are narrower than the Wald intervals. This suggests that even 10, 000 bootstrap replicates might not be large enough to appropriately estimate the tail distributions.

Figure 1.

Q-Q plots of 10, 000 bootstrap replicates ${\widehat{x}}_0^{\ast }$ and ${\widehat{\mathrm{AUC}}}^{\ast }$ for all four cases in the single virus simulation.

3.1.2 Multiple viruses case

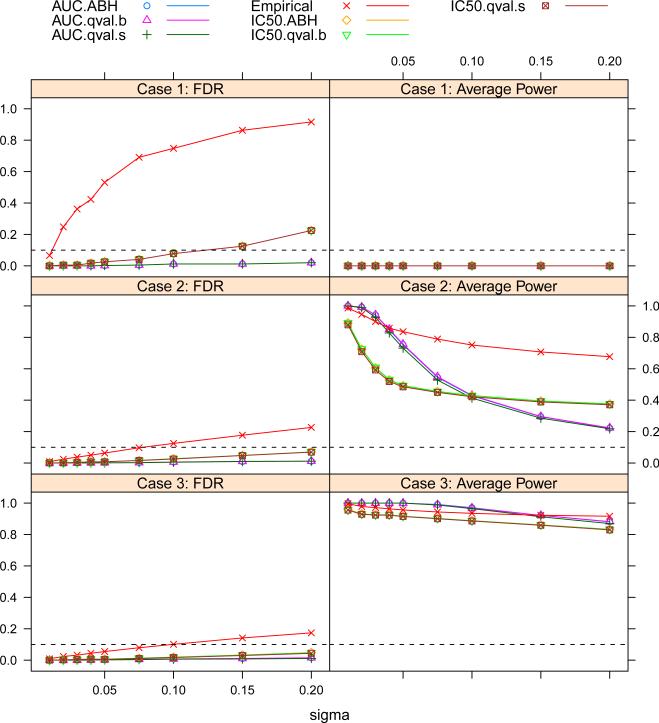
Figure 2 shows the plots of FDR and average power versus σ for the IC50 and AUC methods using different testing methods. As we would expect, the empirical method has much higher estimated FDR than all other FDR-based methods. For the empirical method, the estimated FDR is greater than 10% for all three cases, when the noise level is high (σ ≥ 0.10). For both ABH and q-value methods in case 1, the IC50 methods have elevated estimated FDR at σ > 0.10 when there is low-level neutralization activity such that their IC50 values are not but very close to 50μg/ml. The AUC method controls the FDR well with both ABH and q-value methods for all three cases.

Figure 2.

Plot of the FDR and average power versus σ for all three cases in the multiple viruses simulation. The FDR level is 10%. The dashed horizontal lines are at 0.10.

For case 2, the AUC method is more powerful than the IC50 method at σ < 0.10 but less powerful at σ > 0.10. For case 3, the AUC method is more powerful than the IC50 method across the σ range we examined.

As we see in table 1, the bias and variance of the estimated IC50 increases as neutralization gets weaker while the bias and variance of the estimated AUC does not change. This occurs partly because the IC50 extracts information at a single point while the AUC averages information across the concentration range. Combining information across the concentration range not only reduces the type I error rate but also boosts the power. For a typical TZM-bl assay, 75% of σs are less than 0.08, so for the majority of the data, the AUC method perform best with higher sensitivity and lower false positive rate.

Table 2 shows the simulation results for estimated breadth using both B̂_m0 and B̂_V+T. Not surprisingly, overall B̂_m0 underestimates the breadth for all the methods in cases 2 and 3. Of all the methods we examined, the q-value method using natural cubic splines performs the worst. For B̂_V+T, as we would expect, the AUC method performs at least as well as the IC50 method. The empirical method tends to overestimate the breadth when B = 0 (case 1) or when neutralization level is high (case 3). The ABH and q-value with bootstrap methods perform equally well.

Table 2.

Simulation results for the estimated breadth using the empirical method, ABH and q-value methods. Estimates are computed as averages over the 1000 simulated data sets. The FDR level is 10%. qval.s represents the q-value method using the natural cubic spline smoother for choosing λ, and qval.b represents the q-value method using the bootstrap for choosing λ.

				IC50			AUC
Case	B	Method	Empirical	ABH	qval.s	qval.b	ABH	qval.s	qval.b
σ = 0.05
1	0	B̂mo	-	0.0	0.0	0.0	0.0	0.0	0.0
		B̂V+T	0.6	0.0	0.0	0.0	0.0	0.0	0.0
2	10	B̂mo	-	3.5	0.0	4.0	5.8	0.0	6.8
		B̂V+T	9.0	5.1	5.0	5.1	7.5	7.3	7.5
3	10	B̂mo	-	7.7	0.0	3.3	8.0	0.0	1.4
		B̂V+T	10.2	9.2	9.2	9.2	10.0	10.0	10.0
σ = 0.10
1	0	B̂mo	-	0.0	0.0	0.0	0.0	0.0	0.0
		B̂V+T	1.1	0.1	0.1	0.1	0.0	0.0	0.0
2	10	B̂mo	-	2.9	0.0	3.1	3.3	0.0	4.0
		B̂V+T	8.7	4.4	4.4	4.4	4.3	4.2	4.3
3	10	B̂mo	-	7.4	0.0	3.2	7.8	0.0	5.5
		B̂V+T	10.5	9.1	9.0	9.1	9.8	9.7	9.8

In summary, the empirical method has elevated FDR. In the complete null case the IC50 method does not control the FDR when σ is greater than 0.10, while the AUC method controls the FDR even when σ is larger than 0.10. When the false nulls have weak neutralization, the AUC method is more powerful at σ < 0.10 but less powerful at σ > 0.10 compared to the IC50 method. When the false nulls have strong neutralization, the AUC method is more powerful than the IC50 method over the entire σ range we examined. For estimation of breadth, B̂_V+T using AUC test statistic combined with either the ABH or q-value method with bootstrap for choosing λ are recommended.

3.2 Real data applications

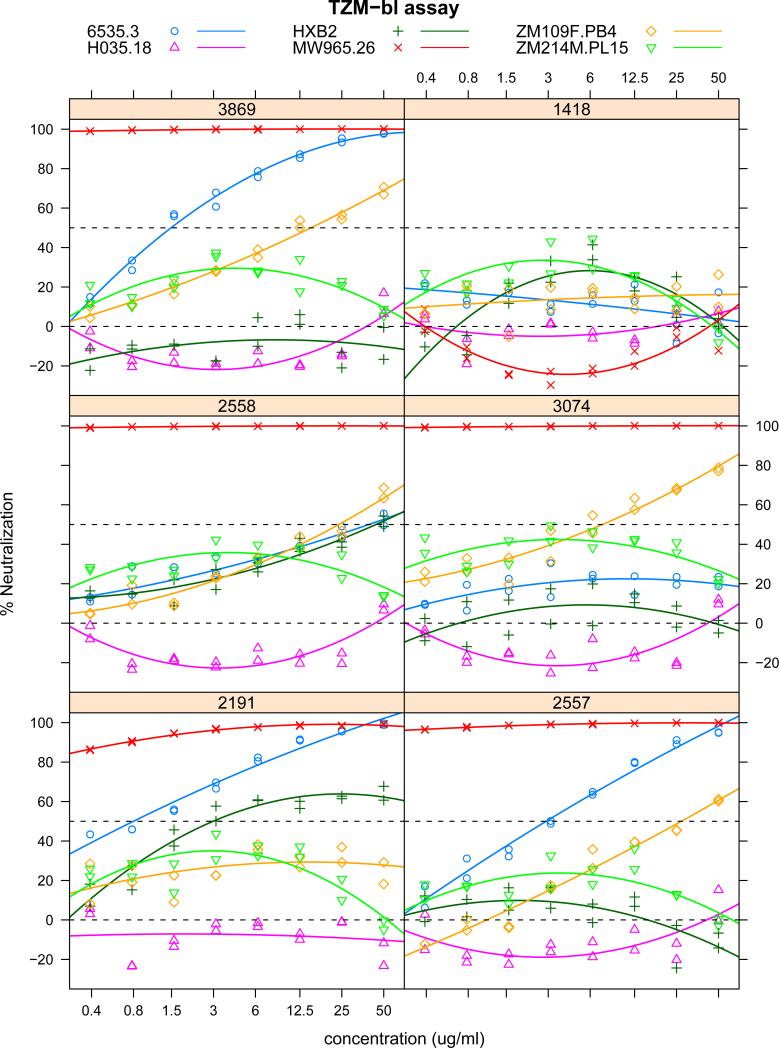
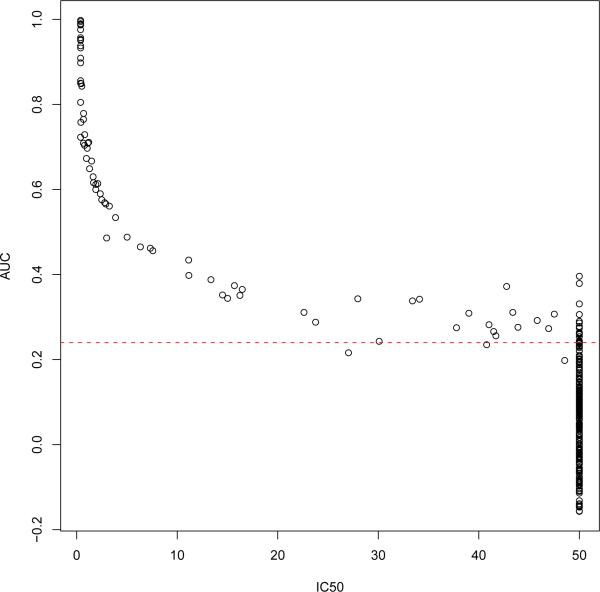
To illustrate the proposed statistical methods, we considered a TZM-bl assay data set from six HIV-1 specific mAbs and one irrelevant parvovirus-specific mAb (1418) tested against a panel of 41 pseudoviruses (Hioe et al., 2010). The titration curves were fitted using polynomial models. Figure 3 shows some of the raw data with fitted titration curves. To estimate breadth for each mAb, we considered several methods: empirical method, IC50 and AUC methods combined with ABH and q-value multiple testing methods. The multiple testing was adjusted for each mAb separately as we were interested in estimating breadth for each mAb rather than the overall number of positive responses across all mAbs. Table 3 shows the breadth for all seven mAbs. The constant c₁ = 50μg/ml was the highest concentration level, and c₂ = 0.24 was derived using the mean plus two sd of AUCs from negative control mAb1418 against 41 viruses. The estimated breadth for the negative control mAb1418 is zero for all methods. Overall, the IC50 method yields the smallest estimated breadth while the AUC method the largest except for mAb2557. These results are generally consistent with the simulation results that the AUC method has higher sensitivity when σ is not large (all σ < 0.15 ). Figure 4 shows the scatter plot of IC50 versus AUC for all mAbs. For those curves with censored IC50 estimates, their estimated AUCs indeed have a wide range from −0.157 to 0.396, some of which are AUC positive but IC50 negative.

Figure 3.

Scatter plot of raw data with fitted titration curves using quadratic polynomial models for the real TZM-bl assay data. The titles in each panel are the mAb ID. The legend gives the viruses ID along with their symbols.

Table 3.

Estimated breadth for each antibody to a panel of 41 viruses using B̂_V+T estimator. The FDR level is 10%. qval.s represents the q-value method using the natural cubic spline smoother for choosing λ, and qval.b represents the q-value method using the bootstrap for choosing λ.

B̂V+T: number of rejected nulls
	IC50 methods				AUC methods
antibody	Empirical	ABH	qval.s	qval.b	ABH	qval.s	qval.b
2219	10	9	9	9	10	10	10
2191	16	14	13	14	17	17	17
1418	0	0	0	0	0	0	0
2557	13	11	11	11	12	12	12
2558	15	11	11	11	16	16	16
3074	12	9	9	9	14	14	14
3869	12	11	11	11	14	14	14

Figure 4.

Scatter plot of the IC50 versus AUC estimates for all seven mAbs tested against 41 viruses in the real TZM-bl assay data. The dotted horizontal line represents c₂ = 0.24.

4. Discussion

We have proposed the AUC measure for summarizing the titration curve in complement to the commonly used IC50 measure, have developed point and interval (Wald and bootstrap) estimators for these parameters, and have investigated the performance of these estimators in simulations. We have also proposed statistical methods for determining positive neutralization of a single virus and for estimating the neutralization breadth.

Though the AUC measure has been widely used to summarize information in various curves, e.g., drug dose-response curves in biopharmaceutics and pharmacokinetics and ROC curves in medical tests (Pepe, 2003), to our knowledge, it has not been considered in the vaccine field. In this study, we present advantages of AUC over IC50, which include no problems with censoring, better coverage probabilities of confidence interval, and improved efficiency of estimators. Of course, the AUC has its own limitations. Like IC50, AUC is a summary measure of the curve, which does not convey all the information in the curve. One important feature missed by both IC50 and AUC is the slope that measures the change rate of neutralizations at certain concentrations. A large slope implies a great potential of reaching higher neutralization at higher concentration. Hioe et al. (2010) incorporated a slope criterion, on top of the AUC method, for determining positive neutralization. Shen et al. (2008) showed that the slope is a key factor in classifying antiretroviral drugs.

In general, the neutralization curves should be monotonic and indicate a dose-response relationship. However, for the negative samples, the neutralization values are low and appear to be non-monotonic. The possible causes of non-monotonicity include technical errors (e.g., dilution errors, reading error due to irregularity in the wells or pipetting errors) and a true biological phenomenon. If it is believed that the neutralization curves are all monotonic, one can apply a constrained polynomial regression such that parameters for the linear and quadratic terms are constrained to be non-negative. One merit of the un-constrained regression is that, when combined with appropriate replication, one can identify when the non-monotonicity happens. What one might do if there is statistical evidence for non-monotonicity would depend on the specific context and is beyond the scope of the paper. We have analyzed the data with both unconstrained and constrained methods. The two methods yield comparable results (Supplementary figure 1 and 2).

IC50 estimates become more biased and less precise as the IC50 gets closer to the highest concentration end. This phenomenon was also observed in calibration curves for immunoassay data (Belanger et al., 1996; Zeng and Davidian, 1997). The estimates were not reliable such that confidence intervals were unacceptably wide when the calibrated values were close to the end of the concentration range. However, AUC estimates are unbiased and equally precise regardless of overall response levels. All of these suggest that the AUC measure is preferable in particular when IC50s are at high concentrations. For positivity calls, however, since the AUC and IC50 methods test different hypotheses, it is not unexpected that some virus-antibody combinations are AUC positive but IC50 negative or vice versa.

Our simulation results indicate that the large-sample approximation confidence interval is valid and performs better than the bootstrap confidence interval. However, Zeng and Davidian (1997) and Belanger et al. (1996) demonstrated through theory and empirical work that Wald confidence intervals for immunoassay may be inaccurate when variance parameters need to be estimated in a heteroscedastic regression model. Therefore, Zeng and Davidian (1997) proposed a bootstrap-adjusted confidence interval that uses the exact quantiles of the test statistics estimated by bootstrapping residuals instead of using z_α/2 and z_1–α/2 from a standard normal distribution. This automatically adjusts for the effect of variance parameter estimation. Not surprisingly, Belanger et al. (1996) found that Wald intervals preformed reasonably well when response heteroscedasticity was not severe or when quadruplicate (r_j = 4) rather than duplicate (r_j = 2) responses were assayed at each of the standard concentrations. This finding is consistent with our results that Wald intervals perform well when the variance of responses are homogeneous.

All simulations and analysis in this paper were implemented in R.