Abstract
Recently, the “Common Disease-Multiple Rare Variants” hypothesis has received much attention, especially with current availability of next generation sequencing. Family-based designs are well suited for discovery of rare variants, with large and carefully selected pedigrees enriching for multiple copies of such variants. However, sequencing a large number of samples is still prohibitive. Here, we evaluate a cost-effective strategy (pseudo-sequencing) to detect association with rare variants in large pedigrees. This strategy consists of sequencing a small subset of subjects, genotyping the remaining sampled subjects on a set of sparse markers, and imputing the untyped markers in the remaining subjects conditional on the sequenced subjects and pedigree information. We used a recent pedigree imputation method (GIGI), which is able to efficiently handle large pedigrees and to accurately impute rare variants. We used burden and kernel association tests, famWS and famSKAT, which both account for family relationships, and heterogeneity of allelic effect for famSKAT only. We simulated pedigree sequence data and compared the power of association tests for: pseudo-sequence data, a subset of sequence data used for imputation, and all subjects sequenced. We also compared, within the pseudo-sequence data, the power of association test using best-guess genotypes and allelic dosages. Our results show that the pseudo-sequencing strategy considerably improves the power to detect association with rare variants. They also show that the use of allelic dosages results in much higher power than use of best-guess genotypes in these family-based data. Moreover, famSKAT shows greater power than famWS in most of scenarios we considered.
Keywords: Kernel statistic, burden test, mixed linear model, sequence data, inheritance vectors, MCMC
Introduction
Genome Wide Association Studies (GWAS) have shown their success in identifying thousands of markers associated with hundreds of complex traits (http://www.genome.gov/gwastudies/). The discovered variants are rather common in the population, have small effect sizes and are mainly identified in data of unrelated individuals using classical single marker tests. Despite their high number, the discovered markers do not explain a substantial fraction of the heritability of any trait so far investigated [Manolio, et al. 2009]. Several hypotheses may explain the missing heritability including the association of multiple rare variants [Bodmer and Bonilla 2008; Cohen, et al. 2004; Cohen, et al. 2006; Iyengar and Elston 2007; Nejentsev, et al. 2009]. Under this hypothesis, GWASs lose power because of two main reasons: (1) rare variants are not captured by genotyping chips, designed to optimally tag common variants only, and (2) single marker tests are underpowered for the detection of variants with low minor allele frequency (MAF) in feasible sample sizes.
To circumvent the lack of power of single marker tests, several methods, known as collapsing methods, have been proposed that take into account multiple rare variants at a time [Li and Leal 2008; Madsen and Browning 2009; Morgenthaler and Thilly 2007; Morris and Zeggini 2010; Price, et al. 2010; Zawistowski, et al. 2010]. The principle of these methods is to test the cumulative effect of multiple rare variants in a genomic unit, such as a gene. This reduces the number of tests performed and potentially increases the effect size associated with each test by accumulating the effects across variants. Collapsing methods use a classical regression framework, and weight (e.g. Weighted Sum Approach “WS” [Madsen and Browning 2009]) or not (e.g. Cumulative Minor Allele Test “CMAT” [Zawistowski, et al. 2010]) the variants’ effect sizes by a function which decreases with increasing MAF. These approaches are sensitive to the collapsing of variants with opposite direction of effects. In this case, new statistical kernel methods (e.g. the Sequence Kernel Association Test “SKAT”), based on a variance component test, have been proposed and show better power [Wu, et al. 2011].
These association tests were proposed mainly for population-based designs. However, family-based designs are also well suited for discovery of rare variants with relatively large effect. Indeed, large and carefully selected pedigrees enrich for multiple copies of such variants [Wijsman 2012]. This enrichment makes the family-based design highly efficient for correctly identifying underlying genes relative to the much larger sample sizes needed for population-based approaches [Hinrichs and Suarez 2011]. In addition, the type 1 error of family-based designs might be better controlled due to the lower effects of population structure [Choi, et al. 2009; Evangelou, et al. 2006]. Collapsing approaches, such as WS and CMAT, have been extended to family-based designs simply by using a linear mixed model framework (famWS and famCMAT [Chen, et al. 2013; Saad, et al. 2011]). For SKAT, a new extension (famSKAT) was proposed recently to account for family relationships between individuals, but is limited to quantitative traits [Chen, et al. 2013; Schifano, et al. 2012]. However, the properties and the performance of these tests are not yet well established in family-based designs, especially in datasets containing large pedigrees.
The most pertinent data to use for detecting association with rare variants is sequence data, such as Whole Genome and Exome Sequence (WGS/WES). However, sequencing large datasets of subjects (thousands of samples) is still prohibitive despite decreasing sequencing costs. On the other hand, in pedigrees, which can yield significant results with much smaller sample sizes, it is not always possible to sequence all samples because of the quality and quantity of available DNA. For example, in multigenerational pedigrees, the DNA of individuals in the top generations is often not available. A cost-effective alternative is to sequence a subset of subjects, who are typed on a set of sparse markers, and use imputation to infer untyped markers in the remaining unsequenced subjects. Several family-based imputation methods exist [Burdick, et al. 2006; Daetwyler, et al. 2011; Kong, et al. 2008]. For example, Burdick and colleagues [Burdick, et al. 2006] developed a method that works for small pedigrees but cannot handle large pedigrees with many markers because of computational constraints. Recently, a computationally efficient approach for imputing dense genotypes in large pedigrees was proposed [Cheung, et al. 2013]. This approach is able to efficiently handle large pedigrees, accurately impute rare variants and also impute genotypes on individuals who do not have any available genetic data. The pseudo-sequencing alternative was originally proposed for population-based designs and has shown a considerable gain of power compared to the use of small sequencing datasets [Zawistowski, et al. 2010]. However, this has not been well established for family-based designs because of the difficulty of carrying out imputation in large pedigrees. In addition, to run imputation in population-based designs, one can use public sequence/dense markers data, such as, the 1000 Genomes Project [Abecasis, et al. 2010] and HapMap [Frazer, et al. 2007] data, rather than sequencing a subset of GWAS subjects. In family-based designs, the sequence/dense marker datasets have to be formed from the same pedigrees in which imputation is carried out.
A natural question when implementing these procedures is how best to take into account uncertainty in imputed genotypes [Zheng, et al. 2011]. In general, imputation methods estimate the posterior probabilities of the three possible genotypes at untyped diallelic markers. Using these probabilities, these methods determine the best-guess genotypes and calculate the expected number of copies of the minor allele, called allelic dosages. Allelic dosages account for imputation uncertainty, in contrast to best-guess genotypes. When imputation is highly accurate, allelic dosages and best-guess genotypes are expected to be very similar. Several studies in population-based designs have showed that the power achieved from using allelic dosages is higher than the power achieved from using best-guess genotypes [Louis, et al. 2010; Zheng, et al. 2011]. On the other hand, a study based on the trio design, which implemented a test to incorporate the probability distribution of possible imputed genotypes in a TDT framework, showed no significant power increase by using the probability distribution (allelic dosages) [Taub, et al. 2012]. Therefore, the comparison of best-guess genotypes and allelic dosages needs more evaluation in family-based designs, especially in large pedigrees where the issue has yet to be investigated.
Here, we propose the pseudo-sequencing strategy in large pedigrees and evaluate its performance to detect association with rare variants, using famWS and famSKAT. In the obtained pseudo-sequence data, we compare the power of association tests using best-guess genotypes and allelic dosages. Finally, we compare famWS and famSKAT for use on sequence data and we evaluate the influence of various factors on the performance of these tests (i.e. the number of causal variants, the mix of negative and positive causal variants’ effects, and the linkage disequilibrium (LD) pattern). To the best of our knowledge, the influence of LD on collapsing and kernel tests has not been evaluated yet for large pedigrees. In addition, LD, which is a major key for imputation in population-based designs and is expected to be minimal between rare variants but not necessarily inexistent, might affect, indirectly, imputation in family-based designs (which capitalizes only on inheritance information in pedigrees), and hence the performance of our pseudo-sequencing strategy.
Methods
Imputation
To perform imputation in large pedigrees, we used the recent method implemented in the program GIGI [Cheung, et al. 2013]. GIGI (https://faculty.washington.edu/wijsman/progdists/gigi/GIGI.html) is a computationally efficient approach for imputing dense genotypes in large pedigrees. This approach uses a sparse set of “framework markers” typed on most subjects plus a set of “dense markers” typed on a few subjects. The imputation relies on correlation resulting from inheritance in pedigrees through the inheritance of shared segments of a chromosome as represented by inheritance vectors (IV) [Thompson 2011]. In brief, this imputation approach consists of four steps: (1) sample IVs at the positions of framework markers conditional on the observed genotypes at these markers using MCMC sampling in large pedigrees or the exact conditional distribution in small pedigrees, (2) sample IVs at the positions of dense markers conditional on the pedigree structure and IVs sampled at the positions of the framework markers and the meiotic map, (3) estimate the probability distribution for each unobserved genotype at the dense marker positions conditional on all observed dense marker genotypes, their allele frequencies and position-specific IVs corresponding to the dense markers, and (4) call genotypes using the estimated probabilities and user-specified thresholds. Using the probability distribution of unobserved genotypes, one can calculate the allelic dosages for each marker, which is the estimated number of copies of minor alleles (i.e. Allelic Dosage = Pr(genotype = 1) + 2 × Pr(genotype = 2) under the additive model).
Association analysis
We used two association tests, famWS and famSKAT [Chen, et al. 2013]. The first test aims to collapse rare variants into a mega-variant and thus test the association with this mega-variant. The second test does not collapse rare variants but treats them as separate variables in a multivariate regression model. famWS suffers from loss of power when individual variant effects are of opposite sign, while famSKAT does not have this limitation.
Weighted Sum approach accounting for family relationship: “famWS”
famWS is based on a linear mixed model, which accounts for relatedness between family members:
Where:
Y is the vector of quantitative trait values of all N individuals;
β is the fixed effect coefficient for the region of interest (e.g. gene);
is the weight of marker j (j=1,…,p) used in Wu et al. [Wu, et al. 2011];
Gj = (G1j,…,GNj) is the vector of genotypes of all individuals at the marker j (Genotypes are coded as 0, 1 or 2 copies of minor allele, i.e., minor allele dosage);
is the vector of individual specific random effects, where:
is the genetic variance;
Φ(N×N) is a matrix of twice of the coefficient of kinship between pairs of individuals, and,
I(N×N) is the identity matrix;
and finally, is the vector of residual errors where is the residual variance.
To test the association between the trait and the region of interest, we used the Wald test: the null hypothesis H0(no association),β = 0, versus the alternative hypothesis H1(association),β ≠ 0.
Sequence Kernel Association Test accounting for family relationship: “famSKAT”
In famSKAT, markers are treated as random effects in the following linear mixed model: Y = Gβ + u + ε
Where:
G(N×p) = [G1 … Gj … Gp] is the genotype matrix of the (N × p) of the N individuals at the p markers; β(p×1)~N(0,τW) is the vector of random effects of markers where τ is a variance component and W is a pre-specified diagonal matrix (p × p) of . The terms Y, , u and ε are defined in the famWS model described above.
Here, the association test is a variance component test of whether τ = 0. The test statistics is written as:
where µ̂ is the mean of Y and .
This statistic follows a sum of chi-square distributions with one degree of freedom each:
where λi are the eigenvalues of the matrix , and P0 = Σ − X(X′Σ−1X)−1X′ where X(N×1) = [1 … 1] (for more details, please see [Chen, et al. 2013; Schifano, et al. 2012; Wu, et al. 2011]). Note that, for both famWS and famSKAT, the matrix G can contain: i) genotype data (coded as 0, 1 and 2) from direct genotyping or from imputation (best-guess genotypes), or ii) allelic dosages.
Simulation
We simulated sequence data on a large collection of extended pedigrees extracted from a set of Alzheimer Disease cohorts under study at the University of Washington. We considered three datasets: (1) all subjects are sequenced, (2) a small number of subjects are sequenced and the remaining subjects are genotyped, and (3) the previous small number of sequenced subjects are combined with the remaining genotyped subjects, who are imputed using GIGI (pseudosequence data). The first dataset represents the ideal scenario where the DNA and the sequence data are available for all subjects. Note that there may be real studies in which not every individual is genotyped (for the sparse markers) because of the absence of DNA, but the general conclusions do not depend on this. The second dataset represents the scenario of using only the small subsets of sequence subjects. The third dataset represents our pseudo-sequencing strategy, in which we try to maximize the information in pedigrees by using both small subset of sequenced subjects and the remaining genotyped subjects. We performed association analyses on a quantitative trait only.
Sequence data simulation
To obtain semi-realistic data, we simulated 100 sequence datasets, which mimic the 1000 Genomes Project sequence data. The procedure of this simulation follows:
A. Haplotype Simulation
From the Ensemble Gene 63 database (3p.37GRCh), we selected an arbitrary gene (ZNF492) with a length similar to the average length of genes in this database (~ 30 Kilo base pairs (kb)), and which contains a large number of rare variants in the exons (22 SNPs with MAF <0.05, MAFs estimated in the 1000 Genomes Project data, Release August 2010, 566 CEU haplotypes). In the literature, different criteria are used to define rare variants and depend on context. The most common criteria is MAF<0.01. We chose the criteria MAF<0.05 to be able to vary the number of causal SNPs in exons. Note that the difference of imputation accuracy for MAF=0.05 and MAF=0.01 is not great [Cheung, et al. 2013] so that the particular choice here of the definition will not change the basic conclusions. This gene contains 168 common and 145 rare variants (313 in total). The distribution of MAFs of rare variants is shown in Figure S1 in supplementary material.
We extracted the sequence in the region of the gene from the 566 CEU phased haplotypes. In addition, we extracted 5 Mega base pairs (Mb) upstream and 5 Mb downstream of the gene, to select the required more distant framework markers needed for the estimation of inheritance vectors, used for imputation (one framework marker each 0.5 Mb ~ 0.5 centiMorgan (cM)) [Cheung, et al. 2013; Thompson 2011].
In our simulation settings, we varied the magnitude of LD in the gene region. By creating different levels of hotspot recombination events (i.e. 42, 22 and 6 events), randomly in the 1000 Genomes Project haplotypes, we obtained three sets of 566 haplotypes with different LD patterns: LowLD, MedLD and HighLD. The mean r2 of all possible pairs of SNPs is 0.09, 0.12 and 0.18, respectively for the three LD level (Figure S2, S3 and S4 in supplementary material show the LD plots). Note that the same SNPs in the original CEU haplotypes are even more highly correlated than in our simulated data (mean r2 = 0.59, Figure S5 supplementary material shows the LD plot). We choose this gene with unusual high LD relative to all genes to be able to create different LD patterns while fixing the number of rare variants and their MAFs in the gene. Finally, for each LD pattern, we used HapSim [Montana 2005] to simulate 10,000 haplotypes similar to the 566 haplotypes already created. This software used the 566 haplotypes as input to simulate haplotypes with similar LD between SNPs and similar allele frequencies.
B. Haplotype dropping in pedigrees
From the set of 10,000 generated haplotypes, we started by randomly selecting haplotypes, without replacement, for the unrelated founders. Then, we passed the haplotypes down through the generations using a recombination rate of 1% per cM per meiosis. We repeated this last step 100 times for each LD pattern to obtain 100 sequence datasets.
We considered 94 pedigrees, which consist of 21 trios, 11 quartet and 62 other large multigenerational pedigrees in which the number of subjects ranges from 5 to 48 (16 pedigrees have more than 10 subjects and 11 pedigrees have more than 20 subjects). The 11 pedigrees with more than 20 individuals each (total of 338 individuals) cannot be imputed efficiently without using GIGI, which can handle even larger (and possibly complex) pedigrees (>100 subjects per pedigree). The pedigrees we considered contain a total of 882 individuals (336 founders) and come from a real study of Alzheimer Disease. They therefore are representative of what may be found in a real study, which will often not contain only large pedigrees. Nonetheless, more than half of our sample size comes from pedigrees with more than 15 individuals (18 pedigrees, total of 457 individuals). Note that we could use a greater number of larger pedigrees but the general conclusions of our study do not depend on this.
Type 1 Error simulation
For each simulated sequence dataset, we simulated 1000 quantitative traits under the null hypothesis of no association. We fitted the model Y = ε where ε follows a multivariate normal distribution N(0,Σ), with Σ = h2Φ + (1 − h2)I as used by Chen et al. [Chen, et al. 2013]. We fixed the variance due to polygenic effects as and the residual variance as , so the heritability is . This model has genetic variation defined by the pedigree structure but not by the gene. We estimated the type 1 error at a threshold α as the proportion of replicates for which the p-value of the association test is lower than α.
Power simulation
Under the alternative hypothesis of association, we simulated 100 quantitative traits for each simulated sequence dataset by fitting the model: Y = Gcβc + ε where βc is the vector of effect sizes of the c causal variants, Gc is the (N × c) matrix of their genotypes and ε is defined in the type 1 error simulation. The effect sizes of the causal variants were determined by the function , where MAFj is the minor allele frequency of the causal variant j estimated in the generated sequence data, and is the total additive variance. We added this information in our power simulation section. The genetic variation of this model is defined by both pedigree structure and causal variants. In our simulation, we set the total additive variance to 5%. We randomly selected causal variants from the set of rare variants in the exons (i.e. 22 rare variants) and we varied the number of causal variants as: six, 12 and 18. We also varied the proportion of causal variants with negative effects: M0: (+)100%|(−)0%, M30: (+)70%|(−)30% and M50: (+)50%|(−)50% where Mi (+)100 – i %|(−)i % indicates that i % of the variants had negative effects for the minor allele. We estimated the power at threshold α as the proportion of replicates for which the p-value of the association test is lower than α.
Imputation Analysis
Framework Markers
Prior to imputation for each genetic dataset, we used the program gl_auto in MORGAN (http://www.stat.washington.edu/thompson/Genepi/MORGAN/Morgan.shtml) [Thompson 2011] to obtain a set of 1000 IVs, at the positions of the framework markers, realized from the joint distribution of marker genotypes given the pedigree and observed data. The framework marker set consisted of 20 markers, approximately equally distant (one marker each 0.5 Mb ~0.5 cM), in linkage equilibrium (LE), highly informative (MAF>0.4) and typed on all individuals. Note that one of the 20 markers is located within the gene.
Dense Markers
We limited our association analysis to the gene. Thus, all the gene’s markers will form the dense marker set (i.e. 313 markers). We refer to the “dense marker individuals” (DMI) as the individuals selected from each pedigree to be typed only at the dense markers and the “framework marker individuals” (FMI) as the remaining individuals.
The selection of DMI is of great importance. This may affect the performance of the association test and hence suggests the need of efficient algorithms for “picking-individuals”. In our study, we did not focus on this problem and simply selected d=20% of subjects, at random, from each pedigree to be the DMI, rounding up the number of selected individuals. The choice of 1-2 DMI in small pedigrees (less than 13 subjects) will not make a big difference in imputation results. However, the choice of 3-10 DMI in larger pedigrees (more than 12 members) is more important and could make a considerable difference. Our selection procedure led to a subset of 184 DMI over all pedigrees. For each sequence dataset, we select different 184 DMI, holding the total in each pedigree constant across the LD pattern scenarios. By selecting different sets of individuals in each replicate of our simulation datasets, we cover the space of possible combinations of DMI. We considered two scenarios of imputation: IMP-1 and IMP-2. In IMP-1, we carried out imputation on all pedigrees (small and large), and in IMP-2, we carried out imputation on large pedigrees while fixing the number of DMI in both scenarios (i.e. 184), which results in a value of d slightly higher than 20% in IMP-2. The reason of considering IMP-2 is the fact that the advantage of family-based designs is more important in large pedigrees, in which the evidence of segregation of rare variants may be higher than in small pedigrees. In addition, family-based designs in large pedigrees results in better imputation due to the large number of possible combinations of DMI and also their family relationships. Thus, we performed this scenario to answer to the following question: under a fixed-sequencing cost constraint, does limiting imputation and association analyses to large pedigrees improve power?
To call best-guess genotypes, we used two imputation calling thresholds (ICT), t1 and t2, proposed by the authors of GIGI [Cheung, et al. 2013]. We can call both alleles (i.e. a and b) if . Otherwise, we can call one allele (i.e. a) if where α/. signifies that one allele can be called at threshold t2. If we cannot call any alleles, the best-guess genotype is set to missing. We used three combinations of these thresholds’ values: C1 (t1=0.6, t2=0.8), C2 (t1=0.8, t2=0.9) and C3 (t1=0.9, t2=0.99). Increasing the values of t1 and t2 lead to an increase in the fraction of best-guess genotypes used for analysis that are highly certain.
Results
We performed association analysis using famSKAT and famWS in two type of data: 1) in the sequence data and 2) in the imputation data (pseudo-sequence data) based on d=20% of DMI. In the sequence data, we ran association analysis on all subjects and also on the 20% of the DMI used for imputation. In the imputation data, we ran association analysis using best-guess genotypes (“BestG”) and also allelic dosages (“AllelicD”).
Type 1 Error results
Table 1 shows the type 1 error rates of the association tests in the sequence and imputation data under the scenario IMP-1 estimated for different thresholds: 10−3 and 10−4. The scenario IMP-2 gave similar type 1 error rates (results not shown). Over all, the type 1 error is well controlled. We observed that famSKAT can be slightly conservative for small sample sizes (Table 1, 20% of DMI). To confirm this trend, we carried out association analysis on the imputation data using d=30%, 40% and 80% of the DMI. In the first two cases, the type 1 error rates were still slightly conservative for famSKAT. In the third case, the type 1 error rates were well controlled (Table S1 in supplementary material). This result is in good agreement with what has been shown in the literature [Lee, et al. 2012; Wu, et al. 2011]. Finally, our results show that the level of LD does not affect the type 1 error rates.
Table I.
Type I error of famSKAT and famWS: in the sequence data (for two proportions of dense markers individuals, d =20% and d =100%) and in the imputation data (using best-guess genotypes and allelic dosages).
| LowLD | MedLD | HighLD | |||||
|---|---|---|---|---|---|---|---|
| α | famSKAT | famWS | famSKAT | famWS | famSKAT | famWS | |
| Sequence data | |||||||
| d =20% | 10−3 | 0.0007 | 0.0010 | 0.0006 | 0.0010 | 0.0006 | 0.0012 |
| 10−4 | 0.00002 | 0.00012 | 0.00004 | 0.00012 | 0.00002 | 0.00009 | |
| d =100% | 10−3 | 0.0010 | 0.0011 | 0.0010 | 0.0011 | 0.0008 | 0.0011 |
| 10−4 | 0.00010 | 0.00012 | 0.00013 | 0.00006 | 0.00012 | 0.00012 | |
| Imputation data$ | |||||||
| Best-guess genotypes |
10−3 | 0.0010 | 0.0012 | 0.0010 | 0.0010 | 0.0009 | 0.0010 |
| 10−4 | 0.00007 | 0.00011 | 0.00008 | 0.00011 | 0.00010 | 0.00015 | |
| Allelic dosages | 10−3 | 0.0010 | 0.0012 | 0.0009 | 0.0011 | 0.0009 | 0.0010 |
| 10−4 | 0.00012 | 0.00013 | 0.00007 | 0.00013 | 0.00011 | 0.00010 | |
Imputation based on the previous d =20% of dense marker individuals
Power results
We present our power analysis results in three parts. In the first part, we focus on the sequence data, in which we compare the performance of famWS and famSKAT and evaluate the influence of three factors on these tests: the mix of protective and risk causal variants, the number of causal variants, and the LD pattern. In the second part, we show the advantage of the pseudo-sequencing strategy by comparing the power of the association analysis conducted on the sequence and imputation data. In the third part, we compare, in the imputation data, the relative performance of association analysis based on BestG versus AllelicD. All power results were estimated at a type 1 error of 10−3.
Part 1: Within sequence data
Mix of protective and risk causal variants
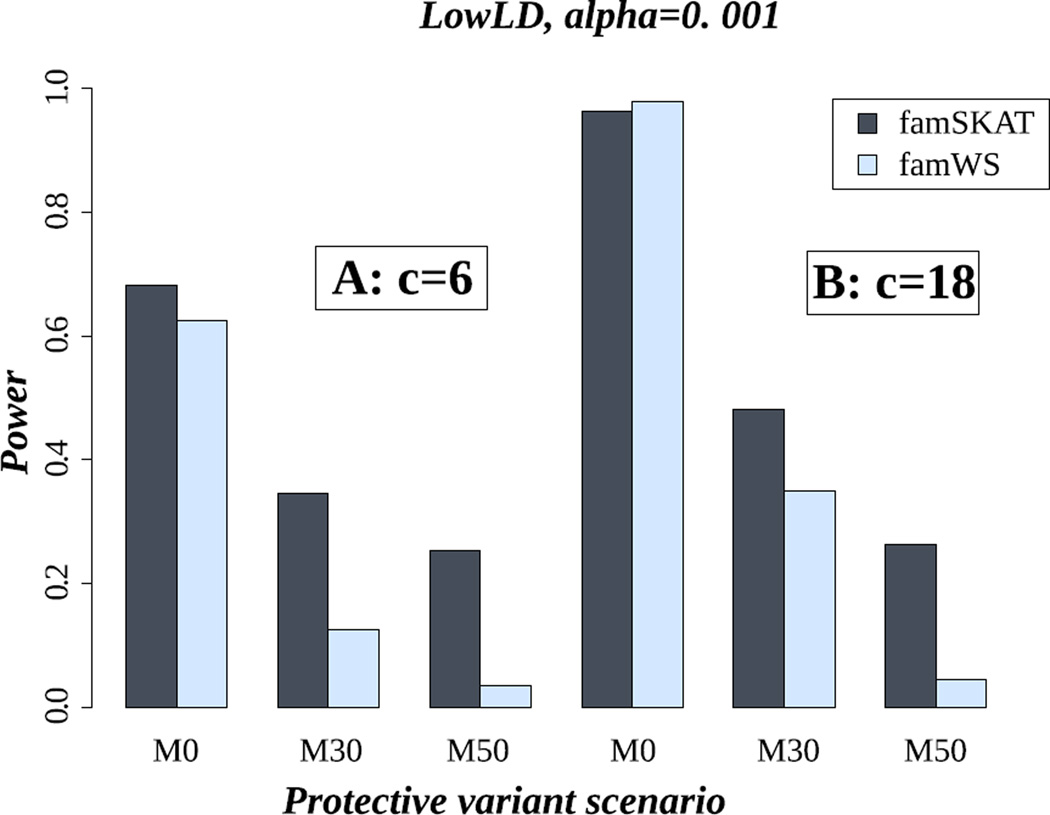
Figure 1 shows the power results of famSKAT and famWS, in the LowLD pattern and for the case of six (Figure 1.A) and 18 causal variants (Figure 1.B). In each part of this figure, we illustrate the results for the three settings of a mix of protective and risk causal variants: M0, M30 and M50 (0%, 30% and 50% protective variants). Our results show that when all causal variants have the same effect direction, the power of famSKAT and famWS is roughly similar (Figure 1.A or Figure 1.B). Nevertheless, famSKAT can be more powerful than famWS when the ratio c/p (#causal variants / #total rare variants) decreases (M0 in Figure 1.A, with c/p= 6/145 versus M0 in Figure 1.B, with c/p= 18/145). When causal variants are a mix of protective and risk variants, famSKAT is clearly more powerful than famWS. This is the advantage of famSKAT, which was designed as a way to deal with the heterogeneity of effect signs of causal variants. For the other LD patterns, the same trends were observed (e.g. MedLD and HighLD, Figure S6 and Figure S7, respectively, in supplementary material).
Figure 1.
Power of famSKAT and famWS in the LowLD pattern. c is the number of causal variants. A) c= 6; B) c= 18. M0, M30 and M50 represent the proportion of protective variants (0%, 30% and 50% respectively).
Number of causal variants
Our results show that the power of both famSKAT and famWS clearly increases with the number of causal variants (Figure 1.A versus 1.B), despite the same total additive variance in both cases. This result can be explained by the increase of the “c/p” ratio and is in good agreement with what has been shown in the literature [Chen, et al. 2013; Oualkacha, et al. 2013; Schaid, et al. 2013].
In the following sections, we will show power results for famSKAT only, because we observed the same trends in the results for famWS.
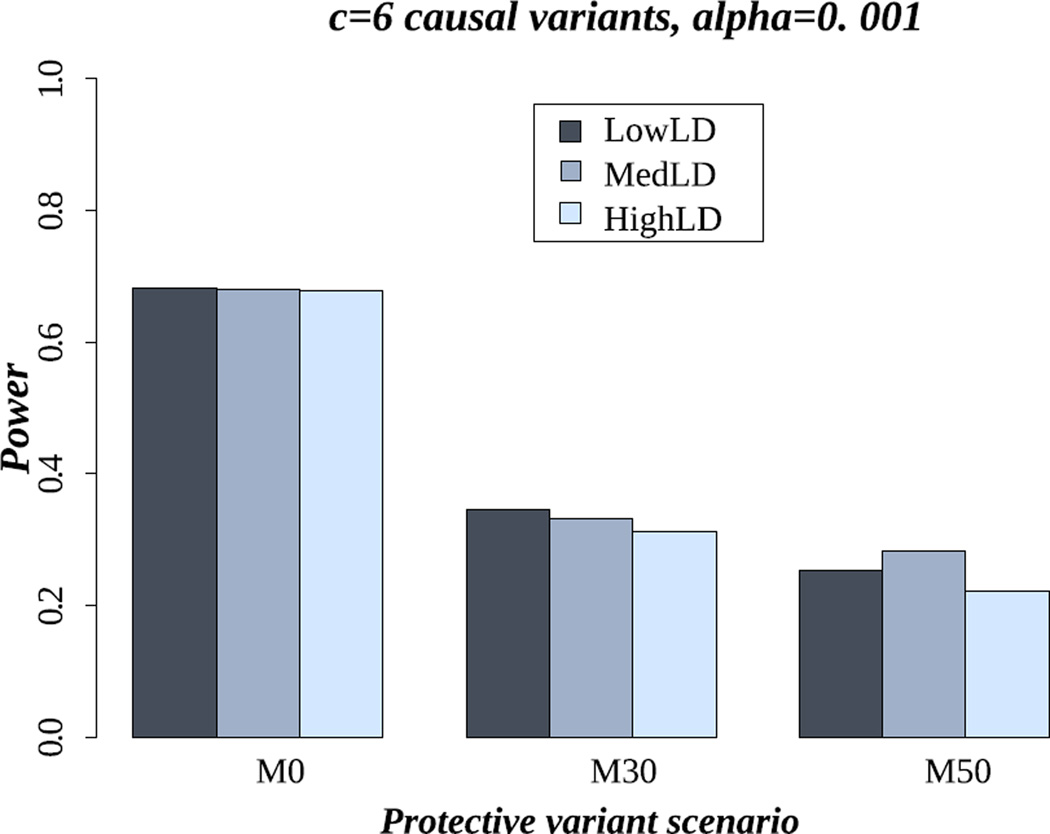
LD pattern
Figure 2 shows that the LD level did not affect power for famSKAT, for the three settings of mix of effects, LD patterns and six causal variants. We observed similar power for all LD patterns, even though we might expect higher power under the HighLD pattern. This was not observed due to the fact that the linkage disequilibrium is expected to be minimal between rare variants, and also between rare and common variants. If some of the risk variants are not genotyped or are filtered out during the quality control steps, a decrease of power might be observed as the LD is minimal and no variants will tag these missing risk variants. We observed the same results for the 18 causal variant setting (Figure S8 in supplementary material).
Figure 2.
Power of famSKAT in the scenario of six causal variants for LowLD, MedLD, and HighLD. M0, M30 and M50 represent the proportion of protective variants (0%, 30% and 50% respectively).
Part 2: Between sequence and imputation data
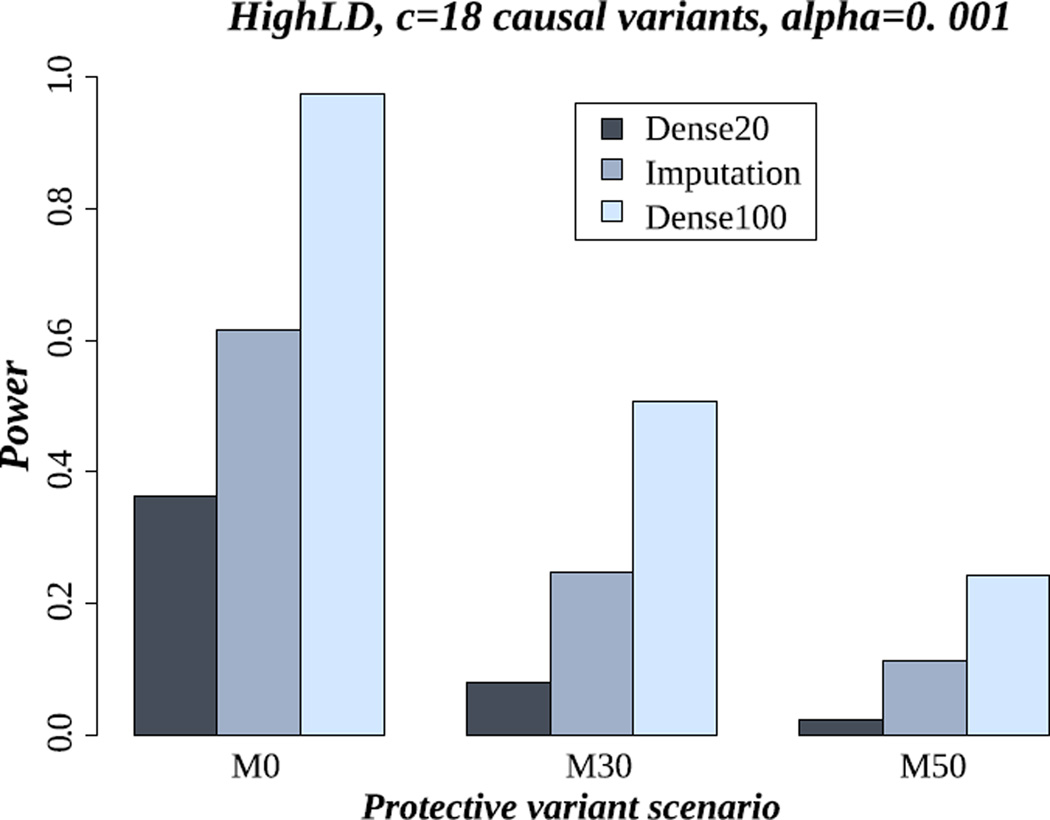
Here, we compare power results of association testing in the sequence data versus imputation data. We of course expect that the use of the sequence data in all subjects would give stronger power. However, we used these data as a reference for comparison with the imputation data. In the imputation data, the association test is based on AllelicD. Figure 3 shows the power results of famSKAT in: (1) all individuals having dense marker data (i.e. Dense100), (2) only a subset of 20% of individuals having dense marker data (i.e. Dense20), and (3) imputation along with the previous 20% of individuals used for imputation (i.e. Imputation). These power results were estimated in the scenario of the setting of HighLD and 18 causal variants. Not surprisingly, the highest power (i.e. 97%) is achieved from using the whole sequence data. More importantly, our results show a consistent gain of power obtained from using imputation data rather than using only Dense20: the power of famSKAT is 36% using only the Dense20 but 61% using the imputation data (almost doubling in power). The increase of power using the imputed data is even more obvious when six or 12 variants are causal: the power achieved from using the imputation data is more than twice that achieved from using only the Dense20 (Figure S9 and Figure S10 in supplementary material).
Figure 3.
Power of famSKAT in the scenario of 18 causal variants and the HighLD pattern. M0, M30 and M50 represent the proportion of protective variants (0%, 30% and 50% respectively). Dense100 is the analysis using all individuals sequenced. Dense20 is the analysis using 20% of individuals sequenced, from each pedigree. Imputation20 is the analysis in imputation data based on the previous sequenced individuals (20%). The association test is based on allelic dosages.
Part 3: Within imputation data: Allelic dosages versus Best-guess genotypes
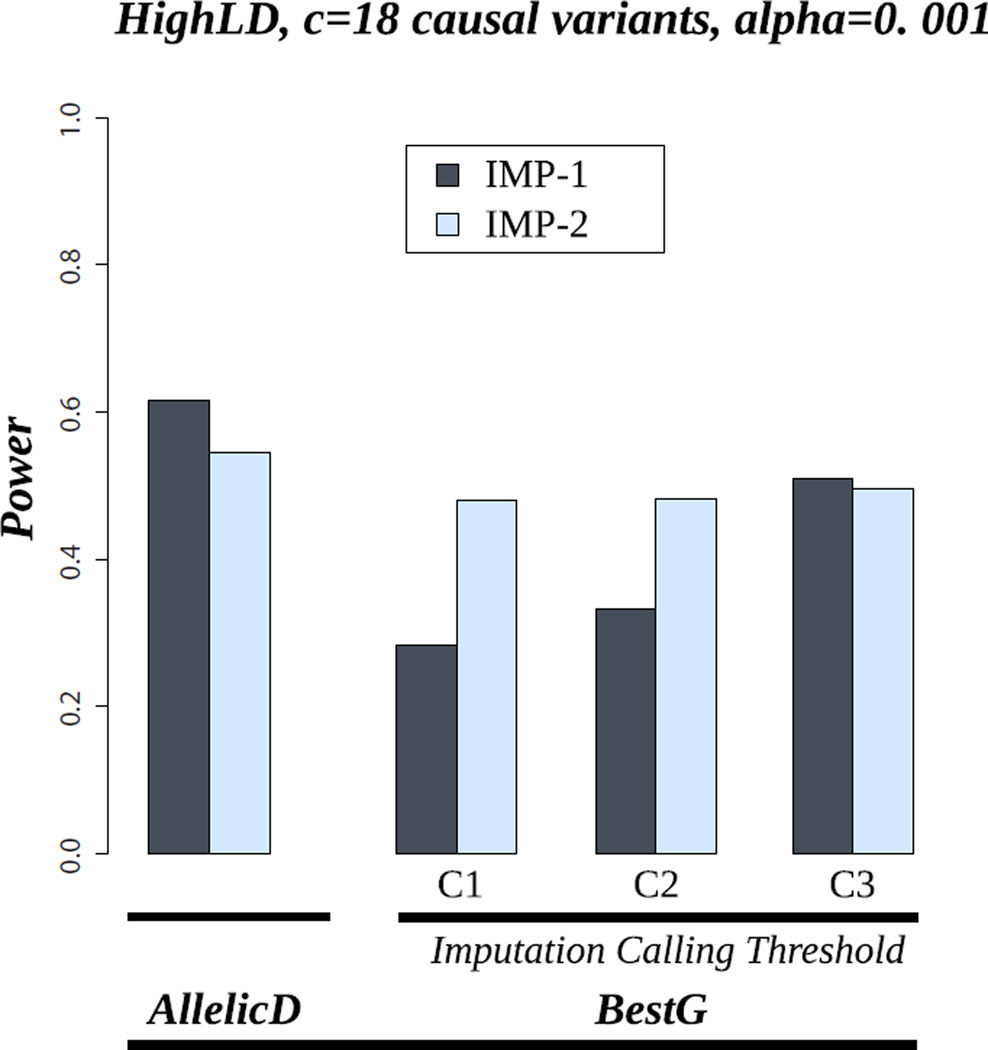
Figure 4 shows the power results for famSKAT in the imputation data, using AllelicD and BestG. These results are shown for the HighLD pattern and 18 causal variants with the same effect direction (M0). We show the results under the two imputation scenarios: IMP-1 and IMP-2. For BestG, we show the power results for the three ICT settings (C1, C2, and C3). Our results show that, for both IMP-1 and IMP-2, the power achieved from using AllelicD is higher than the power achieved from using BestG, for all ICTs we considered (power = 61% for AllelicD versus 28% for BestG using C1 to 51% using C3). In addition, the power achieved from using BestG increases with increasing ICTs. For example, the power using C1 is 28% and it increases to reach the 51% using C3. For IMP-2, the power achieved from using BestG for the different ICT combinations does not vary very much. This is because the BestG are almost certainly more accurate in bigger than smaller pedigrees (results not shown) so that rare alleles are called accurately even with stringent ICTs. Our results show that the power of IMP-1 is higher than that of IMP-2 in the case of AllelicD. The explanation of this result is that the greater amount of data in IMP-1 coupled with the use of AllelicD that captures the uncertainty of the imputation allows more effective use of the imputation data. In addition, this result might depend on pedigree structure. For instance, in a nuclear family with two parents and 10 offspring, sequencing three individuals (ideally two parents and one offspring) would allow accurate imputation in every other individual. Therefore, sequencing more than three individuals will not, almost certainly, add extra information. In this context, choosing only three DMIs from this pedigree and the remaining DMIs from other smaller pedigrees would give more information and hence be better. However, it seems quite possible that a carefully chosen set of individuals from the large pedigrees might yet be better. This shows the importance of the need for wise selection of DMIs. In the case of BestG, IMP-2 has higher power than IMP-1 for small ICTs (C1 and C2) and similar power for higher ICTs (C3). This suggests that for a specific sequencing budget, and hence a specific number of DMI, carrying out sequencing in only large pedigrees results in more power than carrying out sequencing in both small and large pedigrees for association tests based on BestG. Over all, our results suggest that if the test we aim to use can handle AllelicD or probability distributions, the best scenario is IMP-1, which uses all the data (small and large pedigrees together). Otherwise, the use of only large pedigrees appears to be more powerful with the use of stringent imputation calling thresholds (t1=0.9 and t2=0.99 gave the highest power for BestG).
Figure 4.
Power of famSKAT in the scenario of HighLD, 18 causal variants and M0 (the proportion of protective variants is 0%). AllelicD= Allelic dosages. BestG= Best-guess genotypes. IMP-1: imputation scenario using all individuals in all pedigrees. IMP-2: imputation scenario using all individuals in large pedigrees. C1: t1=0.6, t2=0.8; C2: t1=0.8, t2=0.9; C3: t1=0.9, t2=0.99.
Discussion
In the last few years, the “Common Disease-Multiple Rare Variants” hypothesis has received much attention, especially with the fast-moving next generation sequencing era. The advances of this technology have made possible the direct typing of rare variants rather than depending on LD in a panel of SNPs. The technology has been followed by a rapid development of statistical approaches, especially association tests, to efficiently analyze rare variants including burden/collapsing methods (e.g. WS) and kernel methods (e.g. SKAT). Although these tests were proposed initially for unrelated data (population-based designs), they have been modified to take into account relationships between individuals in family-based designs [Chen, et al. 2013; Oualkacha, et al. 2013; Schaid, et al. 2013; Schifano, et al. 2012], and so are well suited for discovery of novel rare variants involved in complex traits. However, the properties and the performance of these tests are not yet well established in large pedigree data. This motivated us to evaluate, here, the performance of two association tests, famWS and famSKAT, and to compare them in simulated sequence data on a collection of large pedigrees and for different scenarios (i.e. Number of causal variants, heterogeneity of the direction of their effects, and LD pattern). We showed that famSKAT is more powerful than famWS for most considered scenarios. Nevertheless, famWS has better power than famSKAT when the ratio of causal variants and the total number of variants in the region of interest is high. This result has been shown in other studies [Basu and Pan 2011; Wu, et al. 2011] and has motivated the development of SKAT-O in population-based designs [Lee, et al. 2012], which uses a linear combination of the burden test and SKAT to maximize the power.
In our study, we proposed the pseudo-sequencing strategy in family-based designs for large extended pedigrees. That is: sequence a small subset of pedigree members, genotype many of the remaining members on a set of sparse markers, and impute the untyped markers in the remaining subjects conditional on the sequenced subjects, to obtain what we call pseudo-sequence data. Our strategy was motivated by three facts: 1) sequencing costs are still relatively high, and hence budgets cannot afford sequencing of a large number of samples in order to achieve high power; 2) in large multigenerational pedigrees, one cannot sequence all subjects because of the absence of DNA or its low quantity and quality (especially for diseases with late onset age); and 3) the sequencing of all pedigrees’ members will result in redundant sequence information due to their familial correlation.
We used a recent family-based imputation method called GIGI [Cheung, et al. 2013]. This method is able to efficiently handle large pedigrees and accurately impute rare variants. We showed a considerable increase in power of association testing in pseudo-sequence data compared to the use of only the data of directly-sequenced subjects. The increase of power is observed here despite a random selection of individuals with such dense marker data. Although this selection of individuals to be sequenced within each pedigree is overly simple, the issue of optimal subject selection is beyond the scope of our paper and will need evaluation in further design studies. Also, a more ideal selection of individuals will not change our main results about the general gain of power obtained using pseudo-sequence data over use of only the data of directly-sequenced subjects. We expect that a careful selection of such dense marker individuals will only increase the accuracy of imputation, thus optimizing the information in each pedigree, and hence will further increase the power of detecting association with rare variants. Many programs have been proposed to pick individuals for sequencing, such as ExomePicks (http://genome.sph.umich.edu/wiki/ExomePicks) and PRIMUS (http://sourceforge.net/projects/primus-beta/). However, the effect of these different algorithms on the power of association tests has also not yet been evaluated and needs to be quantified in future studies before committing to a particular approach. Note also that as in other studies based on imputed marker data, any positive results from an initial analysis of imputed data should be followed up with direct sequencing/genotyping for verification.
Imputation methods estimate the probability distribution of possible genotypes at untyped markers conditional on the observed data (i.e. dense and sparse markers data). Imputation software for both unrelated subjects (e.g. MACH [Li, et al. 2006], IMPUTE [Marchini, et al. 2007], BEAGLE [Browning and Browning 2009]) and related subjects (e.g. GIGI [Cheung, et al. 2013]) use the probability distribution to estimate allelic dosages, and also use pre-specified thresholds to estimate best-guess genotypes. In our study, we compared the performance of the association tests based on allelic dosages and best-guess genotypes. Our results showed that the power of association achieved from using allelic dosages is higher than the power achieved from using best-guess genotypes. In addition, using stringent imputation calling thresholds resulted in higher power for best-guess genotypes. Moreover, in our simulated data, we showed that the use of the most stringent calling thresholds yielded the highest power, even though different values might be evaluated in further studies. We showed also that if we have a collection of small and large pedigrees, and we can sequence a total of N subjects, focusing only on large pedigrees provides more power only in the case of best-guess genotypes. This suggests that if the association test one aims to use can handle allelic dosages, there is an advantage to use of allelic dosages from imputation carried out on all available pedigrees (both small and large), to obtain higher power. Nonetheless, considering large pedigrees only, or both large and small pedigrees, depends on the pedigree structures and sizes. Focusing on large pedigrees only could be a better design with a carefully selected DMI, but we also caution the that detailed study design will also always need to be a function of what kind of pedigrees are actually available.
Supplementary Material
Power of famSKAT in the scenario of 12 causal variants and the HighLD pattern. M0, M30 and M50 represent the proportion of protective variants (0%, 30% and 50% respectively). Dense100 is the analysis using all individuals sequenced. Dense20 is the analysis using 20% of individuals sequenced, from each pedigree. Imputation20 is the analysis in imputation data based on the previous sequenced individuals (20%). The association test is based on allelic dosages.
Power of famSKAT in the scenario of six causal variants and the HighLD pattern. M0, M30 and M50 represent the proportion of protective variants (0%, 30% and 50% respectively). Dense100 is the analysis using all individuals sequenced. Dense20 is the analysis using 20% of individuals sequenced, from each pedigree. Imputation20 is the analysis in imputation data based on the previous sequenced individuals (20%). The association test is based on allelic dosages.
The MAF distribution of rare variants in the selected gene, estimated in the 1000 Genomes Project CEU data, Release August 2010.
LD plot for LowLD pattern. Top: D’ values of LD. Bottom: r2 values of LD.
LD plot for MedLD pattern. Top: D’ values of LD. Bottom: r2 values of LD.
LD plot for HighLD pattern. Top: D’ values of LD. Bottom: r2 values of LD.
LD plot in the real data of the 1000 Genomes Project CEU haplotypes. Top: D’ values of LD. Bottom: r2 values of LD.
Power of famSKAT and famWS in the MedLD pattern. c is the number of causal variants. A) c= 6; B) c= 18. M0, M30 and M50 represent the proportion of protective variants (0%, 30% and 50% respectively).
Power of famSKAT and famWS in the HighLD pattern. c is the number of causal variants. A) c= 6; B) c= 18. M0, M30 and M50 represent the proportion of protective variants (0%, 30% and 50% respectively).
Power of famSKAT in the scenario of 18 causal variants for LowLD, MedLD, and HighLD. M0, M30 and M50 represent the proportion of protective variants (0%, 30% and 50% respectively).
Acknowledgements
Research reported in this paper was supported by National Institutes of Health award numbers P50 AG005136, R01 AG039700, R01 HD054563, R37 GM046255, R01 MH092367, and R01 MH094293. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
References
- Abecasis GR, Altshuler D, Auton A, Brooks LD, Durbin RM, Gibbs RA, Hurles ME, McVean GA. A map of human genome variation from population-scale sequencing. Nature. 2010;467(7319):1061–1073. doi: 10.1038/nature09534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Basu S, Pan W. Comparison of statistical tests for disease association with rare variants. Genet Epidemiol. 2011;35(7):606–619. doi: 10.1002/gepi.20609. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bodmer W, Bonilla C. Common and rare variants in multifactorial susceptibility to common diseases. Nat Genet. 2008;40(6):695–701. doi: 10.1038/ng.f.136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Browning BL, Browning SR. A unified approach to genotype imputation and haplotypephase inference for large data sets of trios and unrelated individuals. Am J Hum Genet. 2009;84(2):210–223. doi: 10.1016/j.ajhg.2009.01.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burdick JT, Chen WM, Abecasis GR, Cheung VG. In silico method for inferring genotypes in pedigrees. Nat Genet. 2006;38(9):1002–1004. doi: 10.1038/ng1863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen H, Meigs JB, Dupuis J. Sequence kernel association test for quantitative traits in family samples. Genet Epidemiol. 2013;37(2):196–204. doi: 10.1002/gepi.21703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheung CY, Thompson EA, Wijsman EM. GIGI: an approach to effective imputation of dense genotypes on large pedigrees. Am J Hum Genet. 2013;92(4):504–516. doi: 10.1016/j.ajhg.2013.02.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choi Y, Wijsman EM, Weir BS. Case-control association testing in the presence of unknown relationships. Genet Epidemiol. 2009;33(8):668–678. doi: 10.1002/gepi.20418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen JC, Kiss RS, Pertsemlidis A, Marcel YL, McPherson R, Hobbs HH. Multiple rare alleles contribute to low plasma levels of HDL cholesterol. Science. 2004;305(5685):869–872. doi: 10.1126/science.1099870. [DOI] [PubMed] [Google Scholar]
- Cohen JC, Pertsemlidis A, Fahmi S, Esmail S, Vega GL, Grundy SM, Hobbs HH. Multiple rare variants in NPC1L1 associated with reduced sterol absorption and plasma low-density lipoprotein levels. Proc Natl Acad Sci U S A. 2006;103(6):1810–1815. doi: 10.1073/pnas.0508483103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daetwyler HD, Wiggans GR, Hayes BJ, Woolliams JA, Goddard ME. Imputation of missing genotypes from sparse to high density using long-range phasing. Genetics. 2011;189(1):317–327. doi: 10.1534/genetics.111.128082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evangelou E, Trikalinos TA, Salanti G, Ioannidis JP. Family-based versus unrelated case-control designs for genetic associations. PLoS Genet. 2006;2(8):e123. doi: 10.1371/journal.pgen.0020123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frazer KA, Ballinger DG, Cox DR, Hinds DA, Stuve LL, Gibbs RA, Belmont JW, Boudreau A, Hardenbol P, Leal SM, et al. A second generation human haplotype map of over 3.1 million SNPs. Nature. 2007;449(7164):851–861. doi: 10.1038/nature06258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hinrichs AL, Suarez BK. Incorporating linkage information into a common disease/rare variant framework. Genet Epidemiol. 2011;35(Suppl 1):S74–S79. doi: 10.1002/gepi.20654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iyengar SK, Elston RC. The genetic basis of complex traits: rare variants or "common gene, common disease"? Methods Mol Biol. 2007;376:71–84. doi: 10.1007/978-1-59745-389-9_6. [DOI] [PubMed] [Google Scholar]
- Kong A, Masson G, Frigge ML, Gylfason A, Zusmanovich P, Thorleifsson G, Olason PI, Ingason A, Steinberg S, Rafnar T, et al. Detection of sharing by descent, long-range phasing and haplotype imputation. Nat Genet. 2008;40(9):1068–1075. doi: 10.1038/ng.216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee S, Emond MJ, Bamshad MJ, Barnes KC, Rieder MJ, Nickerson DA, Christiani DC, Wurfel MM, Lin X. Optimal unified approach for rare-variant association testing with application to small-sample case-control whole-exome sequencing studies. Am J Hum Genet. 2012;91(2):224–237. doi: 10.1016/j.ajhg.2012.06.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li B, Leal SM. Methods for detecting associations with rare variants for common diseases: application to analysis of sequence data. Am J Hum Genet. 2008;83(3):311–321. doi: 10.1016/j.ajhg.2008.06.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Y, Ding J, Abecasis G. Mach 1.0: rapid haplotype reconstruction and missing genotype inference. Am J Hum Genet. 2006;79:S2290. [Google Scholar]
- Louis T, Carvalho B, Fallin M, Irizarry R, Li Q, Ruczinski I. Association Tests that Accommodate Genotyping Errors. In: Bernardo JM, Bayarri MJ, Berger JO, Dawid AP, Heckerman D, Smith AFM, West M, editors. Bayesian Statistics. Vol. 9. Oxford, UK: Oxford University Press; 2010. pp. 393–420. [Google Scholar]
- Madsen BE, Browning SR. A groupwise association test for rare mutations using a weighted sum statistic. PLoS Genet. 2009;5(2):e1000384. doi: 10.1371/journal.pgen.1000384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manolio TA, Collins FS, Cox NJ, Goldstein DB, Hindorff LA, Hunter DJ, McCarthy MI, Ramos EM, Cardon LR, Chakravarti A, et al. Finding the missing heritability of complex diseases. Nature. 2009;461(7265):747–753. doi: 10.1038/nature08494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marchini J, Howie B, Myers S, McVean G, Donnelly P. A new multipoint method for genome-wide association studies by imputation of genotypes. Nat Genet. 2007;39(7):906–913. doi: 10.1038/ng2088. [DOI] [PubMed] [Google Scholar]
- Montana G. HapSim: a simulation tool for generating haplotype data with pre-specified allele frequencies and LD coefficients. Bioinformatics. 2005;21(23):4309–4311. doi: 10.1093/bioinformatics/bti689. [DOI] [PubMed] [Google Scholar]
- Morgenthaler S, Thilly WG. A strategy to discover genes that carry multi-allelic or mono-allelic risk for common diseases: a cohort allelic sums test (CAST) Mutat Res. 2007;615(1-2):28–56. doi: 10.1016/j.mrfmmm.2006.09.003. [DOI] [PubMed] [Google Scholar]
- Morris AP, Zeggini E. An evaluation of statistical approaches to rare variant analysis in genetic association studies. Genet Epidemiol. 2010;34(2):188–193. doi: 10.1002/gepi.20450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nejentsev S, Walker N, Riches D, Egholm M, Todd JA. Rare variants of IFIH1, a gene implicated in antiviral responses, protect against type 1 diabetes. Science. 2009;324(5925):387–389. doi: 10.1126/science.1167728. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oualkacha K, Dastani Z, Li R, Cingolani PE, Spector TD, Hammond CJ, Richards JB, Ciampi A, Greenwood CM. Adjusted sequence kernel association test for rare variants controlling for cryptic and family relatedness. Genet Epidemiol. 2013;37(4):366–376. doi: 10.1002/gepi.21725. [DOI] [PubMed] [Google Scholar]
- Price AL, Kryukov GV, de Bakker PI, Purcell SM, Staples J, Wei LJ, Sunyaev SR. Pooled association tests for rare variants in exon-resequencing studies. Am J Hum Genet. 2010;86(6):832–838. doi: 10.1016/j.ajhg.2010.04.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saad M, Pierre AS, Bohossian N, Mace M, Martinez M. Comparative study of statistical methods for detecting association with rare variants in exome-resequencing data. BMC Proc. 2011;5(Suppl 9):S33. doi: 10.1186/1753-6561-5-S9-S33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schaid DJ, McDonnell SK, Sinnwell JP, Thibodeau SN. Multiple genetic variant association testing by collapsing and kernel methods with pedigree or population structured data. Genet Epidemiol. 2013;37(5):409–418. doi: 10.1002/gepi.21727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schifano ED, Epstein MP, Bielak LF, Jhun MA, Kardia SL, Peyser PA, Lin X. SNP Set Association Analysis for Familial Data. Genet Epidemiol. 2012 doi: 10.1002/gepi.21676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taub MA, Schwender H, Beaty TH, Louis TA, Ruczinski I. Incorporating genotype uncertainties into the genotypic TDT for main effects and gene-environment interactions. Genet Epidemiol. 2012;36(3):225–234. doi: 10.1002/gepi.21615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson E. The structure of genetic linkage data: from LIPED to 1M SNPs. Hum Hered. 2011;71(2):86–96. doi: 10.1159/000313555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wijsman EM. The role of large pedigrees in an era of high-throughput sequencing. Hum Genet. 2012;131(10):1555–1563. doi: 10.1007/s00439-012-1190-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu MC, Lee S, Cai T, Li Y, Boehnke M, Lin X. Rare-variant association testing for sequencing data with the sequence kernel association test. Am J Hum Genet. 2011;89(1):82–93. doi: 10.1016/j.ajhg.2011.05.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zawistowski M, Gopalakrishnan S, Ding J, Li Y, Grimm S, Zollner S. Extending rare-variant testing strategies: analysis of noncoding sequence and imputed genotypes. Am J Hum Genet. 2010;87(5):604–617. doi: 10.1016/j.ajhg.2010.10.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng J, Li Y, Abecasis GR, Scheet P. A comparison of approaches to account for uncertainty in analysis of imputed genotypes. Genet Epidemiol. 2011;35(2):102–110. doi: 10.1002/gepi.20552. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Power of famSKAT in the scenario of 12 causal variants and the HighLD pattern. M0, M30 and M50 represent the proportion of protective variants (0%, 30% and 50% respectively). Dense100 is the analysis using all individuals sequenced. Dense20 is the analysis using 20% of individuals sequenced, from each pedigree. Imputation20 is the analysis in imputation data based on the previous sequenced individuals (20%). The association test is based on allelic dosages.
Power of famSKAT in the scenario of six causal variants and the HighLD pattern. M0, M30 and M50 represent the proportion of protective variants (0%, 30% and 50% respectively). Dense100 is the analysis using all individuals sequenced. Dense20 is the analysis using 20% of individuals sequenced, from each pedigree. Imputation20 is the analysis in imputation data based on the previous sequenced individuals (20%). The association test is based on allelic dosages.
The MAF distribution of rare variants in the selected gene, estimated in the 1000 Genomes Project CEU data, Release August 2010.
LD plot for LowLD pattern. Top: D’ values of LD. Bottom: r2 values of LD.
LD plot for MedLD pattern. Top: D’ values of LD. Bottom: r2 values of LD.
LD plot for HighLD pattern. Top: D’ values of LD. Bottom: r2 values of LD.
LD plot in the real data of the 1000 Genomes Project CEU haplotypes. Top: D’ values of LD. Bottom: r2 values of LD.
Power of famSKAT and famWS in the MedLD pattern. c is the number of causal variants. A) c= 6; B) c= 18. M0, M30 and M50 represent the proportion of protective variants (0%, 30% and 50% respectively).
Power of famSKAT and famWS in the HighLD pattern. c is the number of causal variants. A) c= 6; B) c= 18. M0, M30 and M50 represent the proportion of protective variants (0%, 30% and 50% respectively).
Power of famSKAT in the scenario of 18 causal variants for LowLD, MedLD, and HighLD. M0, M30 and M50 represent the proportion of protective variants (0%, 30% and 50% respectively).