Adaptive Control with State-Dependent Modeling of Patient Impairment for Robotic Movement Therapy

Abstract

This paper presents an adaptive control approach for robotic movement therapy that learns a state-dependent model of patient impairment. Unlike previous work, this approach uses an unstructured inertial model that depends on both the position and direction of the desired motion in the robot’s workspace. This method learns a patient impairment model that accounts for movement specific disability in neuromuscular output (such as flexion vs. extension and slow vs. dynamic tasks). Combined with assist-as-needed force decay, this approach may promote further patient engagement and participation. Using the robotic therapy device, FINGER (Finger Individuating Grasp Exercise Robot), several experiments are presented to demonstrate the ability of the adaptive control to learn state-dependent abilities.

I. Introduction

The use of robotic devices for post-stroke movement therapy continues to be an important and growing research area. Rehabilitation robots have previously demonstrated the ability to administer therapy in a consistent and prescribed manner, with therapeutic efficacy equal to or marginally exceeding conventional therapy (for reviews see [1],[2]). However, exactly how these devices should interact with patients during movement therapy remains an open and active research area. The goal is to create protocols and algorithms by which robotic therapy may maximize the functional recovery experienced by a patient.

Previous works suggest that too much assistance may limit or reverse the effects of therapy. For example, [3], [4] demonstrated that patients will reduce their effort when given the opportunity to do so without drastically affecting the desired motion. That is, if the robot is able to “take over” the movement, patients are willing to allow it to do so. And because patient effort is known to promote motor-plasticity during therapy [5], [6], it is important for robotic devices to only assist as much as necessary for a prescribed therapy motion.

To promote patient effort and engagement, assist-as-needed control strategies aim to restrain the power of a rehabilitation robot in a way that maximizes patient effort while simultaneously completing therapy movements. As noted in [7], a wide-variety of implementation approaches for assist-as-needed control have been investigated, including both static (examples include [8]–[11]) and adaptive (examples include [4], [12], [13]). Unlike static approaches, adaptive strategies change control parameters during and/or between movement therapies in order to modulate assistance based on the patient’s ability.

In previous work by the authors [4], the adaptive assist-as-needed approach was implemented using passivity-based adaptive control [14]. This implementation included an unstructured adaptive model of patient abilities and a force decay term that limited the robotic assistance needed to complete the prescribed movements. The resulting controller demonstrated the ability to modulate patient effort while keeping tracking errors small.

The need for an unstructured model stems from the nature of disability after stroke; each person who has suffered a stroke has unique neuro-muscular impairment. Because passivity-based adaptive control assumes that the system parameters are constants and correlated directly to the geometry and kinematics of the robot, [4] implemented an unstructured model using radial basis functions to adapt to patient’s neuromuscular abilities. This use of radial basis functions allows the controller to create a model of each individual patient’s impairment as a function of position. While other unstructured modeling approaches are possible, radial basis functions are linear in term of their magnitudes, and may thus be incorporated into the passivity-based adaptive control structure.

The work presented in [4] included two significant shortcomings. First, the adaptive model only represented patient force output and excluded inertial and viscous forces and is thus unable to properly assist with dynamic movements requiring higher velocities and specific timing. Increasing the rate of adaptation can improve the dynamic response, but at the expense of decreasing the compliance of the robot. This problem is noted in [15], which also presents a potential solution based on separate models for each target motion.

The second noted problem with the approach in [4] is that the unstructured model assumed patient ability was only a function of position and not a function of velocity or movement direction. In fact, the ability to model patient impairment by movement direction may be significant for rehabilitation. In the hand, for example, it has been shown that stroke survivors with hand impairment often have unequal impairment in metacarpophalangeal (MCP) joint movement. Often patients exhibit a deficiency in extension that is significantly greater than in flexion [16]–[19]. This phenomenon appears to be caused by an inherent weakness in extension activation signal [17] or inappropriate muscle co-activation [16] rather than passive mechanisms such as stiffness and spasticity. Thus, it is important to model directional impairment for providing movement assistance to stroke survivors.

In this paper we present an unstructured model for adaptively learning patient abilities that includes both inertial terms and state dependence (position and direction). By modeling patient impairment with better state-dependent resolution, the robot will be able to further minimize assistance to the minimal amount needed. In the following section, we describe the control algorithm and its implementation on a robotic device developed for finger rehabilitation. We then present experimental results that demonstrate the ability of the presented approach to learn a direction specific inertial model in order to assist with dynamic movements with unbalanced, directionally dependent force disturbances.

II. Methods

A. Robotic Therapy Device

The robotic therapy device, FINGER (Finger Individuating Grasp Exercise Robot) was used for experimental validation of the presented adaptive control approach. FINGER consists of two stacked, planar 8-bar mechanisms each with a single degree-of-freedom (DOF) [18,19]. FINGER is capable of guiding the index and middle fingers individually through a naturalistic grasping motion that was based on motion capture of unimpaired subjects. Range of motion is limited with hard stops and the grasping mechanisms incorporate several easily adjustable components to accommodate physical differences between patients.

Several characteristics of FINGER make it an excellent test platform for the control strategies outlined in this paper. First, the combination of low-friction bearings, precision machining, lightweight components, and high speed linear actuators produce a high bandwidth (about 8Hz at −3dB) of direct force control. Furthermore, because the linear actuators lack any gearing or other high-friction components, FINGER is highly back-drivable.

B. Passivity Based Adaptive Control

One successful model-based adaptive controls system was implemented by [4] and expanded by [15]. This approach follows [14], which defines the adaptive control as

$${\mathbf{F}}_r=\mathbf{Y}\widehat{\mathbf{a}}-{\mathbf{K}}_P(\mathbf{x}-{\mathbf{x}}_d)-{\mathbf{K}}_D(\dot{\mathbf{x}}-{\dot{\mathbf{x}}}_d)=\mathbf{Y}\widehat{\mathbf{a}}-{\mathbf{K}}_P(\tilde{\mathbf{x}})-{\mathbf{K}}_D(\dot{\tilde{\mathbf{x}}}),$$ (1)

where Fr is the assistive force applied by the robot, x is an n × 1 vector of generalized coordinates of the robot (subscript d denotes desired), Y is an n × m matrix of functions of known parameters and system dynamics (x, ẋ, x_d, ẋ_d, ẍ_d), a â is an m × 1 estimate of system parameters a, and K_P and K_D are symmetric, positive-definite gain matrices. In (1), the terms −K_Px̃ and $-{\mathbf{K}}_D\dot{\tilde{\mathbf{x}}}$ are the proportional and derivative feedback portions of the control and Yâ is a model of system dynamics. In this application, Yâ is used to model state-dependent neuromuscular impairment. The regressor matrix, Y is a sparsely populated, quasi-diagonal matrix with the form of

$${\mathbf{Y}}^{n\times m}=\left[\begin{array}{ccc}{\mathbf{g}}^T& \cdots & 0\\ ⋮& \ddots & 0\\ 0& 0& {\mathbf{g}}^T\end{array}\right],$$ (2)

and g is a p × 1 vector (m = np) of radial basis functions (RBFs) that spans the workspace of the robot with elements defined by

$$g_n=\text{exp}(-{\parallel \mathbf{x}-{\mathbf{\mu }}_{\mathbf{n}}\parallel }^2/{\sigma }^2),$$ (3)

where the center of the n^th radial basis function is μ_n. The standard deviation, σ, specifies the width of the RBFs and may be selected to allow proper overlap. Adaptation of the amplitudes of the RBFs is achieved by

$$\dot{\widehat{\mathbf{a}}}=-(1/\tau ){\mathbf{Y}}^T{(\mathbf{Y}{\mathbf{Y}}^T)}^{-1}\mathbf{Y}\widehat{\mathbf{a}}-{\mathbf{\Gamma }}^{-1}{\mathbf{Y}}^T\mathbf{s},$$ (4)

where τ is the decay time constant and Γ is a diagonal, positive-definite gain matrix. The first term governs the “assistance-as-needed”; it exponentially decays the weights in order to address the tendency of patients to allow a stiff controller to take over [4]. The second term in (4) updates the parameter estimates according to the error defined by the sliding surface, s, which is defined as

$$\mathbf{s}=\dot{\tilde{\mathbf{x}}}+\mathbf{\Lambda }\tilde{\mathbf{x}},$$ (5)

where Λ is a diagonal constant gain matrix that specifies the ratio of position error to velocity error. The adaptive controller described above was modified in [15] by splitting up the desired trajectory into multiple segments and utilizing a separate â vector for each, thus reducing the need for fast adaptation which increases controller stiffness. The adaptive control approach presented in this paper also improves controller compliance, but unlike [14], it does so with a continuous workspace model of patient impairment, that is state-dependent. This impairment model represents the inability of a patient to generate forces during movement as a function of both movement position and direction.

C. Inertial Adaptive Control Model

In [4] the regressor matrix Y does not include viscous or inertial components. This limits complexity, but it also restricts the types of dynamic movements that can be effectively assisted. The following describes the implementation of the inertial and viscous components. Since physical validation will be completed on FINGER, the model can be reduced to a single DOF. This is for experimental validation and is not a limitation of the approach, which can be expanded for multi-DOF robotic devices. For the single DOF robotic device FINGER, we define an impairment model according to

$$\mathbf{Y}=[g_1\dot{w}\cdots g_n\dot{w}\dot{x}x],$$ (6)

where g_1−n are n RBFs distributed from full extension to full flexion of the finger, and w = ẋ_d − Λx̃. By using radial basis functions, the system mass is not required to be constant across the range of motion, and more closely match the inertial ability (as mass) of the patient as a function of position. The corresponding system parameter vector is

$$\widehat{\mathbf{a}}={[{\gamma }_1\cdots {\gamma }_n{\mathrm{b}}_{\mathrm{\gamma }}{\mathrm{k}}_{\mathrm{\gamma }}]}^T,$$ (7)

where γ_1−n are the amplitudes of the respective radial basis functions and k_γ and b_γ are adapted stiffness and damping, respectively.

D. State-Dependent Adaptive Control

Many stroke survivors exhibit significant weakness in one direction (typically extension) over the other [16]–[19]. Due to this phenomenon, (6) is modified to account for possible variation in patient impairment between flexion and extension. To achieve this, a separate parameter vector is used for flexion and extension, such that (6) becomes

$$\mathbf{Y}={\left[\begin{array}{c}(.5\text{tanh}80{\dot{x}}_d+.5)\mathbf{y}\\ (-.5\text{tanh}80{\dot{x}}_d+.5)\mathbf{y}\end{array}\right]}^T$$ (8)

where

$$\mathbf{y}={[g_1\dot{w}\cdots g_n\dot{w}\dot{x}x]}^T.$$ (9)

The system parameter vector was expanded from (7) to

$$\widehat{\mathbf{a}}={[{\alpha }_1\cdots {\alpha }_n{\mathrm{b}}_{\mathrm{\alpha }}{\mathrm{k}}_{\mathrm{\alpha }}{\beta }_1\cdots {\beta }_n{\mathrm{b}}_{\mathrm{\beta }}{\mathrm{k}}_{\mathrm{\beta }}]}^T$$ (10)

where α_n represents the amplitude of the n^th radial basis function in flexion and β_n represents the corresponding amplitude in extension. Combining the amplitudes with the RBFs creates distribution models of the effective “mass” in flexion and extension that describes the inability of the subject to create forces necessary to accelerate their fingers according to a desired trajectory. These “mass” distribution models are a function of position and defined for a single mass distribution model, m, a flexion specific model, m_F, and an extension specific model, m_E, according to:

$$m=[{\gamma }_1\cdots {\gamma }_n]{[g_1\cdots g_n]}^T{m}_F=[{\alpha }_1\cdots {\alpha }_n]{[g_1\cdots g_n]}^T{m}_E=[{\beta }_1\cdots {\beta }_n]{[g_1\cdots g_n]}^T.$$ (11)

The hyperbolic tangent functions included in (8) activate either the first or second set of radial basis functions based on the direction of the desired velocity. They also remove the discontinuity that occurs as the desired velocity crosses zero. Thus, in the small region around zero (approximately ±.02 m/s) both the flexion and extension sets of parameters will be proportionally updated and will both influence output. This method could be expanded to a spatial robot by using two sets of radial basis functions for each Euclidean direction.

E. Experimental Protocol

Four experiments were conducted to validate the presented adaptive controller. For each experiment, four unimpaired subjects, securely connected to FINGER (see Fig. 1), were guided by a simple visual interface that displayed two markers on a radial path (see Fig. 2). One marker corresponded to the position of the user’s finger and the other marker represented the desired location. The participants were instructed to follow the desired marker which followed a minimum jerk trajectory between two points pseudo-randomly distributed between the bounds of FINGER’s functional workspace. This point-to-point trajectory operated at 1.5 Hz, regardless of movement size. Each of the three experiments was repeated with adaptation based on a direction specific (using the model defined by (8), (9), and (10)) and a single mass distribution (using the model defined by (6) and (7)) model.

Fig. 1.

Finger INdividuating Grasp Exercise Robot (FINGER) viewed from the top. FINGER can individually guide the index and pointer fingers through a naturalistic grasping motion.

Fig. 2.

The visual interface during experiments. The blue marker shows the desired angle/position and the yellow marker shows the actual angle/position.

These four experiments were designed to investigate the ability of the proposed approach to adapt to directionally dependent patient impairment. In order to simulate impairment, directional viscous force fields were superimposed with the robot.

In the first experiment, only the inertia and friction of the device (both relatively low) impeded the performance of the participants. For the second procedure, the desired trajectory and visual feedback were unchanged. However, a significant viscous field was superimposed in the flexion direction. The experiment was then repeated with the viscous field superimposed in the extension direction. This impeded the ability of the subject to perform the flexion or extension task.

The third experiment follows the same procedure as the second with the inclusion of the forgetting term with a force decay rate of τ = 1. The fourth experiment followed the same procedure as the second, except that the artificial viscous field was removed suddenly after 40 seconds. All four experiments are summarized in Table I.

Table I.

Summary of the experiments.

Test	Task	Controller	τ	Force Field
1	Min. jerk tracking at 1.5 Hz	Both with and without direction specific adaptation.	∞	None
2	Min. jerk tracking at 1.5 Hz	Both with and without direction specific adaptation.	∞	Viscous field applied opposing either flexion or extension.
3	Min. jerk tracking at 1.5 Hz	Both with and without direction specific adaptation.	1	Viscous field applied opposing either flexion or extension.
4	Min. jerk tracking at 1.5 Hz	Both with and without direction specific adaptation.	∞	Viscous field applied opposing flexion or extension for the first 40 seconds.

During testing the controller gains and adaptation parameters were set to K_P = 1.15, K_D = 0.575, Γ = 0.02, and Λ = 0.5. Furthermore, n =15 RBFs were evenly distributed with σ = 0.007 m². The magnitude of the superimposed viscous field was $C=1\frac{N·s}{m}$ in all pertinent experiments.

III. Results

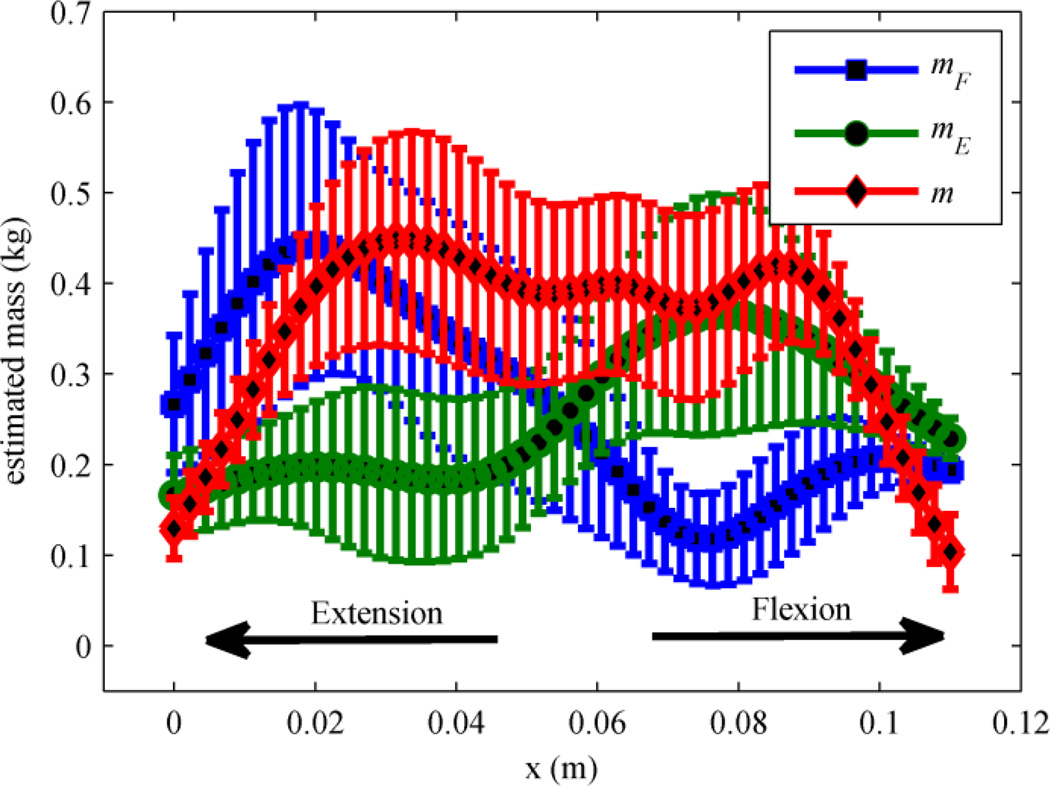
The results from the first experiment shown in Fig. 3 illustrate how RBF coefficients adapt with the either the direction specific or a single mass distribution models. The figure shows the four subject average of the converged mass models for both flexion, m_F, and extension, m_E, using the direction specific model for adaptation. It also shows the converged mass model, m, when adaptation was based on a single mass distribution. In all cases, adaptation is limited near both ends of the workspace (full flexion and full extension) because the desired trajectories lack significant velocity and acceleration in those regions (and thus mass adaptation is limited).

Fig. 3.

Estimated average mass distribution of four subjects from the first experiment. The blue and green markers are the mass distribution in the direction specific model and red is the single mass distribution.

With careful inspection of Fig. 3, it is clear that when direction specific adaptation is present, the mass model for flexion has greater amplitude near full extension (x = 0m). Conversely, the mass model for extension has greater amplitude near full flexion (x = 0.114m). A possible explanation for this phenomenon is that larger motions require higher accelerations which cause faster adaptation, as evident in (6), and larger flexion motions must start near full extension. Thus, the largest adaptation for the flexion model appears near full extension. The same argument is valid for extension motions and the extension mass model. However, adaptation with a single mass distribution does not take advantage of this propensity and all weights increase/decrease regardless of the direction of motion.

In the second experiment, a viscous force field was superimposed on the subjects separately during either flexion or extension. Fig. 4 is analogous to Fig. 3 and shows the mass distribution using the direction specific and single mass distribution models with the viscous field applied in flexion. Because the force field was applied in only one direction, the results show a clear difference in the direction specific modeling versus the single mass distribution.

Fig. 4.

Estimated average mass distribution of four subjects with a viscous field applied in flexion from the second experiment. The blue and green markers are the mass distribution in the direction specific model and red is the single mass distribution.

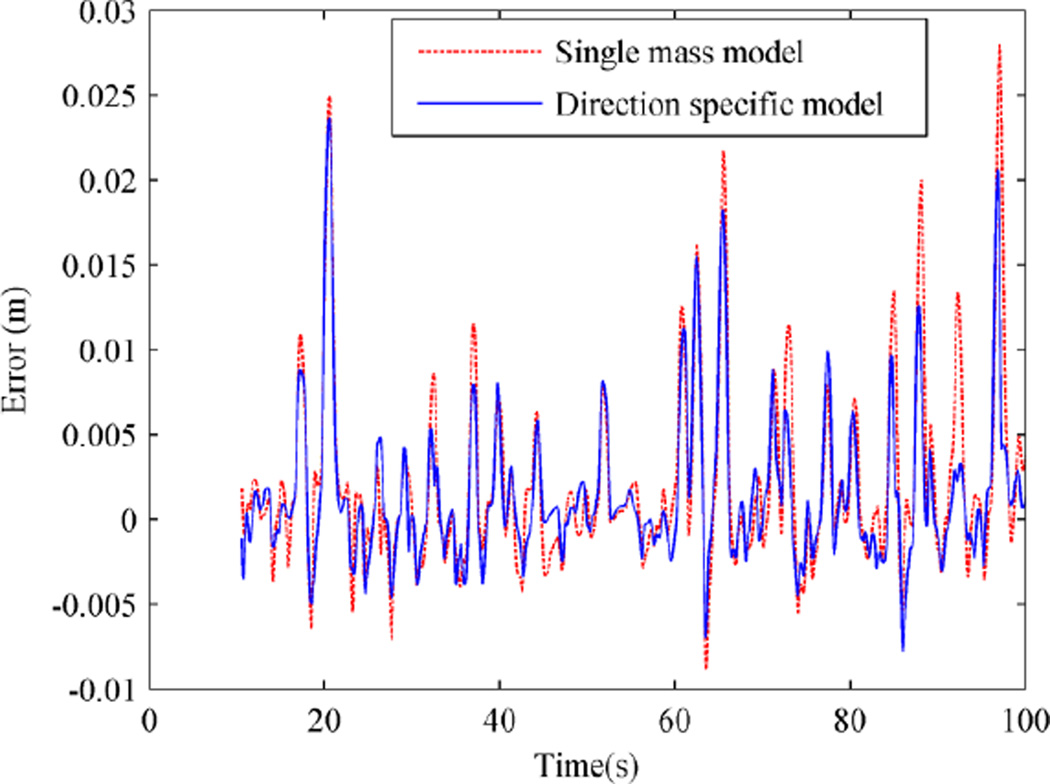
Fig. 5 shows the position error of a subject under the two adaptive control schemes. Position errors are slightly smaller when the direction specific adaptive control is used. Since the viscous field was applied in flexion, the position error doesn’t have a zero mean; the subjects have to overcome the force field and are behind the desired trajectory. This causes the error to be biased toward positive numbers. The results from extension were similar.

Fig. 5.

Position error using the two adaptive control schemes from the second experiment for one patient.

Fig. 6 demonstrates how the adaptation gains evolve throughout a typical trial when the viscous field was applied to subject in the flexion direction. The two adaptive controller schemes were used to assist the subject to follow the same desired trajectory. Fig. 6 (a) shows the instantaneous mean of the mass parameters, γ̄_M, ᾱ_M and β̄_M, versus time. It is observed that, as suggested by Fig. 4, in the direction specific controller, the average mass parameters are smaller than the ones in the controller with single mass distribution. Since there is no apparent stiffness in the system, one could predict a zero estimated stiffness. However, this is not the case when the single mass distribution adaptation is used. In contrast, the direction specific adaptation settles to the predicted zero stiffness as shown in Fig. 6 (b).

Fig. 6.

Parameter adaptation for the second experiment with a viscous field applied in flexion. The solid lines are the directional specific adaptation and the dashed lines are the directional independent adaptation.

Fig. 6 (c) shows how the two damping parameters are independently adapted in the direction specific adaptation. The parameter along the direction that the force field was applied (flexion) continues to adapt while the coefficient associated with extension goes to zero.

In the third experiment, the procedure from the second experiment was repeated with the forgetting portion of the control included ( τ =1 ). Fig. 7 shows the parameter adaptation of a trial with a viscous field applied in extension.

Fig. 7.

Parameter adaptation for the third experiment with τ = 1 and a viscous field applied in extension. The solid lines are the direction specific model and the dashed lines are the single mass distribution.

In the final experiment, the direction specific adaption and a directional force field was applied separately in both directions. However, the force field was removed after forty seconds. As a result, the damping coefficient estimate corresponding to the direction that the force field was applied increased until forty seconds and then suddenly went to zero as force field turned off as predicted by the model. This is shown in Fig. 8 for a case where the viscous field was applied in flexion.

Fig. 8.

Direction specific model parameter adaptation for the fourth experiment with a viscous field applied in flexion for the first 40 seconds. The solid lines are the damping coefficients and the dashed lines are the stiffness coefficients.

IV. Discussion and Conclusions

This paper describes an adaptive control algorithm for robotic assisted movement therapy that includes direction specific mass distributions for modeling neuro-muscular impairment. Previous work in impairment modeling lacks inertial terms or directional dependence which limits its ability to effectively assist with dynamic motions and direction specific impairment. By including direction specific mass distributions modeled with RBFs the proposed adaptive controller can tailor its assistance to individual patients. Combined with the assistance-as-needed force decay, this approach decreases control effort, which is important to promote participation and effort from the patient.

The direction specific model was compared with the single mass distribution, performing with less error. Furthermore, in the presence of a superimposed asymmetric force field, the single mass distribution increased stiffness due to its inability to learn the direction specific behavior. However, with the proposed controller, which includes a direction specific model, the adapted stiffness did not exhibit this increase.

Future efforts will focus on implementing the adaptive control approach on a multiple DOF system. In addition, an expansion of the RBFs to consider the full state space (variable velocity rather than movement direction only) will also be implemented. Future experiments are also planned with impaired and unimpaired subjects to better understand how to model neuro-muscular impairment after stroke. Final validation will include therapeutic evaluation of the proposed approach with impaired subjects.