Simplified and economical 2D IR spectrometer design using a dual acousto-optic modulator

Abstract

Over the last decade two-dimensional infrared (2D IR) spectroscopy has proven to be a very useful extension of infrared spectroscopy, yet the technique remains restricted to a small group of specialized researchers because of its experimental complexity and high equipment cost. We report on a spectrometer that is compact, mechanically robust, and is much less expensive than previous designs because it uses a single pixel MCT detector rather than an array detector. Moreover, each axis of the spectrum can be collected in either the time or frequency domain via computer programming. We discuss pulse sequences for scanning the probe axis, which were not previously possible. We present spectra on metal carbonyl compounds at 5 µm and a model peptide at 6 µm. Data collection with a single pixel MCT takes longer than using an array detector, but publishable quality data are still achieved with only a few minutes of averaging.

I. Introduction

A 2D IR spectrum is a correlation of two vibrational frequency axes. When Hamm, Lim and Hochstrasser collected the first 2D IR spectrum, they collected the data in the frequency-domain by scanning the center frequency of a narrowband pump pulse to generate one axis and frequency-resolved a femtosecond probe pulse for the second axis [1]. A few years later, Hochstrasser and coworkers collected the first time-domain 2D IR spectrum, followed closely by Tokmakoff and coworkers, by using four femtosecond pulses, two to generate the pump axis and two for the probe axis [2,3]. When originally implemented, it took many hours to collect a single 2D IR spectrum. Nonetheless, the information contained in 2D IR spectra is so valuable that the technique was soon applied in fields as diverse as chemical dynamics, material science, and molecular biophysics, regardless of the time consuming data acquisition [4–15]. Now, due to improvements in the technology and a better understanding of the scientific underpinnings of the technique, 2D IR spectra with high signal-to-noise can be generated in seconds [16–18].

One of the most important developments for fast data collection was the use of spectral interferometry, in conjunction with an array detector, to collect the data for the probe axis of the spectra [2,3,19]. To generate the probe axis, the electromagnetic field emitted from the sample must be time-resolved and Fourier transformed. The measurement can be done in the time-domain, by scanning the fourth laser pulse (called the “local oscillator”) and performing a digital Fourier transform or in the frequency domain by utilizing a spectrometer to optically perform the Fourier transform [20]. With a spectrometer, followed by an array detector, all of the frequencies contained in the emitted field are measured simultaneously. This frequency-domain approach is called spectral interferometry. With spectral interferometry, one only needs to incrementally scan the pump axis, which leads to fast data acquisition of the 2D IR spectrum.

Data acquisition with an array detector also has a few practical drawbacks. The drawbacks included grating losses in the spectrometer that leads to lower signal strength, detector noise from each of the many pixels in the array, and a frequency resolution that is ultimately limited by the pixel size. But the biggest drawback may be its cost. The array detector, spectrometer and associated electronics altogether cost about 1/3 the price of a Ti:Sapphire regenerative amplifier. The high price certainly limits the number of researchers that can utilize 2D IR spectroscopy in their laboratories, even if they already own a regenerative amplifier.

In this article, we present a design for a 2D IR spectrometer that utilizes two germanium acousto-optic modulators (AOM). Previously, we reported a 2D IR spectrometer with a single AOM that modulated the pump beam [17,18,21]. The AOM could be used to generate and scan the time delay between a pair of pulses to collect data in the time-domain or it could generate and scan the center frequency of a spectrally narrow pulse to collect data in the frequency-domain. Interferometric methods have also been developed to generate the pump axis data [22]. For all of these methods, a spectrometer and array detector were used to generate the probe axis. With the addition of a second AOM, these two expensive components are no longer needed. The second AOM can create a femtosecond pulse pair to measure the probe data in the time-domain, or it can be spectrally narrowed to measure in the frequency-domain. Either way, a single channel detector replaces the array detector, which greatly simplifies the experimental layout and reduces the cost of the 2D spectrometer since an AOM is significantly less expensive than an array detector, monochromator and the associated electronics. Data collection is still very rapid, because a new pulse sequence can be generated with every laser shot even at multiple kHz repetition rates. In this paper, we demonstrate that even without an array detector, our dual AOM design can collect high signal-to-noise 2D IR spectra in a few minutes.

Rapid time-domain scanning using translation stages has been receiving an increased amount of attention in the past few years [16,22,23]. Continuous scanning of the delay between the two pump pulses, rather than stopping and restarting the translation stages, increases the accuracy and decreases the acquisition time of the pump axis data. Rapid scanning of the pump axis in a style similar to that used in commercial Fourier transform infrared (FTIR) spectrometers has been shown to improve the signal-to-noise [22]. Rapid scanning of the delay between two pump pulses still requires an array detector. Recently, a rapid scan approach has been used for the probe pulse [23]. That method is similar to ours in that a single channel detector is used rather than an array detector, but they used a four-wave mixing phase matching geometry which necessitates a more difficult alignment procedure and requires both the rephasing and non-rephasing spectra to be independently collected, added and phased. Using AOMs in the pump-probe beam geometry, these steps are all done automatically. But there is also an intrinsic difference between delay scanning with translation stages and an AOM. With an AOM, one can precisely control the number of points per period to be collected of the vibrational coherence and thus easily set the frequency bandwidth of the measured spectrum. In contrast, with continuously moving translation stages, the number of points per period is tied to the repetition rate and the speed of the translation stages (a HeNe interferometer is also necessary for calibration of each axis). Thus, moving to higher repetition rates adds more points per period, but those points mainly sample frequencies outside of that spanned by the laser bandwidth unless the scanning speed is also increased. Thus, higher repetition rates do not necessarily correlate with faster data collection. With dual AOMs, data collection time shortens linearly with increased repetition rate. In addition, one can also scan the probe in the frequency-domain, which requires far fewer data points than time-domain data collection. We demonstrate the unique abilities of our spectrometer by collecting 2D IR spectra using various combinations of time and frequency-domain scanning without any mechanical adjustments to the spectrometer.

II. Experimental Implementation

A home built optical parametric amplifier (OPA) is pumped by 1.3 mJ, 45 fs transform limited pulses from a 1 kHz Ti:Sapphire regenerative amplifier. The 800 nm output is downconverted into signal and idler pulses (200 µJ combined) in a type II BBO crystal (θ = 28.0°, 2 mm thick) in two stages with collinear alignment. Mid-IR pulses are generated by difference frequency mixing the signal and idler pulses in a type II AgGaS₂ crystal (θ = 45.4°, 1 mm thick or θ = 41.8°, 1 mm thick). The resulting pulses have FWHM bandwidths of approximately 185 cm⁻¹ at 5 µm or 6 µm respectively, and pulse energies of about 5 µJ.

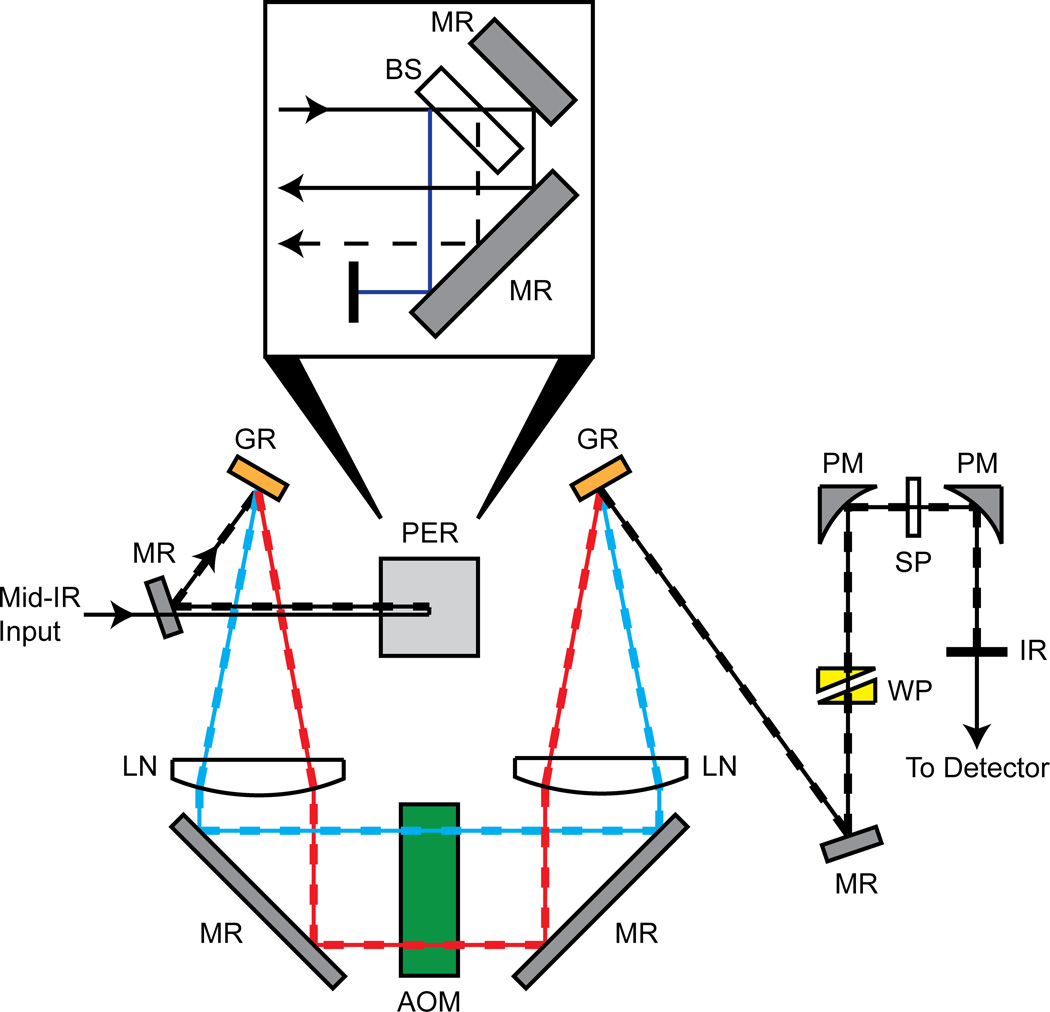
The spectrometer used for experimentation is shown in Fig. 1. A single mid-IR pulse is brought into the spectrometer where it first passes through a custom periscope assembly in order to generate two parallel vertically displaced pulses (inset). The periscope contains a plane parallel CaF₂ window that reflects about 3% of the mid-IR light at both the front and back faces, while the transmitted light is reflected by a gold mirror. All three beams are reflected off a gold mirror at the bottom of the periscope to bring them back parallel to the optical table. The light coming from the front reflection of the CaF₂ window is discarded, leaving two parallel vertically displaced pulses for the pump (0.94*I_input) and the probe (0.03*I_input) beam paths.

Figure 1.

Schematic of dual Ge AOM 2D IR spectrometer. A single mid-IR pulse enters from the left side and goes through a custom periscope (shown from side view in zoom), which splits the single pulse input into vertically displaced pump and probe output pulses. Overlapped solid and dashed lines indicate the path where the vertically displaced pump and probe pulses travel in parallel. PER: Periscope Assembly, BS: CaF₂ Beam Splitter, MR: Mirror, GR: Grating, LN: CaF₂ Lens, AOM: Dual Ge Acousto-Optic Modulator, WP: ZnSe Wedge Pair, PM: Parabolic Mirror, SP: Sample, IR: Iris.

The two parallel vertically displaced pulses are reflected off a gold mirror and sent into a 4-f pulse shaper setup. First, the pulses are frequency dispersed using a goldcoated grating (200 grooves/mm, 5.0 µm blaze or 150 grooves/mm, 5.4 µm blaze) in a near-Littrow configuration. The frequency components are then collimated with a custom 12.5 cm focal length CaF₂ cylindrical lens. A folding mirror reflects the light and sends each pulse through its own germanium acousto-optic modulator (AOM). The first-order diffracted light from the AOM is reflected toward a second CaF₂ lens, where the frequency components are focused down at a second grating. The second grating recombines the frequencies of each individual pulse, transforming them back into the time-domain. Theoretical throughput of the spectrometer for the pump pathway is between 0.37*I_input and 0.47*I_input, but in practice is heavily dependent on the efficiency of the grating pair used. Experimental throughput of the pump is typically measured to be between 0.3*I_input and 0.4*I_input.

The pump and probe beams are reflected off stacked gold mirrors toward a 90° off-axis parabolic gold focusing mirror (2 inch focal length). The stacked mirrors are horizontally offset to compensate for differences in time delays. The probe beam passes through a ZnSe wedge pair that is positioned using a translation stage for controlling the pump-probe delay time. With this arrangement we can vary the waiting time, t₂ in the 2D IR experiment from 0 to 15 ps.

Following the sample, a second 90° off-axis parabolic gold mirror collimates the pump and probe beams. The pump beam is blocked with an iris, while the probe beam is detected by either a spectrometer and an array detector, as is usual with spectral interferometry detection, or by rotating the spectrometer grating to zero-order so that it acts as a mirror and use only a single pixel on the array for detection (in practice, we sum three pixels to account for slight frequency dispersion). With this detection arrangement, we can quickly switch between array and single channel detection in order for comparison studies. The spectrometer is 150 mm focal length with either a 150 or 75 grooves/mm grating followed by a 64-channel array detector, which results in a frequency resolution of 2.5 or 5 cm⁻¹ per pixel, respectively. We use the spectrometer to calibrate the AOMs, but one could use other calibration methods instead, which we are currently devising. Windowing functions are not used in this paper as to not complicate the method comparisons.

III. Results

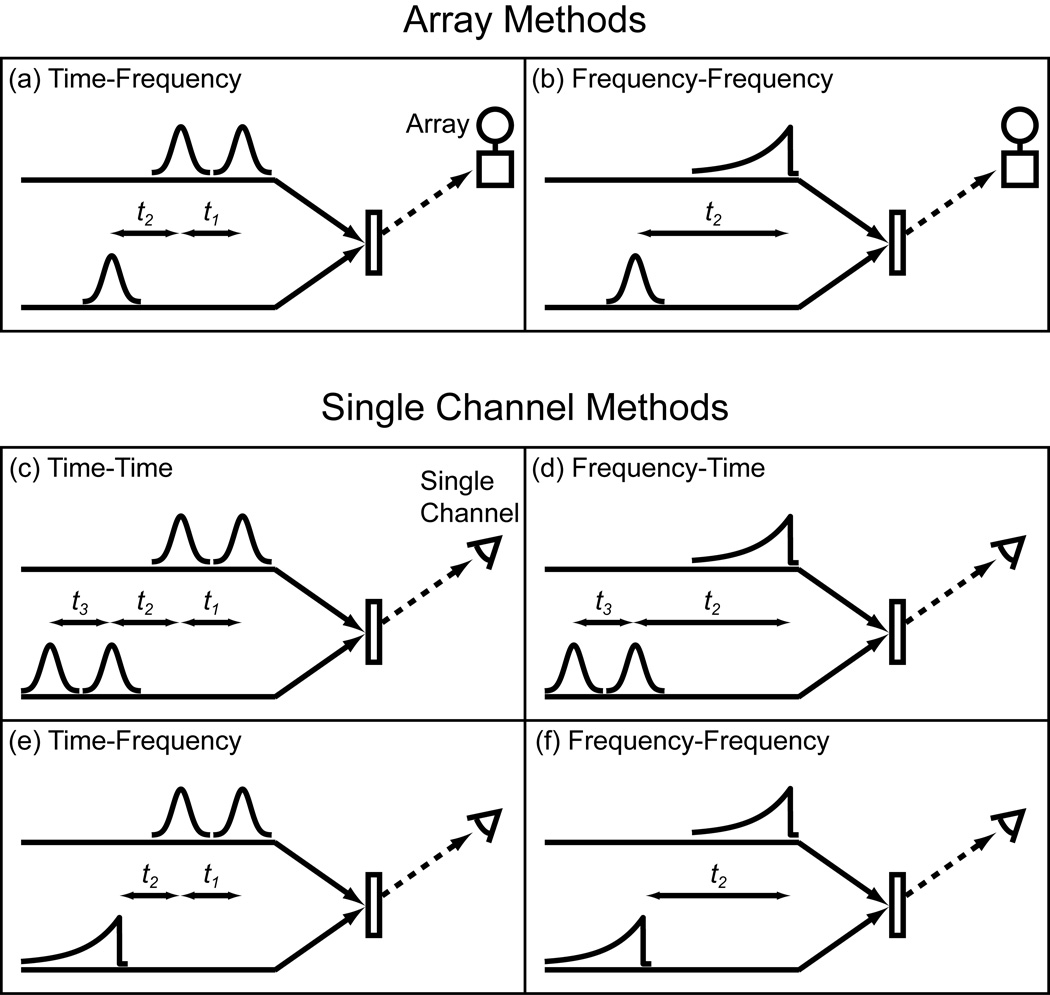
Shown in Fig. 2a and b are two common ways of collecting 2D IR spectra. They both utilize a femtosecond probe pulse, a spectrometer, and an array detector. They differ in that (a) one has its pump axis collected in the time-domain while (b) the other is collected in the frequency-domain. In time-domain data collection, the delay (t₁ for the pump axis) is incremented and the resulting data computationally Fourier transformed. For frequency-domain data collection, the center frequency of a narrowband pump is scanned while measuring the transient absorption. For the frequency-domain pulse sequence, we draw the pulse envelope as if it were generated by an etalon as Hamm, Lim and Hochstrasser first used, although more optimized pulse shapes are now available with pulse shapers [1,17].

Figure 2.

2D IR pulse sequences. (a)-(b) Array detector methods with the pump shaped by an AOM. (c)-(f) Single channel methods with pump and probe shaped by AOMs.

In this paper, we demonstrate methods in which the array is replaced by a single channel detector. To do so, the probe pulse must be scanned in either frequency or time, giving four combinations of pulse sequences shown in Fig. 2c-f. In what follows, we compare spectra collected using a single channel detector to spectra collected with an array detector. While some of the spectra shown below could have been generated using conventional optics, it is the use of a dual AOM 2D IR spectrometer that enables the fast and efficient data collection that we illustrate below.

A. Time-domain data collection with a single channel detector

In this section, we collect 2D IR spectra completely in the time-domain using a single channel detector (Fig. 2c) and compare the results to data collected using an array detector (Fig. 2a). 2D IR is a third-order spectroscopy that requires molecular samples to interact three times with an electric field, which we refer to as E₁, E₂ and E₃ that are separated by time delays t₁ and t₂, respectively. The emitted third-order electric field, E_sig, is then heterodyne detected with a local oscillator pulse, E_LO, following t₃ after E₃.

To collect a 2D IR spectrum, the two coherence time periods t₁ and t₃ need to be sampled in discrete steps. We use one AOM to produce a pair of pulses that act as E₁ and E₂, and the other AOM to generate E₃ and E_LO. Since E₁ and E₂ are collinear, E_sig is emitted collinearly to E₃ and E_LO. A single pixel MCT detector measures the total intensity in this direction. The intensity is collected as a function of t₁ and t₃ by applying a sequence of masks. A 2D IR spectrum is generated by calculating the two-dimensional cosine transform from the resulting matrix of data [24].

We need to measure the signal created by the interference of E_LO and E_sig, but since E₃, E_LO and E_sig are all collinear, we also get other interferences. We remove these background signals by phase cycling [20]. Phase cycling is easily and accurately performed using a pulse shaper [21]. We use the phase cycling scheme

$$S(\mathrm{\Delta }{\varphi }_{12}=0,\mathrm{\Delta }{\varphi }_{3LO}=0)+S(\mathrm{\Delta }{\varphi }_{12}=\pi ,\mathrm{\Delta }{\varphi }_{3LO}=\pi )-S(\mathrm{\Delta }{\varphi }_{12}=0,\mathrm{\Delta }{\varphi }_{3LO}=\pi )-S(\mathrm{\Delta }{\varphi }_{12}=\pi ,\mathrm{\Delta }{\varphi }_{3LO}=0)=4\cdot 2\text{Re}(E_{LO}{E}_{\mathit{\text{sig}}}^{*})$$ (Eq.1)

to eliminate all but the desired heterodyned third-order term 2Re $(E_{LO}{E}_{\mathit{\text{sig}}}^{*})$, where Δϕ₁₂ is the difference in phase of E₁ and E₂ and Δϕ_3LO is the difference in phase of E₃ and E_LO. Other phase cycling schemes can be used to eliminate all potential scattering terms in the experiment [25]. Mechanical chopping can be used instead, but chopping reduces the effective repetition rate of signal collection [26]. Phase cycling can be mimicked with small time delays, just so long as the envelope of E_sig is slowly varying, which is not the case in 2D electronic spectroscopy nor in complicated 2D IR spectra [25]. With pulse shaping, the phase is truly controlled independent of the pulse envelope.

Shown in Fig. 3a and b are 2D IR spectra of tungsten hexacarbonyl, W(CO)₆ collected using the dual AOM spectrometer and a single channel detector using the time-domain approach discussed above. W(CO)₆ is dissolved in heptane with an OD = 0.41 at 1983 cm⁻¹. The coherence times t₁ and t₃ were incremented from 0 to 5700 fs in steps of 60 fs. Thus, the number of (t₁, t₃) pairs used to generate a single spectrum is 9216, which takes 9.2 seconds to collect at a laser repetition rate of 1 kHz. Consecutive sets of data were averaged until the desired signal-to-noise was achieved. Even though 60 fs steps were taken, we were not undersampling the coherence oscillations because we were working in the rotating frame in order to convert the fundamental signal frequency from 1983 cm⁻¹ to 160 cm⁻¹ [21].

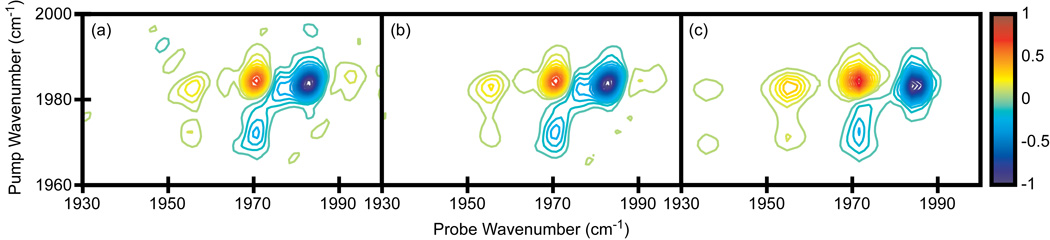
Figure 3.

2D IR spectra of W(CO)₆ in heptane. (a)-(b) Single pixel detection with a time scanned probe axis. Spectra averaged for 5 and 20 minutes, respectively. (c) Array detection, averaged for 5 minutes. Contours levels show 6.67% increments with zero level contours omitted.

The spectra exhibit a bleach at the fundamental frequency (1983 cm⁻¹) and transient absorption at the 1^st overtone frequency (1971 cm⁻¹). The other peaks are due to fifth-order signals in which either E₁ or E₂ has interacted with the sample three times instead of just once. These spectra are plotted with contours at 6.67% increments and zero level contours are omitted. Within five minutes of averaging, the signal-to-noise ratio is comparable to previously reported 2D IR spectra of W(CO)₆ [17,27]. The signal-to-noise ratio doubles after 20 minutes of averaging (Fig. 3b).

For comparison, we also collected a W(CO)₆ spectrum with a spectrometer and an array detector (Fig. 3c). The coherence time t₁ was incremented the same as above. Therefore, the 96 steps along the t₁ axis determined the amount of time necessary to collect a single spectrum, which was about 0.1 seconds at 1 kHz. To eliminate all other experimental differences between the single pixel and array detection methods, we did not send the probe beam around the pulse shaper as is usually done. Instead, the probe pulse was still sent through the second pulse shaper, but the pulse shaper applied a uniform mask that left the probe pulse unchanged. Fig. 3c is a five minute average using the array detector. The peaks in the 2D IR spectra have the same width along the pump axis, as for the spectra collected with a single channel detector, but are broader along the probe axis. The frequency resolution of the array detector matches that of the single pixel spectra but the peaks are not as well resolved because the array is pixilated. To increase the resolution one needs a longer pathlength spectrometer or higher density gratings for array detection. But the resolution of the time-domain method can be easily increased simply by scanning to larger values of t₃ [28]. The spectrum collected with the array detector has higher signal-to-noise compared to the time-domain method when averaged the same amount of time. Thus, data collection is faster with the array, but high quality spectra can be obtained with a single channel detector in just a few minutes. Additionally, windowing of the time-domain data can be applied to improve the signal-to-noise ratio and enhance resolution [20,29].

B. Rapidly versus slowly scanning time delays

The standard way of incrementing time delays is to use translation stages. One sets the t₁ delay (or t₃ delay, if under explicit control) and then averages for typically 50 or 100 laser shots. The delay is then incremented and data acquisition is repeated. No data is collected while the stage moves to the next position. With pulse shaping using an acousto-optic modulator, arbitrary pulse sequences can be generated on a shot-to-shot basis. As a result, the time delay between pulses can be incremented with every laser shot at repetition rates of many kilohertz. Thus there is no loss of data due to moving parts. Fast data acquisition not only decreases the amount of time necessary to acquire a 2D IR spectrum, but also improves the signal-to-noise and quality of the data because the rate of data acquisition lies further from the frequency of the laser fluctuations (which is the primary source of noise in 2D IR spectra). To illustrate this effect, we collected data at both fast and slow scanning rates. For rapid scanning, we incremented t₁ and t₃ from 0 to 2820 fs in steps of 60 fs (2304 data points), and collected only a single laser shot of data for each point to generate a 2D IR data set in 2.3 seconds. One hundred data sets of each phase were collected in series, and averaged to generated a 2D IR data set that took a total of 15 minutes to acquire. For the slow scanning, we mimicked the operation of translation stages by averaging for 100 laser shots at each time delay before incrementing the delays. We added a 100 ms time lag between sets of 100 data points to account for the time it takes the translation stage to reposition. Because of the lag time, collecting the full data set takes 30 minutes. Thus, both experiments are averaged for the exact same number of laser shots, albeit in different orderings (in both cases, we collected data in the rotating frame, which is not possible with translation stages). Fig. 4 shows the results of the two scanning methods. The comparison reveals that rapidly scanning results in 5.8x higher signal-to-noise 2D spectra. Higher repetition rate lasers would further improve the signal-to-noise.

Figure 4.

2D IR spectra of W(CO)₆ in heptane. Single pixel detection with a time scanned probe axis. (a) Rapid scanning - time delays varied on a shot-to-shot basis and cycled through 100 times. (b) Slow scanning - time delays static for 100 laser shots and cycled through 1 time. Contours levels show 6.67% increments with zero level contours omitted.

As discussed in the Introduction, rapid scanning of the delays using fast moving translation stages has recently been investigated in a number of different scenarios [16,22,23]. We note that rapid scanning with translation stages is not equivalent to the shot-to-shot capabilities of an AOM pulse shaper. With translation stages, one does not actually synchronize the laser repetition rate with the translation stage motion. As a result, time delays at which the data is measured differs from scan to scan, so that the data must be binned in order to average it. Moreover, the laser repetition rate and scanning speed are intimately connected with the sampling of the time delays. As a result, it is difficult to sample at the Nyquist frequency or at other controllable delays, such as delays for undersampling the data. Finally, the amount of time it takes to collect a 2D IR spectrum does not scale inversely with the laser repetition rate, because the limiting factor is the stage motion. The shot-to-shot increments in time delays made possible by AOM pulse shaping does not have these drawbacks. With pulse shaping, no binning is necessary, one can sample at the Nyquist frequency or any other frequency, and data collection time is linearly proportional to laser repetition rates, even at many kilohertz.

C. Frequency-domain data collection with a single channel detector

So far we have demonstrated the ability to collect 2D IR spectra with a single pixel detector by creating two pulse pairs and scanning the coherence times t₁ and t₃. Thus, data for both axes of the 2D IR spectrum are collected in the time-domain (Fig. 2c). In this section, we collect the probe axis in the frequency-domain by using one pulse shaper to narrow the mid-IR probe pulse down to a few wavenumbers and scan its center frequency. The data for the pump axis is collected either in the time-domain, by using the shaper to scan a pulse pair like above (Fig. 2e), or in the frequency-domain by narrowing the pump pulse and scanning its center frequency in a similar manner to the probe pulse (Fig. 2f).

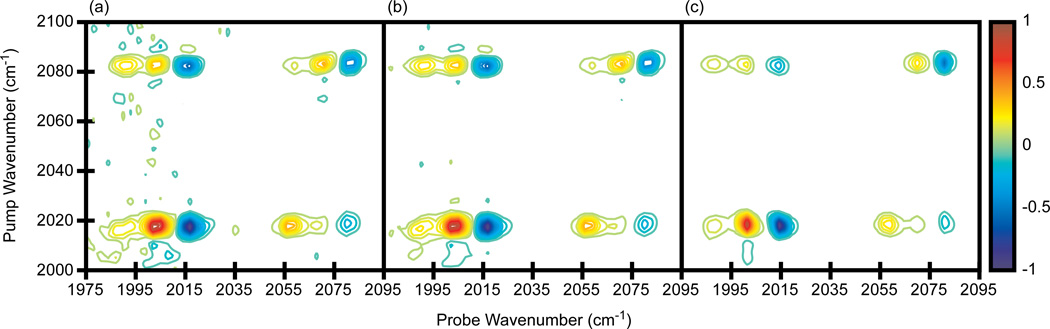
Shown in Fig. 5 are 2D IR spectra of dicarbonylacetylacetonato rhodium(I) (RDC) in heptane. The concentration was set to give an OD = 0.30 at 2083 cm⁻¹ and an OD = 0.39 at 2014 cm⁻¹. The pump and probe polarizations are perpendicular to each other (ZZYY), which increases the intensity of the cross peaks relative to the diagonal peaks although the overall signal is 3x smaller than for parallel polarization (ZZZZ). The waiting time for the experiment, t₂, is 5.3 ps. Shown in Fig. 5a and b are spectra in which the pump axis is collected in the time-domain by scanning a pair of pulses for t₁ = 0 to 4000 fs in 80 fs steps (in the rotating frame with a fundamental signal frequency set to 130 cm⁻¹), while the probe axis is collected in the frequency-domain by narrowing the bandwidth of the probe pulse to 4 cm⁻¹ FWHM with a Gaussian profile and scanning its center frequency from 1960 cm⁻¹ to 2110 cm⁻¹ in steps of 3 cm⁻¹. Thus, 2601 data points are collected to generate a single spectrum. The spectra were averaged for 5 and 20 minutes, respectively (Fig. 5a and b). For comparison, we show data collected using an array detector and averaged for five minutes in Fig. 5c. The coherence time t₁ was incremented in the same fashion as above so it took 51 data points to collect a single spectrum.

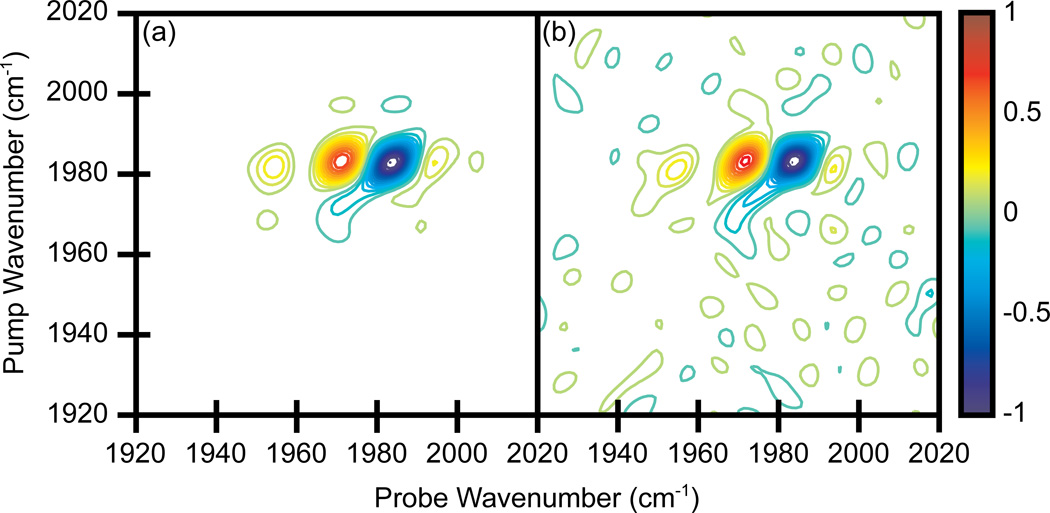
Figure 5.

2D IR spectra of RDC in heptane. (a)-(b) Single pixel detection with a frequency scanned probe axis. Spectra averaged for 5 and 20 minutes, respectively. (c) Array detection, averaged for 5 minutes. Contours levels show 6.67% increments with zero level contours omitted.

The two spectra are very similar to one another. Once again, array detection produces a spectrum with higher signal-to-noise for equivalent averaging times, but using a single pixel detector still produces a publishable quality spectrum in a short amount of time. More importantly, the 2D lineshapes are not distorted by the frequency narrowed probe pulse. Frequency scanning the probe pulse is similar to the original method used by Hamm, Lim and Hochstrasser to generate the pump axis of the first 2D IR spectrum [1]. They used an etalon to narrow the bandwidth and scan the center frequency of the pump pulse. As is now better understood, the frequency dependent amplitude and phase of the narrowed pulse distorts the 2D IR spectrum along the pump axis [17,30]. In this work, a similar convolution distorts the spectrum along the probe axis, but since we have a pulse shaper, we can create less perturbative pulse shapes. A Gaussian narrowed pulse was chosen because it has smaller wings and flat phase profile, which minimizes the distortions. Thus, a single pixel detector can replace an array detector and produce a high quality 2D IR spectrum in a few minutes. Data collection in the frequency-domain can be done more quickly than in the time-domain because fewer data points are needed.

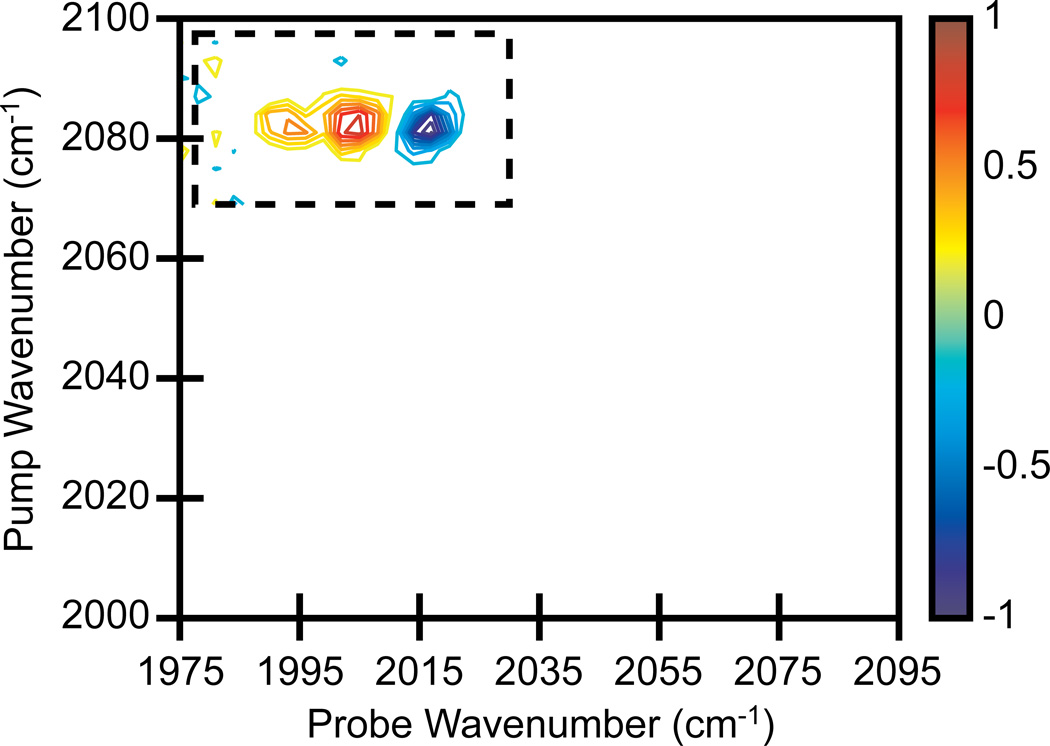
With two pulse shapers, we can also collect both axes in the frequency-domain. Frequency-frequency scans do not have to span an entire 2D IR spectrum, but can be restricted to small frequency regions, such as cross peaks. Shown in Fig. 6 is a 2D IR spectrum in which only the RDC cross peaks in one quadrant of the spectrum were collected. This was carried out by scanning the frequency-narrowed Gaussian pump pulse from 2055 cm⁻¹ to 2115 cm⁻¹ and a Gaussian narrowed probe pulse from 1975 cm⁻¹ to 2035 cm⁻¹. For both the pump and probe, a 3 cm⁻¹ step size and 4 cm⁻¹ FWHM was used (441 data points per single spectrum). The spectrum was averaged for 5 minutes. We notice that higher signal-to-noise spectra can be obtained for equivalent averaging times since fewer data points are required to scan the small region. Scanning small regions of 2D IR spectra may be useful when rapid data collection is necessary for measuring real-time kinetics, for example, or when high resolution cross peaks are needed, since cross peaks measured in the frequency-domain will have absorptive lineshapes whereas those measured in the time-domain will not [20].

Figure 6.

2D IR spectrum of RDC in heptane. Single pixel detection with frequency scanned pump and probe axes, averaged for 5 minutes. The frequency range of scanning restricted to the small spectral region that contains a set of cross peaks (dashed box). Contours levels show 10% increments.

One technical issue should be mentioned regarding the functioning of the dual Ge AOM before concluding this section. Due to a small amount of electronic cross talk between the two commonly housed AOMs, a reproducible feature appears in the 2D IR spectrum that is not due to the response of the molecular system. For this reason, we have experimentally collected background scans, with the pump blocked, that are subtracted off all the spectra shown in Fig. 5 (and also later in Fig. 7). We anticipate the correction of this electronic issue with an updated version of the dual Ge AOM, because this problem does not occur for spectra collected with two individually housed AOMs.

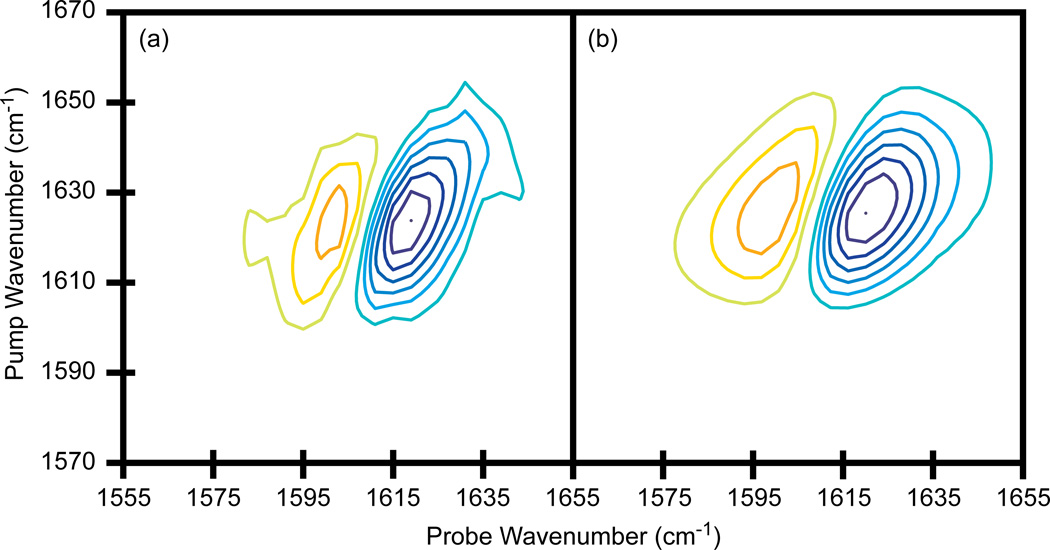
Figure 7.

2D IR spectra of N-methylacetamide in D₂O. (a) Single pixel detection with a frequency scanned probe axis, averaged for 15 minutes. (b) Array detection, averaged for 5 minutes. Contours levels show 14% increments with zero level contours omitted.

D. Demonstration of single pixel data collection at protein amide I wavelengths

The W(CO)₆ and RDC systems presented above are often used as model systems because they have very strong vibrational modes and absorb in the 5 µm region of the infrared spectrum for which mid-IR laser pulse generation is efficient and does not suffer from water vapor absorption. The 6 µm region is often utilized with 2D IR spectroscopy because it corresponds to double bond stretch modes such as the carbonyl stretch motions of the amide I band of proteins. At 6 µm, the vibrational modes are weaker absorbers, mid-IR pulse generation is less efficient, and there is strong water vapor absorption that necessitates dry air purging of the spectrometer. In order to assess the performance of single pixel detection with our dual AOM 2D IR spectrometer in this region of the spectrum, we have collected the spectrum of N-methylacetamide in D₂O. The sample has an OD = 0.38 at its fundamental absorption at 1622 cm⁻¹. Shown in Fig. 7a is a 2D IR spectrum collected in the time-domain for the pump axis and the frequency-domain for the probe axis. The pump pulse delay was stepped from t₁ = 0 to 1000 fs in 40 fs steps (in the rotating frame), while the probe was scanned from 1555 to 1655 cm⁻¹ with a 4 cm⁻¹ step size and a FWHM of 8 cm⁻¹ (676 data points per single spectrum). The spectrum was averaged for 15 minutes. For comparison, a 2D IR spectrum was collected using an array detector with a femtosecond probe pulse, which was averaged for 5 minutes (Fig. 7b). The t₁ delay was incremented in the same way as above which means 26 data points are collected to generate a single spectrum. Once again, for a fixed amount of time, the signal-to-noise using the array detector is superior, but a high-quality 2D IR spectrum can still be obtained in a short amount of time using a single pixel detector.

In the 2D IR spectra of RDC in Fig. 5 above, using a frequency narrowed probe pulse did not distort the spectra, but for NMA, the spectrum collected with the bandwidth narrowed probe pulse is narrower than when using a femtosecond probe. The narrowing is a consequence of an unequal weighting of rephasing and non-rephasing diagrams caused by time overlap between the pump and probe pulses. The frequency narrowed probe pulse has a FWHM of 8 cm⁻¹, which corresponds to a FWHM in time of 3.7 ps. The waiting time is t₂ = 0, which means that the probe pulse can interact with the sample before either E₁ or E₂ of the pump beam. The time-ordering dictates the Feynman path being measured. In the RDC experiments, signals generated from reversed time-orderings were less apparent because the long lifetime of RDC permitted data collection with t₂ = 5.3 ps so that E₃ was always last.

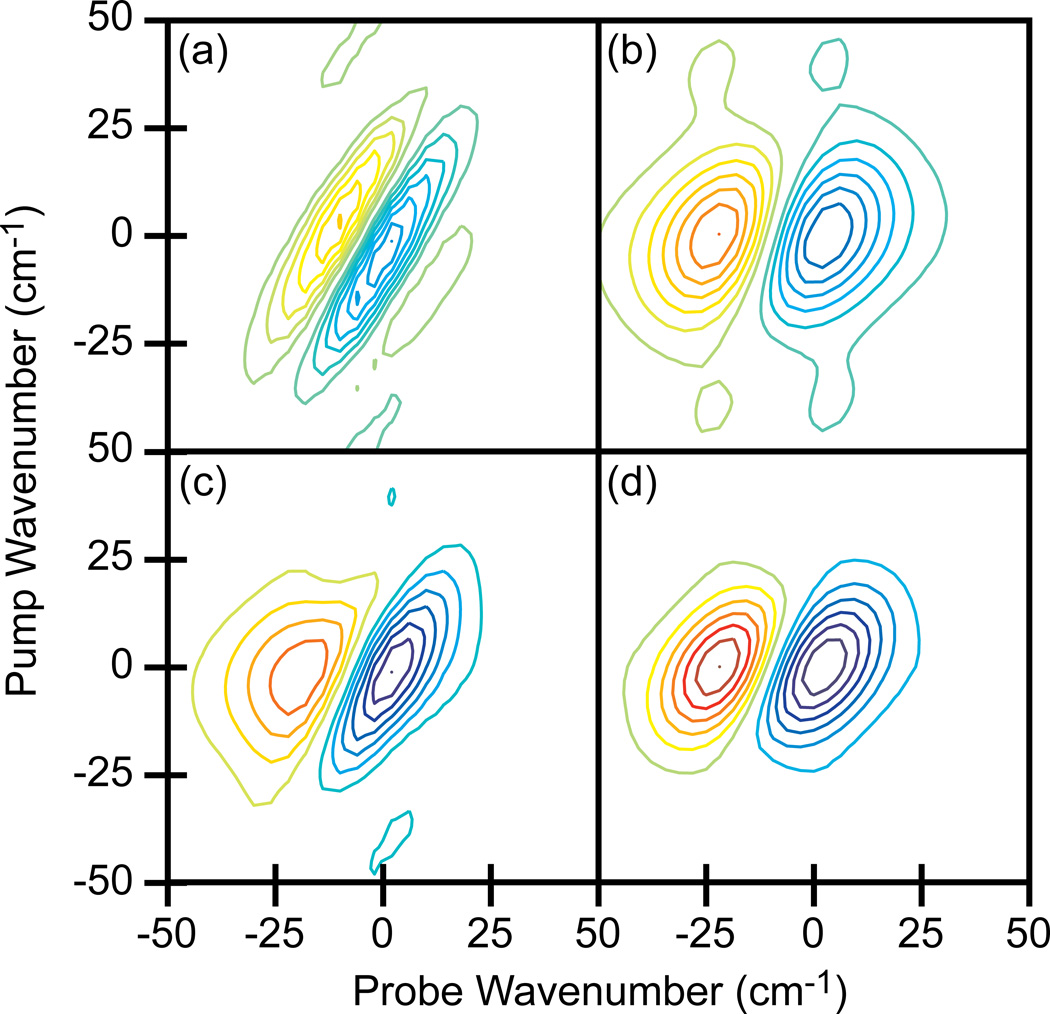
To better understand the contributions of rephasing and non-rephasing signals to the spectra, we simulated the 2D IR spectra in a calculation that included the full convolution of the molecular response with the time-dependent electric fields of the broadband pump and narrowband probe pulses. Shown in Fig. 8a and b are simulations of 2D IR spectra that would be generated if E₃ acts before either E₁ or E₂ and if E₃ acts after both E₁ and E₂, respectively. The 2D IR spectrum with fully weighted Feynman pathways is calculated by summing the two spectra, which is shown in Fig. 8c. The complete spectrum in Fig. 8c reproduces the narrowing seen in the experimental results. For comparison, a simulated 2D IR spectrum generated from only broadband femtosecond pulses is also shown (Fig. 8d), which matches the array detected experimental data. Based on these results, we conclude that the spectral distortions are indeed caused by contributions from pathways with switched time-orderings.

Figure 8.

Simulated 2D IR spectra of N-methylacetamide. (a) Spectrum generated when E₃ acts before either E₁ or E₂. (b) Spectrum generated when E₃ acts after both E₁ and E₂. (c) Summation of (a) and (b) which simulates the single pixel measurement. (d) Spectrum generated from only femtosecond pulses which simulates the data collected with the array. Spectra are plotted with the fundamental vibrational frequency set to 0 cm⁻¹. Contours levels show 14% increments with zero level contours omitted.

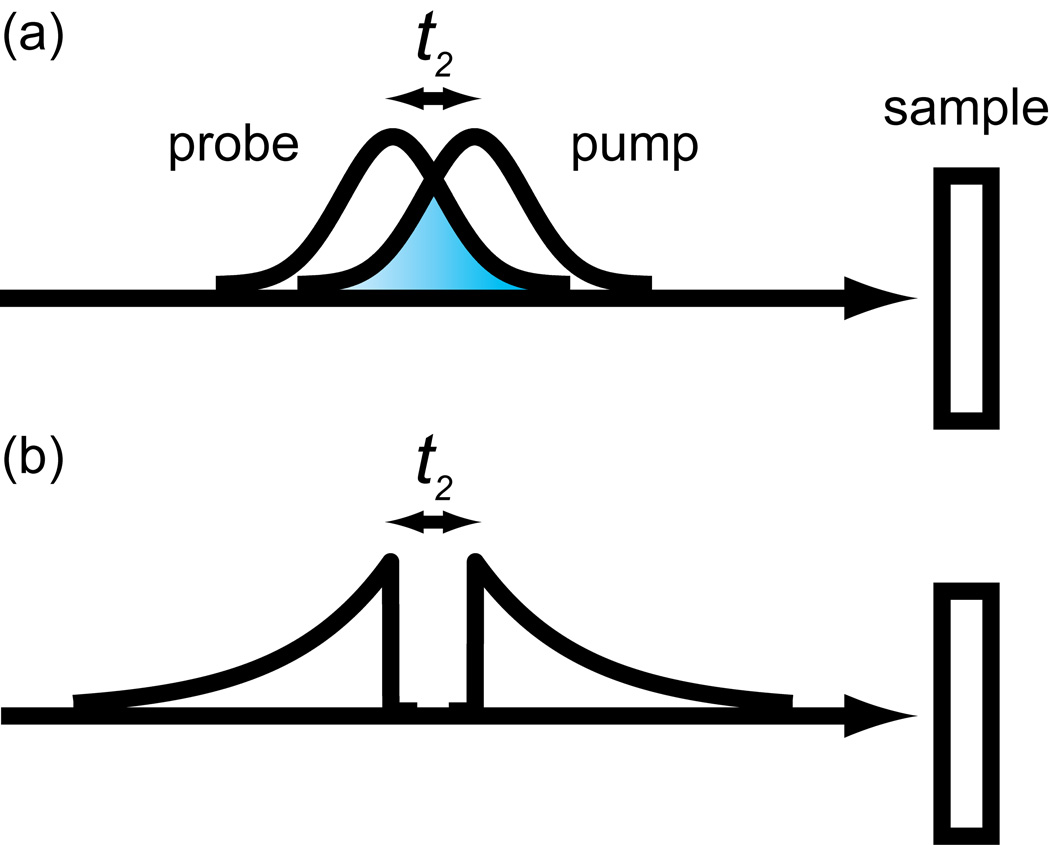
These distortions are similar to those that occur in frequency-domain experiments that utilize etalons [17,30]. Etalons create pulse envelopes with a fast rise followed by an exponential decay (see Fig. 2) which is why their spectrum is Lorentzian. When the exponential tail overlaps in time with the probe pulse, one gets pulse reorderings and distorted spectra like discussed above. Of course, this distortion will be minimal for large t₂ waiting times. With a pulse shaper there are more sophisticated ways to improve the spectrum. It was shown that a “reverse” etalon, in which the pulse envelope had an exponential rise rather than a decay, enabled short t₂ times to be measured artifact free [17]. Another example is shown in Fig. 9. For frequency-frequency scans at short waiting times with Gaussian pulses there will be pulse overlap (Fig. 9a). Instead, a pulse sequence like shown in Fig. 9b, which consists of an etalon and reverse etalon can be used. Pulse shaping allows one to optimize the pulse sequences for the problem at hand.

Figure 9.

2D IR pulse sequences for single channel frequency scanning. (a) Gaussian pump and probe profiles overlap at short t₂ times, which causes distortions. (b) Etalon and reverse etalon profiles have no overlap at short t₂ times.

IV. Conclusion

In this paper we demonstrated the usefulness of a novel 2D IR spectrometer that uses two Ge AOMs to independently control the pulse shapes of the pump and probe beams. Pulse shaping enables rapid scanning, phase cycling, and the ability to shift data collection between the time and frequency domains. By shaping the probe beam, one can replace the expensive array detector and its associated spectrometer and electronics with an economical single pixel detector. Data collection in the time-domain provides the highest resolution 2D IR spectra, because the resolution is simply set by scanning to longer delays. Frequency-domain scanning allows specific regions of the 2D IR spectra to be scanned and produces truly absorptive rather than phase-twisted cross peak lineshapes. The choice of pulse shape for frequency-domain scanning optimizes the 2D IR spectrum. The way in which noise is distributed in the spectrum is probably influenced by the data collection method, and thus might be optimized by appropriate choice of pulse sequence. Of course, with pulse shaping, altering the pulse sequence is simply a matter of computer programming.

Our dual AOM spectrometer uses a pump-probe beam geometry so that the emitted signal field is automatically heterodyned, which makes alignment straightforward and robust. Moreover, due to the phase matching geometry, one obtains 2D IR spectra automatically since both rephasing and non-rephasing signals are collected simultaneously. While not discussed here, one can use a two-dimensional Fourier transform to independently extract these signals, if desired [21,26]. No matter which type of signal is measured, the 2D IR spectra are properly phased, so that one does not need to calibrate the 2D IR data to a pump-probe spectrum [31,32]. The signal-to-noise might also be improved with use of polarization schemes that independently control the probe background to the signal amplitude [33,34].

Our approach is similar to that of a commercial FTIR spectrometer. FTIR spectrometers use an interferometer to generate two parallel traveling infrared beams whose interference is measured on a single pixel detector. The interferometer is scanned as rapidly as possible to move the frequency at which the signal is collected as far away as possible from zero frequency experimental noise. Time-domain scanning is what enabled robust and inexpensive commercial infrared spectrometers. Our spectrometer utilizes AOM pulse shapers because they provide more control over the pulses than do interferometers, but the principle is the same.

We have found that data collection is slower without an array detector, but we have also demonstrated that 2D IR spectra of samples at typical concentrations can be collected in only a few minutes. While already short enough for practical applications, in the future this time will decrease further as improvements are made, such as the straightforward implementation of a higher repetition rate laser. All the data was collected at 1 kHz, but we recently started working at 2 kHz so it now takes ½ as long to collect the same spectra. It may be possible to do similar experiments at visible wavelengths as well. Visit our website at http://zanni.chem.wisc.edu/ to see a video demonstration of our spectrometer.

Highlights.

• We demonstrate the viability of a novel 2D IR spectrometer that uses a dual Ge acousto-optic modulator (AOM).

• The spectrometer uses a single pixel MCT detector rather than an array detector.

• The use of a dual AOM permits ways of scanning 2D IR spectra not previously possible.

• We compare data collection with a single pixel MCT detector to an array detector at 5 µm and 6 µm.

• We find improved signal-to-noise using a dual AOM because time delays are varied on a shot-to-shot basis.