Abstract
The catalytic asymmetric thiazolium- and triazolium-catalyzed benzoin condensations of aldehydes and ketones were studied with computational methods. Transition-state geometries were optimized by using Morokuma's IMOMO [integrated MO (molecular orbital) + MO method] variation of ONIOM (n-layered integrated molecular orbital method) with a combination of B3LYP/6–31G(d) and AM1 levels of theory, and final transition-state energies were computed with single-point B3LYP/6–31G(d) calculations. Correlations between experiment and theory were found, and the origins of stereoselection were identified. Thiazolium catalysts were predicted to be less selective then triazolium catalysts, a trend also found experimentally.
The use of computational theory to understand and predict the stereoselectivity of catalytic asymmetric reactions has undergone rapid development. The introduction of faster computers and improved algorithms will likely make computational techniques of even greater importance in the years to come. Recent examples of the computational elucidation of stereoselectivities include studies by our group of the enantioselective proline catalyzed aldol and Mannich reactions (1–3) and Kozlowski's (4) introduction of the functionality mapping technique, which offers promise for the design of asymmetric catalysts. We now report the modeling of stereoselective benzoin condensations catalyzed by thiazolium and triazolium salts by using quantum mechanical methods.
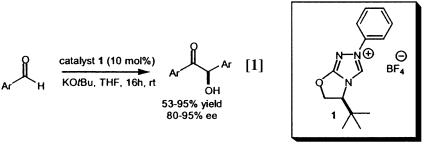
Over the last three decades synthetic chemists have investigated the use of chiral thiazolium catalysts in the benzoin condensation (5–10). Regrettably, these catalysts have performed poorly and afforded acyloin products of only moderate optical enrichment. The highest recorded enantiomeric excess (ee) for a thiazolium-catalyzed benzoin condensation (51% ee) was reported by Sheehan et al. (10), using the chiral catalyst (S)-(–)-4-methyl-3-α-(1-napthyl)ethylthiazolium tetrafluoroborate that afforded the product in only 6% yield. Chiral triazolium salts have fared better (5, 11, 12). For example, the chemically robust triazolium catalyst 1 recently prepared by Enders et al. (11) affords benzoin products in high yields with enantiomeric excesses as high as 95% (Eq. 1). To date this is the highest recorded ee for an organic catalyzed benzoin reaction.
 |
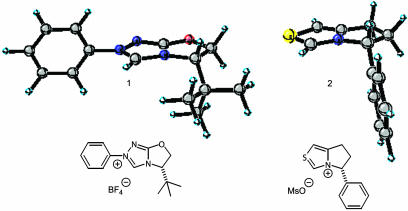
The origin of the dramatic difference in product yields and selectivities observed between thiazolium and triazolium catalysts is not readily apparent. For example, Knight et al. (6) have reported the preparation and use of the bicyclic thiazolium catalyst 2 (Fig. 1) for the condensation of benzaldehyde, isolating essentially racemic (10.5% ee) benzoin product in 20% yield. The structural similarity of thiazolium catalyst 2 relative to the triazolium catalyst 1 of Enders makes this result surprising, although the lack of a N-phenyl substituent in catalyst 2 likely has a significant effect.
Fig. 1.
Triazolium catalyst 1 and thiazolium catalyst 2.
What is the chemical basis for this difference, and might it be possible to predict a priori what catalysts are worthy of investigation? We have addressed these issues by using theoretical methods and demonstrate that IMOMO [integrated MO (molecular orbital) + MO method] multilayer calculations offer a viable approach for modeling stereoselective reactions of large molecular systems.
Background: Transition State for Stereoselective C–C Bond Formation.
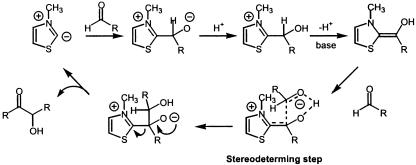
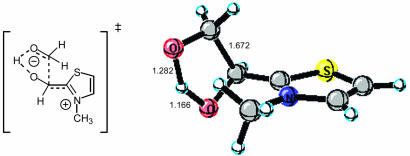
Debate over the mechanism of the thiazolium-catalyzed benzoin condensation during the last 50 years has led to the proposal of several different mechanistic scenarios (13, 14). A related dimer–monomer crossover mechanism based on the work of Lemal et al. (15) has also been proposed. Of the well established mechanisms for the benzoin condensation, both monomer- and dimer-catalyzed pathways have been proposed. We have recently studied this question computationally (unpublished work). Pertinent to the present study is the finding that the preferred reaction pathway for the benzoin condensation is calculated to be a monomer-catalyzed process that is in accord with the original proposal of Breslow (Scheme 1) (13). The transition state corresponding to C–C bond formation for the simple reaction system of formaldehyde addition to N-methylthiazolium, obtained by B3LYP/6–31(d) calculation, is depicted in Fig. 2. This transition structure was used as a starting template from which the larger systems discussed here were constructed. Of special note is the intramolecular proton transfer that occurs in the stereoselective-determining step of chirally substituted cases. This transfer rigidifies the transition state and is an important factor in controlling stereoselectivity.
Scheme 1.
Mechanism for the benzoin condensation as proposed by Breslow.
Fig. 2.
Transition state for stereoselective C–C bond formation in the benzoin condensation of formaldehyde.
Methods
Transition-state structures for catalysts, 1–5 (Fig. 4), were optimized by using Morokuma's (see ref. 16, ref. 17 for an application in biochemistry, ref. 18 for an application in catalysis, and ref. 19) IMOMO variation of ONIOM (n-layered integrated molecular orbital method) as implemented in gaussian 98 (20). The internal region where bonding changes occurs was treated with hybrid density functional theory B3LYP with the 6–31G(d) basis set. The remainder of the system was optimized by using AM1. The region in which the two levels of theory interface, known as the boundary region, was treated by using IMOMO as implemented in gaussian 98; bonds between atoms in the core and outer layer are broken and replaced by hydrogen atoms (link atoms) for the higher-level part of the IMOMO calculation on the core system. The energy of the system (IMOMO energy) is then calculated as the total energy of the whole system at the lower level of theory Elarge(low level theory) plus the energy of the core system at a high level of theory Ecore(high level theory) minus the energy of the core system at a lower level of theory Ecore(low level theory). This relationship is expressed in Eq. 2. It assumes that the error in the lower level method for the core is transferable to the total system.
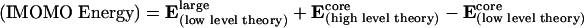 |
[2] |
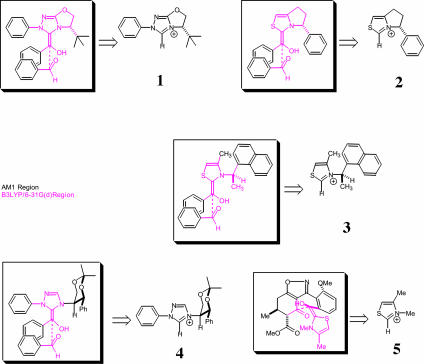
Fig. 4.
IMOMO–ONIOM layering scheme and catalysts for the five reaction systems studied.
Single-point B3LYP/6–31G(d) calculations were preformed on the optimized ONIOM structures. The transition-state structure corresponding to C–C bond formation for the simple reaction system of formaldehyde addition to N-methylthiazolium was calculated by using B3LYP/6–31(d) (Fig. 2). All transition states were characterized by analysis of the normal modes corresponding to their imaginary frequencies.
Results and Discussion
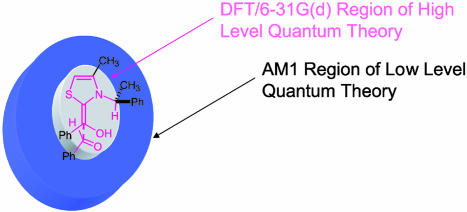
The prediction of product stereoselectivities computationally is an important challenge. A limitation of computational approaches is that most catalytic systems of interest are prohibitively large in size. The use of reliable theoretical methods, such as the well established hybrid density functional method, B3LYP, is often not feasible for catalyzed reactions of interest [exceptions to this general limitation include the modeling of proline-based catalysis by using B3LYP/6–31G(d) (1–3) and the Sharpless asymmetric dihydroxylations by quantum mechanics (on model system only) and force field calculations reported by Norrby and coworkers (21)]. This limitation was the impetus behind the selection of Morokuma's IMOMO variation of ONIOM for the present study. The basic premise of the IMOMO approach involves optimizing a small core region involving bond changes in the transition state by using a high level of theory while at the same time treating the remainder of the system with a simpler theoretical model (Fig. 3). In general, it was found that the ONIOM relative energies do not mirror experimental results. B3LYP/6–31G(d) single-point energies calculated by using ONIOM geometries were found to provide qualitative agreement with the sense and magnitude of the stereoselectivities.
Fig. 3.
Layering in the IMOMO–ONIOM method.
We have studied five different known stereoselective benzoin condensations. Four involve chiral catalysts, and one involves the reaction of a chiral ketone with an achiral thiazolium salt catalyst. For the diastereoselective crossed aldehyde-ketone benzoin condensation of Hachisu et al. (23), a structurally simplified achiral thiazolium catalyst was used and the ethyl ester group of the reacting substrate was replaced by a methyl ester (catalyst 5, Fig. 4). Depicted in Fig. 4 are the ONIOM layering schemes for the five reactions studied alongside the corresponding individual catalysts.
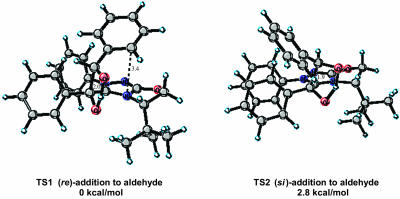
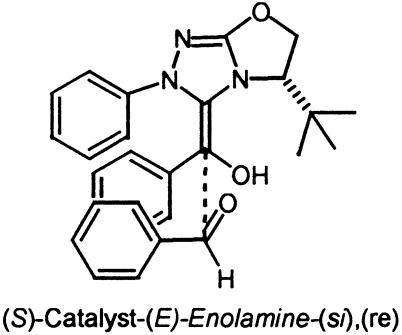
Catalyst 1, a highly selective triazolium catalyst prepared by Enders et al., was recently reported to afforded benzoin products from substituted benzaldehydes with enantioselectivities as high as 95%. The (S)-benzoin product from benzaldehyde was isolated in 83% yield and 90% ee in the presence of the (S)-catalyst. The two lowest-energy transition states for re and si addition on the benzaldehyde, both on the less-hindered si face of the enolamine, transition state (TS)1 and TS2, are depicted in Fig. 5. The calculated energies for the eight possible diastereomeric transition states are listed in Table 1. For this case, we report both the ONIOM energies and B3LYP/6–31G(d) single-point energies from optimized ONIOM geometries. In TS1 and TS2 the phenyl group of the enolamine is anti to the bulky tert-butyl group as shown in Fig. 5. In the lower-energy TS1 the aldehyde substituent is situated anti to the aromatic substituent of the enolamine and is also anti to the N-aryl group of the catalyst. The decisive factor influencing the relative energies of the two structures is the orientation of the aldehyde side chain with respect to the aromatic substituent of the enolamine and the N-aryl group of the catalyst. In addition, some π-aryl–iminium ion interaction may be present in the favored re transition state, TS1. The distance from the iminium ion to the aryl group of the approaching aldehyde is ≈3.4 Å, which is consistent with experimentally observed π-aromatic–iminium interactions (for a recent review discussing aromatic interactions in chemical and biological systems, see ref. 22). The calculations predict that the (S)-benzoin product will be formed in high ee, with re addition being preferred by 2.8 kcal/mol. A Boltzmann distribution using B3LYP/6–31G(d) single-point energies incorporating all structures residing within 4.0 kcal/mol of the lowest-energy structure (Table 1) predicts (S)-product formation with a selectivity of 98.2%. This predicted result correlates well with the experimental isolation of the (S)-benzoin product in 90% ee. In this example the magnitude of the ONIOM energies are overestimated. However, they do predict the correct sense of stereoinduction. For the remaining examples, only the B3LYP/ONIOM energies are reported.
Fig. 5.
Low-energy si and re transition-state structures for catalyst 1.
Table 1. Relative energies of the eight diastereomeric transition states for the benzoin condensation of benzaldehyde with catalyst I.
 Transition-state geometry* |
|||||
|---|---|---|---|---|---|
| Catalyst | Enolamine | Enolamine face | Aldehyde face | Product configuration | ΔGrel, kcal/mol† |
| S | E | si | re [TS1]‡ | S | 0 (0) |
| S | E | si | si [TS2]‡ | R | 2.8 (15.0) |
| S | Z | re | re | S | 2.9 (23.4) |
| S | E | re | re | S | 7.3 (21.6) |
| S | Z | si | re | S | 7.8 (4.5) |
| S | E | re | si | R | 8.4 (12.0) |
| S | Z | re | si | R | 9.8 (30.0) |
| S | Z | si | si | R | 17.8 (23.4) |
See Data Set 1, which is published as supporting information on the PNAS web site, for figures of structures and Cartesian coordinates.
Relative energies obtained by single-point B3LYP/6-31G(d) calculations. Energies in parentheses are relative energies calculated by using IMOMO (B3LYP/6-31G(d)//AM1).
Depicted in Fig. 5.
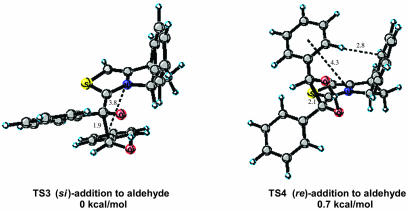
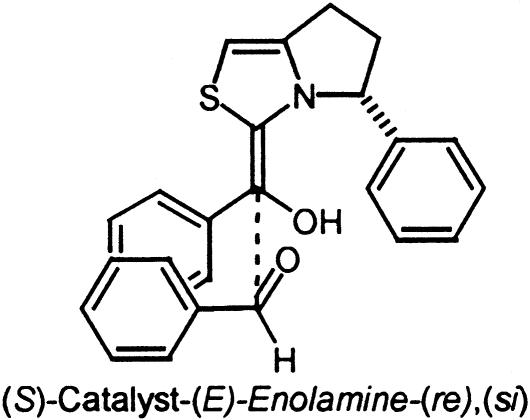
The bicyclic thiazolium catalyst 2 prepared by Knight et al. is reported to afford the (S)-benzoin product from benzaldehyde with low enantioselectivity (10.5% ee). The relative energies of the eight diastereomeric transition states for this system are listed in Table 2. The two transition states corresponding to the lowest energy si versus re modes of addition are depicted in Fig. 6. Within the IMOMO layering scheme for this system the aryl substituents are placed within the lower AM1 level of theory domain while the rest of the system is calculated by using higher-level B3LYP/6–31G(d) theory. In both TS3 and TS4 a π-aryl–iminium ion interaction is present. A noticeable difference between the two transition states is a repulsive aryl–aryl steric interaction noted in TS4 drawn in Fig. 6 between the aldehyde substituent and phenyl group of the catalyst. The si transition state TS3 is favored by 0.7 kcal/mol. The presence of this steric interaction results in less effective π-aryl–iminium ion stabilization, apparent from the larger displacement of the aldehyde aryl group away from the iminium ion in re transition state TS4. The distance between the iminium ion and aryl group in TS4 is ≈4.3 Å compared to ≈3.8 Å in the favored si transition state TS3. The greater stability of the si mode of addition is also reflected in a shorter C–C forming distance of 1.9 Å versus 2.1 Å in the re transition state.
Table 2. Relative energies of the eight diastereomeric transition states for the benzoin condensation with catalyst 2.
 Transition-state geometry* |
|||||
|---|---|---|---|---|---|
| Catalyst | Enolamine | Enolamine face | Aldehyde face | Product configuration | ΔGrel, kcal/mol† |
| S | E | re | si [TS3]‡ | R | 0 |
| S | E | si | re [TS4]‡ | S | 0.7 |
| S | Z | si | re | S | 0.8 |
| S | Z | re | re | S | 0.8 |
| S | E | si | si | R | 1.6 |
| S | E | re | re | S | 1.7 |
| S | Z | si | si | R | 5.9 |
| S | Z | re | si | R | 9.8 |
See Data Set 1 for figures of structures and Cartesian coordinates.
Relative energies obtained by single-point B3LYP/6-31G(d) calculations.
Depicted in Fig. 6.
Fig. 6.
Low-energy si and re transition-state structures for catalyst 2.
The relatively small energy difference (0.7 kcal/mol) between si and re addition is indicative of a nonselective process, as found experimentally (10.5% ee), in contrast to the predicted selectivity of 2.8 kcal/mol for the triazolium catalyst 1 of Enders. A Boltzmann distribution using those transition-state structures within 4.0 kcal/mol of the lowest-energy structure indicates that the (R)-product will be formed in 9.5% ee, in good agreement with the low level of stereoinduction observed experimentally [10.5% ee favoring (S)].
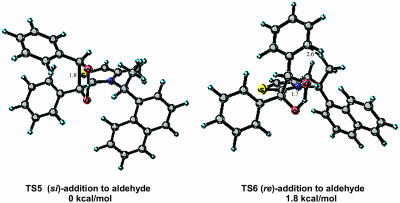
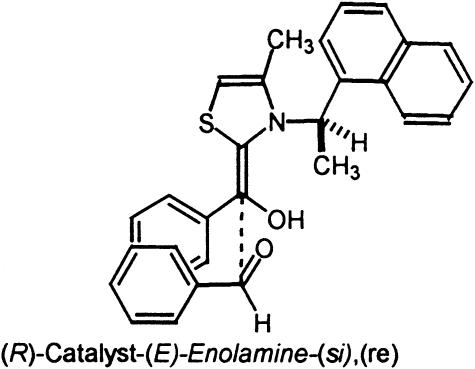
Next we turned our attention to the chiral catalyst 3 (R)-(+)-4-methyl-3-α-(1-naphthyl)ethylthiazolium prepared by Sheehan et al. (10). Catalyst 3 is reported to provide benzoin product of moderate optical enantiomeric enrichment (51% ee). Although moderate, this level of stereoinduction represents the highest enantioselectivity for any known thiazolium catalyst. In Fig. 7 are the two lowest-energy si and re transition states, TS5 and TS6. In general an (E)-stereoisomeric relationship of the enolic bond resulting in a trans relationship between the phenyl group and the sulfur atom was energetically preferred. The relative energies for the eight diastereomeric transition states are listed in Table 3. A repulsive α-CH3–aryl interaction of the aldehyde aryl substituent in transition state TS6 corresponding to re addition (calculated 2.6 Å) is destabilizing, resulting in a si selective process favoring TS5. The calculated Boltzmann distribution incorporating all transition-state structures residing within 4 kcal/mol of the lowest-energy transition-state structure predicts that catalyst 3 will afford the (R)-product in 91% ee (1.8 kcal/mol based on Boltzmann distribution). Experimentally, si addition leading to (R)-product formation in 51% ee is observed. The trend predicted by our model is correct, although the ee is overestimated. The computed 1.8 kcal/mol energy difference between the re and si transition-state structures is consistent with a moderately selective catalyst, as compared to the calculated energy preference of 2.8 kcal/mol for the highly selective bicyclic triazolium catalyst 1.
Fig. 7.
Low-energy si and re transition-state structures for catalyst 3.
Table 3. Relative energies of the eight diastereomeric transition states for the benzoin condensation with catalyst 3.
 Transition-state geometry* |
|||||
|---|---|---|---|---|---|
| Catalyst | Enolamine | Enolamine face | Aldehyde face | Product configuration | ΔGrel, kcal/mol† |
| R | E | si | si [TS5]‡ | R | 0 |
| R | E | si | re [TS6]‡ | S | 1.8 |
| R | E | re | re | S | 4.9 |
| R | Z | re | si | R | 7.3 |
| R | Z | re | re | S | 7.9 |
| R | E | re | si | R | 8.2 |
| R | Z | si | si | R | 10.3 |
| R | Z | si | re | S | 11.4 |
See Data Set 1 for figures of structures and Cartesian coordinates.
Relative energies obtained by single-point B3LYP/6-31G(d) calculations.
Depicted in Fig. 7.
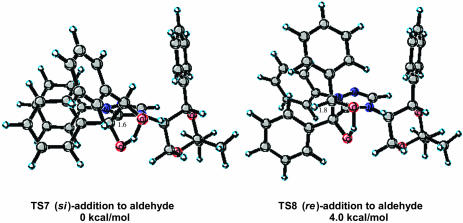
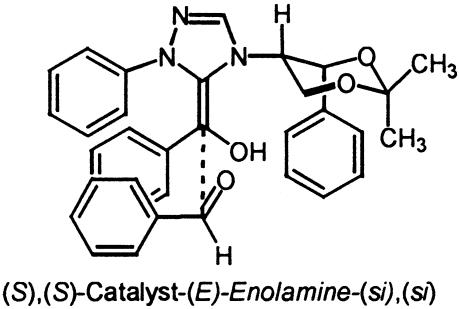
A more challenging system of study was the chiral catalyst 4 reported by Enders et al. (12) based on the large number of possible conformational isomers that might be available to this catalyst. Experimentally, this catalyst is reported to afford the (R)-benzoin product in 75% ee. The authors note that the enantioselectivity of the product decreased with increasing reaction time and increasing catalyst load, presumably because of partial racemization of the product by the catalyst. The isolated 75% ee represents that value optimized for catalyst turnover number (TON), product yield, and selectivity. From a computational perspective, factors of importance are as follows: (i) the expectation that calculated selectivities for this system would be overestimated because of product racemization; (ii) the accurate modeling of such as large system; and (iii) the large number of conformational states available to this catalyst. Key structural aspects of the stereodetermining low energy si transition state TS7 are the projection of the incoming aldehyde aryl substituent away from the catalyst and a short C–C bond length of 1.6 Å (Fig. 8). The competing low-energy re transition state TS8 suffers from an unfavorable steric interaction between the aldehyde aryl substituent and the phenyl group of the chiral auxiliary portion of the catalyst.
Fig. 8.
Low-energy si and re transition-state structures for catalyst 4.
In all of the transition states, the chiral dioxane group maintains the same conformation with an axial triazolium and equatorial phenyl (Fig. 8 and Data Set 1). The CH at the stereogenic center α to the triazolium ring has the CH pointing toward the enol oxygen, leaving the top face relatively crowded, because of the projecting phenyl, and the bottom face relatively unhindered. The calculations predict that the (R)-benzoin product will be formed in high ee. Carrying out a Boltzmann distribution as before predicts that the (R)-product will be formed in >99.8% ee. In practice the calculated high selectivity represents an experimental upper limit that is never realized, because of product racemization under the reaction conditions (Table 4).
Table 4. Relative energies of the eight diastereomeric transition states for the benzoin condensation with catalyst 4.
 Transition-state geometry* |
|||||
|---|---|---|---|---|---|
| Catalyst | Enolamine | Enolamine face | Aldehyde face | Product configuration | ΔGrel, kcal/mol† |
| S,S | E | si | si [TS7]‡ | R | 0 |
| S,S | E | si | re [TS8]‡ | S | 4.0 |
| S,S | E | re | si | R | 4.1 |
| S,S | E | re | re | S | 6.3 |
| S,S | Z | re | re | S | 8.8 |
| S,S | Z | si | re | S | 9.0 |
| S,S | Z | si | si | R | 10.1 |
| S,S | Z | re | si | R | 12.9 |
See Data Set 1 for figures of structures and Cartesian coordinates.
Relative energies obtained by single-point B3LYP/6-31G(d) calculations.
Depicted in Fig. 8.
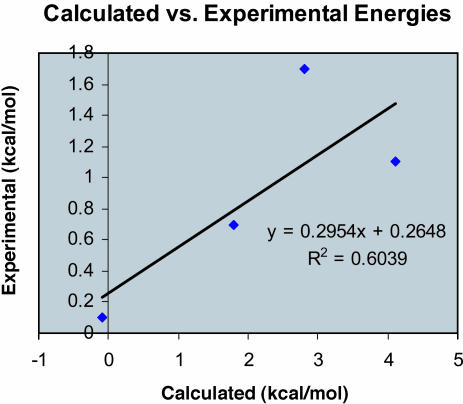
A comparison between calculated and experimental stereoselectivities for the four enantioselective catalysts, 1–4, was carried out to determine the relative accuracies of the method used. Table 5 lists the calculated and experimental energies, as well as the difference between the two. Fig. 9 is a graph of experimental versus calculated energies for catalysts 1–4.
Table 5. Comparison of prediction and experiment for enantioselective reactions for catalysts 1–4.
| Catalyst | Calculated ΔΔG≠* | Experimental ΔΔG≠ | ΔΔΔG≠ (Calc-Exp) |
|---|---|---|---|
| 1 | 2.8 | 1.7 | 1.1 |
| 2 | -0.1† | 0.1 | -0.2 |
| 3 | 1.8 | 0.7 | 1.1 |
| 4 | 4.1 | 1.1 | 3.0 |
| Mean absolute average error = 1.4 kcal/mol | |||
Energies are in kcal/mol and represent values derived from calculated Boltzmann distributions.
Negative value means a theoretical preference for the minor isomer found experimentally.
Fig. 9.
Graph of calculated versus experimental differences in free energies of activation for reactions involving catalysts 1–4.
With the exception of 2, for which no selectivity is predicted, the selectivities for the other three catalysts is overestimated by 1.4 kcal/mol on average. Unfortunately, this error is comparable to the ΔΔG≠ values found for these catalysts. The prediction of the correct major product is useful and will aid in studies directed toward the development of new catalysts, but greater accuracy will be required for the useful prediction of selectivities.
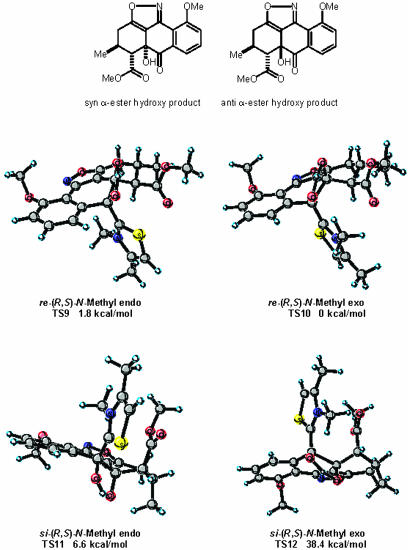
We have also modeled a diastereoselective intramolecular crossed aldehyde-ketone benzoin reaction recently reported by Hachisu et al. (catalyst 5) (23). To simplify these calculations, the N-ethyl group of the catalyst was exchanged for an N-methyl and the ethyl alcohol substituent truncated. In addition the ethyl ester of the substrate was replaced with a methyl ester. The four diastereomeric transition states for this reaction are depicted in Fig. 10. In the two lowest-energy transition states, TS9 and TS10, the catalyst and α-ester group are on opposite faces of the substrate with respect to one another. Moreover, of these two, an (E)-stereomeric relationship of the enolic bond as in TS10 in which the N-methyl group of the thiazolium catalyst possess an exo-orientation is preferred by 1.8 kcal/mol. The preference for TS10 is the result of an unfavorable steric interaction between the endo-oriented N-methyl group and substrate in TS9 that is not present TS10. In transition states TS11 and TS12 the thiazolium catalyst and α-ester group are eclipsing and reside on the same face of the substrate. As a result of the unfavorable eclipsing interaction between the α-ester and thiazolium catalyst, TS11 and TS12 are higher in energy and would led to product having a relative stereochemistry with an anti α-ester hydroxy group orientation. Experimentally, the α-ester and hydroxy group derived from umpolung addition of aldehyde to ketone share a syn relationship and reside on the same face of the molecule (Fig. 10, syn α-ester hydroxy product). The energetically preferred transition states, TS9 and TS10, would lead to the formation of a product having the same relative stereochemistry as that observed by experiment. The experimental diastereo-selectivity of this process is reported to be >20:1 with the α-ester and hydroxy group of the product possess a syn relationship. Based on the 6.6 kcal/mol energy difference between the stereodivergent transition states, TS10 and TS11, a diastereo-selectivity of >20:1 is predicted. This calculated result correlates well with observed experiment.
Fig. 10.
Transition-state structures for the intramolecular crossed aldehydeketone benzoin reaction of Hachisu et al. (23).
Conclusion
The enantioselective organocatalyzed benzoin condensation has been studied by using Morokuma's IMOMO–ONIOM method. The use of IMOMO B3LYP/6–31G(d)/AM1 for transition-state optimization, followed by single-point B3LYP/6–31G(d) calculations, afforded predictions in qualitative agreement with experiment. By using this methodology it was possible to model large reaction systems. The present approach can be a useful predictive tool for exploring and understanding the origins of stereoselectivities of large catalytic systems. This computational methodology represents a valuable method that should be an aid to the de novo design of new asymmetric catalysts.
Supplementary Material
Acknowledgments
This work was supported by the National Institute of General Medical Sciences of the National Institutes of Health.
This paper was submitted directly (Track II) to the PNAS office.
Abbreviations: IMOMO, integrated MO (molecular orbital) + MO method; ONIOM, n-layered integrated molecular orbital method; TS, transition state.
References
- 1.Bahmanyar, S. & Houk, K. N. (2001) J. Am. Chem. Soc. 123, 12911–12912. [DOI] [PubMed] [Google Scholar]
- 2.Bahmanyar, S., Houk, K. N., Martin, H. J. & List, B. (2003) J. Am. Chem. Soc. 125, 2475–2479. [DOI] [PubMed] [Google Scholar]
- 3.Bahmanyar, S. & Houk, K. N. (2003) Org. Lett. 5, 1249–1251. [DOI] [PubMed] [Google Scholar]
- 4.Kozlowski, M. C. & Panda, M. (2003) J. Org. Chem. 68, 2061–2076. [DOI] [PubMed] [Google Scholar]
- 5.Knight, R. L. & Leeper, F. J. (1998) J. Chem. Soc. Perkins Trans. 1, 1891–1893.
- 6.Knight, R. L. & Leeper, F. J. (1997) Tetrahedron Lett. 38, 3611–3614. [Google Scholar]
- 7.Gerhard, A. U. & Leeper, F. J. (1997) Tetrahedron Lett. 38, 3615–3618. [Google Scholar]
- 8.Tagaki, W., Tamura, Y. & Yano, Y. (1980) Bull. Chem. Soc. Jpn. 53, 478–480. [Google Scholar]
- 9.Sheehan, J. C. & Hunneman, D. H. (1966) J. Am. Chem. Soc. 88, 3666–3667. [Google Scholar]
- 10.Sheehan, J. C. & Hara, T. (1974) J. Org. Chem. 39, 1196–1199. [Google Scholar]
- 11.Enders, D. & Kallfass, U. (2002) Angew. Chem. Int. Ed. Engl. 41, 1743–1745. [DOI] [PubMed] [Google Scholar]
- 12.Enders, D. & Breuer, K. (1996) Helv. Chim. Acta 79, 1217–1221. [Google Scholar]
- 13.Breslow, R. (1958) J. Am. Chem. Soc. 80, 3719–3726. [Google Scholar]
- 14.Martí, J., López-Calahorra, F. & Bofill, J. M. (1995) Theochem 339, 179–194. [Google Scholar]
- 15.Lemal, D. M., Lovald, R. A. & Kawano, K. I. (1964) J. Am. Chem. Soc. 86, 2518–2519. [Google Scholar]
- 16.Dapprich, S., Komiromi, I., Byun, K. S., Morokuma, K. & Frisch, M. J. (1999) Theochem 461–462, 1–21. [Google Scholar]
- 17.Torrent, M., Vreven, T., Musaev, D. G., Morokuma, K., Farkas, O. & Schlegel, H. B. (2002) J. Am. Chem. Soc. 124, 192–193. [DOI] [PubMed] [Google Scholar]
- 18.Liu, Z., Torrent, M. & Morokuma, K. (2002) Organometallics 21, 1056–1071. [Google Scholar]
- 19.Humbel, S., Sieber, S. & Morokuma, K. (1996) J. Chem. Phys. 105, 1959–1967. [Google Scholar]
- 20.Frisch, M. J., Trucks, G. W., Schlegel, H. B., Scuseria, G. E., Robb, M. A., Cheeseman, J. R., Zakrzewski, V. G., Montgomery, J. A., Jr., Stratmann, R. E., Burant, J. C., et al. (1998) gaussian 98 (Gaussian, Pittsburgh), Revision A.7.
- 21.Norrby, P.-O., Rasmussen, T., Haller, J., Strassner, T. & Houk, K. N. (1999) J. Am. Chem. Soc. 121, 10186–10192. [Google Scholar]
- 22.Meyer, E. A., Castellano, R. K. & Diederich, F. (2003) Angew. Chem. Int. Ed. Engl. 42, 1210–1250. [DOI] [PubMed] [Google Scholar]
- 23.Hachisu, Y., Bode, J. W. & Suzuki, K. (2003) J. Am. Chem. Soc. 125, 8432–8433. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.