Assessing blood coagulation status with laser speckle rheology

Abstract

We have developed and investigated a novel optical approach, Laser Speckle Rheology (LSR), to evaluate a patient’s coagulation status by measuring the viscoelastic properties of blood during coagulation. In LSR, a blood sample is illuminated with laser light and temporal speckle intensity fluctuations are measured using a high-speed CMOS camera. During blood coagulation, changes in the viscoelastic properties of the clot restrict Brownian displacements of light scattering centers within the sample, altering the rate of speckle intensity fluctuations. As a result, blood coagulation status can be measured by relating the time scale of speckle intensity fluctuations with clinically relevant coagulation metrics including clotting time and fibrinogen content. Our results report a close correlation between coagulation metrics measured using LSR and conventional coagulation results of activated partial thromboplastin time, prothrombin time and functional fibrinogen levels, creating the unique opportunity to evaluate a patient’s coagulation status in real-time at the point of care.

1. Introduction

The normal coagulation process, termed hemostasis, is the body’s defense mechanism to prevent severe blood loss due to uncontrolled bleeding. Blood coagulation involves multiple plasma proteins (coagulation factors), platelets, and red blood cells (RBCs) that work together through a cascade of biochemical processes to stop bleeding following injury [1]. Coagulopathy, a condition in which blood coagulation is impaired, can result from a variety of conditions including severe trauma, illness or surgery [2, 3], and can cause life-threatening bleeding or thrombotic disorders. For instance, deficient blood coagulation can lead to ‘hypo-coagulable’ states resulting in prolonged or uncontrolled bleeding, which may cause severe anemia, shock and multiple organ failure [4, 5]. In other cases, coagulation defects may manifest as ‘hyper-coagulable’ states, causing increased clotting that can result in potentially fatal complications such as deep vein thrombosis and pulmonary embolism [6]. Coagulopathies may also be inherited [7], occurring due to abnormalities in levels of coagulation factors and defective platelet function, or may be acquired due to chronic illness or the use of certain anti-inflammatory or anticoagulant agents further complicating clinical care [2, 8].

During surgery, trauma care and chronic disease management, clinicians often encounter the challenging task of maintaining a precarious balance between bleeding and coagulation. The early identification and management of coagulopathic patients to reverse coagulation defects is a desirable goal, in effort to save lives and significantly improve patient outcome. Traditionally, most clinicians rely on a battery of conventional coagulation tests (CCTs), conducted in a central coagulation laboratory to measure key coagulation metrics, mainly activated thromboplastin time (aPTT), prothrombin time (PT), and fibrinogen levels, to assess a patient’s coagulation status [9]. However, given the requirement to transport and centrifuge the specimen, the turnaround time is often too long (1-5 hours) for CCTs to be reliable for informing blood transfusion or anti-coagulant therapy particularly in the context of rapidly changing coagulation conditions in critically ill or injured patients [10] Therefore, novel methods that enable the assessment of a patient’s coagulation status rapidly at the point of care are critical in identifying patients at an elevated risk of bleeding defects and tailoring treatment protocols to improve patient recovery.

A real-time indicator of blood coagulation status can be obtained by monitoring changes in the viscoelastic properties of clotting blood, in turn associated with key underlying biochemical process in the coagulation cascade. A key mechanism in the coagulation process involves the conversion of fibrinogen into insoluble stands of fibrin through catalytic action of the protease thrombin. This is followed by subsequent fibrin cross-linking and platelet adhesion leading to the formation of a platelet-fibrin mesh which increases the viscoelastic modulus of clotting blood [11]. As a result, by measuring changes in the viscoelastic properties of blood, clotting time can be assessed, which is an important indicator of the patient’s coagulation status. As coagulation progresses the viscoelastic modulus of the blood clot attains a plateau level after the fibrin mesh has been formed. Because fibrin cross-linking is dependent in part on fibrinogen content, the maximum plateau modulus provides information on blood fibrinogen levels [12].

In this study, we have investigated and validated a new optical approach, Laser Speckle Rheology (LSR) [13–19], for assessing the viscoelastic properties of blood during coagulation, therefore opening the opportunity to assess the patient’s coagulation state rapidly using just a few drops of whole blood.

Laser speckle, a random intensity pattern that occurs by the interference of coherent light scattered from tissue, is exquisitely sensitive to the passive Brownian motion of intrinsic light scattering particles [20]. In a viscoelastic medium such as blood, the Brownian motion of light scattering centers is directly related to the viscoelastic properties of the medium [21–23]. Consequently, during the coagulation process, the increasing stiffness of the blood clot caused by the formation of a fibrin-platelet mesh restricts scatterer displacements, eliciting a slower rate of speckle intensity fluctuations compared to un-clotted blood. Because scatterer motion causes a modulation of the laser speckle pattern (Fig. 1(A) ), the measurement of the time scale of speckle intensity fluctuations should provide information about the viscoelastic properties of clotting blood.

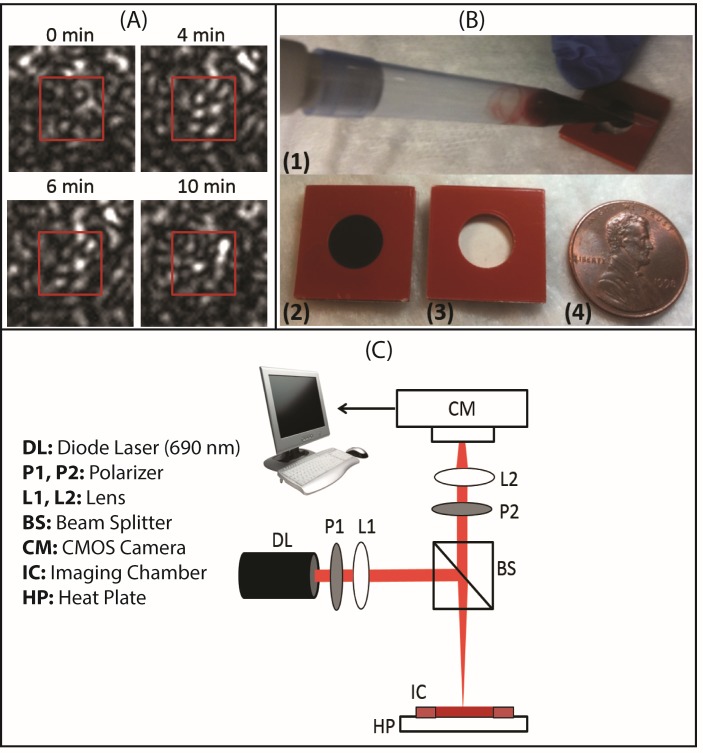
Fig. 1.

(A) Laser speckle patterns captured from a human blood sample showing time-dependent speckle intensity modulation during coagulation at 0, 4, 6 and 10 min following coagulation activation with kaolin. (B) Blood sample cartridge employed for LSR measurements (Grace Bio-Labs). The cartridge consists of a small chamber (volume = 100 μL) made of a blood compatible silicon base sandwiched between thin (0.15 mm) polycarbonate sheets. The clear polycarbonate sheet provides a clear optical window for LSR measurements. (C) Schematic diagram of the LSR optical setup used for blood coagulation assessment. Polarized light (690 nm, 9 mW) from a diode laser (Newport Corp., LPM690-30C) was focused (spot size 100 µm) on the imaging chamber containing ~100 µL of kaolin-activated blood. Cross-polarized laser speckle patterns were acquired at 180° back-scattering geometry via a beam-splitter using a high speed CMOS camera (Basler AG, acA2000-340km) equipped with a focusing lens (Edmund Optics, NT59-872). The captured speckle patterns were transferred to a computer for further processing.

In the current study, we first evaluate the accuracy of LSR in assessing changes the viscoelastic modulus of human blood during coagulation via comparison with standard reference mechanical testing. Next, we investigate the capability of LSR to measure clotting time and functional fibrinogen levels in whole blood samples obtained from patients and compare LSR findings with corresponding conventional coagulation tests (CCTs). The close correlation between LSR and CCT results observed in this study establishes the capability of estimating the coagulation status of patients in real-time from laser speckle fluctuations.

2. Materials and methods

2.1 Blood sample preparation

The human blood protocol was approved by the institutional review board (IRB) of the Massachusetts General Hospital (MGH). Whole blood samples from fifty patients were obtained from the MGH special coagulation laboratory and collected in 3.2% citrate blue top tubes (volume = 3 ml) for analysis. Prior to LSR evaluation, blood coagulation was initiated in each sample via kaolin-based activation of the intrinsic coagulation pathway using published protocols that have been well established for use in prior coagulation studies using other devices [24–28]. Briefly, each citrated blood sample was warmed to 37 °C in a water bath (for 5 minutes) and 1 ml of blood was pipetted into vials pre-loaded with a kaolin buffer solution (Haemoscope Corp, Kaolin 6300). To activate coagulation, the blood sample was re-calcified by adding 0.2M calcium chloride (~60µL) to the kaolin vial. After 5 gentle vial inversions, ~100 µL of the kaolin-activated whole blood was immediately loaded into a blood sample cartridge consisting of a silicone base and transparent optical window (Fig. 1(B), Grace Bio-Labs, RD475023) to begin LSR evaluation as described below.

2.2 LSR evaluation during blood coagulation

The optical setup shown in Fig. 1(C) was employed to capture time-varying laser speckle patterns from the blood sample during coagulation [13–17]. Linearly polarized light from a laser diode source (690 nm, Newport Corp.) was directed and focused to a 100 µm spot on the imaging chamber containing the kaolin-activated blood sample. The power on the sample was 9 mW. In back-scattering geometry, cross-polarized laser speckle patterns (Fig. 1(A)) were acquired via a beam-splitter using a high speed CMOS camera (Basler AG, acA2000-340km). Speckle patterns were detected in cross-polarized mode to minimize specular reflections of incident linearly polarized laser light in the captured speckle pattern and isolate the detection of randomly polarized backscattered light that has interacted with the blood sample. The imaging region of interest (ROI) covering an 8 × 8 mm area of the sample was imaged to 512 × 512 pixels of the CMOS sensor (5.5 × 5.5 μm pixel size). The speckle size was adjusted to at least twice the CMOS pixel size to ensure sufficient spatial sampling of each speckle spot and to avoid averaging of multiple speckles over a single pixel that could increase blurring and reduce speckle contrast in the measured speckle intensity autocorrelation curve [29–31]. To evaluate temporal speckle intensity fluctuations during coagulation, time series of laser speckle patterns were acquired at a frame rate of 480 frames per second (fps) for 0.5 s at a time, at 30 s time increments during coagulation. For each sample, LSR evaluation was performed for a total imaging duration of 20 minutes to evaluate the entire blood coagulation process. As a result, a total of 40 time series of 240 speckle frames (2 time series acquisitions per minute) were captured for each blood sample. A heating plate was incorporated in the setup to maintain the temperature of the blood sample at 37 °C during LSR evaluation.

2.3 Analyzing temporal speckle intensity fluctuations during blood coagulation

Laser speckle patterns acquired during blood coagulation were analyzed to measure the clotting time and maximum clot stiffness. In order to measure the rate of speckle intensity fluctuations during blood coagulation, the temporal speckle intensity autocorrelation curve, g₂(t), (Fig. 2(A) ) was measured via cross-correlation analysis of the first speckle frame with each subsequent frame within the frame series using previously described methods [13–17]. To obtain adequate ensemble averaging and improve the accuracy of speckle temporal statistics, spatial averaging was performed over (512x512 pixels) and temporal averaging was performed over multiple g₂(t) curves that evolved over 0.5 s duration as follows [13–17, 19, 22, 23]:

$$g_2(t)={\langle \frac{{\langle I(t_0)I(t_0+t)\rangle }_{pixels}}{\sqrt{{\langle I{(t_0)}^2\rangle }_{pixels}{\langle I{(t_0+t)}^2\rangle }_{pixels}}}\rangle }_{t_0}$$ (1)

In the equation above, I(t₀) and I(t₀ + t) defines the speckle intensities at times t₀ and t₀ + t, and < >pixels and < >t₀ indicates spatial and temporal averaging over all the pixels and over the 0.5 s duration respectively. The speckle intensity temporal autocorrelation function, g₂(t) therefore represents the correlation between speckle intensities at times t₀ and t₀ + t. Therefore, while the average speckle intensity remains relatively constant over different frames, the correlation between the first speckle pattern and subsequent patterns decreases for temporally fluctuating speckle patterns. The spatial (or ensemble) averaging operation is performed on the product of speckle intensities at times t₀ and t₀ + t for individual pixels, <I(t₀)I(t₀ + t)>_pixels and the product is then normalized to the $\sqrt{{\langle I{(t_0)}^2\rangle }_{pixels}{\langle I{(t_0+t)}^2\rangle }_{pixels}}$to ensure that g₂(t = t₀) = 1. Additionally temporal averaging is performed over multiple g₂(t) curves that evolve in time to improve the statistical accuracy of the final g₂(t) curve. The time scale of temporal speckle intensity fluctuations was measured by calculating the speckle autocorrelation time constant, τ, computed by fitting a single exponential model function to the g₂(t) curve measured as above and calculating time constant of exponential model function [13–17, 19]. Because the time scale of speckle fluctuations is directly related to the viscoelastic properties of the blood sample, the speckle autocorrelation time constant, τ, of the g₂(t) curve provided an index of clot viscoelasticity. Time constants, τ, were similarly measured for each speckle time series at 30 s time increments and plotted over the entire imaging time, 0<t≤ 20 min, to obtain a time constant trace, τ(t) (Figs. 2(B) and 3 ). For comparison with mechanical rheometry, the LSR measurements were replicated three times for a human blood sample and the average τ at each time increment was plotted during coagulation, with the error bars representing the standard deviation (Fig. 2(B)).

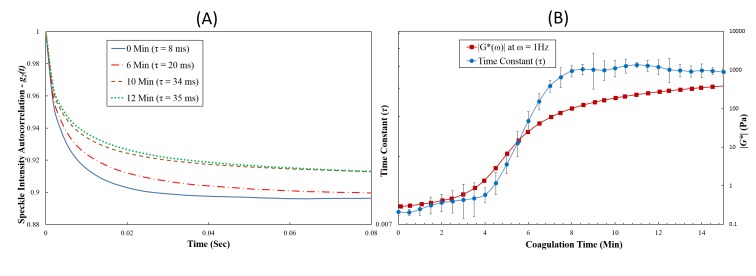
Fig. 2.

(A) Speckle intensity autocorrelation curve, g₂(t), measured at 0, 6, 10, and 12 minutes during coagulation process from a human blood sample. It was observed that g₂(t) decay slowed down as blood coagulation progressed. No significant change in the g₂(t) decay trend was observed after completion of clot formation. Slower g₂(t) decay and the corresponding increase in speckle autocorrelation time constant (τ) indicated an increase in clot viscoelastic modulus during coagulation process. (B) Speckle autocorrelation time constant, τ (primary y-axis), and the viscoelastic modulus |G*(ω)|_{ω = 1} Hz (secondary y-axis) plotted as a function of coagulation time for a human blood sample. Similar trends were observed for both the τ, and |G*| curves during coagulation. In each case, the average value of the three LSR τ-measurements is plotted and the error bars depict standard deviations.

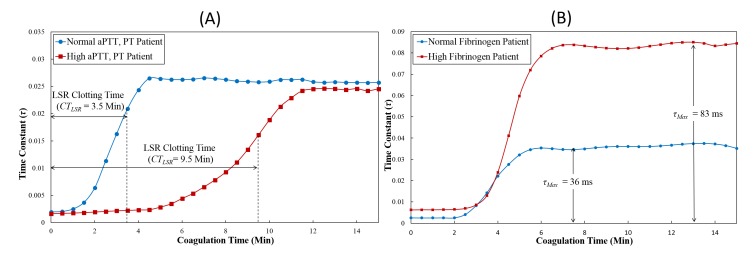
Fig. 3.

Time trace of the speckle autocorrelation time constant, τ(t), (A) Blood sample with normal aPTT and PT showed shorter clotting time, CT_LSR in comparison to blood sample with prolonged aPTT and PT values. (B) Maximum clot stiffness (τ_Max) can also be estimated from the τ(t) curve. Increased τ_Max is measured for the blood sample from the patient with high fibrinogen level indicating increased clot viscoelastic modulus in comparison with the blood sample from a normal fibrinogen patient.

2.4 Measurement of blood viscoelastic properties using standard mechanical testing

The accuracy of the LSR approach in estimating the viscoelastic properties of clotting blood was investigated by comparing the LSR time constant trace, τ(t) with standard mechanical testing measurements. A standard mechanical rheometer (AR-G2, TA Instruments, MA) was used in a time-lapsed fashion to measure the magnitude of the viscoelastic modulus, |G*|, during blood coagulation (Fig. 2(B)). A sample of whole blood (2 mL) was loaded between the bottom plate and a 40 mm stainless steel parallel top plate. To minimize the delay between coagulation activation and mechanical measurements, re-calcification of kaolin-activated citrated blood was directly performed on the rheometer tool by mixing ~120 µL of CaCl₂ on the bottom plate followed by quickly lowering the top plate in position to begin measurement. Using a strain of 1% as the control variable, a time sweep measurement of |G*| was performed at single tool oscillation frequency of 1 Hz over 20 minutes following kaolin activation of the coagulation process. Similar to the LSR procedure, viscoelastic moduli, |G*|, were recorded every 30s during coagulation. All measurements were performed at 37 °C. The time trace of |G*| measured using the AR-G2 rheometer during coagulation was compared with the corresponding speckle autocorrelation time constant, τ(t) trace measured using LSR (Fig. 2(B)).

2.5 Assessing blood coagulation metrics using LSR

For each patient blood sample, the LSR clotting time (CT_LSR), and maximum clot stiffness (τ_Max) were calculated from the τ(t) trace (Fig. 3). To measure CT_LSR values, the first-order derivative of the τ(t) curve was calculated and the time at which the derivative reached a maximum value was recorded (Fig. 3(A)). The maximum clot stiffness (equal to τ_Max) was calculated as the average plateau value of the speckle autocorrelation time constant, τ, measured over a 5 minute duration (Fig. 3(B)). For all samples, the clotting time, CT_LSR measured from LSR was compared with corresponding values of blood clotting time based on CCT results of activated partial thromboplastin time (aPTT) and prothrombin time (PT) using the linear regression analysis (Figs. 4(A) , 4(B)). CT_LSR was compared with aPTT because both tests initiate coagulation by kaolin-activation of the intrinsic pathway of blood coagulation [32]. A number of coagulation abnormalities in patients that affect aPTT also influence PT similarly; therefore, we also compared CT_LSR with PT values [1]. Additionally, the levels of soluble fibrinogen in blood is directly related to the extent of the polymerization of insoluble fibrin strands, which in turn influences the maximum viscoelastic modulus of the fully formed blood clot [11]. Therefore, the maximum clot stiffness metric, τ_Max, measured by LSR was compared with functional fibrinogen levels on subset of samples (N = 25) for which fibrinogen levels were clinically reported (Fig. 4(C)).

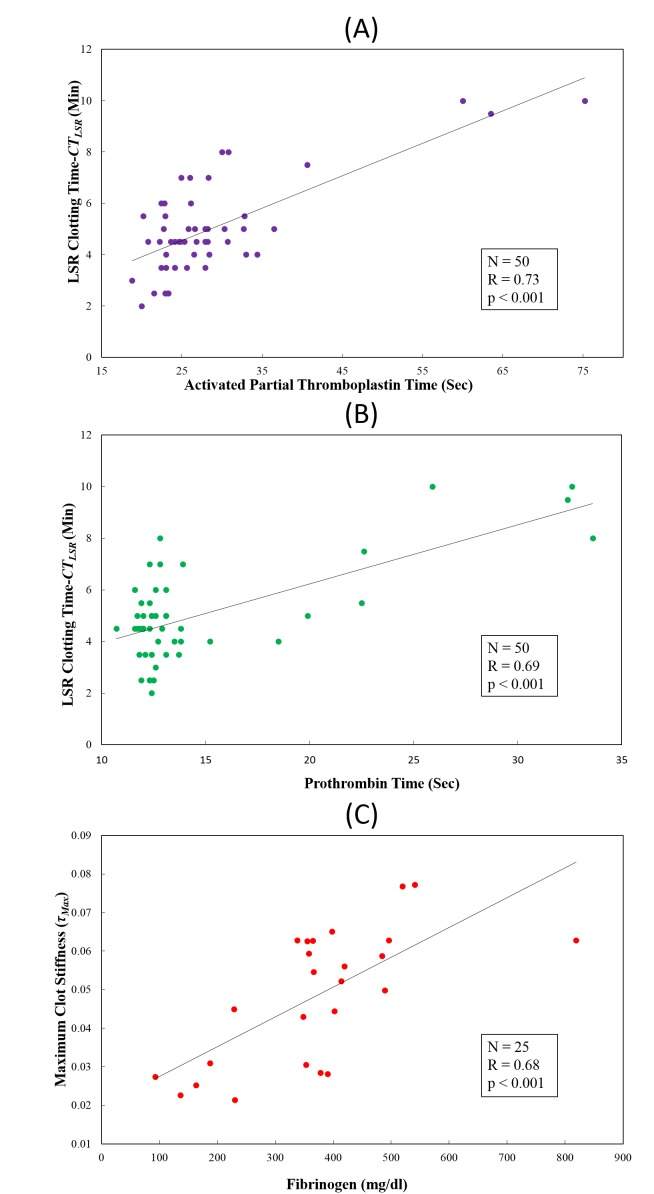
Fig. 4.

Comparison of LSR clotting time (CT_LSR) measured with (A) activated partial thromboplastin time (aPTT) and (B) Prothrombin time (PT) in 50 patient blood samples. (C) Comparison of maximum clot stiffness, τ_Max with fibrinogen levels in 25 blood samples. A statistically significant strong positive correlation with conventional coagulation tests (CCT) results in all cases demonstrates the utility of LSR for blood coagulation assessment.

3. Results

3.1 LSR versus mechanical rheometry of human whole blood

In this section we present results of the time-lapse analysis of blood mechanical properties during coagulation using both LSR and standard reference mechanical rheometry. Figure 2(A) shows temporal intensity autocorrelation curves, g₂(t) plotted with the corresponding speckle autocorrelation time constant, τ, values reported prior to kaolin activation (0 min), and at 6, 10 and 12 minutes following kaolin activation of blood coagulation. It is clear that the decay rate of the g₂(t) curve was modulated throughout the coagulation process. Prior to kaolin activation, the low viscosity blood specimen exhibited a fast decay of the g₂(t) curve due to the rapid displacements of scattering particles, corresponding to a τ-value of ~8 ms. Following re-calcification and kaolin activation of coagulation factors, g₂(t) curves exhibited a slower trend with a corresponding increase in τ (τ = 20 ms at 6 min to τ = 34 ms at 10 min) as seen in Fig. 2(A). After the blood coagulation process attained equilibrium characterized by a fully-formed, fibrin-platelet clot, there was only a negligible change in the decay rate of the g₂(t) curves, as indicated by measured time constants (τ = 34 ms at 10 Min and τ = 35 ms at 12 Min). We also observed the plateau level at longer times of the g₂(t) curve is raised during coagulation (as shown in Fig. 2(A)) due to changes in both the mechanical and optical properties of the clotting blood as discussed later.

Figure 2(B) shows results of the time-lapsed LSR measurements of speckle autocorrelation time constant, τ(t), measured at 30s intervals in a human blood sample during coagulation (blue line with circular marker). The corresponding |G*| values measured for the same blood sample using the AR-G2 rheometer following kaolin activation of blood coagulation are plotted in the same graph for comparison (red line with square marker). A close correspondence between the trends of both τ(t) and |G*| was observed as coagulation progressed. During early coagulation times (t< 4 min) τ exhibited only a negligible change (from 8 ms at t = 0 min to 9 ms at t = 4 min) consistent with the low |G*| values (from 0.3 to 1.4 Pa at identical clotting times) evaluated by the mechanical rheometer. This indicates that initially, blood exhibits the characteristics of a viscous material of low modulus exhibiting rapid temporal speckle fluctuations with low τ and corresponding low |G*| values. During the progression of coagulation (between 4 to 8 min) due to the slower rate of temporal speckle fluctuations, τ increased exponentially with time in a manner consistent with the growth of viscoelastic moduli. Subsequently, at t = 8 min, the τ value increased to 33 ms with the corresponding increase of the viscoelastic modulus (|G*| = 100 Pa). Following stabilization of the coagulation process at later clotting times (t > 8 min), both the τ(t) and |G*| traces approached saturation levels.

3.2 LSR versus CCT results in patients

In this section, we compare LSR and CCT results for the 50 patient blood samples analyzed in the current study. A large variation in CCT results was reported with aPTT values ranging from 20.2 to 75.2 s, PT values from 11.6 to 33.6 s and fibrinogen levels from 93 to 819 mg/dl. Figure 3(A) shows representative time-lapse LSR plots for two patient blood samples, describing the temporal evolution of the τ(t) trace during coagulation for a blood sample with normal aPTT (24.9 s) and PT (12.8 s), and coagulopathic sample with high aPTT (63.5 s) and PT (32.4 s). The normal ranges of aPTT and PT are 22.0-35.0 s and 11.0-14 s respectively. In the blood sample obtained from the normal patient, τ(t) remained a constant low value during early coagulation times of t < 1.5 min indicating a negligible alteration in the viscoelastic modulus of the blood sample during the initial phases following coagulation activation. Following this phase, a rapid increase in the τ-value was observed, during coagulation times corresponding to t < 4.5 min likely due to fibrin polymerization and platelet adhesion within the fibrin network during clot progression. In the plateau phase of τ(t) plot (>4.5 min), no significant change in τ was observed indicating completion of the clot formation process. For the blood sample obtained from a coagulopathic patient with prolonged aPTT and PT values, the τ-value remained a constant low value until ~5 min after kaolin-activation compared with <1.5 min for the normal patient. The prolonged clotting duration observed for the coagulopathic blood sample may be the result of delayed fibrin polymerization due to low levels of coagulation factors characterized by the prolonged aPTT and PT values. After a duration of 5 minutes, the measured τ increased to attain a maximum plateau level at ~12 min, but at a significantly slower rate than the normal sample, indicating a diminished rate of fibrin polymerization in the coagulopathic sample. As a result, the LSR clotting time, CT_LSR = 9.5 minutes, measured for the coagulopathic sample was significantly higher than that of the normal blood sample with CT_LSR = 3.5 minutes. LSR τ(t) trace was also used to provide information about maximum clot stiffness indicated with τ_Max which was expected to indicate levels of fibrinogen. Figure 3(B) shows the time lapse trace of τ from a patient with normal fibrinogen level and a patient with high fibrinogen level (378 and 541 mg/dl fibrinogen respectively). The normal range of fibrinogen level in patients is 150-400 mg/dl. We observed that the maximum clot stiffness for the patient with high fibrinogen level was larger (τ_Max = 83 ms) in comparison to the normal patient (τ_Max = 36 ms).

In Figs. 4(A) and 4(B) the LSR clotting time, CT_LSR measured from for all 50 patient blood samples are plotted versus aPTT and PT values obtained from CCTs. It is evident that for the pooled data, clotting times measured using LSR demonstrated a statistically significant positive correlation with aPPT (r-value = 0.73, p < 0.001) as well as with PT (r-value = 0.69, p < 0.001). Furthermore, for the subset of 25 samples, the maximum clot stiffness (τ_Max) measured by LSR demonstrated a close correlation with the available CCT results of functional fibrinogen levels (r-value = 0.68, p < 0.001) as shown in Fig. 4(C). The strong positive correlation between clot viscoelasticity index measured with LSR and fibrinogen levels may be associated with the fact that the time scale of speckle intensity fluctuations, given by τ_Max of the stabilized clot is proportional to total fibrin generation which is in turn related to fibrinogen levels in blood as discussed below.

4. Discussion

In this study, we have investigated the capability of LSR to evaluate blood coagulation status by estimating the viscoelastic properties of clotting blood in real-time from time-varying speckle intensity fluctuations. The results demonstrate that the temporal evolution of the speckle autocorrelation time constant, τ, during coagulation is closely associated with alterations in viscoelastic moduli measured by reference standard mechanical rheometry. Blood coagulation metrics derived from the time-lapsed LSR trace, τ(t), showed a close correlation with the CCT values of clotting time given by aPTT and PT, as well as with functional fibrinogen levels in patients. The capability of LSR to assess blood coagulation status in real-time as demonstrated in this study will open new opportunities for assessing a patient’s blood coagulation status at the point of care.

The analysis of laser speckle patterns has been investigated for a number of biomedical applications such as the measurement of blood flow and tissue perfusion [33, 34] and for skin surface roughness assessment [35]. LSR is distinct in that as it measures the viscoelastic properties of blood from time-resolved laser speckle intensity fluctuations to determine blood coagulation status in patients. We have previously demonstrated the capability of LSR for characterizing the viscoelastic properties of phantom materials, bio-fluids, and solid tissue [13–17, 19]. In LSR, the viscoelastic properties of a material are estimated by relating laser speckle intensity fluctuations with the viscoelastic susceptibility of the surrounding medium [21, 36–38]. By employing a high-speed CMOS camera to simultaneously probe multiple speckle spots, we can measure spatially and temporally averaged g₂(t) curves that are highly sensitive to heterogeneous dynamic changes in the viscoelastic properties of clotting blood.

We have been previously shown that the decay rate of the measured g₂(t) curve given by the speckle autocorrelation time constant, τ, correlates with the viscoelastic modulus, |G*|, measured by a conventional mechanical rheometer for phantoms and tissue samples over a wide range of mechanical moduli [17]. Here, we investigate these methods to estimate the coagulation status of patient blood samples. During blood coagulation, an increase in the viscoelastic modulus of clotting blood affects the rate of speckle fluctuations via reduction of the extent of passive thermal displacements of light scattering particles such as platelets and red and white blood cells. The displacement of light scattering centers can be defined by the mean square displacement (MSD), denoted by <Δr²(t)>, which is related with the measured speckle autocorrelation function, g₂(t) as [21, 38, 39]:

$$g_2(t)=\beta e^{-2\gamma \sqrt{k^2\langle \Delta r^2(t)\rangle +\frac{3{\mu }_a}{{\mu }_s(1-g)}}}+1$$ (2)

where k is the wave vector in the scattering medium which can be further expressed as k = 2πn/λ (n is the refractive index of the medium and λ is the wavelength of the incident laser light), γ is an experimental parameter related to the source-detector distance and polarization state of light, β corresponds to the coherence of the collected light, and µ_a, µ_s, and g define the absorption and scattering coefficients and the anisotropy factor of the blood sample respectively [37, 40]. Further, MSD of the scattering particles is related with viscoelastic modulus of the sample via generalized Stokes-Einstein equation as [21, 36, 41]

$$G^{*}\left(\omega \right)=\frac{K_{b}T}{a\pi \langle \Delta r^2(1/\omega )\rangle \Gamma \left[1+\alpha (\omega )\right]}$$ (3)

where K_b is the Boltzmann constant, a is the average radius of light scattering particle, and T is the temperature in Kelvin, the local power law $\alpha (\omega )$ is given by${\left|\alpha (\omega )=\frac{dln\langle \Delta r^2(t)\rangle }{d\ln t}\right|}_{t=1/\omega }$ and Γ denotes the gamma function. From Eq. (2), (3) and Figs. 2(A) and 2(B), it is evident that during early stages of the coagulation process, due to the lower viscoelastic modulus of blood (~0.1 Pa) increased MSD contributes to a rapid decay of g₂(t) eliciting a low value of the time constant, τ. As coagulation progresses, the rapid increase in the viscoelastic modulus of blood (0.1 to 100 Pa) elicits reduced MSD of light scattering particles (Eq. (3) causing a deceleration of the g₂(t) curve and a higher resultant τ (Eq. (2). After completion of coagulation, the viscoelastic modulus and the associated MSD approach saturation levels imposing no further change in the decay rate of g₂(t). In Fig. 2(A) we also observe a rise in the plateau of the g₂(t) curve at longer times during the progression of coagulation which further indicates changes in the mechanical properties of clotting blood. During blood coagulation, the formation of the fibrin network entraps platelets and RBC’s within the clot, subsequently restricting the motion of light scattering centers. As a result, scatterers may initially diffuse freely at early times represented by the rapid decay of the g₂(t) curve, and at later times particle motion is restricted by interaction with the fibrin mesh characterized by saturated particular MSD. This time-dependent evolution of the MSD can be described as: $\langle r^2(t)\rangle =r_0^2(1-e^{-t/{\tau }_D})$, where $r_0$ is the saturated MSD and ${\tau }_D$ is the diffusion time constant of Brownian particles [22, 42]. As previously described, the viscoelastic modulus, G*(ω) for this model can be re-written as [17, 23, 36, 39, 41]-

$$G^{*}\left(\omega \right)=\frac{K_{B}T}{\pi a{r}_0^2}(1+j{\tau }_D\omega )=\frac{K_{B}T}{\pi a{r}_0^2}+j\frac{K_{B}T{\tau }_D\omega }{\pi a{r}_0^2}$$ (4)

As shown earlier for phantom materials [17], the first term on the right hand side of the Eq. (4) corresponds to the elastic or storage modulus, G’(ω) and the second term correspond to the loss or viscous modulus, G”(ω). Equation (4) suggests that at low frequencies (ω), G*(ω) is dominated by G’(ω), and the low frequency behavior of G*(ω) corresponds to the behavior of g₂(t) at long times (t α 1/ω). As a result, the longtime behavior of g₂(t) measured during coagulation may have a major contribution from clot elastic modulus and the increase in the plateau of g₂(t) during coagulation is likely a result of increase in the blood clot elasticity. In addition to the effects of sample mechanics, the evolution of the g₂(t) curve is also influenced in part by factors such as the optical properties of blood (Eq. (2) and speckle contrast [19, 43, 44]. We have previously demonstrated that an increase in optical scattering can accelerate the decay rate of the measured g₂(t) curve independent of sample mechanical properties due to an increase in the number of scattering events per optical path [19]. Also, absorption of light can reduce the contribution of longer optical paths resulting slower speckle decorrelation at initial times of g₂(t) decay. During coagulation, the optical properties of blood change due to platelet aggregation, formation of fibrin monomers, their polymerization and crosslinking, and trapping of blood cells in fibrin-platelet clot, which all likely result in the change in the number and average size of the light scattering centers. Therefore, blood optical properties, in particular scattering coefficient, µ_s, anisotropy factor, and g, are altered during the coagulation process. By incorporating methods to accurately estimate blood optical properties during coagulation from laser speckle patterns, the effects of blood viscoelastic properties can be isolated from optical factors from the measured g₂(t) curves [14, 19, 45].

To evaluate the viscoelastic properties of clotting blood using a mechanical rheometer (Fig. 2(B)), the |G*| trace was evaluated at a single frequency of ω = 1 Hz, defining the low frequency mechanical properties of the blood specimen. The close association observed between mechanical testing and LSR is evident from the temporal trends of τ and |G*| during the course of blood coagulation. From these results we infer that LSR is highly sensitive to small changes in the mechanical properties of clotting blood arising from the sensitivity of the g₂(t) curve to minute displacements of scattering particles in the order of an optical wavelength. In other words the intensity of the captured speckle pattern will be modulated if intrinsic particles in the illuminated blood sample are displaced by a fraction of an optical wavelength. During the blood clotting process, the low viscosity blood sample evolves to form a viscoelastic solid clot eliciting constrained motion of intrinsic scattering particles. LSR quantifies these small gradual changes in viscoelastic properties with high sensitivity because it can measure optical phase shifts caused by particle displacements by measuring changes in speckle intensity. In our analysis τ values were obtained by fitting a single exponential to the speckle autocorrelation g₂(t) curve over the first 300 ms. In the case of a complex viscoelastic material such as blood however, the trend of the g₂(t) curve can be better described as a combination of multiple exponential functions each with distinct time constants. Therefore, depending on the time interval over which a single exponential function is fitted (300 ms in this case), the measured τ reflects an average of particle relaxation times.

The LSR time trace for normal and coagulopathic blood samples are plotted in the Fig. 3(A) and 3(B). The longer CT_LSR value (coagulopathic patient with high aPTT, PT in Fig. 3(A)) indicates abnormalities in the levels of coagulation factors which likely reduce the rate of thrombin generation and in turn influence the conversion of fibrinogen into fibrin. This subsequently also contributes to a slower rate of clot formation, as evidenced by the rising slope of the τ(t) trace. Clotting time, CT_LSR measured with LSR showed good correlation with aPTT as both measurements were performed by utilizing kaolin-based activation which initiates the intrinsic pathway of coagulation by activating coagulation factor XII [32]. Our results also demonstrate a strong correlation with PT, which is measured using tissue factor which initiates coagulation via the extrinsic pathway by activating coagulation factor VII [32]. Although CT_LSR and PT activate different pathways of coagulation cascade, the observed correlation is likely due to the fact that most pathological conditions affect both coagulation pathways similarly. For instance, liver dysfunction, vitamin K deficiency, disseminated intravascular coagulation (DIC), coagulation factor II, V, or X deficiency, or the use of anticoagulants such as Coumadin, heparin, argatroban, dabigatran, etc., prolong both aPTT and PT [1]. Due to these reasons, in our study we indeed observed a strong correlation between aPTT and PT (r-value = 0.81, p < 0.001).

The plateau phase of the time trace, τ(t), at later times of the coagulation process (Figs. 3(A), 3(B)) provides information on the maximum clot stiffness (expressed as τ_Max) of a fully stabilized blood clot. The maximum clot stiffness is dependent on the extent of fibrin network formation and is in turn proportional to the fibrinogen content in blood [11, 46]. Therefore, in our study we observe a larger τ_Max in patients with abnormally high fibrinogen levels in comparison with normal patients (Fig. 3(B)). It is important to mention here that the presence of aggregated platelets may also contribute to the increased viscoelastic modulus of the stabilized clot. During blood coagulation, platelets serve as cross-linking sites during formation of fibrin network and exert contractile forces on the fibrin scaffold via the protein thrombosthenin which further increases the stiffness of the blood clot [47]. As a result, platelet count and platelet function may also likely to affect τ_Max which will be further evaluated in future studies.

The close correlation between LSR-based coagulation metrics and CCT results of aPTT, PT, and fibrinogen (Fig. 4) demonstrate the utility of LSR for blood coagulation assessment in real-time. In Fig. 4(A) and 4(B) it can be observed that while a strong positive correlation exists, the absolute values of clotting time measured with LSR and CCT are not identical. These differences may be attributed to the differences in the coagulation activator concentration and the use of whole blood employed in LSR versus CCT protocols. An additional advantage of LSR over CCT tests is that CCT is conducted on blood-derived plasma, while LSR is conducted on whole blood which more closely resembles the hemostasis process in vivo in comparison to CCTs. Our current LSR system can provide coagulation result in < 10 minutes which is much faster than is typically possible with conventional CCTs. We anticipate that the LSR reporting time can be further significantly reduced by activating both intrinsic and extrinsic pathway of coagulation with kaolin and tissue factor, based on studies done with a different system [48]. The LSR instrument requires only few drops of blood for assessing blood coagulation status. Thus, LSR may be implemented in the future using a simple finger prick blood test, reducing the need for excess blood draws as in the case of CCTs. The illumination and detection mechanism of LSR which requires a miniature laser source to illuminate the blood sample and a small CMOS sensor to capture the speckle pattern time series, can be miniaturized to fabricate a hand-held device for point of care or home use. The laser source employed in LSR is similar to a commonly used laser pointer and although risk of retinal damage during use is very unlikely; in future devices for clinical use, the laser beam can be entirely enclosed within an opaque device housing to mitigate any potential risk of eye damage by the laser beam.

To address the need for point of care blood coagulation sensing, devices such as Thromboelastography (TEG) and rotational thromboelastometry (ROTEM) have been investigated [10]. These methods involve mechanically stirring blood in a cup and measuring changes in blood viscoelastic properties during clotting. However, both TEG and ROTEM are large instruments that are difficult to operate and require specialized operators and training, and interpreting results can be challenging. These limitations have restricted the clinical adoption of TEG and ROTEM for use at the bedside. To overcome these limitations, new approaches for point of care coagulation assessment have been recently reported. Some of these approaches include the use of quartz crystal [49–51], magnetoelastic transducers [52, 53] or MEMS based devices [54]. These sensing methodologies measure clotting time via contact based mechanical perturbation of the sample which likely interferes with the natural coagulation process. As a result, new non-contact techniques such as surface plasmon resonance sensor [55, 56] and ultrasound-based methods [57–59] have also been investigated. However, surface plasmon resonance sensor evaluates coagulation status by monitoring changes in the refractive index of clotting and is not sensitive to clot stiffness, whereas ultrasound based techniques require significant amount of blood (> 1 ml) for coagulation measurement. Recently, other optical methods that include speckle analysis have also been reported that measure changes in speckle contrast via low frame rate image acquisition to estimate coagulation status [60, 61].

The demonstrated capability of LSR for the non-contact and rapid assessment of the viscoelastic properties of blood during coagulation opens unique opportunities for detecting coagulation defects in patients in real-time at the bedside. In the future, we anticipate that the development and translation of a hand-held LSR instrument for coagulation assessment will likely serve as a powerful tool for detecting bleeding and thrombotic conditions, optimizing treatment or blood transfusion protocols, and monitoring anti-coagulation therapy at the patient bedside.