Abstract
We propose a novel blind compressive sensing (BCS) frame work to recover dynamic images from under-sampled measurements. This scheme models the the dynamic signal as a sparse linear combination of temporal basis functions, chosen from a large dictionary. The dictionary and the sparse coefficients are simultaneously estimated from the under-sampled measurements. Since the number of degrees of freedom of this model is much smaller than that of current low-rank methods, this scheme is expected to provide improved reconstructions for datasets with considerable inter-frame motion. We develop an efficient majorize-minimize algorithm to solve for the dynamic images. We use a continuation strategy to minimize the convergence of the algorithm to local minima. Numerical comparisons of the BCS scheme with low-rank methods demonstrate the significant improvement in performance in the presence of motion.
1. INTRODUCTION
Dynamic MRI (DMRI) is a key component of many clinical exams such as cardiac, perfusion, and functional imaging. Achieving high spatio-temporal resolution in DMRI is often challenging due to fundamental hardware limitations. Several acceleration schemes that exploit the compact structure or sparsity in pre-determined transform domains (eg: temporal Fourier, wavelet domains) [1, 2] were introduced to accelerate breath-held cardiac MRI. However, these methods fail to give good reconstructions when the motion or contrast changes are not periodic because the structure/sparsity of the signal in the Fourier transform domain is considerably disturbed. Recently, several authors have proposed to model the dynamic signal as a linear combination of few principal temporal basis functions (eg: [3, 4, 5]). Since the bases and its corresponding coefficients are directly estimated from the data, these low-rank promoting schemes are also termed as blind linear models (BLM). These schemes are capable of providing high accelerations, when inter-frame motion is not significant. However, when the inter-frame motion is large (eg. free breathing imaging), many basis functions are required to accurately represent the signal; this often limits the maximum possible acceleration. Specifically, in such scenarios, these methods can result in spatio-temporal blurring when operated at high accelerations.
To overcome the above mentioned challenges, we introduce a novel dynamic imaging scheme based on blind compressive sensing (BCS) [6]. This is the first application of the BCS scheme to dynamic imaging, to the best of our knowledge. In classical compressive sensing, the transform or dictionary is fixed. In contrast, BCS estimates the optimal dictionary from the data. While this approach is similar to BLM, the main difference is that the profiles at each voxel are modeled as a sparse linear combination of basis functions from a larger dictionary than in BLM. Since only very few basis functions are active at each voxel, this is essentially a locally low-rank representation. Note that the basis functions in the dictionary are not necessarily orthogonal to each other (see Fig. 1). The significantly larger number of basis functions in the BCS dictionary considerably improves the approximation of the dynamic signal, especially for datasets with significant inter-frame motion. While the approximation quality of BLM schemes can also be improved by increasing the number of basis functions, the overhead in estimating them grows linearly with the size of the dictionary, thus limiting the maximum possible acceleration. Specifically, the degrees of freedom (DOF) in the BLM representation is approximately r(M + N − 2r), where M is the number of voxels in one frame, N is the number of temporal frames, and r is the number of basis functions. Since the number of voxels is often much greater than the number of frames (eg: M = 17100 and N = 50 in our application), the degrees of freedom can be approximated as rM. In contrast, the degrees of freedom associated with BCS is Mk + RN, where k is the average sparsity of the coefficients and r is the number of basis functions in the dictionary. Thus, the degrees of freedom in the BCS scheme is dominated by the average sparsity and not the size of the dictionary, for realistic dictionary sizes. Since k << r, we expect the blind compressive sensing representation to be more compact than the blind linear model. Hence, we expect the BCS scheme to provide improved reconstructions in datasets with significant inter-frame motion.
Fig. 1.

Comparison of BCS and BLM representations of dynamic imaging data: The Casorati form of the dynamic signal Γ is shown in (a). The BLM and BCS decompositions of Γ are shown respectively in (b), (c). BCS uses a large over-complete dictionary, unlike the orthogonal dictionary with few basis functions in BLM. Note that the coefficients/ spatial weights in BCS are sparser than that of BLM. The temporal basis functions in the BCS dictionary are representative of specific regions, since they are not constrained to be orthogonal. For example, the 1st, 2nd columns of UM × R in BCS correspond respectively to the temporal dynamics of the right and left ventricles in this myocardial perfusion data with motion. We observe that only 2–3 coefficients per pixel are sufficient to represent the dataset.
We introduce a novel algorithm to jointly estimate the sparse coefficients (denoted by the M × R matrix U) and the dictionary of temporal basis functions (indicated by the R×N matrix V) directly from the under-sampled DMRI data. The Casorati matrix of the dataset is the product of these matrices Γ = UV (see Fig. 1). We pose the recovery of the coefficients and the dictionary as an unconstrained optimization problem, where we use the sparsity promoting ℓ1 prior on the entries of U and a Frobenius norm penalty on V. We use a majorize minimize algorithm to simplify the problem into three simpler problems; the proposed alternating minimization scheme cycles through the solutions of these problems to determine the optimal solution. We use a continuation strategy using a Huber penalty, parameterized by a single parameter β. The penalty is quadratic in nature when β is small, when the solution is equivalent to the nuclear norm solution, since R >> r [7]. As we increase β, the solution converges to that of the BCS problem. Our experiments confirm that this approach is able to eliminate the local minima problems.
This approach has some similarity to the local low rank scheme in [8]. However, the basis functions at each voxel are independent from each other in [8]. In contrast, pixels that are not close can still share the same basis functions in the BCS method. The proposed scheme encourages the exploitation of similarities between voxels that are far away (for eg: see the 3rd column of UM × R in Fig. 1). Hence, we expect these non-local interactions to provide improved reconstructions.
2. BCS FOR DYNAMIC MRI
Denoting the spatio-temporal signal by γ(x, t), the goal is to recover it from sparse noisy Fourier samples b(ki, ti):
| (1) |
Here, (ki, ti) represents the ith sampling location in the k − t space and n, the additive white noise. The above expression can be rewritten in a vector form as b = 𝒜(γ) + n, where 𝒜 represents the Fourier sampling operator.
2.1. The objective function
Using the Casorati matrix representation [3], BCS models the dynamic signal as a product of a sparse coefficient matrix U and a dictionary matrix V containing over-complete temporal basis functions:
| (2) |
Recall that the columns of Γ correspond to the voxels of each time frame. The ith column of U contains the coefficients, of the ith temporal basis function (ith row of the dictionary V). We pose the simultaneous estimation of U and V subject to data consistency constraint as:
| (3) |
We use a sparsity promoting l1 norm on the entries of U and an energy minimizing Frobenius norm on V to make the problem well posed. We use a continuation strategy, where we start by solving for simpler problems and progressively update the solution to promote l1 sparsity, to minimize local minima problems.
2.2. The optimization algorithm
We approximate the l1 norm penalty in (3) by a Huber induced norm, which is parametrized by β, resulting in the below cost:
| (4) |
Here, is the Huber-induced norm; (ui,j are the entries of U). The Huber function is specified as:
| (5) |
Note that when β = 0, the Huber norm is the quadratic Frobenius norm; as shown in [7], the solution to (4) would be equivalent to the minimum nuclear norm solution, since R here is greater than the rank of Γ. When β → ∞, the Huber norm approximates the l1 norm and the problem in (4) approximates the original problem in (3).
We now majorize the Huber function as:
| (6) |
where L is an auxiliary variable. Substituting (6) in (4), we obtain the following modified cost, which has to be now minimized with respect to three variables U, V and L:
| (7) |
We use an alternating minimization scheme to solve (7) with respect to each variable, assuming the other two variables to be fixed. This results in the following subproblems:
| (8) |
| (9) |
| (10) |
(8) involves l1 shrinkage of Un and can be solved analytically as:
| (11) |
where ‘+’ represents the shrinkage operator defined as (τ)+ = max{0, τ}. The problems in (9) and (10) are quadratic; we solve it by using simple conjugate gradient (CG) algorithms.
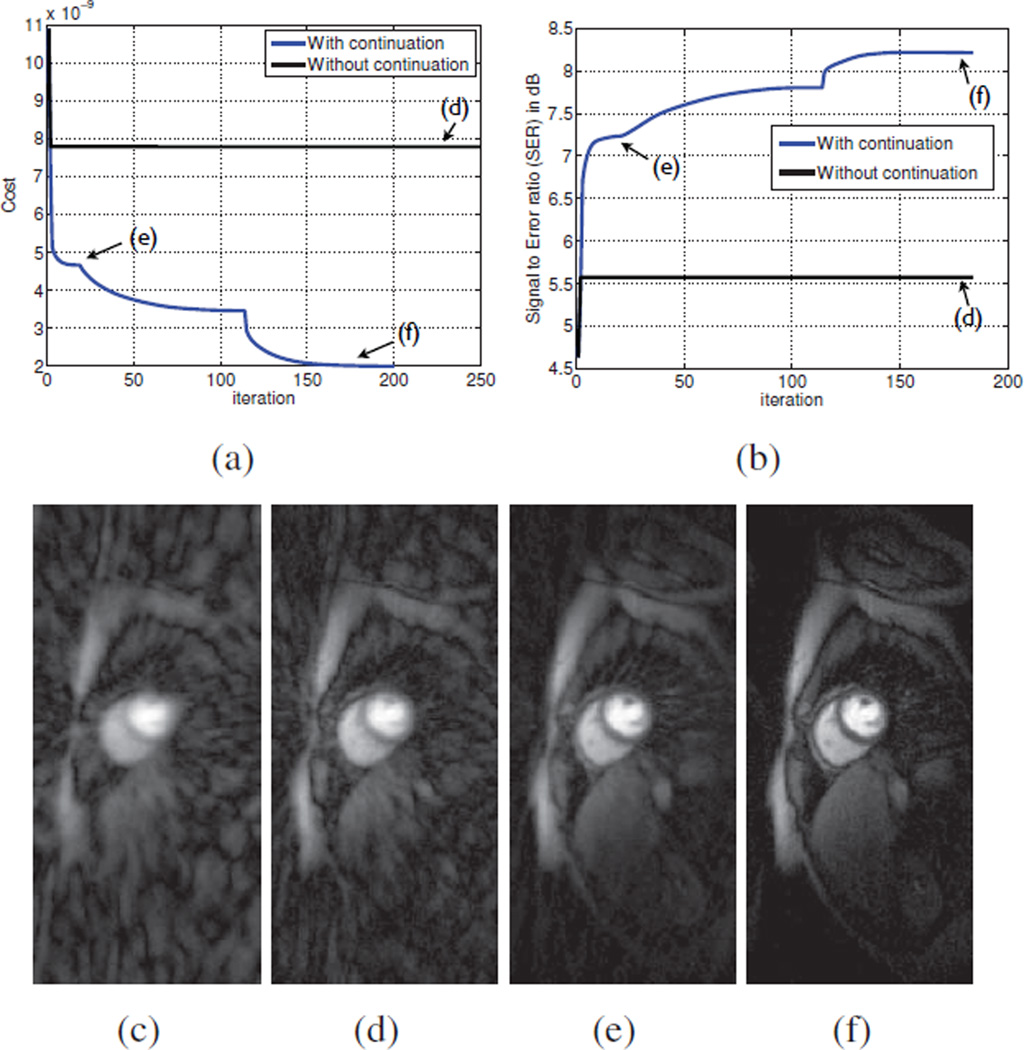
Iterating between (8) to (10) using a high value of β can have many CG steps (due to ill conditioning of (9)). In addition, the algorithm may converge to a local minimum if it is initialized directly with a large value of β. Hence, we use a continuation approach to solve for simpler problems initially and progressively increase the complexity. Specifically, starting with random matrix initializations of U and V, the algorithm iterates between (8) and (10) in an inner loop, while progressively updating β starting with a small value in an outer loop. The inner loop is terminated when the cost in (3) stops decreasing and the outer loop is terminated when a large enough β is achieved. The role of continuation in avoiding local minima is described in figure 2 on a myocardial perfusion data set (see section 3 for the data specifications, the sampling mask and the BCS model order used).
Fig. 2.
(a): Cost in (3) v/s iteration, (b): SER (dB) v/s iteration, (c): Direct IFFT reconstruction for reference. A spatial frame of the reconstructions (d): without continuation, fixed β = 1010, (e): with low β = 105 and (f): with continuation, start with β = 105 and increment till β = 1010. The cost with continuation decreases monotonically avoiding any possible local minima as seen while fixing β to a large value in (d). Specifically (d) gets stuck in modeling the basis functions corresponding to error artifacts; (compare d and c). Also shown is the iterate during low β in (e), which is an equivalent nuclear norm solution. As β is increased during continuation, the algorithm converges to the BCS solution in (f).
3. EXPERIMENTS
We demonstrate the utility of BCS in reconstructing a myocardial perfusion data set with significant motion content. We consider retrospectively down sampling one slice from a fully sampled Cartesian acquisition (phase × frequency encodes × time = 90 × 190 × 70) acquired using a saturation recovery FLASH sequence on a Siemens 3T scanner (3 slices, TR/TE =2.5/1.5 ms, sat. recovery time = 100 ms). The motion in the data was due to improper gating and/or breathing; (see the ripples in the time profile in fig 2(c)). We consider a radial trajectory with 12 uniformly spaced rays within a frame with subsequent random rotations across frames to achieve incoherency. This corresponded to a net acceleration level of 7.5. This acceleration can be capitalized to improve many factors in the scan (eg: increase the number of slices, improve the spatial resolution).
A total number of 45 temporal bases were considered in BCS. The regularization parameters λ1 and λ2 were tuned based on maximizing the signal to error (SER) ratio between the reconstructions and the fully sampled data.
| (12) |
We observe that setting λ2 significantly lower than λ1 yields better reconstructions. We evaluated different continuation schemes in terms of speed of convergence to the same solution (different thresholds in the inner loop and different increments of β in the outer loop). We picked the best one which converged in about 45 mins using a MATLAB implementation on a linux work station with a quad core AMD processor and 16 GB RAM. We expect a significant speedup by using methods such as the augmented Lagrangian [9] and by capitalizing on the parallelism in the code and using graphical processing units.
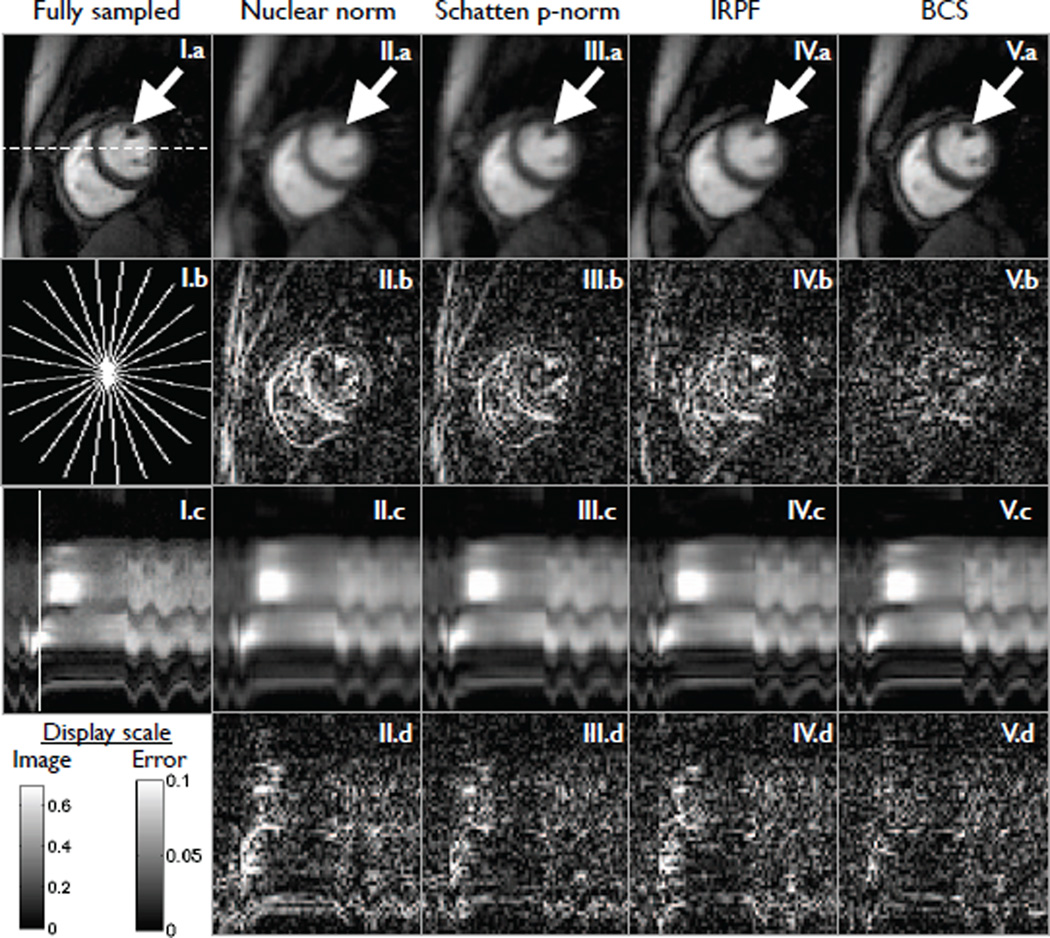
We compare BCS algorithm against the following BLM schemes: (a) nuclear norm (NN) minimization [5], (b) Schatten p-norm (Sp-N) (p = 0.1) minimization [5] and (c) incremented rank power factorization (IRPF) schemes [4]. A total of 14 bases were considered in the IRPF method. The optimum number of bases in IRPF, optimum regularization parameters in NN and Sp-N were chosen based on maximizing the SER between the reconstructions and the fully sampled data. We observe BCS to obtain efficient reconstructions, which are robust to several compromises observed with the BLM schemes. Specifically, at this acceleration level, the frames with significant motion content and contrast are considerably blurred with the BLM methods, due to aggressive rank reduction. In contrast as the BCS scheme promotes efficient selection of the temporal bases, it robustly represents these regions with minimum spatio-temporal blur.
4. CONCLUSION
We introduced a novel frame work for blind compressed sensing in the context of dynamic imaging. The model represents the dynamic signal as a sparse linear combination of temporal basis functions from a large dictionary. An efficient majorize-minimize algorithm with continuation was used to simultaneously estimate the sparse coefficient matrix and the dictionary bases. Results against low rank models show significant improvement with the proposed scheme in being robust to spatio-temporal blurring and efficiently preserving fine structural details in the reconstructions.
Fig. 3.
Retrospective downsampling of a fully-sampled myocardial perfusion data set with motion at 7.5 fold acceleration: The radial trajectory for one frame is shown in (I.b). The trajectory is rotated by random shifts in each temporal frame. Different schemes along with the fully sampled data are shown in (I) to (V). (a), (b), (c), (d) respectively show a spatial frame, corresponding error image, image time profile, corresponding error time profile. The image time profile in (c) is through the dotted line in (I.a). The ripples in (I.c) correspond to the motion due to inconsistent gating and/or breathing. The location of the spatial frame along time is marked by the solid line in (I.c). We observe the BCS scheme to be robust to spatio-temporal blurring, compared to the BLM schemes; eg: see the white arrows where the details of the papillary muscles are blurred in the nuclear norm, Schatten p-norm and the IRPF schemes while maintained well with BCS. This is depicted in the error images as well, where BCS (V.b) has diffused errors while the BLM schemes (II–IV.b) have structured errors corresponding to the anatomy of the heart. Similar behavior was seen in other frames as well, especially in frames that contain motion and contrast variations.
ACKNOWLEDGEMENT
We thank Dr. Edward DiBella, University of Utah for providing the myocardial perfusion data set used in this study.
This work is supported by NSF awards CCF-0844812 and CCF-1116067.
REFERENCES
- 1.Jung H, Park J, Yoo J, Ye JC. Radial k-t focuss for high-resolution cardiac cine mri. Magn Reson Med. 2009 Oct; doi: 10.1002/mrm.22172. [DOI] [PubMed] [Google Scholar]
- 2.Lustig M, Santos J, Donoho D, Pauly J. kt sparse: High frame rate dynamic mri exploiting spatio-temporal sparsity. Proceedings of the 13th Annual Meeting of ISMRM; Seattle. 2006. p. 2420. [Google Scholar]
- 3.Liang Z. Spatiotemporal imaging with partially separable functions. Biomedical Imaging: From Nano to Macro, 2007. ISBI 2007. 4th IEEE International Symposium on; IEEE; 2007. pp. 988–991. [Google Scholar]
- 4.Haldar J, Liang Z. Spatiotemporal imaging with partially separable functions: a matrix recovery approach. Biomedical Imaging: From Nano to Macro, 2010 IEEE International Symposium on; IEEE; 2010. pp. 716–719. [Google Scholar]
- 5.Lingala S, Hu Y, DiBella E, Jacob M. Accelerated dynamic mri exploiting sparsity and low-rank structure: k-t slr. IEEE Transactions on Medical Imaging. 2011;vol. 30(no. 5):1042–1054. doi: 10.1109/TMI.2010.2100850. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Gleichman S, Eldar Y. Blind compressed sensing. Information Theory, IEEE Transactions on. 2011;vol. 57(no. 10):6958–6975. [Google Scholar]
- 7.Recht B, Fazel M, Parrilo P. Guaranteed minimum-rank solutions of linear matrix equations via nuclear norm minimization. Arxiv preprint arxiv:0706.4138. 2007 [Google Scholar]
- 8.Trzasko J, Manduca A. Local versus global low-rank promotion in dynamic mri series reconstruction. ISMRM. 2011:4371. [Google Scholar]
- 9.Afonso M, Bioucas-Dias J, Figueiredo M. An augmented lagrangian approach to the constrained optimization formulation of imaging inverse problems. Image Processing, IEEE Transactions on. 2011;vol. 20(no. 3):681–695. doi: 10.1109/TIP.2010.2076294. [DOI] [PubMed] [Google Scholar]