Predicting reading outcomes with progress monitoring slopes among middle grade students

Abstract

Effective implementation of response-to-intervention (RTI) frameworks depends on efficient tools for monitoring progress. Evaluations of growth (i.e., slope) may be less efficient than evaluations of status at a single time point, especially if slopes do not add to predictions of outcomes over status. We examined progress monitoring slope validity for predicting reading outcomes among middle school students by evaluating latent growth models for different progress monitoring measure-outcome combinations. We used multi-group modeling to evaluate the effects of reading ability, reading intervention, and progress monitoring administration condition on slope validity. Slope validity was greatest when progress monitoring was aligned with the outcome (i.e., word reading fluency slope was used to predict fluency outcomes in contrast to comprehension outcomes), but effects varied across administration conditions (viz., repeated reading of familiar vs. novel passages). Unless the progress monitoring measure is highly aligned with outcome, slope may be an inefficient method for evaluating progress in an RTI context.

1.1 Assessing Response to Intervention

Response to intervention (RTI) is an instructional framework that integrates assessment with instruction to “identify students at risk for poor learning outcomes, monitor student progress, provide evidence-based interventions, and adjust the intensity and nature of those interventions based on a student's responsiveness” (National Center on Response to Intervention, June 2010). Successful operationalization of RTI frameworks hinges on the effective use of progress monitoring measures to evaluate intervention response (Vaughn & Fuchs, 2003). These evaluations are typically conducted by repeatedly assessing achievement with criterion- or norm-referenced progress monitoring measures (Stecker, Fuchs, & Fuchs, 2005).

For reading outcomes, progress monitoring measures may involve timed reading of words or passages, or a maze procedure in which students provide a missing word to reflect their understanding of a passage. Student progress is typically evaluated relative to grade appropriate standards. Methods frequently used to measure instructional response include: (a) final status; (b) slope-discrepancy; and (c) dual discrepancy (Fuchs & Fuchs, 1998). Using a final status method, instructional response is determined by comparing the student's observed final status score – that is, the post-intervention progress monitoring score, to an established criterion (e.g., performing below the 25th percentile on a norm-referenced test or below a cut-point on an empirically derived reading benchmark; Good, Simmons, & Kame'enui, 2001; Torgesen et al., 2001). With the slope-discrepancy method, rate of growth (i.e., slope) for an individual student is compared to the rate of growth for a referent group, e.g. of same age peers or classroom. The “dual discrepancy” method considers both slope as well as final status to determine a student's response to instruction (Fuchs, 2004; Fuchs & Fuchs, 1998).

Although final progress monitoring status is often used to evaluate instructional response at the end of an intervention period, evaluating initial progress monitoring status may be used at the beginning of the school year to predict how well students are likely to perform by the end of the year. This may inform teachers' plans for instruction or specific interventions. If information about slope adds value to either initial or final status or both, then slope may be used in specific ways to make decisions about instruction or response to intervention. However, the utility of these methods depend on how well initial status, final status and/or slope predict outcomes. In particular, the value added of using slope to monitor progress should be critically examined because greater resources (e.g., number and timing of assessments, added teacher training for evaluating slope) are required to use slope in evaluating response. If slope does not add to prediction about student outcomes beyond initial or final progress monitoring status, then initial or final status methods may be preferred over slope-discrepancy and dual-discrepancy methods.

1.2 Predictive Validity of Slope for Reading Outcomes

Group level studies of progress monitoring slope have typically focused on psychometric properties of slope or sensitivity of slope for measuring group level differences (Ardoin, Christ, Morena, Cormier, & Klingbeil, 2013). One study evaluated agreement between classifications of students based on progress monitoring slopes and performance on a standardized reading outcome (i.e., Iowa Test of Basic Skills, VanDerHeyden, Witt, & Barnett, 2005). None of these studies evaluated the relation between slope and reading outcomes using a model-based approach. We identified three studies that evaluated the relation between slope and reading outcomes, controlling for status and using model-based approaches (Kim, Petscher, Schatschneider, & Foorman, 2010; Schatschneider, Wagner, & Crawford, 2008; Wanzek et al., 2010). Using passage reading fluency measures, Schatschneider et al. (2008) found that within year slope did not explain unique variance in end-of-year reading achievement when controlling for final progress monitoring status among first grade students. However, Kim et al. (2010) found that within year slope explained unique variance in end-of-year reading achievement when controlling for initial progress monitoring status during first grade, but not during second or third grade among the same cohort of students. In addition, grade 1 but not grade 2 slope predicted grade 3 reading when controlling for initial status. Similarly, Wanzek et al. (Wanzek et al., 2010) found that across year slope from grade 1 through grade 3 predicted likelihood of passing state- and nationally-normed reading tests when controlling for initial (i.e. grade 1) progress monitoring status.

These studies were similar in several ways. All three focused on elementary-age students; the progress monitoring measure (oral reading fluency of connected text) was the same across all three studies; the reading outcomes were measures of reading comprehension in all three studies (i.e., the same measure in Schatschneider et al. and Kim et al., different but state- and nationally-normed tests in Wanzek et al.); initial and final status measures as well as growth were estimated from growth models then entered separately into regression models; and initial/final status and slope were evaluated as predictors of end-of-year reading achievement without controlling for beginning-of-year reading achievement. The primary difference between the studies was whether slope was compared to initial or final progress monitoring status; and the difference in results suggests that the validity of slope as a predictor of reading outcome is influenced by its comparison to initial versus final progress monitoring status and by student age or reading experience level. These may not be the only factors that influence the predictive validity of slope on reading outcomes. Factors related to the progress monitoring measure may also influence the predictive validity of slope.

1.3 Psychometric Issues in Progress Monitoring: Validity and Reliability

1.3.1 Validity

If the progress monitoring measure is not a valid predictor of the intended outcome, it is unlikely that progress monitoring slope would be a valid predictor of the outcome. Alignment between the progress monitoring measure and the outcome may be a factor in the predictive validity of the slope. For example, Tolar et al. (2012) found that initial status and final status on a maze progress monitoring measure (a measure of comprehension and connected text reading fluency) generally correlated more highly with an outcome measure of reading comprehension than one of word list fluency; similarly, maze slope also correlated more highly with reading comprehension than word list fluency. These results are descriptive because it was not the goal of the study to evaluate the predictive validity of progress monitoring slope on outcomes. However, these findings suggest that, for example, if the reading outcome is reading comprehension, then the slope of a progress monitoring measure of reading comprehension is likely a more valid predictor than the slope of a progress monitoring measure of word list fluency.

A factor that may uniquely influence the predictive validity of slope (as compared to the predictive validity of initial or final status), is the alignment between method of measuring progress and the method of measuring outcome (i.e., progress monitoring growth may be a better predictor of outcome gains than final outcome alone). None of the three studies described above (Kim et al., 2010; Schatschneider et al., 2008; Wanzek et al., 2010) controlled for beginning-of-year reading in evaluating the effect of progress monitoring slope on end-of-year reading.

1.3.2 Reliability

Statistically, the validity of a measure is no better than its reliability. Slope reliability is likely to be lower than intercept (e.g., initial or final status) reliability. For example, in Schatschneider et al. (2008), final status reliability was .97 whereas slope reliabilities were .81 (linear model) and .57 (quadratic model). However, even with low reliability, slope may be a better predictor than initial or final status if there are factors affecting the predictive power of progress monitoring status. Schatschneider et al. (2008), Kim et al. (2010), and Wanzek et al. (2010) used a measure of oral reading fluency to index growth (DIBELS ORF; Good, Kaminski, Smith, Laimon, & Dill, 2001). At the beginning of the school year, there are large floor effects in DIBELS ORF performance among first grade students, but these floor effects diminish substantially by the end of first grade and are minimal at the beginning of second grade (Catts, Petscher, Schatschneider, Bridges, & Mendoza, 2009). Floor effects diminish the ability of initial progress monitoring status to predict reading outcomes. Floor effects in initial status but highly reliable final status (especially relative to slope reliability) may be why DIBELS ORF slope was a significant predictor of reading outcomes when controlling for initial status (Kim et al., 2010; Wanzek et al., 2010) but not when controlling for final status (Schatschneider et al., 2008).

The same phenomenon may occur if there are ceiling effects in final progress monitoring status. Although the presence of floor or ceiling effects may be an indicator of the quality of the progress monitoring measure, it is also possible that as students are beginning to learn a skill (e.g., initial status among younger students) or plateauing in a well-developed skill (e.g., final status among older students), slope may be a more valid predictor of reading outcome than progress monitoring status. As described before (see section 1.2), age or reading experience level may be a factor in the predictive validity of slope on reading outcomes. Regardless of the context (initial/final status is a good or poor predictor of outcome), the more reliable the measure of slope, the more likely it will be a good predictor of outcome.

A key factor that affects slope reliability is form effects. Alternate forms (e.g., different passages or word lists) are frequently used across assessments in progress monitoring. Differences in difficulty level across forms significantly alter the shape of students' growth trajectories and influence growth rate estimates (Betts, Pickart, & Heistad, 2009; Christ & Ardoin, 2009; Francis, Santi, et al., 2008). As a consequence of these form effects, measurement error may exceed observed rates of change in observed oral reading fluency performance (Christ, 2006). The simplest way to control for form effects is by using the same form at each progress monitoring assessment. Tolar et al. (2012) demonstrated that among middle grade students, mean standard errors of slopes were descriptively smaller when the same form (i.e., familiar condition) was administered across assessments than when different forms (i.e., novel condition) were administered. Also, correlations between slope and reading outcomes were consistently higher in the familiar condition than in the novel condition.

1.4 Student Population Factors in Evaluating Progress Monitoring Slope

There are two other student population factors that may influence progress monitoring slope evaluations: ability level and type of instructional experience. For example, higher reading ability students may be near plateau on basic reading skills (e.g., decoding, fluency) but in the steep part of the developmental curve in reading comprehension whereas lower ability students may be experiencing relatively high rates of change in basic skills but near floor in comprehension. Similarly, group differences in type of instruction or level of intervention may translate to differences in growth trajectories. Growth trajectory differences may translate to differences in predictive validity or reliability of progress monitoring measures and/or slope.

Using multi-group factor analyses, Cirino et al. (2013) demonstrated that among middle school students, typical and struggling readers differed in measurement and structural relations between reading decoding, fluency, and comprehension. For example, word list fluency loadings on a fluency factor were substantially higher among struggling students (.87, .85) than among typical students (.60, .67); whereas, passage fluency loadings were comparable (.91 and .98 among struggling and typical students, respectively). This pattern of results suggests that word list fluency progress monitoring measures may be more reliable measures of fluency among struggling than typical students. Tolar et al. (2012) demonstrated that practice effects (i.e., difference in growth trajectories between familiar and novel form conditions) were greater among typical than struggling students. These group differences may be symptomatic of other group differences related to slope (e.g., reliability, predictive validity). Tolar et al. (2012) also demonstrated that practice effects were greater among struggling students who were receiving a research based reading intervention (in addition to regular classroom instruction) than struggling students who were not receiving the reading intervention.

1.5 Study objectives

The combined evidence from progress monitoring research suggests that several factors may influence the predictive validity of slope on reading outcomes: age or reading experience level of students, reading ability of students (e.g., struggling, typical), level of reading intervention, alignment of the progress monitoring measure with the outcome, condition of progress monitoring form administration (e.g., familiar, novel), whether initial or final progress monitoring status is the control, and whether progress monitoring slope is predicting final reading outcome or change in reading outcome.

Previous studies of the predictive validity of progress monitoring slope have focused on final reading outcomes among beginning readers (Kim et al., 2010; Schatschneider et al., 2008; Wanzek et al., 2010). The first objective of this study was to provide evidence about the predictive validity of progress monitoring slope for gains in reading outcomes among older, more experienced readers. We did this by examining the effects of slope on end-of-year reading achievement controlling for beginning-of-year reading achievement among middle school students.

The second objective was to evaluate the effects of progress monitoring alignment, administration condition, initial versus final progress monitoring status, reading ability level, and level of reading intervention on progress monitoring slope predictive validity. We did this by evaluating multi-group structural equation models comparing six groups of students formed by crossing three reading groups with two conditions of progress monitoring administration (viz., familiar, novel). The three reading groups varied by reading ability and intervention level (viz., typical readers, struggling readers who received research based intervention, struggling readers who did not receive intervention). The models differed by the degree to which the progress monitoring and outcome measures were aligned, e.g. word list fluency progress monitoring measure with word list fluency outcome (high alignment) or reading comprehension outcome (low alignment). Finally, for each of the models, the effects of progress monitoring slope on reading outcome were evaluated while controlling for either initial or final progress monitoring status (i.e., intercepts were set at the first and last progress monitoring assessments in separate models).

2. Methods

2.1 Participants

The participants were 1,343 middle school students (grades 6– 8) in seven urban schools who were among first-year participants in a multi-year reading intervention study (Vaughn, Cirino, et al., 2010; Vaughn, Wanzek, et al., 2010). Fifty-two percent of the students were female; 39% African American, 37% Hispanic, and 20% White. Eighty-one percent of the students received free or reduced lunch.

A school wide screening identified all struggling readers and a randomly selected group of typically achieving readers (see Tolar et al., 2012, for a detailed description of participant selection). Students were defined as struggling readers if they scored at or below one-half of one standard error of measurement above the pass-fail cut-point on the state reading achievement test (Texas Assessment of Knowledge and Skills; TAKS; Texas Educational Agency, 2008). The participants were assigned to one of three groups: adequate readers (typical, N=588), struggling readers who received no intervention other than regular classroom instruction (struggling-NI, N = 284), and struggling readers randomly selected to receive large or small group intervention (struggling-I, N = 471). To monitor progress in reading performance during the school year, students were randomly assigned to one of two progress monitoring administration conditions: familiar and novel. Students assigned to the familiar condition read the same passages or word lists across assessments. Students assigned to the novel condition read different passages or word lists across assessments.

2.2 Measures

Progress monitoring measures included a fluency measure for reading word lists and two passage reading assessments administered at baseline, posttest, and three additional intervals. The progress monitoring assessments were linearly equated to remove form effects (see Tolar et al., 2012). Outcome measures included norm-referenced assessments of word reading fluency and comprehension.

2.2.1 Progress Monitoring Measures

The AIMSweb Maze CBM Reading Comprehension subtest (AIMS, Shinn & Shinn, 2002) is a 3-minute, group administered assessment of fluency and comprehension. Students are presented with a 150–400 word passage and are required to identify the correct target among three choices for each omitted word in the passage. Fifteen different equated passages were used for each grade. Howe and Shinn (2002) report a median test re-test reliability of .85 for students in Grade 6, .79 for students in grade 7, and .92 for students in grade 8. The score was the number of correct targets minus the number of incorrect targets.

The Oral Reading Fluency CBM -Passage Fluency (ORF-PF, Francis, Barth, Cirino, Reed, & Fletcher, 2008) was developed for this study. It consists of graded passages administered as short (approximately 500 words) 1 minute probes to assess oral reading fluency. At each assessment time, students read three to five passages. The mean inter-correlation of passages read at pre-test in a grade 6 sample of 327 struggling readers and 249 typical readers was .87; and in a grade 7–8 sample of 436 struggling readers and 440 typical readers was .98. The score for each student was the mean across three passages of the linearly equated, corrected words per minute.

The Oral Reading Fluency- Word Fluency (ORF-WF, Francis, Barth, et al., 2008) was developed for this study and consists of word lists (approximately 150 words each) that are administered as 1 minute probes similar to the way in which the ORF-PF is administered. At each assessment time, students read three word lists. At pretest, the mean inter-correlation of word lists among grade 6 students (327 struggling, 249 typical readers) was .92 and among grade 7–8 students (436 struggling, 440 typical readers) was .97. The score for each student was the mean across three word lists of the linearly equated, corrected words per minute.

2.2.2 Outcome Measures

The Woodcock-Johnson III Passage Comprehension subtest (WJPC, Woodcock, McGrew, & Mather, 2001) uses a cloze procedure to assess sentence level comprehension. Students are required to read a sentence or short passage and fill in the missing words based on overall context. The split-half reliability for this measure is .83 – .96. Standard scores were used in all analyses.

The Test of Word Reading Efficiency (TOWRE, Torgesen, Wagner, & Rashotte, 1999) consists of two subtests: Phonemic Decoding Efficiency (non-words, PD) and Sight Word Efficiency (real words, SW). The raw score is the number of non-words or words read correctly within 45 seconds. Alternate forms and test retest reliability coefficients are at or above .90 for students in grades 6–8. The results for PD and SW were practically identical, so we report only the results for SW.

2.3 Familiar Versus Novel Condition Assignments

Students were randomly assigned to familiar (assessed with the same passages or word lists every 2 months) or novel (assessed with passages or word lists that differed across measurement times) progress monitoring administration conditions (see Table 1 for final group N's, demographic, and achievement information). Students were initially assigned to the same conditions for all progress monitoring measures. Due to a design change after the first assessment, 450 students read the same ORF-PF passages in the subsequent four assessment times which were different from the first assessment time. Because these students were assessed with the same passages 4 out of 5 times, they were included in the familiar condition for ORF-PF analyses. Due to error in administration, 46 students in the novel condition were assessed with the same AIMS passages at times 3 and 5; however because they were assessed with different passages 4 out of 5 times, they were kept in the novel condition for AIMS analyses.

2.4 Testing Procedures

Examiners who assessed students for this study completed an extensive training program. Prior to testing study participants, each examiner demonstrated at least 95% accuracy on test administration and scoring procedures during practice assessments. All assessments were completed at the students' middle school in quiet locations designated by the school (i.e., library, unused classrooms, theatre, etc.).

2.5 Analytical Approach

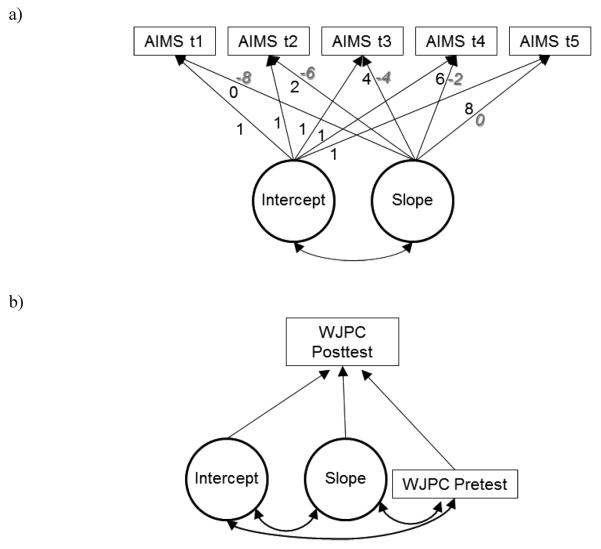
Multi-group structural equation models (SEM) were evaluated in MPlus (Muthen & Muthen, 2007) for AIMS, ORF -PF and ORF–WF. The six groups were composed of typical, struggling-NI, and struggling-I students in familiar or novel progress monitoring administration conditions. Two sets of multi-group models were evaluated: unconditional growth models and models in which intercept and slope as well as a pretest measure of the outcomes (i.e., WJPC and SW) were predictors of a posttest measure of the outcome (see Figure 1). Unconditional growth models were evaluated to determine the most likely growth trajectory (e.g., linear, quadratic) and error structure (e.g., error variances fixed equal across time points).

Figure 1.

Structural equation models of (a) unconditional growth and (b) effect of intercept and slope on reading outcome when controlling for beginning reading (pretest). Models were evaluated for all combinations of the three progress monitoring measures (AIMS, ORF-PF, ORFWF) and the two outcome measures (WJPC and TOWRE SW). The loadings for slope are in months. Loadings in regular/shaded font are for models in which the intercepts are set at the first/last assessment times. For simplicity, error variances and variances for the observed and latent variables are not represented in the figures.

Another purpose of evaluating unconditional growth models was to estimate slope reliabilities. We used two methods for evaluating slope reliability. Both methods are functions of the ratio of true variance to total variance in slopes. The first method was based on recommendations of the progress monitoring tools review committee from the National Center on Response to Intervention (National Center on Response to Intervention, 2011). For this method, true variance was the unconditional growth model estimates of slope variance. Total variance was the estimated variance in individual OLS estimated slopes. True slope variance was estimated for each of the six groups using SAS PROC MIXED (SAS Institute Inc., 2009).

The second method was based on Fornell and Larcker's (1981) proposal for evaluating the average latent construct variance in relation to SEM measurement model error variance. For this study, the average variance extracted by slope, ρ_ve (η_s) was calculated as follows:

$${\rho }_{\mathit{ve}}\left({\eta }_s\right)=\frac{{\Sigma }_i{T_i}^2\mathit{VAR}\left({\eta }_s\right)}{{\Sigma }_i{T_i}^2\mathit{VAR}\left({\eta }_s\right)+{\Sigma }_p\mathit{VAR}\left({\epsilon }_i\right)}$$

where i is the observed measure on which slope loads; T_i is the relative time at which the observed measure was collected (i.e., loading value); VAR(η_s) is the estimated slope variance; and VAR(ε_i) is the model estimated error variance for the observed measure. The average variance extracted by slope will vary as a function of the timing of the intercept, so we calculated ρ_ve (η_s) for models in which the intercepts were set at initial and final status times. Extracted slope variance estimates were based on the SEM model variances estimated in MPlus (Muthen & Muthen, 2007).

Conditional models were evaluated to determine if growth in reading fluency or comprehension predicts end-of-year reading performance (outcome posttest) when controlling for intercept and beginning-of-year reading performance (outcome pretest). Models were evaluated with the intercepts set at the beginning- and end-of-year to evaluate whether slope provides additional information about reading outcomes beyond beginning and end status on progress monitoring measures.

To evaluate model fit, we used the following absolute fit indices: the standardized root mean-square residual (SRMR), the Steiger-Lind root mean square error of approximation (RMSEA, Steiger, 1990), and the Bentler comparative fit index (CFI, Bentler, 1990).

3. Results

3.1 Group Demographics and Achievement

Tables 1a and b show demographic and achievement information for the reader/intervention groups by passage protocol conditions. We compared demographics and achievement between familiar and novel administration conditions within each reader/intervention group and between struggling– intervention and struggling–no intervention groups because the randomization processes were designed to control for differences across these levels of assignment.

Table 1a.

Demographic information and reading performance by growth assessment condition and intervention group (AIMS, ORF-WF Groups)

Measure	Familiar			Novel
	Typical	Struggling-NI	Struggling-I	Typical	Struggling-NI	Struggling-I
N	279	162	234	309b	122	237
Age: M (SD) years	12.6 (0.9)	12.9 (0.9)	12.7 (1)	12.6 (0.9)	12.9 (1)	12.7 (1)
	%
Gender (female)	55	49	50	59	46	46
African American	35	39	39	41	33	45
Hispanic	29	43	46	28	48	40
White	30	14	14	27	16	11
Other	6	4	2	5	2	4
Free or Reduced Luncha	69	89	91	77	87	86
Grade 6	36	33	40	39	36	49
Grade 7	25	23	23	22	23	19
Grade 8	39	44	37	39	41	32
	Standard Score M (SD)
WJPC (pretest)	99.2 (9.8)	85.5 (11.9)	85.9 (10.8)	99.7 (9.4)	88.3 (10.3)	87.3 (10.2)
WJPC (posttest)	101.0 (10.4)	86.6 (12.8)	88.0 (10.7)	101.9 (10.0)	88.5 (10.2)	88.8 (9.7)
TOWRE SW (pretest)	101.9 (11.5)	90.8 (11.5)	92.3 (10.5)	102.8 (11.2)	92.9 (10.9)	93.8 (10.2)
TOWRE SW (posttest)	104.5 (10.9)	92.2 (12.4)	94.2 (11.6)	104.9 (12.0)	94.2 (11.3)	95.6 (11.5)

Note. Struggling-NI, I = No intervention (Tier 1), Intervention (Tier 2).

^aReduced-price or free lunch status were missing for 28 (0.2%) students.

^bOne Typical student in the Novel condition did not complete TOWRE SW (posttest).

Table 1b.

Demographic information and reading performance by growth assessment condition and intervention group (ORF-PF Groups)

Measure	Familiar			Novel
	Typical	Struggling-NI	Struggling-I	Typical	Struggling-NI	Struggling-I
N	374	197	320	214b	87	151
Age: M (SD) years	12.6 (0.9)	13 (1)	12.8 (1)	12.6 (0.9)	12.9 (1)	12.7 (1.1)
	%
Gender (female)	57	50	48	57	43	48
African American	35	35	40	44	39	47
Hispanic	31	47	45	24	41	37
White	30	15	13	26	16	11
Other	5	3	2	6	3	5
Free or Reduced Luncha	70	89	90	77	85	86
Grade 6	37	32	41	38	38	52
Grade 7	25	22	23	21	24	17
Grade 8	38	45	36	41	38	30
	Standard Score M (SD)
WJPC (pretest)	99.1 (9.9)	86.0 (11.4)	86.3 (10.6)	100.1 (8.9)	88.2 (11.1)	87.3 (10.3)
WJPC (posttest)	101.1 (10.5)	86.9 (12.3)	88.2 (10.3)	102.1 (9.5)	88.5 (10.5)	88.9 (10.2)
TOWRE SW (pretest)	102.2 (11.6)	91.2 (11.4)	92.7 (10.4)	102.7 (10.8)	92.8 (11.0)	93.8 (10.2)
TOWRE SW (posttest)	104.7 (11.4)	92.6 (12.2)	94.8 (11.8)	104.8 (11.7)	94.0 (11.3)	95.2 (11.0)

Note. Struggling-NI, I = No intervention (Tier 1), Intervention (Tier 2).

^aReduced-price or free lunch status were missing for 28 (0.2%) students.

^bOne Typical student in the Novel condition did not complete TOWRE SW (posttest).

The only significant difference in demographics between familiar and novel conditions was that a greater percentage of typical students in the AIMS/ORF-WF Novel condition were provided reduced-price or free lunch compared to typical students in the familiar condition, 77% versus 69%, χ²₍₁₎ = 4.83, p < .05. For the struggling groups, there were significant differences in the proportions of Grade 6 (45% vs. 34%), 7 (21% vs. 23%), and 8 students (34% vs. 43%) between the intervention and no-intervention groups, χ²₍₂₎ = 8.73, p < .05.

We conducted ANOVAs to determine if the groups differed in age or beginning-of-year achievement (WJPC and TOWRE SW pretests). The only significant difference between familiar and novel conditions was that AIMS/ORF-WF struggling-NI students in the novel condition scored significantly higher on the WJPC pretest (M = 88.3, SD = 10.3) than struggling-NI student in the familiar condition (M = 85.5, SD = 11.9), F_{(1, 282)} = 4.53, p < .05. For the struggling groups, the no-intervention students were significantly older (M = 12.9, SD = 1.0) than the intervention students (M = 12.7, SD = 1.0), F_{(1, 753)} = 6.99, p < .05, although the difference is relatively negligible in terms of academic time, (d = .2 years, or 2.4 months), when one considers that these are students with six to eight years of school experience at the outset of data collection.

In summary, although there were a few statistical group differences, the differences do not appear to be practically significant nor does there appear to be systematic bias with respect to assignment to familiar and novel conditions or between intervention groups.

3.2 Unconditional Growth Models

The unconditional growth models with intercepts set at time 1 for AIMS, ORF-PF, and ORF-WF are shown in Tables 2a–c.

Table 2a.

AIMS observed means (variances) and unconditional growth model by assessment condition and intervention group

Measure/Parameter	Familiar			Novel
	Typical	Struggling-NI	Struggling-I	Typical	Struggling-NI	Struggling-I
	Observed M (VAR)
AIMS time 1	23.2 (67.4)	12.7 (72)	13.9 (67.3)	23.8 (71.6)	14.5 (67)	14.6 (70.3)
AIMS time 2	27.1 (79.9)	15.3 (107.8)	15.9 (66.1)	24.8 (76.5)	15.2 (86.3)	15.4 (73.9)
AIMS time 3	31.0 (113.4)	16.5 (142.3)	18.0 (106.8)	26.9 (89.6)	16.9 (75.7)	15.6 (76)
AIMS time 4	35.1 (119.3)	19.2 (139.9)	21.2 (118.6)	29.1 (98.4)	17.1 (104.2)	17.5 (95)
AIMS time 5	37.2 (121.9)	21.0 (199.9)	24.6 (130.9)	29.8 (106.1)	19.3 (106.3)	18.1 (109.5)
	Unconditional Growth Model Estimates
Means
I	23.4	12.8	13.4	23.5	14.3	14.4
S	1.82	1.04	1.32	0.83	0.58	0.46
Variances/Covariances
I	55.7	65.7	45.3	51.5	49.8	39.2
S	0.25	0.59	0.37	0.17	0 Fixed	0.25
I with S	2.46	3.46	2.08	1.42	0 Fixed	1.51
Residual
AIMS time 1	15.8	9.4	20.7	23.5	25.9	29.7
AIMS time 2	14.1	18.2	14.6	18.2	30.2	27.1
AIMS time 3	20.9	28.5	33.5	20.3	32.2	26.8
AIMS time 4	21.6	32.5	31.3	20.6	56.3	25.7
AIMS time 5	23.6	35.7	33.7	28.7	42.1	29.3
	Slope Properties
Reliability a	.33	.46	.35	.32		.30
Variance Extracted b
Time 1 Intercept	.27	.38	.28	.19	NA	.22
Time 5 Intercept	.29	.44	.30	.20	NA	.21

Note. CFI = .99, RMSEA = .07, SRMR = .05. All effects are unstandardized. 0 Fixed means variance/covariance was fixed to 0 in order to obtain proper estimates.

^aThe ratio between model estimated true slope variance and observed variance in OLS estimated individual slopes (National Center on Response to Intervention, 2011).

^bThe average variance extracted by slope, ρ_ve (η_s) (Fornell & Larcker, 1981).

Table 2c.

ORF – WF observed means (variances) and unconditional growth model by assessment condition and intervention group

Measure/Parameter	Familiar			Novel
	Typical	Struggling-NI	Struggling-I	Typical	Struggling-NI	Struggling-I
	Observed M (VAR)
ORF- WF time 1	95.3 (515.5)	72.6 (909.4)	72.1 (563.6)	92.7 (540.8)	76.4 (618.3)	74.5 (621.1)
ORF- WF time 2	99.3 (538.1)	74.2 (945.1)	76.3 (690.9)	93.9 (554.4)	78.5 (708.1)	76.5 (595.1)
ORF- WF time 3	102.9 (546.7)	78.0 (936.1)	79.9 (626.7)	95.6 (584.6)	78.3 (620)	77.7 (578.4)
ORF- WF time 4	106.1 (520.4)	80.5 (948)	83.1 (657.9)	96.3 (580.8)	78.6 (635.9)	79.3 (559.9)
ORF- WF time 5	109.3 (539.8)	84.2 (895.4)	86.0 (719.9)	97.0 (624.3)	79.1 (657.1)	81.0 (632.3)
	Unconditional Growth Model Estimates
Means
I	95.7	72.1	72.6	92.9	77.1	74.6
S	1.73	1.46	1.73	0.56	0.27	0.79
Variances/Covariances
I	471.9	879.8	533.2	489.7	599.6	552.3
S	0.84	0.77	1.02	0.94	0 Fixed	0.71
I with S	−1.21c	−2.88c	4.47c	2.12c	0 Fixed	−2.78c
Residual
ORF- WF time 1	71.8	43.2	57.3	64.5	66.1	61.6
ORF- WF time 2	54.2	63.0	81.7	55.2	52.9	53.8
ORF- WF time 3	54.1	77.3	41.3	39.9	26.8	33.1
ORF- WF time 4	28.5	38.3	36.4	35.9	33.7	28.9
ORF- WF time 5	49.4	41.0	59.1	52.0	72.2	61.6
	Slope Properties
Reliabilitya	.45	.25	.44	.48	NA	.45
Variance Extracted (%)b
Time 1 Intercept	.35	.30	.36	.38	NA	.32
Time 5 Intercept	.33	.29	.36	.37	NA	.32

Note. CFI = 1.0, RMSEA = .05, SRMR = .03. All effects are unstandardized. 0 Fixed means variance/covariance was fixed to 0 in order to obtain proper estimates.

^aThe ratio between model estimated true slope variance and observed variance in OLS estimated individual slopes (National Center on Response to Intervention, 2011).

^bThe average variance extracted by slope, ρ_ve (η_s) (Fornell & Larcker, 1981).

3.2.1 AIMS

There was significant linear growth (p < .05) in AIMS for all groups (see Table 2a) and significant variance in linear growth among all groups except struggling-NI students in the novel condition. For all subsequent analyses, slope variance was fixed to 0 for this group in order to obtain proper estimates (e.g., correlation between intercept and slope ≤ 1) and because there was not significant variance in slope.

It should be noted that although the magnitude of the slope variance among struggling-NI students in the novel condition (0.17) was the same as that of typical students, the standard errors were twice as large among struggling-NI (0.15) than typical (0.08) students. In addition, the standard errors of mean slope estimates were greater among struggling-NI students (0.08, familiar; 0.09, novel) than among typical (0.05, familiar and novel) or struggling-I (0.07, familiar; 0.06, novel) students.

AIMS slope reliabilities were low (range .30 to .35, see Table 2a) among typical and struggling-I students and similar across progress monitoring administration conditions (novel, familiar). Slope reliability was slightly higher (.46) but still low among struggling-NI students in the familiar condition.

The average variances extracted by slope were slightly higher in the familiar than novel conditions among both typical (e.g., .27 versus .19 for time 1 intercepts, see Table 2a) and struggling-I (e.g., .28 versus .22 for time 1 intercept models) students. The extracted variance was higher among struggling-NI students in the familiar condition (.38, time 1 intercept model) than among the other groups of students in the familiar condition. In addition, the average slope variance extracted was greater when the intercepts were set at time 5 than time 1 (e.g., .27 versus .29, time 1 and 5 intercept models, among typical students in the familiar condition, see Table 2a) and this differences was greatest among struggling-NI students (.38 versus .44, time 1 and 5 intercept models).

It should be noted that growth model error variances increased from times 1 to 5 among all groups and the greatest increase was among struggling-NI students in the familiar condition (e.g., growth model error variances increased by a factor of 3.8, 1.6, and 1.5 among struggling-NI, struggling-I, and typical students in the familiar conditions, see Table 2a for variance estimates). Because of the way average slope variance extracted is calculated (see section 2.5), differences in the values between time 1 and time 5 intercept models are strictly a function of differences between the time 1 and 5 error variances. Greater time 5 error variances results in greater average slope variance extracted values for time 5 intercept models and the greater the difference between time 1 and 5 error variances, the greater the difference in average slope variances extracted.

3.2.2 ORF-PF

Quadratic growth models were the better fitting models than linear models for ORF-PF (quadratic model: CFI = .99, RMSEA = .09, and SRMR = .07; linear model: CFI = .97, RMSEA = .15, and SRMR = .06); however, model fits were not substantially different. In addition, there was no variability in quadratic growth among any of the groups and the linear slope effects on reading outcomes did not differ across linear and quadratic growth models. Therefore, in order to evaluate the effects of average linear growth on outcomes, only linear model results are reported.

There was significant linear growth (p < .05) in ORF-PF for all groups (see Table 2b) and significant variance in linear growth among all familiar groups. There was no significant variance in growth among the novel groups (p > .05). For all subsequent analyses, slope variance was fixed to 0 for the novel groups.

Table 2b.

ORF-PF observed means (variances) and unconditional growth model by assessment condition and intervention group

Measure/Parameter	Familiar			Novel
	Typical	Struggling-NI	Struggling-I	Typical	Struggling-NI	Struggling-I
	Observed M (VAR)
ORF - PF time 1	145.4 (862.4)	109.8 (1230.6)	113.2 (999.4)	147.1 (924.5)	114.3 (1109.6)	116.1 (821.5)
ORF - PF time 2	157.3 (1035.6)	122.0 (1284.8)	125.7 (1094.5)	155.7 (966.9)	125.6 (1116.6)	124.1 (897.9)
ORF - PF time 3	165.4 (1123.7)	127.6 (1345.2)	131.8 (1078.6)	158.4 (1040.6)	125.9 (1024.6)	125.4 (886.1)
ORF - PF time 4	171.4 (1152.9)	133.5 (1397.8)	136.7 (1139.8)	161.7 (950.2)	126.4 (1127.8)	128.4 (895)
ORF - PF time 5	174.7 (1164.8)	138.1 (1396.7)	142.9 (1221.2)	162.5 (1091)	127.8 (1023.1)	130.8 (937.2)
	Unconditional Growth Model Estimates
Means
I	148.92	113.94	116.85	150.27	119.03	118.50
S	3.61	3.18	3.40	1.74	1.23	1.64
Variances/Covariances
I	830.45	1187.66	940.93	836.96	990.32	793.52
S	1.65	1.65	1.93	0.18c	0 Fixed	0 Fixed
I with S	12.25	5.06c	4.90c	8.11	0 Fixed	0 Fixed
Residual
ORF - PF time 1	166.08	129.34	137.20	118.77	108.05	112.26
ORF - PF time 2	105.73	56.77	85.85	85.66	98.78	91.59
ORF - PF time 3	96.14	66.89	62.10	88.89	83.00	76.06
ORF - PF time 4	94.47	61.38	66.09	99.84	126.96	118.29
ORF - PF time 5	154.75	58.38	103.83	85.19	48.50	101.40
	Slope Properties
Reliabilitya	.44	.50	.54	.10	NA	NA
Variance Extracted (%)b
Time 1 Intercept	.31	.45	.42	.06	NA	NA
Time 5 Intercept	.30	.39	.40	.05	NA	NA

Note. CFI = .97, RMSEA = .15, SRMR = .06. All effects are unstandardized. 0 Fixed means variance/covariance was fixed to 0 in order to obtain proper estimates.

^aThe ratio between model estimated true slope variance and observed variance in OLS estimated individual slopes (National Center on Response to Intervention, 2011).

^bThe average variance extracted by slope, ρ_ve (η_s) (Fornell & Larcker, 1981).

Slope reliabilities were moderate among all three familiar groups (range .44 to .54, see Table 2b)). Average slope variances extracted were greater among struggling than typical students (e.g., .45 and .42, struggling students versus .31 typical students, time 1 intercept models, see Table 2b). Unlike AIMS, ORF-PF error variances were greater at time 1 than time 5 resulting in greater average slope variance extracted for time 1 intercept models than for time 5 models (e.g., .45 versus .39, time 1 and time 5 intercept models among struggling-NI students in the familiar condition).

3.2.3 ORF-WF

Similar to AIMS, there was significant linear growth (p < .05) in ORF-WF for all groups (see Table 2c) and significant variance in linear growth among all groups except struggling-NI students in the novel condition. For all subsequent analyses, slope variance was fixed to 0 for this group. Similar to AIMS, the standard error of the slope variance estimate was greater among struggling-NI students in the novel condition (0.24) than among the other groups in the novel condition (0.20 and 0.22, typical and struggling-I); however, unlike AIMS, the magnitude of the variance estimate was virtually 0 among struggling-NI students (0.004). Similar to AIMS and ORF-PF, ORF-WF slope reliabilities were low to moderate (range .25 to .48, see Table 2c) across groups. However, unlike the other progress monitoring measures, ORF-WF slope reliabilities were substantially lower among struggling-NI students in the familiar condition (.25) than among the other groups (> .44 in all cases, see Table 2c).

The average variances extracted by slope were generally low and similar across groups and intercept models (range .29 to .38, see table 2c). Because there was generally no substantial difference in error variance from time 1 to time 5, average slope variances extracted were similar for time 1 and time 5 models.

3.3 Growth as a Predictor of End-of-Year Performance

3.3.1 AIMS

In general, AIMS slope was not a predictor of reading achievement when controlling for either initial or final AIMS status (see Table 3a). There were only three exceptions, all in the familiar condition. AIMS slope was a significant positive predictor of WJPC controlling for initial AIMS status (β = .23, z = 2.56, p < .05) and a significant negative predictor of TOWRE SW controlling for final AIMS status (β = −.24, z = 2.05, p < .05) among struggling-NI students. Slope was a significant positive predictor of TOWRE SW controlling for initial AIMS status (β = .28, z = 2.46, p < .05) among struggling-I students.

Table 3a.

AIMS intercept and growth as predictors of end-of-year reading performance when controlling for beginning-of-year reading performance

Parameter	Familiar			Novel
	Typical	Struggling-NI	Struggling-I	Typical	Struggling-NI	Struggling-I
	Passage Comprehension
Posttest on
Pretest	.58	.69	.61	.47		.63
Intercept T1 (T5)	.20a (.29a)	.06a (.09a)	.17 (.25)	.41 (.53)		.23 (.33)
Slope T1 (T5)	.05a (−.06a)	.23 (.18a)	.15a (.03a)	−.03a (−.22a)		.01a (−.13a)
Correlation
Pretest, Intercept T1 (T5)	.58 (.60)	.59 (.59)	.61 (.63)	.59 (.60)		.61 (.66)
Pretest, Slope	.52	.43	.46	.40		.52
Intercept, Slope T1 (T5)	.67 (.85)	.55 (.84)	.49 (.81)	.49 (.73)		.50 (.79)
Model R-square (%)	56	72	65	60		65
	Sight Word Oral Reading Fluency
Posttest on
Pretest	.53	.70	.88	.55		.68
Intercept T1 (T5)	.32 (.46)	.27 (.42)	−.18a (−.28a)	.23 (.29)		.08a (.11a)
Slope T1 (T5)	−.04a (−.21a)	−.03a (−.24)	.28 (.41a)	.17a (.07a)		.12a (.07a)
Correlation
Pretest, Intercept T1 (T5)	.33 (.37)	.62 (.62)	.68 (.58)	.45 (.50)		.63 (.56)
Pretest, Slope	.36	.45	.26	.42		.24
Intercept, Slope T1 (T5)	.67 (.85)	.54 (.84)	.48 (.81)	.47 (.73)		.44 (.77)
Model R-square (%)	47	77	74	60		60

Note. Estimates standardized. T1, T5 = intercept set at times 1 and 5. Bolded estimates are cases in which slope is a significant predictor. No model was estimated for Novel Struggling-NI students because there was no significant variance in AIMS slope among these students (see Table 2a). CFI = .99, RMSEA = .05, SRMR = .04 for both models.

^aNon-significant effects (p > .05).

3.3.2 ORF-PF

Similar to AIMS, ORF-PF slope was generally not a significant predictor of reading achievement (see Table 3b). Because slope variance was fixed to 0 for all three groups in the novel conditions, ORF-PF slope could only predict reading achievement among students in the familiar condition. However, ORF-PF slope was a significant predictor only when controlling for initial ORF-PF status and only for the following outcomes-groups: WJPC Typical (β = .18, z = 2.48, p < .05) and TOWRE SW typical (β = .22, z = 2.91, p < .05) and struggling-I (β = .10, z = 2.03, p < .05).

Table 3b.

ORF-PF intercept and growth as predictors of end-of-year reading performance when controlling for beginning-of-year reading performance

Parameter	Familiar			Novel
	Typical	Struggling-NI	Struggling-I	Typical	Struggling-NI	Struggling-I
	Passage Comprehension
Posttest on
Pretest	.61	.72	.73
Intercept T1 (T5)	.12 (.14)	.16 (.17)	.07a (.07a)
Slope T1 (T5)	.18 (.14a)	.04a (.00a)	.08a (.06a)
Correlation
Pretest, Intercept T1 (T5)	.49 (.52)	.48 (.48)	.45 (.46)
Pretest, Slope	.34	.13a	.15a
Intercept, Slope T1 (T5)	.33 (.59)	.11a (.38)	.12a (.43)
Model R-square (%)	58	67	61
	Sight Word Oral Reading Fluency
Posttest on
Pretest	.44	.56	.62
Intercept T1 (T5)	.38 (.44)	.34 (.37)	.25 (.27)
Slope T1 (T5)	.22 (.08a)	.09a (−.01a)	.10 (.01a)
Correlation
Pretest, Intercept T1 (T5)	.53 (.44)	.79 (.76)	.80 (.74)
Pretest, Slope	−.05a	.11a	.03a
Intercept, Slope T1 (T5)	.32 (.59)	.12a (.39)	.11a (.44)
Model R-square (%)	60	76	70

Note. Estimates standardized. T1, T5 = intercept set at times 1 and 5. Bolded estimates are cases in which slope is a significant predictor. No model was estimated for Novel students because there was no significant variance in ORF-PF slope among these students (see Table 2b). CFI = .97/.97, RMSEA = .12/.13, SRMR = .04/.04 for Passage Comprehension and Sight Word Oral Reading Fluency, respectively.

^aNon-significant effects (p > .05).

3.3.3 ORF-WF

The pattern of relations between ORF-WF slope and reading outcomes was different than the patterns for AIMS and ORF-PF. Although ORF-WF slope was not a significant predictor of WJPC, it was a relatively robust predictor of TOWRE SW (see Table 3c).

Table 3c.

ORF-WF intercept and growth as predictors of end-of-year reading performance when controlling for beginning-of-year reading performance

Parameter	Familiar			Novel
	Typical	Struggling-NI	Struggling-I	Typical	Struggling-NI	Struggling-I
	Passage Comprehension
Posttest on
Pretest	.71	.77	.75	.66		.75
Intercept T1 (T5)	.07a (.07a)	.11 (.11)	.05a (.06a)	.14 (.15)		.10 (.10)
Slope T1 (T5)	.05a (.03a)	.06a (.03a)	.04a (.02a)	−.08a (−.13a)		.02a (−.01a)
Correlation
Pretest, Intercept T1 (T5)	.32 (.26)	.39 (.41)	.38 (.36)	.35 (.34)		.38 (.34)
Pretest, Slope	−.15a	.06a	.08a	.05a		−.15a
Intercept, Slope T1 (T5)	−.06a (.27)	−.11a (.13a)	.19a (.48)	.10a (.41)		−.14a (.15a)
Model R-square (%)	52	68	61	51		62
	Sight Word Oral Reading Fluency
Posttest on
Pretest	.45	.69	.75	.61		.90
Intercept T1 (T5)	.42 (.43)	.28 (.28)	.06a (.06a)	.25 (.27)		.02a (.02a)
Slope T1 (T5)	.25 (.11a)	.20 (.13a)	.18 (.16)	.37 (.28)		.53 (.52)
Correlation
Pretest, Intercept T1 (T5)	.53 (.45)	.79 (.72)	.77 (.74)	.60 (.52)		.74 (.65)
Pretest, Slope	−.21	−.27	.16a	−.10a		−.30
Intercept, Slope T1 (T5)	−.07a (.27)	−.13a (.13a)	.19a (.48)	.09a (.41)		−.16a (.14a)
Model R-square (%)	58	80	72	72		83

Note. Estimates standardized. T1, T5 = intercept set at times 1 and 5. Bolded estimates are cases in which slope is a significant predictor. No model was estimated for Novel Struggling-NI students because there was no significant variance in ORF-WL slope among these students (see Table 2c). CFI = 1.0/0.99, RMSEA = .04/.06, SRMR = .02/.02 for Passage Comprehension and Sight Word Oral Reading Fluency, respectively.

^aNon-significant effects (p > .05).

Excluding struggling-NI students in the novel condition (for whom slope variance was fixed 0 as described in section 3.2.3), ORF-WF slope was a significant predictor of TOWRE SW in all cases when controlling for initial status (familiar: typical, β = 0.25, z = 3.82, p < .05; struggling-NI, β = 0.20, z = 3.45, p < .05; struggling-I, β = 0.18, z = 2.97, p < .05; novel: typical, β = 0.37, z = 6.48, p < .05; struggling-I, β = 0.53, z = 6.44, p < .05). ORF-WF slope was also a significant predictor of TOWRE SW when controlling for final status among struggling-I (β = 0.16, z = 2.13, p < .05) students in the familiar condition and typical (β = 0.28, z = 3.87, p < .05) and struggling-I (β = 0.52, z = 5.27, p < .05) students in the novel condition, but not among typical (β = 0.11, z = 1.43, p > .05) or struggling-NI (β = 0.13, z = 1.87, p > .05) students in the familiar condition.

Descriptively, standardized slope effects were greater in the novel than the familiar condition (e.g., .53 versus .18, novel versus familiar struggling-I students) and, within the novel condition, greater among struggling-I (.53, .52) than typical (.37, .28) students. To determine if these differences were statistically significant, we compared three models: (1) slope effects fixed the same across all groups and conditions (2) slope effects fixed the same across typical, struggling-NI, and struggling-I groups within condition but allowed to differ between familiar and novel conditions; and (3) slope effects fixed the same across groups in the familiar condition but allowed to differ across groups in the novel condition. Controlling for initial ORF-WF status, the slope effects were significantly greater in the novel condition (standardized effects .37 and .58) than in the familiar condition (.18 to .25, model 1 vs. 2, Δχ²(1) = 9.98, p < .05). However, the slope effects were not statistically different between typical and struggling-I students in the novel condition, model 2 vs. 3, Δχ²(1) = 1.72, p > .05.

In addition to the more robust relations (across groups and conditions) between ORF-WF slope and TOWRE SW outcome, there were two other notable differences in the pattern of relations between ORF-WF and TOWRE SW as compared to other progress monitoring slope and reading outcome combinations. First, the combined effects of reading outcome pretest and progress monitoring intercept and slope accounted for consistently greater variance in reading outcome posttest for the ORF-WF/SW combinations (> 72% among all groups accept typical students in the familiar condition, see Table 3c) than the other combinations (< 70 % in all but one case when WJPC was the outcome, Tables 3a–c). Second, when correlations between progress monitoring slopes and pretest were significant, they were negative when the progress monitoring measures was ORF-WF and the pretest was TOWER SW but positive in all other cases.

4. Discussion

4.1 Study Objectives

The first objective of this study was to evaluate the predictive validity of progress monitoring slope for reading outcomes among middle school students as a comparison to earlier studies of elementary students (Kim et al., 2010; Schatschneider et al., 2008; Wanzek et al., 2010). The most comparable models to the earlier studies are of ORF-PF slope predicting WJPC among students in the novel condition because the earlier studies used oral reading fluency of connected text to predict reading comprehension without controlling for form effects. Among middle school students in the novel condition, there was no significant variance in ORF-PF slope. Even in the familiar condition where there was variability in slopes, ORF-PF slope was a significant predictor of ORF-PF only among typical students and only when controlling for initial progress monitoring status. These results are consistent with those of Schatschneider et al. (2008) who reported that progress monitoring slope did not add to the prediction of final progress monitoring status when the progress monitoring measure was oral reading fluency for connected text and the outcome was reading comprehension. Our results are generally (with the exception of typical students in the familiar condition) consistent with Kim et al. (2010). In Kim et al. progress monitoring slope predicted reading outcome controlling for initial progress monitoring status among first grade students, but slope did not predict reading outcome among older students (grades 2 and 3). Under similar conditions in this study, progress monitoring slope also did not predict outcomes among middle school students. It is more difficult to compare the results of Wanzek et al. (2010) to this study. They did control for initial status in grade 1 but estimated growth across three years (grades 1 to 3) to predict grade 3 pass rates on reading comprehension tests. It may be that by capturing grade 1 growth as part of the three years of progress monitoring, this influenced the significant effect of growth on reading. As described before (see section 1.3.2), a progress monitoring measure of oral reading fluency of connected text may only add to the predictive power of initial progress monitoring status for reading comprehension among beginning readers who are developing basic reading skills (i.e., decoding and fluency).

It is not clear why ORF-PF slope predicted WJPC among typical students but not struggling students in the familiar condition. It may be because correlations between reading comprehension pre- and posttest were lower among typical than struggling students (regardless of condition) perhaps because variance in WJPC was lower among typical than struggling students (see Tables 1b and 3b). In addition, the correlation between ORF-PF slope and WJPC pretest was higher among typical than struggling students. These group differences provide evidence related to the second goal of the study.

The second objective of this study was to evaluate the effects of progress monitoring alignment, administration condition, initial versus final progress monitoring status, reading ability level, and level of reading intervention on progress monitoring slope predictive validity. To our knowledge, this is the first study to evaluate these factors in relation to the effects of progress monitoring slope on outcomes, especially among middle school students.

4.1.1 Progress monitoring-outcome alignment

The evidence from this study provides strong support that the level of alignment between the progress monitoring and outcome measures influences the predictive validity of progress monitoring slope, but this effect appears to interact with administration condition and comparison assessment (i.e., initial or final progress monitoring status). ORF-WF/TOWRE SW was the most aligned progress monitoring/outcome combination and ORF-WF /WJPC was the least aligned. In the unaligned case, slope did not predict outcome in any context. In the aligned case, controlling for initial progress monitoring status, progress monitoring slope predicted outcome across all groups in both conditions (with the exception of struggling-NI students in the novel condition), but the effect of slope on outcome was stronger in the novel than in the familiar condition. Controlling for final progress monitoring status, progress monitoring slope predicted outcome in the familiar condition only among struggling-I students and in the novel condition among typical and struggling-I students.

4.1.2 Administration Condition

There does not appear to be a consistent effect of administration condition (familiar versus novel) across contexts. As already stated, when the progress monitoring and outcome measures are highly aligned, progress monitoring slope has a stronger effect in the novel condition than in the familiar condition. However, when the progress monitoring and outcome measures are less aligned, if there is a slope effect, it is only in the familiar condition.

Administration condition may interact with both degree of alignment between progress monitoring and outcome and the level of skill development assessed. In the case of ORF-WF/TOWRE SW, not only were the measures highly aligned, but also as measures of word list fluency they assess basic reading skills that are likely relatively well-developed in middle school students. There may be a plateau effect in growth at this point in reading development. This may be why the ORF-WF/TOWRE SW combination was also the only case in which slope was negatively correlated with outcome pretest (i.e., students with lower initial word list fluency skills increased their skill at a higher rate than did students with higher initial skill). For AIMS and ORF-WF, when significant, slope was positively correlated with outcome pretest (i.e., students with higher initial abilities on the outcome measure increased their progress monitoring skills at a higher rate than students with lower initial abilities). The influence of administration condition in these two situations may be a function of the types of processes each administration condition is capturing. Significant slope effects in the familiar administration condition may be a function of less measurement error, but may also reflect the development of new cognitive strategies that would not be observed in the novel administration condition (Tolar et al., 2012). On the other hand, significant slope effects in the novel administration condition may be a better reflection of generalized skill. It may be that for highly aligned measures of generally well-developed skills, capturing generalized skill has a greater influence on slope validity whereas for less developed skills, minimizing measurement error and capturing other types of developmental processes related to reading achievement has a greater influence on slope validity.

4.1.3 Initial versus Final Progress Monitoring Status

Slope is more likely to predict outcome when controlling for initial than final progress monitoring status. The exception is when the progress monitoring-outcome measures are highly aligned. Even in this case, there is a trend for the strengths of the slope effects to be slightly higher when controlling for initial than final progress monitoring status. This may be a consequence of slope correlating more highly with final than initial progress monitoring status. In the case of initial progress monitoring status, the relative lack of shared variance between slope and progress monitoring status means that any shared variance between slope and outcome is likely to be unique (as compared to shared variance between status and outcome). In the case of final progress monitoring status, a greater amount of the variance in outcome explained by slope is also explained by progress monitoring status. The exception may be when the collection of growth curves is such that slopes are more correlated with initial status than final status.

4.1.4 Reading Ability and Intervention Level

The only consistent effect of reading or intervention level on slope validity is that among struggling students not receiving research based intervention in the novel condition there is no variability in progress monitoring slopes, regardless of which progress monitoring measure is used. In some cases this was likely due to measurement error (see AIMS, section 3.2.1), in other cases the slope variance was virtually 0 (see ORF-WF, section 3.2.3). It may be that among struggling students who are not receiving targeted intervention, measuring progress may be especially problematic perhaps due to uniformly low performance combined with difficulty in obtaining reliable estimates of growth.

4.2 Limitations

Slope reliability was low across progress monitoring measures and administration conditions (range .30 to .54). Progress was measured only five times, each assessments spaced two months apart. Because slope reliability is partly a function of the number and spacing of time points, more frequent assessments would have increased slope reliability and consequently the power to detect slope effects on outcomes.

Although we hypothesized that progress monitoring-outcome alignment influenced the results of this study, this factor was not systematically evaluated. Neither AIMS nor ORF-PF are as highly aligned with either WJPC or TOWRE SW as ORF-WF was with TOWRE SW (see Cirino et al., 2013 for factor analyses relating these measures). Future studies should include progress monitoring-outcome combinations that are more closely aligned for passage reading fluency and reading comprehension than was the case in this study.

Finally, this study did not examine the practical value of measuring growth over time. Past research indicates that teachers who use progress monitoring data to inform instructional decisions produce significant gains in student achievement relative to teachers not using progress monitoring data to inform instruction (Stecker et al., 2005). Progress monitoring data may help teachers estimate student learning, set reasonable learning goals, and tailor instruction to meet those goals. For these reasons, the value of evaluating progress monitoring slope may not be in the validity of slope for predicting end of year reading outcomes, but in the ways in which the evaluation process influences teachers to modify instructional programs to achieve higher levels of instructional response.

4.3 Conclusions

There does not appear to be value added in evaluating slope to predict outcomes except when the progress monitoring measure is highly aligned with the outcome and when students are just beginning to develop the skill or are plateauing. When evaluating response-to-instruction, it may be that the most recent progress monitoring assessment evaluated against a research-based or norm-referenced criterion is the most efficient method for determining a student's progress and predicting his or her performance in similar contexts. However, evidence to support this conclusion is sparse; systematic research evaluating the effects of progress monitoring-outcome alignment and administration conditions (e.g., form effects, number of assessments) among different student populations is needed to build a convincing body of evidence.

4.4 Practical Implications

For practitioners making judgments about individual students, the combined research to date suggests that at any point in the school year, the best predictor of a student's score on a norm-referenced or criterion-referenced reading achievement test is the student's most recent score on the progress monitoring measure. For example, a middle school administers oral reading fluency probes five times a year. At the end of the first semester (middle of year), the school is interested in identifying which students will potentially not meet criteria on the state reading test administered at the end of the school year. Using all available data, each student's most recent score (middle of year) on the progress monitoring measure is the better predictor of performance on the state reading exam. In this case, a student's growth (i.e., slope) from beginning to middle of the school year is unlikely to provide additional information. This would especially be the case if the evaluation of the student's progress is made close in time to the state achievement test administration (i.e., end-of-year measure of progress predicting performance on the state exam).

However, if there is high alignment between the progress monitoring measure and the state exam at the level of the underlying construct, the combination of student's initial progress monitoring score and growth may be a better predictor of that student's gain in reading achievement from one year to the next than just a single progress monitoring score. In the case of middle school, the combination of a student's initial progress monitoring score on an assessment of oral reading fluency (beginning of the school year) plus growth calculated during the school year (i.e., 5 data points if collecting data five times during the year) may be the best predictor of improvements on an achievement measure that emphasizes oral reading fluency from the end of the previous school year to the end of the current school year. Nonetheless, there are many factors that may influence this rule-of-thumb including the students age, experience level with the skill or content being evaluated, and the student's status (e.g., typical or struggling). Therefore, the best use of the extant research for practitioners is as a guide of the kind of data that should be collected as part of regular practice (e.g., progress monitoring scores on measures most aligned with reading achievement measures, student factors as described above) and methods for evaluating that data (e.g., using single scores to predict single scores, growth to predict gains, and student factors to moderate inferences) then modifying both based on the context and outcomes produced.

Highlights

• Progress monitoring slope predicts reading in some contexts but not others.

• Evaluating slope, we controlled for initial/final status and beginning reading.

• Slope may only predict reading when progress monitoring is highly aligned with the reading outcome.

• Slope may only predict reading when negatively correlated with beginning reading.