Applying Quantitative Genetic Methods to Primate Social Behavior

Abstract

Increasingly, behavioral ecologists have applied quantitative genetic methods to investigate the evolution of behaviors in wild animal populations. The promise of quantitative genetics in unmanaged populations opens the door for simultaneous analysis of inheritance, phenotypic plasticity, and patterns of selection on behavioral phenotypes all within the same study. In this article, we describe how quantitative genetic techniques provide studies of the evolution of behavior with information that is unique and valuable. We outline technical obstacles for applying quantitative genetic techniques that are of particular relevance to studies of behavior in primates, especially those living in noncaptive populations, e.g., the need for pedigree information, non-Gaussian phenotypes, and demonstrate how many of these barriers are now surmountable. We illustrate this by applying recent quantitative genetic methods to spatial proximity data, a simple and widely collected primate social behavior, from adult rhesus macaques on Cayo Santiago. Our analysis shows that proximity measures are consistent across repeated measurements on individuals (repeatable) and that kin have similar mean measurements (heritable). Quantitative genetics may hold lessons of considerable importance for studies of primate behavior, even those without a specific genetic focus.

Introduction

Quantitative genetics is a body of theory and set of statistical techniques that link directly with rich evolutionary population genetic models, and that incorporate and formally arrange information on variation in traits and their fitness consequences (Arnold 1994; Lande 1982).; One of the primary applications of quantitative genetic techniques is to characterize the genetic variation underlying phenotypic traits. This includes heritability analyses, whereby heritability is broadly defined as the proportion of phenotypic variance that can be attributed to genotypic variance (broad-sense heritability, H²). Heritability is most often examined as the proportion of phenotypic variance that is explained by additive genetic variance in particular (narrow-sense heritability, h²), with additive genetic variance representing the fact that an individual’s mean genotypic value arises from the sum of the average effects of his parents’ alleles (Visscher et al. 2008).

Genetic variation is necessary for evolution to respond to selection on any phenotype and quantitative genetic techniques have been used to examine the genetic basis of many types of traits e.g., morphology and life history (Blomquist 2009b; Cheverud and Dittus 1992; Lawler 2006). Demonstrating that there is a genetic basis to behavior may be especially important because behaviors are often viewed as infinitely plastic or reflective of unique experiences during an individual’s lifetime (Jones 2005). We consider quantitative genetic methods as complementary to the other more common approaches for studying the ecology and evolution of behavior because no other approach provides the requisite information for a realistic evolutionary model about genetic variation or covariation in traits (Cheverud and Moore 1994).

Human behavioral geneticists have labored for many decades to describe the genetic basis of human behavior (Plomin et al. 2009), and many ecologists have done much the same in other taxa (Boake 1994; Dingemanse and Réale 2005; Weiss et al. 2002). Historically, this work has been conducted using family studies, e.g., twins, siblings, or ancestor–descendant pairs, in humans, whereby phenotypic differences between family members are associated with genotypic differences, or by examining the effects of well-characterized genetic loci on phenotypes in other animals (Bennett and Pierre 2010; Boake et al. 2002), whereby variation in behavioral phenotypes is associated with genetic and/or genomic information. In contrast, primate behavioral ecology has typically lacked a quantitative genetic dimension in spite of accepting the premise that observed behaviors are the product of selection on genetic variation in past generations (Grafen 1984; Hadfield et al. 2007; van Oers and Sinn 2011). This divergence can be explained largely by technical and logistic limitations common to the study of nonhuman primate behavior. This is especially true for primates living in unmanaged populations (wild or free-ranging), for which rich information on behavioral phenotypes exist, but that often is not accompanied by the detailed pedigree data required to conduct quantitative genetic analyses. When pedigree information is available, researchers must cope with the fact that many primate groups are characterized by complex relatedness structures, i.e., complex pedigrees, and are relatively small, resulting in small samples sizes. In addition, primate behavioral data are often recorded as counts or proportions that are non-Gaussian, all of which pose challenges to quantitative genetic (or indeed regular statistical) analyses.

With recent advances in noninvasive DNA extraction and genotyping techniques (Bradley and Lawler 2011; Tung et al. 2010; Perry, this issue), the availability of genetic pedigree data is increasing in nonhuman primate populations at a rapid pace. This, coupled with advances in computational power and statistical techniques, particularly generalized linear mixed models, lead us to propose that the time is ripe for adding a genetic dimension to primate behavioral ecology through expanded application of quantitative genetics (Adams 2011; Bradley and Lawler 2011; Tung et al. 2010; Brent et al., this issue).

There is now a large body of work applying quantitative genetic techniques to phenotypes in wild animal populations, including several accessible reviews (Kruuk et al. 2008; Wilson et al. 2010). However, unlike much of the behavioral data collected by primatologists, most of the phenotypes studied follow the normal (Gaussian) distribution of data that quantitative genetic models were developed to describe, and are sometimes based on data from subjects with simple relatedness structures, e.g., sets of siblings, which are difficult to obtain in adequate sample sizes in most studies of primates. In this article we provide a brief introduction to current quantitative genetic methods with a focus on the common challenges faced when analyzing behavioral data collected in wild or unmanaged primate populations. We introduce the typical “animal model” used to analyze normally distributed phenotypes and then explore a generalized linear mixed model (GLMM) version of it adapted for Poisson-distributed counts. We demonstrate the use of such a model through a simple case study of spatial association in adult rhesus monkeys living in a free-ranging colony with a complex pedigree. We conclude this overview by noting opportunities for more detailed quantitative genetic investigations.

A Brief Introduction to the Animal Model

The core tenet of quantitative genetics is that kin should resemble one another phenotypically because they have copies of the same alleles. These alleles in common are said to be identical by descent because the copies are made by DNA replication during gamete production and transmitted across generations in fertilization. The number of genes involved and where they are located in the genome are usually unknown, although if molecular data are available they can be used to map genes that affect a given phenotype (Visscher et al. 2008). Instead, the standard assumption is that the traits are polygenic—there is a very large number of genes whose summed action results in a continuous distribution of genotypes and phenotypes. The statistical match between phenotypic resemblance and predictions from rules of Mendelian inheritance, e.g., parent and offspring have 1/2 their alleles identical by descent, half siblings on average have 1/4 of their alleles identical by descent, is then used to partition phenotypic variance into genetic and nongenetic sources. Many methods are available for performing this statistical partitioning of phenotypic variance, but all require sets of kin.

In recent decades, ecologists have borrowed techniques developed by animal breeders and medical geneticists to use all of the genealogical information in complex pedigrees efficiently and flexibly model phenotypes to control for known environmental factors. This increases statistical power and helps reduce bias due to shared (or divergent) environments. Animal breeders and ecologists call the most common of these approaches the “animal model” (Kruuk 2004; Lynch and Walsh 1998). The typical animal model for normally distributed phenotypes is given in matrix form in Eq. (1). This is a linear mixed model containing fixed effects and random effects (Kruuk et al. 2008; Wilson et al. 2010).

$$\mathbf{y}=\mathbf{X}\mathbf{\beta }+{\sum }_i^n{\mathbf{Z}}_i{\mathbf{u}}_i+\mathbf{e}$$ (1)

Here, y is the vector of phenotypic measurements, and X is an incidence matrix for fixed effects with β as a vector of regression coefficient estimates. Fixed effects are measured differences among phenotypic records such as sex or age. Z_i is an incidence matrix for random effect i with u_i as the vector of solutions for the random effect, and e is residual error, i.e., $y-(X\beta +{\sum }_i^n{Z}_i{u}_i)$. The residual error can also be described for normally distributed phenotypes as the difference between observed and expected values e=y–E[y]. For genetic analysis in an animal model, a random effect is fit with a level for each individual animal. The covariance of these animal random effect solutions is modeled through a relatedness matrix (A) that documents autosomal allele–sharing predicted by Mendelian rules. A has elements equal to 2θ_ij where θ_ij is the coefficient of coancestry between individuals i and j (Lynch and Walsh 1998). Representing kinship via a matrix allows quantitative genetic analyses to cope with unbalanced designs typical of wild and unmanaged primate populations.

A is typically derived from identification of parents to build up a complete pedigree. For primates this is often a social pedigree of maternal links and paternities using parentage assignment based on molecular markers. Methods have been proposed to approximate A exclusively from molecular markers, though they have yet to receive wide use (Frentiu et al. 2008; Pemberton 2008; Sillanpää 2011). Additional random effects can be used to account for repeated observations on individuals and maternal effects (see later, and Wilson et al. 2010). Quantitative genetic models for handling genomic imprinting, an additional potential source of phenotypic resemblance among some kin, are complex and currently still in development (Spencer 2009).

Estimates of variance components for each random effect are often reported as ratios to the total phenotypic variance. For example, the narrow sense heritability is h²=σ_a²/σ_p², the ratio of additive genetic variance to total phenotypic variance. Numerical procedures for estimating variance components are complex, computationally intensive, and typically use maximum likelihood or Bayesian Markov chain Monte Carlo (MCMC) techniques (Lynch and Walsh 1998; Sorensen and Gianola 2002). Although likelihood is much faster, MCMC estimates are more appropriate for the size and structure of data sets commonly used by primatologists (Hadfield 2010; Adams, this issue). A particular advantage of Bayesian MCMC model fitting over restricted maximum likelihood is that the fixed effects are not assumed to be known without error when estimating variance components of the random effects (O’Hara et al. 2008).

Generalized linear mixed models (GLMMs) allow the same methods to be used with non-normal traits (Bolker et al. 2009). Because behavioral data are often expressed as counts or proportions, this is extraordinarily valuable (Silk 2002). In brief, a generalized linear model uses a link function to transform the expected value of the phenotype (E[y]) onto a scale on which it can be predicted by the linear sum of model effects, e.g., using the log-link, which is common for count data assuming a Poisson distribution, ${log}_e(E[\mathbf{y}])=\mathbf{X}\mathbf{\beta }+{\sum }_i^n{\mathbf{Z}}_i{\mathbf{u}}_i+\mathbf{e}$. Note that this is not just taking the log of y, but rather the mean value of the phenotype is predicted on the log scale by the sum of effects in the linear model. The inverse of the link, which is exponentiation in this case, can be used to write the same model (Eq. 2).

$$E[y]={\mathbf{e}}^{\mathbf{X}\mathbf{\beta }+{\sum }_i^n{\mathbf{Z}}_i{\mathbf{u}}_i+\mathbf{e}}$$ (2)

To illustrate the differences between the typical animal model and that based on a GLMM for non-Gaussian data in greater detail, we provide an example case of spatial proximity data (count data) in adult rhesus macaques. Our analysis of this dataset focuses on four outcomes.

1. First, we ensure that the proximity phenotype can be analyzed as a typical count variable using a Poisson GLMM.

2. Next, we extend the model to include a random effect for individual monkeys. This accounts for the many repeated observations on each individual in the data set and allows for the direct estimation of repeatability, i.e., how consistent individual differences in proximity are across repeated measurements.

3. We then identify a suitable fixed effects model for predicting proximity from known differences among individuals or observations, e.g. sex, time of year. These first three steps are likely familiar to ecologists who have dealt with count data before (Zuur et al. 2009). Here they are also important precursors to genetic analysis.

4. Finally, we leverage the pedigree to estimate the heritability of proximity.

Case Study: Spatial Proximity on Cayo Santiago

Data Collection

We collected behavioral data on adult male and female rhesus macaques (Macaca mulatta) living on Cayo Santiago Island, Puerto Rico. This free-ranging colony was established in 1938 with a single founding population of Indian-origin (Rawlins and Kessler 1986). At the time of study there were six social groups on the island. We based analyses on 2 yr of observation of 107 adults (6–25 yr of age) in group F (2010: N = 26 males, N = 58 females; 2011: N = 33 males, N = 68 females). Although this is a large data set compared to those in most primate field studies of behavior, it is small by the standards of quantitative genetics, which is cause for concern over low statistical power to detect genetic variance. Simulation of phenotypes on a known pedigree can be used to describe power for a given data structure. Further, the effects of any uncertainty in the pedigree can be gauged through further simulations (Kruschke 2011; Morrissey and Wilson 2010; Quinn ). Although this is a large data set compared to those in most primate field studies of behavior, it is small by the standards of quantitative genetics, which is cause for concern over low statistical power to detect genetic variance. Simulation of phenotypes on a known pedigree can be used to describe power for a given data structure. Further, the effects of any uncertainty in the pedigree can be gauged through further simulations (Kruschke 2011; Morrissey and Wilson 2010; Quinn et al. 2006).

We used the same protocol in both years collecting 10-min continuous focal individual samples. We collected 1293.3 h of focal individual data with means (SD) of 4.07 (0.39) and 5.02 (0.11) h per subject in 2010 and 2011, respectively. We recorded the identity of all adults (male and female) ≤2 m of the focal subject at three evenly dispersed intervals during focal individual samples, i.e., at 0, 5, and 10 min). From this, we calculated the total number of individuals of unique identity found in proximity to the focal subject during each 10-min observation. For example, if individual A was found ≤2 m of the focal subject at all three data collection intervals of a 10-min observation, we counted this individual once toward the number of unique individuals in proximity to the focal subject during that observation. We determined dominance rank from the direction and outcome of submissive interactions. Further details on the Cayo Santiago population and our collection of behavioral data are found in Brent et al.(this issue).

To enable quantitative genetic analysis, we obtained genealogical information linking all of these individuals in a single, large interlocking pedigree (N = 428 members) from the Caribbean Primate Research Center (CPRC) long-term database (Table I). This database contains maternal assignments based on census information, i.e., based on behaviors of putative mothers, such as lactation) for all individuals from the founding population onwards, as well as maternity and paternity based on analysis of 29 microsatellite markers for most individuals born since 1990 (≈2900 monkeys). Further details on the CPRC pedigree data are found in Brent et al. (2013a) and Brent et al. (this issue).

Table I.

Description of the pedigree used in the heritability models for Cayo Santiago, PR rhesus macaques (Macaca mulatta)

Phenotyped IDs	107
Pedigree members	428
Maximum generations	8
Founders	13
Maternities	415
Paternities	160
F>0	33
F≥1/16	0
% largest family	100
Āij	0.013
% Aij>0	26.440
% Aij≥1/16	6.870

Analysis and Results

We performed the entire analysis using various functions from packages in R (R Development Core Team 2012). This is convenient, because all data manipulation, graphical display, and analysis can be done in a single free, open-source, cross-platform, environment that has many features standalone genetics software lack, e.g. ASREML, DMU, WOMBAT, SOLAR. In general, their support for generalized linear mixed models is either absent or very limited. Here, we explore a single model for count data but note a variety of alternatives are available for counts and proportions (Nakagawa and Schielzeth 2010; Zuur et al. 2009). We used a Poisson model with log-link for additively overdispersed counts and we focus on Bayesian MCMC results because of important disadvantages of likelihood in GLMMs (Bolker et al. 2009). We analyze the proximity data in sequence of building progressively more elaborate models to illustrate the difficulties and power of GLMM for primate behavioral phenotypes and describe the four outcomes noted in the Introduction.]

1. Overdispersion, variance components, and the appropriateness of a Poisson GLMM. As introduced in the preceding text, a GLMM differs from the standard animal model in a variety of ways. An important difference is the relationship between mean and variance. This is crucial because it affects interpretation of variance components that are used to construct heritabilities. With normally distributed phenotypes, the mean and variance are separate descriptors of the distribution. For the animal model with a single additive genetic random effect one could write $\mathbf{y}~N(\mathbf{X}\mathbf{\beta },{\sigma }_a^2{\mathbf{ZAZ}}^T+{\sigma }_e^2\mathbf{I})$ to state that the phenotype has been treated as a random normal/Gaussian variable with mean X β and variance ${\sigma }_a^2\mathbf{Z}\mathbf{A}{\mathbf{Z}}^T+{\sigma }_e^2\mathbf{I}$. In other words, X β is a vector of fitted values determined by the fixed effects. The variance components only describe a matrix of covariance among the observations in y. For other distributions there may only be a single value that controls the entire shape of the distribution. This is true for the Poisson distribution in which the mean and variance are equal (E[y]=λ, the rate parameter). Using Eq. 2, one would write $\mathbf{y}~\mathit{Poisson}\left({\mathbf{e}}^{\mathbf{X}\mathbf{\beta }+{\sum }_i^n{\mathbf{Z}}_i{\mathbf{u}}_i+\mathbf{e}}\right)$ to state that y is Poisson distributed with mean and variance equal to ${\mathbf{e}}^{\mathbf{X}\mathbf{\beta }+{\sum }_i^n{\mathbf{Z}}_i{\mathbf{u}}_i+\mathbf{e}}$. In this case, ${\mathbf{e}}^{\mathbf{X}\mathbf{\beta }+{\sum }_i^n{\mathbf{Z}}_i{\mathbf{u}}_i+\mathbf{e}}$ is a long vector of Poisson rate parameters fit to the observed data. Observed distributions of count data often have variance > mean, which is called overdispersion. A generalized linear mixed model fits heterogeneity in this rate parameter to explain overdispersion through known differences among observations either through fixed, e.g. sex, age, or random effects, e.g., individual identity in the case of repeated observations. It is important to note that e is no longer just the difference between observed and expected values of each observation in y. Instead, it is additional variation in the Poisson rate parameter corresponding to each observation in y. The observed values in y are the result of one draw from a Poisson distribution having λ equal to the estimated rate parameter for that observation (E[y]). On the link scale, however, the rate parameter is modeled in the same way as the normal animal model: random effects, and the additive residual e, are assumed to be Gaussian/normal, i.e., this is a Poisson log-normal model.

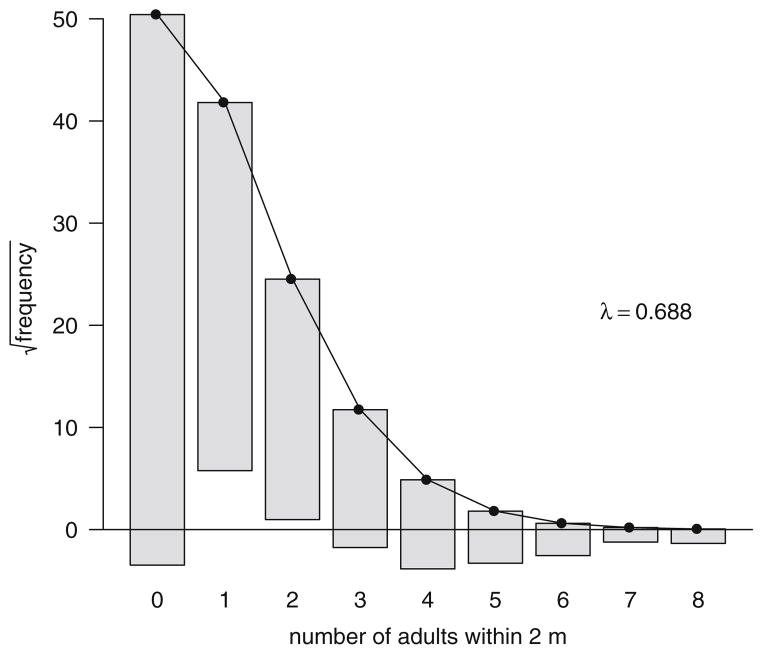
   Overdispersion is a common situation, and it usually indicates there is heterogeneity among the observations in the underlying biological processes generating the data. The adult proximity data were overdispersed and did not precisely fit a Poisson distribution (Fig. 1). This is not surprising considering there are many repeated observations on each individual; they cover a variety of different demographic categories of sex, age, and rank; and were collected at different times of the year. The MCMCglmm function from the package of the same name (Hadfield 2010) can be used in R to fit a GLMM to this data with just an intercept to estimate the mean and a single random effect (Elston et al. 2001). This model is E[y]=e^1β+e, where e^β is a single baseline rate parameter common to all observations and e is a vector of observation-level random effects that are added to β and adjust the rate parameter for each observation. A numerical measure of overdispersion is provided by the variance of this observation-level random effect, ${\sigma }_e^2=0.584$. Rather than a single value, MCMC estimates rely on description of a simulated posterior distribution (Gelman and Shirley 2011; Geyer 2011). We retained 1000 samples of posterior distributions for all models reported. Variance component estimates are taken as the posterior mode. A Bayesian credible interval is also available from the quantiles of the posterior distribution. Here, the 95% credible interval for ${\sigma }_e^2$ was 0.517–0.676, indicating there is a 0.95 probability that the true level of overdispersion falls within this interval (Sorensen and Gianola, 2002; Hadfield and Nakagawa, 2010). This level of overdispersion is small and it declines as other factors are added to the model (Table II). Moreover, a set of graphical checks on the final model explored below indicate the Poisson assumption is not severely violated (Elston et al., 2001).

   If the level of overdispersion were more severe, or the number of zero counts was much larger than expected for a Poisson distribution (zero-inflation), alternatives would have to be explored. These include zero-inflated Poisson and hurdle models (Loeys et al. 2012), modeling the counts with a negative binomial distribution (Hilbe 2011), or collapsing the counts into 0/1 scores and using a logit or probit model (Nakagawa and Schielzeth 2010). However, for this data set, the Poisson model is adequate and there is little reason to try alternatives.

2. Estimating repeatability. Establishing that adult proximity is repeatable is important to justify undertaking a quantitative genetic study. Repeatabilities can only be calculated in the case of repeated measures on individuals and are a ratio of variance components recording the proportion of among individual variance to total variance. Typically, repeatabilities set an upper bound on heritabilities (Nakagawa and Schielzeth 2010). Only if an individual has a consistent, measureable “signal” in his behavioral phenotype should we expect to also detect similarities among kin. Repeatabilities will be familiar to readers who have performed measurement error studies and are particularly commonly reported for morphometric traits. Values calculated for behavioral measures are often low (Bell et al. 2009). This would be disappointing if we expected them to be highly repeatable, e.g., adult tibia length. However, 1–R for behavioral phenotypes is not simply measurement error because behavior is typically much more dynamic than adult morphology. Although heritabilities can still be estimated in cases of single measurements per individual, they offer no indication of this intraindividual variation that is likely to be common for behavioral phenotypes. Repeatabilities can be estimated from GLMMs. As was noted in the previous section, heterogeneity among the observations results in overdispersion and a major source of heterogeneity is the repeated records on each of the monkeys. This can be dealt with directly by adding a random effect such that the model becomes E[y]=e^1β+Zm+e, where m is the vector of individual monkey effects and Z is its incidence matrix relating the 5056 observations to the 107 monkeys. We estimated two variance components with this model; one is the individual monkey variance ( ${\sigma }_m^2=0.351$, CI: 0.246–0.497; Table II), and the other is the observation-level random effect representing remaining overdispersion ( ${\sigma }_e^2=0.371$, CI: 0.312–0.452). These variance components can be used to calculate a repeatability. Although this would simply be a ratio of the monkey variance to the total phenotypic variance for a normally distributed phenotype [ ${\sigma }_m^2/({\sigma }_m^2+{\sigma }_e^2)$], a repeatability on the observed scale for the Poisson log-normal GLMM with additive overdispersion is more complex (Carrasco 2010; Nakagawa and Schielzeth 2010).

   $$R_o=\frac{E_{u,e}[y]\left(e^{{\sigma }_m^{2-1}}\right)}{E_{u,e}[y]\left(e^{{\sigma }_m^2+{\sigma }_e^{2-1}}\right)+1}\text{where}{E}_{u,e}[y]=e^{\mathbf{X}\mathbf{\beta }+\left({\sigma }_m^2+{\sigma }_e^2\right)/2}$$ (3)

   In Eq. 3, exponentiated variance components appear in the numerator and denominator along with the expected mean marginalized over the random effects (E_u,e[y]). This marginal mean reflects the dependence of the total variance in a Poisson GLMM on the mean. E_u,e[y] is the predicted value for an observation given its known fixed effects and any random effect in the sample (as opposed to its calculated random effect solution). Applying $e^{\mathbf{X}\mathbf{\beta }+\left({\sigma }_m^2+{\sigma }_e^2\right)/2}$ produces a vector of predictions for each observation for each MCMC sample. We used the median of these predictions as the estimate of E_u,e[ y] for that sample (Foulley et al. 1987) and then applied Eq. 3 to it, the fixed effect coefficients, and variance components in each MCMC sample to generate a posterior distribution of the repeatability. Applying Eq. 3 yields a posterior mode repeatability on the observed count scale of R_o=0.157 (CI: 0.112–0.228).

   There are two other things worth noting about this repeatability. First, it is not truly comparable to repeatabilities calculated for normally distributed phenotypes in which the denominator is the sum of the variance components. For this reason, some authors prefer to call these pseudo-repeatabilities and pseudo-heritabilities from GLMMs (Foulley et al. 1987; Olesen et al. 1994). Because of the dependence on the mean and requirement that variance components be positive, the Poisson repeatability cannot be equal to one. This is common regardless of the link and variance functions used. Second, a variety of additional information about the individual monkeys or the observations has been left out of this model. Incorporating these effects is the next task.

3. Adjusting for other effects. The repeatability just described could be upwardly or downwardly biased by not accounting for other sources of heterogeneity. Upward bias likely results from not accounting for differences among individuals that are constant but not necessarily a property of the individual. These are sometimes referred to as “group level” effects (Nakagawa and Schielzeth 2010). Sex is the best example of this in the present data set. Males and females have different mean proximity measures. Not accounting for this inflates the mean dissimilarity among individuals and the resulting repeatability (Wilson 2008). However, repeated measurements on each individual might be taken under very different conditions. Not accounting for this would depress the repeatability because an individual monkey’s measurements are more variable than they would be if it were not for these changing conditions. These are often called “data level” effects. A good example of this here is seasonal changes in proximity. Each monkey was measured many times often weeks or months apart. Any additional factors could enter the GLMM as fixed or random effects. The distinction is somewhat arbitrary, but random effects generally should only be used when there are many levels sampled, i.e., enough that estimating a variance makes sense, and they are considered to be drawn from a common distribution (Bolker et al. 2009; McCulloch and Searle 2001). Sex and seasonality are best modeled as fixed effects. Sex is a simple two-level factor. Seasonal changes could be modeled in a variety of ways. We chose to use natural cubic splines. These are local piecewise polynomial fits constrained to be smooth at knot points (Fox 2008; Meyer 2005). We used a single knot, placed at the median of days after January 1, based on visual inspection of the smoothness of the fitted curve and its overall correspondence with monthly sex-specific means. Finding seasonal differences between the sexes, we used the interaction between these variables as part of the fixed effect model. We also used the interaction of sex and linear effect of social rank. We standardized rank within sexes and years to fall on a −1 to +1 scale with highest ranks at −1. Age was the only other variable we tested and found it to have little effect on proximity in either sex, with or without the other fixed effects.

   To make the intercept more interpretable in our full model, we also mean-centered observation date such that it reflected the rate parameter for a female measured on the mean day after January 1 (241.2 d≈ September 1) of middle rank (Schielzeth 2010). In the notation used above, this expanded model is E[y]=e^Xβ+Zm+e where the additional fixed effects are reflected in the expanded design matrix X and vector of coefficients β.

   A common avenue for identifying a suitable set of fixed effects is to run a large set of models and select the best fitting based on information criteria. However, this is often frowned on by statisticians and we do not advocate it for several reasons (Burnham and Anderson 2002). First, the behavior of information criteria is not well understood for many GLMMs, potentially making their ranking of models unreliable (Spiegelhalter et al. 2002; Wilson et al. 2010). Second, MCMC models must run on the computer for a much longer time to obtain trustworthy results in comparison to traditional likelihood routines for fitting models. Although hardware improvements and parallel processing ease this pain, it makes running a large number of models impractical for most investigators. Finally, no software can substitute for the careful consideration of the biological questions at hand and limitations of collected data to identify suitable models rather than “letting the computer decide.” Along these lines, we would echo the recommendation of Bolker et al. (2009) of a long phase of exploratory analysis of graphical displays, descriptive statistics, and models with data subsets before attempting to fit a full GLMM.

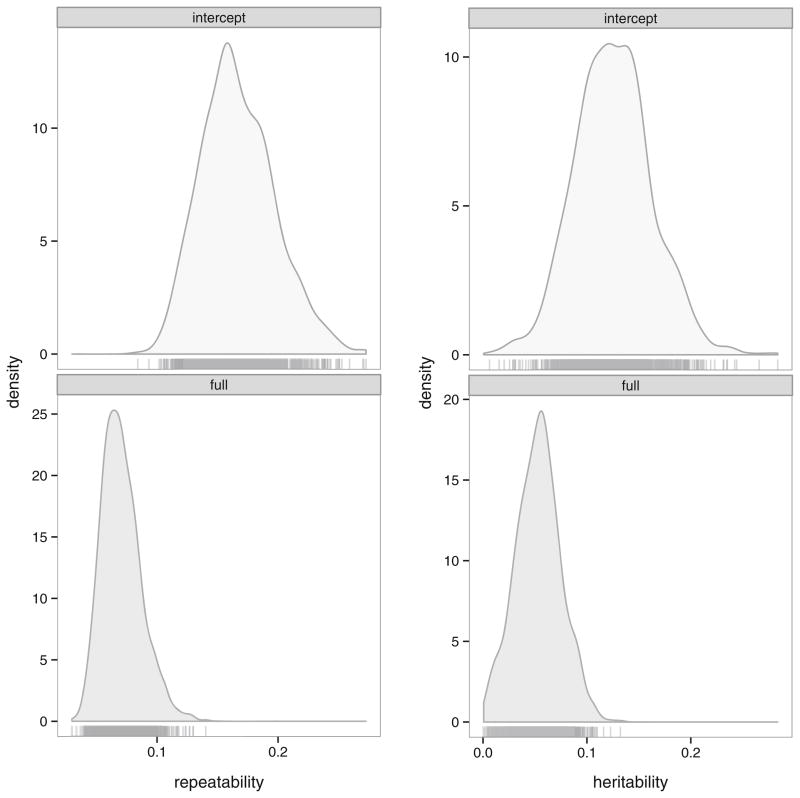
   In our case study, the addition of sex*observation date and sex*rank fixed effects depressed the repeatability of adult proximity, though it clearly remained greater than zero (R_o=0.062, CI: 0.040–0.102; Table II, Fig. 3). This was primarily because most of the fixed effects are at the “group” level, i.e., individual monkeys. There is another less obvious difference from the intercept-only repeatability. Along with the changes in variance components, the distributions of E_u,e[y] also differ. This difference is relatively small and is one reason for using the marginal mean (Carrasco 2010). Alternatively, one could report a range of repeatabilities using different levels of the fixed effects. However, this is unwieldy, because there is a unique repeatability for each combination of the fixed effects (Nakagawa and Schielzeth 2010).

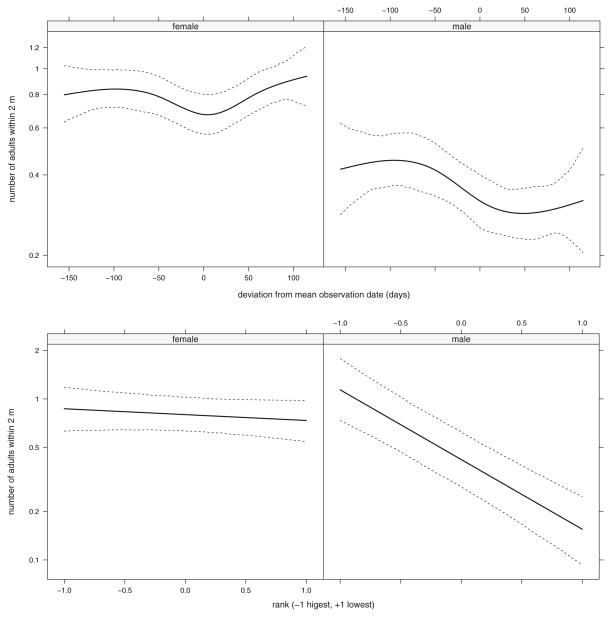
   Fixed effect coefficients are given on the log scale and should be exponentiated to interpret them on the original count scale. These are straightforward for the intercept and sex and rank effects (Fig. 3, Table II). For example, the intercept is mid-ranked females (e^−0.452=0.636); the coefficient for males is −0.659, which means their mean proximity value is e^−0.659=0.517 times the intercept (e^−0.452e^−0.659=0.329). Spline coefficients are typically explored graphically. Effect plots show a distinct seasonal pattern of a drop in mean proximity in the late summer corresponding to the beginning of the birth season that is more persistent for males (Fig. 2, cf. Brent et al. 2013b), and that rank effects are much stronger in males. Precision of the fixed and random effect estimates can be assessed from their credible intervals and these are straightforward to use in graphical displays.

4. Estimating heritability. Our final step is estimating a heritability of proximity. This is accomplished by the addition of a random effect for individual monkeys that is linked to the pedigree which allows calculation of an additive genetic variance component that is separate from the monkey variance and overdispersion variance described previously. A corresponding ratio can be constructed for the heritability. For that reason, we have called these heritability models to distinguish them from the repeatability models above. Here the GLMM becomes E[y] = e^{Xβ+Z_mm+Z_aa+e} if the fixed effects are included, and E[y] = e^{1β+Z_mm+Z_aa+e} if only the intercept is modeled. In these heritability models, a is the vector random effect solutions for individual monkeys linked to the pedigree. In other words, it has the covariance ${\sigma }_a^2\mathbf{A}$. In contrast, m is the vector of random effect solutions for individual monkeys that is not linked to the pedigree. As before, it has the covariance ${\sigma }_m^2\mathbf{I}$. Conceptually, the monkey variance ( ${\sigma }_m^2$) of the repeatability models is being broken down into a portion that reflects resemblance among kin ( ${\sigma }_a^2$) and one that reflects stable but nonfamilial differences among monkeys (σ_m²), or the “permanent environment” of an individual monkey (Lynch and Walsh 1998).

   The estimated additive genetic variances and heritabilities in our heritability models were greater than zero, but they had much broader posterior distributions and larger credible intervals than the variances or ratios in the repeatability models (Fig. 3). Including the set of fixed effects caused a reduction of the heritability estimate similar to the repeatability models (intercept only model, $h_o^2=0.139$ CI: 0.057–0.198; full fixed effects model, $h_o^2=0.057$ CI: 0.009–0.093). Large credible intervals are caused by using a very small data set to estimate a pair of strongly correlated variance components ( ${\sigma }_a^2-{\sigma }_m^2$ lag 0 correlation = −0.686).

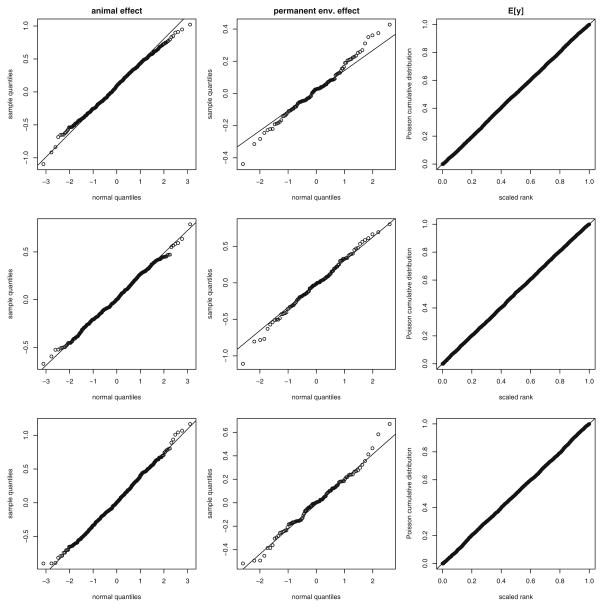
   Posterior distributions of all the fixed effects can be explored graphically. Figures 2 and 3 provide these displays from the heritability model with the full set of fixed effects. Coefficients for the full repeatability and heritability model were very similar (Table II), which is typical when heritabilities are small. A final set of checks on the adequacy of the Poisson distribution for this full model is also given in Fig. 4. In truth, this is the most important check on how suitable the Poisson distribution is for the counts because the full model accounts for all sources of heterogeneity in the data we found to be important. Ideally, the animal and monkey random effects would be normally distributed (assessed by quantile plots) and the predicted rate parameters (E[y]) would be Poisson distributed (assessed by a probability–probability plot). These plots can be produced for each MCMC sample, but only three randomly selected sets are shown (Elston et al. 2001).

Fig. 1.

A “rootogram” of the raw proximity data frequencies as grey bars (Wainer, 1974) for Cayo Santiago, PR rhesus macaques (Macaca mulatta). Expected frequencies if the counts conformed to a Poisson distribution with the same rate parameter (λ) are shown with the black line and dots. Bars for the observed frequencies are shifted up or down to match the Poisson line, making their overlap with the horizontal axis a simple check on whether the frequency is greater or less than expected. There is an excess at counts ≥3 and at 0, and deficiency at counts 1 and 2.

Table II.

Results of repeatability and heritability models for Cayo Santiago, PR rhesus macaques (Macaca mulatta) with either a full set of fixed effects or an intercept only

	Repeatability	Heritability	Repeatability	Heritability
Intercept	−0.751 (−0.878,−0.623)	−0.854 (−1.050,−0.669)	−0.452 (−0.660,−0.208)	−0.480 (−0.720,0.240)
Rank			−0.122 (−0.294,0.029)	−0.084 (−0.272,0.102)
Male			−0.659 (−1.087,−0.187)	−0.642 (−1.082,−0.185)
Male: rank			−0.877 (−1.203,−0.596)	−0.912 (−1.223,−0.613)
σa2		0.304 (0.144,0.455)		0.114 (0.013,0.175)
σm2	0.351 (0.246,0.497)	0.010 (0.000,0.163)	0.123 (0.082,0.194)	0.016 (0.000,0.108)
σe2	0.371 (0.312,0.452)	0.377 (0.305,0.452)	0.362 (0.313,0.448)	0.380 (0.308,0.446)
μ	0.662 (0.606,0.783)	0.614 (0.499,0.732)	0.743 (0.681,0.819)	0.722 (0.640,0.846)
Ro	0.157 (0.112,0.228)		0.062 (0.040,0.102)
ho2		0.139 (0.057,0.198)		0.057 (0.009,0.093)

Posterior means of the fixed effect coefficients and 95% credible intervals are reported. Variance components and ratios have posterior modes and credible intervals reported. In the full models, the intercept is mid-ranked female from the mean observation date. Natural cubic spline coefficients for sex*observation date effects are omitted because they are easiest to interpret graphically (Fig. 2). μ is the posterior mode of the MCMC sample marginal medians.

Fig. 3.

Posterior distributions of repeatabilities and heritabilities from the intercept only and full models Cayo Santiago, PR rhesus macaques (Macaca mulatta). Posterior modes and credible intervals are given in Table II.

Fig. 2.

Fixed effect predictions of proximity in the full heritability model Cayo Santiago, PR rhesus macaques (Macaca mulatta). The upper panels show the observation date*sex interaction and the lower panels give the rank*sex interaction. Random effects are marginalized in all panels. Points correspond to predictions for each record (middle curve/line) using the posterior mean coefficients and posterior mode of the sum of the variance components while the outer curves give quantiles (2.5% and 97.5%) from the individual MCMC samples. These mimic plots produced by the effects package (Fox 2003; Fox and Hong 2009).

Fig. 4.

Diagnostic q–q and p–p plots from the full heritability model for Cayo Santiago, PR rhesus macaques (Macaca mulatta). Each row shows a single randomly selected MCMC sample. Each column displays q–q plots for the animal additive genetic effects, q–q plots for the permanent environment effect, and p–p plots for the predicted Poisson counts (Elston et al. 2001). In each plot, points are expected to fall along the diagonal line. Departures would indicate a poor fit of the Poisson log-normal GLMM. Deviation in these plots and those for other samples are quite small.

Discussion

We have demonstrated that the tendency for free-ranging rhesus macaques to be found within two meters of other adults has a narrow-sense heritability somewhere in the range of 5–15%, depending on how we accounted for covariates such as sex, rank, and seasonality. So what? One answer to this question is very basic. Genetic variation is necessary for populations to respond to selection on any phenotype and demonstrating that there is a genetic basis to primate behavior is therefore an important first step in describing its potential evolutionary trajectory. Although behavioral measurements have been included in heritability estimates for multivariable abstractions such as social network statistics (Brent et al. 2013a), and behavioral tendencies (Williamson et al. 2003; Adams et al. 2012; Brent et al. .this issue) to our knowledge, this is the first demonstration that tendency for adult primates to be in proximity with one another is heritable. The increased availability of pedigrees and power of animal model methods may change this in the near future. However, there is much more that can and should be done with quantitative genetic models and methods.

Before exploring useful applications of a heritability estimate and extensions, it is worth recalling some of the pitfalls of interpretation. These are well known and have been discussed by many authors but are worth recounting (Adams 2011; Roff 1997; Vitzthum 2003; Visscher et al. 2008). First, high heritabilities should not always be expected for phenotypes where genes are thought to play an important role. Heritabilities are fractions of phenotypic variance. Many traits that undoubtedly require interacting networks of genes, e.g. the presence of a brain in adults, do not vary and therefore have undefined heritabilities. Moreover, because heritabilities are dependent on allele frequencies and environmental conditions in a population, a large heritability could be the result of small environmental variance (Charmantier and Garant 2005). Animal model heritabilities are also dependent on how the phenotypic variance is calculated. If fixed effects primarily affect the phenotypic variance, then removal of their variance from the denominator of the heritability will result in higher heritabilities (Wilson 2008). GLMM “pseudo-heritabilities” may also have additional quirks such as the dependence on the overall mean in the Poisson case explored in the preceding text. Second, a low heritability does not mean genes play no role in shaping phenotypic variance. Again, because heritabilities are ratios, a low value could result from large environmental variance even when additive genetic variance is greater than zero. Price and Schluter (1991) argue this is likely a common situation for behavioral and life history traits that are contingent on other physiological and social circumstances. Finally, heritabilities describe intrapopulation variation. Therefore, a simple heritability estimate is next to useless for describing intergroup differences. For example, the difference in mean proximity between monkeys in group F and those in any other social group probably have nothing to do with genetics, and a heritability estimate of 5% certainly would not mean that 5% of any mean difference in proximity between groups is due to the additive effect of genes (Brommer 2011).

Avoiding these pitfalls, we would highlight some appropriate uses of heritability estimates and areas for extension. First, heritabilities link very directly to simple quantitative models of evolutionary change, such as response to directional selection in the breeder’s equation (R=h²S; Roff 1994, 1997). In this equation, intergenerational change in the mean (R =response) is always a fraction of the selection differential (S) equal to h². A small heritability such as the one estimated for adult proximity implies very slow response to selection. This is typical of behavioral phenotypes which often have lower heritabilities than morphological traits (cf. Stirling et al. 2002). The response to directional selection of phenotypes with non-normal distributions, such as Poisson counts, is somewhat different because of the mean–variance equality but it has been modeled (Korsgaard et al. 2002).

Second, heritability estimates are often an effective tool for initial screening of phenotypes amenable to exploring the molecular signatures of inheritance through genome-wide association (GWAS) and or linkage mapping (Visscher et al. 2010). Once identified, loci can be subjected to a variety of tests for departures from equilibrium including molecular signatures of selection. Well-characterized loci from laboratory settings that have documented associations with behavioral patterns can also be incorporated, e.g., neurotransmitter production and regulation; Brent et al. 2013a). These are enticing research projects that are treated in great detail by other authors and emphasize the “genetic” side of quantitative genetics (Bradley and Lawler 2011; Tung et al. 2010). The allure of molecular genetics need not overshadow the advantages of quantitative genetic techniques themselves.

Instead of fretting over the molecular details of inheritance, we should also consider quantitative genetic methods relevant for addressing the equally exciting complexity of environments primates experience and construct for each other. Lengthy developmental periods in primates have often been argued to be opportunities for parental and peer effects on behavioral phenotypes (Leigh 2001; Maestripieri 2009). There are sophisticated quantitative genetic models for describing such effects through variance components or covariances between social partner phenotypes and they often have very different dynamics from the intuitive breeder’s equation (Cheverud and Wolf 2009; Moore et al. 2002; Adams, this issue). Moreover, the flexibility of primate behavior and depth of longitudinal measurements on known individuals are an opportunity for studying the evolution and genetics of plasticity. Plasticity itself can be treated as a phenotype (Schlichting and Pigliucci 1998) when individuals are measured across environmental gradients and individual reaction norms can be calculated (Dingemanse and Dochtermann 2013; Dingemanse et al. 2010; Martin et al. 2011). For example, in our case study we treated spatial association as the same trait regardless of season of measurement. In other words, if proximity in the birth and nonbirth seasons were, in fact, two different traits our case study analysis requires we assume the genetic correlation between these traits is 1 and their heritabilities are equal. It is an open question as to how realistic these assumptions are. Given large enough data sets, they can be tested with multivariate and random regression quantitative genetic models (Brommer et al. 2012).

Power concerns will often limit the applicability and complexity of quantitative genetic models for unmanaged primate populations. The number of such populations with well-resolved pedigrees is rapidly increasing, thus removing the other major barrier to the application of quantitative genetics to studies of primate behavior. We would encourage primatologists wishing to employ these techniques to use simulations on their pedigrees to identify the necessary number of individuals to measure to achieve sufficient power, e.g., for detecting nonzero genetic variance). For example, Quinn et al. (2006) showed a total of 300 measured individuals was sufficient to generate precise estimates of heritabilities and genetic correlations in two bird populations. Although this figure is currently unattainable for most any primate behavioral study, our analysis of spatial association used considerably fewer individuals, but was still able to detect a nonzero genetic variance. Because of the strong influence of pedigree structure, the locations of measured individuals within the pedigree, measurement error, and how well environmental effects are accounted for, there is no clear “rule of thumb” to guide when quantitative genetic analysis is or is not worthwhile. However, we would suggest samples<100 are unlikely to be of much use. This places a considerable limit on the current applicability of quantitative genetics to all but the longest-running primate field sites, and may preclude such analysis with understudied and endangered species. Nevertheless, large-scale sampling efforts are currently underway at a number of field sites, and would be feasible to implement over relatively short periods of time at others. We therefore encourage primatologists in the future to consider the requirements of quantitative genetic techniques when designing data collection protocols.

We close by noting an indirect but potentially far-reaching contribution of quantitative genetics by wondering, should behavioral ecology become like comparative biology? Hardly any interspecific comparative study is published today that does not somehow account for the phylogenetic relationships among study species (Freckleton 2009; Housworth et al. 2004). Primate behavioral ecologists face a similar problem of non-independence among the individual members of the populations they study because many primate groups consist of sets of kin, and kin may not be randomized across environments (Blomquist 2009a; Silk 1984). In comparative studies the phylogenetic history of species is most influential for identifying interspecific patterns, e.g., evolutionary allometries, when those patterns are weak (Klingenberg 1996). Because ecological trends are typically quite weak (Nee et al. 2005; Peters 1991), the genealogy of primate groups could make a huge difference for establishing how population members respond to changing social and climatic conditions that are the foundation of primate theoretical and field ecology (Campbell et al. 2011; Clutton-Brock and Janson 2012). The increasing availability of pedigrees, or techniques to construct them, for wild primates begs for deeper appreciation and direct treatment of this problem. Just as comparative biologists use a phylogeny as a tool for analysis of interspecific data without any direct interest in discovering phylogeny, perhaps ecologists should be using pedigrees even when they are uninterested in genealogy or estimating heritabilities.