Large sample randomization inference of causal effects in the presence of interference

Abstract

Recently, increasing attention has focused on making causal inference when interference is possible. In the presence of interference, treatment may have several types of effects. In this paper, we consider inference about such effects when the population consists of groups of individuals where interference is possible within groups but not between groups. A two stage randomization design is assumed where in the first stage groups are randomized to different treatment allocation strategies and in the second stage individuals are randomized to treatment or control conditional on the strategy assigned to their group in the first stage. For this design, the asymptotic distributions of estimators of the causal effects are derived when either the number of individuals per group or the number of groups grows large. Under certain homogeneity assumptions, the asymptotic distributions provide justification for Wald-type confidence intervals (CIs) and tests. Empirical results demonstrate the Wald CIs have good coverage in finite samples and are narrower than CIs based on either the Chebyshev or Hoeffding inequalities provided the number of groups is not too small. The methods are illustrated by two examples which consider the effects of cholera vaccination and an intervention to encourage voting.

1 Introduction

When assessing the causal effect of a treatment or exposure, it is typically assumed that individuals (or units) do not interfere with each other (Cox 1958). This assumption is part of the stable unit treatment value assumption (SUTVA) (Rubin 1980). Under the no interference assumption, the potential outcomes of any individual are assumed to be determined solely by the treatment of that individual, unaffected by the treatment of other individuals under study. However, in many settings this assumption may not hold. For example, in vaccine studies, the outcome of an individual may depend not only on that individual's vaccine status but also on the vaccination status of other individuals (Halloran and Struchiner 1995). In educational studies, a student's academic performance may depend on the retention or promotion of that student as well as of fellow classmates (Hong and Raudenbush 2006). In econometric studies, interference may be present between households in the same neighborhood (Sobel 2006) or other settings where individuals interact socially (Manski 2012). Interference can occur within an individual over time, e.g., as in functional MRI studies (Luo et al. 2012), or between units that are proximal spatially (e.g., Zigler et al. 2012). Rosenbaum (2007) presents several other examples where interference may be present.

Increasing attention has been placed on relaxing the no interference assumption (see Tchetgen Tchetgen and VanderWeele (2012) and references therein). Inference in this setting is particularly interesting because a treatment may have different types of effects, but challenging because individuals may have many potential outcomes due to interference. One approach has been to consider settings where individuals can be partitioned into groups such that interference is possible between individuals within the same group but not across groups. This is sometimes called `partial interference' (Sobel 2006), a terminology adopted here. In the nomenclature of Manski (2012), partial interference is an example of a `constant treatment response' assumption where the `reference groups' are `treatment invariant' and `symmetric'. The partial interference assumption will be reasonable when groups are sufficiently separate socially, temporally, or spatially.

Drawing inference about treatment effects often relies on knowledge or modeling of the mechanism by which individuals are assigned or select treatment. Assuming partial interference, one possible assignment mechanism is a two stage randomization design, where in the first stage groups are randomized to different treatment allocation strategies and in the second stage individuals are randomized to treatment or control conditional on the strategy assigned to their group in the first stage. For example, schools might be randomized to high or low vaccine coverage, and then students in the schools randomized to vaccine or control with vaccination probability dependent on whether their school was assigned to high or low coverage (Longini et al. 1998). Similarly, Borm et al. (2005) described a trial where general practitioners were randomized to two allocation strategies and then different proportions of each practitioner's patients were randomly assigned either a traditional or new method of care. Sinclair et al. (2012) conducted a two stage randomization experiment to determine the direct and indirect (or `spillover') effects of social pressure mailings on voter mobilization in a special election in 2009. In that study zip-codes were randomly assigned to one of four allocation strategies, and then households within a zip-code were randomly assigned to receive mailings (postcards) conditional on the allocation strategy assigned to that zip-code. For other examples, see Duflo and Saez (2003) and Ichino and Schündeln (2012). This two-stage randomization design has been referred to as split-plot or pseudo-cluster randomization.

Assuming partial interference and a two stage randomization design, Hudgens and Halloran (2008) proposed unbiased estimators for different causal effects of treatment. They also derived variance estimators which under certain assumptions are conservative unless the corresponding causal effect is additive. These results can be viewed as generalizations of the classic results of Splawa-Neyman (1923) to the setting of interference. In this paper, the large sample distributions of the causal effect estimators proposed by Hudgens and Halloran (2008) are derived for two stage randomization studies. The outline of the remainder of this paper is as follows. In Section 2 we introduce notation and define various causal effects. Unbiased estimators of these effects and the corresponding variance estimators are reviewed briefly in Section 3.1. The asymptotic distributions of these estimators are then derived when either the number of individuals within the groups grows large (Section 3.2.1), or the number of groups grows large (Section 3.2.2). These results can be utilized to construct Wald type confidence intervals (CIs) or tests for the different treatment effects. In Section 4 a simulation study is presented comparing Wald CIs with CIs based on Hoeffding and Chebyshev inequalities. Section 5 includes two applications which consider the various effects of a cholera vaccine and an intervention to encourage voting. Proofs of the results in Section 3 and some technical details regarding the voting encouragement analysis are given in the Appendix.

2 Notation, Assumptions and Estimands

Consider a population of m groups with n_i individuals in group i for i = 1, …, m. Suppose individuals can receive treatment or control, denoted by 1 or 0. Let z_ij denote the treatment indicator for individual j in group i, where z_ij = 1 indicates treatment and z_ij = 0 denotes control. Let z_i(−j) denote the vector of treatment indicators for the individuals in group i other than individual j and let z_i = (z_ij, z_i(−j)) denote the vector of treatment indicators for all individuals in group i. Let y_ij(z_i) = y_ij(z_ij, z_i(−j)) denote the potential outcome of individual j when individuals in group i receive treatment z_i. Randomization based inference is employed in this paper wherein the potential outcomes are viewed as fixed (i.e., non-random) features of the population of ${\sum }_{i=1}^m{n}_i$ individuals. Note the notation y_ij(z_i) encompasses the partial interference assumption that the outcome for individual j does not depend on the treatment of individuals in groups i′ ≠ i.

Just as individuals can receive treatment or control, suppose groups can take on different treatment allocation strategies corresponding to the proportion of individuals within the group that receive treatment. For simplicity we consider only two allocation strategies, denoted by α₁ and α₀. For instance, α₁ could correspond to assigning treatment to 50% of individuals in a group and α₀ could correspond to assigning treatment to 10% of individuals in a group. Let g_i = s when the allocation strategy for group i is α_s and let g = (g₁, …, g_m) denote the vector of group level allocation strategies.

Assume a two-stage randomization design where in the first stage groups are assigned allocation strategies α₁ or α₀. Denote the random assignment indicator for group i by G_i and let G = (G₁, …, G_m). Let $l={\sum }_{i=1}^m{G}_i$ denote the number of groups assigned α₁. Assume allocation strategies are assigned using permutation randomization such that l is fixed for some integer l ∈ {1, …, m − 1}, i.e., $\mathrm{Pr}(G=g)=1∕{(}_l^m)$ for all g such that ${\sum }_{i=1}^m{g}_i=l$ and Pr(G = g) = 0 otherwise. In the second stage of randomization, individuals are randomly assigned treatment or control conditional on G_i = g_i from the first stage. Let the individual treatment assignment of individual j in group i be denoted by Z_ij and let Z_i = (Z_i1, …, Z_ini) such that the observed outcome for individual j is y_ij(Z_i). Throughout, it is assumed that the assignment of an individual to a particular treatment is equivalent to receipt of that treatment, i.e., there is perfect compliance. Likewise, it is assumed groups are always compliant with their assigned allocation strategy. Let $k_{i{\alpha }_s}={\sum }_{j=1}^{n_i}{Z}_{\mathit{ij}}$ denote the number of individuals in group i assigned treatment when group i is assigned allocation strategy α_s. Assume that treatment is assigned using permutation randomization such that k_iαs is fixed given G_i. Let $R_k^n$ denote the set of vectors of length n with elements 0 or 1 that sum to k, i.e., $R_k^n=\{v\in {\{0,1\}}^n:{\sum }_{i=1}^n{v}_i=k\}$. Under the two stage randomization design described above, $g\in R_l^m$, $z_i\in R_{k_{i{\alpha }_s}}^{n_i}$ and $z_{i(-j)}\in R_{k_{i{\alpha }_s}-z_{\mathit{ij}}}^{n_i-1}$ when G_i = s.

Define the average potential outcome for individual j in group i when individual j is assigned treatment z and group i is assigned allocation strategy α₁ by

$${\stackrel{‒}{y}}_{\mathit{ij}}(z,{\alpha }_1)=\sum _{z_{i(-j)}\in R_{k_{i{\alpha }_{1^{-z}}}}^{n_{i-1}}}{y}_{\mathit{ij}}(z_{\mathit{ij}}=z,z_i(-j\left)\right)\mathrm{Pr}\left(Z_i\right(-j)=z_{i(-j)})\mid Z_{\mathit{ij}}=z,G_i=1).$$

. See VanderWeele and Tchetgen Tchetgen (2011) for alternative approaches to defining average potential outcomes for an individual. Averaging over individuals, define the group average potential outcome under group allocation α₁ and individual treatment assignment z as ${\stackrel{‒}{y}}_i(z,{\alpha }_1)={\sum }_{j=1}^{n_i}{\stackrel{‒}{y}}_{\mathit{ij}}(z,{\alpha }_1)∕n_i$. Similarly, averaging over groups, define the population average potential outcome as ${\stackrel{‒}{y}}_i(z,{\alpha }_1)={\sum }_{i=1}^m{\stackrel{‒}{y}}_i(z,{\alpha }_1)∕m$. Define the marginal individual average potential outcome by ${\stackrel{‒}{y}}_{\mathit{ij}}\left({\alpha }_1\right)={\sum }_{z\in R_{k_{i{\alpha }_1}}^{n_i}}{y}_{\mathit{ij}}\left(z\right)\mathrm{Pr}(Z_i=z\mid G_i=1)$, that is, the average potential outcome for individual j in group i when group i is assigned α₁. Similarly, define the marginal group and population average potential outcomes by ${\stackrel{‒}{y}}_i\left({\alpha }_1\right)={\sum }_{j=1}^{n_i}{\stackrel{‒}{y}}_{\mathit{ij}}\left({\alpha }_1\right)∕n_i$ and $\stackrel{‒}{y}\left({\alpha }_1\right)={\sum }_{i=1}^m{\stackrel{‒}{y}}_i\left({\alpha }_1\right)∕m$.

Various causal effects can be defined by considering contrasts of different average potential outcomes. For example, at the group level, a direct effect can be defined as ${\overline{\mathit{DE}}}_i\left({\alpha }_1\right)={\stackrel{‒}{y}}_i(1,{\alpha }_1)-{\stackrel{‒}{y}}_i(0,{\alpha }_1)$. That is, ${\overline{\mathit{DE}}}_i\left({\alpha }_1\right)$ is the difference between the average potential outcome when group i receives allocation strategy α₁ and an individual in that group receives treatment compared to when an individual in that group receives control. At the population level define the direct effect $\overline{\mathit{DE}}\left({\alpha }_s\right)=\stackrel{‒}{y}(1,{\alpha }_s)-\stackrel{‒}{y}(0,{\alpha }_s)$ for s = 0, 1, the indirect effect $\overline{\mathit{IE}}({\alpha }_1,{\alpha }_0)=\stackrel{‒}{y}(0,{\alpha }_1)-\stackrel{‒}{y}(0,{\alpha }_0)$, the total effect $\overline{\mathit{TE}}({\alpha }_1,{\alpha }_0)=\stackrel{‒}{y}(1,{\alpha }_1)-\stackrel{‒}{y}(0,{\alpha }_0)$, and the overall effect $\overline{\mathit{OE}}({\alpha }_1,{\alpha }_0)=\stackrel{‒}{y}\left({\alpha }_1\right)-\stackrel{‒}{y}\left({\alpha }_0\right)$. In words, the indirect (or spillover) effect compares the average potential outcome when an individual receives control and their group receives allocation strategy α₁ compared to when their group receives α₀. Because the individual treatment assignment is held fixed, the indirect effect will be non-zero only if interference is present. Note that the indirect effect can also be defined for individuals who receive treatment, i.e., in terms of $\stackrel{‒}{y}(1,{\alpha }_s)$ for s = 0, 1, but for simplicity we do not consider this other indirect effect here. The total effect equals the sum of the direct and indirect effects, while the overall effect provides a single summary measure of the effect of allocation strategy α₁ versus α₀. See Tchetgen Tchetgen and VanderWeele (2012) for further discussion about these estimands.

Assuming only partial interference, an individual in a group with n_i individuals will have 2ⁿⁱ potential outcomes. For groups of even moderate size the large number of potential outcomes per individual makes inference challenging. One possible additional assumption about the structure of interference that reduces the number of potential outcomes considerably is:

$$y_{\mathit{ij}}\left(z_i\right)=y_{\mathit{ij}}\left(z_i^{\prime }\right)\text{for all}{z}_i,z_i^{\prime }\in R_{k_{i{\alpha }_s}}^{n_i}\text{such that}{z}_{\mathit{ij}}=z_{\mathit{ij}}^{\prime }.$$ (1)

Assumption (1) has been referred to as `stratified interference' (Hudgens and Halloran 2008) and `anonymous interaction' (Manski 2012). Under this assumption the potential outcome of any individual in a group may be affected only by that individual's treatment and the aggregate treatment assignment of others in the same group. For example, consider a study of vaccines in children attending school and assume no interference between schools. Assumption (1) implies the outcome for an individual vaccinated child will be the same when k — 1 schoolmates receive vaccine regardless of which particular k — 1 schoolmates are actually vaccinated. Under (1), the number of potential outcomes reduces from 2ⁿⁱ to 2n_i for any individual in a group of size n_i. Given permutation allocation strategy α_s is assigned to group i, individual j will have only two potential outcomes depending on whether z_ij = 1 or z_ij = 0. That is, $y_{\mathit{ij}}(z_{\mathit{ij}},z_{i(-j)})={\stackrel{‒}{y}}_{\mathit{ij}}(z_{\mathit{ij}},{\alpha }_s)$ for all $z_i\in R_{k_{i{\alpha }_s}}^{n_i}$. In the sequel, the stratified interference assumption (1) is made throughout. Thus for notational simplicity ${\stackrel{‒}{y}}_{\mathit{ij}}(z,{\alpha }_s)$ will be denoted by y_ij(z, α_s) for z, s = 0, 1.

3 Inference

3.1 Estimators

Hudgens and Halloran (2008) derived unbiased estimators for the causal estimands defined in Section 2 above. Specifically, assuming partial interference and two stage permutation randomization, a conditionally unbiased estimator for ${\stackrel{‒}{y}}_i(z,{\alpha }_s)$ given G_i = s is ${\widehat{Y}}_i(z,{\alpha }_s)={\sum }_{j=1}^{n_i}{y}_{\mathit{ij}}\left(Z_i\right)1(Z_{\mathit{ij}}=z)∕{\sum }_{j=1}^{n_i}1(Z_{\mathit{ij}}=z)$ and an unbiased estimator for $\stackrel{‒}{y}(z,{\alpha }_s)$ is $\widehat{Y}(z,{\alpha }_s)={\sum }_{i=1}^m{\widehat{Y}}_i(z,{\alpha }_s)1(G_i=s)∕{\sum }_{i=1}^{m}1(G_i=s)$, where 1(·) is the usual indicator function. At the group level a conditionally unbiased estimator given G_i = s of the direct effect is ${\widehat{\mathit{DE}}}_i\left({\alpha }_s\right)={\widehat{Y}}_i(1,{\alpha }_s)-{\widehat{Y}}_i(0,{\alpha }_s)$, and at the population level unbiased estimators for the direct, indirect, total, and overall effects are $\widehat{\mathit{DE}}\left({\alpha }_s\right)=\widehat{Y}(1,{\alpha }_s)-\widehat{Y}(0,{\alpha }_s)$ for s = 0, 1, $\widehat{\mathit{IE}}({\alpha }_1,{\alpha }_0)=\widehat{Y}(0,{\alpha }_1)-\widehat{Y}(0,{\alpha }_0)$, $\widehat{\mathit{TE}}({\alpha }_1,{\alpha }_0)=\widehat{Y}(1,{\alpha }_1)-\widehat{Y}(0,{\alpha }_0)$ and $\widehat{\mathit{OE}}({\alpha }_1,{\alpha }_0)=\widehat{Y}\left({\alpha }_1\right)-\widehat{Y}\left({\alpha }_0\right)$ where ${\widehat{Y}}_i\left({\alpha }_1\right)={\sum }_{j=1}^{n_i}{y}_{\mathit{ij}}\left(Z_i\right)∕n_i$, $\widehat{Y}\left({\alpha }_1\right)={\sum }_{i=1}^m{\widehat{Y}}_i\left({\alpha }_1\right)1(G_i=1)∕{\sum }_{i=1}^{m}1(G_i=1)$ and $\widehat{Y}\left({\alpha }_0\right)$ is defined analogously.

Hudgens and Halloran also proposed estimators of the variances of these estimators. In particular, under (1) unbiased estimators for $\mathit{Var}\left\{{\widehat{Y}}_i\right(1,{\alpha }_1)\mid G_i=1\}$ and $\mathit{Var}\left\{\widehat{Y}\right(1,{\alpha }_1\left)\right\}$ are given by $\widehat{\mathit{Var}}\left\{{\widehat{Y}}_i\right(1,{\alpha }_1)\mid G_i=1\}=(1-k_{i{\alpha }_1}∕n_i){\widehat{\sigma }}_{i1}^2\left({\alpha }_1\right)∕k_{i{\alpha }_1}$ where ${\widehat{\sigma }}_{i1}^2\left({\alpha }_1\right)={\sum }_{j=1}^{n_i}{\left\{y_{\mathit{ij}}\right(Z_i)-{\widehat{Y}}_i(1,{\alpha }_1\left)\right\}}^2{Z}_{\mathit{ij}}∕(k_{i{\alpha }_1}-1)$ and $\widehat{Var}\left\{\widehat{Y}\right(1,{\alpha }_1\left)\right\}=(1-l∕m){\widehat{\sigma }}_{g1}^2\left({\alpha }_1\right)∕l+{\sum }_{i=1}^m(1-k_{i{\alpha }_1}∕n_i){\widehat{\sigma }}_{i1}^2\left({\alpha }_1\right)G_i∕\left(k_{i{\alpha }_1}\mathit{ml}\right)$ where ${\widehat{\sigma }}_{g1}^2\left({\alpha }_1\right)={\sum }_{i=1}^m{\left\{{\widehat{Y}}_i\right(1,{\alpha }_1)-\widehat{Y}(1,{\alpha }_1\left)\right\}}^2{G}_i∕(l-1)$. They also proposed estimators of the variance of the various causal effect estimators which are positively biased unless certain additivity conditions hold. For example, if there exist constants η₁, …, η_m such that y_ij(1, α_s) = y_ij(0, α_s) + η_i for all i = 1, …, m and j = 1, …, n_i, then their estimator for the variance of $\widehat{\mathit{DE}}\left({\alpha }_s\right)$ is unbiased; otherwise their estimator is positively biased. Similar additivity conditions exist for the variance estimators of the other causal effect estimators.

3.2 Asymptotic Distributions

Below the asymptotic distributions of the causal effect estimators defined in Section 3.1 are derived. In Section 3.2.1, the setting where the numbers of individuals per group n₁, …, n_m grow large is considered. These results might be applicable, for instance, when groups are defined to be all individuals in a particular geographic region. For example, Sur et al. (2009) estimated the indirect, total, and overall effects of typhoid vaccination in groups of people within contiguous geographic areas in India, where the average group size was over 700. The results in Section 3.2.1 do not require the number of groups to be large. On the other hand, Section 3.2.2 considers the setting where the number of groups m grows large. These results do not require that the number of individuals per group is large and could be applied, for instance, in household based studies when the households (i.e., groups) are small but the number of households in the study is large. For example, Millar et al. (2008) studied the indirect effect of vaccination against pneumococcal disease in over 900 households containing on average fewer than four individuals per household.

3.2.1 Large Groups

Propositions 1 – 3 below show that under certain conditions the group average potential outcome estimators, group average direct effect estimator and the marginal group average potential outcome estimators are asymptotically Normal (i.e., Gaussian). The notation $\stackrel{d}{\to }\mathcal{N}(0,1)$ will be used to denote convergence in distribution to a standard Normal random variable.

Proposition 1. Let ν_ij = y_ij(z, α_s) and ν_i. = (ν_i1 + … + ν_i,ni)/n_i for z, s ∈ {0, 1}. If

$$k_{i{\alpha }_s}\to \infty ,n_i-k_{i{\alpha }_s}\to \infty$$ (2)

and

$$\frac{\max {(v_{\mathit{ij}}-v_{i.})}^2}{\sum _{j=1}^{n_i}{(v_{\mathit{ij}}-v_{i.})}^2}\max \left\{\frac{n_i-k_{i{\alpha }_s}}{k_{i{\alpha }_s}},\frac{k_{i{\alpha }_s}}{n_i-k_{i{\alpha }_s}}\right\}\to 0\mathit{as}{n}_i\to \infty$$ (3)

where max(ν_ij − ν_i.)² = max{(ν_ij − ν_i.)² : j = 1, …, n_i}, then

$$\frac{{\widehat{Y}}_i(z,{\alpha }_s)-{\stackrel{‒}{y}}_i(z,{\alpha }_s)}{\sqrt{V{\mathit{ar}}_{{\alpha }_s}\left\{{\widehat{Y}}_i\right(z,{\alpha }_s\left)\right\}}}\mid G_i=s\stackrel{d}{\to }\mathcal{N}(0,1)\phantom{\mid }$$

where ${\mathit{Var}}_{{\alpha }_s}\left\{{\widehat{Y}}_i\right(z,{\alpha }_s\left)\right\}=\mathit{Var}\left\{{\widehat{Y}}_i\right(z,{\alpha }_s)\mid G_i=s\}$.

Proposition 2. Assume (2) and that (3) holds for ν_ij = y_ij(1, α_s)/k_iαs +y_ij(0, α_s)/(n_i − k_iαs). Then

$$\frac{{\widehat{DE}}_i\left({\alpha }_s\right)-{\overline{DE}}_i\left({\alpha }_s\right)}{\sqrt{V{\mathit{ar}}_{{\alpha }_s}\left\{{\widehat{DE}}_i\right({\alpha }_s\left)\right\}}}\mid G_i=s\stackrel{d}{\to }\mathcal{N}(0,1)\phantom{\mid }$$

where ${\mathit{Var}}_{{\alpha }_s}\left\{{\widehat{\mathit{DE}}}_i\right({\alpha }_s\left)\right\}=\mathit{Var}\left\{{\widehat{\mathit{DE}}}_i\right({\alpha }_s)\mid G_i=s\}$.

Proposition 3. Assume(2) and that (3) holds for ν_ij = y_ij(1, α_s) − y_ij(0, α_s). Then

$$\frac{{\widehat{Y}}_i\left({\alpha }_s\right)-{\stackrel{‒}{y}}_i\left({\alpha }_s\right)}{\sqrt{V{\mathit{ar}}_{{\alpha }_s}\left\{{\widehat{Y}}_i\right({\alpha }_s\left)\right\}}}\mid G_i=s\stackrel{d}{\to }\mathcal{N}(0,1)\phantom{\mid }$$

where ${\mathit{Var}}_{{\alpha }_s}\left\{{\widehat{Y}}_i\right({\alpha }_s\left)\right\}=\mathit{Var}\left\{{\widehat{Y}}_i\right({\alpha }_s)\mid G_i=s\}$.

Propositions 4.1 – 4.4 below show that, under certain conditions, the population direct, indirect, total and overall effect estimators are asymptotically distributed as a mixture of Normal random variables as the numbers of individuals per group grow large, i.e., as n_min = min{n₁, …, n_m} → ∞. Recall a random variable X follows a finite Normal mixture distribution (McLachlan et al. 1988) if there exists a discrete random variable U with support u₁, …, u_h and parameter vectors μ = (μ⁽¹⁾, …, μ^(h)) and σ = (σ⁽¹⁾, …, σ^(h)) such that the density of X satisfies

$$f_X\left(x\right)=\sum _{i=1}^h{\omega }^{\left(i\right)}f(x\mid {\mu }^{\left(i\right)},{\sigma }^{\left(i\right)})$$

where ω⁽ⁱ⁾ = Pr(U = u_i) and f(x | μ⁽ⁱ⁾, σ⁽ⁱ⁾) is the density of a Normal random variable with mean μ⁽ⁱ⁾ and standard deviation σ⁽ⁱ⁾. Equivalently, $(X-{\mu }^{\left(i\right)})∕{\sigma }^{\left(i\right)}\mid U=u_i~\mathcal{N}(0,1)$ for i = 1, …, h. Define a sequence of random variables {X_n} to have an asymptotically Normal mixture distribution if there exists a discrete random variable U with support u₁, …, u_h and sequences of parameter vectors {μ_n} and {σ_n} such that

$$\frac{X_n-{\mu }_n^{\left(i\right)}}{{\sigma }_n^{\left(i\right)}}\mid U=u_i\stackrel{d}{\to }\mathcal{N}(0,1)\phantom{\mid }\text{as}n\to \infty$$ (4)

for i = 1, …, h, where ${\mu }_n^{\left(i\right)}$ and ${\sigma }_n^{\left(i\right)}$ denote the i^th components of μ_n and σ_n. When (4) holds, for notational convenience we suppress the subscript n and write $(X-\mu )∕\sigma \stackrel{d}{\to }\mathcal{M}(w,h)$. The following proposition is stated in terms of α₁; the analogous result holds for α₀.

Proposition 4.1. Assume (2) and that (3) holds for ν_ij = y_ij(1, α₁)/k_iα1+y_ij(0, α₁)/(n_i− k_iα1) for i = 1, …, m. Assume for any simple random sample {i₁, …, i_l} drawn without replacement from {1, …, m} that lim ${\mathit{Var}}_{{\alpha }_1}\left\{{\widehat{\mathit{DE}}}_i\right({\alpha }_1\left)\right\}∕{\sum }_{i\in \{i_1,\dots ,i_l\}}{\mathit{Var}}_{{\alpha }_1}\left\{{\widehat{\mathit{DE}}}_i\right({\alpha }_1\left)\right\}$ as n_min → ∞ exists for i ∈ {i₁, …, i_l}. Then for m < ∞, $\widehat{\mathit{DE}}\left({\alpha }_1\right)$ has an asymptotically Normal mixture distribution, i.e.,

$$\frac{\widehat{DE}\left({\alpha }_1\right)-{\mu }_{\mathit{DE}}}{{\sigma }_{\mathit{DE}}}\stackrel{d}{\to }\mathcal{M}(\omega ,{(}_l^m))$$

as n_min → ∞. The parameter vectors, each of length ${(}_l^m)$, are given by $w=\left(1∕{(}_l^m)\right)$, ${\mu }_{\mathit{DE}}=\left({\mu }_{\mathit{DE}}^{(i_1,\dots ,i_l)}\right)$ and ${\sigma }_{\mathit{DE}}=\left({\sigma }_{\mathit{DE}}^{(i_1,\dots ,i_l)}\right)$, where the elements of the vectors correspond to all possible simple random sample {i₁, …, i_l} without replacement from {1, …, m}, with ${\mu }_{\mathit{DE}}^{(i_1,\dots ,i_l)}={\sum }_{i\in \{i_1,\dots ,i_l\}}{\overline{\mathit{DE}}}_i\left({\alpha }_1\right)∕l$ and ${\sigma }_{\mathit{DE}}^{(i_1,\dots ,i_l)}={\left[{\sum }_{i\in \{i_1\dots ,i_l\}}{\mathit{Var}}_{{\alpha }_1}\left\{{\widehat{\mathit{DE}}}_i\right({\alpha }_1\left)\right\}\right]}^{1∕2}∕l$.

Note in Proposition 4.1 and below the dependence of the parameters μ_DE and σ_DE on α_s and n_min are suppressed for notational convenience. From a single experiment or trial, only one element from each of the vectors μ_DE and σ_DE is identifiable from the observed data; in particular, only the parameters ${\mu }_{\mathit{DE}}^{i_1,\dots ,i_l}$ and ${\sigma }_{\mathit{DE}}^{i_1,\dots ,i_l}$ are identifiable where {i₁, …, i_l} = {i ∈ {1, …, m} : G_i = 1}. Hence the asymptotic distribution of $\widehat{\mathit{DE}}\left({\alpha }_1\right)$ as the groups grow large is not identifiable without additional assumptions. One special case of Proposition 4.1 occurs when the groups are homogeneous in a certain sense as described by the following corollary.

Corollary. If the assumptions of Proposition 4.1 hold and there exists ${\mu }_{\mathit{DE}}^{\left(0\right)}$ and ${\sigma }_{\mathit{DE}}^{\left(0\right)}$ such that ${\mu }_{\mathit{DE}}^{(i_1,\dots ,i_l)}={\mu }_{\mathit{DE}}^{\left(0\right)}$ and ${\sigma }_{\mathit{DE}}^{(i_1,\dots ,i_l)}={\sigma }_{\mathit{DE}}^{\left(0\right)}$ for all simple random samples {i₁, …, i_l}, then ${\mu }_{\mathit{DE}}^{\left(0\right)}=\overline{\mathit{DE}}\left({\alpha }_1\right)$, ${\sigma }_{\mathit{DE}}^{\left(0\right)}=\sqrt{\mathit{Var}\left\{\widehat{\mathit{DE}}\right({\alpha }_1\left)\right\}}$ and for m < ∞,

$$\frac{\widehat{DE}\left({\alpha }_1\right)-\overline{DE}\left({\alpha }_1\right)}{\sqrt{V\mathit{ar}\left\{\widehat{DE}\right({\alpha }_1\left)\right\}}}\stackrel{d}{\to }\mathcal{N}(0,1)$$ (5)

as n_min → ∞.

Note that the condition ${\mu }_{\mathit{DE}}^{(i_1,\dots ,i_l)}={\mu }_{\mathit{DE}}^{\left(0\right)}$ and ${\sigma }_{\mathit{DE}}^{(i_1,\dots ,i_l)}={\sigma }_{\mathit{DE}}^{\left(0\right)}$ for all simple random samples {i₁, …, i_l} is equivalent to ${\overline{\mathit{DE}}}_1\left({\alpha }_1\right)=\cdots ={\overline{\mathit{DE}}}_m\left({\alpha }_1\right)$ and ${\mathit{Var}}_{{\alpha }_1}\left\{{\widehat{\mathit{DE}}}_1\right({\alpha }_1\left)\right\}=\cdots ={\mathit{Var}}_{{\alpha }_1}\left\{{\widehat{\mathit{DE}}}_m\right({\alpha }_1\left)\right\}$. In other words, if the group level direct effect estimators have the same mean and variance, then (5) holds.

The next three propositions and corollaries give analogous results for the population average indirect, total and overall effect estimators.

Proposition 4.2. Assume (2) and that (3) holds for v_ij = y_ij(0, α_s), s = 0, 1 and i = 1, …, m. Assume for any simple random sample {i₁, …, i_l} drawn without replacement from {1, …, m} that $\lim \sqrt{{\mathit{Var}}_{{\alpha }_1}{\widehat{Y}}_i(0,{\alpha }_1)}∕\left\{l{\sigma }_{\mathit{IE}}^{(i_1,\dots ,i_l)}\right\}$ exists for i ∈ {i₁, …, i_l} and $\lim \sqrt{{\mathit{Var}}_{{\alpha }_1}{\widehat{Y}}_i(0,{\alpha }_1)}∕\left\{\right(m-l\left){\sigma }_{\mathit{IE}}^{(i_1,\dots ,i_l)}\right\}$ exists for i ∉ {i₁, …, i_l} as n_min → ∞. Then for m < ∞,

$$\frac{\widehat{IE}({\alpha }_1,{\alpha }_0)-{\mu }_{\mathit{IE}}}{{\sigma }_{\mathit{IE}}}\stackrel{d}{\to }\mathcal{M}(\omega ,{(}_l^m))$$

as n_min → ∞. The parameter vectors, each of length $\left(\underset{l}{\overset{m}{}}\right)$, are given by $\omega =\left(1∕\left(\underset{l}{\overset{m}{}}\right)\right)$, ${\mu }_{\mathit{IE}}=\left({\mu }_{\mathit{IE}}^{(i_1,\dots ,i_l)}\right)$, ${\sigma }_{\mathit{IE}}=\left({\sigma }_{\mathit{IE}}^{(i_1,\dots ,i_l)}\right)$, where

$${\mu }_{\mathit{IE}}^{(i_1,\dots ,i_l)}=\sum _{i\in \{i_1,\dots ,i_l\}}\frac{{\stackrel{‒}{y}}_i(0,{\alpha }_1)}{l}-\sum _{i\notin \{i_1,\dots ,i_l\}}\frac{{\stackrel{‒}{y}}_i(0,{\alpha }_0)}{m-l}$$

$${\sigma }_{\mathit{IE}}^{(i_1,\dots ,i_l)}={\left[\sum _{i\in \{i_1,\dots ,i_l\}}\frac{V{\mathit{ar}}_{{\alpha }_1}\left\{{\widehat{Y}}_i\right(0,{\alpha }_1\left)\right\}}{l^2}+\sum _{i\notin \{i_1,\dots ,i_l\}}\frac{V{\mathit{ar}}_{{\alpha }_0}\left\{{\widehat{Y}}_i\right(0,{\alpha }_0\left)\right\}}{{(m-l)}^2}\right]}^{\frac{1}{2}}$$

Corollary. If the assumptions of Proposition 4.2 hold and there exists ${\mu }_{\mathit{IE}}^{\left(0\right)}$ and ${\sigma }_{\mathit{IE}}^{\left(0\right)}$ such that ${\mu }_{\mathit{IE}}^{(i_1,\dots ,i_l)}={\mu }_{\mathit{IE}}^{\left(0\right)}$ and ${\sigma }_{\mathit{IE}}^{(i_1,\dots ,i_l)}={\sigma }_{\mathit{IE}}^{\left(0\right)}$ for all {i₁, …, i_l}, then ${\mu }_{\mathit{IE}}^{\left(0\right)}=\overline{IE}({\alpha }_1,{\alpha }_0)$, ${\sigma }_{\mathit{IE}}^{\left(0\right)}=\sqrt{\mathit{Var}\left\{\widehat{IE}\right({\alpha }_1,{\alpha }_0\left)\right\}}$ and for m < ∞,

$$\frac{\widehat{IE}({\alpha }_1,{\alpha }_0)-\overline{IE}({\alpha }_1,{\alpha }_0)}{\sqrt{V\mathit{ar}\left\{\widehat{IE}\right({\alpha }_1,{\alpha }_0\left)\right\}}}\stackrel{d}{\to }\mathcal{N}(0,1)$$ (6)

as n_min → ∞.

Proposition 4.3. Assume (2) and that (3) holds for v_ij = y_ij(z, α_s), (z, s) ∈ {(1, 1), (0, 0)} and i = 1, …, m. Assume for any simple random sample {i₁, …, i_l} drawn without replacement from {1, …, m} that $\lim \sqrt{{\mathit{Var}}_{{\alpha }_1}{\widehat{Y}}_i(1,{\alpha }_1)}∕\left\{l{\sigma }_{\mathit{TE}}^{(i_1,\dots ,i_l)}\right\}$ exists for i ∈ {i₁, …, i_l} and $\lim \sqrt{{\mathit{Var}}_{{\alpha }_1}{\widehat{Y}}_i(0,{\alpha }_1)}∕\left\{\right(m-l\left){\sigma }_{\mathit{TE}}^{(i_1,\dots ,i_l)}\right\}$ exists for i ∉ {i₁, …, i_l} as n_min → ∞. Then for m < ∞,

$$\frac{\widehat{TE}({\alpha }_1,{\alpha }_0)-{\mu }_{\mathit{TE}}}{{\sigma }_{\mathit{TE}}}\stackrel{d}{\to }\mathcal{M}(\omega ,{(}_l^m))$$

as n_min → ∞. The parameter vectors, each of length $\left(\underset{l}{\overset{m}{}}\right)$, are given by $\omega =\left(1∕\left(\underset{l}{\overset{m}{}}\right)\right)$, ${\mu }_{\mathit{TE}}=\left({\mu }_{\mathit{TE}}^{(i_1,\dots ,i_l)}\right)$, ${\sigma }_{\mathit{TE}}=\left({\sigma }_{\mathit{TE}}^{(i_1,\dots ,i_l)}\right)$, where

$${\mu }_{\mathit{TE}}^{(i_1,\dots ,i_l)}=\sum _{i\in \{i_1,\dots ,i_l\}}\frac{{\stackrel{‒}{y}}_i(1,{\alpha }_1)}{l}-\sum _{i\notin \{i_1,\dots ,i_l\}}\frac{{\stackrel{‒}{y}}_i(0,{\alpha }_0)}{m-l}$$

$${\sigma }_{\mathit{TE}}^{(i_1,\dots ,i_l)}={\left[\sum _{i\in \{i_1,\dots ,i_l\}}\frac{V{\mathit{ar}}_{{\alpha }_1}\left\{{\widehat{Y}}_i\right(1,{\alpha }_1\left)\right\}}{l^2}+\sum _{i\notin \{i_1,\dots ,i_l\}}\frac{V{\mathit{ar}}_{{\alpha }_0}\left\{{\widehat{Y}}_i\right(0,{\alpha }_0\left)\right\}}{{(m-l)}^2}\right]}^{\frac{1}{2}}$$

Corollary. If the assumptions of Proposition 4.3 hold and there exists ${\mu }_{\mathit{TE}}^{\left(0\right)}$ and ${\sigma }_{\mathit{TE}}^{\left(0\right)}$ such that ${\mu }_{\mathit{TE}}^{(i_1,\dots ,i_l)}={\mu }_{\mathit{TE}}^{\left(0\right)}$ and ${\sigma }_{\mathit{TE}}^{(i_1,\dots ,i_l)}={\sigma }_{\mathit{TE}}^{\left(0\right)}$ for all {i₁, …, i_l}, then ${\mu }_{\mathit{TE}}^{\left(0\right)}=\overline{TE}({\alpha }_1,{\alpha }_0)$, ${\sigma }_{\mathit{TE}}^{\left(0\right)}=\sqrt{\mathit{Var}\left\{\widehat{TE}\right({\alpha }_1,{\alpha }_0\left)\right\}}$ and for m < ∞,

$$\frac{\widehat{TE}({\alpha }_1,{\alpha }_0)-\overline{TE}({\alpha }_1,{\alpha }_0)}{\sqrt{V\mathit{ar}\left\{\widehat{TE}\right({\alpha }_1,{\alpha }_0\left)\right\}}}\stackrel{d}{\to }\mathcal{N}(0,1)$$ (7)

as n_min → ∞.

Proposition 4.4. Assume (2) and that (3) holds for v_ij = y_ij(1, α_s) − y_ij(0, α_s), s = 0, 1 and i = 1, …, m. Assume for any simple random sample {i₁, …, i_l} drawn without replacement from {1, …, m} that $\lim \sqrt{{\mathit{Var}}_{{\alpha }_1}{\widehat{Y}}_i\left({\alpha }_1\right)}∕\left\{l{\sigma }_{\mathit{OE}}^{(i_1,\dots ,i_l)}\right\}$ exists for i ∈ {i₁, …, i_l} and $\lim \sqrt{{\mathit{Var}}_{{\alpha }_1}{\widehat{Y}}_i\left({\alpha }_1\right)}∕\left\{\right(m-l\left){\sigma }_{\mathit{OE}}^{(i_1,\dots ,i_l)}\right\}$ exists for i ∉ {i₁, …, i_l} as n_min → ∞. Then for m < ∞,

$$\frac{\widehat{OE}({\alpha }_1,{\alpha }_0)-{\mu }_{\mathit{OE}}}{{\sigma }_{\mathit{OE}}}\stackrel{d}{\to }\mathcal{M}(\omega ,{(}_l^m))$$

as n_min → ∞. The parameter vectors, each of length $\left(\underset{l}{\overset{m}{}}\right)$, are given by $\omega =\left(1∕\left(\underset{l}{\overset{m}{}}\right)\right)$, ${\mu }_{\mathit{OE}}=\left({\mu }_{\mathit{OE}}^{(i_1,\dots ,i_l)}\right)$, ${\sigma }_{\mathit{OE}}=\left({\sigma }_{\mathit{OE}}^{(i_1,\dots ,i_l)}\right)$, where

$${\mu }_{\mathit{OE}}^{(i_1,\dots ,i_l)}=\sum _{i\in \{i_1,\dots ,i_l\}}\frac{{\stackrel{‒}{y}}_i\left({\alpha }_1\right)}{l}-\sum _{i\notin \{i_1,\dots ,i_l\}}\frac{{\stackrel{‒}{y}}_i\left({\alpha }_0\right)}{m-l}$$

$${\sigma }_{OE}^{(i_1,\dots ,i_l)}={\left[\sum _{i\in \{i_1,\dots ,i_l\}}\frac{V{\mathit{ar}}_{{\alpha }_1}\left\{{\widehat{Y}}_i\right({\alpha }_1\left)\right\}}{l^2}+\sum _{i\notin \{i_1,\dots ,i_l\}}\frac{V{\mathit{ar}}_{{\alpha }_0}\left\{{\widehat{Y}}_i\right({\alpha }_0\left)\right\}}{{(m-l)}^2}\right]}^{\frac{1}{2}}$$

Corollary. If the assumptions of Proposition 4.4 hold and there exists ${\mu }_{\mathit{OE}}^{\left(0\right)}$ and ${\sigma }_{\mathit{OE}}^{\left(0\right)}$ such that ${\mu }_{\mathit{OE}}^{(i_1,\dots ,i_l)}={\mu }_{\mathit{OE}}^{\left(0\right)}$ and ${\sigma }_{\mathit{OE}}^{(i_1,\dots ,i_l)}={\sigma }_{\mathit{OE}}^{\left(0\right)}$ for all {i₁, …, i_l}, then ${\mu }_{\mathit{OE}}^{\left(0\right)}=\overline{\mathit{OE}}({\alpha }_1,{\alpha }_0)$, ${\sigma }_{\mathit{OE}}^{\left(0\right)}=\sqrt{\mathit{Var}\left\{\widehat{OE}\right({\alpha }_1,{\alpha }_0\left)\right\}}$ and for m < ∞,

$$\frac{\widehat{OE}({\alpha }_1,{\alpha }_0)-\overline{OE}({\alpha }_1,{\alpha }_0)}{\sqrt{V\mathit{ar}\left\{\widehat{OE}\right({\alpha }_1,{\alpha }_0\left)\right\}}}\stackrel{d}{\to }\mathcal{N}(0,1)$$ (8)

as n_min → ∞.

3.2.2 Large Number of Groups

In this section the asymptotic distributions of the causal effect estimators are derived when the number of groups m grows large, in particular when l → ∞ and m − l − ∞. These results rely on the following Lindeberg condition (Lehmann 1998, eq. A.128): Let {W_h} be a sequence of independent random variables, each having finite expected value μ_h and variance ${\sigma }_h^2$. Define $s_t^2={\sum }_{h=1}^t{\sigma }_h^2$. If for every ε > 0

$$\underset{t\to \infty }{\lim }\frac{1}{s_t^2}\sum _{h=1}^{t}E\left[{(W_h-{\mu }_h)}^{2}1\right\{\mid W_h-{\mu }_h\mid >\epsilon s_t\left\}\right]=0,$$ (9)

then ${\sum }_{h=1}^t(W_h-{\mu }_h)∕s_t\underrightarrow{d}\mathcal{N}(0,1)$ as t → ∞. The propositions below indicate that, under different versions of (9), the distributions of the causal effect estimators are approximately Normal as m grows large. These results will have applicability in studies with large numbers of groups even if the groups are small (e.g., households). Unlike in Section 3.2.1, here the mean homogeneity assumption is not needed to justify the Normal approximation.

Proposition 5.1. Suppose for any simple random sample {i₁, …, i_l} that (9) holds for the sequence {W_h} defined by $W_h={\widehat{\mathit{DE}}}_{i_h}\left({\alpha }_1\right)\mid G_{i_1}=\cdots =G_{i_l}=1$ for h = 1, …, l and there exists ${\sigma }_{\mathit{DE}}^{\left(0\right)}$ such that ${\sigma }_{\mathit{DE}}^{(i_1,\dots ,i_l)}={\sigma }_{\mathit{DE}}^{\left(0\right)}$. Let ${\tilde{v}}_i={\overline{\mathit{DE}}}_i\left({\alpha }_1\right)$ and ${\tilde{v}}_{.}=({\tilde{v}}_1+\dots +{\tilde{v}}_m)∕m$. If ${\lim }_{m\to \infty }{\sigma }_{\mathit{DE}}^{\left(0\right)}∕\sqrt{\mathit{Var}\left\{\widehat{\mathit{DE}}\right({\alpha }_1\left)\right\}}$ exists and

$$\frac{\max {({\tilde{\upsilon }}_i-{\tilde{\upsilon }}_{.})}^2}{\sum _{i=1}^m{({\tilde{\upsilon }}_i-{\tilde{\upsilon }}_{.})}^2}\max \left\{\frac{m-l}{l},\frac{l}{m-l}\right\}\to 0asm\to \infty$$ (10)

where $\max {({\tilde{v}}_i-{\tilde{v}}_{.})}^2=\max \{{({\tilde{v}}_i-{\tilde{v}}_{.})}^2:i=1,\dots ,m\}$, then (5) holds as m → ∞.

Proposition 5.2. Suppose for any simple random sample {i₁, …, i_l} that (9) holds for the sequence {W_h} defined by $W_h=\left\{{\widehat{Y}}_{i_h}\right(0,{\alpha }_1\left)1\right(G_{i_h}=1)∕l-{\widehat{Y}}_{i_h}(0,{\alpha }_0\left)1\right(G_{i_h}=0)∕(m-l\left)\right\}\mid G_{i_1}=\cdots =G_{i_l}=1$ for h = 1, …, l and there exists ${\sigma }_{\mathit{IE}}^{\left(0\right)}$ such that ${\sigma }_{\mathit{IE}}^{(i_1,\dots ,i_l)}={\sigma }_{\mathit{IE}}^{\left(0\right)}$. If (10) holds for ${\tilde{v}}_i={\stackrel{‒}{y}}_i(0,{\alpha }_1)∕l+{\stackrel{‒}{y}}_i(0,{\alpha }_0)∕(m-l)$ and ${\lim }_{m\to \infty }{\sigma }_{\mathit{IE}}^{\left(0\right)}∕\sqrt{\mathit{Var}\left\{\widehat{\mathit{IE}}\right({\alpha }_1,{\alpha }_0\left)\right\}}$ exists, then (6) holds as m → ∞.

Proposition 5.3. Suppose for any simple random sample {i₁, …, i_l} that (9) holds for the sequence {W_h} defined by $W_h=\left\{{\widehat{Y}}_{i_h}\right(1,{\alpha }_1\left)1\right(G_{i_h}=1)∕l-{\widehat{Y}}_{i_h}(0,{\alpha }_0\left)1\right(G_{i_h}=0)∕(m-l\left)\right\}\mid G_{i_1}=\cdots =G_{i_l}=1$ for h = 1, …, l and there exists ${\sigma }_{\mathit{TE}}^{\left(0\right)}$ such that ${\sigma }_{\mathit{TE}}^{(i_1,\dots ,i_l)}={\sigma }_{\mathit{TE}}^{\left(0\right)}$. If (10) holds for ${\tilde{v}}_i={\stackrel{‒}{y}}_i(1,{\alpha }_1)∕l+{\stackrel{‒}{y}}_i(0,{\alpha }_0)∕(m-l)$ and ${\lim }_{m\to \infty }{\sigma }_{\mathit{TE}}^{\left(0\right)}∕\sqrt{\mathit{Var}\left\{\widehat{\mathit{TE}}\right({\alpha }_1,{\alpha }_0\left)\right\}}$ exists, then (7) holds as m → ∞.

Proposition 5.4. Suppose for any simple random sample {i₁, …, i_l} that (9) holds for the sequence {W_h} defined by $W_h=\left\{{\widehat{Y}}_{i_h}\right({\alpha }_1\left)1\right(G_{i_h}=1)∕l-{\widehat{Y}}_{i_h}({\alpha }_0\left)1\right(G_{i_h}=0)∕(m-l\left)\right\}\mid G_{i_1}=\cdots =G_{i_l}=1$ for h = 1, …, l and there exists ${\sigma }_{\mathit{OE}}^{\left(0\right)}$ such that ${\sigma }_{\mathit{OE}}^{(i_1,\dots ,i_l)}={\sigma }_{\mathit{OE}}^{\left(0\right)}$. If (10) holds for ${\tilde{v}}_i={\stackrel{‒}{y}}_i\left({\alpha }_1\right)∕l+{\stackrel{‒}{y}}_i\left({\alpha }_0\right)∕(m-l)$ and ${\lim }_{m\to \infty }{\sigma }_{\mathit{OE}}^{\left(0\right)}∕\sqrt{\mathit{Var}\left\{\widehat{\mathit{OE}}\right({\alpha }_1,{\alpha }_0\left)\right\}}$ exists, then (8) holds as m → ∞.

3.3 Confidence intervals and testing

3.3.1 Large sample approximations

The results in the previous two sections establish the limiting distributions of the different effect estimators when either the number of individuals per group or the number of groups grows large. These results can be used to construct CIs when the limiting distribution is a single Normal. For example, under the conditions stated in the Corollary to Proposition 4.1, we have $\left\{\widehat{DE}\right({\alpha }_1)-\overline{\mathit{DE}}({\alpha }_1\left)\right\}∕\sqrt{\mathit{Var}\left\{\widehat{DE}\right({\alpha }_1\left)\right\}}\stackrel{d}{\to }\mathcal{N}(0,1)$. Thus, by Slutsky's theorem, for γ ∈ (0, 1) an asymptotic 1 − γ CI of $\overline{\mathit{DE}}\left({\alpha }_1\right)$ is

$$\widehat{DE}\left({\alpha }_1\right)\pm z_{1-\gamma ∕2}\sqrt{\widehat{V\mathit{ar}}\left\{\widehat{DE}\right({\alpha }_1\left)\right\}}$$

where z_1−γ/2 is the 1−/2 quantile of the standard Normal distribution and $\widehat{\mathit{Var}}\left\{\widehat{\mathit{DE}}\right({\alpha }_1\left)\right\}$ is a consistent estimator of $\mathit{Var}\left\{\widehat{\mathit{DE}}\right({\alpha }_1\left)\right\}$.

These CIs can be used in the large sample setting to test various null hypotheses about the different treatment effects by examining whether the CI for a particular effect contains the corresponding null value. Equivalently, test statistics can be constructed to directly assess the null hypothesis of interest. For example, consider testing the null hypothesis that the group level direct effects are all zero, i.e., $H_0:{\overline{\mathit{DE}}}_1\left({\alpha }_1\right)=\dots ={\overline{\mathit{DE}}}_m\left({\alpha }_1\right)=0$. Under the assumption that ${\mathit{Var}}_{{\alpha }_1}\left\{{\widehat{\mathit{DE}}}_1\right({\alpha }_1\left)\right\}=\cdots ={\mathit{Var}}_{{\alpha }_1}\left\{{\widehat{\mathit{DE}}}_m\right({\alpha }_1\left)\right\}$, the statistic $T=\widehat{\mathit{DE}}\left({\alpha }_1\right)∕\sqrt{\widehat{\mathit{Var}}\left\{\widehat{\mathit{DE}}\right({\alpha }_1\left)\right\}}$ will be approximately $\mathcal{N}(0,1)$ under H₀, provided either n_min or l is large.

The Wald CIs are applicable when the groups are homogeneous. Certain of these homogeneity assumptions can be tested. For instance, the assumption that the direct effects are homogeneous across groups can be tested as follows. Suppose ${\mathit{Var}}_{{\alpha }_1}\left\{{\widehat{\mathit{DE}}}_1\right({\alpha }_1\left)\right\}=\cdots ={\mathit{Var}}_{{\alpha }_1}\left\{{\widehat{\mathit{DE}}}_m\right({\alpha }_1\left)\right\}={\sigma }_{\mathit{DE}}^2$, where ${\sigma }_{\mathit{DE}}^2$ is an unknown constant and the goal is to test $H_{0h}:{\overline{\mathit{DE}}}_1\left({\alpha }_1\right)=\cdots ={\overline{\mathit{DE}}}_m\left({\alpha }_1\right)$. Let $\tilde{T}={\sum }_{i=1}^m{\left\{{\widehat{\mathit{DE}}}_i\right({\alpha }_1)-\widehat{\mathit{DE}}({\alpha }_1\left)\right\}}^{2}1(G_i=1)∕{\widehat{\sigma }}_{\mathit{DE}}^2$, where ${\widehat{\sigma }}_{\mathit{DE}}^2$ is a consistent estimator for ${\sigma }_{\mathit{DE}}^2$. Then based on Proposition 2, $\tilde{T}~{\chi }_{l-1}^2$ under H_0h as n_min → ∞. Without further assumptions about the potential outcomes, tests of mean homogeneity cannot be developed for indirect, total and overall effects. To see this, consider the homogeneity assumptions given in the Corollary to Proposition 4.2 that are sufficient for the indirect effect estimator to have a single Normal distribution asymptotically. The mean homogeneity assumption that there exists ${\mu }_{\mathit{IE}}^{\left(0\right)}$ such that ${\mu }_{\mathit{IE}}^{(i_1,\dots ,i_l)}={\mu }_{\mathit{IE}}^{\left(0\right)}$ for all simple random samples {i₁, …, i_l} is equivalent to assuming $(m-l){\stackrel{‒}{y}}_1(0,{\alpha }_1)+l{\stackrel{‒}{y}}_1(0,{\alpha }_0)=\cdots =(m-l){\stackrel{‒}{y}}_m(0,{\alpha }_1)+l{\stackrel{‒}{y}}_m(0,{\alpha }_0)$. Because only one element of each pair $\left\{{\stackrel{‒}{y}}_i\right(0,{\alpha }_1),{\stackrel{‒}{y}}_i(0,{\alpha }_0\left)\right\}$ is identifiable from the observable data, this assumption is not subject to empirical test.

In the absence of homogeneity, the observed data do provide some information about the asymptotic distributions such that inference relying on large sample approximations may still be possible. For instance, CIs can be constructed using Chebyshev's inequality. For example, for the direct effect the interval $\widehat{\mathit{DE}}\left({\alpha }_s\right)\pm \sqrt{\mathit{Var}\left\{\widehat{\mathit{DE}}\right({\alpha }_s\left)\right\}∕\gamma }$ will contain $\overline{\mathit{DE}}\left({\alpha }_s\right)$ with at least probability 1 – γ. Because the Chebyshev inequality holds for all distributions, such CIs are expected to often be conservative, i.e., have coverage probability greater than 1 – γ. In practice $\mathit{Var}\left\{\widehat{\mathit{DE}}\right({\alpha }_s\left)\right\}$ will be unknown and can be replaced with a consistent estimator $\widehat{\mathit{Var}}\left\{\widehat{\mathit{DE}}\right({\alpha }_s\left)\right\}$ which asymptotically will still give a 1 – γ CI.

3.3.2 Exact method

Rather than relying on large sample approximations, Tchetgen Tchetgen and VanderWeele (2012) derived exact CIs for various casual effects in the setting where the outcome is binary based on the Hoeffding inequality. In particular, they showed under two-stage permutation randomization that for any γ ∊ (0, 1), the interval $\widehat{\mathit{DE}}\left({\alpha }_1\right)\pm {∊}_{\mathit{DE}}^{\ast }(\gamma ,{\alpha }_1,q,m)$ is a (1 - γ) CI of $\overline{\mathit{DE}}\left({\alpha }_1\right)$, where

$${∊}_{DE}^{\ast }(\gamma ,{\alpha }_1,q,m)=\sqrt{\log (2∕\gamma )\left\{4{\left(\frac{1}{q}-1\right)}^2+\sum _{i=1}^m\frac{L_{DE,i}{\left({\alpha }_1\right)}^2}{q^{2}m}\right\}∕\left(2m\right)}$$

q = Pr(G_i = 1) l/m and $L_{\mathit{DE},i}\left({\alpha }_1\right)=2\left\{1-1∕\left(\begin{array}{c}\hfill n_i\hfill \\ \hfill k_{i{\alpha }_1}\hfill \end{array}\right)\right\}$ for i = 1, …, m. Similarly, the interval $\widehat{\mathit{IE}}({\alpha }_1,{\alpha }_0)\pm {∊}^{\ast }(\gamma ,{\alpha }_1,{\alpha }_0,q,m)$ is a (1 – γ) CI of $\overline{\mathit{IE}}({\alpha }_1,{\alpha }_0)$, where

$${∊}_{DE}^{\ast }(\gamma ,{\alpha }_1,{\alpha }_0,q,m)=\sqrt{\log (2∕\gamma )\left[\max \{\frac{1}{q^2},\frac{1}{{(1-q)}^2}\}+\sum _{i=1}^m{L}_{IE,i}{({\alpha }_1,{\alpha }_0,q)}^2∕m\right]∕\left(2m\right)}$$

and $L_{\mathit{IE},i}({\alpha }_1,{\alpha }_0,q)=\max \left[\{1-1∕\left(\begin{array}{c}\hfill n_i\hfill \\ \hfill k_{i\alpha 1}\hfill \end{array}\right)\}∕q,\left\{1-1∕\left(\begin{array}{c}\hfill n_i\hfill \\ \hfill k_{i\alpha 0}\hfill \end{array}\right)\right\}∕(1-q)\right]$ for i = 1, …, m. Likewise, exact (1–γ) CIs of $\overline{\mathit{TE}}({\alpha }_1,{\alpha }_0)$ and $\overline{\mathit{OE}}({\alpha }_1,{\alpha }_0)$ can be constructed by $\widehat{\mathit{TE}}({\alpha }_1,{\alpha }_0)\pm {∊}^{\ast }(\gamma ,{\alpha }_1,{\alpha }_0,q,m)$ and $\widehat{\mathit{OE}}({\alpha }_1,{\alpha }_0)\pm {∊}^{\ast }(\gamma ,{\alpha }_1,{\alpha }_0,q,m)$ respectively. These CIs are exact in the sense that the probability the interval contains the true parameter is at least 1 – γ for any m and n₁, …, n_m. The exact CIs are appealing in that the only assumptions required for the intervals to be valid are partial interference and two-stage permutation randomization. However, in the simulation study in Section 4 below it is demonstrated these CIs tend to be conservative, i.e., the exact CIs tend to be very wide and cover the target parameter with probability greater than 1 – γ. The form of the exact CIs suggests several reasons why they are conservative. First, the widths of the CIs are not data dependent, i.e., they do not depend on the observed outcomes y_ij(Z_i). Second, the widths of these CIs do not go to 0 as γ → 1. Finally, for any given data set and fixed γ, the widths of the CIs for the indirect, overall, and total effects will be the same.

4 Simulations

Simulations were conducted to verify the asymptotic distributions of the causal e ect estimators derived in Sections 3.2.1 and 3.2.2 as well as to evaluate the finite sample performance of the CIs described in Section 3.3. Simulations were conducted under four scenarios: (i) continuous outcomes with heterogeneity between groups, (ii) continuous outcomes, homogeneous groups, (iii) binary outcomes, heterogeneous groups, and (iv) binary outcomes, homogeneous groups. For scenario (i), the simulation study was conducted in the following steps:

• Step 1: A hypothetical population with m = 4 groups and n₁ = ⋯ = n₄ = 1000 individuals within each group was created as follows. For i = 1, …, 4 and j = 1, …, 1000, b_ij was randomly sampled from $\mathcal{N}(0,1)$. Then for z_ij = 0, 1 and g_i = 0, 1 the potential outcomes for individual j in group i were set to y_ij(z_ij, α_gi) = g_i + 0.7z_ij + b_ij + b_ijz_ij for i = 1, 2 and y_ij(z_ij, α_gi) = g_i + b_ij + b_ijz_ij for i = 3, 4.

• Step 2: Groups were assigned α₁ or α₀ and individuals assigned z = 1 or z = 0 using two-stage permutation randomization with l = 2, k_iα1 = 500, and k_iα0 = 200.

• Step 3: The various causal effect estimators defined in Section 3.1 were calculated based on the observed data from Step 2. The corresponding Wald and Chebyshev CIs as described in Section 3.3.1 were also computed, using the variance estimators proposed by Hudgens and Halloran (2008).

• Step 4: Steps 2 – 3 were repeated 5000 times.

Note the model used to generate the potential outcomes in Step 1 assumes partial and stratified interference, such that under two-stage permutation randomization each individual has four potential outcomes. The true causal effects for the simulated population were $\overline{\mathit{DE}}\left({\alpha }_1\right)=\overline{\mathit{DE}}\left({\alpha }_0\right)=0.35$, $\overline{\mathit{IE}}({\alpha }_1,{\alpha }_0)=1.00$, $\overline{\mathit{TE}}({\alpha }_1,{\alpha }_0)=1.35$, $\overline{\mathit{OE}}({\alpha }_1,{\alpha }_0)=1.10$.

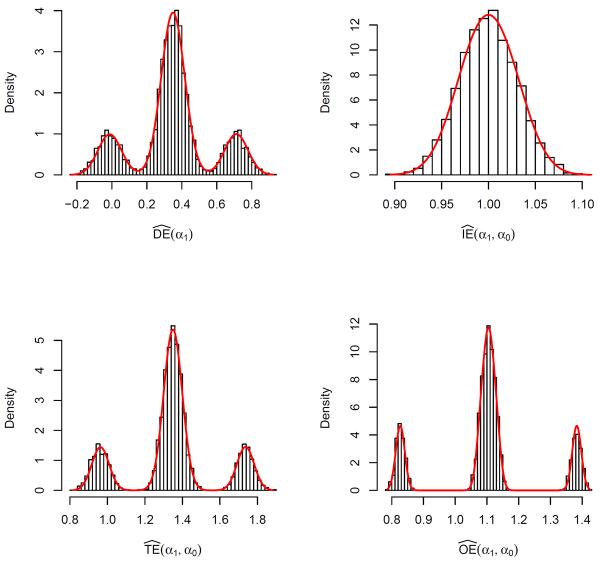
For these simulation n₁ = ⋯ = n₄ = 1000, such that the asymptotic results for large groups derived in Section 3.2.1 apply. Figure 1 shows the accuracy of the Normal mixture approximation to the distribution of the direct, indirect, total and overall effect estimators. For simplicity, here and in the sequel results for $\widehat{\mathit{DE}}\left({\alpha }_0\right)$ are omitted. The histograms give the empirical distributions of the estimators based on the 5000 simulated data sets. The solid lines, created using the R package nor1mix (Mächler 2011), show the density of the Normal mixtures used to approximate the distributions of the estimators. For the direct effect estimator the $\left(\begin{array}{c}\hfill m\hfill \\ \hfill l\hfill \end{array}\right)=\left(\begin{array}{c}\hfill 4\hfill \\ \hfill 2\hfill \end{array}\right)=6$ conditional means of the Normal mixture were 0.71, 0.36, 0.35, 0.35, 0.34, −0.01. Because four of these means are nearly identical, the approximate distribution of $\widehat{\mathit{DE}}\left({\alpha }_1\right)$ is trimodal (Figure 1 upper left panel). The distributions of the total and overall effect estimators are similar. From the model in Step 1 above the simulated groups were approximately homogeneous with respect to the indirect effect. For instance, the indirect effect conditional means were 1.02, 1.01, 1.00, 1.00, 0.98 and 0.98. Thus, in accordance with the Corollary to Proposition 4.2, the distribution of $\widehat{\mathit{IE}}({\alpha }_1,{\alpha }_0)$ for large groups is approximately Normal (Figure 1 upper right panel).

Figure 1.

Empirical distribution of the direct effect $\overline{\mathit{DE}}\left({\alpha }_1\right)$, indirect effect $\overline{\mathit{IE}}({\alpha }_1,{\alpha }_0)$, total effect $\overline{\mathit{TE}}({\alpha }_1,{\alpha }_0)$ and overall effect $\overline{\mathit{OE}}({\alpha }_1,{\alpha }_0)$ estimators for simulations in scenario (i) with m = 4 groups, n_i = 1000 individuals per group, and continuous outcomes. The solid line is the density of the approximating distribution.

Additional simulations were conducted under scenario (i) for various values of m and n₁ = … = n_m. In each case we let l = m/2, k_iα1 = 0.5n_i, and k_iα0 = 0.2n_i, with non-integer values rounded up to the nearest integer. Table 1 shows the empirical coverage and width (i.e., average length) of the Wald and Chebyshev 95% CIs. Recall that justification of the Wald CIs for small m requires certain mean homogeneity assumptions as stated in the corollaries in Section 3.2.1. Therefore, because of the mean heterogeneity between groups for the direct, total, and overall effects in scenario (i), the Wald CIs were not necessarily expected to perform well for small m. Indeed, Table 1 shows the Wald CIs for these effects tend to under-cover for m ≤ 10. These results demonstrate the Wald CIs may not be particularly robust to violation of the mean homogeneity assumption when m is small. On the other hand, the Wald CIs perform well for m ≥ 30, corroborating the results in Section 3.2.2. In contrast to the other effects, the mean homogeneity assumption does approximately hold for the indirect effect in scenario (i), suggesting that the corresponding Wald CIs should perform well for small m provided n_i is suffciently large. To the contrary, the results in the bottom of Table 1 show the Wald CIs of the indirect effect under-cover for n_i = 1000 when m is small. Further investigation revealed this under-coverage was attributable to the estimated variance of the indirect effect estimator; when the true variance was used to construct the Wald CIs, the coverage was approximately 95% (results not shown). The Chebyshev CIs tended to perform better than the Wald CIs for small m, although for n_i = 1000 and m = 4 the Chebyshev CIs also under-covered due to using the estimated variance. For m ≥ 30 the Chebyshev CIs were overly conservative, with 100% coverage for all effects for both n_i = 6 and n_i = 1000.

Table 1.

Empirical width and coverage [in brackets] of Wald (W) and Chebyshev (C) 95% CIs of the direct effect $\overline{\mathit{DE}}\left({\alpha }_1\right)$, indirect effect $\overline{\mathit{IE}}({\alpha }_1,{\alpha }_0)$, total effect $\overline{\mathit{TE}}({\alpha }_1,{\alpha }_0)$ and overall effect $\overline{\mathit{OE}}({\alpha }_1,{\alpha }_0)$ for simulations under scenario (i) with numbers of groups m, number of individuals per group n_i, and continuous outcomes.

			m
			4	6	10	30	100
ni = 6	$\overline{\mathit{DE}}\left({\alpha }_1\right)$	W	3.70[0.88]	2.67[0.91]	2.03[0.93]	1.27[0.95]	0.73[0.95]
		C	8.04[1.00]	5.92[1.00]	4.54[1.00]	2.88[1.00]	1.66[1.00]
	$\overline{\mathit{IE}}({\alpha }_1,{\alpha }_0)$	W	1.89[0.80]	1.60[0.87]	1.26[0.91]	0.88[0.93]	0.42[0.95]
		C	3.92[0.94]	3.49[0.99]	2.82[1.00]	2.01[1.00]	0.96[1.00]
	$\overline{\mathit{TE}}({\alpha }_1,{\alpha }_0)$	W	3.79 [0.76]	2.31 [0.87]	2.32[0.91]	1.40[0.94]	0.74[0.96]
		C	7.57[0.93]	4.95[0.98]	5.14[1.00]	3.17[1.00]	1.69[1.00]
	$\overline{\mathit{OE}}({\alpha }_1,{\alpha }_0)$	W	2.54[0.77]	1.44[0.88]	1.69[0.90]	1.04[0.94]	0.51 [0.94]
		C	5.46[0.94]	3.21[1.00]	3.83[1.00]	2.37[1.00]	1.17[1.00]
ni = 1000	$\overline{\mathit{DE}}\left({\alpha }_1\right)$	W	0.86[0.66]	0.65[0.90]	0.50[0.90]	0.28[0.94]	0.15[0.95]
		C	1.75[0.74]	1.44[0.91]	1.12[0.99]	0.63[1.00]	0.34[1.00]
	$\overline{\mathit{IE}}({\alpha }_1,{\alpha }_0)$	W	0.12[0.80]	0.10[0.88]	0.11[0.91]	0.06[0.94]	0.03[0.95]
		C	0.24[0.95]	0.22[0.99]	0.25[1.00]	0.14[1.00]	0.08[1.00]
	$\overline{\mathit{TE}}({\alpha }_1,{\alpha }_0)$	W	1.21[0.66]	0.89[0.90]	0.69[0.97]	0.38[0.98]	0.20[0.99]
		C	2.35[0.69]	1.95[0.90]	1.56[0.99]	0.87[1.00]	0.46[1.00]
	$\overline{\mathit{OE}}({\alpha }_1,{\alpha }_0)$	W	0.68[0.66]	0.48[0.90]	0.39[0.92]	0.21[0.96]	0.11[0.97]
		C	1.31[0.66]	1.06[0.90]	0.88[0.99]	0.49[1.00]	0.26[1.00]

For scenario (ii), potential outcomes were simulated as above except in Step 1 we let y_ij(z_ij, α_gi) = g_i + b_ij + b_ijz_ij for j = 1,…, n_i, i = 1,…, m. Various values of m and n₁ = … = n_m were considered for scenario (ii) as in scenario (i). In this scenario the groups were approximately homogeneous; for example, the direct effects ${\widehat{\mathit{DE}}}_i\left({\alpha }_1\right)$ for i = 1,…, m were all approximately 0 and the variances of the estimators V ar_α1 $\left\{{\widehat{\mathit{DE}}}_i\right({\alpha }_1\left)\right\}$ were all approximately the same. Table 2 gives the empirical coverage and width of the Wald and Chebyshev CIs for scenario (ii). Results for the indirect effect are identical to those in Table 1 because the same values were generated for y_ij(0, α₀) and y_ij(0, α₁) in scenarios (i) and (ii). For the other effects, coverage for the Wald CIs tends to be slightly better in Table 2 compared to Table 1 for small m and large n_i, but under-coverage persists despite mean homogeneity; this anti-conservative performance of the Wald CIs can again be attributed to use of the estimated variances. Coverage of the Chebyshev CIs was approximately 0.95 or greater for all effects and all values of n_i and m considered.

Table 2.

Empirical width and coverage [in brackets] of Wald (W) and Chebyshev (C) 95% CIs of the direct effect $\overline{\mathit{DE}}\left({\alpha }_1\right)$, indirect effect $\overline{\mathit{IE}}({\alpha }_1,{\alpha }_0)$, total effect $\overline{\mathit{TE}}({\alpha }_1,{\alpha }_0)$ and overall effect $\overline{\mathit{OE}}({\alpha }_1,{\alpha }_0)$ for simulations under scenario (ii) with numbers of groups m, number of individuals per group n_i, and continuous outcomes.

			m
			4	6	10	30	100
ni = 6	$\overline{\mathit{DE}}\left({\alpha }_1\right)$	W	3.51[0.89]	2.72[0.92]	1.92[0.94]	1.27[0.95]	0.71[0.95]
		C	7.66[1.00]	6.05[1.00]	4.32[1.00]	2.87[1.00]	1.62[1.00]
	$\overline{\mathit{IE}}({\alpha }_1,{\alpha }_0)$	W	1.89[0.80]	1.60[0.87]	1.26[0.91]	0.88[0.93]	0.42[0.95]
		C	3.92[0.94]	3.49[0.99]	2.82[1.00]	2.01[1.00]	0.96[1.00]
	$\overline{\mathit{TE}}({\alpha }_1,{\alpha }_0)$	W	3.14[0.78]	2.66[0.87]	2.06[0.91]	1.44[0.95]	1.44[0.95]
		C	6.30[0.94]	5.73[0.98]	4.56[1.00]	3.25[1.00]	1.58[1.00]
	$\overline{\mathit{OE}}({\alpha }_1,{\alpha }_0)$	W	2.01[0.84]	1.81 [0.88]	1.50[0.91]	1.09[0.95]	0.48[0.94]
		C	4.38[0.97]	4.05[0.99]	3.40[1.00]	2.47[1.00]	1.10[1.00]
ni = 1000	$\overline{\mathit{DE}}\left({\alpha }_1\right)$	W	0.27[0.93]	0.22[0.93]	0.18[0.94]	0.10[0.95]	0.06[0.95]
		C	0.60[1.00]	0.49[1.00]	0.40[1.00]	0.23[1.00]	0.13[1.00]
	$\overline{\mathit{IE}}({\alpha }_1,{\alpha }_0)$	W	0.12[0.80]	0.10[0.88]	0.11[0.91]	0.06[0.94]	0.03[0.95]
		C	0.24[0.95]	0.22[0.99]	0.25[1.00]	0.14[1.00]	0.08[1.00]
	$\overline{\mathit{TE}}({\alpha }_1,{\alpha }_0)$	W	0.21[0.78]	0.18[0.85]	0.19[0.91]	0.11[0.94]	0.06[0.95]
		C	0.41[0.93]	0.37[0.98]	0.41[1.00]	0.24[1.00]	0.13[1.00]
	$\overline{\mathit{OE}}({\alpha }_1,{\alpha }_0)$	W	0.11[0.82]	0.10[0.88]	0.13[0.91]	0.07[0.93]	0.04[0.95]
		C	0.23[0.96]	0.22[0.99]	0.30[1.00]	0.17[1.00]	0.09[1.00]

For scenario (iii), simulations were conducted as in scenario (i) with m = 4 groups each having n_i = 1000 individuals but with the first step replaced by the following:

• Step 1: Of the 4000 individuals in the population, 480 were randomly sampled to have x_ij = 0, another 480 were randomly sampled to have x_ij = 1, and x_ij = 2 for the remaining individuals. If x_ij = 2, the potential outcomes were set to y_ij(z_ij, α_gi) = g_iz_ij for i = 1, 2 and y_ij(z_ij, α_gi) = g_i(1 − z_ij) for i = 3, 4; otherwise y_ij(z_ij, α_gi) = x_ij for i = 1,…, 4.

For this scenario there was heterogeneity between groups for the direct, indirect and total effects. Similar to Figure 1 for scenario (i), the Normal mixture distributions provided an excellent approximation to the empirical distributions of the estimators (not shown). Simulations were also conducted under scenario (iii) for populations of 1000m individuals where 120m individuals had x_ij = 0, 120m individuals had x_ij = 1, and the remaining individuals had x_ij = 2 for m = 6, 10, 30, 100. Because the outcomes in scenario (iii) were binary, for each simulated data set the exact CIs described in Section 3.3.2 were computed in addition to the Wald and Chebyshev CIs. Empirical coverage and width of the three types of CIs are given in Table 3. Coverage of the Wald and Chebyshev CIs was similar to scenario (i), which also entailed heterogeneous effects. The exact CIs were very conservative, with 100% coverage for all effects and all values of m considered. Compared to the Wald and Chebyshev CIs, the exact CIs tended to be as wide or wider, especially for the overall effect where the exact CIs were at least an order of magnitude wider than the other CIs.

Table 3.

Empirical width and coverage [in brackets] of Wald (W), Chebyshev (C) and exact (E) 95% CIs of the direct effect $\overline{\mathit{DE}}\left({\alpha }_1\right)$, indirect effect $\overline{\mathit{IE}}({\alpha }_1,{\alpha }_0)$, total effect $\overline{\mathit{TE}}({\alpha }_1,{\alpha }_0)$ and overall effect $\overline{\mathit{OE}}({\alpha }_1,{\alpha }_0)$ for simulations under scenario (iii) with m groups, n_i = 1000 individuals per group, and binary outcomes.

		m
		4	6	10	30	100
$\overline{\mathit{DE}}\left({\alpha }_1\right)$	W	1.73[0.67]	1.33[0.90]	0.99[0.79]	0.55[0.98]	0.30[0.93]
	C	3.26[0.67]	2.89[0.90]	2.25[0.99]	1.26[1.00]	0.68[1.00]
	E	6.07[1.00]	4.96[1.00]	3.84[1.00]	2.22[1.00]	1.21[1.00]
$\overline{\mathit{IE}}({\alpha }_1,{\alpha }_0)$	W	1.22[0.67]	0.93[0.90]	0.70[0.99]	0.39[0.98]	0.21[0.99]
	C	2.31[0.67]	2.02[0.90]	1.59[0.99]	0.89[1.00]	0.48[1.00]
	E	3.84[1.00]	3.14[1.00]	2.43[1.00]	1.40[1.00]	0.77[1.00]
$\overline{\mathit{TE}}({\alpha }_1,{\alpha }_0)$	W	1.22[0.67]	0.96[0.90]	0.70[0.99]	0.39[0.98]	0.21[0.99]
	C	2.31[0.67]	2.08[0.90]	1.59[0.99]	0.90[1.00]	0.48[1.00]
	E	3.84[1.00]	3.14[1.00]	2.43[1.00]	1.40[1.00]	0.77[1.00]
$\overline{\mathit{OE}}({\alpha }_1,{\alpha }_0)$	W	0.03[0.85]	0.04[0.87]	0.02[0.92]	0.01[0.95]	0.01[0.96]
	C	0.06[0.98]	0.09[1.00]	0.05[1.00]	0.03[1.00]	0.02[1.00]
	E	3.84[1.00]	3.14[1.00]	2.43[1.00]	1.40[1.00]	0.77[1.00]

For scenario (iv), simulations were repeated as in scenario (iii) but the potential outcomes were set to y_ij(z_ij, α_gi) = g_iz_ij if x_ij = 2 and y_ij(z_ij, α_gi) = x_ij otherwise. In this scenario the groups were approximately homogeneous. Empirical coverage and width of the three CIs are given in Table 4. For m ≥ 30 the Wald CIs gave the correct coverage and were the narrowest. For small m the Chebyshev and exact CIs both provided at least 95% coverage, but the Chebyshev CIs were substantially narrower. The widths of the exact CIs depend only on m, l, k_iα1, k_iα0, n_i, γ and thus are the same for the simulations carried out in scenario (iii) and (iv). Coverage of the exact CIs was always 100% in scenario (iv), as in scenario (iii).

Table 4.

Empirical width and coverage [in brackets] of Wald (W), Chebyshev (C) and exact (E) 95% CIs of the direct effect $\overline{\mathit{DE}}\left({\alpha }_1\right)$, indirect effect $\overline{\mathit{IE}}({\alpha }_1,{\alpha }_0)$, total effect $\overline{\mathit{TE}}({\alpha }_1,{\alpha }_0)$ and overall effect $\overline{\mathit{OE}}({\alpha }_1,{\alpha }_0)$ for simulations under scenario (iv) with m groups, n_i = 1000 individuals per group, and binary outcomes.

		m
		4	6	10	30	100
$\overline{\mathit{DE}}\left({\alpha }_1\right)$	W	0.06[0.94]	0.04[0.96]	0.03[0.97]	0.02[0.97]	0.01[0.97]
	C	0.12[1.00]	0.09[1.00]	0.08[1.00]	0.05[1.00]	0.03[1.00]
	E	6.07[1.00]	4.96[1.00]	3.84[1.00]	2.22[1.00]	1.21[1.00]
$\overline{\mathit{IE}}({\alpha }_1,{\alpha }_0)$	W	0.04[0.80]	0.05[0.87]	0.03[0.90]	0.02[0.94]	0.01[0.94]
	C	0.08[0.95]	0.10[0.99]	0.07[1.00]	0.04[1.00]	0.02[1.00]
	E	3.84[1.00]	3.14[1.00]	2.43[1.00]	1.40[1.00]	0.77[1.00]
$\overline{\mathit{TE}}({\alpha }_1,{\alpha }_0)$	W	0.04[0.87]	0.04[0.88]	0.03[0.93]	0.02[0.95]	0.01[0.98]
	C	0.09[0.97]	0.10[0.99]	0.06[1.00]	0.04[1.00]	0.02[1.00]
	E	3.84[1.00]	3.14[1.00]	2.43[1.00]	1.40[1.00]	0.77[1.00]
$\overline{\mathit{OE}}({\alpha }_1,{\alpha }_0)$	W	0.03[0.85]	0.04[0.87]	0.02[0.92]	0.01[0.95]	0.01[0.96]
	C	0.06[0.98]	0.09[1.00]	0.05[1.00]	0.03[1.00]	0.02[1.00]
	E	3.84[1.00]	3.14[1.00]	2.43[1.00]	1.40[1.00]	0.77[1.00]

In summary, the simulation results suggest for m ≥ 30 the Wald CIs tend to yield nominal coverage levels while being narrower than the Chebyshev and exact CIs. For m < 30 and continuous outcomes, the simulations suggest the Chebyshev CIs may be preferred, although for m = 10 the Wald CIs tend to be narrower while still providing approximately correct coverage. For m < 30 and binary outcomes, only the exact CIs tend to provide the correct coverage when the effects are heterogeneous (scenario (iii)), whereas the Chebyshev CIs tend to provide the correct coverage and are narrower than the exact CIs when the effects are homogeneous (scenario (iv)).

5 Examples

5.1 Cholera Vaccine Trial

The indirect effects of vaccination have important public health implications. In an analysis of data from an individually-randomized, placebo-controlled trial of two oral cholera vaccines in Matlab, Bangladesh, Ali et al. (2005) found a significant association between the level of vaccine coverage (i.e., the proportion of individuals vaccinated) and the incidence of cholera in unvaccinated individuals, suggesting an indirect effect of the vaccines. Motivated by the results given in Ali et al., Hudgens and Halloran (2008, Table 2) provided data from a hypothetical two-stage randomized vaccine trial wherein the first stage l = 3 of m = 5 geographically separate groups were randomly assigned α₁ and the other two groups α₀, and in the second stage 50% of individuals in groups assigned α₁ were randomly assigned vaccine and 30% of individuals in groups assigned α₀ were randomly assigned vaccine. The number of individuals in the five groups n₁, …, n₅ ranged from roughly 19,000 to 36,000 such that the results from Section 3.2.1 apply.

Table 5 gives point estimates and Wald, Chebyshev, and exact 95% CIs for the different vaccine effects (cases of cholera per 1000 individuals per year) based on the data from Hudgens and Halloran (2008) (see also VanderWeele and Tchetgen Tchetgen (2011) for an analysis of these data). To obtain the results in Table 5 we let y_ij(Z_i) = 1 if individual j in group i did not develop cholera and y_ij(Z_i) = 0 otherwise, such that positive values of the estimates reflect beneficial effects of the vaccine. For example, $\widehat{\mathit{DE}}\left({\alpha }_1\right)$ indicates 1.30 fewer cases of cholera per 1000 person-years would be expected among vaccinated individuals compared to unvaccinated individuals when vaccine coverage is 50%. Wald CIs for the α₀ direct effect, the total effect, and the overall effect all exclude zero. However, the empirical results from Section 4 suggest Wald CIs should be interpreted with caution when m = 5. The test for mean homogeneity of the direct effect based on $\tilde{T}$ indicates significant heterogeneity for α₁ (p = 0.01) but not for α₀ (p = 0.54), providing additional reason to interpret the Wald CI for $\overline{\mathit{DE}}\left({\alpha }_1\right)$ skeptically. The Chebyshev CI for the α₀ direct effect excludes zero, suggesting the risk of cholera is significantly lower when vaccinated compared to when not vaccinated if the group level coverage is low. The Chebyshev CI for the total effect also excludes zero. In contrast to the Wald and Chebyshev CIs, the exact CIs are very wide and uninformative. As pointed out by Tchetgen Tchetgen and VanderWeele (2012), the exact CI width is proportional to $1∕\sqrt{m}$ and thus these CIs are expected to be wide when m is small.

Table 5.

Wald (W), Chebyshev (C) and exact (E) 1 − γ CIs of the direct effect $\overline{\mathit{DE}}\left({\alpha }_s\right)$, indirect effect $\overline{\mathit{IE}}({\alpha }_1,{\alpha }_0)$, total effect $\overline{\mathit{TE}}({\alpha }_1,{\alpha }_0)$ and overall effect $\overline{\mathit{OE}}({\alpha }_1,{\alpha }_0)$ for the cholera vaccine trial described in Section 5.1 and the voting encouragement experiment discussed in Section 5.2

		Estimate	W	C	E
Vaccine	$\overline{\mathit{DE}}\left({\alpha }_1\right)$	1.30	[−0.52, 3.11]	[−2.84, 5.43]	[−3540, 3543]
Trial	$\overline{\mathit{DE}}\left({\alpha }_0\right)$	3.64	[2.81, 4.46]	[1.75, 5.52]	[−2177, 2184]
γ = 0.05	$\overline{\mathit{IE}}({\alpha }_1,{\alpha }_0)$	2.81	[−0.63, 6.25]	[−5.03, 10.7]	[−2145, 2150]
	$\overline{\mathit{TE}}({\alpha }_1,{\alpha }_0)$	4.11	[2.50, 5.71]	[0.44, 7.77]	[−2143, 2151]
	$\overline{\mathit{OE}}({\alpha }_1,{\alpha }_0)$	2.37	[0.03, 4.71]	[−2.98, 7.72]	[−2145, 2150]
Voting	$\overline{\mathit{DE}}\left({\alpha }_1\right)$	0.04	[−2.7e–3, 0.07]	[−0.04, 0.11]
Experiment	$\overline{\mathit{IE}}({\alpha }_1,{\alpha }_0)$	0.08	[0.01, 0.15]	[−0.06, 0.22]
γ = 0.1	$\overline{\mathit{TE}}({\alpha }_1,{\alpha }_0)$	0.12	[0.04, 0.19]	[−0.03, 0.26]
	$\overline{\mathit{OE}}({\alpha }_1,{\alpha }_0)$	0.09	[0.02, 0.16]	[−0.05, 0.22]

5.2 Voting Encouragement Experiment

Assessing the indirect effects on an intervention is important in many areas beyond public health, including econometrics and political science. Nickerson (2008) described an experiment where households in Denver and Minneapolis with two registered voters were randomly assigned to one of three conditions: (i) receive encouragement to vote; (ii) receive encouragement to recycle; or (iii) receive nothing. Households assigned to (i) or (ii) were contacted one week prior to the 2002 primaries by canvassers knocking on the households' doors. In households where the door was answered, the canvassers provided either voting or recycling encouragement to whichever individual of voting age answered the door and recorded the name of that individual. Whether each registered member of the household subsequently voted in the 2002 primary was then determined by voter turnout records. Nickerson found that individuals not directly contacted by the canvassers tended to vote more often if the individuals belonged to households assigned to voting encouragement compared to households assigned to recycling encouragement. This suggests an indirect effect of the voting encouragement intervention, which Nickerson referred to as a `secondary effect.'

For the analysis here we take the m = 392 households contacted in Minneapolis (excluding one household where apparently both voters in the household were contacted by canvassers) as the finite population of interest. Of these 392 households, 201 or 51.2% were randomly assigned to voting encouragement. The randomization process by which these households were assigned to receive encouragement to vote or recycle was complicated (see Nickerson (2005), (2008) for details); for simplicity we assume each household was independently assigned to receive voting encouragement with probability 0.5. In the nomenclature of Tchetgen Tchetgen and VanderWeele (2012), this corresponds to Bernoulli randomization at the group level. By design, at the individual level exactly one (α₁) or none (α₀) of the n_i = 2 registered voters in each of the households received voting encouragement. Although the experimenters did not randomly assign one of the two individuals in the household to receive the intervention, for illustrative purposes assume among households assigned to α₁ that each individual received the intervention with equal probability. Under these assumptions, Wald and Chebyshev CIs can be computed as described in Section 3.3.1, with slight modifications owing to Bernoulli randomization at the group level (see the Appendix for details). Here we let y_ij(Z_i) = 1 if individual j in group i voted in the election and y_ij(Z_i) = 0 otherwise, such that positive values of the effects indicate increased voter turnout due to the encouragement intervention. Point estimates as well as Wald and Chebyshev 90% CIs for the different voting encouragement effects are given in Table 5 (90% CIs were computed following Nickerson (2008), who interpreted p-values of hypothesis tests for secondary effects at the γ = 0.1 level). The exact CIs were not computed because permutation randomization was not employed at the group level. The Wald CIs indicate the presence of indirect, total and overall effects. Based on a similar result in the Denver experiment, Nickerson concluded the null hypothesis of no indirect effect was unlikely. That is, there is likely interference between individuals within the same household. The indirect effect estimate suggests that for every 100 households that receive the encouragement intervention, on average an additional eight individuals will vote despite never coming into direct contact with a canvasser.

6 Discussion

In this paper, we consider inference about treatment effects when the population consists of groups of individuals where interference is possible within groups but not between groups. The asymptotic distributions of effect estimators were derived when either the number of individuals per group or the number of groups grows large. Under certain assumptions about homogeneity across groups, the asymptotic distributions provide justification for Wald type CIs and tests. Empirical results suggest the Wald CIs may be preferred provided there are a large number of groups; otherwise, for a small number of groups, the Chebyshev CIs tend to provide correct coverage while being narrower than the exact CIs.

The asymptotic distributions were derived under several key assumptions, such as partial and stratified interference. The partial interference assumption may be reasonable when groups are suffciently separated in space, in time, or socially. Methods for assessing the stratified interference assumption are needed in future research, perhaps building upon VanderWeele et al. (2012). The results in this paper also rely on the assumption that certain two-stage randomization designs are employed to assign groups to allocation strategies and individuals to treatment. Further research remains to be conducted for other randomization designs and for observational studies where interference may be present.

Appendix

Proof of Propositions 1–3

Proposition 1 follows directly from Lehmann (1998) Appendix 4 Theorem 6. To prove Proposition 2, set $S_{n_i}\left({\alpha }_1\right)={\sum }_{j=1}^{n_i}{v}_{ij}1(Z_{ij}=1)$ and note the same theorem from Lehmann (1998) implies

$$\left[S_{n_i}\right({\alpha }_1)-E_{{\alpha }_1}\{S_{{\alpha }_1}\left({\alpha }_1\right)\left\}\right]\sqrt{V{\mathit{ar}}_{{\alpha }_1}\left\{S_{n_i}\right({\alpha }_1\left)\right\}}\stackrel{d}{\to }\mathcal{N}(0,1)$$ (11)

where E_α1{S_ni(α₁)} = E{S_ni(α₁)|G_i = 1}. Next note that

$$\begin{array}{cc}\hfill {\widehat{DE}}_i\left({\alpha }_1\right)& ={\widehat{Y}}_i(1,{\alpha }_1)-{\widehat{Y}}_i(0,{\alpha }_1)\hfill \\ \hfill & =\frac{1}{k_{i{\alpha }_1}}\sum _{j=1}^{n_i}{y}_{\mathit{ij}}(1,{\alpha }_1)1(Z_{\mathit{ij}}=1)-\frac{1}{n_i-k_{i{\alpha }_1}}\sum _{j=1}^{n_i}{y}_{\mathit{ij}}(0,{\alpha }_1)1(Z_{\mathit{ij}}=0)\hfill \\ \hfill & =\sum _{j=1}^{n_i}\left\{\frac{1}{k_{i{\alpha }_1}}{y}_{\mathit{ij}}(1,{\alpha }_1)+\frac{1}{n_i-k_{i{\alpha }_1}}{y}_{\mathit{ij}}(0,{\alpha }_1)\right\}1(Z_{\mathit{ij}}=1)-\frac{1}{n_i-k_{i{\alpha }_1}}\sum _{j=1}^{n_i}{y}_{\mathit{ij}}(0,{\alpha }_1)\hfill \end{array}$$

implying

$$\begin{array}{cc}\hfill {\widehat{DE}}_i\left({\alpha }_1\right)-{\overline{DE}}_i\left({\alpha }_1\right)& =\sum _{j=1}^{n_i}\left\{\frac{1}{k_{i{\alpha }_1}}{y}_{\mathit{ij}}(1,{\alpha }_1)+\frac{1}{n_i-k_{i{\alpha }_1}}{y}_{\mathit{ij}}(0,{\alpha }_1)\right\}1(Z_{\mathit{ij}}=1)\hfill \\ \hfill & -\frac{1}{n_i-k_{i{\alpha }_1}}\sum _{j=1}^{n_i}{y}_{\mathit{ij}}(0,{\alpha }_1)-\frac{1}{n_i}\sum _{j=1}^{n_i}{y}_{\mathit{ij}}(1,{\alpha }_1)+\frac{1}{n_i}\sum _{j=1}^{n_i}{y}_{\mathit{ij}}(0,{\alpha }_1)\hfill \\ \hfill & =\sum _{j=1}^{n_i}\left\{\frac{1}{k_{i{\alpha }_1}}{y}_{\mathit{ij}}(1,{\alpha }_1)+\frac{1}{n_i-k_{i{\alpha }_1}}{y}_{\mathit{ij}}(0,{\alpha }_1)\right\}1(Z_{\mathit{ij}}=1)\hfill \\ \hfill & =\sum _{j=1}^{n_i}\left\{\frac{1}{k_{i{\alpha }_1}}{y}_{\mathit{ij}}(1,{\alpha }_1)+\frac{1}{n_i-k_{i{\alpha }_1}}{y}_{\mathit{ij}}(0,{\alpha }_1)\right\}\frac{k_{i{\alpha }_1}}{n_i}\hfill \end{array}$$

such that ${\widehat{\mathit{DE}}}_i\left({\alpha }_1\right)-{\overline{\mathit{DE}}}_i\left({\alpha }_1\right)=S_{n_i}\left({\alpha }_1\right)-E_{{\alpha }_1}\left\{S_{n_i}\right({\alpha }_1\left)\right\}$. Also note ${\widehat{\mathit{DE}}}_i\left({\alpha }_1\right)=S_{n_i}\left({\alpha }_1\right)-{\sum }_{j=1}^{n_i}{y}_{ij}(0,{\alpha }_1)∕(n_i-k_{i{\alpha }_1})$, i.e., ${\widehat{\mathit{DE}}}_i\left({\alpha }_1\right)$ and S_ni(α₁) differ by a constant. Therefore ${\mathit{Var}}_{{\alpha }_1}\left\{{\widehat{\mathit{DE}}}_i\right({\alpha }_1\left)\right\}={\mathit{Var}}_{{\alpha }_1}\left\{S_{n_i}\right({\alpha }_1\left)\right\}$, implying

$$\frac{{\widehat{DE}}_i\left({\alpha }_1\right)-{\overline{DE}}_i\left({\alpha }_1\right)}{\sqrt{V{\mathit{ar}}_{{\alpha }_1}\left\{{\widehat{DE}}_i\right({\alpha }_1\left)\right\}}}=\frac{S_{n_i}\left({\alpha }_1\right)-E_{{\alpha }_1}\left\{S_{n_i}\right({\alpha }_1\left)\right\}}{\sqrt{V{\mathit{ar}}_{{\alpha }_1}\left\{S_{n_i}\right({\alpha }_1\left)\right\}}}$$

which by (11) completes the proof of Proposition 2. Using the fact that ${\widehat{Y}}_i\left({\alpha }_s\right)-{\overline{Y}}_i\left({\alpha }_s\right)={\sum }_{j=1}^{n_i}\left\{y_{ij}\right(1,{\alpha }_s)-y_{ij}(0,{\alpha }_s\left)\right\}\left\{1\right(Z_{ij}=1)-k_{i{\alpha }_s}∕n_i\}∕n_i$, Proposition 3 can be proved similarly to Proposition 2.

Proof of Propositions 4.1–4.4

To prove Proposition 4.1, let {i₁, …, i_l} = {i ∈ {1, …, m} : G_i = 1} and let $c_i=\lim \sqrt{{\mathit{Var}}_{{\alpha }_1}\left\{{\widehat{\mathit{DE}}}_i\right({\alpha }_1\left)\right\}}∕\sqrt{{\sum }_{i\in \{i_1,\dots ,i_1\}}{\mathit{Var}}_{{\alpha }_1}\left\{{\widehat{\mathit{DE}}}_i\right({\alpha }_1\left)\right\}}$ as n_min → ∞ for i ∈ {i₁, …, i_l}. By assumption c_i1, …, c_il exist. Then conditional on G₁ = g₁, …, G_m = g_m,

$$\begin{array}{cc}\hfill \frac{\widehat{DE}\left({\alpha }_1\right)-{\mu }_{DE}^{(i_1,\dots ,i_l)}}{{\sigma }_{DE}^{(i_1,\dots ,i_l)}}& =\frac{\sum _{i\in \{i_1,\dots ,i_l\}}\left[{\widehat{DE}}_i\right({\alpha }_1)-E_{{\alpha }_1}\{{\widehat{DE}}_i\left({\alpha }_1\right)\left\}\right]}{\sqrt{\sum _{i\in \{i_1,\dots ,i_l\}}V{\mathit{ar}}_{{\alpha }_1}\left\{{\widehat{DE}}_i\right({\alpha }_1\left)\right\}}}\hfill \\ \hfill & =\sum _{i\in \{i_1,\dots ,i_l\}}\frac{\left[{\widehat{DE}}_i\right({\alpha }_1)-E_{{\alpha }_1}\{{\widehat{DE}}_i\left({\alpha }_1\right)\left\}\right]}{\sqrt{V{\mathit{ar}}_{{\alpha }_1}\left\{{\widehat{DE}}_i\right({\alpha }_1\left)\right\}}}\frac{\sqrt{V{\mathit{ar}}_{{\alpha }_1}\left\{{\widehat{DE}}_i\right({\alpha }_1\left)\right\}}}{\sqrt{\sum _{i\in \{i_1,\dots ,i_l\}}V{\mathit{ar}}_{{\alpha }_1}\left\{{\widehat{DE}}_i\right({\alpha }_1\left)\right\}}}\hfill \\ \hfill & \stackrel{d}{\to }\sum _{i\in \{i_1,\dots ,i_l\}}{Z}_{i{C}_i}\sim \mathcal{N}(0,1)\hfill \end{array}$$

where Z_i1, …, Z_il are i.i.d $\mathcal{N}(0,1)$ and the last line follows from Proposition 2 and that ${\sum }_{i\in \{i_1,\dots ,i_l\}}{c}_2^i=1$.

To prove Proposition 4.2, note that

$$\begin{array}{cc}\hfill \widehat{IE}({\alpha }_1,{\alpha }_0)& =\widehat{Y}(0,{\alpha }_1)-\widehat{Y}(0,{\alpha }_0)\hfill \\ \hfill & =\sum _{i=1}^m\left\{\frac{{\widehat{Y}}_i(0,{\alpha }_1)}{l}1(G_i=1)-\frac{{\widehat{Y}}_i(0,{\alpha }_0)}{m-l}1(G_i=0)\right\}\hfill \end{array}$$

Thus conditional on {G_i = 1 : i ∈ {i₁, …, i_l},

$$\begin{array}{cc}\hfill & \frac{\widehat{IE}({\alpha }_1,{\alpha }_0)-{\mu }_{IE}^{\{i_1,\dots ,i_l\}}}{{\sigma }_{IE}^{\{i_1,\dots ,i_l\}}}\hfill \\ \hfill & =\sum _{i\in \{i_1,\dots ,i_l\}}\frac{{\widehat{Y}}_i(0,{\alpha }_1)-{\stackrel{‒}{y}}_i(0,{\alpha }_1)}{l{\sigma }_{IE}^{\{i_1,\dots ,i_l\}}}-\sum _{i\notin \{i_1,\dots ,i_l\}}\frac{{\widehat{Y}}_i(0,{\alpha }_0)-{\stackrel{‒}{y}}_i(0,{\alpha }_0)}{(m-l){\sigma }_{IE}^{\{i_1,\dots ,i_l\}}}\hfill \\ \hfill & =\sum _{i\in \{i_1,\dots ,i_l\}}\frac{{\widehat{Y}}_i(0,{\alpha }_1)-{\stackrel{‒}{y}}_i(0,{\alpha }_1)}{\sqrt{V{\mathit{ar}}_{{\alpha }_1}\widehat{Y}(0,{\alpha }_1)}}\frac{\sqrt{V{\mathit{ar}}_{{\alpha }_1}{\widehat{Y}}_i(0,{\alpha }_1)∕l^2}}{{\sigma }_{IE}^{\{i_1,\dots ,i_l\}}}\hfill \\ \hfill & =\sum _{i\notin \{i_1,\dots ,i_l\}}\frac{{\widehat{Y}}_i(0,{\alpha }_0)-{\stackrel{‒}{y}}_i(0,{\alpha }_0)}{\sqrt{V{\mathit{ar}}_{{\alpha }_1}\widehat{Y}(0,{\alpha }_1)}}\frac{\sqrt{V{\mathit{ar}}_{{\alpha }_1}{\widehat{Y}}_i(0,{\alpha }_1)∕{(m-l)}^2}}{{\sigma }_{IE}^{\{i_1,\dots ,i_l\}}}\hfill \\ \hfill & \stackrel{d}{\to }\sum _{i\in \{i_1,\dots ,i_l\}}{Z}_i\frac{\sqrt{V{\mathit{ar}}_{{\alpha }_1}{\widehat{Y}}_i(0,{\alpha }_1)∕l^2}}{{\sigma }_{IE}^{\{i_1,\dots ,i_l\}}}-\sum _{i\notin \{i_1,\dots ,i_l\}}{Z}_i\frac{\sqrt{V{\mathit{ar}}_{{\alpha }_1}{\widehat{Y}}_i(0,{\alpha }_1)∕{(m-l)}^2}}{{\sigma }_{IE}^{\{i_1,\dots ,i_l\}}}\hfill \\ \hfill & \sim \mathcal{N}(0,1)\hfill \end{array}$$

where Z₁, …, Z_m are i.i.d. $\mathcal{N}(0,1)$ and the penultimate step follows from Proposition 1. The proofs for Propositions 4.3 and 4.4 are similar.

Proof of Propositions 5.1–5.4

To prove Proposition 5.1, let ${\mu }_{\mathit{DE}}^G={\sum }_{i=1}^m{\overline{\mathit{DE}}}_i\left({\alpha }_1\right)1(G_i=1)∕l$ and ${\tilde{\sigma }}_{\mathit{DE}}^2=\mathit{Var}\left\{{\mu }_{\mathit{DE}}^G\right\}$. Note ${\mu }_{\mathit{DE}}^G=E\left\{\widehat{\mathit{DE}}\right({\alpha }_1)\mid G_1,\dots ,G_m\}$ and the assumptions of Proposition 5.1 imply that ${\sigma }_{\mathit{DE}}^{\left(0\right)}=\sqrt{\mathit{Var}\left\{\widehat{\mathit{DE}}\right({\alpha }_1)\mid G_1,\dots ,G_m}\}$. Therefore, because we assume that (9) holds for the sequence $W_h={\widehat{\mathit{DE}}}_{i_h}\left({\alpha }_1\right)\mid G_{i_1}=\cdots =G_{i_l}=1,h=1,\dots ,l$ for any i₁ ≠ … ≠ i_l, it follows that $\left\{\widehat{\mathit{DE}}\right({\alpha }_1)-{\mu }_{\mathit{DE}}^G\}∕{\sigma }_{\mathit{DE}}^{\left(0\right)}\mid G_{i_1}=\cdots =G_{i_l}=1\stackrel{d}{\to }N(0,1)$ for any i₁ ≠ … ≠ i_l. Because the limiting distribution is the same regardless of G₁, …, G_m, it follows that $\left\{\widehat{\mathit{DE}}\right({\alpha }_1)-{\mu }_{\mathit{DE}}^G\}∕{\sigma }_{\mathit{DE}}^{\left(0\right)}\stackrel{d}{\to }N(0,1)$. Note also this indicates that $\left\{\widehat{\mathit{DE}}\right({\alpha }_1)-{\mu }_{\mathit{DE}}^G\}∕{\sigma }_{\mathit{DE}}^{\left(0\right)}$ is asymptotically independent of G₁, …, G_m and thus asymptotically independent of $\{{\mu }_{\mathit{DE}}^G-\overline{\mathit{DE}}({\alpha }_1\left)\right\}∕{\tilde{\sigma }}_{\mathit{DE}}$, which is a function of G₁, …, G_m. Next note that because we assume ${\overline{\mathit{DE}}}_i\left({\alpha }_1\right)$ satisfies (10), Lehmann (1998) Appendix 4 Theorem 6 implies $\{{\mu }_{\mathit{DE}}^G-\overline{\mathit{DE}}({\alpha }_1\left)\right\}∕{\tilde{\sigma }}_{\mathit{DE}}\stackrel{d}{\to }N(0,1)$. Note $\mathit{Var}\left\{\widehat{\mathit{DE}}\right({\alpha }_1\left)\right\}={\sigma }_{\mathit{DE}}^{\left(0\right)2}+{\tilde{\sigma }}_{\mathit{DE}}^2$ such that

$$\frac{\widehat{DE}\left({\alpha }_1\right)-\overline{DE}\left({\alpha }_1\right)}{\sqrt{V\mathit{ar}\left\{\widehat{DE}\right({\alpha }_1\left)\right\}}}=\frac{{\sigma }_{DE}^{\left(0\right)}}{\sqrt{{\sigma }_{DE}^{\left(0\right)2}+{\tilde{\sigma }}_{DE}^2}}\frac{\widehat{DE}\left({\alpha }_1\right)-{\mu }_{DE}^G}{{\sigma }_{DE}^{\left(0\right)}}+\frac{{\tilde{\sigma }}_{DE}}{\sqrt{{\sigma }_{DE}^{\left(0\right)2}+{\tilde{\sigma }}_{DE}^2}}\frac{{\mu }_{DE}^G-\overline{DE}\left({\alpha }_1\right)}{{\tilde{\sigma }}_{DE}}$$

Following Slutsky's theorem, (5) is obtained. The proofs of Propositions 5.2–5.4 can be derived along the same lines.

Details for Voting Experiment Analysis

For the voting experiment described in Section 5.2, we assume households were independently assigned encouragement to vote with probability 0.5. This group-level Bernoulli type randomization is different from the permutation randomization assumed throughout the rest of the paper and therefore some adaptations of the various results are needed. First, it is helpful to re-express the estimators in an inverse probability weighted (IPW) form. Namely, now define $\widehat{Y}(z,{\alpha }_s)={\sum }_{i=1}^m{\widehat{Y}}_i(Z,{\alpha }_s)1(G_i=s)∕\left\{m\mathrm{Pr}\right(G_i=s\left)\right\}$ and $\widehat{Y}\left({\alpha }_s\right)={\sum }_{i=1}^m{\widehat{Y}}_i\left({\alpha }_s\right)1(G_i=s)∕\left\{m\mathrm{Pr}\right(G_i=s\left)\right\}$, where ${\widehat{Y}}_i(z,{\alpha }_s)$ and ${\widehat{Y}}_i\left({\alpha }_s\right)$ are defined as before. When the group-level assignment entails permutation randomization, these IPW estimators are equivalent to those presented in Section 3.1. Assuming group-level Bernoulli randomization, it is straightforward to show the IPW estimators are unbiased. Deriving the limiting distributions of the IPW estimators is also straightforward because G₁, …, G_n are independent under group-level Bernoulli randomization. For example, if (9) holds for $W_h={\widehat{\mathit{DE}}}_h\left({\alpha }_1\right)1(G_h=1)∕\mathrm{Pr}(G_h=1)$, h = 1, …, m, then it follows immediately that (5) holds as m → ∞; similarly, if (9) holds for $W_h={\widehat{Y}}_h(0,{\alpha }_1)1(G_h=1)∕\mathrm{Pr}(G_h=1)-{\widehat{Y}}_h(0,{\alpha }_0)1(G_h=0)∕\mathrm{Pr}(G_h=0)$, then it follows immediately that (6) holds as m → ∞. Similar results can be obtained for the total and overall effect IPW estimators. Note that no homogeneity assumptions are required here, in contrast to when there is permutation group-level randomization.

Computing Wald and Chebyshev CIs requires estimating the variances of the different IPW estimators. For the direct effect one possible estimator is $\widehat{\mathit{Var}}\left\{\widehat{\mathit{DE}}\right({\alpha }_1\left)\right\}={\sum }_{i=1}^m{\widehat{\mathit{DE}}}_i^2\left({\alpha }_1\right)1(G_i=1)∕\left\{m^2\mathrm{Pr}{(G_i=1)}^2\right\}$, which is a positively biased estimator for $\mathit{Var}\left\{\widehat{\mathit{DE}}\right({\alpha }_1\left)\right\}$ with bias ${\sum }_{i=1}^m{\overline{\mathit{DE}}}_i^2\left({\alpha }_1\right)∕m^2$. To see this, note

$$\begin{array}{cc}\hfill V\mathit{ar}\left\{\widehat{DE}\right({\alpha }_1\left)\right\}& =E\left[V\mathit{ar}\left\{\widehat{DE}\right({\alpha }_1)\mid G_1,\dots ,G_m\}\right]+V\mathit{ar}\left[E\left\{\widehat{DE}\right({\alpha }_1)\mid G_1,\dots ,G_m\}\right]\hfill \\ \hfill & =\sum _{i=1}^m\frac{E\left[V{\mathit{ar}}_{{\alpha }_1}\left\{\widehat{DE}\right({\alpha }_1\left)\right\}1(G_i=1)\right]}{m^2\mathrm{Pr}{(G_i=1)}^2}+\sum _{i=1}^{m}V\mathit{ar}\left[\frac{{\overline{DE}}_i\left({\alpha }_1\right)1(G_i=1)}{m\mathrm{Pr}(G_i=1)}\right]\hfill \\ \hfill & =\sum _{i=1}^m\frac{V{\mathit{ar}}_{{\alpha }_1}\left\{{\widehat{DE}}_i\right({\alpha }_1\left)\right\}}{m^2\mathrm{Pr}(G_i=1)}+\sum _{i=1}^m\frac{{\widehat{DE}}_i^2\left({\alpha }_1\right)\{1-\mathrm{Pr}(G_i=1\left)\right\}}{m^2\mathrm{Pr}(G_i=1)}\hfill \\ \hfill & =\sum _{i=1}^m\frac{E_{{\alpha }_1}\left\{{\widehat{DE}}_i\right({\alpha }_1\left)\right\}}{m^2\mathrm{Pr}(G_i=1)}-\sum _{i=1}^m\frac{{\overline{DE}}_i^2\left({\alpha }_1\right)}{m^2}\hfill \\ \hfill & =E\left\{\sum _{i=1}^m\frac{{\widehat{DE}}_i^2\left({\alpha }_1\right)1(G_i=1)}{m^2\mathrm{Pr}{(G_i=1)}^2}\right\}-\sum _{i=1}^m\frac{{\overline{DE}}_i^2\left({\alpha }_1\right)}{m^2}\hfill \end{array}$$

where $E_{{\alpha }_1}\left\{{\widehat{\mathit{DE}}}_i^2\right({\alpha }_1\left)\right\}=E\left\{{\widehat{\mathit{DE}}}_i^2\right({\alpha }_1)\mid G_i=1\}$. Similarly, one can define $\widehat{\mathit{Var}}\left\{\widehat{\mathit{IE}}\right({\alpha }_1,{\alpha }_0\left)\right\}={\sum }_{i=1}^m{\widehat{Y}}_i^2(0,{\alpha }_1)1(G_i=1)∕\left\{m^2{\mathrm{Pr}}^2\right(G_i=1\left)\right\}+{\widehat{Y}}_i^2(0,{\alpha }_0)1(G_i=0)∕\left\{m^2{\mathrm{Pr}}^2\right(G_i=0\left)\right\}$, $\widehat{\mathit{Var}}\left\{\widehat{\mathit{TE}}\right({\alpha }_1,{\alpha }_0\left)\right\}={\sum }_{i=1}^m{\widehat{Y}}_i^2(1,{\alpha }_1)1(G_i=1)∕\left\{m^2{\mathrm{Pr}}^2\right(G_i=1\left)\right\}+{\widehat{Y}}_i^2(0,{\alpha }_0)1(G_i=0)∕\left\{m^2{\mathrm{Pr}}^2\right(G_i=0\left)\right\}$ and $\widehat{\mathit{Var}}\left\{\widehat{\mathit{OE}}\right({\alpha }_1,{\alpha }_0\left)\right\}={\sum }_{i=1}^m{\widehat{Y}}_i^2\left({\alpha }_1\right)1(G_i=1)∕\left\{m^2{\mathrm{Pr}}^2\right(G_i=1\left)\right\}+{\widehat{Y}}_i^2\left({\alpha }_0\right)1(G_i=0)∕\left\{m^2{\mathrm{Pr}}^2\right(G_i=0\left)\right\}$, as positively biased estimators for $\mathit{Var}\left\{\widehat{\mathit{IE}}\right({\alpha }_1,{\alpha }_0\left)\right\}$, $\mathit{Var}\left\{\widehat{\mathit{TE}}\right({\alpha }_1,{\alpha }_0\left)\right\}$ and $\mathit{Var}\left\{\widehat{\mathit{OE}}\right({\alpha }_1,{\alpha }_0\left)\right\}$ with bias ${\sum }_{i=1}^m{\left\{{\overline{y}}_i\right(0,{\alpha }_1)-{\overline{y}}_i({\alpha }_0\left)\right\}}^2∕m^2$, ${\sum }_{i=1}^m{\left\{{\overline{y}}_i\right(1,{\alpha }_1)-{\overline{y}}_i(0,{\alpha }_0\left)\right\}}^2∕m^2$ and ${\sum }_{i=1}^m{\left\{{\overline{y}}_i\right({\alpha }_1)-{\overline{y}}_i({\alpha }_0\left)\right\}}^2∕m^2$ respectively. Because these variance estimators are positively biased, Wald and Chebyshev CIs constructed using these estimators (as in the lower part of Table 5) are expected in practice to be conservative, i.e., cover with probability greater 1 − γ.