Similarity enhancement for automatic segmentation of cardiac structures in computed tomography volumes

Abstract

The aim of this research is proposing a 3–D similarity enhancement technique useful for improving the segmentation of cardiac structures in Multi-Slice Computerized Tomography (MSCT) volumes. The similarity enhancement is obtained by subtracting the intensity of the current voxel and the gray levels of their adjacent voxels in two volumes resulting after preprocessing. Such volumes are: a.- a volume obtained after applying a Gaussian distribution and a morphological top-hat filter to the input and b.- a smoothed volume generated by processing the input with an average filter. Then, the similarity volume is used as input to a region growing algorithm. This algorithm is applied to extract the shape of cardiac structures, such as left and right ventricles, in MSCT volumes. Qualitative and quantitative results show the good performance of the proposed approach for discrimination of cardiac cavities.

I. INTRODUCTION

Each year many people die due to cardiovascular diseases [1]. In particular, ventricles malfunction is one of factors leading to cardiac failure.

The main function of right ventricle (RV) is to pump the de–oxygenated blood toward the pulmonary artery; whereas the left ventricle (LV) pumps the oxygenated blood through the aorta to every part of human body.

Multi-Slice Computerized Tomography (MSCT) is a medical imaging modality that performs simultaneous acquisition of several slices using an array of X-rays detectors [2]. This imaging modality provides the necessary time resolution for representing the cardiac volume during the entire cardiac cycle [3] after tomographic reconstruction [4].

Heart cavities segmentation is necessary for studying and monitoring the cardiovascular function [5]. This is a very interesting problem for the international research community. However attaining an accurate solution is a challenge due to the following undesirable aspects: a.- the heart is a moving structure. b.- MSCT images show a low contrast between blood and heart’s tissues. c.- noise and some artifacts are present in the images.

Reduction of these limitations is a requirement for attaining an accurate segmentation. For attaining this goal, a preprocessing stage is proposed in [6]. It is based on a similarity enhancement aiming at improving the region growing segmentation. Such enhancement technique was first formulated in bi–dimensional (2–D) space. This methodology includes feature vectors obtained from preprocessed images considering Gaussian and morphological filters. Then, a similarity image is obtained by taking into account the similarity between the intensity of the current pixel and the gray level of their adjacent pixels in both preprocessed images. This similarity image includes uniform regions that are easier to segment using region growing techniques.

Additionally, cardiac segmentation methods are important in analysis and geometric modelling of cardiac images, in diagnosis of cardiovascular diseases and biomechanical model construction [7]. Several cardiac segmentation methods have been proposed. Among them are:

Fleureau et al. [8][9], proposed a new technique for general purpose, semi-interactive and multi-object segmentation in N-dimensional images, applied to the extraction of cardiac structures in MSCT imaging. The proposed approach makes use of a multi-agent scheme combined with a supervised classification methodology allowing the introduction of prior information and presenting fast computing times. The multi-agent system is organized around a communicating agent which manages a population of situated agents (associated to the objects of interest) which segment the image through cooperative and competitive interactions. The proposed technique has been tested on several patient data sets, providing first results to extract cardiac structures such as LV, left atrium, RV and right atrium.

A model–based framework for detection of heart structures has been reported by Ecabert et al. [10]. The heart is represented as a triangulated mesh model including RV, LV, atria, myocardium, and great vessels. The heart model is located near the target heart using the 3–D generalized Hough transform. Finally, in order to detect the cardiac anatomy parametric deformable adaptations are applied to the model. These adaptations do not allow removal or insertion of triangles to the model. The deformation is attained by triangle correspondence. The mean point–to–surface error reported when applying the model–based method to 28 MSCT volumes was 0.82 ± 1.00 mm.

A very efficient and robust algorithm for four heart chambers segmentation was proposed by Zheng et al. [11]. They developed that algorithm applying marginal space learning and steerable filters over 137 MSCT sequences. The worse Point-To-Mesh error obtained was 1.57 ± 0.48 mm.

Bravo et al. [12], performed LV segmentation and motion analysis in MSCT sequences using support vector machines and a region growing technique. They proposed the validation test that considers several metrics obtaining an average position error of 1.38 mm.

Zhuang et al. [13], developed a new technique for segmentation of cardiac structures present on MRI, implementing two methods called: locally affine registration and the adaptative control point status free–form deformations. They establish the correspondence of the anatomical structures with the initial shapes using the first method. Then, they refine local details using a constrained optimization scheme based on the second method. The technique has been applied to 37 MRI heart volumes. The rms surface–to–surface error obtained was 4.1 mm.

The algorithm proposed in this paper is an extension of the work reported in [14]. First, we introduce an extension from two-dimensional to three-dimensional domain for calculating the similarity enhanced volume [6]. In this extension, we proposed a compact and simple mathematical formulation, that enables quantification of the 3–D similarity enhanced volume. Then, the segmentation is performed for both ventricle cavities during the entire cardiac cycle.

II. Method

A. Cardiac Databases

Two human MSCT databases are used. The acquisition process is performed using the helical computed tomography General Electric medical system, Light Speed⁶⁴. The acquisition has been triggered by the R wave of the electrocardiography signal. Each dataset contains 20 volumes to describe the heart anatomical information for a cardiac cycle. The resolution of each volume is (512×512×325) voxels. The spacing between pixels in each slice is 0.488 mm and the slice thickness is 0.625 mm.

B. Pre-processing

1. Cropping the database

In order to exclude anatomical structures, that are not considered in this research, a plane (Np) automatically calculated was used for separating LV and left atrium. For this, it was necessary to incorporate prior knowledge about the spatial location of several cardiac structures. Thus, a point in the plane (denoted as Nc) was located at the junction of the mitral and aortic valves by a cardiologist. The normal to the plane orientation is determined by the anatomical axis obtained by joining the point Nc with the apex point. Subsequently, for cropping the database, it was considered the following criterion: the gray level of a voxel is assigned to zero if this voxel is located at a distance less than zero with respect to Np; otherwise, the gray level of the voxels is not modified. Figure 1 presents the location of the plane in the heart and the axial views of an original image and the corresponding cropped image.

Fig. 1.

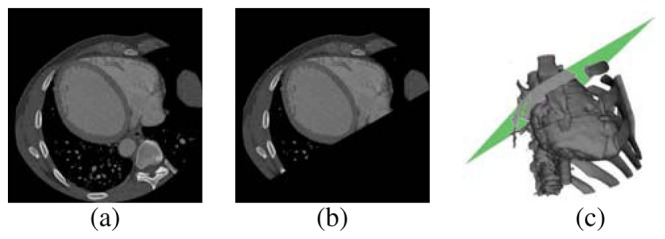
Cropped database. (a) Slice in the original volume. (b) Slice in the cropped volume. (c) Heart + cropping plane.

2. Filtering

In order to enhance information about the ventricles, a filtering process was applied to each database using the following filters.

• Averaging Filter: an averaging filter is applied to the input volumes. This kind of filter uses a 3–D kernel mask where the gray level of the current voxel is changed by the averaging gray level of a 3–D neighborhood of the current voxel according to (1). The size of 3–D neighborhood was 3 × 3×3 voxels.

  $$\mid f(x,y,z)-\mu \mid >\sigma .$$ (1)

  where: f(x, y, z) is the gray level of the current voxel, μ is the average gray level of a 3–D neighborhood of the current voxel and σ is the standard deviation of the input volume.

• Gaussian filter: this filter is applied to the input volume for reducing the noise and smoothing. A discrete Gaussian distribution could be expressed as a density mask according to (2). The size of density mask was 3×3×3 voxels. This filter is implemented by convolving a Gaussian kernel with the input volume. [15].

  $$G(x,y,z)=\frac{1}{{(\sqrt{2\pi })}^3{\sigma }_x{\sigma }_y{\sigma }_z}{e}^{-\left(\frac{x^2}{2{\sigma }_x^2}+\frac{y^2}{2{\sigma }_y^2}+\frac{z^2}{2{\sigma }_z^2})\right)}$$ (2)

  where 0 ≤ x, y, z ≤ n; n is the size of density mask and σ_x, σ_y and σ_z are the standard deviation for each spatial dimension.

• Morphological filters: these filters are based on nonlinear operations. They use neighborhoods or masks, called structuring elements (SE). The SE may have different shapes [16]. The parameter considered, for these filters, was the radius that defines the size of SE. The SE used corresponds with an ellipsoidal shape. The Gaussian smoothed volumes (I), were processed using morphological operators, such as: closing (•) and top-hat. Equation (3), shows the mathematical formulation of the top-hat filter. Figure 2, shows the axial slice view of a processed volume using the described filters.

  $$\mathbf{I}•\mathbf{SE}-\mathbf{I}=(\mathbf{I}\oplus \mathbf{SE})⊝\mathbf{SE}-\mathbf{I}$$ (3)

  where ⊕ and ⊝ are the dilation and erosion operators, respectively.

Fig. 2.

Filtering stage. (a) Averaging image. (b) Gaussian image. (c) Top-hat image.

C. 3–D Similarity

The 2–D similarity enhancement technique reported in [6] is reformulated and extended to 3–D space. This enhancement technique allows to compare a smoothed version of the input volume with respect to original volume processed using an edge enhancement morphological filter. In the smoothed volume the ventricles edges are blurred while these edges are enhanced in the morphological volume. The difference between the smoothed and edge enhanced volumes is maximized at the edges and minimized in the rest of image volume. The proposed 3–D similarity enhancement can be structured as follows: a.– An original volume is preprocessed with the top–hat morphological filter (resulting in volume Vth) and the averaging filter (resulting in volume Vp). b.– To capture the attribute in the volumes (gray level of the voxels) both volumes are processed with a square neighborhood centered on the current voxel. c.– Then, equation (4) is applied in order to obtain the intra and inter volume similarity. Equation (4) is simply the unweighted sum of squares of the differences of the attribute.

In Fig. 3, the voxels belonging to Vth are denoted with i and their respective sub-index. So, i₁ represents the gray level information of the voxel at position (x, y, z) (current voxel); whereas i₂, i₃, i₄ and i₅ represent the gray level values for the voxels (x, y +1, z), (x, y, z +1), (x−1, y, z) and (x, y, z −1), respectively. Similarly, the voxels of Vp are denoted with k and their respective sub-index.

Fig. 3.

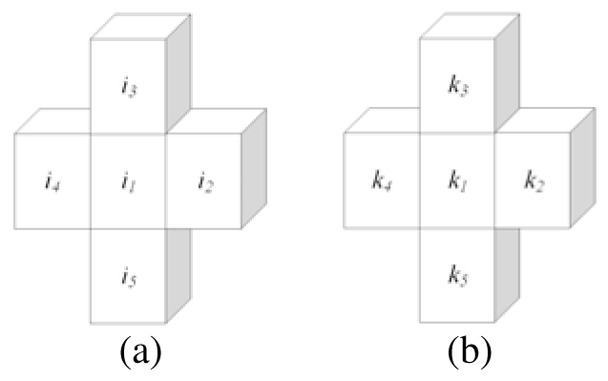
Similarity stage. a) Voxels into top-hat volume. b) Voxels into averaging volume.

$$\mathbf{S}=\sum _{n=2}^{N+1}[{(i_1-i_n)}^2+{(i_1-k_n)}^2+{(k_1-i_n)}^2]$$ (4)

where N ={2, 3, …, 26} is the number of neighbor voxels.

In this way, 25 cases corresponding to the 26 adjacent voxels of the current voxel were analyzed. Each of the 25 cases are obtained by incorporating the corresponding neighbors. In the first case, two adjacent voxels were considered. In the second were considered three adjacent voxels and so on. For example, the third case includes the gray levels of four neighboring voxels as shown in Fig. 3. It was determined, empirically, that 6 adjacent voxels give the best compromise between computational cost and quality of segmentation. The resulting volume attains a enhanced local similarity as shown in Fig. 4.a and Fig. 4.b.

Fig. 4.

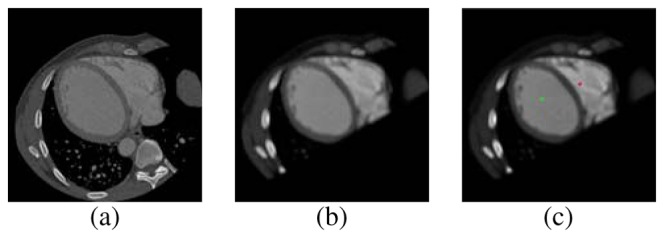
Similarity enhancement and seed localization process. (a) Original image. (b) Similarity image.(c) Seeds placed on the similarity Image.

D. Segmentation

The 3–D segmentation of ventricles is performed using a region growing technique. This technique requires a seed voxel. Starting from this seed, the algorithm extracts all voxels belonging to connected regions. A voxel is added to a region if and only if the voxel meets a predefined criterion. In this research, the criterion was the comparison of the gray level of the current voxel with respect to the average gray level of a neighborhood around the seed voxel. If the absolute difference is less than or equal than a certain threshold the current voxel is added to the region. The threshold was calculated as the product of the variance of the input volume and a constant determined empirically by the user. The segmentation process was performed on the similarity enhanced volume S. To segment the LV the seed was placed at the midpoint of the normal axis connecting the plane and the apex while for the RV the seed point was located using the Generalized Hough Transform (GHT), proposed by Ballard [17]. A detailed description of the stages of GHT is presented in [14]. In Fig. 4.c the location of seeds in the ventricles is shown.

E. Validation

The validation of the algorithm proposed was performed by comparing the automatic and the manual segmentation generated by a cardiologist. The metrics used to quantify this difference were: the area error, the contour error and the Dice coefficient. These metrics are reported in [18] and [19].

III. RESULTS

A 3–D visualization of first segmented database is shown in Fig. 5. The visualization of the internal walls of ventricles is performed using the Visualization Toolkit libraries [20]. The LV is shown in red while the RV is presented in gray. A second database that includes artifacts shown as horizontal stripes (see Fig. 6) was segmented using the proposed method. Qualitative results are shown in Fig. 7. Quantitative results of the validation process are presented in Table I. Error metrics were calculated for both segmented databases and they are close to results reported in [14]. Results of de LV segmentation are better than the RV segmentation because RV segmentation is more difficult due to the high level of contrast inhomogeneity of RV.

Fig. 5.

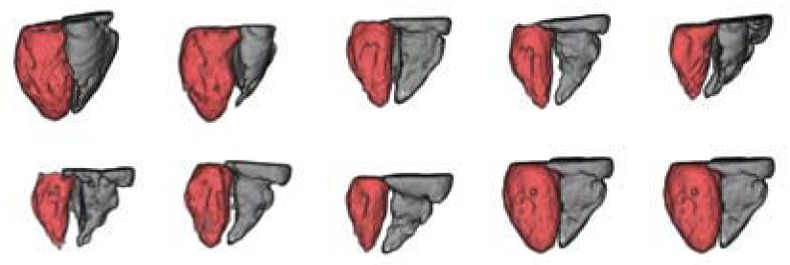
3–D visualization of segmented ventricles. First database.

Fig. 6.

Second validation database. (a) Axial view. (b) Coronal view.(c) Sagittal view.

Fig. 7.

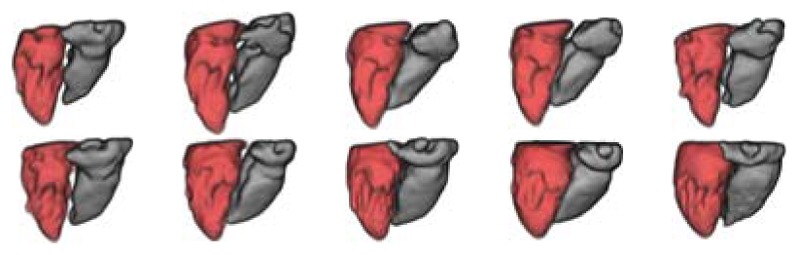
3–D visualization of segmented ventricles. Second database.

TABLE I.

AVERAGE ERRORS OBTAINED FOR BOTH PROCESSED DATABASES

	LV	RV
Metric	μ ± σ	μ ± σ
Area error (%)	0.70 ± 0.66	9.67 ± 6.41
Contour error (%)	11.94 ± 0.27	15.91 ± 1.49
Dice’s coefficient	0.92 ± 0.03	0.87 ± 0.03

IV. CONCLUSIONS AND FUTURE RESEARCH

An algorithm based on similarity enhancement techniques and region growing has been proposed. This algorithm performs the 3–D segmentation of ventricular chambers (LV and RV) in cardiac MSCT volumes. The originality of this work is based on improving the quality of images before the segmentation process by using a similarity enhancement technique. The area errors obtained for LV are smaller than errors reported in [14]. However, the contour errors are greater. The proposed approach shows high accuracy in LV detection which is reflected in both a mean area error of 0.70 % and an average Dice coefficient of 0.92. The proposed approach takes 3 minutes to extract both cavities in a MSCT volume. The computational cost to segment one entire sequence (6500 MSCT slices) was 1 hour using a Core 2 Duo 2GHz processor with 2Gb RAM. A more extensive validation of the proposed algorithm is still necessary. It should be tested using a larger number of databases. Additionally, several parameters describing the mechanical function of ventricles could be calculated such as the volume and the ejection fractions. The validation should include a comparison with results obtained in other cardiac imaging modalities and other research groups.