Abstract
Advances in salivary bioscience enable the widespread integration of biological measures into the behavioral and social sciences. While theoretical integration has progressed, much less attention has focused on analytical strategies and tactics. The statistical literature warns that common methods for comparing groups and studying associations can have relatively poor power compared to more modern robust techniques. Here we illustrate, in secondary data analyses using the USC Well Elderly II Study (n = 460, age 60-95, 66% female), that modern robust methods make a substantial difference when analyzing relations between salivary analyte and behavioral data. Analyses are reported that deal with the diurnal pattern of cortisol and the association of the cortisol awakening response with depressive symptoms and physical well-being. Non-significant results become significant when using improved methods for dealing with skewed distributions and outliers. Analytical strategies and tactics that employ modern robust methods have the potential to reduce the probability of both Type I and Type II errors in studies that compare salivary analytes between groups, across time, or examine associations with salivary analyte levels.
Keywords: robust statistical techniques, cortisol awakening response, depressive symptoms, well-being, Well Elderly II study
Introduction
Perhaps more so than any time in recent history, behavioral and social science research is integrating biological processes into their models and theories. This paradigm shift is, at least partially, due to advances in technology that make the assessment of biological variables minimally invasive (in saliva). The collection of saliva is relatively straightforward, samples can be self-collected, and collection can take place under a wide range of circumstances (e.g., Granger et al., 2012). Knowledge regarding the correlates and concomitants of salivary indices reflecting the activity of the immune, autonomic, and hypothalamic-pituitary-adrenal axis is accumulating at a very rapid rate. Salivary analytes are most often employed in studies exploring the effects or consequences of change in environmental demands or exposures on individual differences in environmentally sensitive biological systems . Individual differences in biological sensitivity and susceptibility to context are considered to reflect variation in risk versus resilience to a variety of negative outcomes. At a theoretical and practical level the integration of salivary analytes in behavioral and socially-oriented research is highly evolved. Yet, from the perspective of statistical analysis and tactics, the approach is perhaps under developed.
One of the possibilities that has received almost no empirical attention is whether discoveries are lost when analyzing salivary analyte data due to violations of standard assumptions underlying commonly used statistical techniques. Granger et al. (2012) report that skewed distributions are routinely encountered as evidenced by the frequently used strategy of transforming the data. And there is ample evidence that outliers are often encountered as well. But to what extent does standard practice deal effectively with skewed distributions and outliers in salivary analyte data? Insights reported in the statistics literature indicate that serious concerns remain in terms of both Type I errors and power (e.g., Staudte and Sheather, 1990; Marrona et al., 2006; He et al., 1990; Heritier et al., 2007; Huber and Ronchetti, 2009; Wilcox, 2012a, 2012b). The simple strategy of transforming the data can be effective in some situations. But under general conditions it is relatively ineffective, in terms of both power and Type I errors, when comparing means (e.g., Doksum and Wong, 1983; Rasmussen, 1989; Wilcox, 2012a).
Simultaneously, many new and improved methods have been derived that are aimed at dealing with violation of assumptions in a more effective manner. These new methods stem from a deeper understanding of why conventional techniques can be unsatisfactory plus improved strategies for dealing with non-normality. Under general conditions, for example, non-significant results are found to be significant when dealing with outliers in a more effective manner than is currently done. Even small departures from normality can result in relatively low power when using conventional methods based on means. Moreover, modern robust methods offer much better control over the probability of a Type I error. But modern robust methods are rarely applied in research employing salivary analyte data, and it is evident that by not doing so we may not be fully utilizing our data. That is, significant differences are missed and alternative perspectives are being ignored that might provide a deeper understanding of data. Under utilization of these data is problematic from a global perspective because laboratory derived data are very costly to generate in terms of both time and money.
The primary purpose of this study is to illustrate these issues by directly comparing results based on modern robust methods to results based on traditional statistical approaches using data from the Well Elderly II study (Clark et al., 1997; Jackson et al., 2009). These data are convenient because (1) the sample sizes are relatively large, (2) multiple samples were collected per participant per day, (3) samples were collected pre and post intervention.
Some introductory comments, from a substantive point of view, are in order. The hypothalamus-pituitary-adrenal (HPA) axis and the sympathetic-adrenomedullary system (SAM) are two major biological systems involved in homeostatic and allostatic adaptations to environmental and internal stimuli (Kopin 1995; Goldstein and McEwen 2002; McEwen 2002, 2005; de Kloet 2003). Dysfunction in the HPA axis is implicated in the development of a variety of sub-clinical and clinical conditions (Herbert et al., 2006; McEwen, 2007; Belmaker and Agam, 2008). Cortisol, the primary hormone product secreted by the HPA axis, is considered to be a biomarker of HPA axis activity (e.g., Ghiciuc et al., 2011). There is an extensive literature indicating an association between various psychological measures and measures of salivary cortisol (e.g., Van Niekerk, 2001; Strahler et al., 2007; Chida and Steptoe, 2009).
Past studies have found that mean cortisol levels exhibit an initial rise after awakening, referred to as the cortisol awakening response (CAR), followed by a decline in cortisol during the remainder of the day. Here, CAR is taken to be the cortisol level measured upon awakening minus the cortisol level measured again 30-45 min after awakening. Pruessner et al. (1997) were the first to propose that the repeated assessment of the salivary cortisol increase after awakening might represent a useful and easy measure of cortisol regulation. In most studies an increase in salivary cortisol levels of about 50-75% within 30-45 min after awakening have been found. The CAR is increasingly used in psychoneuroendocrinology as an indicator of HPA axis activity. For reviews of the literature, see Clow et al. (2009), Chida and Steptoe (2009) and Fries et al. (2009). The CAR is considered to be a marker of the integrity of the HPA axis (Hellhammer et al. (2007). Exhibiting an absence or an exacerbation of this increase is associated with several adverse psychological and physiological outcomes (e.g., Pruessner et al., 1999; Portella et al. , 2005). Both enhanced and reduced CARs are associated with various psychosocial factors (Kirschbaum et al. 1995; Chida and Steptoe 2009), including depression and anxiety disorders (e.g., Pruessner et al., 2003; Stetler and Miller, 2005; Bhattacharyya et al., 2008; Vreeburg et al., 2009, 2010).
As noted in Jackson et al. (2009), lifestyle interventions have been shown to reduce age-related declines under carefully controlled conditions, which was found to be the case in the Well Elderly study. A secondary goal in this paper is to expand on these results by addressing three fundamental issues. First, for older adults, if modern methods for comparing medians are used, to what extent are the diurnal patterns consistent with past studies? Second, can the CAR be impacted by intervention? Finally, can intervention impact the association between the CAR and a measure of depressive symptoms as well as a measure of physical well-being? And if the answer is yes, how?
Material and methods
Participants and study design
The data stem from the Well Elderly II study (Clark et al., 1997; Jackson, et al., 2009), which tested the hypotheses that a six-month lifestyle, activity-based intervention leads to reduced decline in physical health, mental well-being and cognitive functioning among ethnically diverse older people. Clark et al. (1997) summarize details of the study. Here, only a few of these details are described that are relevant for present purposes. The participants were 460 men and women aged 60 to 95 years (mean age 74.9). All participants were residents of, users of, or visitors to the study recruitment sites, demonstrated no overt signs of psychosis or dementia (based on a cursory screening procedure), and were able to complete the study assessment battery (with assistance, if necessary). Demographic details are summarized in Table 1. All prospective participants completed the informed consent process prior to study entry. Participants were recruited from 21 sites in the greater Los Angeles area, including nine senior activity centers, eleven senior housing residences, and one graduated care retirement community. Recruitment strategies included providing sign-up booths, giving presentations at meetings and social events, and distributing flyers and posters. Recruitment was undertaken in two successive cohorts to reduce temporal influences on study outcomes, overcome logistical difficulties, minimize interactions among participants, and allow adjustments in ethnic stratification. Individuals in cohort 1 (n =205) began participation between November (2004) and June (2005), whereas those in cohort 2 (n = 255) began participation between March and August (2006). Here, the two cohorts are combined in all analyses. Among the 460 participants, 379 agreed to provide salivary samples across a single day of sampling, 355 of whom provided at least 3 of the 4 required samples. After intervention, n = 328 participants remained.
Table 1.
Demographic Variables at Baseline (n=460)}
| Treatment (n=232) | Control (n=228) | Total (n=460) | |
|---|---|---|---|
| Sex | |||
| Male | 70 (30.2%) | 87 (38.2%) | 157 (34.1%) |
| Female | 162 (69.8%) | 141 (61.8%) | 303 (65.9%) |
| Age (Years)a | 75 (7.8) | 75 (7.6) | 75 (7.7) |
| 60-64 | 24 (10.3%) | 23 (10.1%) | 47 (10.2%) |
| 65-69 | 40 (17.2%) | 39 (17.1%) | 79 (17.2%) |
| 70-74 | 50 (21.6%) | 44 (19.3%) | 94 (20.4%) |
| 75-79 | 45 (19.4%) | 59 (25.9%) | 104 (22.6%) |
| 80-85 | 51 (22.0%) | 38 (16.7%) | 89 (19.4%) |
| 85+ | 22 (9.5%) | 25 (11.0%) | 47 (10.2%) |
| Race | |||
| White | 85 (36.6%) | 87 (38.2%) | 172 (37.4%) |
| Black/African American | |||
| 78 (33.6%) | 71 (31.1%) | 149 (32.4%) | |
| Hispanic or Latino | |||
| 49 (21.1%) | 43 (18.9%) | 92 (20.0%) | |
| Asian | 10 (4.3%) | 8 (3.5%) | 18 (3.9%) |
| Other | 10 (4.3%) | 19 (8.3%) | 29 (6.3%) |
| Education | |||
| < high school | 72 (31.0%) | 64 (28.1%) | 136 (29.6%) |
| High school | 45 (19.4%) | 44 (19.3%) | 89 (19.4%) |
| Some college technical school | |||
| 77 (33.2%) | 81 (35.5%) | 158 (34.4%) | |
| Four years of college or more | |||
| 38 (16.4%) | 39 (17.1%) | 77 (16.7%) | |
| Annual Incomeb | |||
| 0- $11,999 | 123 (53.7%) | 117 (53.2%) | 240 (53.5%) |
| $12,000− $23,999 | 51 (22.3%) | 56 (25.5%) | 107 (23.8%) |
| $24,000− $35,999 | 25 (10.9%) | 24 (10.9%) | 49 (10.9%) |
| $36,000+ | 30 (13.1%) | 23 (10.4%) | 53 (11.8%) |
Mean(SD)
Income: 11 refused (3 in the Treatment group, 8 in the Control group)
The intervention largely followed the one manualized in the original Well Elderly study (Clark et al., 1997). Intervention in the Well Elderly II study (Jackson et al., 2009) consisted of small group and individual sessions led by a licensed occupational therapist. Typically, each group had six to eight members, all recruited from the same site and treated by the same intervener. Monthly community outings were scheduled to facilitate direct experience with intervention content such as the use of public transportation. Due to the overt nature of lifestyle programs, neither the therapists nor the treated participants were blind to the intervention. However, the interveners and participants were blind to the study design and hypotheses. Key elements of intervention were: Identification and implementation of feasible and sustainable activity-relevant changes, development of plans to overcome mundane obstacles to enacting activity-relevant changes (e.g., bodily aches or transportation limitations), and participation in selected activities; rehearsal and repetition of changes to everyday routine. Therapists completed 40h of training to standardize provision of the Lifestyle Redesign protocol in accord with manualized specifications. Therapists participated in weekly or biweekly meetings with the on-site project director and manager to ensure intervention fidelity and quality control. Weekly 2h small group sessions were used, led by a licensed occupational therapist. Included were didactic presentations, peer exchange, direct experience (participation in activities) and personal exploration (application of content to self). There were up to 10 individual one h sessions with an occupational therapist in homes or community settings.
Assessment
Testing sessions typically occurred in groups of 4 to 29 elders and took place in recreation or meeting rooms at the study sites. The Center for Epidemiologic Studies Depressive Scale (CESD) was used to measure depressive symptoms. The CESD (Radloff, 1977) is sensitive to change in depressive status over time and has been successfully used to assess ethnically diverse older people (Lewinsohn et al., 1988; Foley et al., 2002). Physical health was assessed with the Physical Component Summary (PCS) scores from Version 2 of the Short Form-36 (SF-36v2) Item Health Survey (Ware, Kosinski and Dewey, 2000). The SF-36 is a well validated instrument for measuring health-related quality of life in a wide array of populations, including older adults (Hayes, Morries, Wolfe and Morgan, 1995). Reliability estimates using both internal consistency and test-retest methods for the PCS and the MCS have usually exceeded .90 (Ware et al, 2000).
Before and six months following the intervention, participants were asked to provide, within 1 week, four saliva samples over the course of a single day, to be obtained on rising, 30 min after rising, but before taking anything by mouth, before lunch, and before dinner. The participants were told to complete all samples on the same day and record the time of day for each sample. Regarding the second saliva sample, before intervention, 94% were obtained within 45 min or less of the first sample. After intervention this proportion was 95%. The proportion recording a time of exactly 30 min was 72% and 78% before and after intervention, respectively. Samples were assayed for cortisol using a highly sensitive enzyme immunoassay without modifications to the manufacturers recommended protocol (Salimetrics, State College, LLC). The test uses 25ul test volume, ranges in sensitivity from .007 to 3.0 ug/dl, and has average intra- and inter-assay coefficients of variation of 4.13% and 8.89%, respectively. After each collection, samples were immediately placed by the participants in their home freezers.
Data analysis and statistics
All analyses were performed with the software R (R Development Core Team, 2013) in conjunction with functions contained in the R package WRS (Wilcox Robust Statistics).
As will be seen, the data in the present study are skewed with outliers suggesting that conventional methods for comparing means might have relatively low power and poor control over the Type I error probability. (e.g., Staudte and Sheather, 1990; Marrona et al., 2006; He et al., 1990; Heritier et al., 2007; Huber and Ronchetti, 2009; Wilcox, 2012a). Indeed, even a single outlier might result in poor power as illustrated, for example, in Wilcox (2012a, p. 322). Concerns about relatively low power remain even when distributions appear to be approximately normal. To provide a rough indication of why outliers are a concern, recall from basic principles that when comparing means, power is determined in part by both the standard deviation and the sample size. More precisely, power is determined by the standard error of the mean, which is the standard deviation divided by the square root of the sample size. Even a single outlier can inflate that standard deviation resulting in relatively low power.
One strategy for dealing with outliers is to use improved methods for comparing medians. Here, the median cortisol levels were compared using a percentile bootstrap method that deals effectively with tied (duplicated) values. (For summaries of bootstrap methods, see Efron and Tibshirani, 1993; Chernick, 1999; Davison and Hinkley, 1997; Hall and Hall, 1995; Lunneborg, 2000; Mooney and Duval, 1993; Shao and Tu, 1995.) The precise details of the bootstrap method used here, as well as an R function for applying it, are described in Wilcox (2012b, sections 5.9.11 and 5.9.12.) The method is nonparametric, meaning that it makes no assumptions about the distributions when comparing, for example, cortisol levels upon awakening and shortly after. They do, however, assume that the data are a representative sample of the population under study. To provide a rough indication of the strategy, consider the goal of comparing median cortisol levels at times 1 and 2 based on n individuals. A bootstrap sample is obtained by randomly sampling, with replacement, n individuals from the observed data and noting whether the resulting median at time 1 is less than the median at time 2. This process is repeated many times (2000 times here) and the proportion of times the median at time 1 is less than the median at time 2 is noted. This proportion can then be used to compute a p-value based on general theoretical results in Liu and Singh (1993).
Classic nonparametric (rank-based) methods are sometimes suggested for comparing medians. There are exceptions, but under general conditions, nonparametric methods do not compare medians (e.g., Fung, 1980; Hettmansperger and McKean, 2011; Brunner, et al., 2002). Also, there have been important improvements related to classic nonparametric methods (e.g., Cliff, 1996; Brunner, et al., 2002; Wilcox, 2012b), but the details go beyond the scope of this paper.
The simple strategy of transforming the data can be effective in some situations. But under general conditions it is relatively ineffective, in terms of power, when comparing means (e.g., Doksum and Wong, 1983; Rasmussen, 1989; Wilcox, 2012a). For example, taking logs, typically outliers remain and distributions are still skewed, which proved to be the case for the data at hand. In practical terms, even when data are transformed, it can be advantageous to use more modern methods that are less sensitive to outliers and deal more effectively with skewed distributions. For additional concerns about classic methods for comparing means when distributions are skewed or when distributions differ in shape, see for example Pratt (1964), Westfall and Young (1993) and Wilcox (2012a).
When using least squares regression, again outliers can wreak havoc on power and they can result in a highly misleading summary of the association among the bulk of the points. Here, outliers among the dependent variable were addressed using the estimator derived by Theil (1950) and Sen (1964). The resulting regression equation is designed to predict the median value of the dependent variable, rather than the mean, given some value for the independent variable. A criticism of this estimator is that tied (duplicated) values among the dependent variable can negatively impact power. This concern can be addressed using a simple modification of the Theil–Sen estimator (via the R function tshdreg), details of which can be found in Wilcox and Clark (in press). Hypothesis testing was done via the R function regci, which uses a percentile bootstrap method. As is the case when dealing with means, simply discarding outliers among the dependent variable and applying least squares regression to the remaining data generally yields poor control over the probability of a Type I error. The resulting estimate of the standard error is incorrect regardless of how large the sample size might be. As for the independent variable, theory allows one to remove outliers. This was done here using an outlier detection method (the so-called MAD-median rule) that has been studied extensively in the statistics literature (e.g., Rousseeuw and Leroy, 1987; Wilcox, 2012b, section 3.13.4). This literature also explain and illustrate why outlier detection techniques, based on the mean and variance, are highly unsatisfactory. Briefly, outliers can be missed due to the inordinate influence they have on the sample variance.
The usual linear model assumes the regression line is straight, but modern methods make it clear that often this assumption is unsatisfactory. Moreover, the more obvious parametric methods for dealing with curvature can be unsatisfactory relative to more recently derived techniques. For a summary of the many details and various methods for dealing with curvature, often called smoothers or nonparametric regression estimators, see for example Härdle (1990), Efromovich (1999), Eubank (1999), Fox (2001) and Györfi, et al. (2002). The method used here is generally known as LOESS and was derived by Cleveland and Devlin (1988). LOESS provides some protection against outliers, but it is possible for outliers to negatively impact this method. As a check on this possibility, an initial fit was obtained using a running interval smoother (e.g., Wilcox, 2012b, section 11.5.4), which was then smoothed again using LOESS. (The R function rplot was used).
The familywise error rate (the probability of one or more Type I errors) was set at .05 and controlled using the method derived by Rom (1990), which improves on the Bonferroni method.
To add perspective, a portion of the analyses are based on the sign test. The particular variation used is based on results in Pratt (1968).
RESULTS
We begin by summarizing results based on robust methods. Then we contrast these results with those obtained via more conventional techniques.
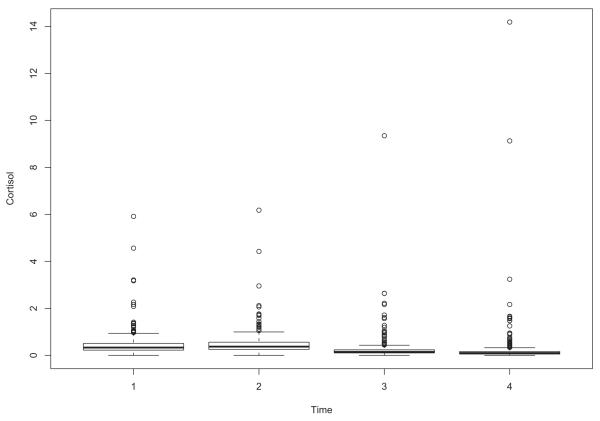
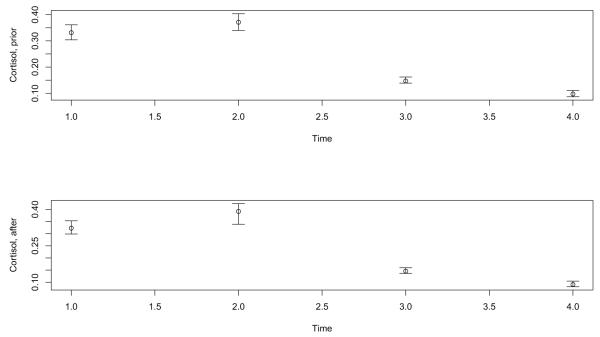
First consider cortisol prior to intervention. Evidence of skewness and outliers is provided by the four boxplots in Figure 1,which shows the cortisol measures at times 1-4. The number of outliers at the four times are 34, 37, 48 and 51, respectively. Taking logs, the number of outliers is 26, 25, 39 and 47. Boxplots after intervention are very similar to those in Figure 1. Figure 2 shows the medians prior to intervention with the bars indicating a distribution-free .95 confidence interval. That is, the confidence intervals assume random sampling only. No assumption about the distributions is needed. (The R function ebarplot.med was used.)
Figure 1.
Boxplots of the cortisol data at Times 1, 2, 3 and 4
Figure 2.
Medians at times 1, 2, 3 and 4
All pairwise comparisons of the marginal medians are significant both before and after intervention. That is, the pattern of the (marginal) medians is consistent with past studies based on means: the medians initially increase and then decline during the remainder of the day.
Regarding times 1 and 2, a possible criticism of the results just described is that it includes individuals who took the second sample up to 60 minutes after awakening. Repeating the analysis using only those individuals who report exact compliance (the recorded time for the second saliva sample is exactly 30 minutes after awakening), again a significant difference is found both before intervention (p = .04) and after (p < .001).
The results using the entire sample do not necessarily mean that for the typical individual, cortisol increases shortly after awakening. Prior to intervention, the probability that cortisol increases shortly after awakening is estimated to be .527, which does not differ significantly from .5 (p = .3). After intervention, the estimate is .58, which differs significantly from .5 (p = .013). Using exact compliance data only, prior to intervention, the estimate before intervention is .51 (p = .72) and after intervention it is .64 (p < .001).
No significant difference between CAR prior to intervention and after intervention was found based on medians. Also, the probability that CAR increases after intervention was estimated to be .486, which does not differ significantly from .5 (p = .73).
Cortisol levels among ethnic groups were compared and no significant differences were found when using means or medians. This remained the case after intervention.
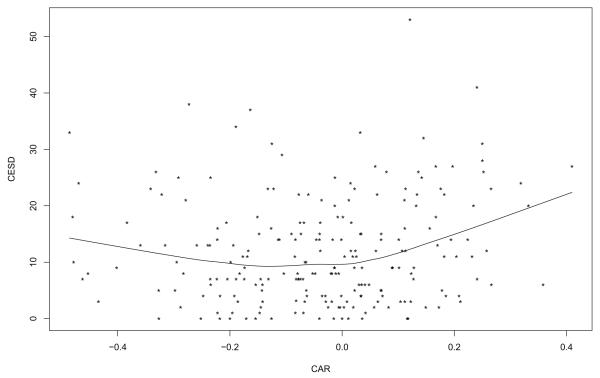
Prior to intervention, no association was found between CAR and CESD. However, after intervention, a smoother suggests that there is curvature as indicated in Figure 3. (Five CAR values greater than .5 were flagged as outliers and are not shown in Figure 3.) A test of the hypothesis that the regression line is straight was significant (p < .001). Note that there appears to be a distinct bend close to where CAR is equal to zero. For CAR greater than zero, a positive association is found (p = .038). But for CAR less than zero, no association is found. That is, the more cortisol tends to decrease immediately after awakening, the higher the predicted level of depressive symptoms. But when cortisol tends to increase after awakening, the amount it increases has little or no association with the predicted level of depressive symptoms.
Figure 3.
Regression line for predicting CESD with CAR after intervention
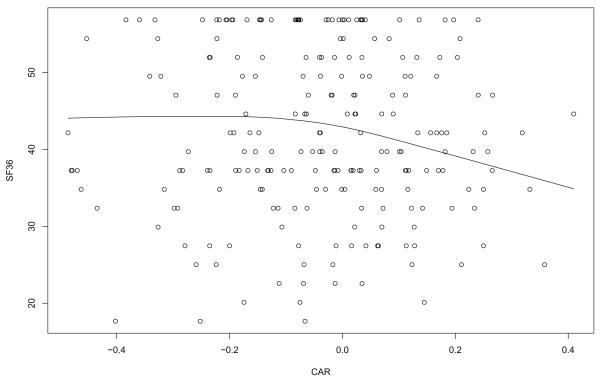
Figure 4 shows an estimate of the regression line for predicting SF-36 after intervention. Prior to intervention, no association was found. Consistent with CESD, the plot suggests that there is little or no association when cortisol increases after awakening. But there appears to be a distinct bend close to where CAR is equal to −.1. Using only the data for which the CAR is greater than −.1, with outliers among the CAR values removed, the slope differs significantly from zero (p = .003).
Figure 4.
Regression line for predicting SF36 with CAR after intervention
Results Using More Conventional Methods
To underscore the practical importance of more modern methods aimed at dealing with skewed distributions and outliers, analyses using more conventional methods are reported and discussed. First consider the diurnal patterns prior to intervention. Based on means, awakening cortisol levels do not differ significantly from levels shortly after awakening (p = .73), in contrast to p = .049 when comparing medians. Comparing times 3 and 4, again a nonsignificant result is obtained using means (p = .96). Comparing medians, p < .001. If the analysis is limited to exact compliance, again the means are not significantly different at times 1 and 2 (p = .51), which is consistent with results based on the median.
There are two features of the data that explain why comparing medians can yield substantially different results in some situations. Prior to intervention, the standard error of the sample means, corresponding to the four times used here, are 0.027, 0.027, 0.031 and 0.051, respectively. In contrast the standard errors of the medians are 0.015, 0.015, 0.006 and 0.005, which are substantially smaller, particularly at times 3 and 4. (The standard error of the median refers to the standard deviation of the median over many studies.) The other feature that impacts power is that when distributions are skewed, comparing means is not the same as comparing medians. For example, the difference between the means at times 1 and 2 is −0.008 while the difference between the medians is −0.068.
Note that the mean can poorly reflect the typical value, roughly because it is sensitive to outliers. In contrast, the median is highly insensitive to outliers because it trims all but the middle one or two values. Also, the median is arguably a better reflection of the typical value because half of all values are less than the median. That is, the median tends to be closer to the bulk of the values when a distribution is skewed. Here, prior to intervention, the proportion of values less than the mean is equal to .68, .68, .77 and .84 at times 1-4, respectively. So, if the goal is to characterize the typical value, the mean performs poorly, particularly at time 4. Taking logs reduces this problem somewhat. For example, at time 4, the proportion drops from .84 to .78. The standard error is now .014, nearly three times larger than the standard error of the median. After intervention, the proportion of values less than the mean is .67, .74, .82 and .76.
Consistent with results based on medians, the CAR prior to intervention did not differ significantly from the CAR after intervention based on means.
Now consider the association between the CAR and CESD. Consistent with results based on the Theil–Sen estimator, least squares regression finds no association before intervention. This remains the case even after removing outliers among the CAR values. Regarding the data after intervention, first it is noted that if a CAR value is declared an outlier when it is two standard deviations from the mean, only one positive value is declared an outlier: 2.01. In contrast, a boxplot finds five outliers greater than zero, namely the values greater than or equal .75. The discrepancy is due to the sensitivity of the standard deviation to outliers. That is, outliers inflate the standard deviation causing them to be missed.
Consider again the positive CAR values in Figure 3. The least squares slope does not differ significantly from zero (p = .22). Ignoring the outliers among the CAR values (CAR values greater than or equal to .75), again a nonsignificant result is obtained (p = .095). To provide some sense of why this result differs from using the Theil–Sen estimator, which yields p = .038, note that least squares regression cannot deal with outliers among the dependent variable. Simply removing them results in an incorrect estimate of the standard error and poor control over the Type I error probability regardless of how large the sample size might be. In contrast, the Theil–Sen estimator, coupled with the hypothesis testing method used here, deals with outliers among the dependent variable in a technically sound manner. The least squares estimate of the slope, after removing outliers among the independent variable, is 15.7. The Theil–Sen estimate is 21.3.
Consider again the association between SF-36 and the CAR. As previously noted, an association was found using the Theil–Sen estimator when focusing only on the data for which the CAR is greater than −.1. If least squares regression is applied instead, no association is found (p = .098).
DISCUSSION
In summary, the present study found that despite having skewed distributions with outliers, the diurnal pattern of cortisol, based on medians at times 1-4, is similar to past studies. This is in contrast to an analysis based on means. That is, had the analysis been performed on means only, the results would not be consistent with past studies. Moreover, closer examination suggests that a more nuanced understanding of diurnal patterns is needed, at least for the population studied here. The results based on medians or means do not necessarily reflect the probability that cortisol increases shortly after awakening. Prior to intervention, this probability did not differ significantly from .5, as might be expected. Also, the distribution of the CAR did not differ significantly from a symmetric distribution. That is, for the typical participant prior to intervention, an increase in cortisol shortly after awakening was not found to be more or less prominent than a decrease. But after intervention, the probability that cortisol increases shortly after awakening was found to be significantly greater than .5.
Because the CAR is known to be associated with various forms of stress, there was some expectation that prior to intervention, there would be an association with CESD. But no association between the CAR and CESD was found even when using robust methods.
The more important result here is that after intervention, an association was found based on improved techniques for dealing with violations of standard assumptions. In contrast, if more conventional methods are used, no association is found despite the reasonably large sample size. The results based on robust methods indicate that if cortisol increases shortly after awakening, depressive symptoms tend to be relatively low, but otherwise there is little or no association. That is, in terms of depressive symptoms, there is little or no difference between individuals with a small increase in their cortisol levels compared to those with a large increase. However, when cortisol decreases, the larger the decrease, the higher is the typical level of depressive symptoms. A similar result was obtained based on a measure of physical well-being. After intervention, SF-36 measures tend to be lower when cortisol decreases after awakening. The reason for finding an association only after intervention is unclear. The CAR, for example, was not found to change significantly after intervention.
Regarding cortisol, the presence of outliers found here is consistent with other recent papers (e.g., Joergensen, 2011; Looser et al. 2010; Seltzer et al., 2010; Zilioli and Watson, 2013). Using a boxplot, Zilioli and Watson (2013) report that 6.7% of their data were flagged as outliers. These results provide supporting evidence that something other than the mean might provide higher power when studying individual differences in salivary analyte data. It is stressed that the mere presence of outliers does not necessarily mean that conventional methods will have relatively low power. Nor does it necessarily mean that more modern methods for dealing with non-normality will have substantially higher power. But to assume that power will be reasonably high based on conventional techniques is not supported by extant publications.
Because the median trims all but one or two values, standard training might suggest that it could not possibly have more power (a smaller standard error) than a method based on means. However, it has been known for over two centuries that the median can indeed have a much smaller standard error. The details go beyond the scope of this paper, but a relatively non-technical explanation can be found in Wilcox (2012a).
Observe that the median belongs to the family of trimmed means: the median trims all but one or two values. Despite this, the median performs well, in terms of power, when the number of outliers tends to be relatively high. But a possibility is that for the typical situation when dealing with cortisol and other biomarkers, less trimming might provide better power. That is, some compromise between no trimming (the mean) and the maximum amount of trimming (the median) might be better for general use. The issue of how much to trim has been studied extensively in the statistics literature. A common recommendation is 20%. Technically sound inferential methods, based on a 20% trimmed mean, have been derived and have both theoretical and practical advantages compared to methods based on means (e.g., Wilcox, 2012a, 2012b). Using a 20% trimmed mean when analyzing the diurnal patterns considered here, the results mirror those obtained using medians. When comparing cortisol levels at times 1 and 2 the p-values and standard errors are smaller than the values based on medians. At times 3 and 4, the standard errors are virtually identical. Another possibility is to use a Winsorized mean as was done by Seltzer et al. (2010) in their analysis of cortisol data.
There are practical reasons for considering robust regression methods beyond what is indicated here. For a recent non-technical overview, plus more a more comprehensive summary of why violations of assumptions can result in poor power, see Wilcox et al. (2013).
The results reported here suggest that understanding the role of salivary analtyes might require multiple perspectives that can now be achieved with recently developed statistical techniques. Here, for example, several techniques were used to better understand the association between the CAR and CESD: smoothers, modern outliers detection techniques, and regression methods that deal with outliers among the dependent variable. Even when focusing on diurnal patterns, different perspectives can make a practical difference. The extent this is the case, when dealing with other biomarkers, measures of psychological stress and other populations of individuals, remains to be determined.
Anecdotal reports suggest that individual differences in salivary cortisol data are the norm rather than the exception. Our analyses of the Well Elderly II cortisol data suggest that employing modern statistical techniques for dealing with skewness, curvature, and outliers is superior to traditional techniques that assume normality, homoscedasticity, or that simple transformations of data necessarily deal effectively with violations of standard assumptions. To the best of our knowledge, this is the first study to address this important knowledge gap. The findings raise the possibility that the literature on salivary cortisol, which typically employs traditional statistical techniques, may have underestimated relationships between salivary cortisol and social, behavioral, and health-related variables. The use of modern statistical techniques in the next generation of studies, as well as in the re-analysis of existing data sets, seems well worthwhile.
Highlights.
Modern robust statistical methods for analyzing psychobiological data are studied Violations of standard assumptions can result in poor power using standard strategies Improved methods for dealing with curvature make a practical difference Highly nonsignificant results can become significant using modern methods Diurnal patterns for cortisol were similar to past studies based on medians but not means. Cortisol associations with depressive symptoms and perceived health are described
Acknowledgments
The Well Elderly II study was supported by NIH grant R01 AG021108.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
DAG is founder and Chief Scientific and Strategy Advisor at Salimetrics LLC and SalivaBio LLC. These relationships are managed by the policies of the committee on conflict of interest at Johns Hopkins University School of Medicine and the Office of Research Integrity at Arizona State University
Contributor Information
Rand R. Wilcox, Dept. of Psychology University of Southern California
Douglas A. Granger, Institute for Interdisciplinary Salivary Bioscience Research Arizona State University
Sarah Szanton, School of Nursing, Bloomberg School of Public Health, and School of Medicine Johns Hopkins University.
Florence Clark, Division of Occupational Science & Occupational Therapy University of Southern California.
References
- Belmaker RH, Galila Agam G. N Engl J Med. 2008;358:55–68. doi: 10.1056/NEJMra073096. [DOI] [PubMed] [Google Scholar]
- Bhattacharyya MR, Molloy GJ, Steptoe A. Depression is associated with flatter cortisol rhythms in patients with coronary artery disease. J Psychosom Res. 2008;65:107–113. doi: 10.1016/j.jpsychores.2008.03.012. [DOI] [PubMed] [Google Scholar]
- Brunner E, Domhof S, Langer F. Nonparametric Analysis of Longitudinal Data in Factorial Experiments. Wiley; New York: 2002. [Google Scholar]
- Chernick MR. Bootstrap Methods: A Practitioner’s Guide. Wiley; New York: 1999. [Google Scholar]
- Chida Y, Steptoe A. Cortisol awakening response and psychosocial factors: A systematic review and meta-analysis. Bio Psych. 2009;80:265–278. doi: 10.1016/j.biopsycho.2008.10.004. [DOI] [PubMed] [Google Scholar]
- Clark F, Azen SP, Zemke R, et al. Occupational therapy for independent-living older adults. A randomized controlled trial. JAMA. 1997;278:1321–1326. [PubMed] [Google Scholar]
- Cleveland WS, Devlin SJ. Locally-weighted Regression: An Approach to Regression Analysis by Local Fitting. J Amer Stat Assoc. 1988;83:596–610. [Google Scholar]
- Cliff N. Ordinal Methods for Behavioral Data Analysis. Erlbaum; Mahwah, NJ: 1996. [Google Scholar]
- Clow A, Thorn L, Evans P, Hucklebridge F. The awakening cortisol response: Methodological issues and significance. Stress. 2004;7:29–37. doi: 10.1080/10253890410001667205. [DOI] [PubMed] [Google Scholar]
- de Kloet ER. Hormones, brain and stress. Endocr Regul. 2003;37:51–68. [PubMed] [Google Scholar]
- Davison AC, Hinkley DV. Bootstrap Methods and Their Application. Cambridge University Press; Cambridge, UK: 1997. [Google Scholar]
- Doksum KA, Wong C-W. Statistical tests based on transformed data. J Amer Stat Assoc. 1983;78:411–417. [Google Scholar]
- Efromovich S. Nonparametric Curve Estimation: Methods, Theory and Applications. Springer-Verlag; New York: 1999. [Google Scholar]
- Efron B, Tibshirani RJ. An Introduction to the Bootstrap. Chapman & Hall; New York: 1993. [Google Scholar]
- Eubank RL. Nonparametric Regression and Spline Smoothing. Marcel Dekker; New York: 1999. [Google Scholar]
- Foley K, Reed P, Mutran E, et al. Measurement adequacy of the CES-D among a sample of older African Americans. Psychiat Res. 2002;109:61–9. doi: 10.1016/s0165-1781(01)00360-2. [DOI] [PubMed] [Google Scholar]
- Fox J. Multiple and Generalized Nonparametric Regression. Sage; Thousands Oaks, CA: 2001. [Google Scholar]
- Fries E, Dettenborn L, Kirschbaum C. The cortisol awakening response (CAR): Facts and future directions. Int J Psychophys. 2009;72:67–73. doi: 10.1016/j.ijpsycho.2008.03.014. [DOI] [PubMed] [Google Scholar]
- Fung KY. Small sample behaviour of some nonparametric multi-sample location tests in the presence of dispersion differences. Statistica Neerlandica. 1980;34:189–196. [Google Scholar]
- Ghiciuc CM, Cozma-Dima CL, Pasquali V, Renzi P, Simeoni S, Lupusoru CE, Patacchiol FR. Awakening responses and diurnal fluctuations of salivary cortisol, DHEA-S and alpha-amylase in healthy male subjects. Neuroendocrinol Lett. 2011;32:475–480. [PubMed] [Google Scholar]
- Goldstein DS, McEwen B. Allostasis, homeostats, and the nature of stress. Stress. 2002;5:55–58. doi: 10.1080/102538902900012345. [DOI] [PubMed] [Google Scholar]
- Granger DA, Fortunato CK, Beltzer EB, Virag M, Bright M, Out D. Salivary Bioscience and research on adolescence: A integrated perspective. J Adolescence. 2012;32:1081–1095. doi: 10.1016/j.adolescence.2012.01.005. [DOI] [PubMed] [Google Scholar]
- Györfi L, Kohler M, Krzyzk A, Walk H. A Distribution-Free Theory of Nonparametric Regression. Springer Verlag; New York: 2002. [Google Scholar]
- Hall PG, Hall D. The Bootstrap and Edgeworth Expansion. Springer Verlag; New York: 1995. [Google Scholar]
- Hampel FR, Ronchetti EM, Rousseeuw PJ, Stahel WA. Robust Statistics. Wiley; New York: 1986. [Google Scholar]
- Härdle W. Applied Nonparametric Regression. Cambridge University Press; Cambridge, UK: 1990. Econometric Society Monographs No. 19. [Google Scholar]
- Hayes V, Morris J, Wolfe C, Morgan M. The SF-36 Health Survey questionnaire: Is it suitable for use with older adults? Age Ageing. 1995;24:120–125. doi: 10.1093/ageing/24.2.120. [DOI] [PubMed] [Google Scholar]
- He X, Simpson DG, Portnoy S. Breakdown Robustness of Tests. J Amer Stat Assoc. 1990;85:446–452. [Google Scholar]
- Herbert J, Goodyer IM, Grossman AB, Hastings MH, De Kloet DR, Lightman SL, Lupien SJ, Roozendaal B, Seckl JR. Do Corticosteroids Damage the Brain? J Neuroendocrinology. 2009;18:393–411. doi: 10.1111/j.1365-2826.2006.01429.x. [DOI] [PubMed] [Google Scholar]
- Hellhammer DH, Wüst S, Kudielka BM. Salivary cortisol as a biomarker in stress research. Psychoneuroendocrinology. 2009;34:163–171. doi: 10.1016/j.psyneuen.2008.10.026. [DOI] [PubMed] [Google Scholar]
- Herbert J, Goodyer IM, Altham PME, Secher S, Shiers HM. Adrenal steroid secretion and major depression in 8 to 16 year olds II. Influence of comorbidity at presentation. Psychol Med. 1996;26:257–263. doi: 10.1017/s0033291700034656. [DOI] [PubMed] [Google Scholar]
- Heritier S, Cantoni E, Copt S, Victoria-Feser M-P. Robust Methods in Biostatistics. Wiley; New York: 2009. [Google Scholar]
- Hettmansperger TP, McKean JW. Robust Nonparametric Statistical Methods. 2nd Ed Chapman Hall; New York: 2011. [Google Scholar]
- Huber PJ, Ronchetti E. Robust Statistics. 2nd Ed Wiley; New York: 2009. [Google Scholar]
- Jackson J, Mandel D, Blanchard J, Carlson M, Cherry B, Azen S, Chou C-P, Jordan-Marsh M, Forman T, White B, Granger D, Knight B, Clark F. Confronting challenges in intervention research with ethnically diverse older adults: the USC Well Elderly II trial. Clinical Trials. 2009;6:90–101. doi: 10.1177/1740774508101191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joergensen A, Broedbaek K, Weimann A, Semba RD, Ferrucci L, et al. Association between Urinary Excretion of Cortisol and Markers of Oxidatively Damaged DNA and RNA in Humans. PLoS ONE. 2011;6(6):e20795. doi: 10.1371/journal.pone.0020795. doi:10.1371/journal.pone.0020795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kopin IJ. Definitions of stress and sympathetic neuronal responses. Ann NY Acad Sci. 1995;771:19–30. doi: 10.1111/j.1749-6632.1995.tb44667.x. [DOI] [PubMed] [Google Scholar]
- Lewinsohn PM, Hoberman HM, Rosenbaum M. A prospective study of risk factors for unipolar depression. J Abnorm Psychol. 1988;97:251–64. doi: 10.1037//0021-843x.97.3.251. [DOI] [PubMed] [Google Scholar]
- Liu RG, Singh K. Notions of limiting P values based on data depth and bootstrap. J Amer Stat Assoc. 1997;92:266–277. [Google Scholar]
- Looser RR, Metzenthin P, Helfricht S, Kudielka BM, Loerbroks A, Thayer JF, Fischer JE. Cortisol Is Significantly Correlated With Cardiovascular Responses During High Levels of Stress in Critical Care Personnel. Psychosomatic Medicine. 2010;72:281–289. doi: 10.1097/PSY.0b013e3181d35065. [DOI] [PubMed] [Google Scholar]
- Lunneborg CE. Data Analysis by Resampling: Concepts and Applications. Duxbury; Pacific Grove, CA: 2000. [Google Scholar]
- Maronna RA, Martin DR, Yohai VJ. Robust Statistics: Theory and Methods. Wiley; New York: 2006. [Google Scholar]
- McEwen BS. Sex, stress and the hippocampus: allostasis, allostatic load and the aging process. Neurobiol Aging. 2002;23:921–939. doi: 10.1016/s0197-4580(02)00027-1. [DOI] [PubMed] [Google Scholar]
- McEwen BS. Stressed or stressed out: what is the difference? J Psychiatry Neurosci. 2005;30:315–318. [PMC free article] [PubMed] [Google Scholar]
- McEwen BS. Physiology and neurobiology of stress and adaptation: Central role of the brain. Physiol Rev. 2007;87:873–904. doi: 10.1152/physrev.00041.2006. doi:10.1152/physrev.00041.2006. [DOI] [PubMed] [Google Scholar]
- Mooney CZ, Duval RD. Bootstrapping: A Nonparametric Approach to Statistical Inference. Sage; Newbury Park, CA: 1993. [Google Scholar]
- Portella MJ, Harmer CJ, Flint J, Cowen P, Goodwin GM. Enhanced early morning salivary cortisol in neuroticism. Amer J Psychiatry. 2005;162:807–809. doi: 10.1176/appi.ajp.162.4.807. [DOI] [PubMed] [Google Scholar]
- Pratt JW. Robustness of some procedures for the two-sample location problem. J Amer Stat Assoc. 1964;59:665–680. [Google Scholar]
- Pratt JW. A normal approximation for binomial, F, beta, and other common, related tail probabilities, I. Journal of the American Statistical Association. 1968;63:1457–1483. [Google Scholar]
- Pruessner JC, Hellhammer DH, Kirschbaum C. Burnout, perceived stress, and cortisol responses to awakening. Psychosomatic Med. 1999;61:197–204. doi: 10.1097/00006842-199903000-00012. [DOI] [PubMed] [Google Scholar]
- Pruessner M, Hellhammer JC, Pruessner JC, Lupien SJ. Self-reported depressive symptoms and stress levels in healthy young men: associations with the cortisol response to awakening. Psychosomatic Med. 2003;65:92–99. doi: 10.1097/01.psy.0000040950.22044.10. [DOI] [PubMed] [Google Scholar]
- Pruessner JC, Wolf OT, Hellhammer DH, Buske-Kirschbaum AB, von Auer K, Jobst S, Kirschbaum C. Free cortisol levels after awakening: A reliable biological marker for the assessment of adrenocortical activity. Life Sci. 1997;61:2539–2549. doi: 10.1016/s0024-3205(97)01008-4. [DOI] [PubMed] [Google Scholar]
- R Development Core Team . R: A language and environment for statistical computing. R Foundation for Statistical Computing; Vienna, Austria: 2013. ISBN 3-900051-07-0, URL http://www.R-project.org. [Google Scholar]
- Radloff L. The CES-D scale: a self report depression scale for research in the general population. Appl Psych Meas. 1977;1:385–401. [Google Scholar]
- Rasmussen JL. Data transformation, Type I error rate and power. Brit J Math Stat Psych. 1989;42:203–211. [Google Scholar]
- Rom DM. A sequentially rejective test procedure based on a modified Bonferroni inequality. Biometrika. 1990;77:663–666. [Google Scholar]
- Rousseeuw PJ, Leroy AM. Robust Regression & Outlier Detection. Wiley; New York: 1987. [Google Scholar]
- Seltzer MM, Greenberg JS, Hong J, Smith LE, Almeida DM, Coe C, Stawsk RS. Maternal Cortisol Levels and Behavior Problems in Adolescents. J Autism Dev Disord. 2010;40:457–69. doi: 10.1007/s10803-009-0887-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shao J, Tu D. The Jackknife and the Bootstrap. Springer-Verlag; New York: 1995. [Google Scholar]
- Staudte RG, Sheather SJ. Robust Estimation and Testing. Wiley; New York: 1990. [Google Scholar]
- Stetler C, Miller G. Blunted cortisol response to awakening in mild to moderate depression: Regulatory influences of sleep patterns and social contacts. J Abnormal Psych. 2005;114:697–705. doi: 10.1037/0021-843X.114.4.697. [DOI] [PubMed] [Google Scholar]
- Strahler J, Berndt C, Kirschbaum C, Rohleder N. Aging diurnal rhythms and chronic stress: Distinct alteration of diurnal rhythmicity of salivary α-amylase and cortisol. Bio Psych. 2010;84:248–256. doi: 10.1016/j.biopsycho.2010.01.019. [DOI] [PubMed] [Google Scholar]
- Van Niekerk JK, Huppert FA, Herbert J. Salivary cortisol and DHEA: Association with measures of cognition and well-being in normal older men, and effects of three months of DHEA supplementation. Psychoneuroendocrinology. 2001;26:591–612. doi: 10.1016/s0306-4530(01)00014-2. [DOI] [PubMed] [Google Scholar]
- Vreeburg SA, Kruijtzer BP, van Pelt J, van Dyck R, DeRijk RH, Hoogendijk WJ, Smit JH, Zitman FG, Penninx BW. Associations between sociodemographic, sampling and health factors and various salivary cortisol indicators in a large sample without psychopathology. Psychoneuroendocrinology. 2009;34:1109–1120. doi: 10.1016/j.psyneuen.2009.04.024. [DOI] [PubMed] [Google Scholar]
- Vreeburg SA, Hartman CA, Hoogendijk WJ, van Dyck R, Zitman FG, Ormel J, Penninx BW. Parental history of depression or anxiety and the cortisol awakening response. Br J Psychiatry. 2010;197:180–185. doi: 10.1192/bjp.bp.109.076869. [DOI] [PubMed] [Google Scholar]
- Ware JE, Kosinski M, Dewey JE. How to score version 2 of the SF-36 Health Survey. QualityMetric Incorporated; Lincoln, RI: 2000. [Google Scholar]
- Westfall PH, Young SS. Resampling Based Multiple Testing. Wiley; New York: 1993. [Google Scholar]
- Wilcox RR. Modern Statistics for the Social and Behavioral Sciences: A Practical Introduction. Chapman & Hall/CRC press; New York: 2012a. [Google Scholar]
- Wilcox RR. Introduction to Robust Estimation and Hypothesis Testing. 3rd Edition Academic Press; San Diego, CA: 2012b. [Google Scholar]
- Wilcox RR, Carlson M, Azen S, Clark F. Avoid lost discoveries, due to violations of standard assumptions, by using modern, robust statistical methods. Journal of Clinical Epidemiology. 2013;66:319–329. doi: 10.1016/j.jclinepi.2012.09.003. [DOI] [PubMed] [Google Scholar]
- Wilcox RR, Clark F. Robust regression estimators when there are tied values. Journal of Modern and Applied Statistical Methods. in press. [Google Scholar]
- Zilioli S, Watson NV. Winning Isn’t Everything: Mood and Testosterone Regulate the Cortisol Response in Competition. PLoS ONE. 2013;8(1):e52582. doi: 10.1371/journal.pone.0052582. doi:10.1371/journal.pone.0052582. [DOI] [PMC free article] [PubMed] [Google Scholar]