Abstract
The anisotropic g and hyperfine tensors of the Mn di-μ-oxo complex, [Mn2(III,IV)O2(phen)4](PF6)3·CH3CN, were derived by single-crystal EPR measurements at X- and Q-band frequencies. This is the first simulation of EPR parameters from single-crystal EPR spectra for multinuclear Mn complexes, which are of importance in several metalloenzymes; one of them is the oxygen-evolving complex in photosystem II (PS II). Single-crystal [Mn2(III,IV)O2(phen)4](PF6)3·CH3CN EPR spectra showed distinct resolved 55Mn hyperfine lines in all crystal orientations, unlike single-crystal EPR spectra of other Mn2(III,IV) di-μ-oxo bridged complexes. We measured the EPR spectra in the crystal ab- and bc-planes, and from these spectra we obtained the EPR spectra of the complex along the unique a-, b-, and c-axes of the crystal. The crystal orientation was determined by X-ray diffraction and single-crystal EXAFS (Extended X-ray Absorption Fine Structure) measurements. In this complex, the three crystallographic axes, a, b, and c, are parallel or nearly parallel to the principal molecular axes of Mn2(III,IV)O2(phen)4 as shown in the crystallographic data by Stebler et al. (Inorg. Chem. 1986, 25, 4743). This direct relation together with the resolved hyperfine lines significantly simplified the simulation of single-crystal spectra in the three principal directions due to the reduction of free parameters and, thus, allowed us to define the magnetic g and A tensors of the molecule with a high degree of reliability. These parameters were subsequently used to generate the solution EPR spectra at both X- and Q-bands with excellent agreement. The anisotropic g and hyperfine tensors determined by the simulation of the X- and Q-band single-crystal and solution EPR spectra are as follows: gx = 1.9887, gy = 1.9957, gz = 1.9775, and hyperfine coupling constants are AIIIx = |171| G, AIIIy = |176| G, AIIIz = |129| G, AIVx = |77| G, AIVy = |74| G, AIVz = |80| G.
Introduction
Manganese clusters with μ-oxo bridged structures are known to play an important role at the active site in several metalloenzymes, such as catalase and the oxygen-evolving complex (OEC) of photosystem (PS) II.1–5 The OEC contains a cluster of 4 manganese atoms that catalyzes the oxidation of water to dioxygen. This reaction is a stepwise process wherein 4 photons absorbed sequentially by the reaction center power the advance of the OEC through the S-state intermediates (S0 – S4 states). The first direct spectroscopic evidence for the association of Mn with the S-state intermediates emerged from the discovery of a multiline EPR signal (MLS) centered at g = 2 with hyperfine structure characteristic of 55Mn (I = 5/2).6 On the basis of its flash-number dependence, the MLS was associated with the S2 state. The similarity of this signal to the EPR spectrum of a Mn2(III,IV) complex with S = 1/2 ground state led to a proposal for the oxidation state of the Mn cluster. At present, the generally accepted interpretation of the S2 state MLS is that it arises from an S = 1/2 antiferromagnetically exchange-coupled high spin Mn4(III,IV3) species.5,7 A similar MLS EPR signal has been discovered from the S0 state.8–10
Multinuclear, especially binuclear, Mn model complexes have been extensively studied by several groups11–16 in the hope that a clear understanding of simple model systems would shed light on the much more complicated natural system, which remains poorly understood.17–19 The EPR MLS from the OEC contains key information about electronic structures, oxidation states, and ligand environment of the Mn cluster. A variety of di-μ-oxo-bridged Mn2(III,IV) compounds with a distinct 16 hyperfine line EPR signal, similar to that of the OEC in the S2 state, have been reported. The origin of this MLS was first explained by Cooper et al.20 as an antiferromagnetically coupled 55Mn (I = 5/2) binuclear mixed-valence complex of Mn(III) (S = 2) and Mn(IV) (S = 3/2) with S = 1/2 ground state. Using the spin-coupled model, it was determined that the intrinsic hyperfine constant of Mn(III) is twice as large as that of Mn(IV) for such a system, leading to the characteristic 16 lines assuming isotropic g and 55Mn hyperfine tensors of approximately |167| G for Mn(III) and |79| G for Mn(IV). However, the above explanation ignored the anisotropic characteristics of the experimental spectra, and the clear discrepancy between the experimental and simulated spectra of Mn(III)Mn(IV) complexes remained unexplained. Thus, it was difficult to elaborate further the electronic structures of these molecules. Recent studies, however, have attempted to simulate the EPR signals of the di-μ-oxo-bridged Mn model systems by considering the anisotropic characteristics of the multiline signals by utilizing EPR at different fields and related techniques such as ESEEM and ENDOR.11,13–16,21
In this study, we have utilized single-crystal EPR spectroscopy at two microwave frequencies, X (9 GHz) and Q (34 GHz) bands, to obtain a very precise anisotropic data set for a Mn(III)Mn(IV) complex directly from EPR spectra collected with the external magnetic field aligned along a specific crystal axis. Multiline EPR signals contain contributions from g anisotropy and hyperfine anisotropy. A combination of X- and Q-band measurements allows us to emphasize the contribution of anisotropic characteristics of g-values to the spectra, since the effect is enhanced at the higher magnetic fields, while the hyperfine interactions are not affected. In addition, the EPR study using single crystals provides a direct method of resolving and orientationally selecting EPR features that are unresolved in the spectra of unoriented solution samples. We measured the X-ray diffraction and polarized X-ray absorption spectra (XAS) using the same crystals. The X-ray diffraction and the extended X-ray absorption fine structure (EXAFS) region of XAS together with single-crystal EPR spectra allowed us to relate the principal axes of molecules directly to the g and hyperfine tensors along those axes.
The complex used in the present study is a binuclear di-μ-oxo-bridged Mn compound with phenanthroline terminal ligands, [Mn2(III,IV)O2(phen)4](PF6)3·CH3CN. The synthesis and the crystal structure of this complex has been reported by Stebler et al.22 We chose this crystal for our study because the four molecules in the crystal unit cell line-up in nearly the same orientation; this enormously simplifies making a relation between the crystal and molecular axes, and facilitates determining the hyperfine anisotropy and g anisotropy of a molecule. In single-crystal studies of pure complexes, high magnetic concentrations lead to line-broadening via spin–spin interactions, and this effect often creates a limitation for orientational resolution. In this complex, however, the unique molecular arrangements seemed to avoid significant line-broadening and this made it possible to obtain the unique set of anisotropic g values and hyperfine tensors. These parameters were related to the molecular axes by the results from single-crystal EXAFS measurements and X-ray diffraction. On the basis of these results, we discuss the relationship of EPR features and the electronic environment of the Mn(III)Mn(IV) system. This is the first such study, to our knowledge, of binuclear Mn complexes that has utilized single-crystal EPR studies at different fields to assign anisotropic g and hyperfine parameters.
Experimental Section
Single-Crystal Samples
Three binuclear di-μ-oxo-bridged Mn2(III,IV) compounds with phenanthroline or bipyridine terminal ligands, and PF6– or ClO4– counterions, were used in this study. They are as follows: [Mn2(III,IV)O2(phen)4](PF6)3·CH3CN, [Mn2(III,IV)O2(phen)4](ClO4)3·H2O, and [Mn2(III,IV)O2(bipy)4](ClO4)3·H2O. These crystals have a diamond-shaped plate morphology. The solution samples were prepared by dissolving the crystals in acetonitrile solvent.
EPR Spectra Measurements
Single crystal and solution EPR spectra were collected at 9.25 GHz (X-band) and 34.5 GHz (Q-band) frequencies at 9 K. X-band EPR spectra were collected using a Varian E-109 spectrometer equipped with an E-102 microwave bridge. Temperature was controlled by an Air Products Helitran liquid helium cryostat. Q-band EPR spectra were collected using a Bruker EPR spectrometer (EMX 10/12 with ER5106QT Flexline resonator). Temperature was maintained using a liquid helium cryostat (Oxford Instruments). Both X- and Q-band measurements were taken with 100 kHz magnetic field modulation. The microwave frequency was calibrated using a standard sample of TEMPO (Aldrich, 30 μM, 50 v/v% glycerol solution). The single-crystal sample was rotated in the liquid He dewar/EPR cavity using a home-built goniometer.
EPR Spectra Analysis
In the Mn(III)Mn(IV) system, which has two hyperfine centers, the effective EPR spin Hamiltonian with the total spin of S = 1/2 is written as
| (1) |
where AIII and AIV are the hyperfine coupling tensors for Mn(III) and Mn(IV), I is the nuclear spin (I = 5/2 for 55Mn), B is the magnetic field, βe is the Bohr magneton, g is the effective g tensor, and S is the total electron spin. For a Mn(III)Mn(IV) system with antiferromagnetically coupled SIII (Mn(III)) = 2 and SIV (Mn(IV)) = 3/2 states that generate a S = 1/2 ground state, the g tensor from the coupled Mn(III) and Mn(IV) ions is23–25
| (2) |
where gIII and gIV are the g tensors of monomeric Mn(III) and Mn(IV) ions, J is the isotropic exchange coupling constant (H = –2JSIIISIV), and DIII and DIV are the zero-field splitting tensors of the monomeric MnIII and MnIV ions.25 In the same manner, the magnetic hyperfine tensors of the coupled two nuclei, AIII and AIV, can be written as
| (3) |
| (4) |
where aIII and aIV are hyperfine tensors of the monomeric Mn(III) and Mn(IV) ions.
For a rhombic system, eq 1 is written as
| (5) |
EPR solution spectra were simulated by the programs developed by White and Belford26,27 for the total spin of S = 1/2 systems and modified by our group. The program includes second-order hyperfine interaction up to the second nuclei. The two isolated spin systems were added using the vector projection model for the exchange-coupled system.
For the simulation of single-crystal EPR spectra, we used a modified version of the programs to calculate the EPR spectra at specified angles of the magnetic field with respect to the g and hyperfine tensors. Slightly different microwave frequencies for individual spectra lead to small shifts of the spectra on the magnetic field axis relative to each other. Therefore, the simulation was done using the precise microwave frequencies of the individual spectra.
X-ray Diffraction Measurements
Indexing of the crystals was carried out by standard X-ray diffraction methods (Rigaku/MSC). Crystals were mounted on a 2-circle goniometer, and the diffraction data were collected using a Mar345 imaging plate detector (MAR USA Inc.). The data collection was carried out at room temperature.
X-ray Absorption Measurements
X-ray absorption spectra were taken at the Stanford Synchrotron Radiation Laboratory (SSRL) on beamline 9–3 at an electron energy of 3.0 GeV with an average current of 70–90 mA. The radiation was monochromatized by a Si(220) double-crystal monochromator which was detuned at 6600 eV to 50% of maximal flux to attenuate the X-ray 2nd harmonic. Intensity of the incident X-ray was monitored by an N2-filled ion chamber (I0) in front of the sample. Data were taken as fluorescence excitation spectra using a germanium 30-element energy-resolving detector (Canberra Electronics). Energy was calibrated by the preedge peak of KMnO4 (6543.3 eV), which was placed between two N2-filled ionization chambers after the sample. The sample crystal was mounted on a two-circle goniometer, and spectra were taken at several orientations by rotating the crystal relative to the incident polarized X-ray radiation.
A combination of XANES and EXAFS spectra was collected from 6400 to 7100 eV at room temperature; 3 eV/point from 6400 to 6535 eV, 0.2 eV/point from 6535 to 6576 eV, and 0.05 Å–1/point in k-space from 2.07 to 12.0 Å–1 (6576 eV to 7100 eV). In the k-space region, collection time was weighted using a cubic function from a minimum of 1 s per point at low k values to a maximum of 15 s per point at high k values. The EXAFS analysis was performed following methods described in detail previously.28
Coordinate System and the Crystal Structure of Mn2(III,IV) Di-μ-oxo Bridged Phenanthroline Complex
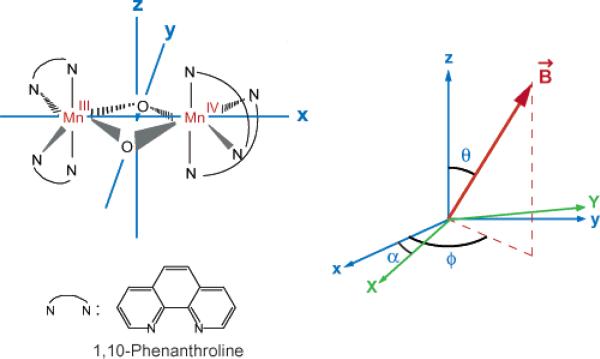
An x,y-rotated coordinate system was used for the definition of g and hyperfine tensors of [Mn2(III,IV)O2(phen)4] according to Gamelin et al. (Figure 1).29 The site symmetry of the Mn2O2 moiety is approximately C2V, and the z-axis is defined to be perpendicular to the di-μ-oxo-plane. The x- and y-axes are defined as two orthogonal axes in the di-μ-oxo-plane; the x-axis is parallel to the Mn–Mn vector, while the y-axis is perpendicular to it.
Figure 1.
Geometrical model of the [Mn2(III,IV)O2(phen)4] molecule with the definition of the coordinate system used for the g and hyperfine tensors. The Mn2O2 unit, which is planar, is in the xy plane, with the x and y axes along the Mn–Mn and the oxo-bridge oxygens, respectively. The z axis is perpendicular to the Mn2O2 plane. On the right is the coordinate system of the g and hyperfine tensors and the relation to the magnetic field (B). θ is the angle between B and the z axis; ϕ is the angle of the projection of B in the xy-plane; α is the noncoincident angle between the g and hyperfine tensors. The X and Y axes define the coordinates of the hyperfine tensor when α ≠ 0 (z as the common axis).
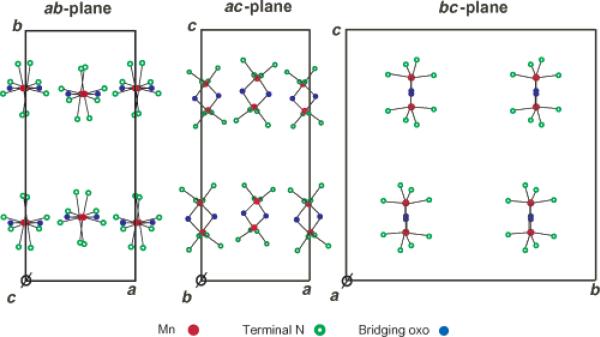
The crystal structure of [Mn2(III,IV)O2(phen)4](PF6)3·CH3CN has been reported.22 It crystallizes in the orthorhombic, space group Pbcn with a = 9.891 (3) Å, b = 22.690 (9) Å, c = 22.858 (8) Å, Z = 4. Figure 2 shows the projections of molecules in the crystal unit cell. The Mn–oxo–Mn planes are in the ac-plane and the Mn–Mn vectors are nearly parallel to the c-axis of unit cell. Table 1 specifies the relation between the molecular axes and the crystallographic axes more precisely. The z-axis of the molecule is parallel to the b-axis and perpendicular to the a- and c-axes. As can be seen in Figure 2, the Mn–Mn vector of each molecule is approximately 7° from the c-axis in the ac-plane, and the neighboring molecules (indicated as Molecule I and II in Table 1) are related by the 2-fold rotation axis symmetry. Thus, the a- and c-axes are nearly parallel to the y- and x-axes of molecules with approximately 7° of deviation.
Figure 2.
Molecular arrangement in the crystal unit cell of [Mn2(III,IV)O2(phen)4](PF6)3·CH3CN; only the Mn, bridging O atoms, and terminal N ligand atoms are shown in the ab-, ac-, and bc-planes.22 The Mn2O2 unit is in the ac-plane and the Mn–Mn vector is almost perpendicular to the ab-plane.
Table 1.
Orientation of g-Tensor Axes of [Mn2((III,IV)O2(phen)4](PF6)3·CH3CN Molecules in the Single-Crystala
| crystal axis | gx axis parallel to the Mn–Mn vector |
gy axis parallel to the O–O vector |
gz axis perpendicular to the Mn2O2 plane |
||
|---|---|---|---|---|---|
| molecule I | molecule II | molecule I | molecule II | molecule I and II | |
| a | 82.8 | –82.8 | –7.5 | 7.5 | 90 |
| b | 90 | 90 | 90 | 90 | 0 |
| c | 7.2 | –7.2 | –82.5 | 82.5 | 90 |
The angles (deg) between the crystallographic a, b, and c axes and the g-tensors.22 I and II are two adjacent molecules in the unit cell of the crystal.
Results
Determination of the Orientation of the Single Crystal
The orientation of a crystal was determined using both polarized EXAFS and X-ray diffraction. X-ray diffraction was used to screen the crystals and index them. The crystals were mounted on small Mylar strips for EPR measurements and, after the EPR measurements, the same crystals were used for polarized EXAFS measurement to obtain the direction of the Mn–Mn vector and Mn2O2 plane to a high degree of accuracy.
The single crystal of [Mn2(III,IV)O2(phen)4](PF6)3·CH3CN was mounted on the goniometer such that the crystal long axis was parallel to the X-ray e-vector and the crystal face was perpendicular to the incoming X-ray beam (ϕcrystal = 0°, χcrystal = 0°) (see Supporting Information). Then polarized XAS spectra were taken by rotating the crystal about the ϕ- and χ-axes. The unique set of polarized spectra were obtained at the three extreme orientations, (ϕcrystal, χcrystal) = (0°, 0°), (0°, 90°), and (90°, 0°) which are parallel to the crystal c-, a-, and b-axes, respectively. A comparison of the crystal structure and the polarization characteristics of Mn EXAFS explains well the relation between the orientation of crystallographic axes and crystal morphology. The c-axis, which is parallel to the Mn–Mn vector, coincides with the direction of the long axis of the crystal, and the b-axis is perpendicular to the crystal face. The a-axis is parallel to the short axis of the crystal. Thus, the molecular geometry and distances obtained from polarized EXAFS coincide well with the crystallographic data. The orientation of the crystallographic axes was also obtained by X-ray diffraction measurement, which confirmed the molecular orientation that emerged from polarized EXAFS.
This methodology allowed us to obtain independent data on the orientation of the same single crystal, in the same sample holder, as was used for EPR measurements after the XRD measurements. These studies provide the underpinning for the assignment of the anisotropic EPR parameters and their correlation to the molecular axes of the complex.
Single-Crystal X- and Q-Band EPR Spectra
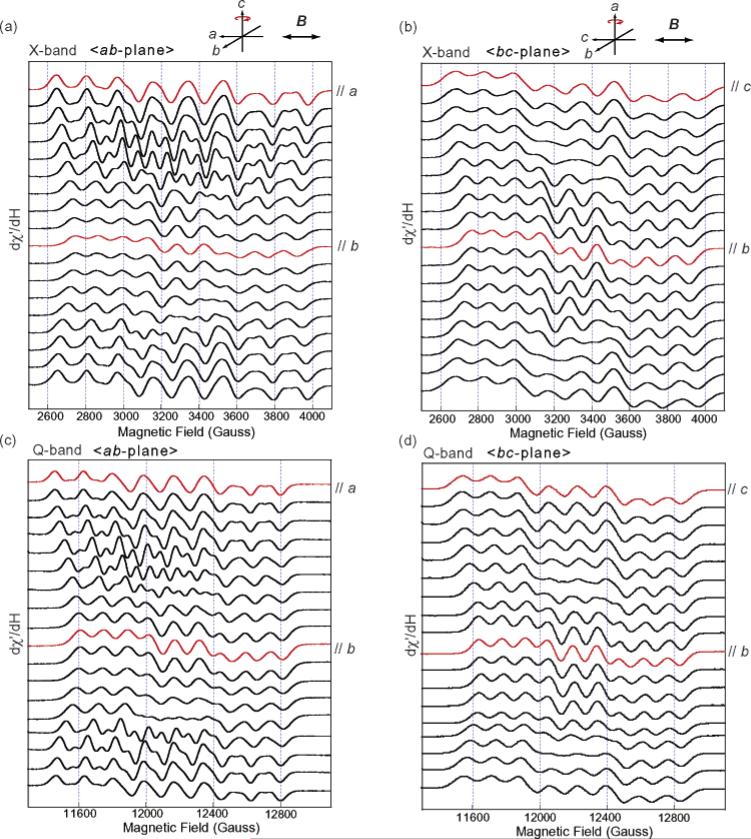
Using the EXAFS and XRD results as an indicator of crystal orientation, the EPR spectra in the crystallographic ab- and bc-planes were collected by rotating the crystal around the c- and a-axes, respectively (Figure 3). Figure 3a shows the X-band spectra in the ab-plane. A crystal was mounted in the EPR cavity such that the magnetic field (B) is parallel to the crystallographic a-axis (0° orientation). Then the crystal was rotated around the c-axis by 10° steps to 170°. At 90°, the magnetic field coincided with the direction of the b-axis of the crystal. In the same manner, single-crystal spectra were taken in the bc-plane. In Figure 3b, the magnetic field is parallel to the c-axis at the 0° setting and parallel to the b-axis at 90°. The spectra show clear hyperfine splitting in all orientations and exhibit a 180° periodicity, as expected from the symmetry of the crystal. Depending on the orientation of the crystal, both the number of hyperfine components and the center of the hyperfine signal change, showing the strong anisotropic characteristics in both ab- and bc-planes. The spectra along the a-, b-, and c-axes, identified in red in Figure 3a,b, exhibit a total width of ~1350 G, ~1170 G, and ~1290 G, respectively.
Figure 3.
Angle dependence of the single-crystal EPR spectra of [Mn2(III,IV)O2(phen)4](PF6)3·CH3CN in the ab-plane (a, c) and in the bc-plane (b, d). The X-band spectra are shown in (a, b) and the Q-band spectra in (c, d). The spectra were taken at 10° steps from 0° to 170°. The inset on top shows the rotation axis. The spectra in red are the unique spectra with the magnetic field, B, parallel to the a, b, and c axes of the crystal. In the Q-band spectra, slightly different microwave frequencies for individual spectra lead to small shifts of the spectra on the magnetic field axis relative to each other. However, the simulations shown in Figure 4 were carried out using the precise microwave frequencies of the individual spectra.
We also measured the Q-band EPR spectra, using the same crystal and following a similar protocol; the Q-band spectra in the ab- and bc-planes are shown in Figure 3c,d. The total width of the spectra is similar to that observed for the X-band data. However, the relative center of the spectrum among three extreme orientations is clearly different, indicating the presence of significant g anisotropy.
These unique spectral features along the a-, b-, and c-axes show the rhombic symmetry of g-values and 55Mn hyperfine couplings. In the following section, we describe the simulation of these three spectra by taking into account the molecular arrangement in the crystal.
Simulation of Single-Crystal EPR Spectra
The molecular site symmetry of the di-μ-oxo bridged Mn2O2 planar unit is approximately C2v. Therefore, this symmetry was used for the definition of the molecular orientation for the simulation of the single-crystal EPR spectra (see Figure 1).30 The angle θ defines the tilt angle of the magnetic field (B) from the z-axis, and ϕ defines the angle of B in the xy-plane. The noncoincident angle, R, between g and hyperfine tensor axes was assumed to be zero in the initial simulation. The spectrum parallel to the b-axis of the crystal was used for the determination of the z-components of g and hyperfine parameters, since b//z ((θ, ϕ) = (0°, 0°)). For the determination of x and y components, the spectra parallel to the c- and a-axes were used, respectively. As indicated in Table 1, the x- and y-axes of the neighboring molecules have a small orientational deviation; those axes are approximately 7° from the crystallographic axes and directed away from each other. Incorporating these deviations, the θ and ϕ angles for the simulation of the polarized spectrum along each crystal-lographic axis were set as (θ, ϕ)) (90°, 83°) for a, (0°, 0°) for b, and (90°, 7°) for the c-axis. The angle dependence of the g value is obtained by the following equation.30-32
| (6) |
with the direction cosines, l = sin θcos ϕ, m = sin θsin ϕ, and n = cos θ.
The angle dependence of the 55Mn hyperfine coupling, A(θ,ϕ), is given by
| (7) |
In the case where the hyperfine tensor axes coincide with the g tensor axes, eq 7 can be simplified as (see Figure 1)
| (8) |
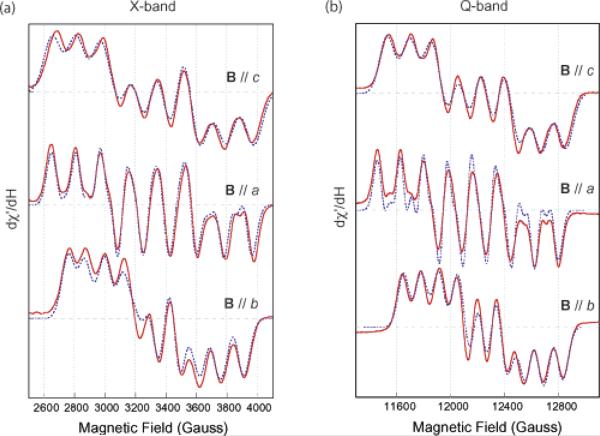
The approximate g values were obtained from the center of the hyperfine lines along each crystallographic axis, first with X-band spectra and then more precisely with Q-band spectra. A set of g values thus obtained was used for fitting the hyperfine parameters, initially assuming a constant Gaussian line width. Fitting was completed when a consistent set of g value and hyperfine parameters for both frequency bands was found that could not be improved further. The best fit was obtained with the Gaussian line width (half width at half-maximum for the absorption spectrum) of 69 G along the c-axis, 45 G along the a-axis, and 57 G along the b-axis, independent of the frequency of the microwaves. In Figure 4, the solid lines show the experimental spectra, and the dotted lines show the results of the single-crystal EPR simulation. The final values obtained from these spectra were, gx = 1.9860 (±0.0010), gy = 1.9935 (±0.0010), gz = 1.9740 (±0.0008), AIIIx = |170 (±2)|, AIIIy = |176 (±2)|, AIIIz = |129 (±2)|, AIVx = |76(±2)|, AIVy = |75 (±2)|, AIVz = |79 (± 2)| G. We also tried to include the effect of the noncoincident angle α between the g and the hyperfine tensors (Figure 1). The quality of simulation improved at an α = 5°, but the effect was not significant.
Figure 4.
Simulation of the single-crystal EPR spectra of [Mn2(III,IV)O2(phen)4](PF6)3·CH3CN collected at X-band (a) and Q-band frequencies (b). The three experimental spectra are shown as solid lines, and with the magnetic field, B, parallel to each of the crystallographic, a, b, and c axis. Simulations are shown as dotted lines. The best fits for all the single-crystal spectra shown here were obtained with the anisotropic tensors of gx = 1.9860 (±0.0010), gy = 1.9935 (±0.0010), gz = 1.9740 (±0.0008), AIIIx = |170 (±2)|, AIIIy = |176 (±2)|, AIIIz = |129 (±2)|, AIVx = |76(±2)|, AIVy = |75 (±2)|, AIVz = |79 (±2)| G, with the Gaussian line width (HWHM for the absorption spectrum) of 69, 45, and 57 G along the c, a, and b-axes, respectively.
The relatively large line width is due to the high spin concentration in the single crystals leading to a low resolution of the anisotropic parameters determined above. Therefore, the final determination of the g and hyperfine tensors was carried out by applying those parameters to the simulation of the solution spectra.
Simulation of Solution Spectra
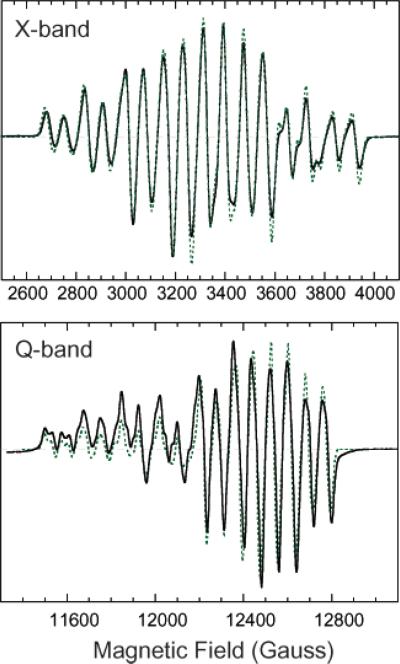
Solution spectra were taken by dissolving crystals of [Mn2(III,IV)O2(phen)4](PF6)3·CH3CN in acetonitrile. The spectra showed a typical 16 line EPR spectrum at X- and Q-bands, as reported in the literature from Mn(III)Mn(IV) exchange-coupled complexes (Figure 5).20 Using the g values and hyperfine constants obtained from the simulation of single-crystal EPR spectra as starting parameters, we carried out the fitting of solution spectra at both frequencies. The line width of hyperfine coupling was kept constant at 15 G, and we kept the noncoincident angle at 0°. The final set of g values and hyperfine constants obtained are listed in Table 2 and the simulated spectra are plotted as dotted lines in Figure 5. The obtained data set yielded consistent results in simulating the solution spectra at both X- and Q-band frequencies. The single-crystal spectra were reasonably reproduced using these values at both frequencies.
Figure 5.
Solution EPR spectra of [Mn2(III,IV)O2(phen)4](PF6)3·CH3CN in acetonitrile (solid lines in black) with the simulation spectra (dotted lines in green); X-band and Q-band. The g and hyperfine tensors of the best simulation for both frequencies are gx = 1.9887, gy = 1.9957, gz = 1.9775, AIIIx = |171| G, AIIIy = |176| G, AIIIz = |129| G, AIVx = |77| G, AIVy = |74| G, AIVz = |80| G, with a line width 15 G (HWHM).
Table 2.
g Values and Hyperfine Constantsa from the Present Single-crystal Study Compared to Other Simulations from EPR and ENDOR Studies Using Solution Spectra
| present study |
Schäfer et al.11 |
Randall et al.15 |
Policar et al.13 |
||
|---|---|---|---|---|---|
| compound |
[(phen)4Mn2III,IV(μ-O)2](PF6)3·CH3CN |
[(phen)4Mn2III,IV(μ-O)2](ClO4)3·CH3COCH3 |
[(phen)4Mn2III,IV(μ-O)2](ClO4)3·H2O |
[(phen)4Mn2III,IV(μ-O)2](ClO4)3 *Solvent not specified |
|
| form | single-crystal | solution | solution | solution | |
| g x | 1.9887 | 1.992 | 1.995 | 2.0002b | |
| g y | 1.9957 | 1.998 | 1.995 | 1.9950b | |
| g z | 1.9775 | 1.98 | 1.982 | 1.9814 | |
| A III | A III x | –481 (–171) | –485 (–173) | –480 | –495b |
| A III y | –493 (–176) | –504 (–178) | –480 | –468b | |
| A III z | –365 (–129) | –387 (–130) | –378 | –339 | |
| A IV | A IV x | 215 (77) | 216 (77) | 213 | 211b |
| A IV y | 206 (74) | 213 (75) | 213 | 211b | |
| A IV z | 227 (80) | 230 (84) | 229 | 233 | |
Unit of hyperfine constants: MHz (the values are also given in Gauss in parentheses for the present study and for the reference when the authors reported it in the paper.)
The definition of gx, gy, gz in the present study, Schäfer et al.,11 and Randall et al.15 are the same with respect to the molecular orientation. The convention gx > gy > gz was used in the study of Policar et al.,13 and the subscripts do not necessarily denote directions in the molecular frame. However, the definition of gz is the same as in the other studies.
Discussion
In this study, the orientation of the g and hyperfine tensor axes of [Mn2(III,IV)O2(phen)4](PF6)3·CH3CN complex with respect to the molecular structure was obtained directly from the single-crystal EPR spectra. We obtained a rhombic g and hyperfine tensor system with gx = 1.9887, gy = 1.9957, gz = 1.9775, AIIIx = |171| G, AIIIy = |176| G, AIIIz = |129| G, AIVx = |77| G, AIVy = |74| G, AIVz = |80| G.
The hallmark of EPR spectrum from exchange-coupled oxo-bridged Mn2(III,IV) clusters was the observation of 16 hyperfine lines assigned to a coupling of the Mn(III) and Mn(IV) nuclei. The presence of 16 hyperfine lines instead of the 36 expected lines (with isotropic g and hyperfine values) was attributed to overlap of the hyperfine lines caused by the two-to-one ratio of the AIII to AIV hyperfine values. Even in studies at Q-band where the presence of anisotropy should be apparent, the solution EPR spectrum still exhibited only 16 lines. The single-crystal EPR spectra shown in Figure 3a–d clearly demonstrate the presence of both g and hyperfine anisotropy; therefore, the traditional explanation for the 16 line spectrum is too simplistic. In the single crystal spectra, the number of lines ranges from 8 to 16 as a function of the orientation. It is because (1) the relatively large line width of single-crystal EPR spectra makes some lines unresolved, (2) the two-to-one ratio of AIII to AIV does not hold in all directions, and (3) the number of lines resolved in a specific orientation depends on the anisotropic line width. In the following part, we discuss the origin of anisotropic g and 55Mn hyperfine parameters and line width by comparing them to the parameters of mononuclear Mn(III) and Mn(IV) ions.
g-Values
The present EPR study of single crystals shows that the rhombic g values are in the order gz < gx < gy. The lowest g value is along the direction of the molecular z-axis, which is perpendicular to the di-μ-oxo plane. The gx value is along the Mn–Mn direction, and it is smaller than gy, which is along the axis that bisects the Mn–O–Mn. The EPR spectra and anisotropic g and A values derived from these spectra clearly indicate the valence-trapped nature of the mixed valence complex. Hence, reviewing the g-values from Mn(III) and Mn(IV) monomers is useful for understanding the origins of g and A anisotropy in this complex.
In a typical Mn(III) monomer33 with d4 configuration (3t2g1eg), a single unpaired electron occupies the σ antibonding dz2 orbital. This leads to the distorted octahedral environment with Jahn–Teller distortion along the dz2 direction,34 with a 5B1 ground state.33 The deviation of the g values along the tetragonally distorted axis and in the equatorial direction for such a ground-state configuration can be described by the equations described in the footnote.35 These show that the g∥ along the dz2 direction will be smaller compared to g⊥ in the x and y direction. No differences have been observed in the g-values in the equatorial directions (x and y) in Mn(III)(dbm)3 and Mn(III) in rutile in which the six oxo ligands are structurally equivalent in the x, y, z directions.33,36 On the other hand, rhombic g values have been reported for the [(terpy)MnIII(N3)3], (terpy, 2,2′:6′2″-terpyridine) complex where the six N ligands are structurally nonequivalent.37
For the Mn(IV) monomer with a d3 configuration (3t2g), the anisotropy in the g values is usually smaller compared to the Mn(III) ion due to the symmetric electronic configuration.38–40 The deviation of the g value is in the vicinity of 0.004 for Mn(IV) depending on the ligand environment, while in the vicinity of ~0.02 for Mn(III).
In the mixed valence system of [Mn2(III,IV)O2(phen)4](PF6)3·CH3CN, the deviation of the g-value is 0.018, with the smallest g value along the molecular z-direction (gz). Although the g tensor derives from both Mn(III) and Mn(IV) centers, the present result clearly shows that most of the g anisotropy of the Mn(III)Mn(IV) system arises from the Mn(III) center. The crystallographic data of Mn(III)Mn(IV) complexes usually exhibit a longer Mn–Nax bond (molecular z-direction) length at the Mn(III) site, indicating the presence of distinct Mn(III) and Mn(IV) sites in the Mn(III)Mn(IV) complexes.41–47 Just as in the case of the Mn(III) monomer, the unpaired electron occupies the dz2 orbital of the Mn(III) site in the Mn(III)-Mn(IV) di-μ-oxo complex.29 By assuming a 5B1 ground state,13 the rhombic g values along each of the molecular axes can be described by the following equations35
| (9) |
| (10) |
| (11) |
where ΔE is the energy difference between the ground state and the excited state and dxy is the excited state in the present case.29 It is clear from eqs 9–11 that gz will be the lowest value, as is observed experimentally. In the Mn(III)Mn(IV) complexes, x and y directions are structurally nonequivalent (Figure 1). In addition, the bonding interactions between the metal d-orbitals and oxygen p-orbitals are different in the x and y directions. The crystallographic data show that the oxo-Mn-oxo angle is 84°, whereas Mn–oxo–Mn angle is 96°. The acute angle of oxo-Mn-oxo indicates stronger interaction along the x-direction. Therefore, the energy level of dxz > dyz and, as a consequence, gx < gy according to eqs 10 and 11. Our experimental data are consistent with this theoretical observation.
Hyperfine Coupling
In the present study we have obtained rhombic hyperfine tensors, AIIIx = –171, AIIIy = –176, AIIIz = –129, AIVx = 77, AIVy = 74, AIVz = 80 G, with the anisotropy of ΔAIII = 47 G and ΔAIV = 76 G. The sign of these hyperfine coupling constants has been explained in the literature.20 The result shows the strong anisotropic character in Mn(III), but less in Mn(IV). In the Mn(IV) d3 monomer,39 the magnetic hyperfine tensors are nearly isotropic due to the symmetric electronic configuration (3t2g). Some exceptions have been observed in strongly perturbed octahedral environments.40 On the other hand, large hyperfine anisotropy has been observed in Mn(III) d4 monomers (3t2g1eg).31,33,48 In addition, the zero-field splitting of the Mn(IV) ions is smaller (|DIV| < 1 cm–1)39,40 than the value of Mn(III) ions (|DIII| ≈ 4 cm–1).33,36,37 In the Mn(III)Mn(IV) mixed valence system, the anisotropy transfer from Mn(III) to Mn(IV) through zero-field splitting perturbation arises from the second term of eqs 3 and 4. We expect from the above observations that the hyperfine anisotropy of Mn(III) can be basically explained by the intrinsic Mn(III) hyperfine anisotropy, while the major source of the Mn(IV) hyperfine anisotropy arises from the transferred zero-field splitting perturbation from Mn(III).11,15,25
In the following section we compare our experimental values with the calculated values using the intrinsic values reported for Mn(III) and Mn(IV) ions. The intrinsic hyperfine tensors for the monomeric Mn(III) ions in TiO2 are from Gerritsen and Sabisky33 who reported values of Ax,y = 88.8 G and Az = 56.5 G with D = –3.4 ± 0.1 cm–1 and E = 0.116 ± 0.001 cm–1. For Mn(IV) ion in TiO2, From et al.40 obtained values of Ax = 77.7 ± 0.5 G, Ay = 75.4 ± 0.5 G, and Az = 80.6 ± 0.5 G with D = 0.8818 ± 0.003 cm–1 and E = 0.2635 ± 0.003 cm–1. When these two isolated spin systems are combined using the vector projection model for exchange-coupled systems, the expected hyperfine terms of Mn(III)Mn(IV) complexes are AIIIx,y = |172| G, AIIIz = |110| G, AIVx = |72| G, AIVy = |69| G, AIVz = |74| G, with anisotropy of ΔAIII = 62 G and ΔAIV = 5 G from eqs 3 and 4, using J = –148 cm–1, DIII = –3.4 cm–1 and DIV = 0.8818 cm–1.
The experimental values are in the range of the theoretically expected values, except for the smaller hyperfine anisotropy for the Mn(III) site. The hyperfine anisotropy of the Mn(IV) site is significantly smaller than that of the Mn(III) site, which is consistent with the trend in the Mn(IV) monomers (AIVy < AIVx < AIVz). For the Mn(III) center, the smallest hyperfine coupling along the z-direction is consistent with the calculated hyperfine coupling value of the Mn(III) monomer with the 5B1 ground state.48 The smaller value along the x-axis (AIIIx) compared with that along the y-axis (AIIIy) could be the consequence of the rhombic electronic environment at the Mn(III) site due to the nonequivalent electron density in the x and y directions, as was mentioned in the previous section. We do not have a definitive explanation for a smaller hyperfine anisotropy for the Mn(III) site compared to the calculated values. However, possible reasons are as follows; (1) In the Mn(III)Mn(IV) mixed valence system, the electron is not completely localized, and the electron density can be transferred from the dz2 orbital on one center (Mn(III)) to the dx2-y2 orbital on the other (Mn(IV)) in C2 symmetry.49,50 This may modify hyperfine anisotropy of the two Mn centers, mostly decreasing the anisotropic effect at the Mn(III) site. (2) The hyperfine tensors (AIII and AIV) and the zero-field splitting tensors (DIII and DIV) of the intrinsic Mn(III) and Mn(IV) ions we used for the calculations are both from the six O-ligand complexes, rather than from mixed N and O ligand complexes. We know of no appropriate Mn monomers which have a mixed ligand environment; therefore, the present calculation does not include this effect.
Interestingly, the crystallographic data of [Mn2(III,IV)O2(phen)4](PF6)3·CH3CN do not show the difference between Mn(III) and Mn(IV), unlike other reported crystal structures of Mn(III)Mn(IV) di-μ-oxo complexes.41–44 This is probably due to the transposition of Mn(III)–Mn(IV) and Mn(IV)–Mn(III) units in the crystal as Stebler et al. mentioned.22 This structural disorder is the possible reason for the small difference between the averaged distances of Mn–Nequatorial and Mn–Naxial (Δ{(Mn–Nequatorial)–(Mn–Naxial)} ≈ 0.02 Å); in other reported crystal structures of Mn(III)Mn(IV) system, the difference is in the range of 0.05–0.1 Å. In fact, the evidence of the trapped Mn(III) and Mn(IV) valences in [Mn2(III,IV)O2(phen)4](PF6)3·CH3CN is clear in the present EPR spectra; two distinct hyperfine couplings of Mn(III) and Mn(IV) are observed in the x, y, and z directions, which we do not expect from the system where the spin is completely delocalized on two Mn centers.
Line Width
In general, hyperfine splitting is not observed in single crystals of Mn(III)Mn(IV) complexes due to the broadening of the individual absorption curves caused by the large spin–spin interaction. In the single-crystal spectra of [Mn2(III,IV)O2(bipy)4](ClO4)3·H2O and [Mn2(III,IV)O2(phen)4](ClO4)3·H2O, for example, only a single broad peak (~1350 G peak-to-peak width of the 1st derivative) was observed at any crystal orientation in the X-band measurement. On the contrary, we have observed clear hyperfine splitting and, therefore, an unique angle dependence of hyperfine couplings from a single crystal of the [Mn2(III,IV)O2(phen)4](PF6)3·CH3CN complex.
In the magnetically concentrated systems, the line width is the result of (A) magnetic dipole–dipole interaction and (B) the exchange interaction between the neighboring spins.51–58 The former factor causes line broadening, while the latter narrows the line width. For the [Mn2(III,IV)O2(phen)4](PF6)3·CH3CN complex, we have not observed any significant difference of the line width at both X- and Q-band measurements, as seen by the clear hyperfine and g anisotropy at both frequencies. We can therefore conclude that the hyperfine interaction and the g anisotropy are much larger than the effect of the intermolecular exchange coupling in our system.
The above fact implies that the significant difference of the line broadening among the [Mn2(III,IV)O2(phen)4](PF6)3·CH3CN, [Mn2(III,IV)O2(bipy)4](ClO4)3·H2O, and [Mn2(III,IV)O2(phen)4](ClO4)3·H2O crystals can be explained mainly by the dipole–dipole coupling caused by the differences of (1) the neighboring spin–spin distances, (2) the angle between the static magnetic field and the vector connecting the two interacting spins, and (3) the position and the kind of counterions and solvent molecules.
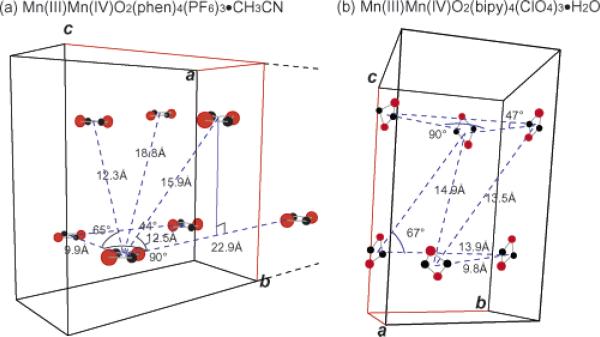
As far as the center-to-center distances of molecules are concerned, we have not observed a significant difference between [Mn2(III,IV)O2(phen)4](PF6)3·CH3CN and [Mn2(III,IV)O2(bipy)4](ClO4)3·H2O crystals (Figure 6). The former crystal has center-to-center distances of the neighboring molecules between 9.9 and 18.8 Å. The shortest Mn–Mn distance is 9.9 Å. For the latter crystal, which has the space group of P21/c, the center-to-center distances are between 9.8 and 14.5 Å. The shortest Mn–Mn distance is 9.7 Å.58
Figure 6.
Molecular arrangement in the unit cell of the crystals of (a) [Mn2(III,IV)O2(phen)4](PF6)3·CH3CN22 and (b) [Mn2(III,IV)O2(bpy)4](ClO4)3·H2O.42 The distances between the molecules in one unit cell and the relevant nearest molecules in neighboring unit cells are shown. The Mn atoms are in red and the O atoms in black.
However, the molecular orientations are significantly different in [Mn2(III,IV)O2(phen)4](PF6)3·CH3CN and [Mn2(III,IV)O2(bipy)4](ClO4)3·H2O crystals. By considering the center-to-center distances of molecules and with these orientations, we calculated the line broadening effect in the following manner. The dipole interaction from a neighboring identical dipole μ can be expressed as μ(1-3cos2θij)/rij3, where θij is the angle between the static magnetic field and the vector connecting the center of two interacting dipoles (i,j) and rij is the distance between dipoles. The approximate line broadening effect of the dipolar-dipolar interaction can be evaluated by the second moment
| (12) |
By considering the neighboring molecules closer than 15 Å, we have obtained ΔH2ave ≈ 23–28 G for [Mn2(III,IV)O2(phen)4](PF6)3·CH3CN and 25–43 G for [Mn2(III,IV)O2(bipy)4](ClO4)3·H2O crystals, depending on the crystal orientation. This is suggestive that the smaller dipolar-dipolar interaction in [Mn2(III,IV)O2(phen)4](PF6)3·CH3CN due to the simple molecular arrangement is one of the main reasons to prevent the severe line broadening, which would otherwise veil hyperfine splitting in a magnetically concentrated system. As mentioned before, however, the best fit of the single-crystal EPR spectra of [Mn2(III,IV)O2(phen)4](PF6)3·CH3CN was obtained with a Gaussian line width of 69 G for c, 45 G for a, and 57 G for the b direction at both X- and Q-band frequencies; the numbers are much larger than the calculated line width for both [Mn2(III,IV)O2(phen)4](PF6)3·CH3CN and [Mn2(III,IV)O2(bipy)4](ClO4)3·H2O.
Concerning the third point, the type of counterions and solvent molecules modifies the space group and the unit cell parameters, and therefore the molecular arrangements.59,60 The counterions and solvent molecules may also weakly coordinate with metal ions, modifying the exchange interaction. Felthouse et al. have discussed the effect of counterions for [Cu2(dien)2(C2O4)](X)2 (counterion X as BPh4, PF6, or ClO4)60 When the counterions are weakly coordinated, they mediate intermolecular exchange interaction between the neighboring spins, resulting in a coalescence of the hyperfine lines into a sharp single resonance. This is not applicable in our present case, because we have observed an EPR signal with a total width of 1350 G in both [Mn2(III,IV)O2(bipy)4](ClO4)3·H2O and [Mn2(III,IV)O2(phen)4](PF6)3·CH3CN systems, which have very different counterions. As for the solvent molecules, positions of CH3CN are not clear in the crystal unit cell of [Mn2(III,IV)O2(phen)4](PF6)3·CH3CN. Although we cannot go further into a detailed discussion in the present study, the differences of the counterions and solvent molecules between [Mn2(III,IV)O2(bipy)4](ClO4)3·H2O and [Mn2(III,IV)O2(phen)4](PF6)3·CH3CN may not be eliminated as a possible reason for the significant differences of EPR line width observed in these molecules.
In addition, a small inhomogeneity in the crystal, such as a crystal defect, might also contribute to the line broadening and the anisotropic line width, although we did not observe any significant differences in line broadening among the several crystals of [Mn2(III,IV)O2(phen)4](PF6)3·CH3CN that we have examined.
Conclusion
The analysis of orientation-dependent EPR spectra in a single crystal of [Mn2(III,IV)O2(phen)4](PF6)3·CH3CN yields precise data on the orientation of the g tensor in the molecule and on the anisotropy of the g and hyperfine tensors. The anisotropic EPR characteristics of the Mn(III)Mn(IV) system obtained here could be applicable to the precise analysis of the EPR spectra of Mn OEC in PSII, in which 18–20 multiline EPR signals are observed in the S2 state. It also shows the anisotropic characteristics in membrane samples.17,61 As observed in the present study, the mixed valence system of Mn(III) and Mn(IV) with oxo-bridged ligands has rhombic g and 55Mn hyperfine couplings, and the relationship of 2AIV = AIII is not a valid approximation. This could contribute a reason for the origin of more than 16 multiline signals in the OEC S states. However, the total width of the EPR multiline of OEC (~2000 G for S2 and ~2400 for S062) is much greater than that of the Mn(III)Mn(IV) di-μ-oxo system (~1350 G). This greater line width cannot be explained by the 2AIV ≠ AIII and g and hyperfine anisotropy. It requires other factors such as the presence of more than two manganese in the OEC.
Supplementary Material
Acknowledgment
This research was supported by a grant from the National Institutes of Health (GM55302) and by the Director, Office of Science, Office of Basic Energy Sciences, Division of Chemical Sciences, Geosciences, and Biosciences, of the U.S. Department of Energy (DOE), under Contract DEAC03-76SF00098. Synchrotron radiation facilities were provided by the Stanford Synchrotron Radiation Laboratory (SSRL), which is operated by the Department of Energy, Office of Basic Energy Sciences. The SSRL Biotechnology Program is supported by the National Institutes of Health, National Center of Research Resources, Biomedical Technology Program, and by the Department of Energy, Office of Health and Environmental Research.
Footnotes
Supporting Information Available: The k3-weighted polarized Mn EXAFS spectra (Figure 1S) and the Fourier Transforms of EXAFS (Figure 2S). This material is available free of charge via the Internet at http://pubs.acs.org.
References
- 1.Khangulov SV, Barynin VV, Antonyukbarynina SV. Biochim. Biophys. Acta. 1990;1020:25–33. [Google Scholar]
- 2.Khangulov SV, Barynin VV, Voevodskaya NV, Grebenko AI. Biochim. Biophys. Acta. 1990;1020:305–310. [Google Scholar]
- 3.Haddy A, Waldo GS, Sands RH, Penner-Hahn JE. Inorg. Chem. 1994;33:2677–2682. [Google Scholar]
- 4.Debus RJ. Biochim. Biophys. Acta. 1992;1102:269–352. doi: 10.1016/0005-2728(92)90133-m. [DOI] [PubMed] [Google Scholar]
- 5.Yachandra VK, Sauer K, Klein MP. Chem. ReV. 1996;96:2927–2950. doi: 10.1021/cr950052k. [DOI] [PubMed] [Google Scholar]
- 6.Dismukes GC, Siderer Y. Proc. Natl. Acad. Sci. U.S.A. 1981;78:274–278. doi: 10.1073/pnas.78.1.274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Britt RD. In: Oxygenic Photosynthesis: The Light Reactions. Ort DR, Yocum CF, editors. Kluwer Academic Publishers; Dordrecht: 1996. pp. 137–164. [Google Scholar]
- 8.Messinger J, Nugent JHA, Evans MC. W. Biochemistry. 1997;36:11 055–11 060. doi: 10.1021/bi9711285. [DOI] [PubMed] [Google Scholar]
- 9.Åhrling KA, Peterson S, Styring S. Biochemistry. 1997;36:13 148–13 152. doi: 10.1021/bi971815w. [DOI] [PubMed] [Google Scholar]
- 10.Messinger J, Robblee JH, Yu WO, Sauer K, Yachandra VK, Klein MP. J. Am. Chem. Soc. 1997;119:11 349–11 350. doi: 10.1021/ja972696a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Schäfer KO, Bittl R, Zweygart W, Lendzian F, Haselhorst G, Weyhermuller T, Wieghardt K, Lubitz W. J. Am. Chem. Soc. 1998;120:13 104–13 120. [Google Scholar]
- 12.Zheng M, Dismukes GC. Inorg. Chem. 1996;35:3307–3319. doi: 10.1021/ic9512340. [DOI] [PubMed] [Google Scholar]
- 13.Policar C, Knüpling M, Frapart YM, Un S. J. Phys. Chem. B. 1998;102:10 391–10 398. [Google Scholar]
- 14.Randall DW, Sturgeon BE, Ball JA, Lorigan GA, Chan MK, Klein MP, Armstrong WH, Britt RD. J. Am. Chem. Soc. 1995;117:11 780–11 789. [Google Scholar]
- 15.Randall DW, Chan MK, Armstrong WH, Britt RD. Mol. Phys. 1998;95:1283–1294. [Google Scholar]
- 16.Schäfer KO, Bittl R, Lendzian F, Barynin V, Weyhermuller T, Wieghardt K, Lubitz W. J. Phys. Chem. B. 2003;107:1242–1250. [Google Scholar]
- 17.Rutherford AW. Biochim. Biophys. Acta. 1985;807:189–201. [Google Scholar]
- 18.Peloquin JM, Campbell KA, Randall DW, Evanchik MA, Pecoraro VL, Armstrong WH, Britt RD. J. Am. Chem. Soc. 2000;122:10 926–10 942. [Google Scholar]
- 19.Peloquin JM, Britt RD. Biochim. Biophys. Acta. 2001;1503:96–111. doi: 10.1016/s0005-2728(00)00219-x. [DOI] [PubMed] [Google Scholar]
- 20.Cooper SR, Dismukes GC, Klein MP, Calvin M. J. Am. Chem. Soc. 1978;100:7248–7252. [Google Scholar]
- 21.Tan XL, Gultneh Y, Sarneski JE, Scholes CP. J. Am. Chem. Soc. 1991;113:7853–7858. [Google Scholar]
- 22.Stebler M, Ludi A, Bürgi H-B. Inorg. Chem. 1986;25:4743–4750. [Google Scholar]
- 23.Bencini A, Gatteschi D. EPR of Exchange Coupled Systems. Springer-Verlag; Berlin: 1990. [Google Scholar]
- 24.Blondin G, Girerd J-J. Chem. ReV. 1990;90:1359–1376. [Google Scholar]
- 25.Zheng M, Khangulov SV, Dismukes GC, Barynin VV. Inorg. Chem. 1994;33:382–387. [Google Scholar]
- 26.White LK, Belford RL. Chem. Phys. Lett. 1976;37:553–555. [Google Scholar]
- 27.White LK. Ph.D. Thesis. University of Illinois; Urbana-Champaign: 1975. [Google Scholar]
- 28.Robblee JH, Messinger J, Cinco RM, McFarlane KL, Fernandez C, Pizarro SA, Sauer K, Yachandra VK. J. Am. Chem. Soc. 2002;124:7459–7471. doi: 10.1021/ja011621a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Gamelin DR, Kirk ML, Stemmler TL, Pal S, Armstrong WH, Penner-Hahn JE, Solomon EI. J. Am. Chem. Soc. 1994;116:2392–2399. [Google Scholar]
- 30.Pilbrow JR, Winfield ME. Mol. Phys. 1973;25:1073–1092. [Google Scholar]
- 31.Abragam A, Pryce MHL. Proc. Royal Soc. London Ser. A- Math. Phys. Sci. 1951;205:135–153. [Google Scholar]
- 32.Blum H, Salerno JC, Leigh JS., Jr. J. Magn. Res. 1978;30:385–391. [Google Scholar]
- 33.Gerritsen HJ, Sabisky ES. Phys. Rev. 1963;132:1507–1512. [Google Scholar]
- 34.This effect is reflected by the longer Mn-ligand bond along the dz2 direction in the crystal structure data.
-
35.The g-values of the tetragonally distorted Mn(III) d4 system with a 5B1 ground state are described by the following equations,
where ge is the g value of the free ion (g = 2.0023), ΔE1 and ΔE2 the energy difference between the corresponding ground state and the excited state, and λ, the spin–orbit coupling constant for a single d electron. - 36.Barra A-L, Gatteschi D, Sessoli R, Abbati GL, Cornia A, Fabretti AC, Uytterhoeven MG. Angew. Chem. 1997;36:2329–2331. [Google Scholar]
- 37.Limburg J, Vrettos JS, Crabtree RH, Babcock GT, de Paula JC, Hassan A, Barra A-L, Duboc-Toia C, Collomb M-N. Inorg. Chem. 2001;40:1698–1703. doi: 10.1021/ic001118j. [DOI] [PubMed] [Google Scholar]
-
38.The g values of a Mn(IV) d3 system with a 4A2 ground state are described by the following equations,
where ΔE1′ and ΔE2′ are the energy differences between the corresponding ground state and the excited state (see ref 35 for other notations). - 39.Geschwind S, Kisliuk P, Klein MP, Pemeika JP, Wood DL. Phys. ReV. 1962;126:1684–1686. [Google Scholar]
- 40.From WH, Dorain PB, Kikuchi C. Phys. ReV. A. 1964;135:A710–714. [Google Scholar]
- 41.Plaksin PM, Stoufer RC, Mathew M, Palenik GJ. J. Am. Chem. Soc. 1972;94:2121–2122. [Google Scholar]
- 42.Jensen AF, Su ZW, Hansen NK, Larsen FK. Inorg. Chem. 1995;34:4244–4252. [Google Scholar]
- 43.Wilson C, Larsen FK, Figgis BN. Acta Crystallogr. Sect. C–Cryst. Struct. Commun. 1998;54:1797–1799. [Google Scholar]
- 44.Baffert C, Collomb M-N, Deronzier A, Pécaut J, Limburg J, Crabtree RH, Brudvig GW. Inorg. Chem. 2002;52:1404–1411. doi: 10.1021/ic0107375. [DOI] [PubMed] [Google Scholar]
- 45.Goodson PA, Glerup J, Hodgson DJ, Michelsen K, Pedersen E. Inorg. Chem. 1990;29:503–508. [Google Scholar]
- 46.Goodson PA, Oki AR, Glerup J, Hodgson DJ. J. Am. Chem. Soc. 1990;112:6248–6254. [Google Scholar]
- 47.In general, elongated Mn–ligandaxial distances are observed along the direction of Jahn–Teller distortion in Mn(III).33,44 In Mn(III)Mn(III) symmetric compounds, the Mn–Naxial distance is close to 2.4 Å, whereas Mn–Nequatorial ≈ 2.1 Å.45 In contrast, the Mn(IV) sites are structurally identical in the Mn(IV)Mn(IV) complex (Mn–N ≈ 2.1 Å).22,46 The structural distortion at the Mn(III) site in the Mn(III)Mn(IV) complexes is smaller (Mn(III)–Naxial ≈ 2.25 Å, Mn(III)–Nequatorial ≈ 2.1 Å) 22,41-44 compared with the Mn(III)Mn(III) complexes, suggesting that the unpaired electron is not completely localized in the dz2 orbital on the Mn(III) center in the mixed valence system.
-
48.For the hyperfine coupling constant of the Mn(III) site with 5B1 ground state, the following equations from Abragam and Pryce31 are applicable:
where β is the Bohr magneton; βn, the nuclear magneton; γ, the nuclear gyromagnetic factor; r, the effective radius of the d shell; and κ, the core polarization parameter. A∥ is comparable to Az, while A⊥ to Ax,y. - 49.Zhao XG, Richardson WH, Chen JL, Li J, Noodleman L, Tsai HL, Hendrickson DN. Inorg. Chem. 1997;36:1198–1217. doi: 10.1021/ic9514307. [DOI] [PubMed] [Google Scholar]
- 50.McGrady JE, Stranger R. J. Am. Chem. Soc. 1997;119:8512–8522. [Google Scholar]
- 51.Kubo R, Tomita K. J. Phys. Soc. Jpn. 1954;9:888–919. [Google Scholar]
- 52.Van Vleck JH. Phys. ReV. 1948;74:1168–1183. [Google Scholar]
- 53.Bleaney B, Penrose RP, Plumpton BI. Proc. Royal Soc. London Ser. A- Math. Phys. Sci. 1949;198:406–428. doi: 10.1098/rspa.1947.0046. [DOI] [PubMed] [Google Scholar]
- 54.McGregor KT, Soos ZG. J. Chem. Phys. 1976;64:2506–2517. [Google Scholar]
- 55.Hennessy MJ, McElwee CD, Richards PM. Phys. ReV. B. 1973;7:930–947. [Google Scholar]
- 56.Hughes RC, Morosin B, Richards PM, Duffy W. Phys. ReV. B. 1975;11:1795–1803. [Google Scholar]
- 57.Velayutham M, Varghese B, Subramanian S. Inorg. Chem. 1998;37:5983–5991. doi: 10.1021/ic980071n. [DOI] [PubMed] [Google Scholar]
- 58.Gatteschi D, Guillou O, Zanchini C, Sessoli R, Kahn O, Verdaguer M, Pei Y. Inorg. Chem. 1989;28:287–290. [Google Scholar]
- 59.Gloux J, Gloux P, Laugier J. J. Am. Chem. Soc. 1996;118:11 644–11 653. [Google Scholar]
- 60.Felthouse TR, Laskowski EJ, Hendrickson DN. Inorg. Chem. 1977;16:1077–1089. [Google Scholar]
- 61.Kim DH, Britt RD, Klein MP, Sauer K. Biochemistry. 1992;31:541–547. doi: 10.1021/bi00117a034. [DOI] [PubMed] [Google Scholar]
- 62.Messinger J, Robblee J, Yu WO, Sauer K, Yachandra VK, Klein MP. J. Am. Chem. Soc. 1997;119:11 349–11 350. doi: 10.1021/ja972696a. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.