Quantification of continuous in vivo flexion–extension kinematics and intervertebral strains

Abstract

Purpose

Healthy subjects performed lumbar flexion and were assessed by video fluoroscopy to measure the in vivo kinematics of the lower lumbar motion segments.

Methods

Fifteen healthy subjects (8 male, 7 female, 28 ± 10 years) performed lumbar flexion and extension back to neutral while their vertebrae were imaged. The sagittal plane vertebral margins of L3–S1 were identified. Lumbar angle, segmental margin strains, axial displacements, anterior–posterior (A–P) translations, and segmental rotations over the course of flexion were measured.

Results

L4–L5 had the largest posterior margin Green strain (65 %). Each segment displayed more axial displacement than A–P translation. Peak vertebral angulation occurred at approximately 75 % of peak flexion during the extension phase.

Conclusion

L4–L5 exhibited the largest anterior and posterior margin strains (29 and 65 %, respectively). Strains in the disc during in vivo lumbar flexion are due to both angular rotation and linear translation.

Introduction

Intervertebral disc degeneration occurs with injury, natural aging, and a combination of the two. Currently, there are numerous treatments for painful disc degeneration, ranging from physical therapy to disc arthroplasty [1, 2]. These treatments are only partially effective, due in part to an incomplete mechanical understanding of the natural deformation of intervertebral disc during physiologic movement.

Much work has been done in vitro to characterize the disc mechanically, both whole sample and isolated annulus fibrosus/nucleus pulposus [3–5]. The annulus has been tested at strains ranging from 2.5 to 50 % in uniaxial tension [4, 6–11] and from 1.25 to 15 % in equibiaxial extension [12, 13]. The wide range of strains utilized in these experiments makes the results difficult to interpret within a functional context. Furthermore, incorporating physiologic strains into tissue testing would ensure the clinical relevance of materials testing of the intervertebral disc.

Ideally, physiologic strains would be determined from in vivo three-dimensional kinematics of intervertebral discs during activities of daily living, such as spinal flexion. MRI is capable of visualizing soft tissue but does not allow for real-time scans during subject movement. Fluoroscopy can image in real time but cannot detect soft tissue and is constrained by patient radiation exposure limits. Due to these imaging limitations, physiologic disc annulus fibrosus strains have not been reported in the lumbar spine literature. Many studies have focused on planar vertebral motion, using adjacent vertebrae as approximations of intervertebral disc margins.

Kinematics of the lumbar spine vertebrae has been well studied in flexion (Tables 1, 2). Cadaveric and in vivo experiments typically report segmental rotation [14–22], with a few also reporting intervertebral strains [23–25]. Takayanagi et al. [21] took fluoroscopic video of healthy males performing flexion. They reported intervertebral margin anterior–posterior translation and segmental angular rotation but not segmental intervertebral margin strains or segmental axial displacement, leaving an incomplete assessment of segmental intervertebral strains. Another study took radiographs of healthy subjects at neutral and full flexion to calculate disc margin strains [25]. With only the endpoints of motion examined, the complex motion of the intervertebral disc throughout flexion was neglected. To date, the full pathway of lumbar kinematics and intervertebral deformation throughout a flexion motion has not been reported. Therefore, the objective of this study was to characterize the in vivo kinematic response of lower lumbar motion segments and intervertebral margin strains throughout a flexion cycle.

Table 1.

Intervertebral kinematic literature (in vitro testing conditions)

Method	Data type	Motion segment(s)	Motion type	Data reported	References
Digital strain indicators	C	L1–L5	Flexion (eccentric compression)	Load–deflection curves	[29]
Stereophotogrammetry	C	T12–L5	Flexion/extension (6.5°, eccentric compression)	Surface fiber strains	[23]
Magnetic resonance imaging	E	L3–L5	Flexion (5°, eccentric compression)	Axial, radial, and shear strains	[24]

C continuous data collection, E data collected at motion endpoints

Table 2.

Intervertebral kinematic literature (in vivo testing conditions)

Method	Data type	Motion segment(s)	Motion type	Data reported	References
External three-dimensional position sensors	C	L1–S1	Standing flexion	Proportion of inter sensor angle	[14]
Lateral radiographs	E	L1–S1	Standing full flexion/full extension	Anterior and posterior disc height changes	[25]
	E	L1–S1	Sitting full flexion/full extension	Segmental angle and anterior–posterior translation	[15]
Neutral lateral radiograph, displacement transducers, and a potentiometric goniometer	C	L3–L4	Prone flexion (60°)/extension (50°)	Segmental angle, anterior–posterior translation, and axial displacement	[16]a
	C	L2–L5	Standing full flexion/full extension	Same as [16]	[17]
Biplanar fluoroscopy	C	L1–S1	Standing full flexion/full extension	Same as [16]	[18]
Single-plane fluoroscopy	C	L3–S1	Standing full flexion/full extension	Same as [15]	[19]
	C	L2–L5	Standing flexion	Segmental angle	[20]
	C	L2–S1	Sitting flexion	Same as [15]	[21]
	C	L3–S1	Standing flexion	Segmental angle	[22]
	C	L3–S1	Standing full flexion (29°)	Proportion of segmental angle and margin anterior–posterior translation and axial Green strains	Present study

C continuous data collection, E data collected at motion endpoints

^aDomestic pigs used

Materials and methods

Fifteen healthy volunteers were recruited to perform flexion, which was captured by fluoroscopic video. Subjects were excluded for musculoskeletal disease, abdominal or pelvic surgery, low back pain in the previous three years, or an Oswestry Disability Index above 5 %. Sex, age, and body mass index (BMI) of subjects are shown in Table 3.

Table 3.

Subject demographics

Subject #	Age	Sex	BMI
1	32	M	22
2	38	M	24
3	18	F	25
4	22	M	26
5	21	M	25
6	29	F	26
7	26	F	22
8	48	F	27
9	46	M	27
10	23	F	26
11	21	M	23
12	19	M	26
13	36	F	30
14	18	F	29
15	19	M	28

Subjects, having been placed in a device to fix the pelvis, were instructed to practice bending forward as far as possible and returning to neutral at least three times. Then, the subjects were imaged performing flexion and extension. Sagittal images of the lumbar spine (L3–S1) were recorded continuously during flexion and extension at 30 Hz using digital fluoroscopic video (12-in. image intensifier, OEC 9800 GE, Fairfield, CT).

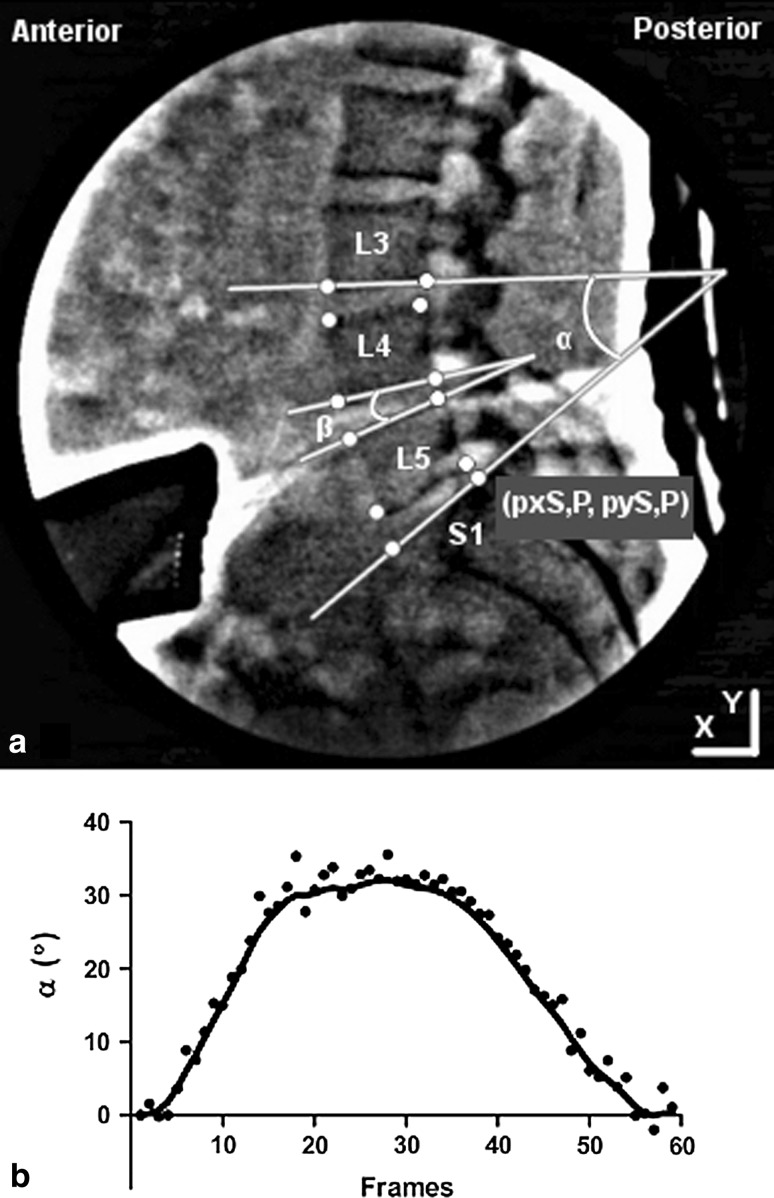
The fluoroscopic videos were randomized, and all data were analyzed by a single investigator. Six data sets were removed due to indistinct anatomy. Video frames were analyzed at 10 Hz using Image J (NIH, Bethesda, MD) to take the point-wise measurements shown on the vertebral margins in Fig. 1a. The data were then analyzed using Matlab (Mathworks, Natick, MA) following the methods of Takayanagi et al. [21]. Briefly, point-wise measurements were used to create local coordinate systems with the origin at the point (px_S,P, py_I,P) for each motion segment (L3–L4, L4–L5, and L5–S1). The origin represents the most superior (S) and posterior (P) point on the inferior vertebra of the motion segment. This local coordinate system was then used to calculate the lower lumbar angle, anterior and posterior margin strain, axial displacement, anterior–posterior (A–P) translation, and intervertebral angle as described in Table 4. A low-pass Butterworth filter with a cutoff frequency of 2 Hz was applied to the calculated data, as shown in Fig. 1b.

Fig. 1.

a Representative fluoroscopic frame with labeled anatomy. Vertebral margin points labeled with circles (representative origin at the superior, posterior point of S1), and computed angles are shown. b Representative profile of the lower lumbar angle as a function of position, raw points and filtered data

Table 4.

Description of vertebral calculations

Name	Description	Calculation
Anterior margin, D A	Anterior margin vector	(pxS,A − pxI,A, pyS,A − pyI,A)
Posterior margin, D P	Posterior margin vector	(pxS,P − pxI,P, pyS,P − pyI,P)
Superior x axis, x S	Superior x axis vector with origin at (pxS,P, pyS,P)	(pxS,P − pxS,A, pyS,P − pyS,A)
Superior y axis, y S	Superior y axis vector with origin at (pxS,P, pyS,P)	[0,0,1] × x S
Inferior x axis, x I	Inferior x axis vector with origin at (pxS,P, pyS,P)	(pxI,P − pxI,A, pyI,P − pyI,A)
Superior distance, D S	Magnitude of superior x axis vector	∥x S∥
Lower lumbar angle, α	Calculated as the angle between the inferior L3 and superior S1 vertebral margin points	cos−1(x S,S1·x I,L3)
Disc margin angle, β	Calculated as the angle between the inferior and superior vertebral margin points of the given motion segment	cos−1(x S·x I)
Margin height, d u	Calculated as the distance between the inferior and superior vertebral points of the given margin (anterior or posterior) of a motion segment	(pxS − pxI, pyS − pyI)
Margin strain	Calculated as the Green strain using the neutral margin height as the original length and the minimum anterior margin height as the deformed length	0.5 × ((d 2u,current − d 2u,neutral)/d 2u,neutral)
Axial displacement	Calculated as the distance moved perpendicular to the superior margin of the inferior vertebra relative to the average disc margin height	d u·y S
Anterior–posterior (A–P) displacement	Calculated as the distance moved parallel to the superior margin of the inferior vertebra relative to the average disc margin height	d u·x S

Directionality was defined as inferior (I), superior (S), anterior (A), and posterior (P) relative to each vertebra (L3–S1)

In this work, Green strain was used rather than linearized strain, often used for bone and other small-deformation systems. The Green strain is commonly used in soft-tissue biomechanics (see, e.g., [12, 26, 27].) to quantify deformation due to its independence from rigid body rotation. The linear strain (i.e., (l − L)/L, where l is the final and L is the initial length) has non-zero rigid body rotation; if the rigid body rotations are small, linear strain remains similar to the Green strain. However, if rigid body rotations are not small, the linear strain becomes an inaccurate measure, and the Green strain must be used.

The Green strain is given by

1

In the limit of small deformations and rotations, the Green strain becomes identical to the linear strain.

Statistical analysis was performed using two-tailed independent sample t tests which assumed equal variances. Observer error was estimated by calculating the standard deviation between intervertebral angles calculated by four observers using one segment from one subject in a single frame.

Results

The peak flexion range-of-motion across L3–S1 was 29 ± 2.9°, and the peak local segmental angular displacements were 6.1 ± 1.5° (L3–L4), 9.0 ± 2.1° (L4–L5), and 7.3 ± 1.1° (L5–S1) (mean ± 95 % CI). Peak local segmental angular displacements are reported as segmental angles, which peak prior to peak flexion range-of-motion across L3–S1 as shown in [19].

In flexion, posterior intervertebral strains were tensile (+) in nature and those on the anterior margin were compressive (−). L4–L5 had the largest anterior and posterior intervertebral margin strains, −29 and 65 %, respectively, which were significantly larger than the posterior margin strain at L5–S1, 29 % (p < 0.001, Fig. 2). The smallest anterior and posterior intervertebral margin strains occurred at L5–S1, −24 and 29 %, respectively. It is emphasized that these results are margin strains, that is, changes in the bone-to-bone distance along the anterior or posterior margin, and not actual intervertebral disc strains; the intervertebral margin strains may be interpreted as an upper bound on the intervertebral disc strains.

Fig. 2.

Peak Green strains on the anterior and posterior margins (mean ± 95 % CI, *p < 0.05, **p < 0.001)

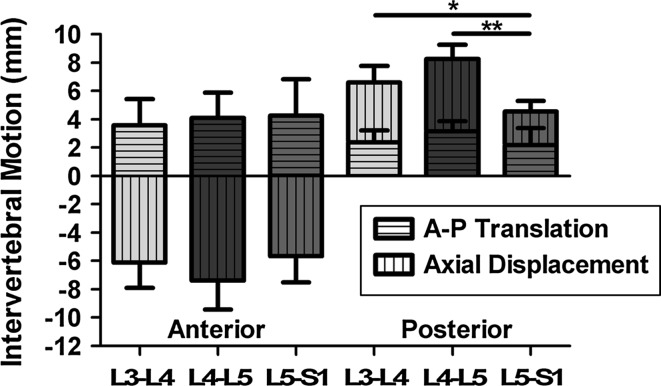
As expected, at the superior vertebra of each motion segment, flexion involved anterior and inferior displacement of the anterior margin and anterior and superior displacement of the posterior margin. Decomposing the intervertebral margin displacement into A–P translation and axial displacement showed that displacements varied by level (Fig. 3). The L4–L5 anterior intervertebral margin produced the greatest axial displacement (compression). At the posterior margin, L4–L5 produced the most axial displacement (tension), which was significantly larger than L5–S1 level (p < 0.001). Furthermore, the L3–L4 spinal level produced posterior margin axial displacements that were significantly larger than L5–S1 (p = 0.008). Posterior margin A–P translation accounted for about a third of the decomposed motion at L3–L4 and L4–L5.

Fig. 3.

Intervertebral margin motion decoupled into anterior–posterior translation and axial displacement (mean ± 95 % CI, *p < 0.05, **p < 0.001)

The posterior margin Green strains were averaged across the nine subjects and fitted with fourth-order polynomials, as shown in Fig. 4. Across the flexion phase, L3–L4 and L5–S1 displayed similar strains, but L4–L5 produced larger strains, culminating in strains four times larger than the other two segments measured.

Fig. 4.

Average posterior margin Green strains in flexion and extension phases 95 % CI shown as filled regions (L3–L4 speckled, L4–L5 left slant [\], L5–S1 right slant [/]). Data were fit with fourth-order polynomials

Intervertebral angle contributions to the summed L3–S1 segment angular displacement were averaged across the nine subjects and filtered with a low-pass Butterworth filter with a cutoff frequency of 250 Hz (Fig. 5). In the early flexion phase, L3–L4 contributes the largest amount, followed by L4–L5. As the flexion phase progresses, the contribution from L4–L5 and L5–S1 increases. At full flexion, L4–L5 contributes the largest amount to the total amount of angular displacement, 37 %. At the start of the extension phase, L5–S1 continues to increase in contribution. At 30 % extension, L5–S1 begins to contribute less and L3–L4 more. These spinal levels also exhibited a different peak contribution time throughout the flexion–extension sequence where the median peak contribution of each segmental angle to the sum of the segmental angles is: L3–L4, 89 % α, L4–L5, 98 % α, L5–S1, 100 % α. This pattern has been seen in previous flexion literature [19]. However, the data herein illustrate angle contributions which are not symmetric about the full flexion point (100 % α). Extracting data at ±70 % α showed significant differences in the L3–L4 A–P translation (p = 0.032) and L4–L5 posterior margin strain (p = 0.021), axial displacement (p = 0.022), and A–P translation (p = 0.038).

Fig. 5.

Intervertebral angle contribution during flexion and extension (filtered using a low-pass Butterworth filter with a cutoff frequency of 250 Hz). Dotted line represents full flexion; area to the left of the dotted line is neutral to full flexion and to the right is flexion to upright neutral

Interobserver error was estimated by calculating the standard deviation of the measured segmental angle in one frame by four observers. This standard deviation was small, 2.81° with respect to the magnitude of the angular displacement measured (9.77°).

Discussion

This work identified the time history of Green strains across lumbar vertebrae throughout a flexion–extension cycle to upright standing. These strain profiles demonstrate the relative strains which presumptively affect the intervertebral disc tissues during a physiologic motion. These data also illustrate the natural human variability between spinal levels and between healthy subjects. To contextualize the results herein, other research efforts aimed at uncovering the intervertebral strains will be examined and compared.

Pearcy and Tibrewal [25] reported percentage changes in disc height on the anterior and posterior margins at the full flexion endpoint. Calculating the Green strains from their published data shows that the data of the present study are similar. On the posterior margin, L4–L5 had 69 % Green strain (present study 65 %), and L5–S1 had 39 % Green strain (present study 29 %), with the exception of the L3–L4 which was lower, 51 and 71 %, respectively. Differences could be the product of Pearcy and Tibrewal’s use of an all-male population and/or differences in the magnitude of lower lumbar angle, which was not reported in Pearcy and Tibrewal.

More recently, Takayanagi et al. [21] reported segmental angular displacement and segmental anterior–posterior translation in flexion–extension. The present study found these outcomes to be similar among levels as opposed to being larger at L3–L4 and L4–L5. Both measurements were similar in L3–L4, 6.5° and 3.2 mm (present study 6.1° and 3.0 mm), and larger in L4–L5, 4.8° and 2.3 mm (present study 9.0° and 3.6 mm), and L5–S1, 2.5° and 0.5 mm (present study 7.3° and 3.2 mm). The present study produced larger magnitudes possibly because of to subjects starting in a standing rather than in a sitting position.

Additional studies have reported segmental angular displacement. Teyhen et al. [22] reported segmental angular displacements as a percentage of maximum segmental angular displacement at 35 % of total flexion. The present study found similar trends but larger magnitudes. Okawa et al. [20] reported segmental angular displacement as the angle from the inferior surface of the vertebrae from the horizontal. Reporting the present study data with this method finds similar trends but again larger magnitudes. These studies [20, 22] do not report flexion range-of-motion, so it is possible that in the present study flexion range-of-motion was higher.

The present study found intervertebral margin motion was mainly composed of axial displacement, but a significant amount of motion was produced by anterior–posterior translation. This result agrees with the previous literature [17], which found 4 mm of anterior–posterior translation on average when considering L2–L5. The present study found 3.27 mm of anterior–posterior translation on average considering L3–S1. This result also agrees with [18], which found 2 mm (L3–L4), 2 mm (L4–L5), and 1 mm (L5–S1) of anterior–posterior translation at the centroid and with [15], which found 2.5 mm (L3–L4), 3.0 mm (L4–L5), and 1.3 mm (L5–S1) of anterior–posterior translation at the centroid averaged for flexion and extension. The present study found 2.98 mm (L3–L4), 3.63 mm (L4–L5), 3.21 mm (L5–S1). The present study found higher magnitudes than in [15], as a result of measuring subjects in standing rather than sitting flexion, and in [18] which does not report flexion range-of-motion, so again, it is possible that in the present study flexion range-of-motion was higher.

Furthermore, the sum of the decomposed motion, axial displacement and anterior–posterior translation, was larger on the anterior margin than the posterior margin. This result is likely due to the posterior elements that resist flexion: supraspinous and infraspinous ligaments, the facet capsular ligaments, and the ligamentum flavum. There is no resistance on the anterior margin to flexion.

The average posterior margin Green strains had the largest magnitude at L4–L5 in the flexion phase. L3–L4 and L5–S1 had similar margin Green strains throughout the flexion phase. The pattern follows published magnitudes of segmental rotation in flexion, where L4–L5 is the largest, 15.3° ± 1.6°, then L5–S1, 12.5° ± 1.9°, then L3–L4, 9.8° ± 3.5° [19].

The intervertebral angle contributions to the summed L3–S1 segment angular displacement followed the same patterns during spinal flexion but displayed hysteresis over the course of the returning extension movement. In flexion, L3–L4 made the dominant contribution, then L4–L5, and then L5–S1. This result agrees with the previous literature [14]. A–P translation, posterior margin strain, and axial displacement compared between the flexion and extension phases suggest that the kinematic response of the flexion phase is different from the extension phase. Differences between the flexion and extension phases have been previously reported in in vitro studies through the neutral zone parameter [e.g., 24]. The intervertebral angles displayed a non-symmetric response between flexion and extension, which is also visible in other measurements at L3–L4 and L4–L5. Interestingly though, the average posterior margin Green strains were symmetric about the full flexion point revealing a decoupling of margin strains and angular displacements.

Typical human subject and sample size limitations must be considered when digesting the results of this study. Only 2D sagittal plane fluoroscopic images were captured, which likely led to errors based upon the 3D nature of spinal motion. Furthermore, intervertebral disc margins were not visible on the fluoroscopic images. As a result, at the neutral position, pre-strain on the anterior margin and slack on the posterior margin could not be assessed. Our results must therefore be viewed as relative to neutral position rather than relative to the unloaded state of the tissue (see further discussion of this issue in [28]).

The challenge of placing margin points on the same segment across the course of the flexion movement created some within-subject errors. The pelvis of each subject was fixed, but it is possible that the data included some out-of-plane motion. As each subject performed flexion, anatomical features of the vertebral margins moved in and out of view, which at times created difficulty in choosing the same margin point. Although all subjects reported to be in good health, it is possible that varying levels of disc health were represented in the sample.

Conclusion

The L4–L5 spinal unit exhibited the largest amount of anterior and posterior margin strain. The presumptive strains in the intervertebral disc during in vivo lumbar flexion are due to segmental angular rotation and linear translations, which together represent physiologic intervertebral disc loading. Peak intervertebral angular displacement occurred at approximately 75 % of the total segment (L3–S1) motion, during the extension phase. As the Green strains across the intervertebral margins are symmetric about the flexion–extension activity and the angles are not, these two measures appear physiologically decoupled. As a result clinically, X-rays at the end points of the flexion–extension motion do not capture the complexity of intervertebral motion. From an engineering perspective, these strain data give an approximation of the physiologic strains which could be used to assess intervertebral disc health and evaluate potential replacements or other therapies. In addition, non-symmetric loading should be considered in segment testing.