Instrumental Variable Analyses. Exploiting Natural Randomness to Understand Causal Mechanisms

Abstract

Instrumental variable analysis is a technique commonly used in the social sciences to provide evidence that a treatment causes an outcome, as contrasted with evidence that a treatment is merely associated with differences in an outcome. To extract such strong evidence from observational data, instrumental variable analysis exploits situations where some degree of randomness affects how patients are selected for a treatment. An instrumental variable is a characteristic of the world that leads some people to be more likely to get the specific treatment we want to study but does not otherwise change those patients’ outcomes. This seminar explains, in nonmathematical language, the logic behind instrumental variable analyses, including several examples. It also provides three key questions that readers of instrumental variable analyses should ask to evaluate the quality of the evidence. (1) Does the instrumental variable lead to meaningful differences in the treatment being tested? (2) Other than through the specific treatment being tested, is there any other way the instrumental variable could influence the outcome? (3) Does anything cause patients to both receive the instrumental variable and receive the outcome?

To understand the mechanisms of our world, we want to understand causation (i.e., how a change in one thing causes a change in another). Over the last decades, the randomized controlled experiment has been refined as a preeminent tool for producing strong proof of causation. However, for a vast number of situations, randomized controlled experiments are not feasible. Here we are faced with two choices: the nihilistic answer that no scientific understanding is possible (implying that perhaps every story is equally good as a “fact”) or an optimistic answer that, by careful observations, progress toward understanding can be made. The optimistic answer is supported by advances in design and analysis that dramatically expand options for testing causation.

Outside of the randomized controlled trial (RCT), instrumental variables are one of the best-established techniques for showing that a treatment causes an outcome. Intuitively, an instrumental variable analysis exploits a little bit of natural randomness in otherwise nonrandomized studies to create a situation that can be examined as if it were an RCT. In this article, we explain the logic behind instrumental variable analyses (Figure 1). We provide several examples of how instrumental variable analyses have given meaningful insight into clinically relevant problems and provide some basic questions that a skeptical reader should consider when evaluating an instrumental variable analysis. However, to understand instrumental variables, we need to begin with RCTs.

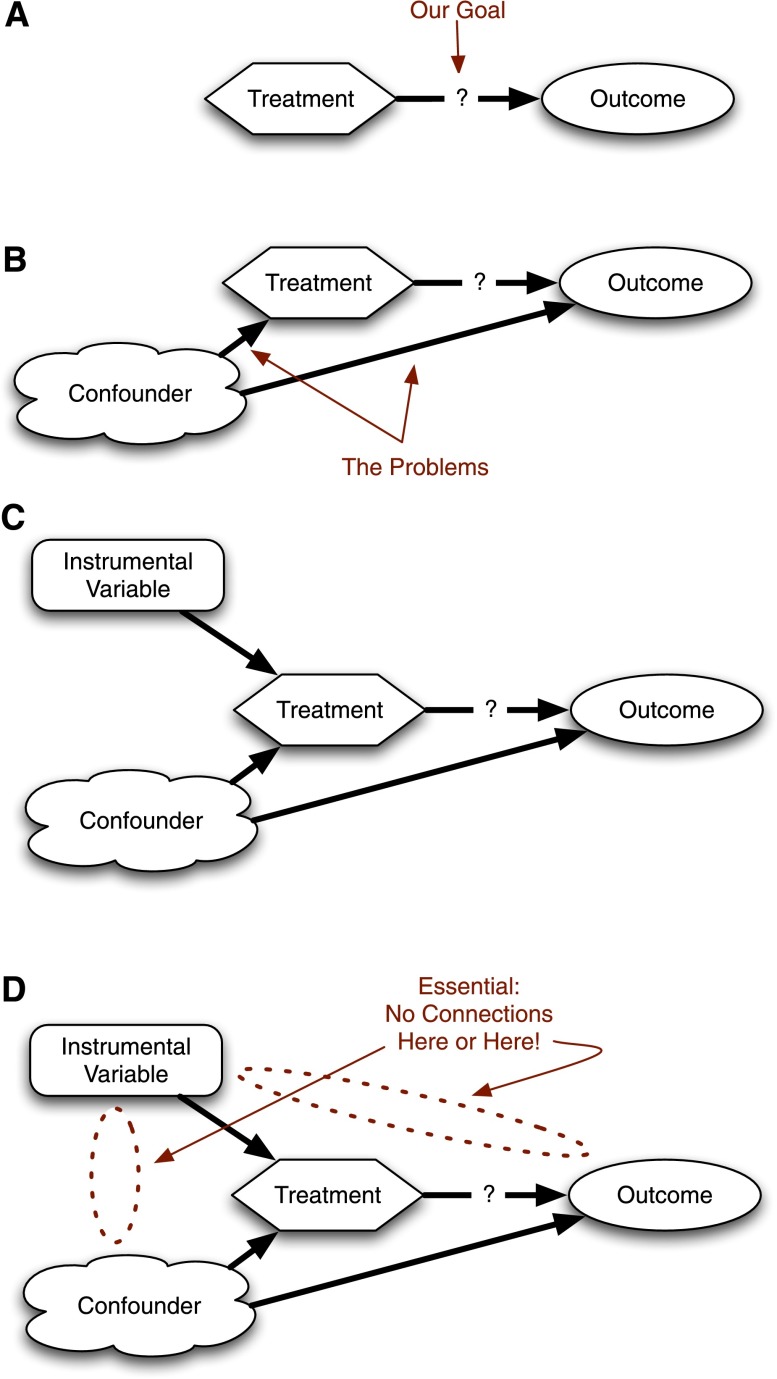
Figure 1.

Causal diagram for instrumental variables. (A) General framework. We need to study whether a treatment causes differences in outcomes. (B) A confounder affects treatment and outcome, so we cannot do a simple comparison between treated and untreated patients. (C) An instrumental variable can provide a solution. (D) The instrumental variable only works if the only connection between the instrumental variable and the outcomes is through the treatment.

Why RCTs Are Easy to Understand

In the simplest RCT, patients are randomly assigned to a treatment or a control. They get the treatment, and then an outcome is measured at some specified time (e.g., survival at 28 d). If all is done well, we can confidently conclude that the difference in the number of people alive at 28 days between the treated and the controlled patients is the result of whether or not they got the treatment.

This is not the same thing as saying that the outcomes are always caused by the treatment. Some people in the control group have the outcome anyway; in critical care trials, some people survive regardless of which group they are in, and some people in the treatment group die anyway. Our standard of success is not complete eradication of the bad outcome; rather, success is determined by sufficient improvement.

Randomization ensures that, on average, there are the same number of frail people and hardy people in the treated and control groups. There are the same number of people for whom your treatment might work in each group and the same number for whom the treatment would be ineffective. Because the investigator randomly and blindly assigns the treatment, there is no way for patients who might do better anyway to be more likely to get treatment.

Randomization ensures that the “confounders” (i.e., things that might lead a patient to successfully get the treatment he or she wants or that might affect whether the patient dies or not) are “balanced” between the two groups. This is what makes RCTs relatively easy to understand. If nobody goofed or cheated, any differences in the groups' outcomes are because of the treatment (Figure 2; missing arrows imply zero effect). A clinician’s review can focus on checking for those sorts of methodological standards, which have been relatively well protocolized, and then proceed to argue about whether or not the outcomes mattered or the control arm was the clinically useful comparison.

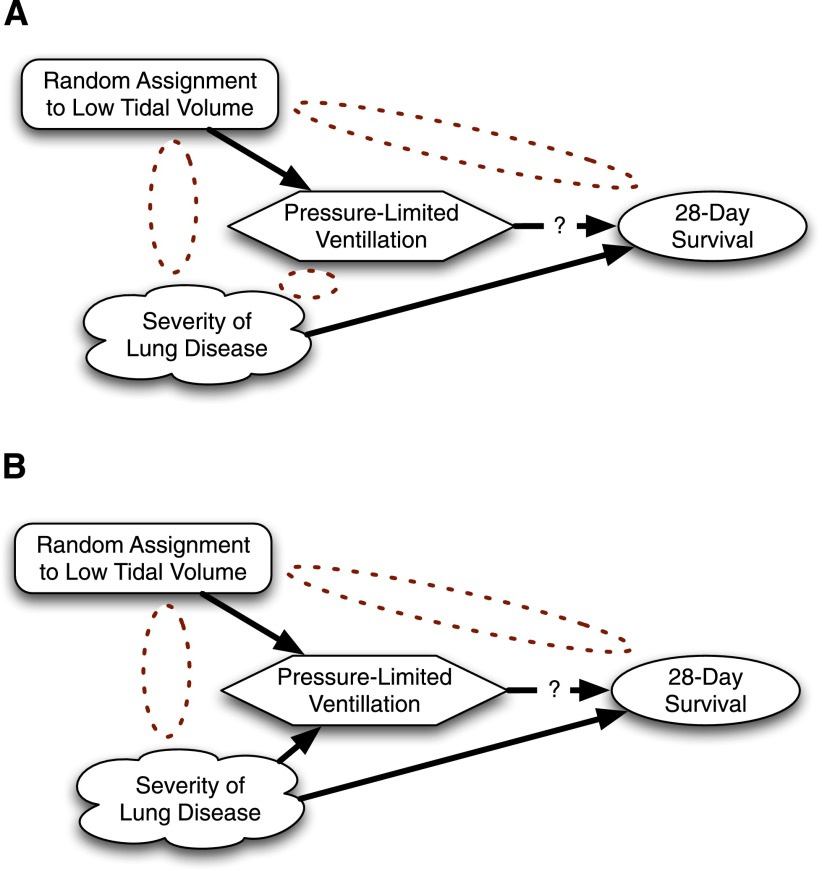
Figure 2.

A first example relating instrumental variables to randomized control trials (RCTs). (A) RCT with perfect compliance. Note the absence of an arrow between the confounder and the treatment. (B) RCT with imperfect compliance. If harder to ventilate patients with worse lung disease are more likely to be protocol deviations, then confounding re-enters.

In contrast, without randomization, one is stuck having to think hard about the process by which patients get the treatment. If we perfectly understand the process or if we know all the different factors that can lead to the outcome, then we can use regression techniques to control for patient differences. In perfect circumstances, we can get the same answer that a RCT would provide. If we fully understand and can measure the process (this is a rare if not impossible circumstance), RCTs are not necessarily better than observational studies. Where RCTs offer the advantage is when we have unknowns because we could not or did not measure something that we know matters or where several centuries of experience have taught us the humility to accept that we do not know everything that matters. With unknowns, standard techniques might get the right answer, but our confidence in that answer is less (i.e., we cannot prove that it is the right answer).

Introducing Instrumental Variables

Often we need to understand the mechanisms of things but have not been able to randomize. In such situations, we have a treated group and a control group, but something other than pure chance selects which patients get the treatment. In other words, we have confounding (i.e., the treated and untreated patients are different in ways that matter for measuring the effect of the treatment).

Getting around such selection is one of the great arts of epidemiology and health services research. One of the most elegant approaches is using a so-called “instrumental variable.” An instrumental variable is a factor that we know influences whether or not a patient gets selected to receive the treatment. However, we also have to believe that this factor does not influence the outcome, except by determining whether or not the treatment gets selected.

To make this more concrete, let us step outside of medicine for the first of several examples. Suppose we wanted to understand the influence of having an extra child on people’s productivity at work. Clearly, people who have two children may be quite different from people who have three children, on average; one might speculate that people who have two children may be more career focused, for example. Being career focused is hard to measure but could lead one to be more productive and to have fewer children (Figure 3). Therefore, a simple analysis would be at risk for confounding. An RCT is impossible because most people are unwilling to leave such family decisions to chance, and those willing to participate in such a hypothetical trial would clearly be different from most other parents.

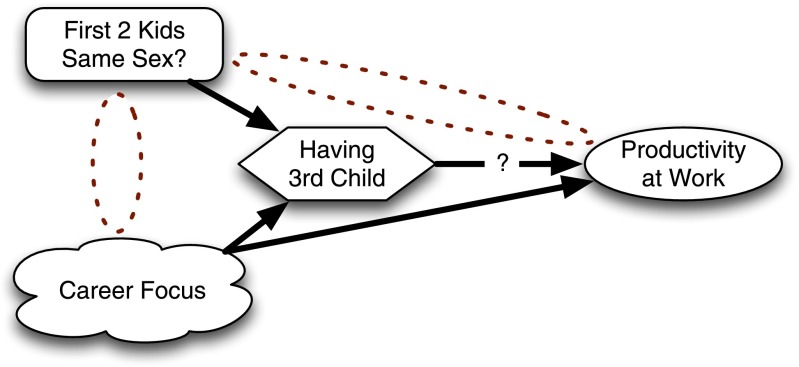
Figure 3.

Using an instrumental variable to examine whether having a third child influences parents’ productivity at work.

Americans like to have children of both genders but have little control of which gender their children turn out to be. This preference for diverse children is manifested in that if a couple’s first two children are of the same gender, the couple is much more likely to have a third child than if the children are of different genders. Equally important for the analysis, it is hard to believe gender concordance of the first two children is going to influence work productivity in any way other than by influencing whether or not the couple has a third child. Some analysts noticed this and realized that the gender concordance of a couple’s first two children could be used as an instrumental variable (1).

The analysis is done like this. Conceptually, you start by looking at the association between gender concordance among the first two children and subsequent productivity. This extracts the unconfounded portion of the treatment and looks at its effect on the outcome. After extracting the unconfounded portion, we rescale that to get the right magnitude because the instrumental variable does not perfectly predict the treatment, and we want our answer to be in units relevant to the treatment, not in units relevant to the instrumental variable.

In practice, this is often done in two steps, as in a procedure called two-stage least squares regression. In a first step, the gender concordance of a couple’s first two children is used to predict whether or not each couple would have a third child. Then, in the second stage, we analyze the association between work productivity and the prediction of having a third child based on gender concordance. We do not look at the association with productivity of having a third child; that would be too confounded. Instead, we examine the association between productivity and whether or not you are more likely to have a third child based on the sex of your first two children. By looking at the associations of the instrumental variable with the treatment and outcome, we can measure the effect of the treatment on the outcome without it being confounded.

This scenario should look a little familiar to anyone used to intention-to-treat analyses of RCTs. When we run a RCT, we know that analyzing the drug that was taken can cause significant selection bias, often giving us the wrong answer (e.g., when only the relatively hardy patients can tolerate the chemotherapy). Instead we analyze the trial not by which drug the patients took but by which drug they were assigned. Because there was randomization, the only way the assignment could influence outcomes is by changing which drug patients get (Figure 2). Because assignment has some effect on the treatment received, it follows that assignment should be an instrument. The intention-to-treat effect (i.e., the effect of the assignment on the outcome) is only one piece of the quantity estimated using instrumental variables; an instrumental variable analysis takes the intention-to-treat effect and divides by the instrument's effect on the treatment to get a potentially more clinically relevant measurement of how much benefit a treatment provides (2).

Instrumental Variables in Medicine

One of the best-accepted instrumental variables in medicine takes advantage of the relative lack of planning in the United States health care system. Authors argue that there are lots of reasons people choose to live wherever they live, but it is rarely because of the specific capabilities of nearby hospitals. Therefore, one of the present authors has argued, people who end up needing a procedure (e.g., non–postoperative mechanical ventilation) and happen to live near a hospital that performs a high volume of that procedure are more likely to get that procedure at a high-volume hospital (3). The instrumental variable is whether or not the nearest hospital is a high-volume provider, and the treatment is whether or not one got the procedure at a high-volume hospital.

Consider a recent example that examined the question of whether or not referral to a long-term acute care hospital (LTAC) affected long-term costs and outcomes for ICU patients (Figure 4) (4). A traditional analysis would have asked whether patients who went to LTACs had different outcomes from ICU patients who did not go to LTACs. However, such an analysis would be confounded because LTACs select their patients on the basis of being sick enough to need prolonged care. In principle, one might conduct a RCT in which patients are randomized to referral to an LTAC or not, but no funders have stepped forward for such a massive undertaking.

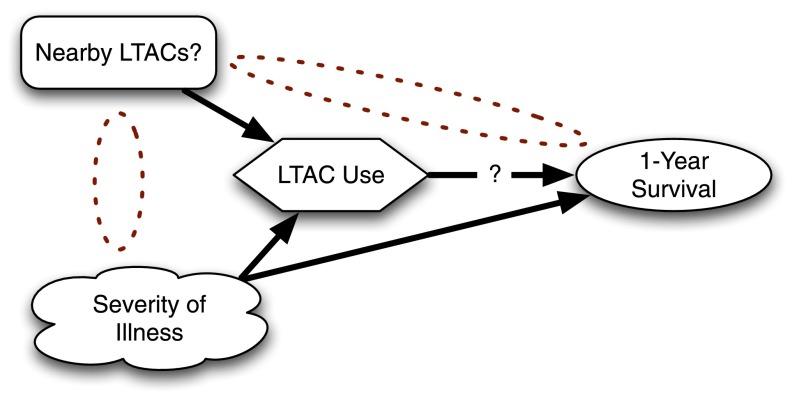
Figure 4.

Using an instrumental variable to examine whether referral to long-term acute care hospitals (LTACs) results in improved 1-year survival for critically ill patients.

Lacking a feasible RCT or simple observational way to get at the problem, Kahn and colleagues reasoned that hospitals that are near lots of LTACs probably use LTACs more than hospitals that are not near LTACs (4). They used as their instrumental variables the distance to the nearest LTAC and the number of LTAC beds in the local area. There is no reason to believe that LTACs are preferentially cropping up near hospitals with unusually less sick patients. Nor is there any reason to think having an LTAC nearby would influence a patient’s outcome in any way other than by patients using an LTAC. Whereas traditional analyses had suggested LTACs were killing patients, Kahn and colleagues’ analysis appropriately controlled for selection and showed no difference in long-term mortality. (They find fascinating results about costs and spending for care as well, but those are beyond the scope of this article.)

Do Instrumental Variables Give the Same Answer as RCTs? Should They?

An important test of any analytic model is whether or not it gives the “right” answer, defined as better outcomes for patients when the results of that analysis are acted upon. Recently, mouse models of severe sepsis have been criticized for failing to predict human responses to severe sepsis (5). Statistical models should be held up to the same standard: Does their use lead to better care?

We are unaware of anyone who has systematically compared the results of instrumental variable analyses to RCTs to evaluate instrumental variables as currently used in the medical literature. There are a number of subtleties that should be considered when interpreting instrumental variable analyses. The first is that instrumental variables are a tool, and, like any tool, can be used well or poorly. We discuss in the next section examples of how to conduct such an evaluation and provide examples of poor use.

Second, instrumental variables and RCTs answer subtly different questions. RCTs answer the question, “Would all patients who met enrollment criteria benefit from treatment on average?” RCTs answer the question well for the average patients who met enrollment criteria, but in practice those enrollment criteria sometimes limit RCTs to studying restricted subpopulations. Instrumental variable analyses typically start with wider patient populations but also only answer the question of whether a specific subgroup of patients would benefit. For example, many instrumental variable analyses are effective at studying those “compliers” or “marginal patients” who would only take the treatment if they were “encouraged” to by the instrument (6).

This difference can be important. For example, suppose one wishes to know if inhaled tobramycin slows the rate of FEV₁ decline for patients with cystic fibrosis (CF). The RCT might answer this for all patients with CF (although this might really be “all patients with CF who were also treated at CF centers and lacking other significant comorbidities and not otherwise concurrently involved in other trials and whatever other enrollment criteria”). An instrumental variable analysis might answer it for those patients who would only take tobramycin if they were treated at institutions that prescribed it frequently and not otherwise (7). Thus, the RCT might include all of the patients “for whom everybody would do this,” whereas the instrumental variable analysis might highlight the patients for whom in practice there might be the greatest question of benefit, possibly leading to different answers to different questions.

Reading Instrumental Variable Analyses Skeptically

In a RCT, randomization will, on average, evenly balance the unobserved confounders between the treated and the control groups. By definition, this is not something we can prove because they are unobserved. We usually scrutinize the first table in any RCT for any hint that such a confounder may have snuck though randomization and threaten our causal understanding.

When an instrumental variable analysis works well, it provides high-quality evidence about a causal relationship. In such a case, the instrumental variable needs to be associated with specific differences in treatment but to not plausibly lead to differences in the outcome. Furthermore, there needs to be no confounder that influences both the instrumental variable and the outcome. A skeptical reader needs to decide whether these conditions (Table 1) are met, at least approximately.

Table 1.

Three key questions for evaluating instrumental variable analysis

1) Does the instrumental variable lead to meaningful differences in the treatment being tested?

2) Other than through the specific treatment being tested, is there any other way the instrumental variable could influence the outcome?

3) Does anything cause patients to both receive the instrumental variable and receive the outcome?

The first step is that the instrumental variable needs to lead to differences in treatment. “Weak” instruments lead to little differences between the treated patients and the control subjects. “Strong” instruments lead to big differences. With weak instruments, the analysis can very easily be biased and will have little power (8). Think of an RCT with substantial crossover between the groups. Most articles report some measure of the strength of their instrument by explaining how well the first stage of the regression explains the variance. Higher is better.

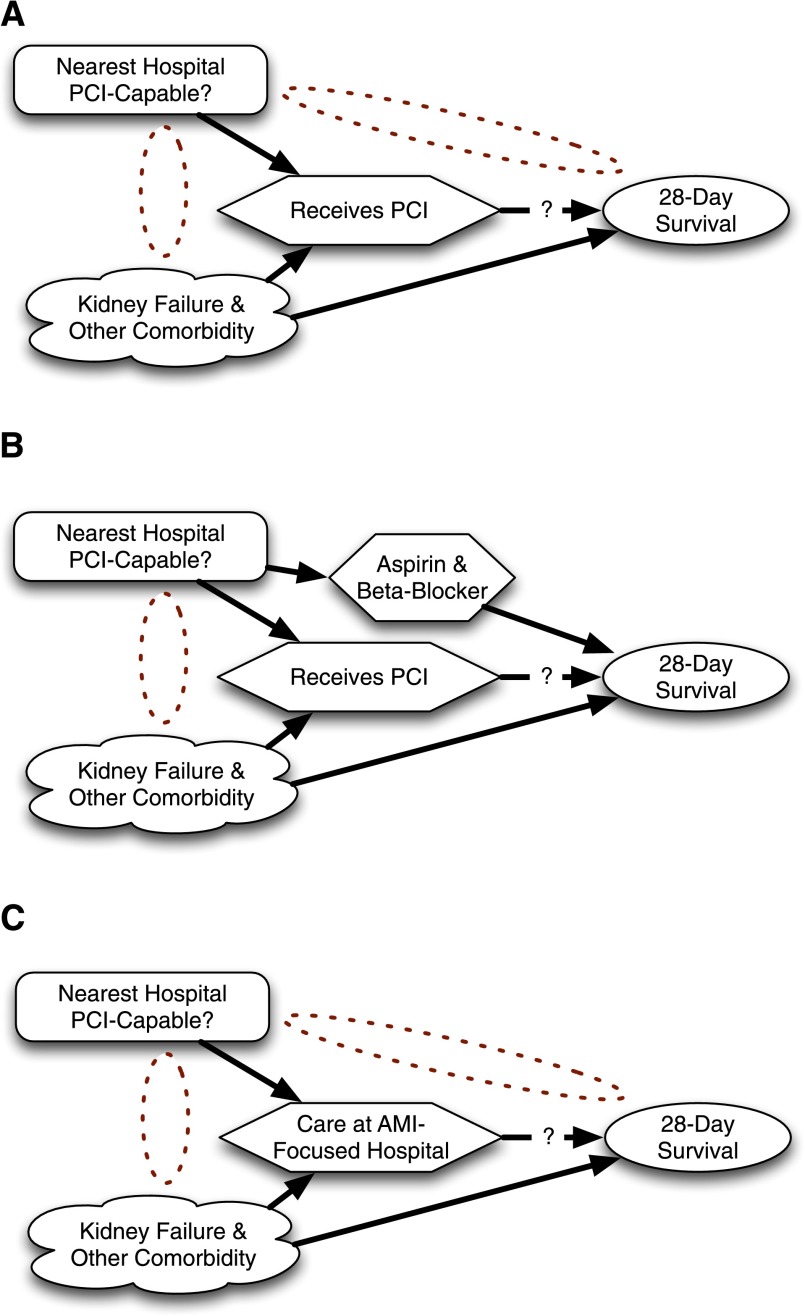
The second step is that the instrument can only influence outcome through the proposed treatment. Deep clinical understanding is necessary to check the plausibility of this assumption. Consider one of the major policy debates that has been influenced by instrumental variable analysis (9). Initially, analysts framed the question as whether receipt of percutaneous coronary intervention (PCI) improved outcome for acute myocardial infarction (AMI). Simple regression analysis was confounded by factors such as kidney failure and clinical instability, not all of which could be adequately controlled using available data (Figure 5). An analysis was planned that used as an instrumental variable whether or not the person’s nearest hospital performed PCI. It was argued that if one lived near a PCI-capable hospital, one was more likely to go to a PCI-capable hospital when having an AMI and that PCI-capable hospitals were more likely to provide prompt PCI. It was also argued that patients living near PCI-capable hospitals were not likely to be sicker or healthier.

Figure 5.

Attempts to use an instrumental variable analysis to understand the impact of availability of percutaneous coronary intervention (PCI) on acute myocardial infarction (AMI) outcomes. (A) Question as originally formulated. (B) Reality of alternate pathway. (C) Reformulated question that could be answered with instrumental variable.

It was discovered, however, that PCI-capable hospitals were also more likely to have good processes in place to provide other aspects of evidence-based care. PCI-capable hospitals tended to have protocols making sure every appropriate patient went home with aspirin and a β-blocker. This required a change in the research question. The instrumental variable analysis could not argue that it was receipt of PCI, per se, that resulted in better AMI outcomes. Instead, they argued that it was care at a PCI-capable hospital that resulted in better outcomes—care that might include not only receipt of PCI but also all the other protocols and focus on excellence (e.g., aspirin and β-blockers) that were more common at PCI-capable hospitals. This was still a potentially valuable finding, while opening new questions about how PCI-capable hospitals were able to do other things better as well.

A skeptical reader needs to be convinced that the differences in care that are associated with the instrumental variable are specific to the research question being posed. Examples where this is patently not the case abound. Once, there were analyses that proposed using state of residence as an instrumental variable for availability of treatment X. The proposers argued that states varied widely in their availability of treatment X and therefore that state of residence would be a strong instrument.

Although state of residence passes the first stage test for an instrumental variable, it fails miserably for the second step. Patients who live in California are definably different from patients who live in Alabama for a host of reasons, are exposed to a wide variety of differences in treatment other than just treatment X, and have large differences in comorbidity. Thus, it is implausible to claim that the only differences in outcomes across states were caused by differences in treatment X. State of residence is not an acceptable instrumental variable for treatment X.

The third condition for a valid instrumental variable analysis is that there is not something that causes both the instrument and the outcome (directly or indirectly). One might wish to use a patient’s physician’s likelihood of prescribing a given drug as an instrumental variable (10). Going to a physician who prescribes more of that drug plausibly increases a patient’s likelihood of getting the drug, although the strength of that association needs to be quantified. We can carefully check to see if there are other differences in practice patterns of high prescribers to convince ourselves it is the drug per se, not just that better physicians prescribe more (or less) of the drug. To test the third condition, we would need to convince ourselves that the patients in a high-prescribing physicians’ practices are not somehow sicker (or healthier). If physicians with sicker patients overall tend to have a more aggressive treatment style, then patient severity of illness may confound the proposed instrumental variable and the outcome, making it a bad instrumental variable.

As with RCTs or any test, these three conditions are not absolute cut-offs. Instead, we must use our clinical judgment to decide how important any violations may be. Sometimes additional data—akin to the data published in RCTs showing balance between the two experimental groups—can help suggest that, although a violation was theoretically possible, in practice the instrumental variable seems to work well. In other cases, that data may help convince us that an instrumental variable that might have worked turned out to be confounded in unexpected ways.

Conclusions

Instrumental variables are a potentially powerful tool in helping us understand the causal mechanisms in the world around us. They complement RCTs, trying to get causal evidence in cases where quirks lead to some degree of random assignment to specific treatments. By exploiting this randomness, they can get around the selection and confounding problems common in observational studies. However, to be effective, an instrumental variable must be associated with the treatment of interest but not with other treatments. Furthermore, the instrument must not be related to the outcome, except through the treatment of interest. Although these conditions can never be proven—just as the fundamental assumptions of RCTs and mice models can never be proven—they can be critically evaluated to allow instrumental variable analyses to inform clinical decision-making.