Detecting Stable Distributed Patterns of Brain Activation Using Gini Contrast

Abstract

The relationship between spatially distributed fMRI patterns and experimental stimuli or tasks offers insights into cognitive processes beyond those traceable from individual local activations. The multivariate properties of the fMRI signals allow us to infer interactions among individual regions and to detect distributed activations of multiple areas. Detection of task-specific multivariate activity in fMRI data is an important open problem that has drawn much interest recently. In this paper, we study and demonstrate the benefits of Random Forest classifiers and the associated Gini importance measure for selecting voxel subsets that form a multivariate neural response. The Gini importance measure quantifies the predictive power of a particular feature when considered as part of the entire pattern. The measure is based on a random sampling of fMRI time points and voxels. As a consequence the resulting voxel score, or Gini contrast, is highly reproducible and reliably includes all informative features. The method does not rely on a priori assumptions about the signal distribution, a specific statistical or functional model or regularization. Instead it uses the predictive power of features to characterize their relevance for encoding task information. The Gini contrast offers an additional advantage of directly quantifying the task-relevant information in a multi-class setting, rather than reducing the problem to several binary classification sub-problems. In a multi-category visual fMRI study, the proposed method identified informative regions not detected by the univariate criteria, such as the t-test or the F-test. Including these additional regions in the feature set improves the accuracy of multi-category classification. Moreover, we demonstrate higher classification accuracy and stability of the detected spatial patterns across runs than the traditional methods such as the recursive feature elimination used in conjunction with Support Vector Machines.

1. Introduction

Functional Magnetic Resonance Imaging (fMRI) allows us to study the relationship between experimental conditions and the brain response at different locations. The traditional analysis methods analyze the data in a univariate fashion, that is, they examine the contributions of different experimental conditions to the fMRI response of each voxel separately (Friston et al., 1994). Recently, a new approach, often referred to as multi-voxel pattern analysis (MVPA), has emerged that considers patterns of responses across voxels that carry information about different experimental conditions (Haxby et al., 2001). In the multi-voxel pattern analysis framework, the response of each voxel is considered relevant to the experimental variables not only on its own, but also in conjunction with the responses of other spatial locations in the brain. Most multi-voxel pattern analysis methods train a classifier on a subset of fMRI images in an experiment and use the classifier to predict the experimental conditions in the unseen subset. This approach has proved successful in a variety of applications (Norman et al., 2006; O’Toole et al., 2007).

One of the major challenges of multi-voxel pattern analysis is that fMRI images contain a large number of uninformative, noisy voxels that carry no useful information about the category label. At the same time, voxels that do contain information are often strongly correlated. When trained with a relatively small number of examples, the resulting classifier is likely to capture irrelevant patterns and suffer from poor generalization performance. To mitigate the first problem, feature selection must be performed prior to, or in conjunction with, training (De Martino et al., 2008; Pereira et al., 2009).

Furthermore, the ultimate goal of most fMRI experiments is not to achieve high classification performance, but to characterize the functional organization of the brain. Identifying the complete set of task-dependent meaningful features promises to not only improve the generalization performance of the learning algorithms, but also to provide insights into the structure of the functional areas in the brain. Specifically, a feature selection method can identify regions that process information related to specific stimuli. In light of this exploratory goal, feature selection becomes more than a mere tool in optimally regularizing the learning algorithm, but the main aim of the analysis.

In this paper, we focus on the problem of reproducible feature selection and examine a fully multi-feature, multi-class method in application to fMRI analysis that improves upon the previous approaches in terms of the generalization ability of the resulting classifiers, the robustness and completeness of the selected voxel sets, and the stability of the voxel score patterns. We employ the Gini importance measure derived from a Random Forest (RF) classifier (Breiman, 2001) or Gini contrast to quantify the predictive power of voxels in the selection procedure. This measure captures multivariate and non-linear relationships among fMRI activations and conditions. The measure is robust to noise, exhibits stability across datasets without a need for explicit regularization, and captures the most informative voxels more accurately than previously demonstrated approaches.

We demonstrate the method on a visual multi-category fMRI study of object perception and recognition. Our experimental results indicate that the proposed method outperforms the commonly used univariate and multivariate feature selection algorithms in terms of reproducibility and ranking of voxels.

This paper is organized as follows. In the next section, we review existing pattern analysis methods used for multi-voxel pattern analysis in fMRI studies. In Section 3, we present the training procedure for the Random Forest classifiers and define the Gini contrast we use for selecting voxels. The same section also reviews our methodology for the empirical comparison across methods. Section 4 contains detailed information on the imaging study we used for empirical evaluation of the methods. Section 5 reports the experimental results, followed by a discussion in Section 6. We conclude in Section 7.

2. Background and Related Work

Conventional localization approaches for fMRI analysis focus on explaining the variation in the response of individual voxels. Univariate statistical tests detect voxels whose fMRI response is highly correlated with the experimental variable of interest in a linear model (Friston et al., 1994). Most methods select a subset of the detected voxels that form contiguous blobs in relevant anatomical locations. For example, in the studies of visual object recognition, the localization approach was used to identify category-selective functional regions, such as the fusiform face area (FFA) and the parahippocampal place area (PPA) in the ventral visual pathway (Epstein and Kanwisher, 1998; Kanwisher et al., 1997; Kanwisher, 2003).

In contrast, multi-voxel pattern analysis aims to associate a robust pattern of response across a large set of brain voxels with each experimental condition. For example, to study the structure of object representation in the visual cortex, this approach yields a distributed pattern in the visual cortex as an alternative to the localized representations implied by category-selective areas such as FFA and PPA (Carlson et al., 2003; Cox and Savoy, 2003; Haxby et al., 2001). Classification-based multi-voxel pattern analysis methods have been employed in a wide variety of neuroscientific problems, including decoding cognitive and mental states (Haynes and Rees, 2006; Mitchell et al., 2004), lie detection (Davatzikos et al., 2005), and low level vision (Haynes and Rees, 2005; Kamitani and Tong, 2005).

2.1. Multi-Variate fMRI Analysis Methods

Unlike the unified framework of the Generalized Linear Models (GLM) used by the univariate fMRI analysis (Friston et al., 1994), there is considerable variety in the preprocessing stages and the classification algorithms used for multi-voxel pattern analysis (Pereira et al., 2009). Earlier studies employed simple correlation-based methods, Linear Discriminant Analysis (LDA), or multiple regression (Haxby et al., 2001; Carlson et al., 2003; Ishai et al., 2000). A comprehensive overview of the basic concepts, and the relationship between univariate and multivariate approaches can be found in (Haynes and Rees, 2006; Norman et al., 2006). Later work compared the more sophisticated Support Vector Machines (SVM) with simple algorithms such as LDA, Gaussian Naive Bayes (GNB), and the k-Nearest Neighbors (k-NN), commonly demonstrating advantages of the linear SVM, which naturally imposes regularization on the learning problem (Cox and Savoy, 2003; Mitchell et al., 2004; Mourão-Miranda et al., 2005). These findings resulted in considerable interest in SVM classifiers for fMRI analysis (LaConte et al., 2005; Mourão-Miranda et al., 2005, 2007; Wang et al., 2007; Wang, 2009).

However, the application of linear SVMs to fMRI data presents several challenges. First, the regularization used by the SVM training procedure results in weights that are not directly informative as spatial maps but require further processing. Examples of representations extracted from the classifier include sensitivity maps (Kjems et al., 2002) and weighting of the feature space based on the distance to the margin (LaConte et al., 2005). Second, the SVM classification framework is intrinsically defined for two-category classification problems. Additional constructs are needed to form multi-class prediction from binary SVM classifiers. Finally, proper regularization of non-linear SVMs is challenging; linear SVMs might be insufficient for modeling non-linear relationships between the experimental conditions and the fMRI responses, in particular when working with more than two categories.

2.2. Feature selection in fMRI studies

Most multi-voxel pattern analysis methods use voxels as features. The problem of feature selection thus reduces to choosing a subset of voxels to be used in the analysis (Cox and Savoy, 2003; Mourão-Miranda et al., 2006; De Martino et al., 2008; Hardoon et al., 2007). Numerous feature selection methods have been developed in machine learning (Guyon and Elisseeff, 2003), many of which also have been employed on the fMRI data (Pereira et al., 2009). Most commonly, statistical significance tests or other univariate criteria are used for selecting relevant voxels. However, this approach departs from the core idea of multi-voxel pattern analysis and fails to fully utilize the predictive power of the underlying signals.

Alternatively, multi-voxel feature selection methods, such as Recursive Feature Elimination (RFE), search for a set of voxels that jointly provide the most information about the experimental conditions (Hanson and Halchenko, 2008; De Martino et al., 2008). Given a classifier of choice, typically a linear SVM, RFE starts with the set of all voxels and incrementally removes voxels with lowest weights (Guyon et al., 2002). Since it is computationally infeasible to re-estimate the classifier after removing each voxel, usually a subset of voxels is removed in each step. However, since the SVM results degrade with the increasing number of features, it is unclear whether the ranking provided by the initially trained classifier is a reliable measure for the elimination of voxels.

Sparse logistic regression with automatic relevance determination (Yamashita et al., 2008) is also based on a regularized linear model. Rather than successively remove features, it directly maximizes the number of zero regression coefficients in the model. A more local “search light” strategy was proposed in (Kriegeskorte et al., 2006). Rather than test individual voxels for correlation with the experimental protocol, the search light selection procedure considers small neighborhoods for inclusion in the analysis. Unfortunately, this approach still fails to capture the joint patterns of response across distant locations in the brain.

An alternative approach to feature selection is to compare the performance of a classifier trained on the full data set with the performance of the classifier on a data set with a particular feature removed, or the values of that feature permuted across training samples (Hanson and Halchenko, 2008; Strobl et al., 2008; Archer and Kimes, 2008). The difference in classification performance is then used as a measure of the feature importance. This perturbation method comes at a high computational cost. Furthermore, it may fail to select relevant variables if several features carry the same information and the removal of one of them does not affect the classification performance significantly, ultimately leading to low reproducibility of the detected patterns. A related approach is discussed in Kjems et al. (2002) where sensitivity maps represent the sensitivity of class labels to the modification of individual voxel values.

Nonlinear feature selection methods promise to improve the performance of the approaches based on linear classification models (Davatzikos et al., 2005). For example, the algorithm developed in (Lao et al., 2004) approximates the nonlinear margin at each support vector by a local linear function, and visualizes the features that contribute the most to the separation between the classes. However, relying on support vectors might overly emphasize the most extreme representatives of each class (De Martino et al., 2008).

For completeness, we note that dimensionality reduction techniques, such as PCA, can be used to reduce the number of features used by the classifier and therefore improve its generalization performance (Mourão-Miranda et al., 2005, 2007). But since these exploratory methods do not reflect the structure of the experimental design, their results are not necessarily predictive of the experimental conditions (O’Toole et al., 2007).

2.3. Random Forests and Gini contrast

In this paper, we propose to use the Gini contrast of the fMRI voxels derived from a Random Forest (RF) classifier (Breiman, 2001) for feature selection in multi-voxel pattern analysis in fMRI studies. The inherently non-linear multi-voxel Gini contrast promises to robustly capture complex relationships between the experimental conditions and the observed fMRI signals.

The method does not rely on neighborhood constraints, linearity, specific kernels, or regularization. The core algorithm is simple and requires only minimal parameter tuning. Moreover, the results appear quite robust to the changes in the values of the parameters.

A Random Forest is an ensemble classifier that uses decision trees as base learners (Breiman, 2001). Each decision tree is trained on a random subset of the training set. The nodes of the decision tree perform thresholding on individual features. To construct the next node of a decision tree, the method searches over a random subset of features (voxels in the fMRI context) to maximize separation among the different classes. The features are tested effectively for their ability to separate the classes, conditioned on the decisions at the higher levels of the tree. The Gini importance of a particular feature quantifies the gain in class separation due to that feature, integrated over all the trees in the random forest.

In contrast to many other training methods, the independent random draws enable highly correlated but predictive features to be included in the classifier, a characteristic referred to as grouping effect. This is particularly relevant when we are interested in detecting all informative voxels in fMRI data as opposed to detecting a subset sufficiently informative to perform accurate decoding. A direct consequence is high reproducibility of the informative regions detected by Gini contrast across trials.

Unlike the classification methods based on SVMs (Pereira et al., 2009), the Random Forest classifiers naturally enable a multi-class setup. As a result, the Gini contrast derived from such a classifier simplifies the interpretation of the resulting feature rankings and highlights the importance of features which are of mutual relevance to differentiating several external stimuli. In addition, the Gini importance measure has been shown to correlate well with measures based on feature perturbations (Breiman, 2001; Archer and Kimes, 2008), providing a surrogate for computationally more expensive statistical permutation tests.

Random forests often perform remarkably well, with very little tuning required (Hastie et al., 2009). The Gini importance and related importance measures derived from the Random Forest classifiers have shown to be useful for feature selection in a variety of high dimensional learning tasks (Breiman, 2004). Examples include micro-array experiments (Diaz-Uriarte and Alvarez de Andres, 2006), chemometrical applications (Svetnik et al., 2003; Menze et al., 2009), classification of spectra (Menze et al., 2007; Granitto et al., 2006), classification of time series and EEG signals (Shen et al., 2007).

3. Methods

In this section, we formally define the Gini contrast and discuss the empirical evaluation procedure we used to compare different feature selection methods. Our review of the Random Forest classifiers follows (Breiman, 2001)¹. (Hastie et al., 2009) offers an excellent introduction to RF.

3.1. Random Forests and Gini Importance for Feature Selection

We let X = [x₁,…, x_T] ∈ R^VxT be the BOLD signal observed in an fMRI experiment in V voxels over T time points. $x_t^v$ represents the response of voxel v at time t. In addition, we have access to the labels [l₁,…, l_T] that specify the experimental condition (stimulus or task) for each time point, l_t ∈ {1,…, L}. We treat the fMRI pattern at each time point as a separate data point for classification purposes. Feature selection then becomes selecting voxels [v₁,…, v_K] whose fMRI responses exhibit robust generalization.

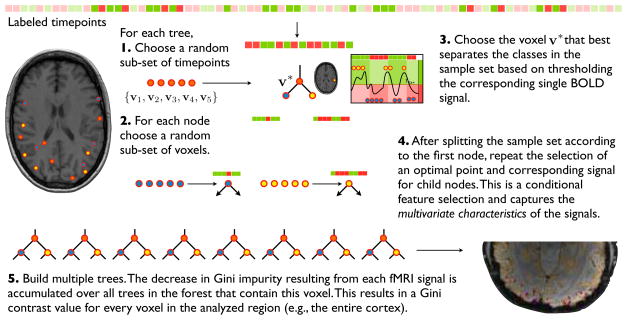
A Random Forest classifier consists of decision trees (Fig. 1) for predicting the category label l from the fMRI pattern x. Majority voting rule yields the final category by integrating decisions over all the trees in the forest. Each tree is trained on a random subset of examples (x_t, l_t).

Figure 1.

Random forest construction and Gini importance calculation.

Let n_w be the total number of examples assigned to node w in the tree and $n_w^l$ be the number of examples at node w that belong to category l. Let $p_w^l$ be the empirical frequency of category l at node w, i.e., $p_w^l=\frac{n_w^l}{n_w}$. The Gini impurity measures the degree of separation among the classes achieved at a particular node:

$$i(w)=\sum _{l=1}^L{p}_w^l(1-p_w^l).$$ (1)

Intuitively Gini impurity measures the probability that two independent draws from the multinomial distribution defined by $p_w^l$ are from two different classes. Each node is associated with a feature (voxel) v and a threshold value η. All the examples at node w are assigned to one of its two children, w₁ and w₂, based on the outcome of the thresholding. We can evaluate the decrease in Gini impurity between node w and its children (w₁, w₂):

$$\mathrm{\Delta }i(w;v,{\eta }_v)=i(w)-\frac{n_{w_1}}{n_w}i(w_1)-\frac{n_{w_2}}{n_w}i(w_2).$$ (2)

During training of the tree, given node w, we choose a random subset of features [v₁, …, v_K]. We then select a single feature v*(w) and a threshold value η*(w, v*) that maximize the reduction in Gini impurity for the node w. This selection defines the two children of the node w. We repeat this procedure recursively, until all leaves of the tree define unique categories.

Given the forest, the Gini importance or contrast of feature v is defined as the reduction in the Gini impurity induced by the feature, integrated over all the trees in the forest:

$$I_G(v)=\sum _{\text{all}\text{trees}}\sum _{\{w:v^{\ast }(w)=v\}}\mathrm{\Delta }i(w;v,{\eta }^{\ast }(w,v)).$$ (3)

In this work, we use the Gini importance to rank voxels for feature selection. We refer to the value as the Gini contrast of a voxel with regard to the classes in the training set of the random forest (e.g., different image categories). The underlying Gini impurity is related to the entropy of the conditional distribution of the labels at node w, $i_e(w)=-{\sum }_{i=1}^L{p}_w^{l}log{p}_i$ by replacing the logarithm log p_i by −(1 − p_i) (Raileanu and Stoffel, 2004). The decrease in Gini impurity quantifies the decrease of labeling uncertainty caused by choosing the feature and the threshold. The Gini contrast approximates the expected information gain in the decision tree. It enables selection of voxels that improve the separation among the classes at some point of any of the hierarchical decisions imposed by decision trees in the forest.

3.2. Gini contrast vs. Univariate Criteria

We compare Gini contrast to three univariate criteria for feature selection: (i) the univariate t-test that compares the average response to stimuli in a particular category to that of fixation, (ii) the omnibus F-test that includes one regressor for each category in the linear model of the signal, and (iii) random selection of features that provides an uninformed baseline. We use identical classification setup, described above, with all four feature selection methods.

We train a random forest of 40,000 trees to rank voxels based on Gini contrast. The Matlab implementation on a standard workstation (Intel Xeon, 8 cores, 2.8GHz each) takes about 2.5 hours to train the classifier.

To illustrate the regions selected by Gini contrast and univariate scores we use the Mutual Information between the labels and the average fMRI signals in individual selected regions, or pairs of regions.

3.3. Gini contrast vs. Recursive Feature Elimination

We compare the Gini contrast to Recursive Feature Elimination based on linear SVMs as described in (Hanson and Halchenko, 2008; Guyon et al., 2002).

During recursive feature elimination, we train a SVM with linear kernel in every step, enforcing strong regularization by setting the error penalty to 10¹⁰ and assigning equal weight to all features by scaling each variable to unit variance. After training, we rank variables according to the absolute value of the coefficient in the prediction function. We remove the features with the lowest rank, retrain the SVM using the remaining features and repeat the elimination process. In each step, about half of the voxels are removed. The process yields data sets with 40, 80, 160, 320, 640, 1280, 2560, 5120, and 10240 voxels.

When using recursive feature elimination, we select features for each category separately, as choosing a unique feature set by merging the feature rankings obtained for all binary subproblems (“one-vs-all”) resulted in poor predictions. We used the same classification setup with both feature selection procedures.

3.4. Classification Setup

Once the ranking of all voxels is established, we proceed to train a classifier based on the top K voxels while varying K. We decouple the choice of the feature selection method from the classifier that uses the features to assign novel examples to one of the categories. In this work, we use three types of classifiers: the Random Forest (Breiman, 2001), the linear SVM and the Gaussian RBF SVM (Schoelkopf and Smola, 2002).

For each subject in the study, we train the classifier on the voxels identified by the feature selection procedure using the first half of the time courses and test it on the remaining time points. While the Random Forest classifiers are inherently multi-class, the SVM classifiers are two-way classifiers for each image category vs. all other categories. We quantify the classification performance of the classifiers by the average area under the ROC curve (AUC), averaged over all categories.

In the absence of ground truth for the regions related to stimuli categories, we evaluate the information encoded in the selected voxels by the classification performance. A fast classification performance increase when starting with the top-ranked features indicates that the top-ranked voxels contain highly relevant information.

3.5. Cross validation scheme

We perform feature selection, classifier training, and testing in a two-fold cross validation fashion. For each subject, we divide the fMRI sequence into two consecutive parts of equal length (300 time points). We then use one of the halves for features selection and training and apply the resulting classifier to the other half. While the signals of adjacent time points in fMRI time courses are highly correlated, this subdivision reduces the effects of correlations to a small region at the split point.

In addition to the classifier performance, we evaluate the stability of the selection by comparing the overlap of the selected voxel subsets between the two halves of the time courses. For each feature selection method (Gini contrast and RFE), we use the Dice measure of overlap (Dice, 1945)

$$\mathit{Dice}(A,B)=2\mid A\cap B\mid /(\mid A\mid +\mid B\mid )$$

to quantify the volume overlap between the two voxel sets identified by the method on the two training sets. We calculate the Dice measure for different numbers of top ranked voxels.

4. Image Data

We evaluated the methods in a high-level vision fMRI study that included five subjects (Kanwisher, 2003). The subjects viewed images from eight different categories (Animals, Bodies, Cars, Faces, Scenes, Shoes, Trees, Vases) in a block-design protocol. During the experiment, subjects viewed sets of eight blocks separated by a fixation period. Each block lasted 16 seconds, during which 20 images of one category were shown. Each block set contained one block for each category, arranged in a random order. Subjects were shown between 8 and 9 blocks for each category. The fMRI data was acquired using a Siemens 3T scanner and a custom 32-channel coil (EPI, flip angle = 90°, TR = 2s, TE = 30ms, 28 axial 128×128 slices, voxel size = 1.5 × 1.5 × 2mm). The image volume was restricted to the occipital cortex and the temporal lobe.

For each subject, structural T1 MRI data was acquired and co-registered to the functional data. We segmented the cortex in the T1 image using the segmentation procedures in FreeSurfer² and transfered this segmentation to the functional images. All calculations were restricted to the voxels on the cortex. We performed motion correction, spike detection, intensity normalization, and Gaussian smoothing with a 3 mm kernel using our standard pipeline employed in localization studies. We discarded all runs that contained signal spikes. In addition, we applied de-trending to voxel time courses, regressing out a constant baseline, a linear trend, and three linear motion correction regressors, using FsFast³.

We calculated the classification labels by convoluting the block labels with the hemodynamic response kernel and thresholding the resulting values at 10% of the maximum value, to exclude ambiguous sections close to the beginning and the end of each block. We excluded the fixation periods from feature selection and classification.

5. Results

We first compare ranking by Gini contrast and univariate criteria, and examine the information contained in the regions selected only by the multivariate criterium. Then, we compare Gini contrast to RFE in terms of classification performance and reproducibility.

5.1. Gini contrast vs. univariate criteria

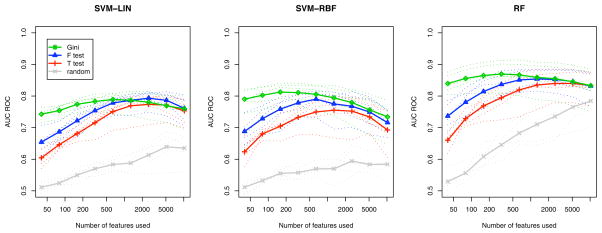
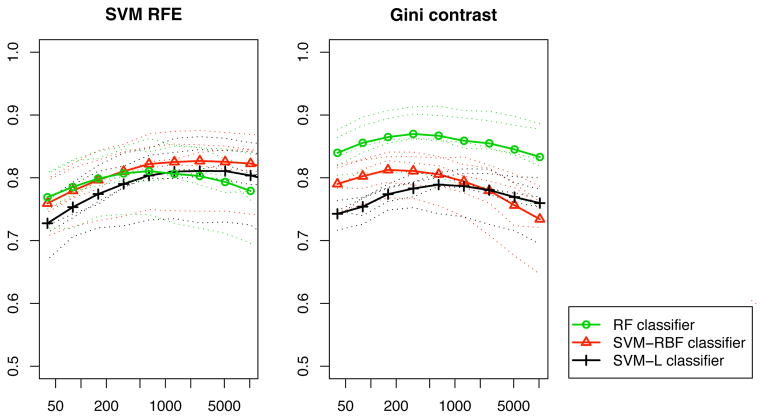
Fig. 2 reports the classification performance for random ranking, t-test, F-test and Gini contrast ranking. The mean performance over all categories is shown for each subject, as well as the average performance over all subjects. Starting with the highest ranked voxels, the voxel sets used for classification have a size of 40, 80, 160, 320, 640, 1,280, 2,560, 5,120, and 10,240 (approximately a quarter of all voxels). Random ranking provides a baseline for the information contained in arbitrary subsets of voxels. As expected, all three feature selection methods perform better than the random ranking. Since RF performs an inherent feature selection during training the accuracy of RF on random ranking increases as more voxels are included. This is not the case for SVM. When using SVM-RBF and RF classifiers the Gini contrast consistently outperforms t-test, and F-test for all voxel subsets. The accuracy of the classifiers based on Gini contrast peaks between 200 and 400 voxels, while t-test, and F-test reach their peak performance only after 1,000 voxels are included.

Figure 2.

Comparison of Gini contrast ranking and univariate rankings for all 5 subjects averaged over all classes: classification accuracy using the top ranked voxels. Three classifiers (SVM-LIN, SVM-RBF, and RF) exhibit consistent differences when trained on the selected voxels. The curves show the AUC for all classes, and all subjects. Dotted lines show subject-specific accuracy; solid lines show the average accuracy across subjects.

RF achieves the best classification results for all selection methods. However, the differences between the feature selection methods (random, t-test, F-test, Gini contrast) are consistent across the three classification methods.

The differences between the feature selection methods are most pronounced for the small voxel sets. An RF classifier trained and tested on the 40 top ranked voxels yields an average 0.84 AUC for Gini contrast ranking, 0.73 for the F-test, and 0.66 for the t-test. It takes 640 voxels for the F-test to reach classification accuracy comparable to that of Gini contrast for 40 voxels, and the t-test ranking never reaches this performance.

5.2. What is gained by multivariate regions?

When increasing size of the selected voxel set, starting from the top-ranked voxels, the classification performance of Gini contrast increases more rapidly, and reaches its peak earlier, than that for t-test and F-test. The latter two capture large blobs in the data, while Gini contrast selects parts of the same blobs, but ranks only a small portion of each blob very high. At the same time, Gini contrast selects other regions that are not identified by the t-test or the F-test.

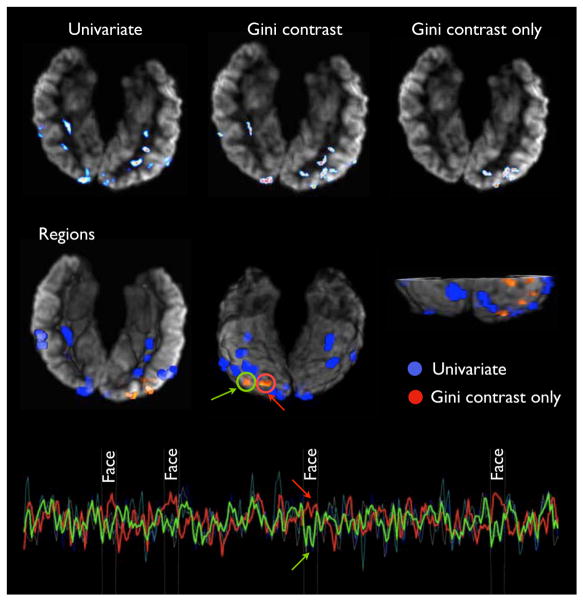
Fig. 3 illustrates the regions selected by t-test and those selected by Gini contrast but not by t-test. It also shows the detrended BOLD signals for the regions selected by Gini contrast only. For one pair of those regions, I(y; x₁), I(y; x₂), and I(y; x₁, x₂) are reported. The corresponding plots illustrate how the signals explain the presense of faces jointly, while each of them alone does not exhibit high selectivity to the stimulus.

Figure 3.

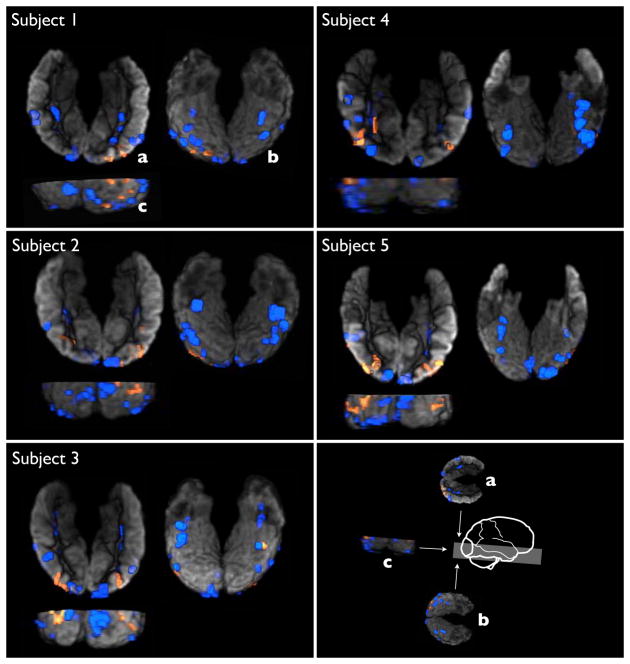
Face category: Top row: top ranked voxels by univeriate t-test, Gini contrast, and exclusively Gini contrast. Second row: comparison between connected regions with more than 9 voxels detected by a univariate criterion (t-test, blue) and regions selected exclusively by Gini contrast (red). The additional regions detected by Gini contrast primarily contribute multivariate relationships to the category. For one pair of regions the de-trended BOLD values are illustrated. Together they hold significantly more information about the category than random regions. Two example regions carrying joint information are indicated by red and green curves. They exhibit characteristic joint behavior for faces: single mutual information vs. face images: I(face; red)=0.11, I(face; green)=0.054, pair-wise mutual information vs. face images: I(face; red, green)= 0.213. U - selected by univariate t-test; Gini only - selected only by Gini contrast.

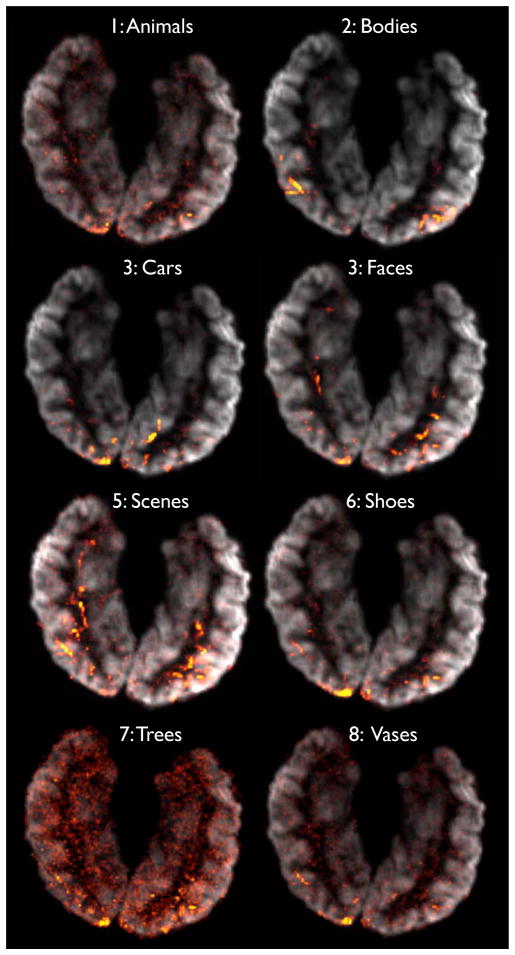
In Fig. 4, the Gini contrast ranking is shown for subject 1 for all 8 image categories. The multi-class Gini contrast takes the interaction between the classes into account and reflects the differentiating features accordingly. In Fig. 5, t-test, and Gini only regions are shown for all 5 subjects in the study. The regions selected only by Gini contrast exhibit a considerable level of consistency across subjects.

Figure 4.

Gini contrasts for all 8 classes, shown in 3D at their positions on the cortex.

Figure 5.

All subjects: regions selected by t-test (blue) and regions selected by Gini contrast but not by t-test (red) analogous to Fig. 3. The regions are shown on top of a 3D rendering of the cortex: view from top, view from behind, view from bottom.

5.3. Gini contrast vs. Recursive Feature Elimination

Fig. 6 reports cross-validation results for the two multivariate ranking methods. We first perform recursive feature elimination based on a linear SVM. We stop removing features when the overall predictive performance starts decreasing. We observe such a peak, for most subjects, after removing 35,000 to 39,000 features. The remaining 2,000 – 5,000 voxels form the feature set used for training of the classifier. When testing the nonlinear classifiers on the same subset of top RFE features the SVM-RBF holds a slight advantage over the linear SVM and shows consistent improvement with the increasing voxel set size. The RF is well within the performance range defined by the two SVMs – with slightly worse results on the larger sets of features and better results on the smaller sets when compared to the SVM-RBF classifier. The RF performs well as long as informative features are part of the feature set it is applied to, with a slight decrease in performance upon the injection of too many irrelevant “noisy” predictors. Many of the 200–400 features required for an optimal RF classifier were removed early in the RFE ranking. Overall, we find that the predictive performance of the two nonlinear classifiers is very close to the performance of the linear classifier which had been used to define the feature ranking and the selected voxel sets. This also implies that features which may be non-linearly related to the categories have been removed early in the recursive feature elimination.

Figure 6.

Comparison of classification performance in a two-fold cross-validation, using (a) random forests, (b) RBF SVM, and (c) Linear SVM. For each classifier voxel ranking was done by RFE, and Gini contrast. Three classifiers (SVM-LIN, SVM-RBF, and RF) exhibit consistent differences when trained on the selected voxels. The curves show the AUC for all classes, and all subjects. Dotted lines show subject-specific accuracy; solid lines show the average accuracy across subjects.

The random forest classifier achieves the best classification performance for both ranking schemes (Gini and RFE) (Fig. 6). More importantly, the Gini contrast ranking has an advantage over the RFE ranking for small voxel sets regardless of which of the two non-linear classifiers (RF, and SVM-RBF) is used for classification. That is, both non-linear classifiers can take advantage of the information in the voxels ranked high by Gini contrast. Gini contrast ranking together with random forests achieves the best classification performance in the entire experiment.

We find the peak performance of the nonlinear classifiers to be at about 200–400 features, i.e., when using at most 1% of the features. The observed advantage of the RF classifier may be attributed to the match between the feature importance measure and the classifier. The two SVMs exhibit comparable performance on larger feature sets, but we observe a significant advantage of the nonlinear classifier on small feature sets. Specifically SVM-RBF with the top 400 features performs equally or better than the linear SVM with any of the voxel subsets selected by Gini contrast or RFE. Overall, the Gini contrast seems to identify features relevant to nonlinear relations between observations and stimuli, better than the recursive feature elimination.

In summary, for all classifiers in the experiment the maximum classification performance is reached by Gini ranking with smaller numbers of voxels than what is required by other rankings. The observations regarding linear SVM and SVM-RBF accuracy are consistent with the expectation that Gini contrast selects voxels with both linear and non-linear relationship to the class label, while RFE with linear SVMs selects those features with a linear relationship to the class label.

5.4. Consistency of the selected regions across data

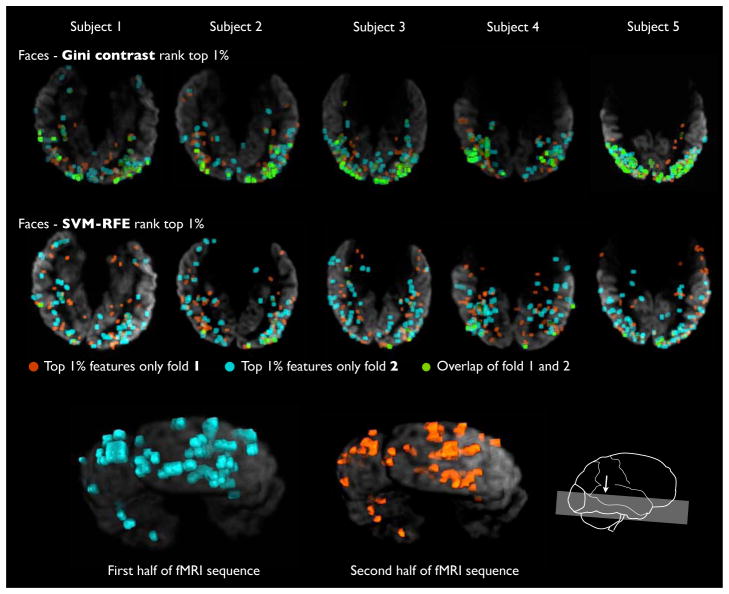
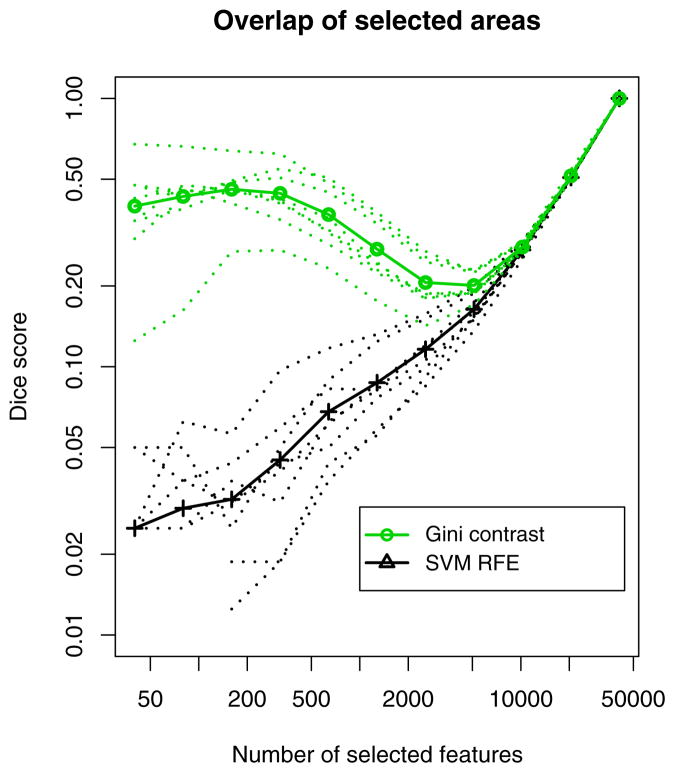
Fig. 7 shows the top 1% of voxels for two folds of the cross-validation for the Gini contrast (top row), and RFE (bottom row). Here we examine face-selective areas of the brain. For each number of chosen voxels, we compute the Dice measure of volume overlap (Dice, 1945) between the sets of top-ranked voxels in the two training sets. The average Dice coefficient between the two sets is 0.35 (ranging from 0.21 to 0.54) for Gini contrast, and 0.06 (ranging from 0.05 to 0.08) for RFE. Fig. 8 reports the Dice measure of overlap between voxel subsets selected by RFE and Gini contrast on two different parts of the fMRI data. For RFE, the amount of overlap scales linearly with the number of selected voxels, indicating that randomness – or lack of appropriate regularization – is present in the recursive feature selection process. In contrast, for Gini contrast, we find a set of several hundred top ranking features (less than 0.5 % of the total number of voxels) that are shared during cross-validation. The Dice scores behave distinctly different from the random scaling found for RFE, until more than approximately 10% of total features are added, which presumably contain more noise than the initial top features.

Figure 7.

Consistency across trials: Gini contrast ranking vs. SVM RFE ranking of voxels. Top 1% of the voxels is shown for the first half of the time course in red, and the second half of the time course in blue. The overlap between the two sets is shown in green. In the bottom row the voxel sets for Subject 1 are shown on the 3D view of the cortex.

Figure 8.

Dice measure of overlap between identified voxels in the two-fold cross-validation. Voxel sets selected by Gini contrast (green) exhibit far higher overlap compared to those selected by RFE (black). The thick lines show the mean over all subjects and all categories. The thin lines show average overlap for each category separately. Both axes use log scale.

6. Discussion

The premise of employing multi voxel pattern analysis in fMRI studies is that the relationship between BOLD signals and stimuli can be captured by multi-voxel classifiers. Furthermore this approach assumes that the patterns detected reveal information about the role of brain regions during cognitive processes.

The search for selective, or diagnostic regions in the neuroscientific context, is equated with the selection of informative features - a preprocessing step for classification. There are different approaches for selecting features, or voxels, driven by the objective to improve the classifier performance. The individual time courses of the selected voxels do not necessarily correlate with the experimental protocol, but are a part of potentially complex patterns that predict the stimulus.

The approaches used in the neuroscientific community transitioned from including anatomical regions known a priori to employing univariate criteria to select regions (Friston et al., 1994), and then to recursive feature elimination schemes that take the properties of a specific classifier explicitely into consideration (Hanson and Halchenko, 2008). This has made the relationship between feature selection and the detection of active regions more complex, and subject to potential bias introduced by the feature selection method (Norman et al., 2006).

In this paper, we use the Gini contrast to rank voxels according to their potentially non-linear and multivariate relationship to the set of the stimuli in the experiment. The scoring is inherently multi-class and captures both the relationship of a voxel’s timecourse to individual categories of stimuli (in our case, different visual object categories), and its contribution for the differentiation among categories. We do not perform any preselection of the regions other than confining the analysis to an anatomical segmentation of the cortex in the recorded fMRI data. No parameter optimization or regularization was performed as part of the Gini contrast computation. The classification of the visual categories is not the focus of this paper but only a means to quantify the information encoded in the voxels in a comparative way. To obtain a balanced view and avoid bias towards a specific classifier and feature selection pair, we performed validation with three different classifiers.

6.1. Experimental Findings

The experiments revealed several interesting findings.

1. Multivariate non-linear scoring of voxels identified regions related to the stimuli that are consistent across cross validation trials and across subjects. Some of these regions are missed by univariate criteria. This suggests that the Gini contrast score yields a more accurate indication of the relation between voxels and stimuli than the t-test and the F-test. Specifically, Gini contrast captures multi-voxel relationships that cannot be detected by univariate criteria. The results substantiate this hypothesis. The performance of the classifiers trained on the voxel sets selected based on the Gini contrast tends to peak at high accuracy for relatively small feature set sizes (Fig. 2), implying that the information about the stimulus in the highest ranked voxels is higher than for univariate criteria. The t-test and F-test do not capture multivariate relations, and thus comparable sizes of top ranked voxel sets include possibly noisy voxels with weak univariate relationships to the stimuli.

Comparing voxel selection by Gini contrast and univariate criteria (t-test, F-test) based on the classification performance of the classifier on a separate test set reveals two important differences in the ranking. The Gini contrast selects regions if they exhibit strong univariate or multivariate relation to the stimulus differentiation. Most of the regions selected by a t-test are also selected by Gini contrast. However with equal number of top-ranked voxels, Gini contrast selects additionally regions that exhibit primarily a multivariate relation to the stimulus, and are completely ignored by the univariate criteria. In a related phenomenon, the voxels selected by the Gini contrast form tighter spatial clusters.

An example of this behavior is illustrated in Fig. 3. The two individual highlighted regions do not differentiate between face and non-face with sufficient specificity to be selected by the t-test. However as a joint feature set, they do relate to faces. The corresponding mean BOLD signals reveal this form of relationship. Fig. 5 depicts the regions selected by Gini contrast but not by the t-test for all subjects in the study. There is a qualitative level of consistency across subjects that indicates that the multivariate regions are characteristic to the face stimuli across subjects.

2. The ranking of the voxels by a multivariate non-linear criterion like Gini contrast more accurately captures the information contained in individual voxels. We quantitatively compared the feature selection methods based on the score assigned to the voxels by random ranking, t-test, F-test, and Gini contrast. We used the classification performance in a two-fold cross validation as an indicator for the information captured in the selected voxels. Fig. 2 shows that the methods outperform random ranking, as expected. The important difference between the univariate rankings and Gini contrast is in the highest ranked voxels. We note that Gini contrast yields higher classification accuracy. The advantage is particularly pronounced in the top 2% of the voxels. While the classifiers based on the univariate criteria gradually improve the performance, as more voxels are included, the Gini contrast selection leads to a fairly early peak in classification accuracy.

It is interesting to compare the classifiers’ performance for the random ranking. In contrast to the SVMs, random forests utilize the information in the randomly selected 10,000 voxels (approximately a quarter of all voxels) to achieve competitive classification performance, even though a majority of the included voxels are not informative. This phenomenon is related to the observations made in (De Martino et al., 2008): high classification performance indicates presence of informative voxels, not the absence of noise.

3. Gini contrast outperforms RFE with linear SVMs in terms of ranking and selection of informative voxels, and in terms of stability of the selection. The effect is similar to but less pronounced than what we observed in comparisons to univariate criteria. RFE reaches the peak performance for larger sizes of the selected voxel sets than Gini contrast. Furthermore, the regions selected by Gini contrast exhibit better stability than those selected by RFE (Fig. 7). While the RFE regions have only small overlap between training sets, Gini contrast regions show significantly higher overlap. Since both methods yield similar classification performance, this calls for caution using classification performance as a singular criterion, if voxel identification is the primary aim. Despite of comparable classification performance, the repeatability of the voxel sets is substantially different for the two ranking methods. Similar observations have been made in prior literature (Kjems et al., 2002; LaConte et al., 2003; Strother et al., 2002; Pereira et al., 2009). The non-linear classifiers like SVM-RBF, and random forests reveal a quantitative classification difference favoring the Gini contrast regions. This is in agreement with the high overlap of the selected regions in different training sets of the cross-validation, and gives reason for confidence in the identified brain regions. It is consistent with the hypothesized robustness of the Gini contrast measure for ranking of the voxels in fMRI.

6.2. Pitfalls of multi voxel pattern analysis

There is a conceptual difference between the activations detected by a general linear model (GLM) that takes the increase of oxygenation as an indicator for the relationship to the stimulus, and the classifier based identification of multi voxel patterns (Haynes and Rees, 2006; Norman et al., 2006). While the former associates the correlation of BOLD signal increase with a specific stimulus, the latter uses multiple voxels to differentiate between stimuli. One criticism of GLM is noted in (Hanson and Halchenko, 2008) where the authors conclude that for example, the efficiency of a brain region in terms of energy consumption can confound the significance of the GLM paradigm. In contrast multi voxel patterns aim to differentiate between stimuli, or conditions, by using BOLD signals in multiple voxels together with statistical classifiers. While this approach makes the observation of complex and interconnected characteristics possible (i.e., beyond the correlation between a single BOLD signal and the stimulus) it can lead to ambiguous results if used for the identification of informative voxels. The patterns might include voxels that are not informative but do not deteriorate the classification results. It can also exclude parts of informative but highly correlated voxels. Both cases result in only partial overlap between regions identified by the algorithm, and those actually related to the stimulus.

For example, a method that treats the reduction in classification performance when a certain voxel is excluded as an indicator of the voxel’s diagnostic value, can detect informative voxels. But such a method would exclude voxels that are informative but highly correlated to other informative voxels. SVM-based rankings tend to score informative but highly correlated voxels lower than single voxels with the same contribution to classification performance that are not strongly correlated with other voxels in the volume. One way of constraining the voxel selection and minimizing this ambiguity is a tolerant univariate activation detection by a standard GLM and only a subsequent restriction of the analysis to the selected regions. In (De Martino et al., 2008; Haynes et al., 2007) a GLM-based detection of voxels that exhibit an activation effect precedes the multi voxel pattern analysis. However, the disadvantage of this strategy is that it can exclude regions with low univariate characteristics but high multivariate predictive power. In our experiments, we did not perform a prior exclusion of regions based on GLM.

In contrast to the methods above, Gini contrast exhibits a grouping effect. It ranks informative voxels equally high, even if their time courses are strongly correlated. Furthermore, bagging and random feature selection during the Random Forest training and Gini contrast calculation provides robustness against noise and ensures stability even though the size of the training set is small (300 time points) compared to the dimensionality of the data (40,000 voxels).

7. Conclusion

Identification of diagnostic brain regions by means of classifiers and multi voxel patterns requires careful choice of the classifier, the voxel selection criterion, and the inference made from the selected regions. In our experiments, we observed that Gini contrast as a voxel selection score identifies regions detected by univariate criteria and additional informative regions consistently missed by univariate criteria. Regions selected by the Gini contrast measure exhibit substantial overlap for different fMRI data trials for the same subject and across subjects. Gini contrast is a multi-class multivariate criterion, that eliminates the need for regularization or pre-selection of regions. The results indicate that it is a promising choice for the detection of multi voxel patterns in fMRI data.