Abstract
Human immunodeficiency virus (HIV-1 or simply HIV) induces a persistent infection, which in the absence of treatment leads to AIDS and death in almost all infected individuals. HIV infection elicits a vigorous immune response starting about 2–3 weeks post infection that can lower the amount of virus in the body, but which cannot eradicate the virus. How HIV establishes a chronic infection in the face of a strong immune response remains poorly understood. It has been shown that HIV is able to rapidly change its proteins via mutation to evade recognition by virus-specific cytotoxic T lymphocytes (CTLs). Typically, an HIV-infected patient will generate 4–12 CTL responses specific for parts of viral proteins called epitopes. Such CTL responses lead to strong selective pressure to change the viral sequences encoding these epitopes so as to avoid CTL recognition. Indeed, the viral population “escapes” from about half of the CTL responses by mutation in the first year. Here we review experimental data on HIV evolution in response to CTL pressure, mathematical models developed to explain this evolution, and highlight problems associated with the data and previous modeling efforts. We show that estimates of the strength of the epitope-specific CTL response depend on the method used to fit models to experimental data and on the assumptions made regarding how mutants are generated during infection. We illustrate that allowing CTL responses to decay over time may improve the fit to experimental data and provides higher estimates of the killing efficacy of HIV-specific CTLs. We also propose a novel method for simultaneously estimating the killing efficacy of multiple CTL populations specific for different epitopes of HIV using stochastic simulations. Lastly, we show that current estimates of the efficacy at which HIV-specific CTLs clear virus-infected cells can be improved by more frequent sampling of viral sequences and by combining data on sequence evolution with experimentally measured CTL dynamics.
Keywords: acute HIV infection, escape mutations, CTL response, cost of escape, mathematical model
1 Introduction
Viruses replicate within cells. In order for the immune system to recognize that a cell is infected, fragments of viral proteins or peptides, typically 8–10 amino acids in length, called epitopes, are presented on the surface of infected cells bound to major histocompatibility complex (MHC) class I molecules [51, 35]. These complexes of viral peptides and MHC-I molecules are then recognized by cytotoxic T lymphocytes (CTLs) and this recognition leads to the death of virus-infected cells [2].
Because CTLs can recognize and kill virus-infected cells, they play an important role in the control of many viral infections. However, many viruses, including cytomegalovirus and HIV persist, developing into chronic infections despite very strong virus-specific CTL responses [49, 34]. Viruses have evolved different strategies to avoid recognition by CTL including downregulation of MHC-I molecules [52, 3] and generation of mutants that are not recognized by CTLs, a process called “escape”. Some of these mutations affect binding of viral peptides to MHC-I molecules and other mutations affect the ability of CTLs to recognize the peptide-MHC complex [22]. Mutations at several different sites within and sometimes outside the epitope sequence can lead to viral escape [1, 12, 22, 43]. As a result, viral mutants that are not recognized by epitope-specific CTLs have a selective advantage and accumulate in the population over time [34].
Escape of HIV from CTL responses has been documented from months to years after infection [8, 26, 20, 34, 1, 12, 22] and escape from T cell immunity may potentially drive disease progression [40]. Also escape from CTL responses may influence the efficacy of vaccines that aim at stimulating T cell responses. Thus, understanding the contribution of different factors to the rate and timing of viral escape from CTL responses may help in designing better HIV vaccines.
A number of mathematical models have been developed to describe the kinetics of viral escape from T cell immunity. Here we review some of these models, show novel model developments, and discuss directions of future research.
2 Modeling viral escape from a single CTL response
During acute HIV infection there are several HIV-specific CTL responses (on average around 7 [48, 20]), each recognizing a different viral epitope. As the virus can escape from all these responses escapes do not generally occur at the same time; some escapes occur very early in infection and some late [16]. Initial models of viral escape only examined virus evolution in response to a single CTL response [13, 4, 15] and we will discuss these first.
2.1 Mathematical model
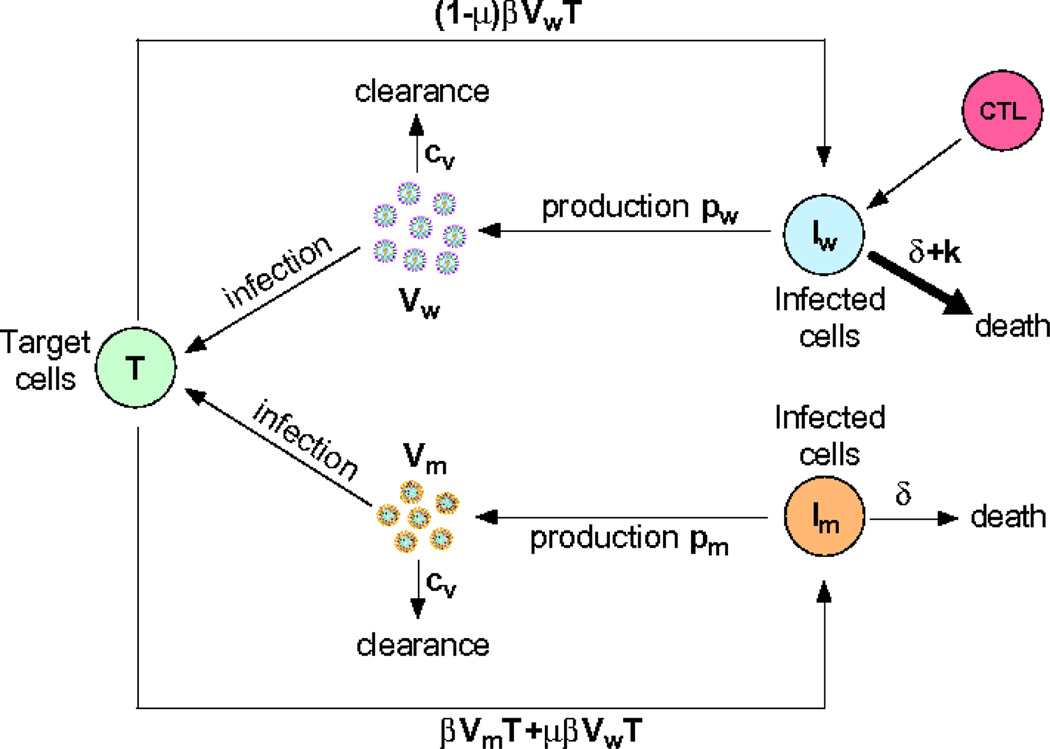
To describe virus escape from a single CTL response we start with the standard model for virus dynamics in which virus infects target cells, i.e., cells susceptible to infection, and infected cells produce virus (Figure 1). The model is formulated as a system of ordinary differential equations
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
where T is the density of uninfected target cells, produced at rate λ and dying at per capita rate d. Infection is assumed to occur via a mass-action like term with rate constant β. Cells can be infected with either wild-type (the infecting strain) virus, Vw, or escape mutant virus, Vm leading to the generation of infected cells, Iw and Im, respectively. Infected cells are assumed to die at rate δ per cell due to viral cytopathogenic effects, and at rate k per cell due to killing by CTLs. Since the escape variant is not recognized by CTLs, the term proportional to k is absent in the Im equation. When an infecting virus is reverse transcribed errors in copying occur at the mutation rate μ. We neglect back mutation from mutant to wild-type but this could easily be added to the model. The constants pw and pm are the rates of virus production by cells that are infected with the wild-type and escape viruses, respectively, and cV is the clearance rate of free viral particles.
Figure 1.
Schematic illustration of the model of virus dynamics and escape from a CTL response. Symbols are defined in the text.
In this model we made several simplifying assumptions. We assumed that the wild-type and escape viruses differ only in the rate of virus production; generally pw ≥ pm (but see [20]). It is also possible that mutations that lead to escape from the CTL response also affect viral infectivity, β, especially if they occur in the envelope, reverse transcriptase or integrase-coding regions of the viral genome. Because viral particles are short-lived in vivo [41, 44, 53], a quasi-steady state is rapidly established in which the density of viral particles is proportional to the density of virus-infected cells, Vw = Iwpw/cV and Vm = Impm/cV. Then by substituting r = pwβT/cV, c = 1 − pm/pw, w = Iw, m = Im, we arrive at a simpler model for the dynamics of the density of wild-type and mutant viruses:
| (6) |
| (7) |
where r and r(1 − c) are the replication rates of the wild type and the mutant, respectively; c is the cost of the escape mutation defined as a selection coefficient [24, 33]. To analyze this model, it is useful to rewrite eqns. (6)–(7) in terms of the dynamics of the ratio of the mutant to the wild-type density, z(t) = m(t)/w(t)
| (8) |
Assuming a constant replication rate, r, and CTL killing rate, k, eqn. (8) can be solved analytically, where the ratio, z(t), increases exponentially with the rate ε = k − r(c − μ) ≈ k − cr (when μ ≪ c) which we call escape rate, i.e.,
| (9) |
where z0 is the ratio at t = 0. In the examples we give below, the initial time, t = 0, is the time when patients are first identified as being HIV-infected and are enrolled in a clinical study. This time of enrollment is likely to be several weeks after initial infection [17, 18]. Similarly, the onset of CTL selection tends to be a few weeks after infection [17, 18]. Equation 9 is only valid after the CTL selection has started and one has to allow for the uncertainty of t = 0 relative to the onset of selection by adjusting z0.
The dynamics of the ratio in eqn. (9) is described by 3 parameters but only 2 parameters can in general be estimated from the available viral sequence data [15, 16]. Therefore, two limiting cases of the general model can be found. If rate of mutation is small and the escape variant is initially present at a non-negligible frequency so that z0 > 0, then the generation of escape variants by mutation may be neglected, and the frequency of the escape variant in the viral population is given by the logistic equation
| (10) |
where f0 = z0/(1 + z0) is the initial frequency of the escape variant in the population. Alternatively, if the initially escape variant is not present and is generated by mutation from the wild-type (i.e., μ > 0 and z0 = 0) then the frequency of the escape variant in the population is given by
| (11) |
where now f0 = μr/ε. It should be noted that at large times (tε ≫ 1), the dynamics predicted by eqn. (11) and eqn. (10) are identical. In a later section we discuss the situation where the escape variant is generated stochastically by mutation. By fitting eqn. (11) or eqn. (10) to experimental data, rates of viral escape ε from a given CTL response can be estimated. In many previous studies, the logistic equation (eqn. (10)) that assumes that both wild-type and escape variant were present at t = 0, has been used [4, 15, 20, 16].
The basic model assumes that the rate of viral escape from a given CTL response is constant over time which in general implies a constant rate of CTL-mediated killing of infected cells (determined by the parameter k). Biologically, however, immune mediated selective pressure is likely to change over time, for example, because of a change in the magnitude of the epitope-specific CD8+ T cell responses [20]. If the CTL killing efficacy, and as result the escape rate, changes exponentially over time, e.g., ε(t) = ε0e−at, the change in the frequency of the mutant virus in the population over time can be obtained analytically by solving eqn. (8)
| (12) |
| (13) |
where . As before to reduce the number of parameters in the model we can assume that either the escape variant is present at t = 0 (z0 > 0 and μ = 0) or is generated by mutation (z0 = 0 and μ > 0).
2.2 Data and estimating model parameters
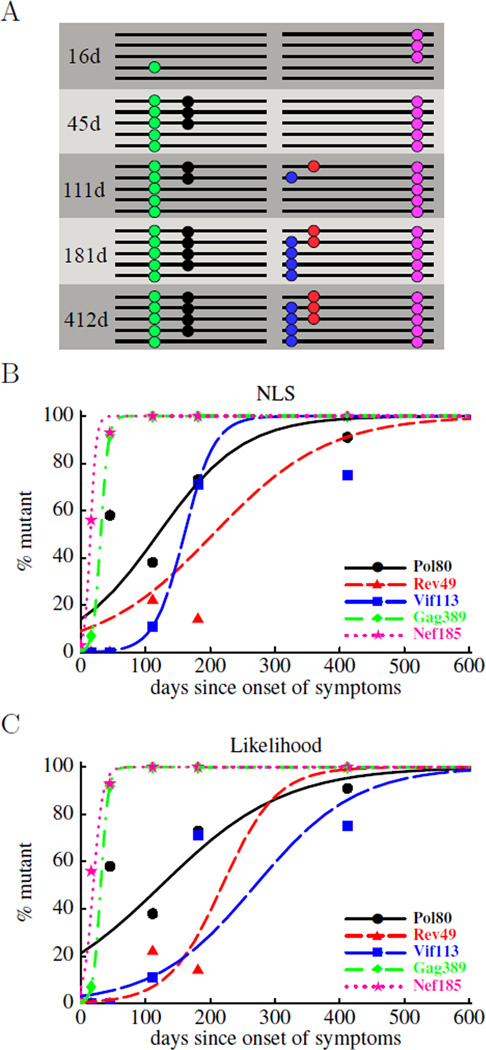
Evasion of the CTL response by HIV occurs as the virus mutates epitopes that are recognized by virus-specific CTLs. This escape process can be studied by monitoring the sequence composition of the viral population during infection. Over the last few years, detection of viral escape mutations has been improved in two major ways. First, HIV RNA isolated from peripheral blood is diluted to the point that a single RNA molecule is expected to be present in a given sample. Then the RNA is reverse transcribed, amplified, and sequenced resulting in the sequence for a given virus being obtained (so-called single genome amplification and sequencing, SGA/S). When multiple viruses are sequenced by SGA/S (in general about 10 to 20 per time point), the sequences are compared at sites coding for a CTL epitope and changes in the percent of the wild-type/transmitted sequence in the population are followed over time [20, Figure 2A]. Second, deep sequencing can be done in which a relatively short RNA region (about 150–300 nucleotides) is sequenced in the population [14]. Although deep sequencing only allows one to follow changes in a small region in the viral genome many more sequences can be obtained than in the SGA/S protocol (from 102 to 104).
Figure 2.
Schematic representation of experimental data on HIV escape from CTL responses (panel A) and fits of the mathematical model to such data (panels B and C). In panel A, a small number of sequences covering either the 3’ or 5’ half of the HIV genome has been obtained at 5 different time points. Escape mutations are indicated as colored dots. Typical sequence sample sizes range between 10 and 20. In panels B and C we show the fits of the mathematical model (eqn. (10)) to experimental data using nonlinear least squares (panel B) or likelihood (panel C) methods. We estimate two parameters: the rate of escape, ε, and the initial frequency of the escape variant in the population, f0. The estimated escape rate obtained by both methods is shown in Table 2.
An example, taken from ref. [20], of such time course data of HIV immune escape is shown in Figure 2. The figure shows a schematic of the sequenced genomes and the frequencies of escape mutations estimated as the fraction of times a mutation is observed in the sample. Since samples are small (about 10–20 sequences each), the frequency estimates come with substantial uncertainty. Using data of this kind, we would like to infer escape rates associated with CTL responses specific to different HIV epitopes using the models discussed above.
Previously, data on viral escape have been analyzed by assuming that some mutants are present at time t = 0, using a logistic equation [13, 4, 15] and fitting the model to the data using nonlinear least squares leaving f0 completely unconstrained. This yields results as shown in Figure 2B. Although this method often provides a reasonable description of the data it does not weight the different data points according to the uncertainty associated with them. Although weighted least squares can take this uncertainty into account, we propose here to use a more direct approach based on calculating the likelihood of the data given our model. Similar methods have been developed in the context of evolution experiments and the evolution of cancer [25]. The likelihood of sampling a certain number of mutants at different time points, given a particular escape rate, ε, and the initial mutant frequency, f0, is derived as follows.
Finding k mutations in a sample of size n when the true frequency is f(t) has the binomial probability
| (14) |
The data set in general contains several samples of different sizes, ni, sampled at different times ti. Given a frequency trajectory, f(t), such a data set therefore has the likelihood
| (15) |
Our model parameterizes the frequency trajectory of individual escapes with the escape rate ε, and the initial frequency f0. Ignoring all terms that do not depend on ε or f0, we obtain up to a constant
| (16) |
By maximizing this log-likelihood we obtain maximum likelihood estimates of the parameters f0 and ε. The confidence interval of this estimator can be obtained by calculating the curvature of the likelihood surface or by bootstrapping the data using a binomial distribution [16]. Furthermore, to constrain some of the parameters of the model (e.g., the initial frequency of the escape variant, see below) we can use a prior favoring some values over other.
We applied both nonlinear least squares and likelihood methods to the data shown in Figure 2B on escape of HIV from five different CTL responses in patient CH40 [20, 16]. While both methods allow a reasonable description of the data, the estimates of the escape rate from a given CTL response obtained by the two methods are often different (Table 2). For example, for viral escape from the Rev49-specific CTL response, likelihood predicts more rapid escape than the nonlinear least-squares method. In part, this arises because of the oscillations in the measured frequency of the mutant sequence in the viral population which initially increased, then decreased, and then increased again. A similar argument applies to the data on escape from the Pol80-specific CTL response.
Table 2.
Estimates of the rate at which HIV escapes from CTL responses specific to different viral epitopes. We fit a mathematical model (eqn. (10)) of HIV escape from a CTL response specific to a single viral epitope using nonlinear least squares (NLS) or maximum likelihood (eqn. (16)). The epitope is given in the first column and the estimated escape rate, ε, in the subsequent columns. To investigate the influence of interference between escapes at different epitopes we performed stochastic multi-locus simulations and determined the escape rates that maximize the likelihood of observing the data averaged over several runs of the stochastic simulation (see main text). In these simulations, we assumed that CTL responses started 30 days before the first patient sample was obtained; the estimated escape rates for early escapes are higher if this delay is shorter. The estimated rates are given in the column labeled “multiple epitopes”. The estimated escape rates can depend strongly on the model and method. One has to strike a delicate balance between a too complicated model whose parameters cannot be determined due to insufficient data, and a too restrictive model with a well-defined optimal solution that is nevertheless inaccurate since the model was inappropriate. The rather exible model used in [16] with two parameters per epitope results in large confidence intervals for estimated rates of viral escape (e.g., see [16]).
| Epitope | Single Epitope | Multiple Epitopes | ||
|---|---|---|---|---|
| ε, day−1 (NLS) | ε, day−1 (Likelihood) | ε, day−1 (Likelihood) | ||
| Pol80 | 0.02 | 0.01 | 0.05 | |
| Rev49 | 0.01 | 0.02 | 0.03 | |
| Vif113 | 0.04 | 0.01 | 0.02 | |
| Gag389 | 0.17 | 0.17 | 0.15 | |
| Nef185 | 0.22 | 0.14 | 0.18 | |
There are two problems with some of the model fits. First, some of the fits predict a very high mutant frequency at time t = 0 (e.g., for Pol80 f0 ≈ 0.2), which is inconsistent with the experimental data. Second, the confidence intervals on the estimated escape rates are very large (results not shown and [16]). The underlying reason for the latter ambiguity is that without sufficient data, the initial mutant frequency and escape rate are correlated, and in general larger initial frequencies lead to lower escape rates. To reliably estimate two parameters, we have to have at least two measurements where the mutant frequency is between 10 and 90% (and the data needs to be consistent with logistic growth; more on that below).
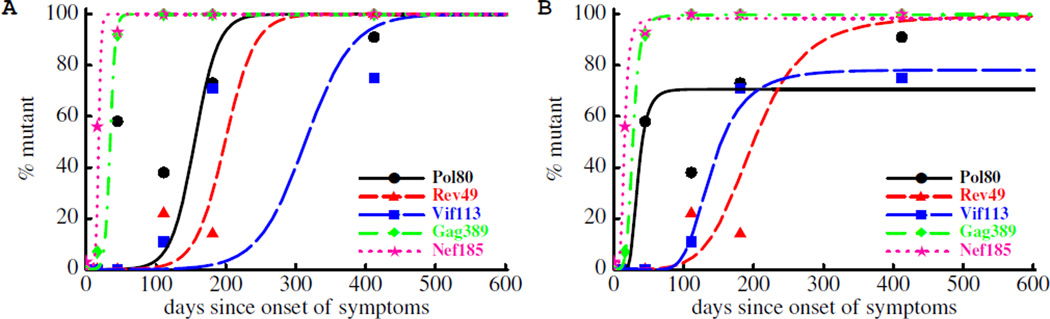
To circumvent both of these problems, one might be inclined to constrain f0 to be less than a prescribed cut-off (e.g., f0 < 10−4). Doing so reduces the variability of the fits and generally results in larger estimates of the escape rates (Figure 3A and Table 3). At the same time, the fits of the model to data on late escapes get substantially worse as early data points are not described by the model. These inferior fits point toward the inadequacy of the model. One potential explanation for this discrepancy between data and the model is that the escape rate may be changing over the course of infection [15]. Indeed, over time the magnitude of the CTL response may decrease leading to a decreased selection pressure on the virus, and as a result, a slower rate of escape later in infection. Indeed, allowing the escape rate to change over the course of infection leads to a significantly better description of the data at least for some escapes (Figure 3B and Table 3). Another feature that is missing from the model is the simultaneous escape from multiple epitopes, which we discuss at greater length below.
Figure 3.
Impact of constraining the initial mutant frequency, f0, on the kinetics of viral escape. In panel A we show fits of the model (eqn. (10)) to the sequence data obtained assuming that the initial frequency of escape variant is lower than fc = 10−4. The fit is done by adding an extra penalizing term 10105(f0−fc) to the log-likelihood (eqn. (16)). The constraint leads to much higher estimates of the escape rate (Table 3) but in a poor description of the data. In panel B in addition to the constraint to the initial mutant frequency we allow the escape rate to decline over the course of infection (eqn. (13)). This extension improves the fit of the constrained model to data for 3 out 5 epitopes (Table 3).
Table 3.
Estimates of the escape rate in the model where the initial frequency of the escape variant is constrained to be lower than fc = 10−4. In the 1st column we list the epitopes in which escape occurs. In the 2nd column we list estimates of the escape rate assuming a constant escape rate and using eqn. (10) and eqn. (16) with a penalizing term 10105(f0−fc) added to the log likelihood. Model fits are shown in Figure 3A. In the 4th and 5th columns we list estimates of the initial escape rate and the rate of decline of the escape rate assuming that the escape rate declines over time using eqn. (13) and eqn. (16). Fits are shown in Figure 3B.
| Model | Constant ε | Decreasing ε | |
|---|---|---|---|
| epitope | ε, day−1 | ε0 day−1 | a, day−1 |
| Pol80* | 0.06 | 2.55 | 0.09 |
| Rev49 | 0.05 | 0.07 | 0.01 |
| Vif113* | 0.03 | 0.76 | 0.02 |
| Gag389 | 0.27 | 0.53 | 0.04 |
| Nef185* | 0.51 | 1.04 | 0.08 |
For the 3 epitopes indicated by * allowing the escape rate to change over time significantly improved the quality of the model fit to data (likelihood ratio test, p < 0.0001).
In summary, the model for viral escape from a single CTL response can be used to estimate CTL-mediated pressure on the wild-type transmitted virus using different statistical methods. If enough data is available for a reliable estimate of ε and f0 and the model predictions are compatible with the observed data, direct estimation by fitting a logistic involves the smallest number of assumptions. The estimated escape rate might still be an underestimate due to variable selection strength and the escape rate estimated using eqn. (11) or eqn. (10) should be treated as the average escape rate in the observed time period [15, 16]. With limited data, more robust estimates can be obtained by constraining the initial frequency of escape mutants at the first time point, but its validity rests on additional data on the time when the CTL response to a given epitope is generated.
With these caveats in mind, the estimates nevertheless suggest that virus-infected cells are killed by the virus-specific CTL responses with rates ranging from 0.01 day−1 to 0.4 day−1 [4, 16, 14], and if the escape rate changes with the time since infection for a given epitope, killing rates could be even higher (Table 3). Given that HIV-infected cells have a death rate of ~ 1 day−1 [41], this work suggests that CTL responses contribute substantially to the control of HIV at least during acute infection.
2.3 Effects of sampling depth and frequency on fitting performance
To perform a more systematic analysis of the fidelity of the different fitting methods, we simulated escape trajectories using the computational model for escape dynamics introduced below. From this simulated data, we can produce a series of samples of different size and mutant frequency and try to reconstruct the parameters that were used in the simulation. The question we address here is: if we want to improve estimates of the escape rate how should the data collection be improved.
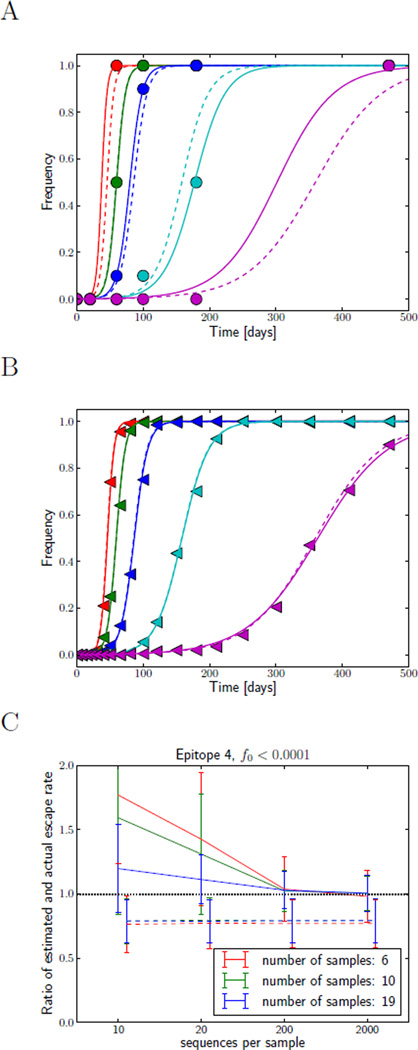
Figure 4 A&B show two runs of the simulation with shallow and infrequent (A) and deep and frequent sampling (B). Deep sampling will be readily achieved in forthcoming experiments since new sequencing technologies allow deep sampling at low cost. The frequency of sampling, however, will likely remain limited. Panel C shows how well the escape rate of epitope 4 can be reconstructed from sample series of different depth and frequency. The fitting procedure that attempts to determine both f0 and ε is rather noisy and biased for small and infrequent sampling. Both deep and frequent sampling allows one to overcome this problem. On the other hand, the method that only fits the escape rate and assumes that variants are present at a small frequency, f0, when selection starts, consistently underestimates the escape rate, but does not fluctuate a lot. We will see below that this underestimate is a consequence of delayed escape due to interference between different epitopes.
Figure 4.
Influence of sampling frequency and sampling depth on fidelity of esimates of the escape rate. Panels A and B show mutation frequencies in population samples for infrequent shallow sampling (n = 10, A), and more frequent deep sampling (n = 200, B). The actual mutation frequencies are shown as dashed lines, the sample frequencies are indicated by symbols, while the fitted trajectories as solid lines. Obviously, more frequent and deeper sampling will improve the estimates of the escape rate. This is quantified in panel C. It shows the mean estimate of the escape rate of epitope 4 (left pointed triangles) and its standard deviation as a function of sampling depth for different sampling frequencies. The estimates are shown relative to the true value of the simulated escape rate, hence a systematic deviation from one represents a bias. The dashed lines show the results of fitting only the escape rate, ε, while fixing f0 = 10−4. Those fits show a systematic bias towards lower estimates, but have small variance and are insensitive to sample depth or frequency. The solid lines correspond to estimates where both ε and f0 were fitted, while constraining f0 to be smaller than 10−4. These fits show much larger variance and a strong bias at small sampling frequencies, but are unbiased at frequent and deep sampling.
In order to estimate the escape rate and the initial frequency reliably, we need to sample a trajectory at least twice at intermediate frequency. This can be achieved both by deep or frequent sampling. We would like to caution, however, that low frequencies are very susceptible to fluctuations and rare variants found in a deep sequencing experiment should not be assumed to follow a deterministic trajectory.
3 Modeling viral escape from multiple CTL responses
While the model of viral escape from a single CTL response gives a general idea of the rates involved in CTL escape, it is not a priori obvious whether ignoring the simultaneous escape of other epitopes is justified. Different epitopes are encoded by the same viral genome and as such are not independent. The analysis of multiple simultaneous CTL escapes is complicated by the large number of possible combinations of epitopes. In the next section, we formulate a model for multiple simultaneous escapes as well as for mutation and recombination that give rise to novel combinations of epitopes.
3.1 Mathematical model
We assume that there are in total n CTL responses that control viral growth and, potentially, the virus can escape from all n responses. A CTL response that recognizes the ith epitope of the virus kills virus-infected cells at rate ki, and escaping from the ith CTL response leads to a viral replicative fitness cost ci. We denote a viral genome by a vector i = (i1, i2,…, in) with ij = 0 if there is no mutation in the jth CTL epitope and ij = 1 if there is a mutation leading to escape from the jth CTL response. The death rate of an escape variant due to the remaining CTL responses is then simply , where k1, k2,…, kn are the death rates of infected cells due to killing by the jth CTL response. Note that we have assumed that killing of infected cells by different CTL responses is additive. Extending models for viral escape with other mechanisms of CTL killing is an important area for future research.
Escape from a given CTL response incurs a fitness cost to the virus. Assuming multiplicative fitness, the fitness of a variant i is ∏j(1 − cjij). Although there is evidence for compensatory evolution in and around individual epitopes, we do not expect strong epistasis between mutations in epitopes in different parts of the genome.
Given that most HIV infections start with a single transmitted/founder virus [28], we need to describe the generation of the escape variants from the founder strain. Even though the viral population during acute infection may attain a large peak where there might be around 1010 infected cells, we cannot assume that all possible viral genotypes are present early on. Because μ3 ≈ 10−14 is so small we do not expect to generate a virus with more than two mutations in a single generation. Multiple mutations therefore have to accumulate in the course of infection and the appearance of these multiple mutants is delayed, as illustrated with simulation data in Figure 6. Mutation dynamics therefore has to be included in the model. Genotype i can arise by mutation with rate μ per epitope if a cell gets infected with a viral strain lacking one of the mutations in i:
| (17) |
where i\j denotes genotype i without mutation j and V (i) is the abundance of virus with genotype i. We are mainly interested in the generation of escape mutations and will therefore ignore back mutations. Similarly, we will for now ignore that genotypes are lost by mutations at all sites that have not yet escaped (this term will be reinstantiated later). Both of these contributions have negligible effects on the dynamics since they do not involve genotypes that are favored by selection. Furthermore, back mutations will occur at a slower rate because escape mutation may occur at several positions in the epitope (8–10 amino acids) while back mutations have to occur in the same place as the escape mutation.
Figure 6.
Influence of stochastic effects on CTL escapes. The rise of escape mutations in the stochastic model (dashed lines, 10 realizations) is delayed relative to the deterministic model (solid lines) at low coinfection rates (left panel, coinfection rate 0.01). This delay is much shorter at increased coinfection frequencies (right panel, coinfection rate 0.2), suggesting that the delay is mainly due to interference between epitopes. The population size is 106.
In addition to mutation, novel genotypes can also be generated by recombination of two existing HIV genomes. Diversifying recombination in HIV requires coinfection of a host cell with virions carrying different genomes, which are crossed over by template switching in subsequent generations [31] (Figure 5). The coinfection frequency was estimated to be on the order of a few percent or less [37, 6, 27] and is denoted here with the symbol ρ. We could extend the model to include cells coinfected with different viral genotypes, but we will simply assume that the fraction of viruses that are heterozygotes (see Figure 5) with genotypes j and k is proportional to product of the fraction of genotypes j and k in the total population, i.e., N−2V (j)V (k), where N = ∑i V (i) is the total number of virus particles. After infection with such a heterozygote virus, template switching will produce a chimeric cDNA which is then integrated into the target cell’s genome. Within this model, cells get infected with the recombinant genotype i at rate
| (18) |
where C(i|j, k) is the probability of producing genotype i from j, k by template switching. In this expression, one factor of N got canceled since eqn. (18) accounts for the total production of recombinant virus, rather than the fraction of total. The genotypes that recombine are lost when producing the recombinant genotype, which can be accounted for by a loss term −βTρV(i). The mutation and recombination terms are easily incorporated into the equations describing the viral population.
| (19) |
| (20) |
| (21) |
where I(i) is the abundance of cells infected with strain i. The fitness costs of escape mutations are hidden in the rate of virus production p(i) = p0∏j(1 − cjij). Assuming the viral population is in a quasi-steady state, we substitute , denote by f(i), and normalize using mi = I(i)/M with M = ∑jI (j), to obtain
| (22) |
The term in big parentheses accounts for selection and the loss due to recombination, while the two terms on the second line account for the gain of genotype i through mutation and recombination, respectively. In the quasi-steady state, the average clearence of infected cells ≈ δM has to equal the number of new infections, given by the product of the number of virus particles N, the infectivity β, and the target cell number T. The prefactor of the recombination term is therefore approximately equal to ρ/δ. Since different viral genotypes reproduce with different efficiency f(i), the effective mutation and recombination rates at the level of infected cells have become genotype dependent. However, we will neglect this strain dependence in the following since it only leads to small changes in the mutational input and the recombination process. Defining the effective growth rate of a strain as and the average growth rate , and an effective recombination rate ρe, we can simplify the above to
| (23) |
where we have restored the loss μ ∑j∉i mi due to mutations at wild-type epitopes.
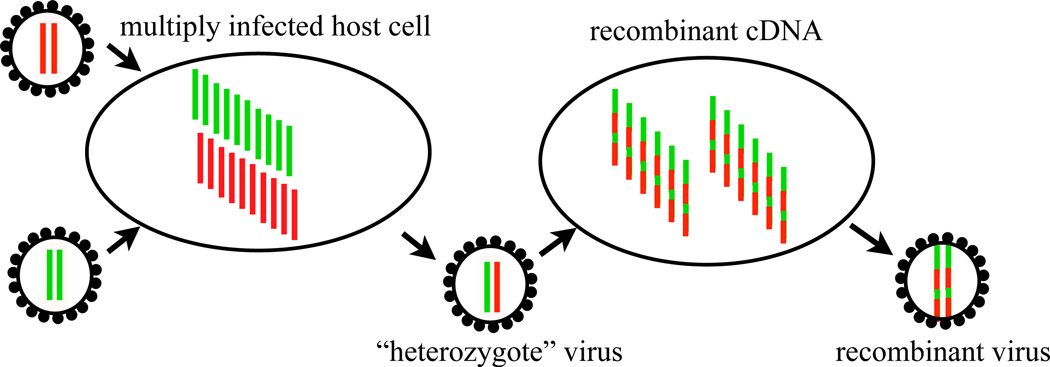
Figure 5.
Each HIV particle contains two copies of its RNA genome, from which one complementary DNA strand is produced and integrated into the host cell genome. The two RNA strands are combined by template switching of the reverse transcriptase enzyme, which can happen up to 10 times per replication [31]. The in vivo recombination rate, however, is limited by the probability that a host cell is infected by genetically distinct viruses, illustrated on the left. The effective recombination rate combining these two processes is estimated to be on the order of 10−5 per nucleotide per generation [37, 6, 27], which implies a coinfection rate on the order of a few percent.
The three terms account for changes in frequency due to differential replication and killing, mutation, and recombination, respectively. The mutation and recombination terms account both for influx and efflux of genotypes. The effective recombination rate should be thought of as the rate at which novel genotypes are produced from existing genotypes and accounts for coinfection, copackaging, and the average relatedness of copacked genomes. Within our additive model, the growth rate εi is a sum of terms accounting for the fitness costs of the escape mutations and the avoided killing.
Equation 23 provides a simpler description of the viral population than eqns. (19)–(21). The dynamics of the free virus has been slaved to the frequencies of infected cells and the complex parameters describing virus reproduction and killing have been subsumed in a simple growth rate. Models of this type have been studied intensively in population genetics. For a review of theoretical work on the evolution of multi-locus systems we refer the reader to [36]. da Silva [10] has introduced a similar model and investigated how different assumptions about mutation rates, coinfection probability, and CTL killing efficacy influence the number and timing of escapes.
Equation 23 still describes deterministic dynamics. Stochastic effects, however, are important whenever a particular genotype is present in small numbers. The stochastic features of the dynamics can be easily incorporated in computer simulations where each individual can replicate, mutate, and recombine with a certain probability each time step, see below. Examples of such stochastic simulations are shown in Figure 6, where the frequencies of escape mutations in stochastic simulations are compared to the deterministic solution of the system. The stochastic trajectories deviate significantly from the deterministic ones, in particular, when the recombination rate is low.
To appreciate how stochasticity, in combination with selection, and recombination can affect the viral population dynamics, it is useful to consider the extreme case of no recombination, i.e., asexual evolution. To produce a genotype with multiple beneficial mutations, a series of mutations in the same lineage is required since mutations happening on different genomes cannot be combined in the absence of recombination. Hence the only mutations that can successfully spread through the population are those that happen on already very fit virus and produce new exceptionally fit genomes. All other mutations, even if beneficial, are lost since they are outcompeted by fitter genotypes – a phenomenon often called selective interference [19]. Since this seeding of new exceptionally fit genotypes is a rare process that involves a very small number of viruses, and the existence or absence of such fit virus determines the future dynamics, the stochasticity of the population dynamics is important.
A particular escape mutation might have to arise multiple times until it is finally falls onto a genome that is successful. This interference can substantially delay the accumulation of mutations as is apparent in Figure 6, which shows that competition between different mutations can have substantial effects on the allele frequency trajectories. When such delays are not accounted for, the estimates of escape rates can be biased as apparent in Figure 4.
At large recombination rates genotypes are constantly taken apart and reassembled from the existing genetic variation. Escape mutations that happen on different genomes can be combined by recombination to produce better adapted virus. Hence recombination accelerates the production of recombinant virus and reduces the fluctuations of allele frequency trajectories.
The crossover between a more or less asexual population to one that behaves like a fully sexual one depends on the strength of selection. Selection operates on the fitness of entire genotypes and changes the genetic composition of the population on time scales that are inversely proportional to the fitness differences in the population. If this time scale is much shorter than the inverse recombination rate, recombination has a small impact on the dynamics. It does, however, occasionally produce new genotypes similar to mutation. If recombination is faster than selection, genotypes are taken apart and reassembled by recombination before their frequency is changed substantially by selection. In this case the frequency of the genotype is the product of the frequencies of the alleles it is composed of. In other words, recombination decouples different loci along the genome and the dynamics of allele frequencies at each locus are well described by the single epitope model.
The recombination rate of HIV is such that both of these limits are important in different phases of the infection. The frequency of recombination between distant parts on the viral genome (distance l > 1 kb) is limited by the probability of coinfection, which is estimated to be on the order of a few percent or less [37, 6, 27]. For loci closer together than a distance l, the recombination rate will be approximately 10−5 × l per generation [37]. The parameters estimated above suggest that changes in genotype frequencies are much more rapid than decoupling by recombination, at least during the early part of the infection. Hence in order to estimate the parameters of the model, we have to take the complex dynamics of a stochastically evolving population into account. During later stages of the infection, changes in genotype frequencies are much less rapid, such that distant parts of the viral genome are essentially decoupled. The effect of selection in partly sexual populations like HIV has been studied in greater detail in [46, 39, 38].
In essence, the two regimes of high and low recombination differ in what the relevant dynamical variables are. In the early regime where selection is strong, fit viral strains are amplified by selection, while mutation and recombination produce novel strains at a smaller rate. The relevant quantities are the frequencies of different strains, which happen to be the variables of our model. Later in infection, however, when recombination dominates over selection, the frequencies of mutations evolve approximately independently of each other and genotypes frequencies are slaved to these mutation frequencies [36].
Whether one or the other description is appropriate matters for the interpretation of the data. The rapid rise of several mutations that occur together as one genotype is most likely driven by the joint effect of all of these mutations. Estimates of an escape rate from the slope of the frequency trajectory would therefore correspond to an escape rate of a genotype rather than an individual mutation. For example, escape of HIV from Gag389- and Nef185-specific CTL responses occurs within the same time frame and therefore, our estimates of viral escape from individual responses (0.17 day−1 and 0.14 day−1, respectively) likely represent simultaneous escape from both responses (≈ 0.16 day−1, see Table 2 and Figure 2C).
Later in the infection, when recombination and selection are of comparable strength, the trajectory of a particular mutations would reflect selection on this mutation alone, even if other mutations escape at the same time.
The problem of the accumulation of competing beneficial mutation in large sexual and asexual population is an active area of research in population genetics [47, 11, 46, 39]. Analytic results have only been obtained for drastically simplified models, which are not suitable for the inference of model parameters of the sort we are interested in here. On the other hand, we are typically interested in the evolution of just a few sites, which can be efficiently simulated.
3.2 Simulation of multiple CTL escapes
We have implemented the simplified model described above as a computer simulation using a discrete time evolution scheme. The simulation keeps track of the abundance mi of each of the 2n possible viral genotypes, where n is the number of epitopes. In each generation, mi is replaced by with mieε(i)−〈ε〉, which accounts for selection. To implement recombination, we calculate the distribution of recombinant genomes resulting from random pairing of genotypes after selection. It is assumed that all loci reassorted at random, which is justified if all epitopes are further apart than 1000 bp. A genetic map could be implemented easily. A fraction, ρ, of the population is replaced by recombinant genomes in each generation. Similarly, mutations change the genotype distribution by moving μmi\j individuals with genotype i\j to genotype mi and vice versa for every possible i and j. To account for the stochastic nature of viral reproduction, the population is resampled according to a Poisson distribution after selection, recombination, and mutation. The average population size can be set at will in this resampling step. The program source code and brief documentation is available as supplementary information. Due to recombination, the computational complexity scales as 3n and a simulation of n = 10 epitopes for 500 days runs for about one second on a typical 2011 desktop computer. The simulation is built using the a general library FFPopSim for multi-locus evolution. The source code, documentation, and a python wrapper are available from http://code.google.com/p/ffpopsim.
3.2.1 Inferring escape rates by multi-locus simulations
Given our model of multi-epitope viral escape and a simulation to generate trajectories, we can try to infer the escape rates by adjusting the parameters of the model to maximize the likelihood of the observed escape trajectories. In absence of any tested fitting procedure for such a problem, we simulated the dynamics for a large number of parameters and determined the likelihood of sampling the observed mutations from the simulation (we tested 21 values of the escape rates for each epitope, i.e., 215 rate combinations).
In addition to the escape rates of the different epitopes, we introduced an additional parameter τ that specifies the onset of CTL selection relative to the time of the first available patient sample. Other parameters such as μ = 2×10−5 and ρ = 0.01 are taken from the literature. The population is initialized as a homogeneous population without any escape mutations τ generations prior to the first sample.
The likelihood of the data given the escape mutant frequencies is calculated using eqn. (15). Empirically, we find that there is a single (broad) maximum of the likelihood surface and that fits are best with CTL selection onset 20 – 30 days before the first sample. The values in Table 2 correspond to τ = −30. However, we would like to emphasize that the agreement between the simulation and the data is never terribly good, which, as discussed above, is possibly due to changing selection pressure over time.
4 Conclusions & Future directions
We have discussed several models of the dynamics of immune escape at single or multiple loci. We have shown how the model fit depends on the assumptions made by the model. By applying the inference procedures to simulated data, we investigated how the sampling depth and sampling frequency affects the fidelity of the estimates.
The models and procedures outlined have a number of short-comings that need to be addressed to obtain more meaningful estimates of the parameters governing the co-evolution of the viral population and the immune system. The models are both too simple and too complex. On one hand, there is mounting evidence that the models miss several important aspects of the immune system/virus interaction. On the other hand, the models already contain too many parameters to allow for their robust estimation from the available data.
It has recently become clear that the adaptive immune system is able to control the virus by other means than the direct killing of infected cells, for example, by production of antiviral cytokines and chemokines [16, 29, 50]. Furthermore, the immune systems produces a very dynamic environment for the virus where the selection pressure on different epitopes is changing. We have generalized the single locus models to allow for exponentially decaying escape rates, but introducing one additional parameter per locus makes the fit near degenerate unless a constraint on the initial frequency of the escape mutant is introduced. We have also ignored the possibility of compensatory mutations, competition between multiple escape variants at a single epitope, and epistatic interactions between mutations.
Another potential extension of the model is to allow the processes of mutation and selection due to escape from CTL responses to start at different times post infection. Indeed, mutation from the founder virus starts at the beginning of infection while most CTL responses do not arise until 2–4 weeks post infection [34]. Also, it is not well understood how multiple CTLs that are specific for different viral epitopes interact to kill virally infected cells, e.g., whether the death rate of cells expressing different viral epitopes is the sum of the killing rates due to individual epitope-specific CTL responses. Recent work has shown that competition between different CTL responses may influence the timing and speed of viral escape [16].
The analysis of multi-locus data is hampered by the large number of possible genotypes, which grows exponentially with the number of loci considered. The dynamics of this genotype distribution is governed by a non-linear equation and solving the model involves considerable computational effort, such that one would expect fitting parameters of the model to be slow and ridden with many suboptimal local minima. The problem, however, is not as daunting as it seems.
The majority of the possible genotypes will never exist and the population is always dominated by a small number genotypes. Furthermore, the escape mutations accumulate in the inverse order of their escape rates, which implies that early mutations affect the dynamics of later mutations, but not vice versa.
Lacking an analytical solution of the multi-locus dynamics, fitting parameters will require repeated simulation of the population dynamics and comparison of the simulated trajectories with the data. The underlying dynamics of the population, however, is stochastic and different runs of a stochastic simulation will result in different outcomes, such that fitting to a stochastic simulation is ambiguous.
All of these additions will provide interesting future directions, particularly when deep and dense data are available to constrain the models.
Table 1.
Parameters determining the dynamics of HIV as estimated in previous studies. Here the viral increase rate is the rate at which HIV RNA accumulates in the blood during first weeks of infection, r = βλpw/(cVd) (see eqn. (2)). There are no direct estimates of virus infectivity β but its value can be adjusted to satisfy the condition r − δ ≈ 1 day−1 observed during acute infection. Estimates of the effective population size, which in the case of HIV infection is the number of virally infected cells, vary dramatically depending on the study. The rate of virus production by infected cells is p = Nδ. Not all virions produced by infected cells are infectious; the ratio of infectious to noninfectious HIV is on the order of 10−2 – 10−4 [21, 23, 42].
| quantity | symbol | value | references |
|---|---|---|---|
| average mutation rate | μ | 2 × 10−5/base/gen | [32] |
| net viral increase rate | r − δ | 0.9 − 1.3 day−1 | [45] |
| free virus decay rate | cV | 23 day−1 | [44] |
| infected cell death rate | δ | 1 – 2 day−1 | [41, 7] |
| virus production per cell (burst size) | B | 5 × 104 | [9] |
| effective population size | Ne | 103 – 107 | [41, 30, 5] |
| virus infectivity | β | varies | — |
Acknowledgements
This work began with discussions between ASP and RN at a Kavli Institute of Theoretical Physics workshop supported by NSF grant PHY05-51164. This work was performed under the auspices of the U.S. Department of Energy under contract DE-AC52-06NA25396, and supported by NIH grant R37-AI028433 and the National Center for Research Resources and the Office of Research Infrastructure Programs (ORIP) through grant 8R01-OD011095-21 (ASP). RAN is supported by ERC Starting Grant no. 260686(HIVEVO).
Abbreviations
- CTL
cytotoxic T lymphocyte
- HIV
human immunodeficiency virus
- SGA
single genome amplification
References
- 1.Allen T, Altfeld M, Yu X, O’Sullivan K, Lichterfeld M, Le Gall S, John M, Mothe B, Lee P, Kalife E, Cohen D, Freedberg K, Strick D, Johnston M, Sette A, Rosenberg E, Mallal S, Goulder P, Brander C, Walker B. Selection, transmission, and reversion of an antigen-processing cytotoxic T-lymphocyte escape mutation in human immunodeficiency virus type 1 infection. J Virol. 2004;78:7069–7078. doi: 10.1128/JVI.78.13.7069-7078.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Anthony DA, Andrews DM, Watt SV, Trapani JA, Smyth MJ. Functional dissection of the granzyme family: cell death and inflammation. Immunol Rev. 2010;235:73–92. doi: 10.1111/j.0105-2896.2010.00907.x. [DOI] [PubMed] [Google Scholar]
- 3.Antoniou AN, Powis SJ. Pathogen evasion strategies for the major histocompatibility complex class I assembly pathway. Immunology. 2008;124:1–12. doi: 10.1111/j.1365-2567.2008.02804.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Asquith B, Edwards C, Lipsitch M, McLean A. Inefficient cytotoxic T lymphocyte-mediated killing of HIV-1-infected cells in vivo. PLoS Biology. 2006;4:e90. doi: 10.1371/journal.pbio.0040090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Balagam R, Singh V, Sagi AR, Dixit NM. Taking multiple infections of cells and recombination into account leads to small within-host effective-population-size estimates of HIV-1. PLoS One. 2011;6:e14531. doi: 10.1371/journal.pone.0014531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Batorsky R, Kearney MF, Palmer SE, Maldarelli F, Rouzine IM, Coffin JM. Estimate of effective recombination rate and average selection coefficient for HIV in chronic infection. Proc Natl Acad Sci USA. 2011;108:5661–5666. doi: 10.1073/pnas.1102036108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Bonhoeffer S, Funk G, Gunthard H, Fischer M, Muller V. Glancing behind virus load variation in HIV-1 infection. Trends Microbiol. 2003;11:499–504. doi: 10.1016/j.tim.2003.09.002. [DOI] [PubMed] [Google Scholar]
- 8.Borrow P, Lewicki H, Wei X, Horwitz MS, Peffer N, Meyers H, Nelson JA, Gairin JE, Hahn BH, Oldstone MB, Shaw GM. Antiviral pressure exerted by HIV-1-specific cytotoxic T lymphocytes (CTLs) during primary infection demonstrated by rapid selection of CTL escape virus. Nat Med. 1997;3:205–211. doi: 10.1038/nm0297-205. [DOI] [PubMed] [Google Scholar]
- 9.Chen HY, Di Mascio M, Perelson AS, Ho DD, Zhang L. Determination of virus burst size in vivo using a single-cycle SIV in rhesus macaques. Proc Natl Acad Sci U S A. 2007;104:19079–19084. doi: 10.1073/pnas.0707449104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.da Silva J. The dynamics of HIV-1 adaptation in early infection. Genetics. 2012;190:1087–1099. doi: 10.1534/genetics.111.136366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Desai MM, Fisher DS. Beneficial mutation selection balance and the effect of linkage on positive selection. Genetics. 2007;176:1759–1798. doi: 10.1534/genetics.106.067678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Draenert R, Le Gall S, Pfafferott K, Leslie A, Chetty P, Brander C, Holmes E, Chang S, Feeney M, Addo M, Ruiz L, Ramduth D, Jeena P, Altfeld M, Thomas S, Tang Y, Verrill C, Dixon C, Prado J, Kiepiela P, Martinez-Picado J, Walker B, Goulder P. Immune selection for altered antigen processing leads to cytotoxic T lymphocyte escape in chronic HIV-1 infection. J Exp Med. 2004;199:905–915. doi: 10.1084/jem.20031982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Fernandez C, Stratov I, De Rose R, Walsh K, Dale C, Smith M, Agy M, Hu S, Krebs K, Watkins D, O’connor D, Davenport M, Kent S. Rapid viral escape at an immunodominant simian-human immunodeficiency virus cytotoxic T-lymphocyte epitope exacts a dramatic fitness cost. J Virol. 2005;79:5721–5731. doi: 10.1128/JVI.79.9.5721-5731.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Fischer W, Ganusov VV, Giorgi EE, Hraber PT, Keele BF, Leitner T, Han CS, Gleasner CD, Green L, Lo CC, Nag A, Wallstrom TC, Wang S, McMichael AJ, Haynes BF, Hahn BH, Perelson AS, Borrow P, Shaw GM, Bhattacharya T, Korber BT. Transmission of single HIV-1 genomes and dynamics of early immune escape revealed by ultra-deep sequencing. PLoS One. 2010;5:e12303. doi: 10.1371/journal.pone.0012303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Ganusov V, De Boer R. Estimating costs and benefits of CTL escape mutations in SIV/HIV infection. PLoS Comput Biol. 2006;2:e24. doi: 10.1371/journal.pcbi.0020024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Ganusov VV, Goonetilleke N, Liu MKP, Ferrari G, Shaw GM, McMichael AJ, Borrow P, Korber BT, Perelson AS. Fitness costs and diversity of the cytotoxic T lymphocyte (CTL) response determine the rate of CTL escape during acute and chronic phases of HIV infection. J Virol. 2011;85:10518–10528. doi: 10.1128/JVI.00655-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Gasper-Smith N, Crossman DM, Whitesides JF, Mensali N, Ottinger JS, Plonk SG, Moody MA, Ferrari G, Weinhold KJ, Miller SE, Reich CF, 3rd, Qin L, Self SG, Shaw GM, Denny TN, Jones LE, Pisetsky DS, Haynes BF. Induction of plasma (TRAIL), TNFR-2, Fas ligand, and plasma microparticles after human immunodeficiency virus type 1 (HIV-1) transmission: implications for HIV-1 vaccine design. J Virol. 2008;82:7700–7710. doi: 10.1128/JVI.00605-08. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Gay C, Dibben O, Anderson JA, Stacey A, Mayo AJ, Norris PJ, Kuruc JD, Salazar-Gonzalez JF, Li H, Keele BF, Hicks C, Margolis D, Ferrari G, Haynes B, Swanstrom R, Shaw GM, Hahn BH, Eron JJ, Borrow P, Cohen MS. Cross-sectional detection of acute HIV infection: timing of transmission, inflammation and antiretroviral therapy. PLoS One. 2011;6:e19617. doi: 10.1371/journal.pone.0019617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Gerrish PJ, Lenski RE. The fate of competing beneficial mutations in an asexual population. Genetica. 1998;102–103:127–144. [PubMed] [Google Scholar]
- 20.Goonetilleke N, Liu MK, Salazar-Gonzalez JF, Ferrari G, Giorgi E, Ganusov VV, Keele BF, Learn GH, Turnbull EL, Salazar MG, Weinhold KJ, Moore S, Letvin N, Haynes BF, Cohen MS, Hraber P, Bhattacharya T, Borrow P, Perelson AS, Hahn BH, Shaw GM, Korber BT, McMichael AJ. The first T cell response to transmitted/founder virus contributes to the control of acute viremia in HIV-1 infection. J Exp Med. 2009;206:1253–1272. doi: 10.1084/jem.20090365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Goto T, Harada S, Yamamoto N, Nakai M. Entry of human immunodeficiency virus (HIV) into MT-2, human T cell leukemia virus carrier cell line. Arch Virol. 1988;102:29–38. doi: 10.1007/BF01315560. [DOI] [PubMed] [Google Scholar]
- 22.Goulder P, Watkins D. HIV and SIV CTL escape: implications for vaccine design. Nat Rev Immunol. 2004;4:630–640. doi: 10.1038/nri1417. [DOI] [PubMed] [Google Scholar]
- 23.Ho D, Neumann A, Perelson A, Chen W, Leonard J, Markowitz M. Rapid turnover of plasma virions and CD4 lymphocytes in HIV-1 infection. Nature. 1995;373:123–126. doi: 10.1038/373123a0. [DOI] [PubMed] [Google Scholar]
- 24.Holland J, de la Torre J, Clarke D, Duarte E. Quantitation of relative fitness and great adaptability of clonal populations of RNA viruses. J Virol. 1991;65:2960–2967. doi: 10.1128/jvi.65.6.2960-2967.1991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Illingworth CJR, Mustonen V. Distinguishing driver and passenger mutations in an evolutionary history categorized by interference. Genetics. 2011;189:989–1000. doi: 10.1534/genetics.111.133975. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Jones NA, Wei X, Flower DR, Wong M, Michor F, Saag MS, Hahn BH, Nowak MA, Shaw GM, Borrow P. Determinants of human immunodeficiency virus type 1 escape from the primary CD8+ cytotoxic T lymphocyte response. J Exp Med. 2004;200:1243–1256. doi: 10.1084/jem.20040511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Josefsson L, King MS, Makitalo B, Brännström J, Shao W, Maldarelli F, Kearney MF, Hu W-S, Chen J, Gaines H, Mellors JW, Albert J, Coffin JM, Palmer SE. Majority of CD4+ T cells from peripheral blood of HIV-1-infected individuals contain only one HIV DNA molecule. Proc Natl Acad Sci USA. 2011;108:11199–11204. doi: 10.1073/pnas.1107729108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Keele BF, Giorgi EE, Salazar-Gonzalez JF, Decker JM, Pham KT, Salazar MG, Sun C, Grayson T, Wang S, Li H, Wei X, Jiang C, Kirchherr JL, Gao F, Anderson JA, Ping LH, Swanstrom R, Tomaras GD, Blattner WA, Goepfert PA, Kilby JM, Saag MS, Delwart EL, Busch MP, Cohen MS, Montefiori DC, Haynes BF, Gaschen B, Athreya GS, Lee HY, Wood N, Seoighe C, Perelson AS, Bhattacharya T, Korber BT, Hahn BH, Shaw GM. Identification and characterization of transmitted and early founder virus envelopes in primary HIV-1 infection. Proc Natl Acad Sci USA. 2008;105:7552–7557. doi: 10.1073/pnas.0802203105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Klatt NR, Shudo E, Ortiz AM, Engram JC, Paiardini M, Lawson B, Miller MD, Else J, Pandrea I, Estes JD, Apetrei C, Schmitz JE, Ribeiro RM, Perelson AS, Silvestri G. CD8+ lymphocytes control viral replication in SIVmac239-infected rhesus macaques without decreasing the lifespan of productively infected cells. PLoS Path. 2010;6:e1000747. doi: 10.1371/journal.ppat.1000747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Kouyos R, Althaus C, Bonhoeffer S. Stochastic or deterministic: what is the effective population size of HIV-1? Trends Microbiol. 2006;14:507–511. doi: 10.1016/j.tim.2006.10.001. [DOI] [PubMed] [Google Scholar]
- 31.Levy DN, Aldrovandi GM, Kutsch O, Shaw GM. Dynamics of HIV-1 recombination in its natural target cells. Proc Natl Acad Sci USA. 2004;101:4204–4209. doi: 10.1073/pnas.0306764101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Mansky LM, Temin HM. Lower in vivo mutation rate of human immunodeficiency virus type 1 than that predicted from the fidelity of purified reverse transcriptase. J Virol. 1995;69:5087–5094. doi: 10.1128/jvi.69.8.5087-5094.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Maree AF, Keulen W, Boucher CA, De Boer RJ. Estimating relative fitness in viral competition experiments. J Virol. 2000;74:11067–11072. doi: 10.1128/jvi.74.23.11067-11072.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.McMichael AJ, Borrow P, Tomaras GD, Goonetilleke N, Haynes BF. The immune response during acute HIV-1 infection: clues for vaccine development. Nat Rev Immunol. 2010;10:11–23. doi: 10.1038/nri2674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Neefjes J, Jongsma MLM, Paul P, Bakke O. Towards a systems understanding of MHC class I and MHC class II antigen presentation. Nat Rev Immunol. 2011;11:823–836. doi: 10.1038/nri3084. [DOI] [PubMed] [Google Scholar]
- 36.Neher R, Shraiman B. Statistical genetics and evolution of quantitative traits. Rev. Mod. Phys. 2011;83:1283–1300. [Google Scholar]
- 37.Neher RA, Leitner T. Recombination rate and selection strength in HIV intra-patient evolution. PLoS Comput Biol. 2010;6:e1000660. doi: 10.1371/journal.pcbi.1000660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Neher RA, Shraiman BI. Genetic drift and quasi-neutrality in large facultatively sexual populations. Genetics. 2011;188:975–996. doi: 10.1534/genetics.111.128876. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Neher RA, Shraiman BI, Fisher DS. Rate of adaptation in large sexual populations. Genetics. 2010;184:467–481. doi: 10.1534/genetics.109.109009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Nowak MA, Anderson RM, McLean AR, Wolfs TF, Goudsmit J, May RM. Antigenic diversity thresholds and the development of AIDS. Science. 1991;254:963–969. doi: 10.1126/science.1683006. [DOI] [PubMed] [Google Scholar]
- 41.Perelson A, Neumann A, Markowitz M, Leonard J, Ho D. HIV-1 dynamics in vivo: virion clearance rate, infected cell lifespan, and viral generation time. Science. 1996;271:1582–1586. doi: 10.1126/science.271.5255.1582. [DOI] [PubMed] [Google Scholar]
- 42.Platt EJ, Kozak SL, Durnin JP, Hope TJ, Kabat D. Rapid dissociation of HIV-1 from cultured cells severely limits infectivity assays, causes the inactivation ascribed to entry inhibitors, and masks the inherently high level of infectivity of virions. J Virol. 2010;84:3106–3110. doi: 10.1128/JVI.01958-09. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Prado JG, Honeyborne I, Brierley I, Puertas MC, Martinez-Picado J, Goulder PJ. Functional consequences of human immunodeficiency virus escape from an HLA-B* 13-restricted CD8+ T-cell epitope in p1 Gag protein. J Virol. 2009;83:1018–1025. doi: 10.1128/JVI.01882-08. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Ramratnam B, Bonhoeffer S, Binley J, Hurley A, Zhang L, Mittler JE, Markowitz M, Moore JP, Perelson AS, Ho DD. Rapid production and clearance of HIV-1 and hepatitis C virus assessed by large volume plasma apheresis. Lancet. 1999;354:1782–1785. doi: 10.1016/S0140-6736(99)02035-8. [DOI] [PubMed] [Google Scholar]
- 45.Ribeiro RM, Qin L, Chavez LL, Li D, Self SG, Perelson AS. Estimation of the initial viral growth rate and basic reproductive number during acute HIV-1 infection. J Virol. 2010;84:6096–6102. doi: 10.1128/JVI.00127-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Rouzine IM, Coffin JM. Evolution of human immunodeficiency virus under selection and weak recombination. Genetics. 2005;170:7–18. doi: 10.1534/genetics.104.029926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Rouzine IM, Wakeley J, Coffin JM. The solitary wave of asexual evolution. Proc Natl Acad Sci USA. 2003;100:587–592. doi: 10.1073/pnas.242719299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Turnbull EL, Wong M, Wang S, Wei X, Jones NA, Conrod KE, Aldam D, Turner J, Pellegrino P, Keele BF, Williams I, Shaw GM, Borrow P. Kinetics of expansion of epitope-specific T cell responses during primary HIV-1 infection. J Immunol. 2009;182:7131–7145. doi: 10.4049/jimmunol.0803658. [DOI] [PubMed] [Google Scholar]
- 49.van Leeuwen EMM, de Bree GJ, ten Berge IJM, van Lier RAW. Human virus-specific CD8+ T cells: diversity specialists. Immunol Rev. 2006;211:225–235. doi: 10.1111/j.0105-2896.2006.00379.x. [DOI] [PubMed] [Google Scholar]
- 50.Wong JK, Strain MC, Porrata R, Reay E, Sankaran-Walters S, Ignacio CC, Russell T, Pillai SK, Looney DJ, Dandekar S. In vivo CD8+ T-cell suppression of SIV viremia is not mediated by CTL clearance of productively infected cells. PLoS Path. 2010;6:e1000748. doi: 10.1371/journal.ppat.1000748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Yewdell J, Reits E, Neefjes J. Making sense of mass destruction: quantitating MHC class I antigen presentation. Nat Rev Immunol. 2003;3:952–961. doi: 10.1038/nri1250. [DOI] [PubMed] [Google Scholar]
- 52.Yewdell JW, Hill AB. Viral interference with antigen presentation. Nat Immunol. 2002;3:1019–1025. doi: 10.1038/ni1102-1019. [DOI] [PubMed] [Google Scholar]
- 53.Zhang L, Dailey PJ, He T, Gettie A, Bonhoeffer S, Perelson AS, Ho DD. Rapid clearance of simian immunodeficiency virus particles from plasma of rhesus macaques. J Virol. 1999;73:855–860. doi: 10.1128/jvi.73.1.855-860.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]