Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 Mar 21;4:4429. doi: 10.1038/srep04429

Robust longitudinal spin-Seebeck effect in Bi-YIG thin films

Gene Siegel 1, Megan Campbell Prestgard 1, Shiang Teng 1, Ashutosh Tiwari 1,a
PMCID: PMC3961741  PMID: 24651124

Abstract

In recent years, the coupling of magnetic insulators (bismuth-doped yttrium iron garnet, Bi-YIG) with platinum has garnered significant interest in spintronics research due to applicability as spin-current-driven thermoelectric coatings. These coatings bridge the gap between spintronics technologies and thermoelectric materials, providing a novel means of transforming waste heat into electricity. However, there remain questions regarding the origins of the spin-Seebeck effect (SSE) as well as claims that observed effects are a manifestation of magnetic proximity effects, which would induce magnetic behavior in platinum. Herewith we provide support that the voltages observed in the Bi-YIG/Pt films are purely SSE voltages. We reaffirm claims that magnon transport theory provides an ample basis for explaining SSE behavior. Finally, we illustrate the advantages of pulsed-laser deposition, as these Bi-YIG films possess large SSE voltages (even in absence of an external magnetic field), as much as twice those of films fabricated via solution-based methods.

The development of a vast array of smart, nano-scale, low-power-consumption devices has been made possible through recent advances in modern sensor technologies. For many such devices, it would be advantageous if the energy required for operation could be partially generated by the device itself. One such means is through the use of thermoelectric devices which can convert ambient temperature gradients into electricity1. However, current thermoelectric generators (TEG) are not capable of efficiently converting thermal energy to electrical energy2. The efficiency of a TEG device is determined by a dimensionless quantity known as the figure of merit ZT = TS2 σ/κ where ‘S' is the Seebeck coefficient, ‘σ' is the electrical conductivity, ‘κ' is the thermal conductivity, and ‘T' is the absolute temperature3. Any improvement in the value of ZT requires a reduction in the thermal conductivity and an increase in the electrical conductivity of the thermoelectric material. However, in traditional thermoelectric materials, these two requirements contradict one another, making further enhancement nearly impossible3,4.

For the last several decades, efforts have been made to overcome the above limitations using nano-technological approaches5,6. However, improvements have been only modest. Recently, a new approach based on the spin-Seebeck effect (SSE) has been proposed7,8,9,10,11,12. In the proposed approach, thermal transport and electrical transport occur in different parts of the device. Hence, the fundamental limit posed by the Wiedmann-Franz law can be overcome13. Utilizing this concept, Kirihara et al.14 demonstrated a spin-current driven thermoelectric coating comprised of a magnetic insulator (bismuth-doped yttrium iron garnet, Bi-YIG) and platinum. The above demonstration opened a new frontier in spintronics research to not only utilize waste heat, but also provide a new basis for sustainable technological developments. However, there remain several questions regarding the implications of platinum in the device and the origins of the SSE which must be answered before this technology can progress further.

The first question to be addressed is the nature of platinum in the structure. Recently, Huang et al.15 claimed that, in a similar structure (YIG/Pt), the platinum film itself becomes ferromagnetic, as magnetic proximity effects induce magnetic behavior in platinum. If this claim stands true, then the observed voltages originally attributed to SSE are not only due to the spin-Seebeck effect, but also possess a contribution resulting from the anomalous Nernst effect in platinum16. Thus, before the origins of the SSE are investigated, this claim must be addressed. In examinations into the origins of the spin-Seebeck effect, the first phenomenon to be investigated is how magnon transport occurs and is influenced by external factors in magnetic insulators. Adachi et al.17 reported that, at low temperatures, SSE in transverse Bi-YIG/Pt devices is enhanced, which was attributed to substrate-induced phonon drag effects influencing the movement of magnons. Similar predictions were likewise made by Kirihara et al.14 for longitudinal SSE structures. Verification of the effects phonon-drag has on magnon movement in longitudinal Bi-YIG/Pt devices will further shed light on the SSE. Finally, from an application standpoint, it is essential that the magnetic films exhibit enhanced coercivity, such that the devices remain functional even in the absence of an external magnetic field.

Here we present a detailed experimental study to address the above stated questions. Our results show that the voltages observed in longitudinal Bi-YIG/Pt films are purely SSE voltages. We observed excellent agreement between the experimentally determined temperature dependence of SSE voltage and the theoretically predicted behavior. This indicates the efficacy of magnon transport theory in explaining the observed SSE phenomenon. Finally, the Bi-YIG films prepared by PLD technique possess large coercivity which makes them useful for practical device applications.

Results

The Bi-YIG films were grown on gadolinium gallium garnet, GGG (111), substrate using a pulsed laser deposition (PLD) technique. The thickness of the Bi-YIG films was ~50 nm while the thickness of GGG (111) substrates was ~0.5 mm. A 10 nm thick platinum film was deposited over the Bi-YIG films using an e-beam evaporation technique. Very extensive characterization of the samples was performed using X-ray diffraction (XRD), atomic force microscopy (AFM), X-ray photoelectron spectroscopy (XPS), and magnetization and magnetoresistance measurements. More details are given in the Methods section.

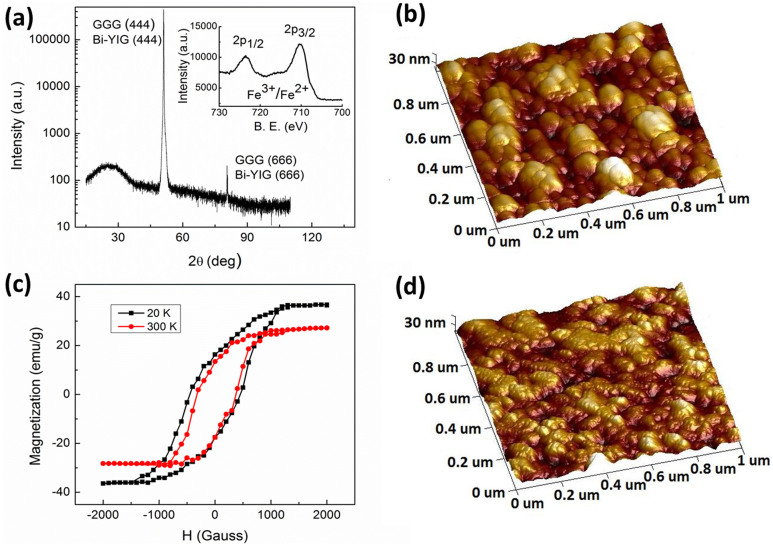
Fig. 1(a) shows the X-ray diffraction (XRD) data of the Bi-YIG film. For collecting XRD data, the BYIG film (5 mm × 5 mm) was placed on a glass slide. The dimension of the X-ray beam was (10 mm × 15 mm). So a fraction of the X-ray beam was incident on the glass slide too giving rise to an amorphous background and a slight hump at lower angles. Except for the above, over the 2θ range of 20–100 degrees, only the peaks corresponding to (444) and (666) planes of GGG and Bi-YIG could be detected indicating highly aligned growth of Bi-YIG on GGG. Because of the exactly similar lattice parameters, the GGG and Bi:YIG reflections could not be separated from each other to extract the film's lattice parameters. Films were further examined using X-ray photoelectron spectroscopy (XPS) which gave an elemental ratio for Bi:Y:Fe of 0.14:2.86:4.87. These values are very close to the target stoichiometry of 0.15:2.85:5. Inset of Fig. 1(a) shows the Fe 2p XPS spectrum for the Bi-YIG film. The peak observed at 710.3 eV lies in between the binding energy (BE) values expected for the 2p3/2 peaks of Fe3+ (711.0 eV) and Fe2+ (709.6 eV)18. Similarly the peak at 723.6 eV lies in between the BE values for the 2p1/2 peaks of Fe3+ (724 eV) and Fe2+ (722.6 eV)18. This indicates that iron in the film, exists both in the Fe2+ as well as Fe3+ state. The presence of Fe in the mixed valence state of Fe2+/Fe3+ is quite surprising because of the isovalence substitution of Y3+ with Bi3+. We speculate the presence of Fe2+ could be due to the introduction of some oxygen vacancies in the material during PLD process. No clear peaks corresponding to metallic Fe were observed in the XPS spectra. However, two shoulders at around 720 eV and 705 eV were observed which prevent us from excluding the possibility of any metallic Fe precipitate on the surface. However, even if any metallic precipitate was present there, that must be on extremely small scale as also suggested by the enormously large surface resistance of the film. Fig. 1(b) displays an AFM image of Bi-YIG film surface indicating a root mean square (rms) roughness of about 4.2 nm. Fig. 1(c) shows magnetization (M) vs magnetic field (H) data recorded at 20 K and 300 K using a squid magnetometer. Films exhibited saturation magnetization values of 36 emu/g at 20 K and 27 emu/g at 300 K which are in close agreement with the reported values for bulk material19. However, the coercivity of the film was significantly higher than the reported bulk values. Large values of coercivity are believed to arise because of strain fields that are expected to be present in the ultra-thin crystalline films20. The other factor, which could equally be responsible for the observed large coercivity, is the film's high surface roughness and the corresponding stray fields. On the thoroughly characterized Bi-YIG films, a 10 nm layer of platinum was deposited using an e-beam evaporator. Fig. 1(d) shows a typical AFM image of the film after platinum deposition (rms roughness ~ 5.1 nm). The features on the surface of Bi-YIG and Pt-coated Bi-YIG films are quite similar indicating that the coating of Pt on Bi-YIG is conformal and is making coherent interfaces.

Figure 1. Bi-YIG films grown by PLD technique.

Figure 1

Open in a new tab

(a) XRD pattern of Bi-YIG film grown on single crystal GGG(111) substrate. Inset shows the Fe 2p XPS spectra. (b) AFM image of the Bi-YIG film. (c) Magnetization vs magnetic field curves for the Bi-YIG film at 20 K and 300 K. (d) AFM image the of Pt film grown on Bi-YIG/GGG(111).

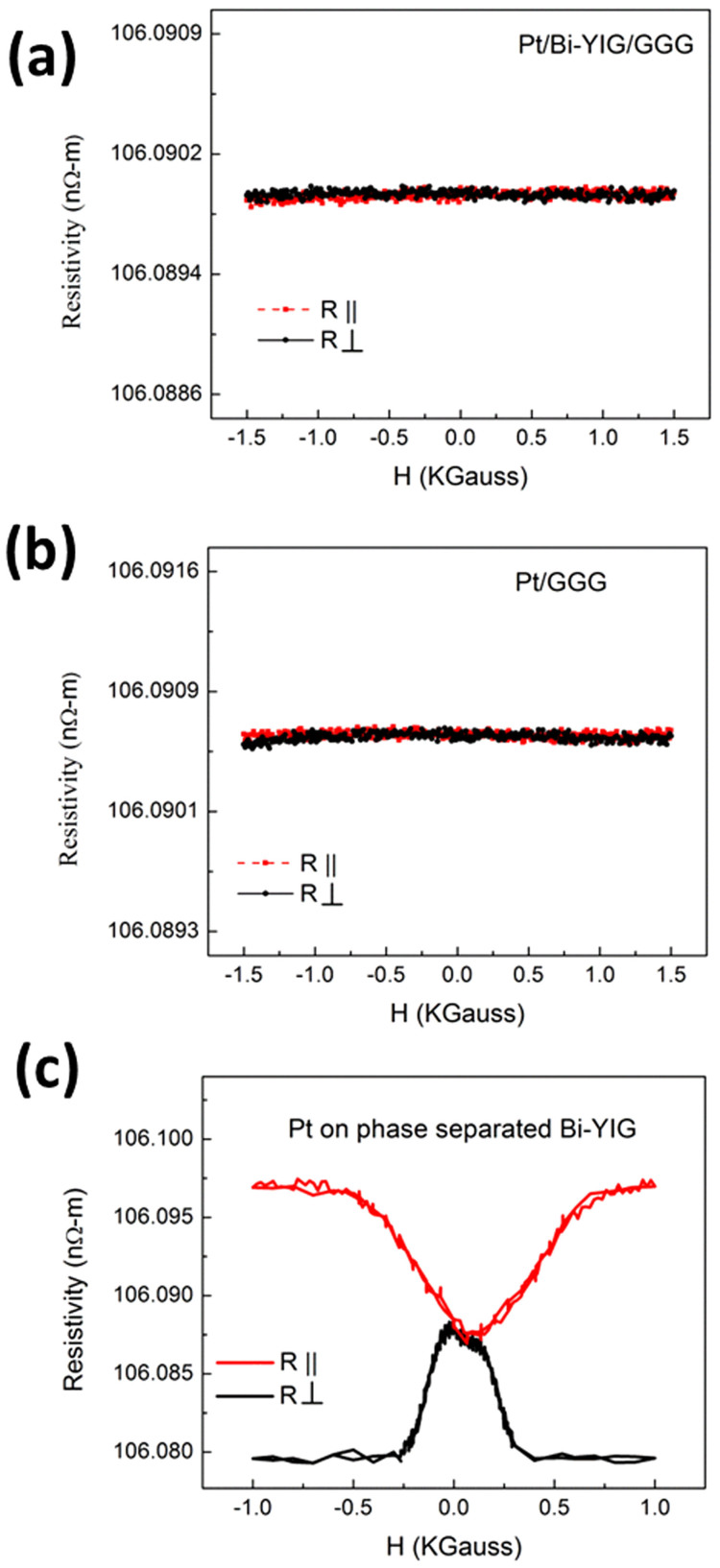
To test the possibility that the platinum film itself turns magnetic due to its proximity with the magnetic Bi-YIG layer, magnetoresistance (MR) measurements were performed on Pt films grown on Bi-YIG layers. For comparison, we also performed MR measurements on Pt film deposited directly on GGG substrate. Fig. 2(a) and 2(b) show room temperature MR vs H data for these films. In contrast to Huang et al.'s15 results, we did not observe MR effect in any of Pt films. These results clearly show that Pt films are not ferromagnetic and also confirm the validity of SSE results reported previously by many groups. In order to further understand what could be the cause of the observed MR in Huang's study, we grew Pt films on Bi-YIG films which XPS had shown to possess quite significant Fe precipitates present on the surface (see Supplementary Material). MR measurements on these samples showed exactly same MR characteristics as reported by Huang et al.15 (see Fig. 2(c)).

Figure 2. Magnetoresistance of Pt film.

Figure 2

Open in a new tab

(a) Electrical resistance vs applied magnetic field for Pt film grown on Bi-YIG/GGG(111). (b) Electrical resistance vs applied magnetic field for Pt film grown directly on GGG(111). (c) Electrical resistance vs applied magnetic field for Pt film grown on phase-separated Bi-YIG/GGG(111).

Here it is in order to mention that in very recent reports, it has been shown that Pt films can exhibit MR even in absence of any proximity effect driven transformation to a ferromagnetic state21. This effect, named as the spin hall magnetoresistance (SMR), arises because of the combined action of spin Hall effect, inverse spin Hall effect and the magnetization direction dependent absorption of the spin current at the ferromagnetic insulator/Pt interface22,23,24. The absence of MR in our Pt films grown on optimized BiYIG film was contrary to the above reports. We speculate that the rougher surface in our films may be responsible for the absence of detectable SMR signal in our films. Our speculations are consistent with the theory of SMR which predicts that the SMR effect depends very sensitively on the spin mixing conductance so that variation in the interface quality could indeed lead to significant changes and suppression in the MR magnitude. It has also been shown that the SMR has a characteristic length scale; so we performed MR measurements on a thinner film too. Results of those measurements are given in the supplementary section.

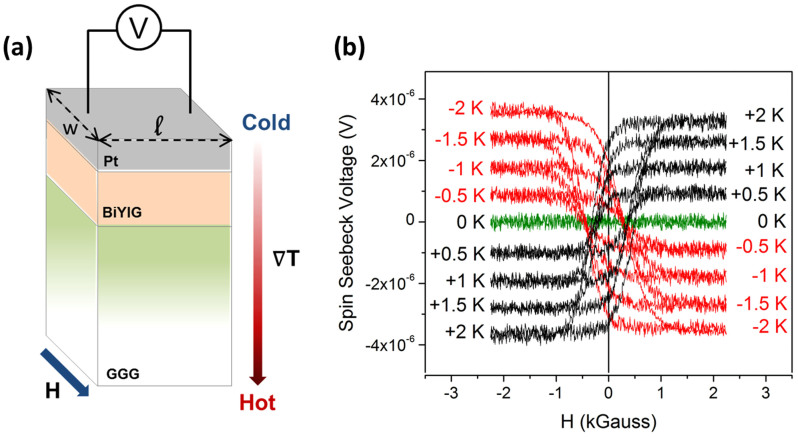
SSE measurements were performed on thoroughly characterized Bi-YIG/Pt coatings. Fig. 3(a) shows a schematic diagram of the longitudinal SSE measurement set-up. An external magnetic field ‘H' was applied in the plane of the device and then a temperature gradient was created between the top of the Pt film and the bottom of the GGG substrate by sandwiching the structure between two copper plates. The spin-Seebeck voltage (VSS) developed across the platinum film was measured using a nanovoltmeter. Fig. 3(b) shows a plot of VSS as a function of the applied magnetic field H at room temperature for ΔT = ±2, ±1.5, ±1, ±0.5, and 0 K. When there was no temperature difference between the top of the platinum layer and the bottom of the GGG substrate (ΔT = 0 K), a negligible voltage was detected between the two ends of the Pt layer. However, when a temperature difference was applied, a voltage difference was recorded which was linearly proportional to the temperature gradient and changed sign upon reversing the temperature gradient as well as upon reversing the direction of the applied magnetic field. This behavior is a clear characteristic of the SSE phenomenon. Further characterization was performed by measuring the angular dependence of the SSE signal which exhibited a cosine dependence as expected for the SSE phenomenon (see supplementary section).

Figure 3. Measurement set-up and measured voltages.

Figure 3

Open in a new tab

(a) Schematic of the SSE measurement set-up. (b) Spin-Seebeck voltage as a function of the applied magnetic field for ΔT = ±2, ±1.5, ±1, ±0.5, and 0 K at 300 K.

Assuming that the thermal conductivities of GGG and Bi-YIG are the same, the temperature difference of 2 K through the GGG/Bi-YIG structure results in a temperature difference of ΔTBi-YIG = 0.2 mK across the Bi-YIG layer. Therefore, the observed voltage of 3.6 μV corresponds to a large spin-Seebeck coefficient of 18 mV/K. The observed SSE voltages are almost twice as compared to those reported by Kirihara et al.14 for films prepared via solution-based method. Moreover, PLD grown Bi-YIG films possess very large coercivity values eliminating the need for any external magnetic field in day-to-day operation. Here, it is also important to note that while estimating the quantitative values SSE above, we determined the temperature difference across the Bi-YIG by using the standard thermal conductance. However, it has been shown that in thin films the thermal interface resistance dominates the thermal transport25. So, in reality, the actual temperature difference across the Bi-YIG layer will be lower than the value estimated above.

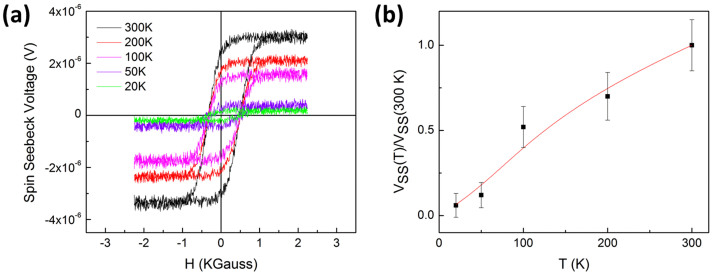
In Fig. 4(a), we have shown the longitudinal VSS vs H data at different temperatures over the range 20–300 K. Fig. 4(b), shows the variation of saturated value of VSS as a function of temperature. A monotonic decrease in the value of VSS with decrease in temperature can clearly be seen. As illustrated below, these results can be explained using magnon transport theory26,27.

Figure 4. Temperature dependence of longitudinal spin-Seebeck voltage.

Figure 4

Open in a new tab

(a) Spin-Seebeck voltage as a function of the applied magnetic field for ΔT = +2 K at different temperatures. (b) Variation of the saturated value of spin-Seebeck voltage as a function of temperature. Symbols represent experimentally determined data while the solid line represents the theoretically calculated data using magnon transport theory. Data has been normalized at T = 300 K for comparison.

Discussion

Magnons are the low-lying excitations of localized spins. In the case of magnetic insulators, where no conduction electrons are present, magnons facilitate the transmission of spin current. In the device geometry shown in Fig. 3(a), when a temperature difference, ΔT, is applied between the Bi-YIG and Pt layers, a magnon-driven spin current, IS, is injected into the Pt layer perpendicular to the Bi-YIG/Pt interface. In the Pt layer, the aforementioned spin current is converted into a charge voltage (spin-Seebeck voltage, VSS) through the process of inverse-Hall effect. The VSS is given by the expression17,26:

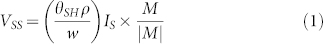graphic file with name srep04429-m1.jpg

where θSH, ρ, w, and M represent the spin-Hall angle of platinum, resistivity of platinum, width of the platinum layer, and magnetization vector of the Bi-YIG layer, respectively. The value of the magnon mediated spin current |IS| can be estimated using the relation17,26,27:

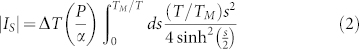graphic file with name srep04429-m2.jpg

here α is the Gilbert damping constant, TM is the magnon temperature, and P is a nearly temperature independent coefficient calculated by Adachi et al.17 The plot of VSS vs T, calculated using Eqn. 1 and Eqn. 2, is shown as a dashed line in Fig. 4(b). An excellent agreement between the experimental and the theoretically calculated data suggest the efficacy of magnon theory in explaining the observed SSE phenomenon.

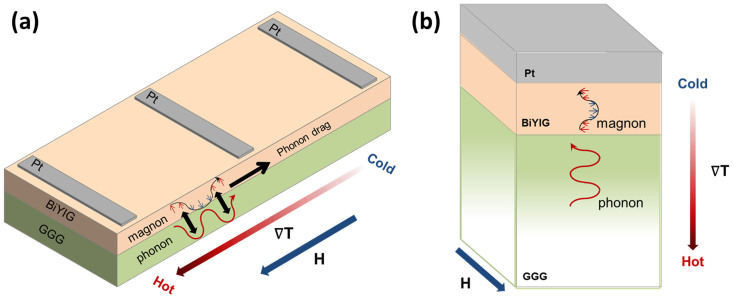
Our findings for the longitudinal SSE devices are very different from those reported by Adachi et al.17 for the transverse device structures. Adachi et al. observed an enhancement in the SSE at low temperatures which was attributed to phonon drag effects in the substrate17,28. In order to understand the cause of discrepancy between ours and Adachi's results, we also fabricated the transverse SSE structures and did temperature dependent SSE measurements. In close agreement with Adachi's results, an enhancement in the values of VSS at lower temperatures was observed (see Supplementary Material). Based on these studies we have concluded that though, in the transverse geometry, phonon drag effects in the substrate enhance SSE, no such phenomenon occurs in the longitudinal geometry. This behavioral difference is understood to arise due to the fact that in the transverse geometry, phonon transport in the substrate and magnon transport in Bi-YIG take place in parallel, while in the longitudinal geometry these two processes take place in series. Further, in the Bi-YIG layer, because of its very small length the effective phonon free length is too small to lead to a significant magnon-phonon drag.(see Fig. 5).

Figure 5. Illustration of substrate induced phonon drag effect on the transport of magnons in Bi-YIG.

Figure 5

Open in a new tab

(a) Illustration of the movement of phonons in the substrate and magnons in the Bi-YIG in transverse geometry. In this geometry, phonons move parallel to magnons and hence can drag them along. (b) Illustration of the movement of phonons in the substrate and magnons in the Bi-YIG in longitudinal geometry. In this case, movement of phonons and magnons take place in series.

In summary, our results have shown that magnon transport theory is valid for explaining observed SSE results. We have also found that substrate-induced phonon-drag effects typically observed in the transverse device setup were not present in the longitudinal device setup. Furthermore, we have refuted claims that magnetic proximity effects are causing Pt films to become magnetic when in contact with magnetic insulators through magnetoresistance testing. Finally, we have demonstrated that PLD grown Bi-YIG films have significantly higher coercivities compared to those grown via solution-based methods. This delineation of the origins of the SSE opens the door for further exploration and device fabrication of next-generation spintronic-based thermoelectric generators.

Methods

Sample preparation

The Bi-YIG films were deposited on GGG (Gd3Ga5O12) substrates using a pulsed laser deposition (PLD) technique. The highly dense Bi-YIG target pellet used for laser ablation was fabricated via a solid-state method. The precursory oxides utilized were bismuth oxide (Bi2O3), yttrium oxide (Y2O3), and iron oxide (Fe2O3) with a ratio of 0.15:2.85:5, thereby achieving the desired composition of Bi0.15Y2.85Fe5O12. Following a uniform mixing and grinding of the precursory powders, a densified pellet was fabricated using a uniaxial press. Then, the pellet was sintered at 900°C for four hours in a box furnace, after which it was again ground up. This process was repeated several times until the X-ray diffraction (XRD) results indicated that a pure Bi-YIG pellet was yielded. The fabricated Bi-YIG pellet was then ablated using a KrF excimer laser, with a laser fluence of 14 J/cm2. During deposition, the substrate temperature and the oxygen pressure in the chamber were kept at 650°C and 5 × 10−5 mbar, respectively. After the deposition, the films were sintered in-situ at 800°C under an oxygen pressure of 1 × 10−1 mbar for 10 minutes. Finally, the films were cooled, in the presence of 1 × 10−1 mbar, to room temperature at a rate of 10°C/min. For making the longitudinal testing devices, a thin film of platinum was deposited over the entire Bi-YIG film using an e-beam evaporation technique. For making the transverse test structures, a stainless steel shadow mask was used to deposit the platinum layer. XRD characterization of the films was performed using a Philips X'PERT diffractometer. Elemental analysis was performed using XPS (Kratos Axis Ultra DLD). AFM was performed using a Bruker Dimension Icon microscope. Magnetization was measured using a quantum design squid magnetometer. Magnetization of the substrate was measured separately and subtracted from the total magnetization of both the substrate and the film in order to determine the net magnetization of the film.

Magnetoresistance measurements

The magnetoresistance measurements were performed on the Pt films grown on Bi-YIG film, as well as on NiFe and Pt films grown directly on GGG substrate (control samples). A traditional four-point probe setup was used for such measurements. An electric current was passed through the outer two contacts while the resulting voltage was measured between the middle two contacts as an in-plane magnetic field was swept from +1.5 kG to −1.5 kG. Measurements were taken for both the cases where the magnetic field direction was parallel to the direction of the current as well as when they were perpendicular to one another.

Spin Seebeck voltage measurement

The SSE measurements on longitudinal devices were performed by sandwiching Bi-YIG/Pt structures between two copper blocks. Each of these copper blocks was equipped with a micro-heater and a silicon-diode temperature sensor. A temperature gradient was created between the top of the Pt film and the bottom of the GGG substrate using these micro-heaters and a magnetic field was applied in the plane of the Bi-YIG film. The voltage developed across the platinum film was measured using a Keithely 2182A nanovoltmeter. For the transverse devices, a temperature gradient as well as a magnetic field was applied along the length of the Bi-YIG film. The voltage developed along the transverse platinum wires was measured using a Keithley 2182A nanovoltmeter.

Author Contributions

G.S. prepared the samples and did structural characterization and SSE measurements. M.C.P. performed magnetoresistance measurements. S.T. did the theoretical calculation of SSE voltages using magnon transport theory. A.T. designed the experiments and supervised the study. All authors discussed the results and contributed in preparing the manuscript.

Supplementary Material

Supplementary Information

Supplementary Material

srep04429-s1.pdf (482.7KB, pdf)

Acknowledgments

Financial support from U.S. National Science Foundation through Award No. 1121252 (MRSEC), Award No. DMR-0746486 (CAREER), and Award No. CMMI-1234338 is thankfully acknowledged.

References

  1. DiSalvo F. J. Thermoelectric cooling and power generation. Science. 285, 703–706 (1999). [DOI] [PubMed] [Google Scholar]
  2. Bell L. E. Cooling, heating, generating power, and recovering waste heat with thermoelectric systems. Science. 321, 1457–1461 (2008). [DOI] [PubMed] [Google Scholar]
  3. Rowe D. M. CRC Handbook of Thermoelectrics: Macro to Nano. (CRC Press, Boca Raton, 2005). [Google Scholar]
  4. Goldsmid H. J. Introduction to Thermoelectricity. (Springer, New York, 2009). [Google Scholar]
  5. Nolas G. S., Sharp J. & Goldsmid H. J. Thermoelectrics: Basic Principles and New Materials Developments. (Springer, New York, 2001). [Google Scholar]
  6. Chowdhury I. et al. On-chip cooling by superlattice-based thin-film thermoelectric. Nature Nanotech. 4, 235–238 (2009). [DOI] [PubMed] [Google Scholar]
  7. Uchida K. et al. Observation of the spin-Seebeck effect. Nature. 455, 778–781 (2008). [DOI] [PubMed] [Google Scholar]
  8. Jaworski C. M. et al. Observation of the spin-Seebeck effect in a ferromagnetic semiconductor. Nature Mater. 9, 898 (2010). [DOI] [PubMed] [Google Scholar]
  9. Uchida K. et al. Observation of the longitudinal spin-Seebeck effect in magnetic insulators. Appl. Phys. Lett. 97, 172505 (2010). [Google Scholar]
  10. Uchida K. et al. Spin Seebeck insulator. Nature Mater. 9, 894–897 (2010). [DOI] [PubMed] [Google Scholar]
  11. Uchida K. et al. Long-range spin Seebeck effect and acoustic spin pumping. Nature Mater. 10, 737–741 (2011). [DOI] [PubMed] [Google Scholar]
  12. Bauer G. E. W., Saitoh E. & van Wees B. J. Spin caloritronics. Nature Mater. 11, 391–399 (2012). [DOI] [PubMed] [Google Scholar]
  13. Ashcroft N. W. & Mermin N. D. Solid State Physics. (Cengage Learning, Philadelphia, 1976). [Google Scholar]
  14. Kirihara A. et al. Spin-current-driven thermoelectric coating. Nature Mater. 11, 686–689 (2012). [DOI] [PubMed] [Google Scholar]
  15. Huang S. Y. et al. Transport magnetic proximity effects in platinum. Phys. Rev. Lett. 109, 107204 (2012). [DOI] [PubMed] [Google Scholar]
  16. Kooi C. F., Horst R. B., Cuff K. F. & Hawkins S. R. Theory of the longitudinally isothermal Ettingshausen Cooler. J. Appl. Phys. 34, 1735–1742 (1963). [Google Scholar]
  17. Adachi H. et al. Gigantic enhancement of spin Seebeck effect by phonon drag. Appl. Phys. Lett. 97, 252506 (2010). [Google Scholar]
  18. NIST X-ray Photoelectron Spectroscopy Database, Version 4.1 (National Institute of Standards and Technology, Gaithersburg, 2012); http://srdata.nist.gov/xps.
  19. Xu H. & Yang H. Magnetic properties of YIG doped with cerium and gadolinium ions. J. Mater. Sci.: Mater. Electron. 19, 589–593 (2008). [Google Scholar]
  20. Dubinko et al. Features of the coercivity of strained epitaxial garnet ferrite films. Tech. Phys. Lett. 31, 979–981, (2005). [Google Scholar]
  21. Nakayama H. et al. Spin Hall Magnetoresistance Induced by a Nonequilibrium Proximity Effect. Phys. Rev. Lett. 110, 206601 (2013). [DOI] [PubMed] [Google Scholar]
  22. Hahn C. et al. Comparative measurements of inverse spin Hall effects and magnetoresistance in YIG/Pt and YIG/Ta. Phys. Rev. B. 87, 174417 (2013). [Google Scholar]
  23. Chen Y. et al. Theory of spin Hall magnetoresistance. Phys. Rev. B. 87, 144411 (2013). [Google Scholar]
  24. Weiler M. et al. Experimental Test of the Spin Mixing Interface Conductivity Concept. Phys. Rev. Lett. 111, 176601 (2013). [DOI] [PubMed] [Google Scholar]
  25. Schrier M. et al. Magnon, phonon, and electron temperature profiles and the spin Seebeck effect in magnetic insulator/normal metal hybrid structures. Phys. Rev. B. 88, 094410 (2013). [Google Scholar]
  26. Xiao J., Bauer G. E. W., Uchida K., Saitoh E. & Maekawa S. Theory of magnon-driven spin Seebeck effect. Phys. Rev. B 81, 214418 (2010). [Google Scholar]
  27. Adachi H., Ohe J., Takahashi S. & Maekawa S. Linear-response theory of spin Seebeck effect in ferromagnetic insulators. Phys. Rev. B. 83, 094410 (2011). [Google Scholar]
  28. Jaworski C. M. et al. Spin-Seebeck effect: A phonon driven spin distribution. Phys. Rev. Lett. 106, 186601 (2011). [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Material

srep04429-s1.pdf (482.7KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES