Non-invasive In vivo measurement of the shear modulus of human vocal fold tissue

Abstract

Voice is the essential part of singing and speech communication. Voice disorders significantly affect the quality of life. The viscoelastic mechanical properties of the vocal fold mucosa determine the characteristics of the vocal folds oscillations, and thereby voice quality. In the present study, a non-invasive method was developed to determine the shear modulus of human vocal fold tissue in vivo via measurements of the mucosal wave propagation speed during phonation. Images of four human subjects’ vocal folds were captured using high speed digital imaging (HSDI) and magnetic resonance imaging (MRI) for different phonation pitches, specifically fundamental frequencies between 110 to 440 Hz. The MRI images were used to obtain the morphometric dimensions of each subject's vocal folds in order to determine the pixel size in the high-speed images. The mucosal wave propagation speed was determined for each subject and at each pitch value using an automated image processing algorithm. The transverse shear modulus of the vocal fold mucosa was then calculated from a surface (Rayleigh) wave propagation dispersion equation using the measured wave speeds. It was found that the mucosal wave propagation speed and therefore the shear modulus of the vocal fold tissue were generally greater at higher pitches. The results were in good agreement with those from other studies obtained via in vitro measurements, thereby supporting the validity of the proposed measurement method. This method offers the potential for in vivo clinical assessments of vocal folds viscoelasticity from HSDI.

1. Introduction

Human voice is produced by airflow expelled from the lungs through the airway and modulated by the self-sustained oscillation of the vocal folds, two membranes located within the larynx at the level of Adam's apple. The oscillation involves mainly a wavy motion of the vocal fold mucosa, commonly referred to as the mucosal wave. This structural wave travels from the lower to upper vocal fold lip over the medial and superior surfaces of the vocal folds at a speed that is commensurate with the elasticity of the tissue. The mucosal wave speed is distinct from the velocity of the glottal edge along the medial-lateral direction. The assessment of mucosal wave propagation is commonly used for clinical voice diagnosis (Dejonckere et al., 2001). The generation and propagation of the mucosal wave depends on the shear viscoelastic mechanical properties of the mucosa. Therefore, a knowledge of the mechanical properties of vocal fold tissue is needed for the development of injectable biomaterials used for vocal fold augmentation and repair (Caton et al., 2007; Heris et al., 2012), for diagnostics to distinguish between scarred and healthy tissue (Thibeault et al., 2002; Rousseau et al., 2004), and for the assessment of surgical procedures used in vocal fold treatment (Thibeault et al., 2011).

In vitro measurements of the viscoelastic shear properties of human vocal fold tissue have been mostly performed using parallel plate or linear skin rheometry (Chan and Titze, 1999; Goodyer et al., 2003; Chan, 2004; Hess et al., 2006; Chan and Rodriguez, 2008; Dailey et al., 2009; Goodyer et al., 2009). For example, Chan and Rodriguez (2008) designed a custom- built, controlled-strain, linear, simple-shear rheometer for the measurement of the viscoelastic properties at frequencies up to 250 Hz. The viscoelastic shear moduli of seven human vocal fold cover specimens were measured. These existing methods are inaccurate for frequencies greater than at most 250 Hz, and cannot be used for in vivo measurements.

In vivo measurements of the vocal fold elastic modulus have been performed (Berke, 1992; Berke and Smith, 1992; Tran et al., 1993; Goodyer et al., 2006; Goodyer et al., 2007a; Goodyer et al., 2007b). Berke and Tran et al. (1992; 1993) constructed an apparatus, which worked based on direct lateral force and displacement measurements, to obtain the vocal folds elastic modulus in vivo. This invasive measurement technique had a limited range of application due to its cumbersome apparatus. Goodyer et al. (2006; 2007a; 2007b) developed a custom built instrument to measure the vocal folds elastic properties in vivo. The shear modulus of eight patients’ vocal folds was measured along the transverse direction at the mid- membranous point. This measurement technique is invasive, and is performed in a quasi-static manner; i.e., the frequency-dependent properties of human vocal fold tissue were not obtained at different phonation frequencies.

The mucosal wave propagation has been assessed clinically by different measurement techniques such as electrography, photoglottography, ultrasound and visualization techniques including videokymography, stroboscopy and high speed imaging (Boessenecker et al., 2007; George et al., 2008; Voigt et al., 2010; Krausert et al., 2011). Krausert et al. (2011) investigated the advantages and disadvantages of each technique. George et al. (2008) studied the generation and propagation of the mucosal waves. They used a laser-triangulation endoscope as well as high-speed cameras to capture the human vocal folds profile during vibration in vivo. Voigt et al. (2010) presented a detection algorithm for mucosal wave propagation using HDSI. No attempt was made, however, to obtain the wave propagation speed.

In the present study, a novel method for non-invasive in vivo measurement of the shear modulus of the human vocal fold mucosa was developed. High-speed and MRI images of the vibrating vocal folds of four human subjects were obtained at different pitches within the fundamental range between 110 to 440 Hz. The pixel size of each set of high-speed images was determined by overlapping images of specific anatomical features obtained from HSDI and MRI. An automatic image processing algorithm was developed to detect and track the mucosal wave propagating on the superior surface of the vocal folds, through which the speed of mucosal wave propagation at different pitches was obtained for different subjects. An inverse surface (Rayleigh) wave propagation problem was solved to calculate the shear modulus of the subjects’ vocal folds mucosa in the transverse direction from the measured wave speeds. The dependency of the mucosal wave speed and the shear modulus on pitch was investigated. In addition, a Voigt viscoelastic model was fitted to the obtained shear wave velocities to calculate an approximate value for the complex shear modulus of vocal fold mucosa over the pitch range of interest. The results were found to be in good agreement with those obtained by Chan and Rodriguez (2008) in vitro, and thus support the validity of the proposed in vivo measurement method for clinical applications.

2. Experiments

The review board of the Research Ethics and Compliance (IRB) of McGill University, Montreal Neurological Institute and Hospital Research Ethics Board (REB) approved the protocol and consent procedure for the HSDI and MRI experiments, respectively. Four non- smoker adults, three men and one woman, aged between 22 to 29, participated in this study. The subjects were healthy with no current or past medical history, and no voice disorders. No subject was a trained voice user or had any background in clinical voice practice. Each subject participated in the HSDI and MRI experiments during two different sessions.

2.1. High speed digital imaging (HSDI)

Color high-speed cameras (Fastcam MC2- Model 10K; Photron Limited, San Diego, CA) attached to a rigid endoscope and a Luxtec® light source (Integra®, Burlington MA, Inc) were used for image recording. The sampling rate was selected to be SR = 4000 frame/s for all the measurements. Higher frame rates resulted in lower image quality and smaller camera field of view. The measurements were performed by an otolaryngologist (the third author) at the voice clinic of the Montreal General Hospital. The subjects were asked to sustain vowel /i/ with a steady volume intensity of 80 dB during the recording. To prevent heat-up from the powerful light, imaging was performed for at most five seconds at the time. Ignoring transients associated with phonation onset and shutoff, the middle three seconds of the recording were selected for image processing. Each subject phonated at different pitches with fundamental frequencies of f₀ = 110, 130, 165, 220, 260 and f₀ = 220, 330, 440 Hz for male and female subjects, respectively. A musical note at the desired pitch frequency was produced for the subjects to adjust his/her voice prior to the start of the imaging.

2.2. Magnetic resonance imaging (MRI)

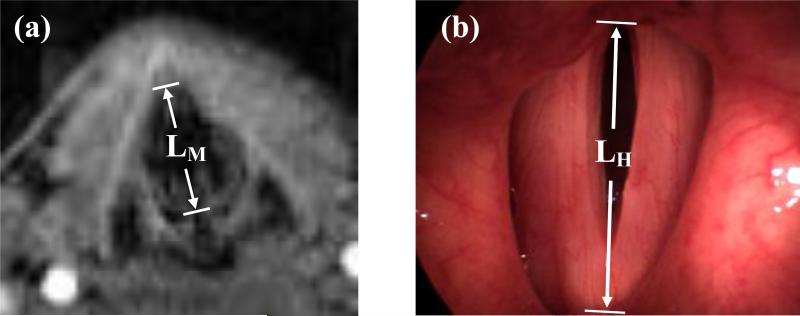
MRI experiments were performed to determine the exact pixel size in the high-speed digital images. The subjects repeated the same tasks as for the HSDI experiments. Three-dimensional MRI was performed using a Siemens 3T (Siemens Medical Solutions, Erlangen, Germany) scanner at the Montreal Neurological Institute. A Siemens “Neck Matrix Coil” and laser alignment was used to fix the position of the subject's larynx. The subjects were scanned in a supine position while phonating normally at their comfort. Subjects were asked to sustain phonation during a scanning period of 12 seconds. The scanning protocol was to acquire T1- weighted (T1W) images and performed with the following parameters: voxel size: 1.0×1.0×2.0 mm, repetition time (TR): 12.0 ms, echo time (TE): 4.01 ms, flip angle: 20 degrees, and an image matrix of 256 pixels, giving a field of view (FOV) of 256 mm. Again, the subject heard a musical note at the desired frequency through an intercom before each scan. The pixel size was obtained for each set of images by comparing a known anatomical feature in images from MRI and HSDI experiments, e.g. the anterior-posterior length of the vocal folds in the MRI image, L_M(m, and the same length in the high-speed digital image, L_H(pixel, as shown in Figure 1.

Figure 1.

Comparison between the anterior-posterior lengths of the vocal fold while performing a similar task. (a) L_M, the length in MRI image (b) L_H, the length in high-speed image.

3. Image processing algorithm

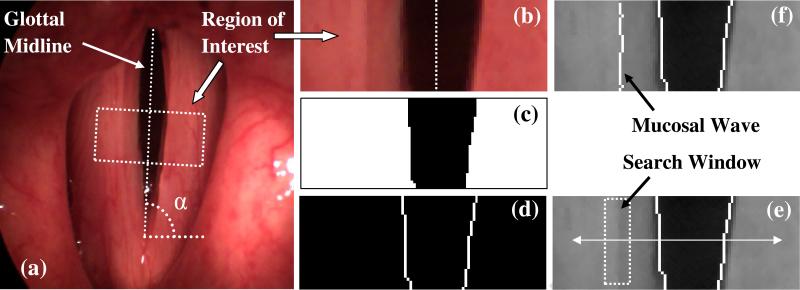
Several methods have been suggested for vocal fold edge detection (Yan et al., 2006; Lohscheller et al., 2007; Zhang et al., 2010). A threshold-based edge detection algorithm was used in the present study. High-speed images were imported in Matlab® for image processing. The glottal midline was defined interactively by selecting and connecting the anterior and posterior commissures points in the first image with the maximum glottal gap (Figure 2 (a)). The same line was considered as the glottal midline for subsequent images in each set of data, because of the high imaging rate and the negligible movement of the larynx within the short imaging time interval. The midline center region of the vocal folds along the anterior-posterior direction was determined as the region of interest and the images were rotated for $\frac{\pi }{2}-\alpha$ to make the glottal midline vertical as shown in Figure 2 (b). To demarcate the vocal fold edges, the cropped high-speed digital images were converted to binary ones and the perimeter of the binary images was identified as shown in Figure 2 (c) and Figure 2 (d), respectively. The conversion threshold was obtained from the first local minimum of the image histogram (Wittenberg et al., 1995; Zhang et al., 2010). The locations where the pixel intensity, I(x,y), became unity in the binary images represented the vocal fold edge location, VF(x,y). The obtained vocal fold edge overlapped on the gray scale image is shown in Figure 2 (e).

Figure 2.

Image processing algorithm, Subject 1 phonating at 130 Hz: (a) pre-processed high-speed image, region of interest and non-vertical glottal midline; (b) magnified region of interest with vertical glottal midline; (c) binary image; (d) perimeter of the binary image, where boundaries represent the vocal fold edge; (e) the search window for mucosal wave detection, obtained vocal fold edge is overlapped on the gray scale image; (f) obtained mucosal wave overlapped on the gray scale image.

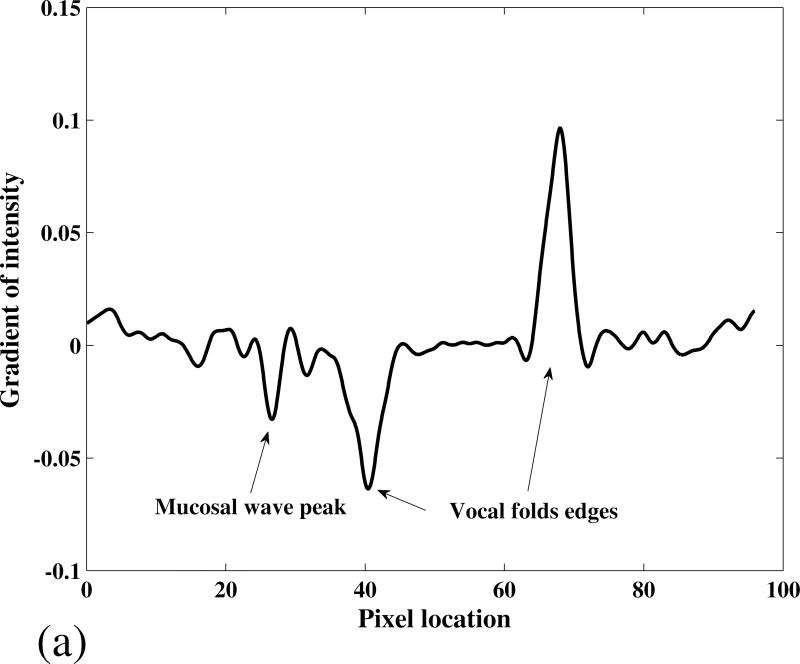
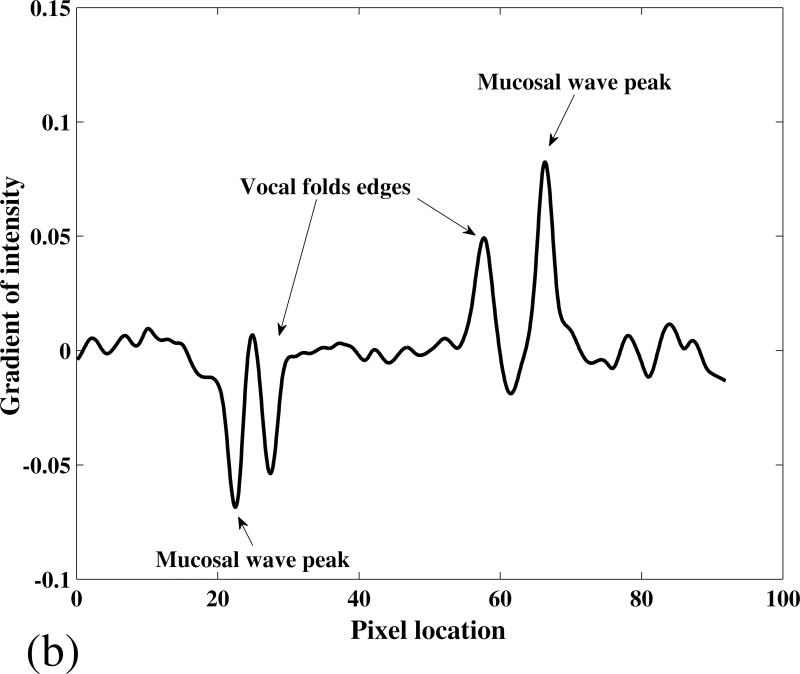
It was observed that I(x,y) changed significantly in the vicinity of the vocal fold edge and the mucosal wave peak. To illustrate this, the gradient of the intensity along the arrow line in Figure 2 (e) is shown in Figure 3 (a). The two main extrema represent the location of the right and left vocal fold edges. A local extremum is also present on the left fold, at the location of the mucosal wave peak amplitude. In the case shown in Figures 2 and 3 (a), the wave on the left fold could not be detected. It might be due to the location of the camera, which was not exactly on the vocal fold's midline and perpendicular to their superior surface. However, in most cases the mucosal wave was detected on both of the folds, as shown in Figure 3 (b). To detect the mucosal wave, a search window was defined near the vocal fold edge as shown in Figure 2 (e). The search window moved in the lateral direction with a velocity equal to the average lateral velocity of the midpoint edge, V̄_edg = ΔVF N, where ΔVF is the displacement of the midpoint edge between the fully closed and fully open phases, and N is the number of frames in which this displacement occurs. The width of the search windows was selected to be equal to ΔVF pixels. The gradient of intensity in the search window was calculated and the location of mucosal wave peak, MW (x,y), was obtained. The mucosal wave peak is shown overlapped with the gray scale image in Figure 2 (f). The mucosal wave propagation speed, c_m , for each row in the image was calculated from:

$$c_m=\Delta MV.SR.L_M∕L_H,$$ (1)

where ΔMV (pixel/frame) is the change in the location of the mucosal wave in the lateral direction. The average of the values obtained from the left and right vocal folds was considered as the mucosal wave speed. For each set of images, the mucosal wave speed was obtained from four different oscillation cycles with at least 1000 frames distance. The variations were found to be negligible, with a standard deviation of less than 6 percent, and thus the mean values were used in the following sections.

Figure 3.

The intensity gradient on a medial-lateral line passing through the vocal folds’ midpoint. (a) Subject 1 phonating at 130 Hz (the arrow line in Figure 2 (e)), and (b) Subject 1 phonating at 110 Hz. The location of the mucosal wave peak and the vocal folds edges are detected by the diagram extrema.

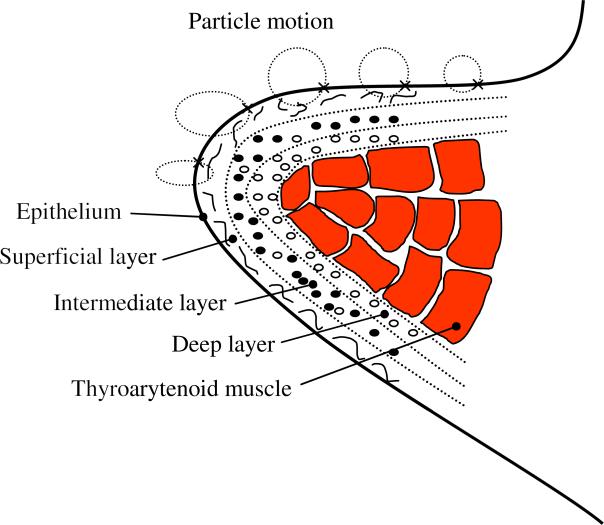
4. Estimation of the shear modulus

The length and the thickness of human vocal folds are approximately 10-15 and 3-5 mm, respectively (Hahn et al., 2006). The thyroarytenoid muscle is approximately 7-8 mm thick (Figure 4). The vocal fold muscle is covered laterally by the lamina propria and the epithelium (Stevens and Hirano, 1981; Titze, 1994). The lamina propria is a layered nonmuscular structure that may be subdivided into three different layers, namely, the superficial, intermediate and deep layers. The thickness of the lamina properia is around 2 mm (Stevens and Hirano, 1981). The self-sustained oscillations of human vocal folds are mostly confined within the mucosa, which consists of the epithelium and the superficial layer of the lamina propria. The frequency of the vocal folds vibrations, and consequently the mucosal wave propagation, is the same as phonation pitch. An inverse wave propagation approach, where the displacement/velocity field is known and the mechanical properties of the medium are unknown, is presented in the following to measure the mechanical properties of the human vocal mucosa.

Figure 4.

Simplified schematic of a coronal section structure of human vocal fold tissue, and the motion of different locations of the vocal fold surface due to the mucosal wave propagation. ● and ○ denote the cross section of elastin and collagen fibers, respectively.

4.1. Wave propagation model

It was shown that the movement of the medial and superior surfaces of vocal folds, featuring the mucosal wave propagation, are respectively elliptical and circular in general (Boessenecker et al., 2007). This suggests that, mucosal waves include motion in both the longitudinal and transverse directions (Figure 4), with respect to the propagation direction. This behavior is similar to that of Rayleigh waves; i.e., a type of surface waves which propagates near stress-free surfaces. Therefore, the well-known Rayleigh wave propagation model was employed to calculate the shear modulus of the vocal fold mucosa from the measured mucosal wave speeds, assuming ideal Rayleigh waves. The Rayleigh wave dispersion equation for a macroscopically homogeneous and isotropic medium is as follows:

$${(2-{\xi }^2)}^4-16(1-{\xi }^2)\left(1-\frac{{\xi }^2}{{\kappa }^2}\right)=0,$$ (2)

where

$${\kappa }^2={\left(\frac{c_c}{c_s}\right)}^2={\left(\frac{k_s}{k_c}\right)}^2=\frac{\lambda +2\mu }{\mu }=\frac{2-3\nu }{1-2\nu },\xi =\frac{k_s}{k_R},$$ (3)

and λ(ω) and μ(ω) are frequency-dependent Lame functions. The Poisson's ratio of the vocal fold tissue, ν, was assumed to be 0.495. The constants k_R , k_c and k_s are the Rayleigh, compressional and shear wavenumbers, respectively, known as (Graff, 1975)

$$k_R=\frac{\omega }{c_R},$$ (4a)

$$k_c=\frac{\omega }{c_c}=\frac{\omega }{\sqrt{(\lambda +2\pi )∕\rho }},$$ (4b)

$$k_s=\frac{\omega }{c_s}=\frac{\omega }{\mu ∕\rho },$$ (4c)

in which ω is the angular frequency, and c_R , c_c and c_s are Rayleigh, compressional and shear wave speeds, respectively.

The mucosal wave propagation speed at different pitches was obtained from the image processing procedure for each of the subjects, c_m, and treated as the Rayleigh wave propagation speed, c_R. Then, the shear wavenumber, k_s, and consequently the shear wave speed, c_s , were obtained from Eqs. (2) and (3). Finally, the shear modulus of the vocal fold mucosa was calculated from $\mu =\frac{{\omega }^2\rho }{k_s^2}$. The vocal fold mucosa density, ρ, was assumed to be 1060 and 1075 kg m³ for male and female subjects, respectively (Titze, 1994).

The shear modulus obtained from such surface wave propagation method is representative over the depth of wave penetration. The mucosal wave propagates mainly within the mucosa during phonation. Therefore, the obtained shear modulus is believed to be that of the vocal fold mucosa.

4.2. Voigt viscoelastic model

The Voigt model, commonly used for soft viscoelastic materials (Royston et al., 1999), was used to obtain an approximate mean value for the shear elasticity (modulus), μ, and the shear viscosity, η, of the vocal fold mucosa over the pitch range of interest. The viscoelastic properties of the medium with a complex shear modulus Ĝ = G′ + iG″ = μ + iωη are related to the shear wave speed via the following equation (Yamakoshi et al., 1990)

$$c_s=\sqrt{\frac{2({\mu }^2+{\omega }^2{\eta }^2)}{\rho (\mu +\sqrt{{\mu }^2+{\omega }^2{\eta }^2})}}.$$ (5)

For an elastic medium with negligible dissipation, where μ >>ωη, Eq. (5) reduces to Eq. (4c). The shear wave speed can be obtained for a medium with known viscoelastic properties at different frequencies using Eq. (5). In the present study, the shear wave speed is known at several different oscillation frequencies (phonation pitches), allowing the calculation of the complex shear modulus of the vocal fold mucosa.

5. Results and discussion

Data were obtained for different phonation pitches in the range from 110 to 260 Hz and 220 to 440 Hz for male and female subjects, respectively. The mean value and standard deviation of the measured data obtained from each subject at each pitch were calculated. The standard deviation values of the measured mucosal wave speed and shear modulus were less than 6 and 12 percent of the corresponding mean values, respectively. Thus, only the mean values are shown.

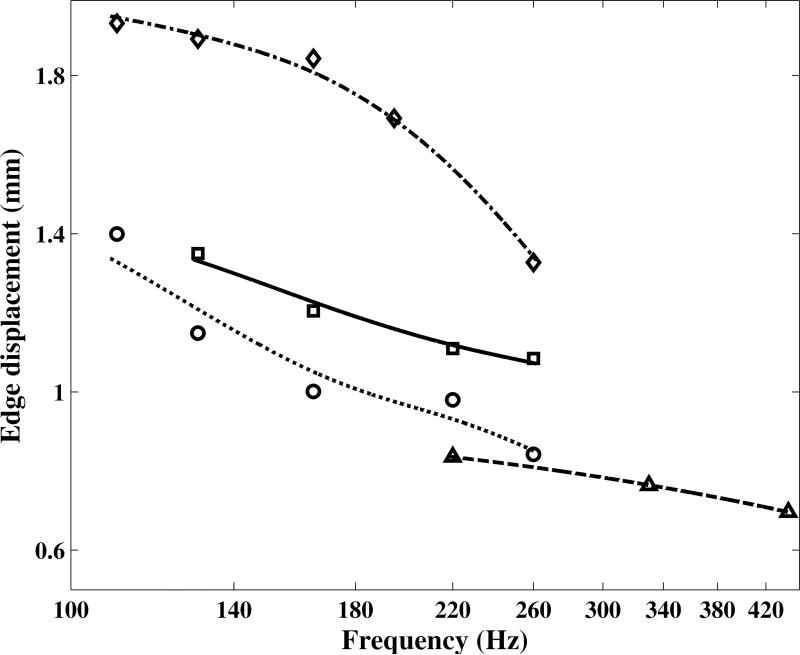
The maximum horizontal (lateral) displacement of vocal fold upper edge at different pitches from 110 to 440 Hz is shown in Figure 5. The vocal folds edge position and glottal area depend on to the viscoelastic mechanical properties of the tissue, as well as lung air pressure, vocal folds geometry, vocal tract inertance, and other parameters that can vary from one subject to another. Therefore, it is not possible to compare the results obtained from different subjects without additional information. Nevertheless, the edge position obtained from each specific subject's vocal fold is expected to decrease with pitch, due to the decrease in the vocal folds width and the expected increase in the shear modulus. This is consistent with the results shown in Figure 5.

Figure 5.

The maximum of the horizontal displacement of vocal fold upper edge during the opening phase at different phonation pitches from 110 to 440 Hz. : Subject 1; : Subject 2; : Subject 3; : Subject 4; : regression for Subject 1; : regression for Subject 2; : regression for Subject 3; : regression for Subject 4. (Regressions are to guide the eye)

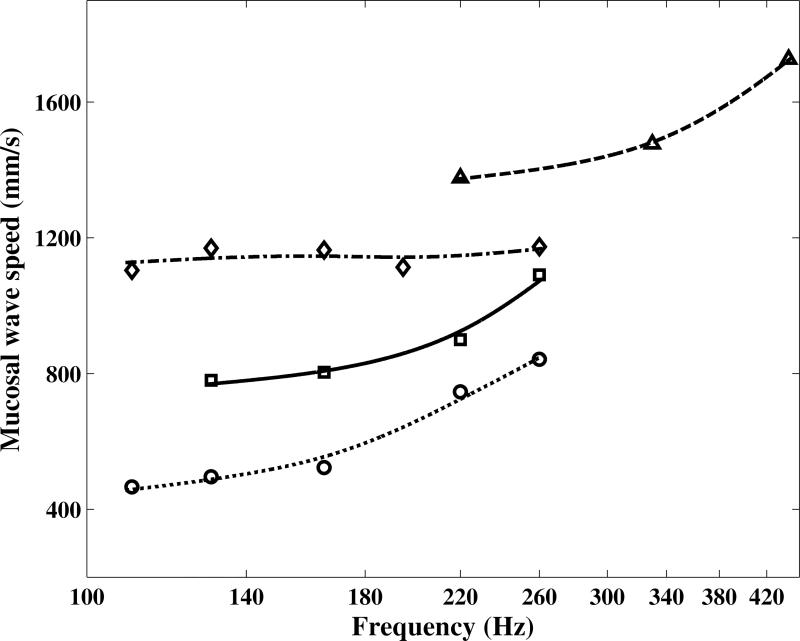
The speed of mucosal wave propagation on the superior surface of vocal folds for four human subjects at different pitches is shown in Figure 6. As seen in this figure, the mucosal wave propagation speed increased with pitch except for Subject 3 where it was almost constant. This is consistent with the expected trend of greater overall stiffness (shear modulus) of the tissue at higher frequencies. Average values of 510 and 810 mm/s were obtained by George et al. (2008) at 149 Hz, which were in good agreement with the results shown in Figure 6, specially those for Subjects 1 and 2.

Figure 6.

The mucosal wave propagation speed at different phonation pitches from 110 to 440 Hz. : Subject 1; : Subject 2; : Subject 3; : Subject 4; : regression for Subject 1; : regression for Subject 2; : regression for Subject 3; : regression for Subject 4. (Regressions are to guide the eye)

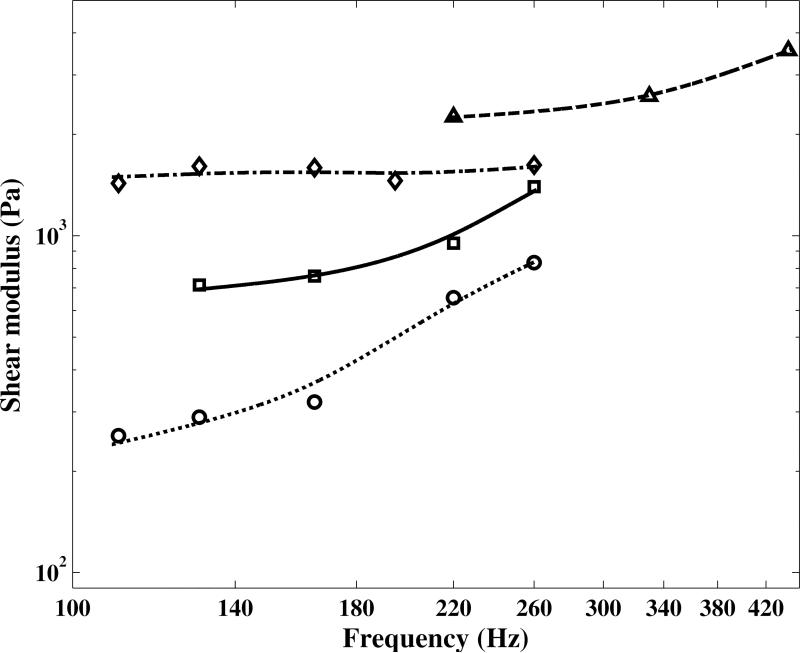
The shear modulus of human vocal fold mucosa in the transverse direction at fundamental frequencies from 110 to 440 Hz is shown in Figures 7. The same trends as those of mucosal wave propagation speed were observed as expected. The frequency-dependent behavior of mechanical properties of human vocal fold tissue is influenced by two main parameters, namely the inherent viscoelastic properties of the tissue and the longitudinal tension.

Figure 7.

The shear modulus of human vocal fold mucosa at different phonation pitches from 110 to 440 Hz. : Subject 1; : Subject 2; : Subject 3; : Subject 4; : regression for Subject 1; : regression for Subject 2; : regression for Subject 3; : regression for Subject 4. (Regressions are to guide the eye)

The vocal fold tissue includes a large concentration of fibers such as elastin and collagen within interstitial fluid (Titze, 1994), and thus feature a highly viscoelastic mechanical behavior. The magnitude of the tissue shear modulus depends on the configurational rearrangements that occur within the time period of one dynamic loading cycle. At low frequencies, the fibers have sufficient time to adjust themselves with the applied deformation by sliding alongside each other. Therefore, the tissue stiffness is relatively small. At higher frequencies, only minor adjustment can take place within the period of deformation, and thus the tissue is stiffer. A longitudinal tension is required for the self-oscillation of vocal folds. This tension is applied by the thyroarytenoid muscle and sustained by collagenous fibers of the ligament, which consists of the intermediate and deep layers of the lamina propria (Titze, 1994). The global (effective) stiffness of the tissue is directly related to vocal fold tension (Titze, 1994). Greater tensions are applied to the vocal folds at higher pitches, which results in greater stiffnesses.

As shown in Figure 7, considerable differences were observed between the obtained shear modulus vales from different subjects’ vocal folds. The rate of increase of shear modulus values with pitch was also different for different subjects. The extension of the vocal fold length varied with pitch. For example, the length of the vocal folds of Subject 1 at 260 Hz was 45 percent greater than that at 110 Hz. For a relative elongation of 45 %, the increase in shear modulus values was 225 % between the corresponding pitches. For Subject 3, for which the rate of increase of the shear modulus was the least, the values for the relative elongation of vocal folds and the increase in shear modulus were 19 % and only 13 %, respectively.

The complex shear modulus values of subjects’ vocal fold mucosa obtained from the Voigt viscoelastic model are shown in Table 1. The Voigt model yields constant values for the shear elasticity and viscosity averaged over all frequencies. The real part of the complex shear modulus, the shear modulus, was found to be a good approximate mean value of the shear modulus values shown in Figure 7. The imaginary part of the obtained complex shear modulus, the viscous modulus, increased linearly with frequency accordingly with the Voigt model, G′′ = ωη. This is in good agreement with data obtained by Chan and Rodriguez (2008) from in vitro measurements. The mean value of shear modulus of four subjects’ vocal fold mucosa was 1378 Pa, which is in excellent agreement with those obtained by Goodyer et al. (2007b) from in vivo measurements; i.e, 1371 Pa. The difference is surprisingly small, only 0.5 percent, considering the data is for different human subjects and is obtained with different measurement methods. In the present study, the shear modulus is obtained during phonation using a dynamic method. Goodyer et al. (2007b) implemented a simple-shear technique in a semi-static manner.

Table 1.

The complex shear modulus, Ĝ, of human subjects’ vocal fold mucosa obtained from the Voigt viscoelastic model.

Subjects	Shear modulus [Pa]
# 1	415 + iω0.40
# 2	878 + iω0.52
# 3	1496 + iω0.67
# 4	2722 + iω1.01

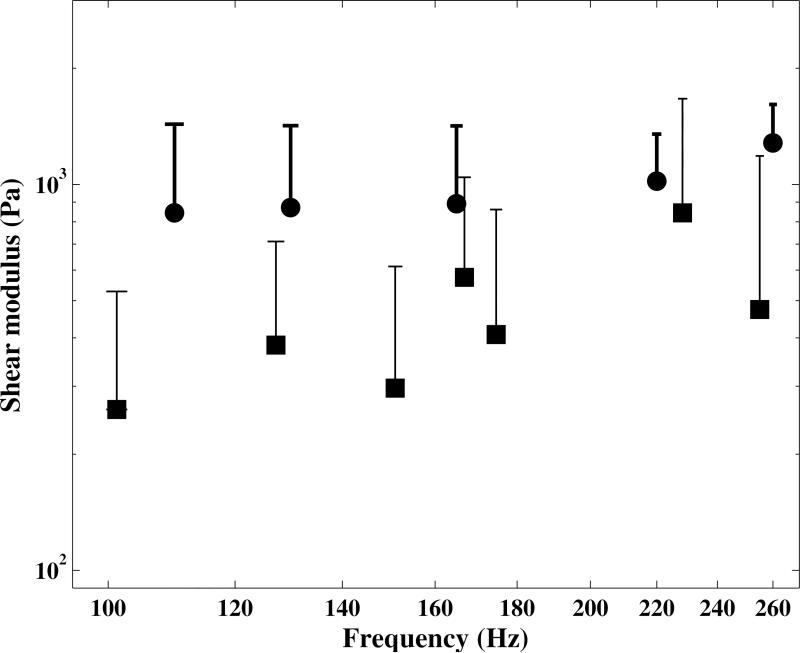
The mean value and standard deviations of the shear modulus of three subjects’ vocal fold mucosa, Subjects 1 to 3, were compared with those obtained by (Chan and Rodriguez, 2008) from in vitro measurements in Figure 8. As seen in this figure, the results fall within the same range while those from in vivo measurements were generally greater than in vitro ones. Chan and Rodriguez (2008), used a parallel rheometer to measure the shear modulus of the human vocal fold cover with no extension (tension). The method used in the present study, however, yields data during phonation, while the vocal folds underwent large extensions. This allowed the effect of vocal fold tension to be taken into account.

Figure 8.

The means and standard deviations (upper error bars) of the shear modulus of human vocal fold mucosa versus frequency in the range from 100 to 260 Hz. ● : the mean value of three male subjects from in vivo measurements (present study); □ : the mean value of seven specimens obtained from in vitro measurements (Chan and Rodriguez, 2008).

6. Conclusions

A novel non-invasive method was developed for the in vivo measurements of the shear modulus of human vocal fold tissue during phonation. Four subjects underwent high speed digital and magnetic resonance imaging tests at different pitches, for fundamental frequencies in the range from 110 to 440 Hz. The images obtained from MRI were used to determine pixel size in those from HSDI. Using the high-speed images and an automatic image processing algorithm, the mucosal wave propagation speed was determined for different human subjects at different phonation pitches. The shear modulus of the subjects’ vocal fold mucosa was then obtained using a surface (Rayleigh) wave propagation model and the measured wave speeds. A Voigt viscoelastic model was also used to calculate the complex shear modulus of the tissue including the shear elasticity and viscosity from the obtained shear wave speeds.

The results, including the vocal fold edge displacement, mucosal wave speed and the mucosa shear modulus, were compared to those of previous studies from in vitro and in vivo measurements and found to be in good agreement. The obtained shear modulus increased with pitch. This was speculated to be because of the inherent viscoelastic properties of the tissue and the increased longitudinal tension applied to vocal folds at higher pitches. The magnitude of the obtained shear modulus and the rate of increase with pitch were considerably different for different subjects. This emphasizes the need for in vivo clinical assessments of any specific patients’ vocal folds for diagnostic purposes or the evaluation of vocal fold treatment procedures.

Several assumptions have been made in the present study, and thus the obtained mucosal wave speed and shear modulus were estimates of such values. For example, the phonation frequency was not measured in MRI experiments, although the musical note was produced to help them to phonate at the required frequencies each time. The actual phonation frequency in MRI experiments, and consequently the vocal fold dimensions, could be slightly different from those of the assumed frequency. Differences between the visible anatomical features from one set of HSDI data to another made it more challenging to overlap these features with the corresponding ones in MRI images. It was done with the help of experienced professionals who were familiar with laryngeal anatomy. Furthermore, ideal Rayleigh wave propagation was assumed on the superior surface of the vocal folds, which might not precisely model the mucosal wave propagation due to the complex geometry.