Uncertainty in Measurement: A Review of Monte Carlo Simulation Using Microsoft Excel for the Calculation of Uncertainties Through Functional Relationships, Including Uncertainties in Empirically Derived Constants

Abstract

The Guide to the Expression of Uncertainty in Measurement (usually referred to as the GUM) provides the basic framework for evaluating uncertainty in measurement. The GUM however does not always provide clearly identifiable procedures suitable for medical laboratory applications, particularly when internal quality control (IQC) is used to derive most of the uncertainty estimates. The GUM modelling approach requires advanced mathematical skills for many of its procedures, but Monte Carlo simulation (MCS) can be used as an alternative for many medical laboratory applications. In particular, calculations for determining how uncertainties in the input quantities to a functional relationship propagate through to the output can be accomplished using a readily available spreadsheet such as Microsoft Excel.

The MCS procedure uses algorithmically generated pseudo-random numbers which are then forced to follow a prescribed probability distribution. When IQC data provide the uncertainty estimates the normal (Gaussian) distribution is generally considered appropriate, but MCS is by no means restricted to this particular case. With input variations simulated by random numbers, the functional relationship then provides the corresponding variations in the output in a manner which also provides its probability distribution. The MCS procedure thus provides output uncertainty estimates without the need for the differential equations associated with GUM modelling.

The aim of this article is to demonstrate the ease with which Microsoft Excel (or a similar spreadsheet) can be used to provide an uncertainty estimate for measurands derived through a functional relationship. In addition, we also consider the relatively common situation where an empirically derived formula includes one or more ‘constants’, each of which has an empirically derived numerical value. Such empirically derived ‘constants’ must also have associated uncertainties which propagate through the functional relationship and contribute to the combined standard uncertainty of the measurand.

Introduction

Since its introduction in 1993 with corrections and updates in 1995 and 2008, the GUM has provided the basic framework for evaluating uncertainty in measurement.¹ The GUM approach provides an alternative focus for uncertainty information to that which may have previously been provided in clinical biochemistry publications in the form of an error analysis or by the total error concept.^2–5 A fundamental premise of the GUM is based on the assumption that all systematic errors are identified and corrected at an early stage in the evaluation process. The quality of a measurement is then expressed by taking the uncertainty associated with random errors and the uncertainty associated with any correction for systematic error (bias) into account on an equal footing. However, section F.2.4.5 of the GUM specifically describes the procedure where a significant systematic effect may be taken into account by enlarging the uncertainty assigned to the result. ‘An example is replacement of an expanded uncertainty U with U+b, where U is an expanded uncertainty obtained under the assumption b = 0 ’.¹ This situation is directly comparable to the calculation of total error as described by Westgard and others, where the total error includes both a bias and an imprecision component as part of the combined standard uncertainty statement.^2–5 The GUM thus recognises that in some circumstances, particularly where time and resources are limited, such a procedure may be unavoidable. The preferred GUM approach however, as described in section 3.2.4 of the GUM, is to eliminate as early as possible in the analytical process any known systematic effect(s) by an appropriate correction(s), with the only uncertainty relating to systematic error being the uncertainty of the correction itself. The uncertainty in the reported value of the measurand will thus comprise the uncertainty due to random errors and the uncertainty of any corrections for systematic errors.

The bottom-up approach as summarised in section 8 of the GUM has previously been given most emphasis.¹ It requires that each step in the analytical process be evaluated in minute detail and that a mathematical model be available to describe the relationship between the various inputs and the output (the measurand). For this reason, the GUM has been criticised as not always providing procedures suitable for medical laboratories, particularly when IQC is used to derive most of the uncertainty estimates.^6,7 Although the bottom-up approach does provide a rigorous methodology for the estimation of uncertainty, other logical approaches are certainly not excluded, for example:

• A top-down approach with the use of IQC for the assessment of precision (imprecision); and external quality assessment for the evaluation of systematic error (bias). The applications of bottom-up and top-down approaches have been reviewed.^8,9

• Numerical procedures such as MCS as outlined in Supplement 1 to the GUM and by others.^10–15

There are many articles in the medical sciences literature describing the use of MCS for the investigation of statistical problems,^16–26 but few for the investigation of combined standard uncertainty associated with the calculation of a measurand through a functional relationship. Interestingly, one uncertainty evaluation used MCS in 1988 for ‘Error estimation in the quantification of alkaline phosphatase isoenzymes by selective inhibition methods’. The MCS procedure was well applied and eminently suited to this application, but certainly did not use the spreadsheet approach which we describe.¹⁶

Supplement 1 to the GUM, Guide to the expression of uncertainty in measurement – Propagation of distributions using a Monte Carlo method provides a detailed discussion which is ‘concerned with the propagation of distributions through a mathematical model of measurement … as a basis for the evaluation of uncertainty of measurement, and its implementation by a Monte Carlo simulation (MCS) method’.¹⁰ Whereas the GUM modelling approach requires advanced mathematical skills for many of its procedures, the MCS method can be applied to most medical laboratory applications using a readily available spreadsheet such as Microsoft Excel. Complex uncertainty calculations can be accomplished by standard spreadsheet applications rather than by technically demanding mathematical procedures.

The aim of this article is to demonstrate the ease with which Microsoft Excel (or a similar spreadsheet) can be used to provide an uncertainty estimate for measurands derived through a functional relationship without the requirement of advanced mathematical knowledge or the detailed assessment required for the bottom-up approach. In addition, we also consider the relatively common situation where an empirically derived formula includes one or more ‘constants’, each of which has an empirically derived numerical value. Such empirically derived ‘constants’ must also have associated uncertainties and therefore should not be considered as true constants. Even though the uncertainties associated with these ‘constants’ are not generally published, any such uncertainty must also propagate through the functional relationship and contribute to the combined standard uncertainty of the measurand. Examples which include plausible estimates of such uncertainties are discussed in Appendices 2 and 3.

Probability Density Function

A probability density function (PDF) or probability density distribution function is a mathematical relationship which describes how the probability density of a continuous random variable may vary over a permitted range of values. A PDF is usually illustrated by means of a graph. For example, the graph of the normal (Gaussian) PDF is a bell-shaped curve with a permitted range from minus infinity to plus infinity (with probabilities in the tails being very low). The horizontal axis of a PDF graph marks off the possible values of a variable, while the vertical axis gives the probability density. In addition, the area under a PDF graph between any two selected values of the variable is the probability that the variable may take any value within the specified interval. It naturally follows that the total area under a PDF graph has a probability of one (certainty), since the variable must take some value within its permitted range.

A probability distribution (with ‘density’ omitted) is a more general statistical term which may include the probability density distribution, but usually refers to other types of distribution such as a cumulative probability distribution or a discrete probability distribution. For brevity in what follows, however, a ‘probability density function’ where appropriate will be referred to as a ‘probability distribution’ or simply a ‘distribution’.

In probability and statistics there are many types of PDF. For medical laboratory applications with respect to uncertainty in measurement, the normal, the Student t, the rectangular and symmetrical triangular distributions are particularly relevant. The importance of correctly allocating the most appropriate distribution for a specified uncertainty is discussed in many sections of the GUM (for example, section 4.4, Graphical illustration of evaluating standard uncertainty),¹ in Supplement 1 to the GUM (section 6, Probability density functions for the input quantities)¹⁰ and in Eurachem/CITAC guide CG4 (appendix E).¹¹ A particularly useful account is also provided in the G104-A2LA guide for estimation of measurement uncertainty in testing.²⁷

In brief:

• A rectangular or uniform PDF is used as a model in situations where the probability of obtaining any value between two stated limits is equal to the probability of obtaining any other value between these limits. The rectangular probability distribution has boundaries or limits which are usually specified as ±a from the central value, where a is the half-width of the distribution. Thus 100% of the values must fall between –a and +a. This is the probability distribution of least knowledge, when all that is known are the limits within which a value will fall. The standard deviation of a rectangular distribution is given by a/√3.^11,27

• The triangular PDF (usually the symmetrical triangular distribution) also contains 100% of the possible values. With this distribution however, the probabilities increase linearly from zero to the peak or central value, and then decrease linearly at the same rate back to zero. In a similar manner to the rectangular distribution, the limits of a symmetrical triangular distribution are usually specified as ±a from the peak. The standard deviation of a triangular distribution is a/√6.^11,27

• The normal or Gaussian PDF represents the statistical behavior of many natural phenomena. It is the symmetrical ‘bell-shaped’ distribution that (in theory) is produced if all that we know about a distribution are its mean and standard deviation. An important reason a normal distribution is often assumed is that other distributions when combined often yield a net distribution which is close to normal (this is the essence of the so-called central limit theorem). It is also the limiting distribution for a measurement which is subject to many small random errors. For many of the measurements in medical laboratory procedures, the distribution of the measurand is assumed to follow, or closely approximate, a normal distribution. This distribution is characterised by its mean and standard deviation, both of which must be specified.

• When the number of observations is relatively small, the Student t distribution with its associated degrees of freedom should be considered. The t distribution applies in situations where high-accuracy analysis is undertaken with a limited number of observations or when the GUM bottom-up approach must be meticulously followed.¹

• The U-shaped PDF models situations where the most likely values are at or near the containment limits.²⁷ A particular example which may be of relevance to laboratory testing is the regulation of ambient temperature by an air-conditioner. Even though several publications comment on room air-conditioning,^10,11 section 3.3.2.4 of the G104-A2LA guide provides the statement ‘… because of the way thermostats work, room temperature tends to be near the maximum allowed deviation from the set point, that is, the room temperature is most likely to be too hot or too cold relative to the set point’. The probability distribution which describes this situation is a U distribution, with containment limits ±a and standard deviation a/√2.²⁷

Some examples associated with the first three of the above distributions and their application to laboratory uncertainty calculations are given in Table 1.

Table 1.

Probability distributions for laboratory measurements: summary of properties, possible laboratory applications and Excel functions for MCS.

Rectangular distribution	Symmetrical Triangular distribution	Normal (Gaussian) distribution
Standard deviation: $s=\frac{a}{\sqrt{3}}$	Standard deviation: $s=\frac{a}{\sqrt{6}}$	Standard deviation: $s=\sqrt{\frac{\sum {\left(x_i-\overline{x}\right)}^2}{n-1}}$
For GUM modelling: u(xi) = s	For GUM modelling: u(xi) = s	For GUM modelling: u(xi) = s
Excel function for MCS given a distribution half-width (a):* (x̄ − a)+(2 * a * (RAND()))	Excel function for MCS given a distribution half-width (a):* (x̄ − a)+(a * (RAND()+RAND()))	Excel function for MCS given a standard uncertainty (expanded uncertainty ÷ k):* NORMINV(RAND(), x̄, u(xi))
Use when there is equal probability of a value falling anywhere within ±a from the mean.12	Use when there is reason to expect that values in the centre of the range are more likely than at the extremes.12	Use when repeated measurements are made of a randomly varying process and analysed statistically to derive a mean and standard deviation.
Use this distribution when a measurement is given as a value ± limits (±a) without a confidence interval or other information with regard to the distribution of values.	Use this distribution when 100% containment limits are known (±a) and values are more likely to be near the mean than at the extremes.	Use this distribution when an uncertainty is given in the form of a 95% (or other) confidence interval or a measurand value ± an expanded uncertainty (for example: measurand ±1.96u, or measurand ±2u).
Example 1: A certificate or specification which gives a range or limits without a confidence interval or other details as to how the range was derived.10,12 Example 2: The uncertainty data for atomic mass should be taken as a rectangular distribution.10,12	Example : The nominal volume of a measuring flask or pipette, as the manufacturing process is such that values near the specified volume are more likely than at the extremes (for example; 100.0 ± 0.1 mL at 20°C, where a = 0.1 mL).10,12	Example: The use of internal quality control specimen(s) to determine analytical imprecision (standard deviation or standard uncertainty).

Symbols: Standard deviation (s); distribution half-width (a); a measured value (x_i); the mean of measured values (x̄); number of observations (n); standard uncertainty of a measured value (u(x_i)); coverage factor (k); Excel function for random number generation (RAND()); Excel function for deriving a value within a given normal distribution (NORMINV(probability, x̄, u(x_i))).

^*In applications such as those described in the appendices, a single determination of a given measurand is usually used in the calculations. In these situations, the mean or centre point of the PDF to be used for the MCS procedure is actually this single measurement value whose standard uncertainty (u(x_i)) must be known in advance. The subscript i for this standard uncertainty implies that it is not the standard uncertainty of a mean (which is sometimes known as the standard error of the mean),²⁹ but denotes a previously estimated standard deviation obtained from several measured values (as might be obtained from an internal quality control).

The GUM Modelling Approach

The separate introduction to the Guide to the Expression of Uncertainty in Measurement and related documents provides an overview of the GUM and its relevance to measurement science.²⁸ It clearly states that the theoretical background for the ‘evaluation of measurement data and evaluation of uncertainty of measurement is supported by mathematical statistics and probability’.

Section 2.2.3 of the GUM defines uncertainty of measurement as a ‘parameter, associated with the result of a measurement, that characterises the dispersion of the values that could reasonably be attributed to the measurand’.¹ Uncertainty of measurement may appear as random variations in the results of repeated measurements, as uncertainty documented from previous experience or as uncertainty estimated by professional judgment. As such, the ‘parameter’ may be evaluated as a sample standard deviation of repeated measurement results, the half-width of an interval having a stated coverage probability, the uncertainty associated with the correction for systematic error (bias), or estimated by other (non-statistical) procedures.²⁹ Whatever method is chosen to provide an uncertainty estimate, GUM outlines the manner in which this can be described in the form of a standard deviation.¹ Expressed in this manner, an uncertainty component is known as a standard uncertainty. Section 2.3.1 of the GUM describes standard uncertainty as ‘uncertainty of the results of a measurement expressed as a standard deviation’. To distinguish the statistical term standard deviation from standard uncertainty, sample standard deviation is given the symbol s, while standard uncertainty is denoted by u. Variance is the standard statistical term for the square of a standard deviation or the square of a standard uncertainty.

The procedural steps proposed by the GUM are outlined in section 8: Summary of procedures for evaluating and expressing uncertainty components.¹ These steps may be summarised as follows:

• Specify the measurand: provide a clear statement of what is being measured and the mathematical functional relationship between the measurand and the input quantities upon which it depends.

• Identify sources of uncertainty.

• Identify and correct for systematic error (bias) where possible.

• Quantify uncertainty components: determine the standard uncertainty associated with each of the input quantities, including any uncertainty associated with the correction for systematic error. An uncertainty estimate obtained by the statistical analysis of serial observations (for example, the standard deviation of an IQC specimen) is described by the GUM as a Type A evaluation of standard uncertainty. An uncertainty estimate obtained by other means (for example, information obtained from an authoritative published report, a calibration certificate, personal experience or a numerical quantity associated with a certified reference material) is described by the GUM as a Type B evaluation. Type B components should be characterised by uncertainty quantities which may be considered as approximations to standard uncertainties.^1,10,11,29

• Calculate the value of the measurand: that is, calculate the result of the measurement from the functional relationship which connects the various input quantities to the measurand.

• Calculate the combined standard uncertainty of the measurand: that is, calculate the combined standard uncertainty of the measurand from the standard uncertainties (and covariances if present) associated with the various input quantities. These standard uncertainties are combined according to the rules based on the law for the propagation of uncertainties.²⁹

• Calculate the expanded uncertainty of the measurand by applying an appropriate coverage factor, k. The expanded uncertainty is equal to the combined standard uncertainty of the measurand multiplied by k. For medical laboratory applications, k is typically given the value of 1.96 (or 2.0). This provides an expanded uncertainty which includes 95.0% (or 95.4%) of the values within the distribution of the measurand. The expanded uncertainty calculated in this manner provides a coverage interval on the assumption that the distribution of the measurand is normal.

Monte Carlo Simulation

MCS provides a practical alternative to the GUM modelling approach and is a general tool for evaluating uncertainty.^10–12 Modern ‘personal’ computers running widely available spreadsheet software can be used for most medical laboratory applications. In contrast to the theoretical GUM modelling approach, MCS may be regarded as ‘experimental statistics’. This comparison between theoretical and experimental statistics is similar to the relationship between theoretical and experimental physics. In both sciences, a complex theoretical analysis can be put to an experimental test. In physics, such experimental testing has long been mandatory. In statistics however, it has only been possible since the development and routine availability of high computing power. Older theoretical statistical results can be (and have been) tested experimentally using MCS. It is now also common practice to use MCS to establish statistical results where a theoretical approach would be difficult or inconclusive.

The MCS procedure uses algorithmically generated pseudo-random numbers (but for simplicity we have used the term random) which are then forced to follow a prescribed probability distribution. For a normal distribution, the spread of random numbers is predetermined by its specified mean and its specified standard deviation. For each input, the MCS procedure generates a numeric value drawn at random from its respective PDF. Numeric values derived in this manner are produced for all inputs to the known functional relationship which is then used to produce a single numeric value as output. This process is repeated a sufficiently large number of times (or ‘trials’) so as to produce a set of simulated results as output. The mean and standard deviation of these output results are then the respective estimates of the measurand and its standard uncertainty.

As these input values are randomly selected from the predefined probability distributions associated with each of the input variables, the overall process may thus be considered as a procedure for the propagation of distributions. Also, as the MCS procedure performs random sampling from the PDFs of the input quantities, it directly provides the probability distribution of the measurand and hence any required coverage interval. Whereas the GUM procedure yields the ‘bare bones’ (the mean and standard uncertainty of the measurand), the MCS procedure ‘fleshes this out’ as it yields the actual PDF of the measurand which contains much more information. This additional information may be used to graph the distribution of output data and to directly determine the coverage interval of the measurand even when the PDF of the measurand has significant asymmetry.

As the GUM modelling approach does not explicitly determine a PDF for the output quantity, the GUM approach can sometimes limit the ability to clearly define an output PDF. The propagation of distributions using MCS however, will always provide a PDF for the output quantity which is consistent with the PDFs of the various inputs. Some further advantages of the MCS procedure over the GUM modelling approach as paraphrased from Supplement 1 to the GUM include:¹⁰

• In contrast to the GUM modelling approach, the MCS procedure ‘automatically’ takes into account any nonlinearities in the functional relationship.

• If two inputs are correlated, the MCS procedure provides joint simulation of a bivariate distribution provided the correlation coefficient (or equivalently the covariance) has been appropriately incorporated into the definition of the input PDF (see below, “Uncertainty in Measurements With and Without Correlation”). In this manner, any correlation will have been explicitly taken into account after the completion of the MCS procedure.

• A graphical representation of the distribution of the measurand can be obtained directly from the MCS procedure. In this manner, any non-normality or asymmetry in this distribution can usually be seen.

• There is a significant reduction in the mathematical skills required for most evaluations.

• The MCS procedure generally provides improved estimates for non-linear models.

• The MCS procedure provides a coverage interval corresponding to a stipulated coverage probability. For medical laboratory applications with a normally distributed measurand, this is typically 95% for a coverage factor of 1.96 or 95.4% for a coverage factor of 2.0. For asymmetric distributions, the coverage intervals (whether 95% or any other value) may vary in length. In such cases, the shortest 95% coverage interval (or any other percentage) is generally quoted, since this provides a narrower uncertainty range and the best location of the measurand.

A fundamental requirement in applying MCS is software for generating random numbers. The period of the numbers so produced (the total number of trials that can be made before the starting point of the sequence of random numbers is again reached) should be as large as possible. This period is often around one billion, which is generally adequate for the great majority of applications.^10,30

Spreadsheet Procedure for MCS

Personal computers running spreadsheet software now provide the computing power and functionality to perform MCS with sufficient numerical precision for most medical laboratory applications. Details for the use of this spreadsheet approach have been described in detail.^10,31,32 However, the very detailed and easy-to-follow procedure described by Chew and Walczyk has been used as the basis for the simulations described in this article.³²

In a similar manner to the GUM modelling procedure, the MCS approach requires a measurement model which can be described by an appropriate functional relationship (equation). From a mathematical perspective, a function can be regarded as a quantity whose value can be derived from one or more input quantities by applying a defined mathematical formula. In laboratory medicine, there are many examples where the measurand is calculated from other measurements by means of a functional relationship.²⁹ In these circumstances, the output from the function is the required measurand, but the input quantities themselves can often be viewed as measurands which may also depend on other quantities, including corrections and correction factors for systematic error. Such interactions may well lead to a complicated functional relationship but one which accurately describes the measurement model. MCS is ideally suited to calculating the combined standard uncertainty of the measurand in this situation. The requirements for implementing an MCS are:

• A clearly defined measurement model which describes the measurement process in terms of the inputs to the measurand.²⁹

• A functional relationship (equation) which describes the measurand (output) as a function of the relevant inputs.

• An assessment of the types of distribution which apply to the various input uncertainties. These uncertainties in the inputs should all be expressed as standard uncertainties and not as expanded uncertainties. If an input uncertainty estimate has been derived by statistical analysis of repeated measurements (as may occur by the repeated analysis of IQC), then this would constitute a GUM Type A evaluation and the associated probability distribution is likely to be normal. If an input uncertainty estimate has been obtained from a report, a certificate or other specification without further information, this would be a GUM Type B evaluation. However, a Type B uncertainty based on repeated measurements made in the past but now reported for use in the present, may often be regarded as a ‘fossilised’ Type A uncertainty and a normal distribution may still be appropriate.

• An uncertainty taken from a report or similar document can often be an expanded uncertainty. If this is so, the quoted value should be converted to a standard uncertainty for use in the MCS procedure. Where the expanded uncertainty refers to a 95% coverage interval, conversion to a standard uncertainty can be performed (usually to a good approximation) simply by halving the expanded uncertainty.

• Some further examples are provided in Table 1.

To demonstrate the power of the MCS procedure, we provide (in the appendices) three examples taken from well-known medical laboratory calculations. The three representative examples are those for calculating serum anion gap (AG),^33,34 the Modification of Diet in Renal Disease Study (MDRD) equation for estimating glomerular filtration rate (eGFR),^35–37 and the equation described by Sartorius et al. for calculating free testosterone (cFT).³⁸ These three equations have been taken as described and were chosen to demonstrate the overall utility of the MCS procedure with:

• A relatively simple calculation using the MCS procedure and comparing this with GUM modelling (the AG equation).

• More complex equations (eGFR and cFT) which involve several mathematical functions including power terms and empirically derived ‘constants’.

• The use of MCS modelling and the effect on the measurand of introducing uncertainty estimates for empirically derived ‘constants’ such as those present in the eGFR and cFT equations.

It is not our intent to discuss the actual validity, derivation, or clinical utility of these equations. They were chosen only to demonstrate the MCS procedure for a medical laboratory application using equations which we believe should be relatively familiar.

For estimating the combined standard uncertainty of the output quantity (u(y)), given the standard uncertainties of the various input quantities (u(x_i)), a spreadsheet is constructed with columns allocated for each of the input quantities and the output quantity (measurand) as described.^31,32 Also required are the statistics which determine the PDF for each of the input quantities. For a normal distribution these are the mean and standard deviation (s) or standard uncertainty (u). In each of the columns allocated to the various input quantities, the appropriate spreadsheet formulae are entered and ‘filled down’ for the required number of trials. When referencing the cells which contain the basic input data (input mean or measurement value; rectangular, triangular or normal distribution limits, etc.), absolute cell references should be used. The inbuilt Excel spreadsheet formulae for generating random numbers according to the specified PDF are given in Table 1. Further information with regard to these formulae can be obtained from Excel ‘help’ or Excel ‘statistical functions’.

The simulated data in the columns which represent the various input quantities are now combined row by row according to the specified measurement model (functional relationship). The results from this set of calculations now represent the many possible values which can be ascribed to the measurand, the mean of which provides an estimate of the measurand and the distribution of values its PDF. The data in the output (measurand) column can now be further evaluated. Some suggestions include:

• Plotting a frequency graph (or frequency histogram) using the Excel chart function.

• Visual inspection of the frequency chart to assess the shape of the distribution.

• Calculation of statistics such as mean, mode, median and standard deviation (standard uncertainty) using standard Excel statistical functions.

• Calculation of the coverage interval for the output quantity or measurand: a good general procedure is to copy the output values into a second column and sort from smallest to largest, exclude the lowest 2.5% and highest 2.5% of values (based on row number) to give a 95% coverage interval (or other percentage as required). If the distribution is symmetrical and approximately normal, this will equate to the usual 95% coverage interval of ±1.96 standard deviations. Alternatively, the Excel PERCENTILE function can be used to determine the required coverage interval boundaries.

• Choice of coverage factor (k): for medical laboratory applications, a coverage factor is typically chosen to include approximately 95% of the distribution (k = 1.96) or 95.4% of the distribution (k = 2.0). In medical laboratory applications, a coverage factor of 2.0 is often used to designate a range which contains 95% of values. From a purist statistical perspective this is not technically correct, as ±2.0 actually represents 95.4% of values within the distribution. In a similar manner, there are many articles which use a coverage factor of 1.96 to correctly represent 95.0% of values. However, section 6.3.3 of the GUM suggests that for most measurement situations ‘where the distribution characterized by y and u(y) is approximately normal and the effective degrees of freedom of u(y) is of significant size … one can assume that taking k = 2 produces an interval having a level of confidence of approximately 95%’.¹

• Calculation of skewness and kurtosis: even though not essential to the MCS procedure, these statistics may provide some additional assistance when considering the shape of the output PDF, its closeness to normality or when determining the coverage interval. For a normal distribution, the skewness coefficient (from the SKEW function in Excel) should be approximately zero with a standard deviation of approximately √(6/N), where N is the number of MCS trials.^39,40 In a similar manner, the kurtosis coefficient of a normal distribution as calculated by Excel (from the KURT function) should also be approximately zero with a standard deviation of approximately √(24/N), where N is the number of MCS trials.^39,40 The Excel kurtosis coefficient of zero contrasts with the usual statistical kurtosis coefficient of 3, as the Excel equation used for the KURT function has an inbuilt −3 correction. If the observed kurtosis is more than about three standard deviations from zero, the distribution may well be non-normal. This tentative conclusion is strengthened if the observed skewness is also about three standard deviations from zero.

Precision Profile and Uncertainty of Measurement

IQC performed in a routine medical laboratory is often evaluated at only two or three measurand values. However, uncertainty of measurement may vary over the analytical range of the method and outside of the range covered by the control material. This can apply irrespective of whether the uncertainty is provided as a standard deviation or as a proportional uncertainty (CV%). The precision or uncertainty profile of an assay is a convenient way to describe the relationship between the concentration of a substance and its measured uncertainty. It is usually presented as a plot of standard deviation or coefficient of variation against measurand value and shows the change in uncertainty at values not directly covered by the routine control material. When deriving uncertainty of measurement values or using precision estimates in GUM modelling or MCS calculations, it is important to consider the use of the actual uncertainty at the measurand value in question. It is generally recommended that an uncertainty profile be established when a method is verified for laboratory use.^29,41

The Number of Trials Required for Each Monte Carlo Simulation

One of the potential disadvantages of MCS is that a single run of trials does not indicate by itself the reliability of the results. However, the greater the number of MCS trials, the more ‘stable’ will be the output standard deviation (that is, the standard uncertainty of the measurand). This property of MCS can thus be used as a direct method for determining the number of trials for a given application. The following procedure is suggested for determining the number of trials required:

1. Perform 20 MC simulations with (say) 1000 trials each and calculate the standard deviation of the output (measurand). Record the standard deviation for each of the 20 simulations.

2. Repeat the 20 simulations, but now with 10,000 trials each. Again calculate and record the standard deviation of the measurand for each of the 20 simulations.

3. Again, repeat with 20 simulations for 100,000 trials each. The variation of the standard deviation will decrease as the number of trials increases. This procedure can be halted when the variation of the standard deviation is below the level considered significant.

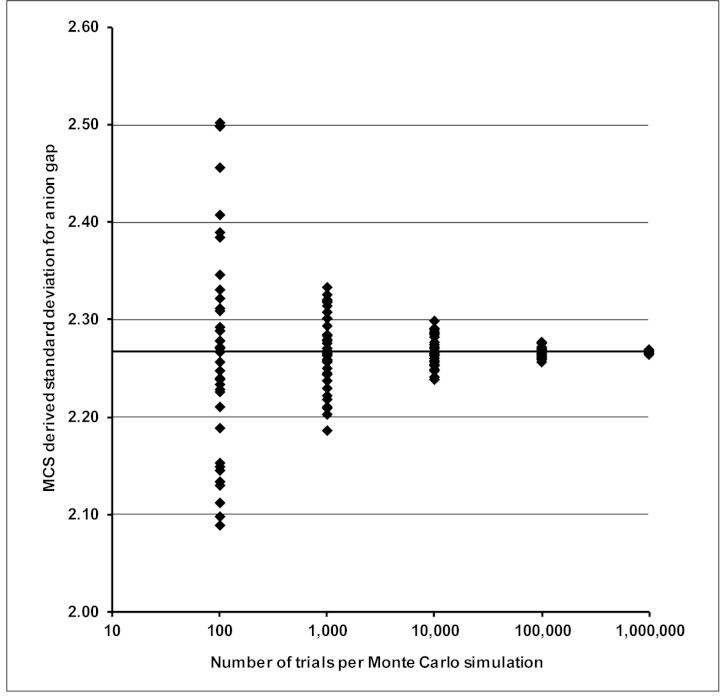
Figure 1 demonstrates this suggested approach for determining the required number of MCS trials. Taking the AG example described in Appendix 1, Figure 1 shows how the output standard deviations change with the number of trials per simulation. As may be expected, the mutual consistency of the output standard deviations increases as the number of trials per simulation increase. However, as whole number percentages provide the uncertainty data for most medical laboratory applications, consistency of output standard uncertainties to one or two decimal places is more than adequate. As can be seen from Figure 1, even a relatively low number of trials (1,000) can often provide standard uncertainties which closely align with those provided by GUM modelling. For the three applications described in the appendices, 10,000 trials provide consistent results with sufficient numerical precision. Where a trustworthy simulation is required for the evaluation of a coverage interval from a PDF which is sparsely populated near its end-points, a higher number of trials may be needed. Section 7.2 of Supplement 1 to the GUM recommends at least 200,000 trials for a 95% coverage interval which is reliable to one or two significant decimal digits.¹⁰

Figure 1.

Variation of the standard deviation for anion gap calculated by 100, 1000, 10,000, 100,000 and 1,000,000 Monte Carlo trials per simulation on 40 separate occasions. As might be expected, a low number of trials per simulation give a wider spread of results. The horizontal line at y = 2.267 is the standard deviation calculated using GUM modelling and the mean standard deviation for each set of simulations performed as outlined in Appendix 1.

Further discussion as to the number of MCS trials can also be found in the Eurachem/ CITAC guide CG4, section E 3.5.¹¹

The GUM and Numerical Precision

The number of significant figures used to report a quantitative result conveys not only its value but also connotes the confidence which may be attached to that result. Section 7 of the GUM provides recommendations on reporting numeric results and their associated uncertainties. In particular, section 7.2.6 of the GUM states ‘The numerical values of the estimate y and its standard uncertainty u(y) or expanded uncertainty U should not be given with an excessive number of digits. It usually suffices to quote u(y) and U … to at most two significant digits, although in some cases it may be necessary to retain additional digits to avoid round-off errors in subsequent calculations’.¹

Another aspect of numerical precision is the truncation or rounding of numbers which may occur within computerised calculations. This particularly applies when very small or very large numbers form part of the procedure. As Excel generally performs its calculations with a numeric precision of 15 significant figures, this is unlikely to be an issue for medical laboratory applications. However, input quantities which have been statistically derived from a sufficiently large number of observations may well be entered with more significant figures than usually reported. For example, IQC derived imprecision may be entered with one more significant figure than usually reported as an estimate of standard uncertainty. Rounding to an appropriate number of significant figures for both measurand and combined standard uncertainty should occur at the output end of the procedure.

Quantitative clinical biochemistry results with whole number percentage expanded uncertainty values (whole number CV%s), should usually not require more than two significant figures for an appropriate uncertainty estimate. That is, the measurand value should be reported with an appropriate number of significant figures consistent with its uncertainty estimate.^41–43

Numerical Accuracy of Excel Statistical Functions

There are many technical evaluations which have identified significant flaws in early versions of Microsoft Excel’s statistical procedures.^44–47 These criticisms are particularly uncomplimentary to versions such as Excel 97, Excel 2000 and Excel 2002 (Excel XP). According to McCullough and Wilson, some of the problems which made Excel ‘unfit for use as a statistical package’ were fixed in Excel 2003, ‘though many were not’.⁴⁵ Of particular importance to the application of MCS is the availability of a reliable random number generator. McCullough et al. have evaluated the generation of random numbers produced by the RAND() function and other statistical procedures in Excel 2003 and Excel 2007. However, while claiming significant improvements over earlier versions, they continue to suggest that some procedures still require improvement.^45,46 Microsoft certainly claim that the previous criticisms have been addressed for Excel 2010.⁴⁸

The Excel based procedures and functions described in the current examples have been used on many occasions with consistent results when compared to GUM modelling and similar MCS procedures using Fortran 95 and Mathematica 5.1. However, whenever spreadsheet calculations are performed (or calculations of any type), the ‘common-sense’ test should always be used to assist with output assessment. In situations such as those currently proposed, exceptionally heavy use of the random number generator (the RAND() function) is not required and Excel should be capable of providing appropriate results. If in doubt, or if heavy-use situations require a robust well defined random number generator, a third-party statistical package with random number generation may be more appropriate. There are many specialised statistical packages currently available which would fulfill this purpose even though at much greater expense (for example, Wolfram Mathematica, IBM SPSS, or Oracle Crystal Ball).

Another factor which may contribute to the suitability of Excel for medical laboratory applications is that the relative or proportional uncertainty of measurement is usually a relatively high percentage of the value being measured. That is, for medical laboratory applications the proportional uncertainty (CV%) is often a whole number percentage compared to many applications in the physical or mathematical sciences which may have proportional uncertainties of less than 0.01%. As a consequence, very small numbers or numbers which only differ in the fifth or sixth decimal place are rarely (if ever) encountered.

The number of trials required for the examples described in the appendices can easily be accomplished with Excel 2003, 2007 or 2010. Excel 2003 provides a work sheet of 65,536 rows by 256 columns, more than sufficient for 10,000 trials (10,000 rows of data). Excel 2007 and 2010 provide 1,048,576 rows by 16,384 columns, thus allowing simulations of up to 1,000,000 trials per simulation. In practice however, this may be limited by available memory and system resources. The examples provided in the three appendices have all been successfully tested using:

• Excel 2003 with 1000, 10,000 and 50,000 trials

• Excel 2010 with 1000, 10,000, 100,000 and 1,000,000 trials

• Fortran 95, Mathematica 5.1 and Origin V6, with a varying number of trials for comparative purposes from 10,000 to 1,000,000.

Uncertainty in Measurements With and Without Correlation

When considering the overall relationship between the various input variables and the output from the functional relationship, any correlation between two (or more) variables requires special consideration. Usually however, the input variables have no relationship with each other, except through the functional relationship which defines the measurand. Under these circumstances, the input variables are described as having zero covariance or correlation. A general overview regarding the effect of correlation on uncertainty calculations has been provided previously,²⁹ with detailed procedures for GUM modelling provided in section F.1.2 of the GUM.¹ The Clinical and Laboratory Standards Institute document C51-A, Expression of Measurement Uncertainty in Laboratory Medicine, Approved Guideline, also provides a good introductory overview of the manner in which correlated variables may influence measurand uncertainty.⁴¹

When input variables are correlated however, both GUM modelling and MCS procedure require a slightly different approach. Even though the inclusion of correlated variables is described in section C.5 of Supplement 1 to the GUM, this description assumes a knowledge of matrix algebra, where correlated variables are described using a variance-covariance matrix such as:

$$\left(\begin{array}{cc}{u}^2\left(x_1\right)& r\left[u\left(x_1\right)u\left(x_2\right)\right]\\ r\left[u\left(x_1\right)u\left(x_2\right)\right]& u^2\left(x_2\right)\end{array}\right)$$

Instead of random sampling from one of the previously described PDFs, the MCS procedure for correlated variables requires sampling from a multivariate PDF. The most useful multivariate distribution for medical laboratory purposes is the bivariate normal distribution and the procedures described below apply specifically to this situation.

When two input variables are correlated, the following sequence should replace the relevant items in the MCS procedures described previously and those in the appendices:

• Determine the correlation coefficient (r) between the two measured input variables (x₁ and x₂).²⁹

• Determine the standard uncertainties (u₁ and u₂) of the two input variables (x₁ and x₂).

• At an appropriate place in the spreadsheet create two data columns. Fill both of these columns with independently derived random numbers (z₁ and z₂) each drawn from a standardised normal distribution (with mean of zero and standard deviation of one). Using Excel, this may be achieved with the function NORMINV(RAND(),0,1).

• Add ‘=NORMINV(RAND(),0,1)’ to the first cell of both ‘z’ columns and fill down the number of rows required for the simulation (say 10,000).

• Let the correlated input variables to the functional relationship (x₁ and x₂) take actual measured values (m₁ and m₂), with standard uncertainties u₁ and u₂.

• The quantities m₁ (a given measured value), m₂ (a given measured value), u₁, u₂ and r are known.

• Create two more data columns corresponding to x′₁ and x′₂. Fill down row by row using the formulae:

  $$\begin{array}{l}{x^{\prime }}_1=m_1+u_1\left[r\times z_2+\left(z_1\times \sqrt{\left(1-r^2\right)}\right)\right]\\ {x^{\prime }}_2=m_2+\left(u_2\times z_2\right)\end{array}$$

• Using the values generated for x′₁ and x′₂ (as replacements for x₁ and x₂), with any other required input variables, calculate the measurand using the relevant functional relationship.

• The output from the functional relationship (the measurand) now takes into account the correlation between measurement data sets x₁ and x₂.

Examples: Calculation of Uncertainty Components through Functional Relationships

As outlined previously, the three equations chosen to demonstrate the MCS procedure are based on functional relationships for the calculation of serum AG, eGFR and cFT. The relatively simple calculation of AG standard uncertainty outlined in Appendix 1 is used to demonstrate the MCS procedure and its comparison to GUM modelling. More complex equations which involve several mathematical functions, including power terms, are then used to further demonstrate the utility of the MCS approach. The use of MCS modelling with the inclusion of uncertainty estimates for empirically derived numerical ‘constants’ is also demonstrated by the examples in Appendix 2 and 3. The three examples provided in the appendices are:

• Appendix 1. The serum AG equation and comparison of MCS with GUM modelling procedures for the calculation of AG standard uncertainty (u(AG)). All variables are assumed to be uncorrelated.

• Appendix 2. The MDRD eGFR equation, comparison of MCS with GUM modelling for the calculation of eGFR standard uncertainty (u(eGFR)) and the inclusion of hypothetical standard uncertainty estimates for empirically derived numerical ‘constants’. All variables are assumed to be uncorrelated.

• Appendix 3. An empirical equation for the calculation of cFT from the measurements of serum total testosterone (T) and serum sex hormone binding globulin (SHBG, S). This example compares MCS with GUM modelling for the calculation of cFT standard uncertainty (u(cFT)) using the equation described by Sartorius et al.³⁸ The proposed procedure includes hypothetical standard uncertainty estimates for the empirically derived numerical ‘constants’. This equation is also of interest from a mathematical perspective as it contains a 1/log₁₀ term. All variables are assumed to be uncorrelated.

Both the eGFR and cFT equations contain empirically derived numerical ‘constants’ which are assumed (in the functional forms provided in the original articles) to be free of inherent uncertainty. However, both of these equations have been derived by statistical procedures using multiple paired measurements as the input variables and contain numerical ‘constants’ which are essentially coefficients derived by the statistical analysis. Empirical equations derived by ‘best fit’ numerical analysis of patient data will always incorporate a degree of variability as shown by the scattering of data points in a ‘y’ versus ‘x’ data plot (scatter plot). Numerical ‘constants’ derived in this manner must also have associated standard uncertainties. As a consequence, the numerical ‘constants’ as shown in the eGFR and cFT functions are not true constants and contribute an unknown degree of uncertainty which is not included in the expressions as usually applied within the clinical laboratory. Unless these standard uncertainties are also provided, the full impact on the output of the functional relationship which is now applied to new input variables cannot be assessed.²⁹

In the absence of any published estimates for the uncertainties likely to be present in the empirically derived numerical ‘constants’ in the eGFR and cFT equations, we have used plausible (although possibly underestimated) values for these uncertainties in Appendices 2 and 3. We would certainly recommend that researchers in the medical sciences explicitly state their estimates of the standard uncertainties of all such empirically derived terms.

Summary

MCS as described in Supplement 1 to the GUM, is a powerful method for evaluating uncertainties through a process that can be regarded as experimental statistics. The theoretical statistics described in the GUM for the calculation of uncertainty in measurement, with its cardinal approach based on the propagation of uncertainties from inputs to measurand, necessitates the use of differential calculus and various theoretical statistical formulas. By contrast, MCS starts with the generation of random numbers which represent the PDFs of the inputs, inserts these random numbers into the particular formula that relates inputs to measurand to produce another set of random numbers that represent the actual PDF of the measurand. This review describes all of these steps using Excel spreadsheet software. The original GUM approach based on the propagation of uncertainties from inputs to measurand is thus subsumed by using MCS. However, MCS also provides a richer output through the propagation of PDFs from inputs to measurand. The statistical coverage interval for the measurand is easily obtained using MCS, even in cases where the measurand PDF is significantly non-normal.

Any severe non-linearities in the functional relationship relating inputs to measurand are automatically taken into account by MCS, whereas the standard GUM procedure relies on a simple linear approximation for the propagation of uncertainties and may lead to errors under such circumstances. In addition, correlations between inputs can be accounted for in a relatively straightforward manner using MCS. However, care must be taken when using MCS that the number of trials is sufficiently large. The larger the number of trials, the more stable will be the resulting standard uncertainty in the measurand. This stability can be tested in a commonsense way by taking (say) 20 simulations with (say) 1000 trials, and then comparing the stability with that obtained from 20 simulations with 10,000 trials, and then again (if necessary) with 100,000 trials for each simulation.

This review considers three medical laboratory-related case studies for illustrating the use of MCS. Two of these case studies involve empirically derived numerical constants, whose uncertainties are not known but have been given plausible (possibly underestimated) values for the purposes of this article. It is recommended that researchers should, as standard practice, estimate and publish the uncertainty attached to each numerical constant in an empirically derived formula.

Appendix 1. Anion Gap Equation

Overview

The serum (or plasma) AG is calculated from the measurements of serum sodium, potassium, chloride and bicarbonate.³³,³⁴ Even though some of these measurement variables may show a degree of correlation, for most usual applications it is assumed that all variables in the AG equation are uncorrelated.²⁹

Thus, assuming uncorrelated measurement variables:

$$\text{AG}=({\text{Na}}^{+}+{\text{K}}^{+})-({\text{Cl}}^{-}+{\text{HCO}}_3^{-})$$

Representative Measurement Values

Representative values for the component serum constituents and their standard uncertainties are given in Table 2. These values have been used to compare the GUM modelling and MCS approaches. Standard uncertainty estimates are given as one standard deviation derived from IQC, the mean value of which being similar to that of the corresponding measurand. All IQC data show a normal distribution.

Table 2.

Representative values used for comparison of anion gap uncertainty.

Serum substance	Quantity	Standard uncertainty (u)	Unit
Sodium (Na+)	140	1.2	mmol/L
Potassium (K+)	4.5	0.10	mmol/L
Chloride (Cl−)	105	1.5	mmol/L
Bicarbonate (HCO3−)	25	1.2	mmol/L

GUM Modelling Calculation

The uncertainty of a result is given by an appropriate combination of the individual uncertainties that are produced at each stage of the measuring process. For results derived from a functional relationship which contains only terms related by sums and/or differences, the variance of the measurand is obtained by adding the variances of the contributing inputs. Assuming no correlation between the individual terms in the AG function, the GUM uncertainty equation is:

$$u^2(\text{AG})=u^2\left({\text{Na}}^{+}\right)+u^2\left({\text{K}}^{+}\right)+u^2\left({\text{Cl}}^{-}\right)+u^2\left({\text{HCO}}_3^{-}\right)$$

$$\begin{array}{l}\text{Thus}:\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{u}^2(\text{AG})={\left(1.2\right)}^2+{\left(0.10\right)}^2+{\left(1.5\right)}^2+{\left(1.2\right)}^2\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=1.44+0.01+2.25+1.44\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=5.14\end{array}$$

$$\text{And}:\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}u(\text{AG})\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}={2.26}_7\text{mmol}/\text{L}(\text{AG}\hspace{0.17em}\text{standard}\hspace{0.17em}\text{uncertainty})$$

$$\begin{array}{l}\text{Expanded}\hspace{0.17em}\text{uncertainty}=2\times u(\text{AG})\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}={4.5}_3\text{mmol}/\text{L}\hspace{0.17em}\text{for}\hspace{0.17em}\text{a}\hspace{0.17em}95.4\%\hspace{0.17em}\text{coverage}\hspace{0.17em}\text{interval}.\end{array}$$

$$\begin{array}{l}\text{Thus}:\hspace{0.17em}\text{Calculated}\hspace{0.17em}\text{anion}\hspace{0.17em}\text{gap}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=14.5\pm 4.5\text{mmol}/\text{L}\hspace{0.17em}(95.4\%\hspace{0.17em}\text{coverage}\hspace{0.17em}\text{interval})\end{array}$$

Monte Carlo Simulation

In contrast to the GUM modelling approach, Table 3 shows part of an Excel spreadsheet using MCS to derive an AG and its associated standard uncertainty. The equation used for the calculation of AG is shown above, with representative values for the relevant variables given in Table 2.

The mean and standard deviation for the 10,000 AG trials in column H provide an estimate of the true value and its coverage interval. A visual assessment of the output PDF may be obtained by determining the frequency (Excel function) of the simulated results in column H using a bin size of 0.5 (for example) and the Excel chart function to plot a histogram or smooth curve.

For the 10,000 simulated AG values in column H, Table 3:

• Mean AG (mean of the trial AG results in column H) = 14.5 mmol/L.

• Combined standard uncertainty for the simulated AG = 2.26₈ mmol/L (average standard deviation for results in column H obtained from 40 simulations of 10,000 trials each, with 95.4% coverage interval (±2s) of 0.029).

• Expanded uncertainty for the simulated AG = 2 × u(AG) = 4.5₄ mmol/L (two standard deviations of the AG results in column H) for a coverage interval of 95.4%. This value can be compared to the 4.5₃ mmol/L obtained by the GUM modelling approach as outlined above.

• Skewness coefficient (calculated using the Excel SKEW function for the AG results in column H) is approximately 0.007 (ideally this should be zero with 95.4% coverage interval of ±0.05 for a normal distribution with 10,000 observations).

• Excel kurtosis coefficient (calculated using the Excel KURT function for the AG results in column H) is approximately 0.050 (ideally this should be zero with 95.4% coverage interval of ±0.10 for a normal distribution with 10,000 observations).

• Each time the spreadsheet is opened or reset, all variables are recalculated (the values entered into cells B3, B4, C3, C4, D3, D4, E3 and E4 are the ‘constants’ which determine the properties of the respective PDFs). Consequently, the actual values for the mean, standard deviation, skewness and kurtosis change slightly for each set of trials or simulation. With 10,000 trials per simulation, the values obtained for the mean and standard deviation always appear to provide the same results with a precision to at least one decimal place, which is more than adequate for the AG calculation.

• Even though the above calculations were based on 10,000 trials per simulation, consistent mean and standard uncertainty values for the AG calculation can also be obtained with as few as 1000 trials as shown in Figure 1.

Table 3.

Anion gap Monte Carlo simulation. Excel spreadsheet representation showing 10,000 anion gap trials (column H) for the quantity values and uncertainty estimates described in Table 2.

	A	B	C	D	E	F	G	H
1	Input quantities					Formula		Output quantity
2		Na+ mmol/L	K+ mmol/L	Cl− mmol/L	HCO3− mmol/L			AG mmol/L
3	Value	140	4.5	105	25	AG = Na+ + K+ − Cl− − HCO3	→	14.5
4	Uncertainty	1.2	0.10	1.5	1.2
5		↓	↓	↓	↓
6								Trial results
7	Trial #							AG
8	1	140.12	4.53	105.99	24.16	AG = Na+ + K+ − Cl− − HCO3−	→	14.50
9	2	140.70	4.39	105.44	24.38		→	15.27
10	3	140.16	4.52	104.46	25.70		→	14.51
11	4	140.52	4.59	104.92	24.40		→	15.79
12	5	140.94	4.36	106.54	26.09		→	12.67
13	6	139.05	4.64	105.54	25.18		→	12.97
14	7	139.51	4.58	104.02	24.92		→	15.15
15	8	138.01	4.55	105.05	25.14		→	12.38
16	9	139.94	4.60	102.73	24.50		→	17.31
17	10	140.58	4.47	108.03	23.62		→	13.39
↓	↓	↓	↓	↓	↓		↓	↓
10007	10000	142.73	4.49	107.31	24.97	AG = Na+ + K+ − Cl− − HCO3−	→	14.94

The simulated anion gap (AG) values in column H are derived from the input variables in columns B, C, D and E, rows 8 to 10007:

• Column B rows 8 to 10007; (NORMINV(RAND(),$B$3,$B$4)),
• Column C rows 8 to 10007; (NORMINV(RAND(),$C$3,$C$4)),
• Column D rows 8 to 10007; (NORMINV(RAND(),$D$3,$D$4)),
• Column E rows 8 to 10007; (NORMINV(RAND(),$E$3,$E$4)).

(The arrows (↓ and →) play no part in the calculations; they have been added to the table for illustrative purposes only.)

Comparison of GUM Modelling and MCS for AG

For the AG and similar equations, calculation of the combined standard uncertainty is relatively straightforward using the GUM modelling approach provided the constituent variables are uncorrelated (or show minimal correlation and can be assumed uncorrelated for practical purposes). Also, the output PDF for the GUM modelling approach is assumed to follow a normal distribution. In contrast, the MCS approach makes no assumptions with regard to the statistical distribution of the output and the coverage interval may be obtained directly from the simulated data as described previously. The MCS calculation for AG and AG standard uncertainty provides equivalent results and can easily be implemented using a spreadsheet such as Excel.

Table 4 summarises the results for the AG calculations obtained by the GUM modelling and MCS procedures.

Appendix 2. Estimated Glomerular Filtration Rate Equation

Overview

The glomerular filtration rate (GFR) is generally considered the best overall index of kidney function. However, an accurate GFR cannot be easily measured in routine medical practice and has usually been estimated by measurement of creatinine clearance. This measure has itself been the subject of much controversy, and GFR estimates are now routinely provided using one of several prediction equations which rely on serum (plasma) creatinine, age, race, gender, and body size.³⁵–³⁷,⁴⁹,⁵⁰ One such equation which has gained widespread clinical acceptance is the MDRD equation.³⁵,³⁷ More recently however, limitations with the MDRD equation have been identified and a new set of equations proposed by the Chronic Kidney Disease Epidemiology Collaboration (the CKD-EPI equations). The CKD-EPI equations relate serum (plasma) creatinine and age, with separate equations for males (with serum creatinine ≤80 or >80 μmol/L), females (with serum creatinine ≤62 or >62 μmol/L), and both with an adjustment for race.⁴⁹,⁵⁰

Although most Australian laboratories will already have changed from the MDRD equation to the CKD-EPI equations, we have chosen the MDRD equation to demonstrate the MCS procedure due to its high profile use over recent years. In addition, the MDRD equation and CKD-EPI equations are of a similar mathematical style; both contain empirical constants with the MCS procedures being easily interchangeable.

Uncertainty of serum creatinine measurement based on IQC should be readily available in all laboratories. However, the uncertainty associated with the calculated GFR requires a relatively complex procedure when using the GUM modelling approach.²⁹ It is more easily accomplished using MCS. The revised MDRD formula for eGFR in male subjects was chosen to demonstrate and compare these two approaches. The formula includes a serum creatinine measurement which has been standardised against isotope dilution mass spectrometry.³⁶,³⁷

A number of similar formulae for the calculation of eGFR have been proposed and recently reviewed, all of which include adjustments for gender and various racial groups.³⁶ As these adjustments all add multiplier terms to the basic equation, the approach used to evaluate uncertainty in the output variable (eGFR) is similar for all forms of this equation.

In addition to the serum creatinine term with its analytical uncertainty of measurement, the various eGFR equations also contain patient age as a variable and numerical ‘constants’ as both multipliers and power terms. Presented in this manner, it may be assumed that these numerical ‘constants’ are free of uncertainty even though the original reports clearly indicate this assumption cannot be correct. Like many empirical equations which have useful applications in medicine, the eGFR equations have been derived by stepwise multiple regression procedures to determine a set of variables that jointly predict eGFR.³⁵,³⁷ With the exception of the factor 0.0113 in the serum creatinine term, the regression coefficients have been derived from data with a wide inherent variability. Thus, in order to provide a more complete uncertainty estimate of the output variable (eGFR) the actual uncertainty associated with each of these numeric terms is also required. As the factor 0.0113 in the serum creatinine term provides a conversion of units from μmol/L to mg/dL, its value is known with sufficient precision to be treated as a true numeric constant.

Table 4.

Comparison of procedures for calculating anion gap (AG) uncertainty.

Calculation procedure	Measurand value (AG) mmol/L	Standard uncertainty u(AG)	Expanded uncertainty (95.4% coverage)
GUM modelling	14.5	2.267	4.53
MCS method*	14.5	2.268	4.54

^*As each MCS generates a new set of values, slight variations in the least significant decimal places are expected from one simulation to the next. The values for the MCS method shown (mean standard uncertainty of 2.268 with a 95.4% coverage interval (± 2s) of 0.029), were obtained from 40 simulations of 10,000 trials each.

Patient age may also present a potential uncertainty depending on how this variable has been programmed within the equation. If age is given as an integer number of years, the uncertainty of this term would be ±0.5 years. If actual years, months and days are programmed to provide an accurate age, then this variable could justifiably be considered to have zero uncertainty.

Representative Measurement Values

Representative values for the variables in the eGFR equation are given in Table 5. These values have been used in comparing the GUM modelling and MCS approaches. In this example a serum creatinine (SCr) of 150 μmol/L has been chosen, as this value may be expected in a patient with possible borderline renal disease. The standard uncertainty of the serum creatinine value is given as one standard deviation derived from IQC, the mean value of which is close to 150 μmol/L. All IQC data show a normal distribution. The numerical ‘constants’ in the eGFR equation are assumed to follow normal distributions. Although it could be argued that these ‘constants’ should be treated as having rectangular distributions in a similar manner to certified values on a calibration certificate, they are essentially regression coefficients which have been derived from data which probably have a normal distribution.

Table 5.

Representative values used for comparison of eGFR uncertainty.

Term in eGFR equation	Quantity	Standard uncertainty (u)	Unit
Serum Creatinine (SCr)	150	5.0	μmol/L
Patient age	60.0	0.0 (zero)	years
175	175	1% (= 1.75)
1.154	1.154	1% (= 0.01154)
0.203	0.203	1% (= 0.00203)

As the actual uncertainty values of the numerical ‘constants’ in the various eGFR equations are not available, we have included standard uncertainty estimates of 1% in order to demonstrate the mathematical procedures involved. The allocation of hypothetical uncertainty values to terms without specified uncertainty and the use of MCS modelling can also provide very useful information regarding the combined effect of uncertainty components on the output value of the functional relationship or measurand (described in more detail below).

GUM Modelling Calculation

The uncertainty of a result is given by an appropriate combination of the individual uncertainties that are produced at each stage of the measuring process. For results derived from a functional relationship which contains terms (coefficients) which are themselves derived by regression analysis of empirical data, the standard uncertainties (standard error of the regression) of these terms should also be included for evaluation.

The MDRD formula for eGFR in white male subjects is:³⁵–³⁷ eGFR = 175 (SCr × 0.0113)^−1.154 (age)−0.203

For the quantity values given in Table 5: eGFR = 41.5 mL/min/1.73m²

The differential equation required for calculating the combined standard uncertainty of the eGFR using the GUM modelling approach is derived from the general equation for the propagation of uncertainty. Assuming no correlation between the individual terms in the eGFR function, the GUM uncertainty equation is:²⁹

$$\begin{array}{l}{(u(\text{eGFR})/\text{eGFR})}^2=\\ {(-1.154(u(\text{SCr})/\text{SCr}))}^2+{(-0.203(u(\text{age})/\text{age}))}^2\\ +{(u(175)/175)}^2+{(-1.154(u(0.0113)/0.0113))}^2\\ +{(\text{ln}(0.0113\hspace{0.17em}\text{SCr}))}^2{(u(-1.154))}^2+{(\text{ln}(\text{age}))}^2{(u(-0.203))}^2\end{array}$$

where:

u(eGFR)/eGFR

relative standard uncertainty in the eGFR

u(SCr)/SCr

relative standard uncertainty in serum creatinine

u(age)/age

relative standard uncertainty in age

u(175)/175

relative standard uncertainty in numerical ‘constant’ 175

u(0.0113)/0.0113

relative standard uncertainty in the creatinine units conversion factor

u(−1.154)

standard uncertainty in numerical ‘constant’ −1.154

u²(−1.154)

squared standard uncertainty in numerical ‘constant’ −1.154

u(−0.203)

standard uncertainty in numerical ‘constant’ −0.203

u²(−0.203)

squared standard uncertainty in numerical ‘constant’ −0.203

ln

logarithm to base e

Evaluating for u(eGFR) using the quantity values given in Table 5, with the creatinine units conversion factor and age having no uncertainty (that is, u(0.0113) = u(age) = 0): u(eGFR) = 1.70 (eGFR standard uncertainty), expanded uncertainty = 2 × u(eGFR) = 3.4₀ for a coverage interval of 95.4%.

Thus, using the GUM modelling approach for the quantity values provided in Table 5: eGFR = 41.5 ± 3.4 mL/min/1.73m².

Monte Carlo Simulation

In contrast to the GUM modelling approach, Table 6 shows part of an Excel spreadsheet using Monte Carlo simulation to derive an eGFR and its associated standard uncertainty using the MDRD equation for white male subjects. As above, representative values for the variables are given in Table 5, with no correlation between the individual terms in the eGFR function and zero uncertainty for the creatinine units conversion term and for age.

The mean and standard deviation for the 10,000 simulations of eGFR in column I provide an estimate of the true value and its coverage interval. A visual assessment of the output PDF may be obtained by determining the frequency (Excel function) of the simulated results in column I using a bin size of 0.5 (for example), and the Excel chart function to plot a histogram or smooth curve.

For the 10,000 simulated eGFR results described in column I, Table 6:

• Mean eGFR (mean of the trial eGFR results in column I) = 41.5 mL/min/1.73 m² (compared to 41.5 mL/min/1.73 m² calculated directly from the stated values in row 3 columns B to F (as shown in cell I3)).

• The combined standard uncertainty of the simulated eGFR (standard deviation of the trial eGFR results in column I) = 1.7 mL/min/1.73 m² (one standard deviation).

• Expanded uncertainty of the simulated eGFR = 3.4 mL/min/1.73 m² (two standard deviations of the eGFR results in column I for a coverage interval of 95.4%). This value can be compared with the 3.4 mL/min/1.73 m² obtained by the GUM modelling approach as outlined above.

• Skewness coefficient (calculated using the Excel SKEW function for the eGFR results in column I) is approximately 0.386 (ideally this should be zero with 95.4% coverage interval of ±0.05 for a normal distribution with 10,000 observations). In our experience, a consistent slight positive skew appears to be present in the simulated eGFR results, which can sometimes also be apparent in the frequency curve obtained from the output data.

• Excel kurtosis coefficient (calculated using the Excel KURT function for the eGFR results in column I) is approximately 0.158 (ideally this should be zero with 95.4% coverage interval of ±0.10 for a normal distribution with 10,000 observations).

• As each time the spreadsheet is opened or reset, all variables are recalculated (the values entered into cells B3, B4, C3, C4, D3, D4, E3, E4, F3 and F4 are the ‘constants’ which determine the properties of the respective PDFs). Consequently, the actual values for the mean, standard deviation, skewness and kurtosis change slightly for each set of simulations. With 10,000 simulations, the values obtained for the mean and standard deviation always appear to provide the same results with a precision to at least one decimal place (more than adequate for an eGFR with an expanded uncertainty of approximately 8% for a 95.4% coverage interval).

• Even though the above calculations were based on 10,000 simulations, consistent mean and standard uncertainty values for the eGFR calculation can also be obtained with as few as 1000 simulations.

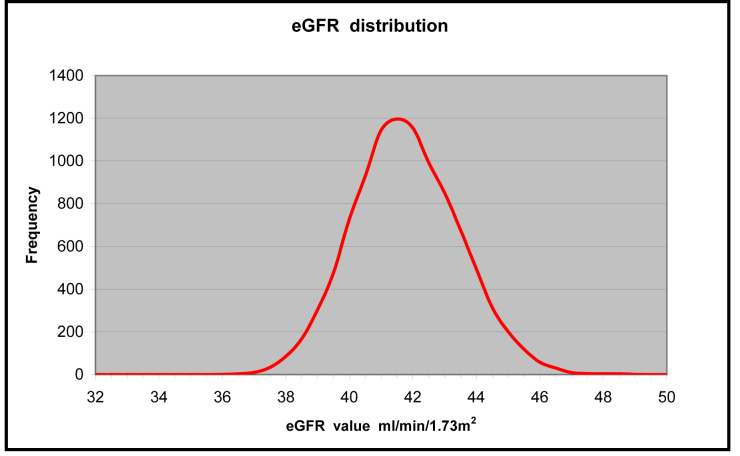
• Figure 2 shows the type of frequency distribution which may be obtained by plotting the simulated eGFR results in column I. This graph was obtained by calculating the frequency of the results in column I using the Excel FREQUENCY function with a bin size of 0.5 mL/ min/1.73 m². As noted above, a slight positive skew is usually present in this simulation suggesting that the output distribution is not truly normal. However, for the purpose of assisting with the interpretation of eGFR results, this slight departure from normality does not substantially alter the uncertainty result obtained. As the relative uncertainty (CV%) in the eGFR calculation is generally quite large, any slight skewness shown in the MCS output does not significantly change the overall interpretation. This also highlights a theoretical difference between GUM modelling and MCS when an expanded uncertainty and a coverage interval are to be calculated. As the MCS procedure delivers an output PDF which may reveal an unsymmetrical or skewed distribution, care must be taken when calculating an expanded uncertainty and coverage interval from MCS output data. In contrast, the GUM procedure assumes a normal distribution of output data and therefore a symmetrical output distribution. When MCS reveals significant skewness, the true coverage interval may be obtained by sorting the output data into numerical order (the results in column I for the eGFR example) and then removing the upper and lower 2.5% of the distribution (by row number), thus leaving a true upper and lower boundary (which contains 95% of the distribution).

Table 6.

eGFR Monte Carlo simulation. Excel spreadsheet representation showing 10,000 simulations of eGFR for white male subjects in column I, with quantity values and uncertainty estimates as described in Table 5.

	A	B	C	D	E	F	G	H	I
1	Input quantities						Formula		Output quantity
2		175	SCr μmol/L	1.154	Age years	0.203			eGFR mL/mim/1.73m2
3	Value	175	150	1.154	60.0	0.203	eGFR = 175(SCr × 0.0113)^ −1.154 (age)^ −0.203	→	41.46
4	Uncertainty	1.75	5.0	0.01154	0.0	0.00203
5		↓	↓	↓	↓	↓
6									Trial results
7	Trial #								eGFR
8	1	175.20	151.35	1.134789	60.00	0.202206	eGFR = 175(SCr × 0.0113)^ −1.154 (age)^ −0.203	→	41.64
9	2	172.32	141.14	1.142378	60.00	0.203425		→	43.96
10	3	175.31	143.07	1.149224	60.00	0.205820		→	43.46
11	4	173.72	159.01	1.152312	60.00	0.203301		→	38.47
12	5	173.94	140.43	1.151667	60.00	0.201352		→	44.81
13	6	175.06	142.18	1.150304	60.00	0.206585		→	43.55
14	7	173.91	153.13	1.152775	60.00	0.203991		→	40.09
15	8	177.15	148.12	1.151006	60.00	0.205686		→	42.18
16	9	174.57	148.74	1.155890	60.00	0.204019		→	41.55
17	10	175.22	156.40	1.140748	60.00	0.203526		→	39.77
	↓	↓	↓	↓	↓	↓		↓	↓
10007	10000	175.31	148.17	1.146714	60.00	0.201389	eGFR = 175(SCr × 0.0113)^ −1.154 (age)^ −0.203	→	42.56

The eGFR simulations in column I are derived from the input variables in columns B, C, D, E and F, rows 8 to 10007:

• Column B rows 8 to 10007; (NORMINV(RAND(),$B$3,$B$4)),
• Column C rows 8 to 10007; (NORMINV(RAND(),$C$3,$C$4)),
• Column D rows 8 to 10007; (NORMINV(RAND(),$D$3,$D$4)),
• Column E rows 8 to 10007; ($E$3),
• Column F rows 8 to 10007; (NORMINV(RAND(),$F$3,$F$4)).

(The arrows (↓ and →) play no part in the calculations; they have been added to the table for illustrative purposes only.)

Figure 2.

Representative frequency distribution curve for 10,000 simulated eGFR results.

Empirically Derived Constants and Their Contribution to Uncertainty

For functional relationships such as the eGFR equation (and free testosterone equations in Appendix 3), where empirically determined numerical ‘constants’ form part of the function but their actual uncertainty values are unavailable, either GUM modelling or MCS procedures can be used to determine the effect which uncertainty associated with the various input variables may have on the functions’ output. The use of modelling procedures and the allocation of hypothetical uncertainty values to terms without specified uncertainty can be used to demonstrate the relative contribution which each of these inputs makes to the combined standard uncertainty of the output.

Figure 3.

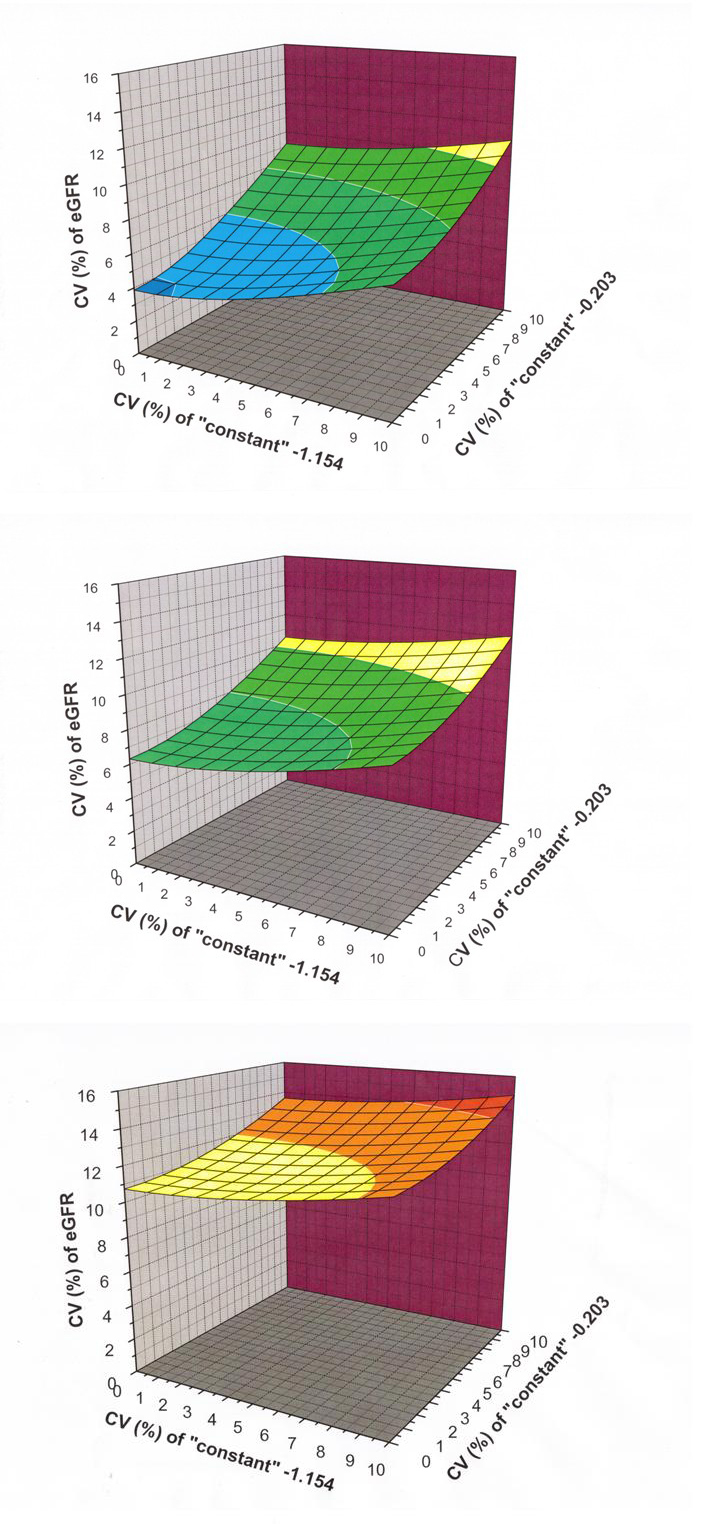
Three dimensional graphs demonstrating the contribution which uncertainty in the empirically derived ‘constants’ may have on the combined standard uncertainty of eGFR calculated using the MDRD equation. Using a fixed serum creatinine of 150 μmol/L with a standard uncertainty of 5.0 μmol/L, proportional uncertainty estimates (CV%) for eGFR are shown using hypothetical standard uncertainty values for the ‘constant’ 175 at 0%, 5% and 10% of its stated value, in association with the ‘constants’ −1.154 and −0.203 at standard uncertainties ranging from 0% to 10% of their stated values. Figure 3(a) shows a graph with the ‘constant’ 175 assumed to have zero uncertainty, with the other two ‘constants’ taking proportional uncertainty values as indicated. In a similar manner, Figure 3(b) and Figure 3(c) show how the eGFR proportional combined standard uncertainty changes when the ‘constant’ 175 is given standard uncertainty values of 5% and 10%.

For example, using the MDRD eGFR equation for white male subjects and uncertainty estimates for the three numerical ‘constants’, the contribution which these estimates provide to the overall combined eGFR uncertainty may be assessed. As indicated previously, the factor 0.0113 in the serum creatinine term is known with sufficient precision to be treated as a true numeric constant as it provides a conversion of units from μmol/L to mg/dL. In a similar manner, age can probably be treated as a variable with very low (zero) uncertainty. On the other hand, the standard uncertainty of the measured serum creatinine (u(SCr)) can be obtained from IQC with a similar mean value.

Using a fixed serum creatinine of 150 μmol/L with a standard uncertainty of 5.0 μmol/L, proportional uncertainty estimates (CV%) for eGFR have been derived using hypothetical standard uncertainty values for the ‘constant’ 175 at 0%, 5% and 10% of its stated value, in association with the ‘constants’ −1.154 and −0.203 at standard uncertainties ranging from 0% to 10% of their stated values. The results obtained using MCS are provided as 3D graphs which demonstrate how each of these components contributes to eGFR uncertainty. Figure 3(a) shows a graph with the ‘constant’ 175 assumed to have zero uncertainty, with the other two ‘constants’ taking proportional uncertainty values as indicated. In a similar manner, Figures 3(b) and 3(c) show how the eGFR proportional combined standard uncertainty changes when the ‘constant’ 175 is given standard uncertainty values of 5% and 10%.

Comparison of GUM Modelling and MCS for eGFR

As the GUM modelling approach does not explicitly determine a PDF for the output quantity, it is often assumed to follow a normal distribution. As discussed previously however, MCS will always provide a PDF for the output quantity which is consistent with the PDFs of the various inputs. Using the MCS procedure described in this example, a slight positive skew is usually apparent in the MCS output for the MDRD eGFR equation which is not sufficient to invalidate using normal distribution statistics. In this situation, the MCS output can be regarded as following a normal distribution.

Table 7.

Comparison of procedures for calculating eGFR uncertainty.

Calculation procedure	Measurand value (eGFR) mL/min/1.73 m2	Standard uncertainty u(eGFR)	Expanded uncertainty (95.4% coverage)
GUM modelling	41.5	1.70	3.40
MCS method*	41.5	1.70	3.40

^*As each MCS generates a new set of values, slight variations in the least significant decimal places are expected from one simulation to the next. The values for the MCS method shown (mean standard uncertainty of 1.70 with a standard deviation (s) of 0.012), were obtained from 20 simulations of 10,000 trials each.

Table 7 summarises the results for the eGFR calculations obtained by the GUM modelling and MCS procedures and demonstrates that equivalent results are obtained by either procedure.

Appendix 3. Free Testosterone Calculation

Overview

Testosterone in blood is present as both protein bound and non-protein bound (free) moieties. In men, approximately 50% is loosely bound to albumin, approximately 44% is strongly bound to sex hormone binding globulin (SHBG or S), 4% is bound to other proteins and approximately 2% is free and non-protein bound (FT). Free testosterone may be calculated or measured. However, because the direct measurement of free testosterone is difficult and impractical for routine laboratory practice, several equations have been developed to provide estimates of free testosterone concentration. The most widely used of these equations are those described by Sodergard et al., Vermeulen et al., Nanjee and Wheeler, Ly and Handelsman, and Sartorius et al.⁵¹–⁵⁴,³⁸

There are essentially two approaches to developing equations for the calculation of free testosterone (cFT). One approach is based on the chemical equilibrium which exists between free testosterone, SHBG (and/or other binding proteins) and bound testosterone. The alternate approach uses patient specimens for the measurement of free testosterone, total testosterone (T) and binding protein(s), which are then used to derive an empirical equation which can be used to relate these three variables. The equations developed by Sodergard and Vermeulen use equilibrium binding as the model,⁵¹,⁵² while Nanjee and Wheeler, Ly and Handelsman, and Sartorius et al. use the empirical approach.⁵³,⁵⁴,³⁸ Even though comparisons of these four equations and their application in routine laboratory practice have been well described,³⁸,⁵⁵ there appears to be no information available as to the uncertainty of calculated free testosterone. In a similar manner to the eGFR example described in Appendix 2, all equations contain numerical ‘constants’ which have been derived as coefficients from data with an inherent variability (uncertainty). This uncertainty in the original data used to derive the various equations will also propagate through the equation and contribute to uncertainty in the output (measurand).

Sartorius et al. have derived an empirical equation by best-fit modelling which they claim provides superior cFT estimates derived from the measurement of T and SHBG (S). This equation is also of interest from a mathematical perspective as it contains a 1/log₁₀ term. This provides an extra challenge when calculating the combined standard uncertainty using the GUM modelling approach. The appropriate differential equation for the combination of terms in the Sartorius equation was not provided in a previous review of the rules for calculating uncertainty components through functional relationships,²⁹ but is provided below for comparison with the MCS procedure.

Representative Measurement Values

The mean values provided in the paper by Sartorius et al. have been used as representative values for serum T and SHBG.³⁸ In a similar manner to the previous examples, the standard uncertainty in the measurement of T and SHBG are given as one standard deviation derived from IQC (with both sets of QC data showing a normal distribution). The uncertainty values used for T and SHBG (S) are consistent with what may be obtained from an automated immunoassay analyser. In the MCS given in this appendix, all four quantities appearing in the Sartorius equation (T, S and the two ‘constants’) have been sampled from normal distributions. In the case of T and S, the relevant distributions relate to the individual serum measurements for a given patient and the uncertainty which surrounds these individual measurements (obtained from IQC data which is normally distributed). Even though the underlying population of serum testosterone measurements may not actually follow a normal distribution, the sample drawn from this population and used as input for the derivation of the Sartorius equation would presumably include this non-normality in a manner which influenced the form of the functional relationship so obtained.

Table 8.

Representative values used for comparison of calculated free testosterone (cFT) uncertainty.

Term in Sartorius cFT equation	Quantity	Standard uncertainty (u)	Unit
Serum testosterone (T)	12.2	5% (= 0.61)	nmol/L
Serum SHBG (S)	36.6	5% (= 1.83)	nmol/L
24.00314	24.00314	1% (= 0.2400314)
0.04599	0.04599	1% (= 0.0004599)

The numerical ‘constants’ in the cFT equation have also been assumed to follow normal distributions even though it could well be argued that they should be treated as having rectangular distributions in a similar manner to certified values on a calibration certificate. However, these ‘constants’ are essentially regression coefficients derived from the evaluation of empirical data where the residuals from such a process are likely to be approximately normally distributed.

As the actual uncertainty values of the numerical ‘constants’ in the various cFT equations are not available, we have again included standard uncertainty estimates of 1% to demonstrate the mathematical procedures involved. The allocation of hypothetical uncertainty values to terms without specified uncertainty and the use of MCS modelling can also provide very useful information regarding the combined effect of uncertainty components on the output value of the functional relationship or measurand (as described previously in Appendix 2).

The representative values used in the example calculations for cFT are given in Table 8.

GUM Modelling Calculation

The uncertainty of a result is given by an appropriate combination of the individual uncertainties that are produced at each stage of the measuring process. For results derived from a functional relationship which contains terms (coefficients) which themselves are derived by regression analysis of empirical data, the standard uncertainties (standard error of the regression) of these terms should also be included for evaluation.

The equation for calculating free testosterone proposed by Sartorius et al. is:

$$\text{cFT}=24.00314\left(\frac{\text{T}}{{\text{log}}_{10}\text{S}}\right)-0.04599\times {\text{T}}^2$$

This may be expressed in a more general mathematical form as:

$$\text{cFT}={\text{K}}_1\left(\frac{\text{T}}{{\text{log}}_{10}\text{S}}\right)-{\text{K}}_2\times {\text{T}}^2$$

where: K₁ = 24.00314, S = SHBG and K₂ = 0.04599.

The differential equation required for calculating the combined standard uncertainty of cFT using the GUM modelling approach is derived from the general equation for the propagation of uncertainty. Assuming no correlation between the individual terms in the Sartorius cFT function, the GUM uncertainty equation is:

$$\begin{array}{l}{u}^2(\text{cFT})={\left(\frac{\text{T}}{{\text{log}}_{10}\text{S}}\right)}^2{u}^2\left({\text{K}}_1\right)+{\left(\frac{{\text{K}}_1}{{\text{log}}_{10}\text{S}}-2{\text{K}}_2\times \text{T}\right)}^2{u}^2(\text{T})+\\ {\left(\frac{{\text{K}}_1\times \text{T}}{S{\text{log}}_{e}10}\right)}^2{\left(\frac{1}{{\text{log}}_{10}\text{S}}\right)}^4{u}^2(\text{S})+{\text{T}}^4\times u^2\left({\text{K}}_2\right)\end{array}$$

Using the representative quantity values provided in Table 8 and evaluating for cFT and u(cFT) gives a cFT of 180.5 pmol/L with a GUM modelling standard uncertainty value of 9.2₅ pmol/L (one standard deviation), or an expanded uncertainty of 18.5₀ pmol/L for a coverage interval of 95.4% (two standard deviations).

Monte Carlo Simulation

In contrast to the GUM modelling approach, Table 9 shows part of an Excel spreadsheet using Monte Carlo simulation to derive a cFT and its associated expanded uncertainty. The function used in the simulation is the Sartorius equation with the representative values for the respective variables given in Table 8.

The mean and standard deviation for the 10,000 simulations of cFT in column H provide an estimate of the true value and its coverage interval. A visual assessment of the output PDF may be obtained by determining the frequency (Excel function) of the simulated results in column H using a bin size of 5 (for example) and the Excel chart function to plot a histogram or smooth curve.

For the 10,000 simulated cFT results described in column H, Table 9:

• Mean cFT (mean of the trial cFT results in column H) = 180.6 pmol/L (compared to 180.5 pmol/L calculated directly from the stated values in row 3 columns B to E (as shown in cell H3)).

• Combined standard uncertainty for the simulated cFT (standard deviation of the trial cFT results in column H) = 9.2₃ pmol/L (one standard deviation).

• Expanded uncertainty for the simulated cFT = 18.4₆ pmol/L (two standard deviations of the cFT results in column H) for a coverage interval of 95.4%. This value can be compared with the 18.5₀ pmol/L obtained by the GUM modelling approach outlined above.

• Skewness coefficient (calculated using the Excel SKEW function for the cFT results in column H) is approximately 0.025 (ideally this should be zero with 95.4% coverage interval of ±0.05 for a normal distribution with 10,000 observations).

• Excel kurtosis coefficient (calculated using the Excel KURT function for the cFT results in column I) is approximately 0.031 (ideally this should be zero with a 95.4% coverage interval of ±0.10 for a normal distribution with 10,000 observations).

• As each time the spreadsheet is opened or reset, all variables are recalculated (the values entered into cells B3, B4, C3, C4, D3, D4, E3 and E4 are the ‘constants’ which determine the properties of the respective PDFs). Consequently, the actual values for the mean, standard deviation, skewness and kurtosis change slightly for each set of simulations. With 10,000 simulations, the values obtained for the mean and standard deviation always appear to provide the same results with a precision to at least one decimal place (more than adequate for a cFT with an expanded uncertainty of approximately 10% for a 95.4% coverage interval).

Table 10.

Comparison of procedures for calculating cFT uncertainty.

Calculation procedure	Measurand value (cFT) pmol/L	Standard uncertainty u(cFT)	Expanded uncertainty (95.4% coverage)
GUM modelling	180.5	9.25	18.50
MCS method*	180.6	9.23	18.46

^*As each MCS generates a new set of values, slight variations in the least significant decimal places are expected from one simulation to the next. The values for the MCS method shown (mean standard uncertainty of 9.23 with a standard deviation (s) of 0.059) were obtained from 20 simulations of 10,000 trials each.

Table 9.

cFT Monte Carlo simulation (Excel spreadsheet representation).

	A	B	C	D	E	F	G	H
1	Input quantities					Formula		Output
2		T nmol/L	SHBG (S) nmol/L	24.00314	0.04599			cFT pmol/L
3	Value	12.2	36.6	24.00314	0.04599	cFT = 24.00314 * T/log(S) − 0.04599 *T^2	→	180.5
4	Uncertainty	0.61	1.83	0.2400314	0.0004599
5
6		↓	↓	↓	↓			Trial results
7	Trial #							cFT
8	1	12.259	37.645	24.159836	0.045892	cFT = 24.00314 * T/log(S) − 0.04599 *T^2	→	181.07
9	2	13.001	35.048	23.765519	0.046060		→	192.24
10	3	12.209	34.061	23.982057	0.045990		→	184.24
11	4	11.421	35.472	23.935677	0.045469		→	170.45
12	5	11.938	37.221	23.981260	0.045930		→	175.72
13	6	12.261	37.897	23.979929	0.046228		→	179.30
14	7	12.068	34.934	23.905895	0.046410		→	180.18
15	8	12.577	38.482	23.873808	0.046113		→	182.12
16	9	12.878	36.382	24.227331	0.045721		→	192.31
17	10	12.249	36.656	23.514162	0.045899		→	177.26
	↓	↓	↓	↓	↓		↓	↓
10007	10000	11.896	34.608	24.165267	0.046522	cFT = 24.00314 * T/log(S) − 0.04599 *T^2	→	180.18

Spreadsheet representation showing 10,000 simulations of calculated free testosterone (cFT) in column H, for quantity values and uncertainty estimates as described in Table 8. The cFT simulations in column H are derived from the input variables in columns B, C, D and E, rows 8 to 10007:

• Column B rows 8 to 10007; (NORMINV(RAND(),$B$3,$B$4)),
• Column C rows 8 to 10007; (NORMINV(RAND(),$C$3,$C$4)),
• Column D rows 8 to 10007; (NORMINV(RAND(),$D$3,$D$4)),
• Column E rows 8 to 10007; (NORMINV(RAND(),$E$3,$E$4)).

The arrows (↓ and →) play no part in the calculations; they have been added to the table for illustrative purposes only.

Even though the above calculations were based on 10,000 simulations, consistent mean and standard uncertainty values for the cFT calculation can also be obtained with as few as 1000 simulations.

Comparison of GUM Modelling and MCS for cFT Using the Sartorius Equation

Even though the GUM modelling approach does not explicitly determine a PDF for the output quantity, it is often assumed to follow a normal distribution. As discussed previously however, MCS will always provide a PDF for the output quantity which is consistent with the PDFs of the various inputs. However, GUM modelling, assuming a normal output distribution, and the MCS procedure described both provide equivalent results for the calculation of combined standard uncertainty for cFT using the Sartorius equation. Table 10 summarises the results for both cFT uncertainty calculations.