“Retention Projection” Enables Reliable Use of Shared Gas Chromatographic Retention Data Across Labs, Instruments, and Methods

Abstract

Gas chromatography-mass spectrometry (GC-MS) is a primary tool used to identify compounds in complex samples. Both mass spectra and GC retention times are matched to those of standards, but it is often impractical to have standards on hand for every compound of interest, so we must rely on shared databases of MS data and GC retention information. Unfortunately, retention databases (e.g. linear retention index libraries) are experimentally restrictive, notoriously unreliable, and strongly instrument dependent, relegating GC retention information to a minor, often negligible role in compound identification despite its potential power. A new methodology called “retention projection” has great potential to overcome the limitations of shared chromatographic databases. In this work, we tested the reliability of the methodology in five independent laboratories. We found that even when each lab ran nominally the same method, the methodology was 3-fold more accurate than retention indexing because it properly accounted for unintentional differences between the GC-MS systems. When the labs used different methods of their own choosing, retention projections were 4- to 165-fold more accurate. More importantly, the distribution of error in the retention projections was predictable across different methods and labs, thus enabling automatic calculation of retention time tolerance windows. Tolerance windows at 99% confidence were generally narrower than those widely used even when physical standards are on hand to measure their retention. With its high accuracy and reliability, the new retention projection methodology makes GC retention a reliable, precise tool for compound identification, even when standards are not available to the user.

Introduction

Advances in fields such as metabolomics hinge on our ability to identify as many compounds as possible from extremely complex biological samples, each of which could contain tens of thousands.^1,2 Gas chromatography-mass spectrometry (GC-MS) is one of the primary tools used for this purpose. It offers both GC retention and mass spectral information, two pieces of complementary information that may be used to narrow the possible identities of unknown peaks. To test whether the GC retention time and mass spectrum match that of unknown peaks, one would ideally have a standard on hand for every potential compound in the sample, but that is impractical. Instead, we must rely on shared databases of GC and MS information. Databases of electron impact-mass spectra have gained wide use because they are adequately reproducible across labs, but alone they do not suffice to identify more than a small fraction of the compounds with high confidence. Considerably more analytes could be positively identified if the MS information could be supplemented with reliable GC retention information. Unfortunately, shared databases of temperature-programmed GC retention data are notoriously unreliable.^3-5

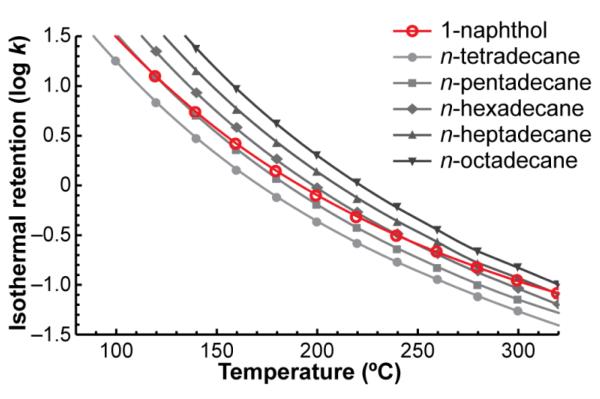
Practically all shared GC retention databases store retention in terms of relative retention (e.g. linear retention indices),⁶ relying on the flawed assumption that the selectivity of a separation is constant regardless of the experimental conditions used. In fact, the selectivity of a temperature-programmed separation strongly depends on a large number of experimental variables. For example, Figure 1 shows retention as a function of temperature for 1-naphthol and 5 n-alkanes. While 1-naphthol elutes between tetradecane and pentadecane at 100 °C, it elutes between heptadecane and octadecane at 320 °C—three alkane pairs over.

Figure 1.

Isothermal retention (log k) vs. temperature for 1-naphthol and five n-alkanes. The relative retention of 1-naphthol is highly temperature-dependent.

In temperature-programmed elution, not only does the selectivity change when the temperature program is changed, but also when the flow rate, inlet pressure, outlet pressure, column length, inner diameter, or phase ratio are changed because they alter the effective steepness of the temperature ramp⁷ (“method translation” provides some exceptions to this rule).^8-10 While some of these variables are easily controlled (e.g. temperature program, flow rate, etc.), others are not (e.g. temperature calibration errors, flow rate non-idealities, imprecise column dimensions, etc.). This means that even when attempts are made to duplicate all of the controllable experimental conditions that were originally used to measure the retention data, retention is still variable due to the uncontrollable, unintentional differences between GC systems. (Retention time locking is a partial exception, as it provides a way for a user to calibrate a GC’s flow rate/inlet pressure to match that of another system,⁸ but it does not account for any non-idealities in the temperature profile.)

Shared GC retention databases present a number of other problems that also limit their utility. Large databases such as the NIST database¹¹ were compiled from multiple sources and therefore contain retention data collected under a diversity of experimental conditions. One compound’s retention may have been measured on a DB-1 column with a 20 °C/min ramp and another compound may have been measured on a DB-5 column with a 5 °C/min ramp. It is rare to find retention data for a set of target compounds that were all measured under nominally the same experimental conditions, much less the conditions of interest. So then one is forced to use retention data that were measured under different experimental conditions, incurring large, unpredictable errors, or not use it at all. With smaller databases such as the Fiehn database,¹² this is less of a problem, as all of the retention data were measured under the same experimental conditions. But one is still restricted to using precisely the same experimental conditions that were originally used to measure the retention data (or to one of a narrow range of translated methods), ^8-10 and even then, unintentional differences between GC systems still cause errors.

In either case, it is entirely unclear what sort of retention time tolerance windows one should use with this data (without significant effort on the part of the user). Both intentional and unintentional differences between experimental conditions contribute an unpredictable amount of error. In addition, inadvertent differences between the selectivity of a user’s column and the same model column (but perhaps with a different history of use) that was used to build the database can cause error, but no standard methodology has as yet been defined to warrant the suitability of a user’s column. By and large, shared temperature-programmed GC retention databases remain experimentally restrictive and offer little more than a rough estimate of retention without providing any estimate of the data confidence intervals. This relegates GC retention information to a minor, often negligible role in compound identification by GC-MS when standards are not on hand despite its potential utility.

Overall, four limitations must be overcome in order for shared GC retention databases (and the associated software) to become more practical, reliable tools for compound identification:

1. They must properly account for unintentional differences between GC systems (e.g. temperature, inlet pressure/flow rate, or column dimension non-idealities).

2. They must properly account for at least some intentional differences between experimental conditions (e.g. different temperature programs, flow rates, column dimensions, etc.).

3. They must provide a user with appropriate retention time tolerance windows at a defined confidence level.

4. They must be able to test whether the GC system is in a suitable state such that the above tolerance windows are applicable.

Retention Projection

Retention indexing cannot satisfy either of the first two limitations because it cannot account for differences in the dependence of retention on temperature (as shown in Figure 1). However, since that data can be measured fairly easily, an alternative, more general approach some researchers have taken^13-18 is to build a shared database of isothermal retention information and use it to calculate temperature-programmed retention times. The general equation used to calculate temperature-programmed retention times is:^10,19

$${\int }_0^{t_{\mathrm{R}}}\frac{\mathrm{d}t}{t_{M,T}(k_T+1)}=1$$ (1)

where t_R is the retention time of the compound, and t_M,T and k_T are the hold-up time and retention factor at temperature T. The equation treats a programmed-temperature run as the sum of a series of infinitesimally small isothermal temperature steps that closely approximate the true temperature program. (Note that while Eq. 1 is always valid under constant inlet pressure mode, it fails in constant flow rate mode with moderate gas decompression,¹⁰ that is, when the inlet pressure, p_i, and the outlet pressure, p_o, are moderately close to one another (e.g. 0.3 < |p_i-p_o|/p_i < 3). This is not usually a problem in GC-MS because it is run under strong gas decompression, but a QuickSwap adapter can put it into moderate gas decompression.) We call this approach “retention projection” because temperature-programmed retention times are projected from isothermal retention data. Theoretically, it can properly account for differences in most of the relevant experimental conditions: the temperature program, flow rate/inlet pressure, outlet pressure, column length, film thickness, and column inner diameter. Only the stationary phase material and the nature of the carrier gas must be held constant.

Unfortunately, retention projection is not accurate unless the temperature program and the hold-up time (as a function of temperature) actually produced by the GC are known with great precision. Small non-idealities can cause considerable error in the projected retention times. These non-idealities can be meticulously measured with high precision and taken into account,¹⁴ but the difficulty and amount of effort required to do it is prohibitive for most GC users. Moreover, they would need to be re-measured every time the experimental conditions are deliberately or inadvertently changed.

Retention Projection with Back-Calculation

Some of us recently described a new approach that solves this problem.²⁰ First, a series of n-alkanes are spiked into a sample and the sample is subjected to temperature-programmed elution. Then the retention times of the n-alkanes are entered into open-source software (available at http://www.retentionprediction.org/gc) that back-calculates what the actual temperature program and hold-up time vs. temperature profiles must have been to give those retention times. It back-calculates them by a convergent, iterative process. The process starts with the ideal temperature and hold-up time profiles and makes a small change to them. After each change, the retention times of the n-alkanes are re-projected. If the change improves the accuracy of the projected retention times, the change is kept, otherwise it is rejected. The process repeats until the difference between the experimental and projected retention times are minimized.

Then, using those back-calculated profiles, the temperature-programmed retention times of other compounds (with known isothermal retention vs. temperature relationships) can then be projected with very high accuracy. We found that the new methodology was far more accurate than retention indexing when the temperature program, the flow rate, or the inlet pressure was altered from that used to measure the retention indices. In one lab, the new methodology proved to be an easy-to-use, reliable and accurate way to harness GC retention information under a wide range of experimental conditions.

In this work, we conducted a multi-lab study to test the new retention projection methodology as a means to overcome all four limitations of conventional GC retention databases. Five independent labs were involved, each with different GC-MS instruments and operators. First, we tested the ability of the methodology to account for unintentional differences between the GC systems in each of the locations. Then we tested the accuracy of the methodology when challenged with a wide range of experimental conditions chosen by each lab. Based on this data, we developed a way to calculate the appropriate retention time tolerance window one should use for a particular compound in a particular method, with a specified confidence level. Finally, we developed a new type of system suitability check capable of testing whether a user’s GC column is “like new” and the above tolerance windows are applicable.

Materials and Methods

Test Mixture

Twelve chemically diverse test compounds and 25 n-alkanes (C7-C26, C28, C30, C32, C34, and C36) made up our test mixture. They were selected to represent each of the 5 types of interactions most common in GC (as represented by the Abraham descriptors).^21-25 There are hydrogen bond donors (e.g. phenol, resorcinol, and 1-naphthol) and hydrogen bond acceptors (e.g. N,N-dimethylisobutyramide, benzamide, and dextromethorphan), compounds that interact by π and/or lone pair interactions (e.g. ethylbenzene, naphthalene, and anthracene), compounds that interact by dipole-dipole and dipole-induced dipole interactions (e.g. N,N-diethylacetamide, 4-nitroaniline, and caffeine), and all vary widely in their gas-liquid partition coefficients.^26,27 The test compounds were also selected so that the set of compounds representing each type of interaction elute over a wide range of retention times. They were all dissolved in ethyl acetate at a concentration of 100 μM.

All chemicals and solvents were purchased from Sigma-Aldrich® (St. Louis, MO), Alfa Aesar® (Ward Hill, MA), or TCI America (Portland, OR).

Software

The new GC retention projection software was compiled for compliance with the Java 1.6 (Oracle, Redwood Shores, CA) runtime environment. It includes the Java OpenGL (JOGL) binding library version 2.0-rc11 (JogAmp, http://jogamp.org), the Unidata netCDF library version 4.2 (Unidata®, Boulder, CO), the Savitzky-Golay filter library version 1.2 by Marcin Rzeźnicki (http://code.google.com/p/savitzky-golay-filter/), the jmzML library,²⁸ and the jmzReader library.²⁹ The source code may be downloaded from http://www.retentionprediction.org/gc/development.

Isothermal Retention Measurements

A detailed description of our measurements of isothermal retention data is described elsewhere,²⁰ along with the measurements themselves. Briefly, we measured isothermal retention factors for each of the 37 compounds in the test mixture at 20 °C intervals from 60 °C to 320 °C, using N₂ as the hold-up time marker. The isothermal retention factors, k, were then calculated from:

$$k=\frac{t_{\mathrm{R}}-t_{\mathrm{M}}}{t_{\mathrm{M}}}$$ (2)

where t_M is the hold-up time and t_R is the retention time (measured from the apex of each peak).

Instrumentation

The isothermal retention data was measured with a Hewlett Packard (HP, Palo Alto, CA) Model 5890 Series II GC equipped with an HP 5970 single quadrupole mass spectrometer. We used He carrier gas (99.999% pure), deactivated, straight quartz liners (2 mm inner diameter) containing deactivated quartz wool, an inlet temperature of 290 °C, and a transfer line temperature of 320 °C.

The five other labs used different instrumentation: Lab A used an Agilent® (Santa Clara, CA) 7890 GC equipped with an Agilent 240 ion trap MS (18 cm transfer line), using a Supelco® 2048605 4 mm split/splitless liner containing deactivated glass wool. Lab B used a Thermo Scientific® (Waltham, MA) Trace GC Ultra equipped with a Thermo DSQ single quadrupole MS (20 cm transfer line), using a Thermo 453T4905 gooseneck liner containing deactivated glass wool. Lab C used an Agilent 5890N GC equipped with an Agilent 5973 single quadrupole MS (16 cm transfer line), using a Restek® 23305.5 Sky 4 mm split liner containing deactivated glass wool. Lab D used an Agilent 6890 GC equipped with an Agilent 5975 single quadrupole MS (10 cm transfer line), using an Agilent 5181-3316 4 mm splitless liner containing no glass wool. A QuickSwap adapter was used with a column outlet pressure of 27 kPa. Lab E used an Agilent 7890A GC equipped with an Agilent 5975C single quadrupole MS (12 cm transfer line), using an Agilent 5188-6576 4 mm split liner containing deactivated glass wool. All used He as carrier gas.

Methods

Each lab was given a new Agilent DB-5MS UI column (30 m long, 0.25 mm inner diameter, 0.25 μm film thickness) on which they ran five different methods. We defined the first two methods—method A and method B. Method A: temperature program, 60 °C for 5 min, then ramp at 26 °C/min to 320 °C, hold for 15 min; inlet pressure, 50 kPa; 1 μL split injection with 1:10 split ratio; inlet temperature, 290 °C; MS transfer line temp, 320 °C; MS scan window, 57 to 271 m/z; scan rate, ≥ 2 Hz; He carrier gas. Method B: same as method A except the temperature ramp rate was 6.5 °C/min. The other three methods were defined independently by each of the other five labs (see Supporting Information).

Of the 300 total retention times reported, a total of 18 were excluded from this study. 15 were excluded because they eluted during the solvent delay and were not detected, or because they eluted before the first reported n-alkane retention time. Three retention times for dextromethorphan were also excluded from Lab D; they gave unusually large error that was 2.6- to 3.4-fold larger than the expected standard deviation in the three relatively fast ramps Lab D chose to run. We expect the QuickSwap adapter, combined with the fast heating rates, confounded these retention projections, as the QuickSwap probably heated more slowly than the rest of the oven, causing a cool spot at the end of the column. Dextromethorphan, being the latest-eluting compound, came out at the highest temperature and therefore was affected the most by the cool spot.

Results and Discussion

To each of the five labs involved in the study, we shipped a new Agilent DB-5MS UI column and a test mixture. The test mixture contained a total of 37 compounds: 25 n-alkane standards that the labs would use to back-calculate the temperature and hold-up time profiles their instruments produced, and 12 chemically diverse test compounds (see Materials and Methods) that were used to test the accuracy of subsequent retention projections.

Accounting for unintentional differences between GC systems

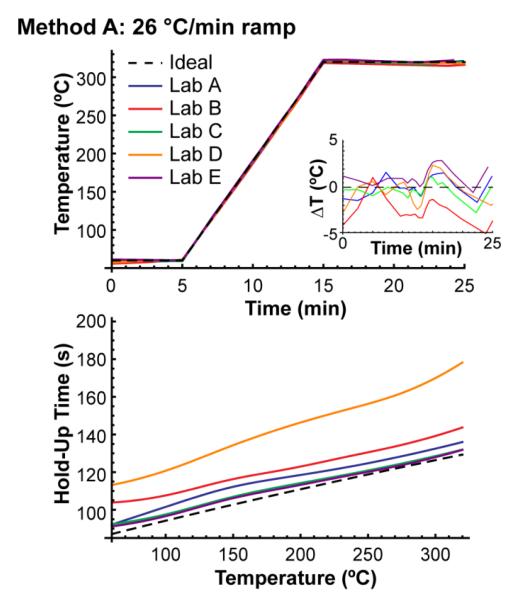
The first two methods, method A and method B, were the same for each lab. Method A was a 26 °C/min ramp and method B was a 6.5 °C/min ramp (see Experimental for details). These two methods allowed us to compare the accuracy of retention projections and retention indices when all controllable experimental conditions were nominally the same in each lab—any differences in experimental conditions were unintentional. Figure 2 shows the temperature and hold-up time profiles that were back-calculated from the n-alkane retention times that each lab reported from method A. Even though each lab used nominally the same temperature program, there were significant differences between the back-calculated temperature profiles. For example, the back-calculated temperature program from Lab E showed the largest positive deviation among the labs, averaging 0.9 °C above the ideal temperature profile, while the temperature program from Lab B had the most negative deviation, averaging 3 °C below the ideal temperature profile. The same trend held in Method B (see Figure S-1), where Lab E averaged 1 °C above the ideal profile and Lab B averaged 1 °C below the ideal temperature profile. These are reasonable deviations considering that most modern GC instruments are specified with oven temperature accuracies of ±3-5 °C (not to be confused with temperature “precision” or “resolution”, which are often specified to 0.01 °C). (Note that the back-calculated temperature profiles are currently not accurate as absolute measures of temperature – they are biased by temperature calibration errors in the original GC oven that was used to measure that isothermal data. We plan to correct this in future work.)

Figure 2.

Back-calculated temperature and hold-up time profiles from method A in each of the five labs (inset shows differences in the back-calculated temperature profiles from the ideal). Even though the experimental conditions were nominally the same, there were significant differences between them.

The back-calculated hold-up time profiles also showed significant differences from the ideal profiles. These could result from a number of unintentional differences: the operators could have cut their columns to different lengths before installing them, the column inner diameters may have been slightly different, or the inlet pressure regulators may have been improperly calibrated. The large deviation in Lab D was the combined result of a QuickSwap adapter that set the column outlet pressure to 28 kPa relative to vacuum and a miscommunication that led the operator to attempt to set the inlet pressure to 50 kPa relative to vacuum (it was supposed to be 50 kPa relative to atmospheric pressure). They increased their inlet pressure to 117 kPa relative to vacuum (16 kPa gauge pressure) for methods A and B before reporting their results to us.

Using the back-calculated temperature and hold-up time profiles, the retention times of the 12 test compounds were then projected. Table 1 shows the overall accuracy (among all 12 test compounds) of the projected retention times from methods A and B in each lab. In method A, the accuracy of retention projections were fairly consistent despite the unintentional differences between the experimental conditions used by each lab, being between ±0.30 and ±0.51 s. In contrast, when linear retention indices measured in our lab (by the usual approach)⁶ were used to predict retention times in each of the other five labs, their accuracies ranged between ±1.1 s and ±2.3 s, averaging over 3-fold less accurate than the retention projections. Retention projections were also better than retention indices in the shallower ramp of method B, where they were nearly 3-fold more accurate.

Table 1.

Accuracies of Retention Projections and Retention Indices in Five Different Labs, Each Running the Same 26 °C/min Ramp (Method A) or 6.5 °C/min Ramp (Method B)

	Lab	Retention projection accuracy (s)a	Linear retention indexing accuracy (s)a
Method A	A	±0.47	±1.1
	B	±0.42	±1.5
	C	±0.30	±1.2
	D	±0.51	±1.6
	E	±0.43	±2.3
	Average:	±0.43	±1.5
Method B	A	±1.5	±2.9
	B	±1.2	±7.5
	C	±1.3	±2.8
	D	±1.2	±4.0
	E	±1.7	±2.2
	Average:	±1.4	±3.9

^aAccuracy was calculated as the root-mean-square of the differences between the experimental and predicted retention times of the 12 test compounds.

Evidently, even when all experimental conditions were nominally the same between labs (which are the conditions under which retention indexing should be most reliable), the retention projection methodology was still more reliable because it could properly measure and account for unintentional differences between each of the GC systems. Table 2 shows one of these experiments in more detail—it shows the measured retention times of the 12 test compounds from Lab E in Method A along with the error in the retention projections and retention indices. Ethylbenzene was the major contributor to the overall error in retention indexing, but it was not the exception; 11 of the 12 compounds were predicted better by retention projection than by retention indexing.

Table 2.

Retention Projections and Retention Indices in the 26 °C/min Ramp (Method A) Run by Lab E

Test Compound	Measured Retention Time (min)	Retention Projection Error (min)	Linear Retention Indexing Error (min)
ethylbenzene	4.808	0.003	0.111
naphthalene	9.556	0.014	0.024
anthracene	13.303	0.009	0.033
N,N-diethyl acetamide	7.402	0.000	0.005
4-nitroaniline	12.210	0.001	0.023
caffeine	13.393	0.007	0.026
phenol	7.113	−0.012	−0.016
resorcinol	10.118	0.000	0.015
1-naphthol	11.704	−0.003	0.023
N,N-dimethylisobutyramide	7.032	0.008	−0.004
benzamide	10.558	−0.002	0.016
dextromethorphan	14.828	0.007	0.029
Overall Errora (min):		±0.0071 (±0.43 s)	±0.038 (±2.3 s)

^aRoot-mean-square of the differe nces between the experimental and predicted retention times of the 12 test compounds.

Accounting for intentional differences in experimental conditions

In previous work, we showed that the retention projection methodology was considerably more accurate than linear retention indexing when the experimental conditions were deliberately changed, but those experiments were performed in one lab, by the same operator. Here, we were interested in determining what sort of accuracy a typical user could expect in a different lab, using a different GC instrument, under whatever experimental conditions they decide to use.

To find out, each of the five labs ran the test mixture using three additional methods. The first two methods used were methods they typically employ in their own labs, while the third was to be a method each thought might “stress the methodology” in some way (see Supporting Information for the specific methods). The labs were provided a set of limits to which the methods had to conform: 1) the oven temperature could not go under 60 °C or exceed 320 °C, 2) hold times could not exceed 60 min, 3) the flow rate or inlet pressure had to stay constant over the course of the run, 4) the transfer line temperature had to be at or above the highest temperature in the temperature program, 5) the mass spectrometer had to scan at a rate of at least 2 Hz, 6) the carrier gas had to be He, and 7) they had to use the DB-5MS UI column they were provided. Notably, all of the methods selected by the labs were different, nor were any of the methods translations of each other. This again points to the need for a shared retention database to be reliable under a wide range of experimental conditions; standard experimental conditions for GC-MS have not been widely adopted nor are they likely to be.

Table 3 shows the accuracy of the retention projection methodology compared to that of retention indexing under the different methods. To calculate the accuracy of retention indexing, we used retention indices measured in our lab under method A (the 26 °C/min ramp) to predict retention times under each of the different methods. Under these wide-ranging conditions, the retention projection methodology was far more reliable than retention indexing; retention projections were up to 165-fold more accurate, averaging 37-fold more accurate among all 15 methods.

Table 3.

Accuracies of Retention Projections and Linear Retention Indices in Five Different Labs, Each Running Three Unique Methods

Lab	Methoda	Retention projection accuracy (s)b	Linear retention indexing accuracy (s)b
A	1	±1.9	±230
A	2	±1.4	±22
A	3	±2.0	±54
B	4	±0.28	±11
B	5	±0.45	±11
B	6	±0.59	±98
C	7	±1.5	±19
C	8	±0.24	±4.4
C	9	±3.8	±80
D	10	±0.88	±3.3
D	11	±0.74	±3.5
D	12	±0.66	±3.9
E	13	±1.2	±21
E	14	±1.4	±54
E	15	±1.1	±47
Average:		±1.2	±44

^aMethods are described in Supporting Information.

^bAccuracy was calculated from the root-mean-square of the difference between the experimental and predicted retention times for all 12 test compounds.

As an aside, we found that the biggest source of error was in transcription of retention times for one or more of the 25 n-alkane peaks. To correct this, we added a feature to the software to automatically extract the retention times from the GC-MS data file. Instructions to convert files from the vendor formats to one of the accepted open source formats (CDF, mzXML, or mzML) are available on the website. We found this to be considerably faster and more reliable than entering the retention times manually—it automatically selected all of the correct retention times in 22 of the 25 methods—and it brings the methodology closer to becoming fully automated.

Calculation of appropriate retention time tolerance windows

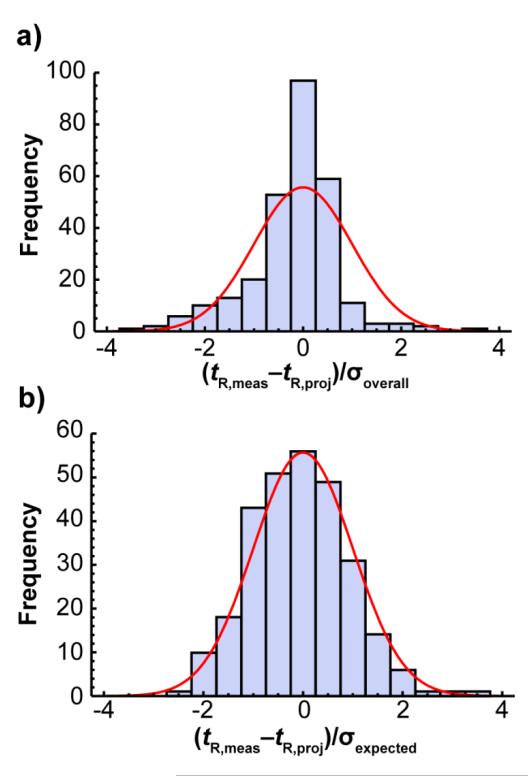
A means to project accurate GC retention times is helpful, but it is of limited value without knowledge of the appropriate retention time tolerance windows. Without them, one cannot quantitatively justify the exclusion of any potential identities based on retention time. Since the retention projection methodology was better able to account for unintentional differences between GC systems, we wondered if it would be possible to calculate retention time windows that are lab-independent; that is, the calculated retention time tolerance windows would be appropriate for any lab, despite the unintentional differences between GC systems. However, we first had to find a way to calculate the error that should be expected for retention projections in different methods. Figure 3a shows a histogram of the errors (measured retention time minus projected retention time) in all 282 retention projections (12 test compounds × 5 experiments × 5 labs minus 18 excluded for reasons discussed in the Experimental section). A normal distribution does not fit the probability distribution well because the error is strongly method-dependent and the methods were not completely random.

Figure 3.

Probability distributions of the error, t_R,meas-t_R,proj, in 282 retention projections divided by a) the overall standard deviation, σ_overall, and b) divided by the calculated standard deviation expected for each compound in each method, σ_expected. The red line shows the best fit normal distribution.

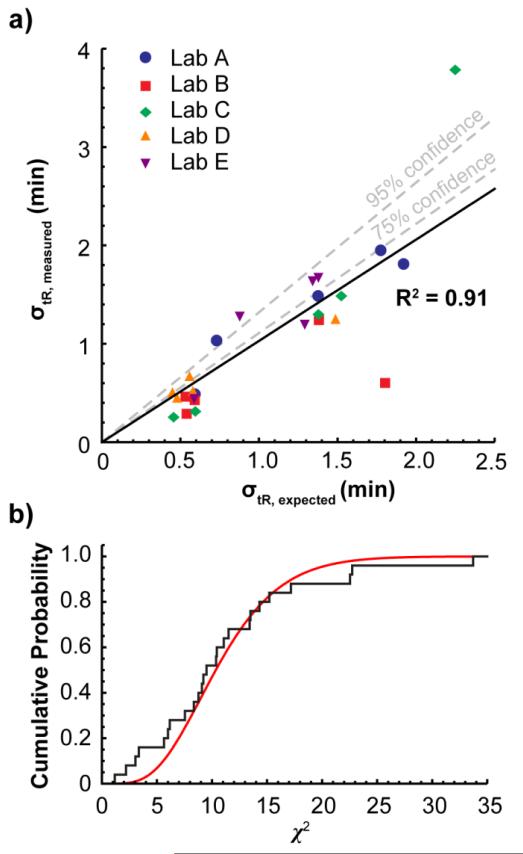
We developed a way to calculate the amount of error that should be expected in a retention projection for a given compound in a given method (see Supporting Information). In short, we assumed that all of the error in the retention projections came from error in the isothermal retention data (using an RSD in k of 0.565%) and propagated that error to the projected retention times. The calculations made it possible to predict the appropriate retention time tolerance windows regardless of the method used. While a histogram of the retention projection error normalized to the overall standard deviation, σ_overall, did not fit a normal distribution, a histogram of the retention projection error normalized to the expected retention projection error, σ_expected, for each compound in each method, did fit a normal distribution (Figure 3b), suggesting that the calculations do indeed predict the correct amount of error. Moreover, a plot of the expected retention projection error vs. the actual retention projection error for each of the 25 runs (Figure 4a) showed a strong correlation (R² = 0.91). The normalized error also fit a chi-square distribution (Figure 4b) as it would if the normalized errors in each method were all drawn from the same normal distribution; that is, the normalized error was method-independent.

Figure 4.

a) The expected retention projection error is strongly correlated with the actual error in the 25 methods. b) The difference between the expected and actual errors for the 25 methods fit a chi-square cumulative distribution.

Once differences between the methods were taken into account, we found that the calculated retention time tolerance windows were indeed lab-independent. The overall normalized error from each lab (across all 12 compounds in all five runs) was as follows: Lab A, 1.02; Lab B, 0.70; Lab C, 0.93; Lab D, 1.03; Lab E, 1.15. With these errors, none of the labs had a statistically different distribution of error as determined by a two-tailed chi-square test (95% confidence level).

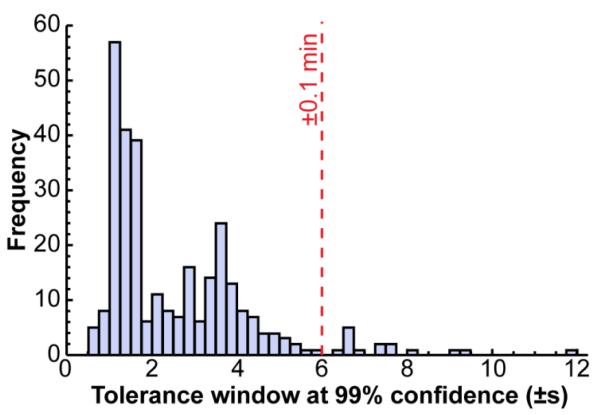
The calculated tolerance windows were not only method-independent and lab-independent, they were also quite narrow, averaging ±2.6 s (0.38 %) at the 99% confidence level. These are generally narrower than those recommended even when a standard is present. For example, the World Anti-Doping Agency specifies that for a positive identification, the retention time of an analyte shall not differ by more than 2% percent or ±0.1 min (whichever is smaller) from that of a reference compound analyzed contemporaneously (Figure 5). None of the 282 calculated tolerance windows exceeded 2% (only 7 exceeded 1%), and only 15 exceeded ±0.1 min.

Figure 5.

The calculated retention time tolerance windows (at 99% confidence) were generally narrower than those widely used when standards are run contemporaneously.

The retention time tolerance window calculations are now built into the online GC retention projection software. The software projects both a retention time and the appropriate retention time tolerance window for each compound in the database at a user-specified confidence level. To the best of our knowledge, this feature is unique, making it possible to reliably exclude possible identities for chromatographic features at a known level of confidence without having standards on hand for them. We must caution, however, that the tolerance windows may not apply when the column is overloaded with one or more components of the sample. As usual, care should be taken to avoid this situation.

System suitability check

The projected tolerance windows are only reliable if the selectivity of the user’s GC system is like one with an unspoiled DB-5MS UI column and a clean, deactivated liner. If the selectivity is different, perhaps because of a dirty liner or column, the tolerance windows cannot be trusted. In fact, we found that sometimes, even with a new DB-5MS UI column, the selectivity appeared to be different. Over the course of two years, we tested 21 new DB-5MS UI columns and with five of them, we experienced relatively poor retention projections right after installation of the columns. We are not sure why this happened, but in each case, nothing short of changing the column could be done to improve retention projection accuracy (e.g. changing the liner, cleaning the inlet, cutting the column, etc.). It seems unlikely, however, that they were faulty columns as received from the vendor, since they showed nearly identical behavior to each other in the vendor’s column performance test. We intend to explore this more in the future, but regardless of the cause, it is essential to test the system suitability before the calculated tolerance windows can be trusted, even when using a new DB-5MS UI column.

We propose a new type of system suitability check for this purpose. A user spikes their sample with both the n-alkanes and the 12 test compounds. Then the user runs the sample in a temperature program, back-calculates their temperature and hold-up time profiles based on the n-alkane retention times, and projects the retention times of the 12 test compounds. If the projections have error below a certain threshold, the selectivity of the system is considered “like new” and subsequent retention time tolerance windows will also likely be accurate. Otherwise the system integrity must be evaluated (e.g. check for leaky septum, proper column installation, etc.) and/or the column/liner replaced until it passes the test.

To determine the threshold for what should be considered a suitable system, we compare the expected distribution of error to the measured distribution of error among the 12 test solutes using a chi-square test. We set the upper threshold for a system that passes the suitability check to the 75% confidence level, anything between the 75% and 95% confidence level should be considered questionable, and anything beyond 95% fails the test. In Figure 4a, the 75% chi-square confidence level and the 95% confidence level are marked. With these thresholds, the vast majority of the runs performed in the five labs passed (19 of 25), 3 fell into the questionable category, and 3 failed, which is close to what would be expected for those confidence levels.

The system suitability check is now built into the online retention projection software. Immediately after the back-calculation step (but before retention times and tolerance windows are projected), the user is prompted to enter the experimental retention times of the 12 test compounds (or automatically extract them from the GC-MS data file). Based on the error in the retention projections of the 12 test compounds, the software gives a numerical score to the GC system that is calculated by dividing the user’s standard deviation of error by the standard deviation that would produce a chi-square value at the 75% confidence level. Therefore a value of 1.0 or less passes the test, and the indicator falls in the green region. Between the 75% and the 95% confidence levels, the indicator falls in the yellow region (questionable), and beyond that, it falls in the red region (fail).

We used the new system suitability check to successfully identify three unsuitable GC systems. In each case, the columns in them were the original ones sent to labs A, B, and C. The system suitability scores from the five methods lab A ran were: 2.1, 2.7, 2.4, 3.8, and 2.7; from lab B they were: 1.0, 1.7, 1.8, 1.7, and 1.9; and from lab C they were: 22.0, 15.0, 20.0, 40.0, and 12.0. Of the 15 scores, 14 failed and the last was on the edge of the acceptable category.

Conclusion

The new retention projection methodology proved considerably more accurate than retention indexing across five different labs. Even when experimental conditions were nominally the same as those used to measure linear retention indices, which should have been the most favorable conditions to accurately reproduce them, the retention projection methodology still averaged three-fold more accurate because it was better able to account for unintentional differences between the GC systems. Evidently, no matter how one predicts temperature-programmed retention, whether by retention projection, retention indexing, de novo calculation, or any other means, the accuracy of the predictions are fundamentally limited unless non-idealities in each GC instrument are measured and properly taken into account. The back-calculation algorithm provides a fast, easy way to measure the precise temperature and hold-up time profiles actually produced by the instrument without the need for any additional equipment.

The new methodology also proved to be robust. Under 15 different experimental conditions selected by the five labs (i.e. the temperature program, flow rate, etc.), the new methodology proved 4- to 165-fold more accurate than retention indexing. The distribution of error under each method was different, but we could calculate the distribution that should be expected for each. Relative to the expected distributions, the accuracy of retention projections was method-independent and far more lab-independent than retention indexing. Therefore, both retention times and appropriate retention time tolerance windows could be calculated, making it possible to use a shared retention database to exclude potential identities for an unknown chromatographic feature with a defined level of confidence, without having standards for each of the compounds on hand. In addition, the calculated tolerance windows were quite narrow, being generally narrower than those widely used for compound identification when a standard is available and contemporaneously analyzed. Finally, to ensure the reliability of the calculated tolerance windows, we developed a new system suitability check that must pass before the tolerance windows may be trusted.

With its high accuracy and reliability, the retention projection methodology has the potential to overcome the major limitations of existing shared retention databases, turning GC retention into a reliable, precision tool for compound identification, even when standards are not physically present. We have made the retention projection software and the beginnings of an isothermal retention database available at www.retentionprediction.org/gc. In the future, we intend to build a much larger database of isothermal retention and to attempt to use the same methodology with other stationary phases besides the DB-5MS UI phase.