Simplifying the complexity of resistance heterogeneity in metastasis

Abstract

The main goal of treatment regimens for metastasis is to control growth rates, not eradicate all cancer cells. Mathematical models offer methodologies that incorporate high-throughput data with dynamic effects on net growth. The ideal approach would simplify, but not over-simplify, a complex problem into meaningful and manageable estimators that predict a patient’s response to specific treatments. Here, we explore three fundamental approaches with different assumptions concerning resistance mechanisms, in which the cells are categorized into either discrete compartments or described by a continuous range of resistance levels. We argue in favor of modeling resistance as a continuum and demonstrate how integrating cellular growth rates, density-dependent versus exponential growth, and intratumoral heterogeneity improves predictions concerning the resistance heterogeneity of metastases.

Heterogeneity in primary tumors and in metastasis

Within an individual tumor, and between a primary tumor and its metastases, there are certain genotypic or phenotypic variations. Intratumoral heterogeneity implies that different parts of a tumor may have different properties, including the existence of different degrees of sensitivity to various cancer drugs. This heterogeneity has significant implications when developing clinical protocols (see [1, 2] and the references within). Heterogeneity can lead to variations in different fundamental cellular behaviors as a function of time and stress, regardless of the specific mechanisms that may induce it [3, 4]. Changes in these rates of cell division, death, mutation, migration, etc. have direct effects on the dynamic of growth and initiation of metastatic cells. For example, mutations in the Ras-Raf pathway, a type of Mitogen-Activated Protein Kinases (MAPK) pathway, may cause increased cell proliferation and resistance to apoptosis [5]. In hepatocellular carcinoma LIM and Cysteine-rich Domains-1 (LMCD1) mutations promote cell migration and tumor metastasis [6]. There are also certain genes that promote genetic stability, including DNA repair genes, DNA damage sensor genes, and cell cycle checkpoint genes. Changes in these stability genes affect the mutation rate [7]. Since these rates are not constant over time, and may vary according to the environment, resistance to chemotherapy becomes a complex dynamic process. Hence, an effective treatment often requires a combination of drugs targeting different resistance mechanisms, based on specific individual genotypic and phenotypic variations.

Along with biological and clinical research, mathematical approaches have been developed to model the development of drug resistance, and have dealt with many of the known aspects of the field [8]. These computational models and their outcomes each have their own definitions of ‘resistance’ for a given treatment, presented in discrete (e.g., two subgroups of ‘sensitive’ and ‘resistant’) or continuous (e.g., a range of values between 0 and 1, where 1 represents the maximum resistance level) ways. In addition to the intrinsic-resistance level, there is another factor, the evolution of resistance, which contributes to the dynamics. This factor determines the ability of a cell with a given resistance level to evolve over time and/or space to a different level, based on the processes that were initially assumed. For example, one of these processes is the development of spontaneous or drug-induced mutations.

Here, we discuss the impact of different assumptions concerning resistance level, resistance evolution, and growth limitation, on the prediction of the dynamics of cancer growth, heterogeneity, and survival. These concepts are described here through the three mathematical models of Stein et al. [9], Lorz et al. [10], and Lavi et al. [11] (see Box 1). In brief, the Stein model assumes exponential growth for all cells, and includes only the mechanism of intrinsic resistance, with no evolutionary process. In addition, they used a discrete definition of the resistance level that categorized the metastatic cells into two main groups: resistant vs. sensitive. While the Lorz model also assumes exponential growth for all metastatic cells, they also include resistance evolution with a continuous description of the resistance level. The Lavi model is an extension of the Lorz model, which shares most of the Lorz assumptions, except that exponential growth is replaced with a growth that depends on the cell density. Furthermore, the Lavi model accounts for the occurrence of changes (e.g., epi-mutations) that occur at higher rates than those of genetic mutations. These realistic assumptions have crucial effects on the predicted level of resistance heterogeneity, and as such integrate differently patient’s information into more accurate predicted clinical outcomes.

Box 1. Mathematical models.

Here, using continuous deterministic models, we describe the problem of drug resistance by including key mechanisms that control the dynamics of a simplified system of metastasis. Three mathematical models are discussed throughout the paper.

Table I.

Main assumptions and equations

Resistance level	Growth	Eq.	Main assumptions and equations	Ref.
Discrete variable	Exponential growth	1	A) The metastatic cells can be categorized into resistant or sensitive compartments, hence a discrete resistance level. B) All metastatic cells grow exponentially. C) The resistance mechanism is intrinsic, with no evolutionary process. $$\rho (t)=e^{-d·t}+e^{g·t}+1$$	Stein et al. [9]
Continuous variable		2	A) A range of values between 0 and 1 describes the resistance of a given cell, hence a continuous resistance level. B) All metastatic cells grow exponentially. C) The evolutionary process of resistance is account for, based on small spontaneous mutations (see Table II). $$\begin{gathered} \frac{\partial n(x,t)}{\partial t}=\left[r(x)(1-\theta (x))-c(x)-d(x)\right]n(x,t \\ )+\underset{0}{\overset{1}{\int }}\theta (y)r(y)M(y,x)n(y,t)dy \end{gathered}$$	Lorz et al. [10]
	Density dependence	3	A) A range of values between 0 and 1 describes the resistance level of a given cell, hence a continuous resistance level. B) Cells grow with cell-density limitations. C) Both the intrinsic and induced evolutionary processes of resistance are account for, based on genetic and non-genetic alterations (see Table II). $$\begin{gathered} \frac{\partial n(x,t)}{\partial t}=[f(\rho (t))\left(r(x)(1-\theta (x)) \\ -c(x,\alpha )\right)-g(\rho (t))d(x)]n(x,t \\ )+f(\rho (t))\underset{0}{\overset{1}{\int }}\theta (y)r(y)M(y,x)n(y,t)dy \end{gathered}$$	Lavi et al. [11]

Table II.

System variables in Equations 2 and 3

Variable	Range	Biological Interpretation
x	[0, 1]	Resistance level
t	R+	Time
ε	[0, 1]	Variance in the ‘alteration kernel function’, M
ρ(t)	R+	Total number of cells as a function of time
n(x, t)	R+	Concentration of cells with trait x at time t
r(x)	R+	Natural division rate of cell with trait x
d(x)	R+	Natural death rate of cell with trait x
c(x,α)	R+	Drug-induced death rate of cell with trait x, and drug dose α
f(ρ)	R+	Density dependence within the cell division rate
g(ρ)	R+	Density dependence within the death rate
θ(x)	[0,1]	Proportion of divisions of cells with trait x undergoing alterations
M(y, x)	[0,1]	The alteration kernel function. Probability that a cell division results in a alteration from state y to state x, given that an alteration occurs

Resistance level as a discrete variable

Although oncologists are aware of the impact of intratumoral heterogeneity, many clinical trials test only one drug. For a given treatment, the clinical response and the treatment efficacy are determined by basic measurements, such as the quantification of tumor shrinkage and overall survival (OS), that are not designed to reveal the underlying complexity of the response based on varying resistance levels in different cells in a tumor. Interesting metastatic studies with clinical and practical implications have been reported by Stein and colleagues [9, 12–15]. These studies offer a method of analyzing tumor response and predict survival using surrogate and direct measures of tumor volume while a metastasis patient is receiving therapy in a clinical trial. Their main hypothesis is that for a given treatment, there are two main cell sub-populations, sensitive and resistant. That is, the resistance level can be described by a discrete variable measuring cellular death/survival. Accordingly, initial tumor shrinkage during treatment is due to a higher portion of sensitive cells in a tumor, and a subsequent increase in the tumor size is a result of the remaining resistant cells that increase in number. The published data [9, 12–15] on patients enrolled in clinical trials receiving chemotherapy, for mainly prostate cancer and renal cell carcinomas, can be divided into four main outcomes: successful treatment, partial response with relapse, no response, or unclear. Stein and colleagues fitted a function that is given as a sum of two exponentials, to estimate tumor size over time (ρ(t)). The tumor size was based on the rates of tumor regression (d) and tumor growth (g) (Box 1, Table I, Equation 1). ρ was normalized with the initial tumor size on day 0, i.e., ρ(0)=1. They proposed that because the growth rate was found to correlate with OS, it would serve to estimate efficacies of different therapies based on the sampled population or the individual patients. Using these assumptions and method, they concluded that bevacizumab reduces the growth rate constants of renal carcinomas [13], and that sunitinib reduces the tumor growth rate more than interferon type I-alpha (IFN-α) [15]. They argued that during treatment, the rate of tumor re-growth (g function in Box 1, Table I, Equation 1) is a constant value, and for certain patients, this indicates that treatment should be continued for a longer period of time since the tumor growth rate is lower than without treatment.

The Stein model describes the net growth of the metastatic cells with no information on cellular rates such as cell division or death rates. Sensitive cells are assumed to be cells that did not survive the treatment, regardless of the value of their drug-induced death rate. Note that a treatment producing low rates of drug-induced death and cell division could have the same net-growth response as a different treatment with higher rates of drug-induced death and cell division. Therefore, with no further information about cellular growth and death rates, the efficacy of a treatment is only expressed by the net-growth response.

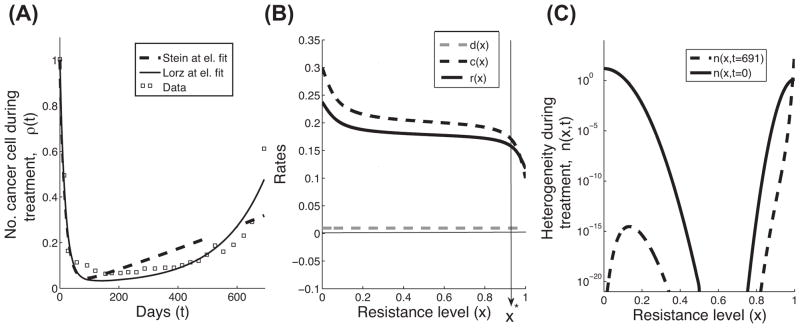
We consider here the approach of Stein et al. with a representative example of partial response (published as part of supplementary Figure S1, case 12 in [9]). Their data set serves us throughout this paper as a way to compare three mathematical models, and discuss their assumptions, approaches and the meaning of their results. We estimated the parameters of Equation 1 (Box 2, Table III) to be d = 0.0541 and g = 0.0005, using a nonlinear least-squares method (for more details see Boxes 1–2). The data points and the curve fitted using Equation 1 are plotted in Figure 1A.

Box 2. Mathematical details and the optimization problem.

Table III.

Parameter and variable details

Fig.	Eq.	Notes	Initial condition (IC)
1A	1, 2	For technical details of the optimization solution, see the optimization problem below. Exponential model (Lorz et al.): Spontaneous death rate as a constant value $$d(x)\equiv 0.0097$$ A sigmoid curve for r(x)−c(x): $$r(x)-c(x)=\frac{p_1-p_2}{\pi }\left(\frac{\pi }{2}-{tan}^{-1}\frac{{\mathrm{p}}_3(\mathrm{x}-{\mathrm{p}}_4)}{\mathrm{x}(1-\mathrm{x})}\right)+p_2$$ where, p1 = −0.0624, p2 = 0.0173, p3 = 0.0846, p4 = 0.6144. A sigmoid curve for c(x): $$c(x)=\frac{a_1-a_2}{\pi }\left(\frac{\pi }{2}-{tan}^{-1}\frac{{\mathrm{a}}_3(\mathrm{x}-{\mathrm{a}}_4)}{\mathrm{x}(1-\mathrm{x})}\right)+a_2$$ where, a1 = 0.3, a2 = 0.1, a3 =0.1, and a4 = 0.6. Also, θ = ε =0 Discrete model (Stein et al.): ρ(t) = e−dt + egt − 1, where, d = 0.0541 and g = 0.0005.	IC1, where: $${IC}_1=\{\begin{array}{cc}\frac{S}{{\sigma }_S}\frac{2}{\sqrt{2\pi }}{e}^{\frac{x^2}{2{{\sigma }_S}^2}}& 0\le x\le 0.5\\ \frac{R}{{\sigma }_R}\frac{2}{\sqrt{2\pi }}{e}^{\frac{{(x-1)}^2}{2{{\sigma }_R}^2}}& 0.5<x\le 1\end{array}$$ S = 0.96, σS= 0.05 R = 0.04, σR= 0.025
1B	2
1C	2
2A	2		IC1- IC4, where: $$\begin{array}{l}{IC}_1\mathit{\text{as}}\mathit{before}.{IC}_2=n_2(x,0)=1\\ {IC}_3=n_3(x,0)=11.2841e^{\frac{{(x-0.5)}^2}{{0.05}^2}}\\ {IC}_4=n_4(x,0)=4.5135e^{\frac{{(x-1)}^2}{{0.25}^2}}\end{array}$$ All Ics ensure: $$\rho (0)={\int }_0^{1}n(x,0)dx=1$$
2B	2
2C	2
2D–E	2	All parameters as in the exponential model described above, except for permuted cellular growth rates (ξ): $$\frac{\partial n(x,t)}{\partial t}=\left[\left(r-c-d\right)(x)+\xi (x)\right]n(x,t)$$ Where ξ(x) ~ N(0, 0.25 (r − c − d)(x))	IC1
3A	3	All cellular rates and parameters as in Figure 2. It has been previously shown [11] that one can mathematically rewrite Eq. 3 by rescaling the time with the term $\tau =\underset{0}{\overset{t}{\int }}f(\rho (s))ds$, and $\frac{\partial n}{\partial t}=\frac{\partial n}{\partial \tau }f(\rho (t))$. These two changes yield $$\begin{gathered} \frac{\partial n(x,\tau )}{\partial \tau }=\left[r(x)(1-\theta (x))-c(x,\alpha )-\frac{g(\rho )}{f(\rho )}d(x)\right]n(x,\tau ) \\ +\theta (x)\underset{0}{\overset{1}{\int }}r(y)M(y,x)n(y,\tau )dy \end{gathered}$$, where the cell-density dependence is described here by: $$\frac{g(\rho )}{f(\rho )}=\sqrt[3]{\rho }{(\rho -2)}^2$$ For panels C and D: $M(y,x)=\frac{C(y)}{\epsilon }{e}^{-\frac{{(y-x)}^2}{{\epsilon }^2}}$ C(y) is included so as to ensure that ${\int }_0^{1}M(y,x)dx=1$, for all y ∈ [0,1]	IC1-IC4
3B	3
3C	3		IC1
3D	3

The optimization problem

We chose to represent r(x)−c(x) as a sigmoid curve with four parameters: $\mathrm{r}(\mathrm{x})-\mathrm{c}(\mathrm{x})=\frac{{\mathrm{p}}_1-{\mathrm{p}}_2}{\mathrm{\pi }}\left(\frac{\mathrm{\pi }}{2}-{tan}^{-1}\frac{{\mathrm{p}}_3(\mathrm{x}-{\mathrm{p}}_4)}{\mathrm{x}(1-\mathrm{x})}\right)+{\mathrm{p}}_2$, and d(x) as a constant, with one parameter: d(x) ≡ p₅ The total density ρ(t) is then obtained via integration over the trait space: $\mathrm{\rho }(\mathrm{t}):={\int }_0^1\mathrm{n}(\mathrm{x},\mathrm{t})\text{dx}$. We solved the linear system described in Equation 2, with no mutations (θ=0 and ε=0) and assumed IC_1. To integrate over x, we discretized [0,1] uniformly, with step size h=1/3999, and used a standard trapezoidal rule on n(x,t). To find the parameters that best fit the data points of the form (t, ρ(t)) in Stein et al. [9], we first performed a random parameter search over the five free parameters p1,…,p5, constraining them to lie within physically realistic values, and solved for ρ(t). This resulted with parameter values that were then used as an initial estimate for a nonlinear least-squares algorithm. The Matlab built-in function ‘lsqcurvefit’ was used to obtain a local minimizer for the norm squared error $\text{Lsq}(\mathrm{p}1,\dots ,\mathrm{p}5):\text{Lsq}({\mathrm{p}}_1,\dots ,{\mathrm{p}}_5):={\sum }_{\mathrm{i}=1}^{25}{\left({\mathrm{\rho }}_{\text{theory}}({\mathrm{t}}_{\mathrm{i}};{\mathrm{p}}_1,\dots ,{\mathrm{p}}_5)-{\mathrm{\rho }}_{\text{data}}({\mathrm{t}}_{\mathrm{i}})\right)}^2$. The parameter values obtained are approximately p1 = −0.0624, p2 = 0.0173, p3 = 0.0846, p4 = 0.6144, and p5 = 0.0097. We then made a qualitative choice, that both r(x) and c(x) should appear sigmoid as well. We chose the same type of sigmoid curve for c(x): $\mathrm{c}(\mathrm{x})=\frac{{\mathrm{a}}_1-{\mathrm{a}}_2}{\pi }\left(\frac{\mathrm{\pi }}{2}-{tan}^{-1}\frac{{\mathrm{a}}_3(\mathrm{x}-{\mathrm{a}}_4)}{\mathrm{x}(1-\mathrm{x})}\right)+{\mathrm{a}}_2$. with a1 = 0.3, a2 = 0.1, a3 = 0.1, and a4 = 0.6. Then, we can simply find r(x) using the above two formulas and the fact that r(x)=[r(x)−c(x)]+[c(x)]. Plotting this with the initial condition n(x,0) above yields Figure 1B.

The same method was used to estimate the parameters of the growth (g) and the regression (d) rates in the Stein model, with an initial estimate given by the rates found in [9]. The values we obtained for their parameters are d = 0.0541 and g = 0.0005 using in ρ(t) = e^−dt + e^gt − 1.

Figure 1.

Comparison between the Stein and Lorz models, with resistance-level variables that are discrete vs. continuous. (A) Patient response data and two mathematical predictions of the total number of cancer cells during treatment are plotted. The data set (boxes) illustrates a representative relapse response (case 12, Fig. S1 in [9]). The Stein model, given in Equation 1, describes the discrete approach of grouping the cells into two categories: resistant and sensitive (dashed line). The Lorz model, given in Equation 2, describes the continuous approach to resistance level (solid line). (B) The cellular rates of cell division (r(x), black solid line) and drug-induced death (c(x), black dashed line) are assumed to be sigmoid curves, and the natural death rate (d(x), grey dashed line) is assumed to be a low constant value. X* is the transition where the net growth rates change from negative to positive values (see arrow). All parameters are given in Box 2. (C) The trait distributions, n(x,t), at the beginning (t=0) and at the end (t=691 days) of the treatment. This plot is the solution of the exponential growth model described in Equation 2, where θ=0 and ε=0, using initial condition IC₁ and cellular rates that are described in panel B (Box 2, Table III).

Resistance level as a continuous variable

The significant variation that has been observed in intratumoral heterogeneity indicates there is a variation in cell division and death rates of cells within a tumor; thus, drug resistance is far from being a black-and-white, resistant or not resistant phenomenon. In view of that, our hypothesis is that a continuous variable is a more appropriate way to describe, estimate, and measure the resistance level. Several direct and indirect interdisciplinary approaches have been suggested to estimate the drug resistance level, depending on the type of data that is analyzed. For instance, clinical data that combine clinical staging, gene expression, and survival data from the same patient can help to categorize a patient as a ‘good’ or a ‘poor’ responder in a continuous manner. Such a score can then be used as a more comprehensive method to estimate the different cancer cell phenotypes and their drug sensitivities.

Exponential growth

From a mathematical perspective, Lorz et al. [10] proposed a model for the evolution of cancer cells, ρ, over time, t (Box 1, Table I, Equation 2). Their model is based on an approach previously developed in part by several other groups [16–22]. It was assumed that the cancer cells had no growth limitations, and grow exponentially. The model was designed to estimate the heterogeneity, n, as a function of the resistance level, x, and time, t. Using this notation, the total number of the cancer cells is described by $\rho (t)=\underset{0}{\overset{1}{\int }}n(x,t)dx$. Each subpopulation, n(x, t), is based on the rate of cell division, r(x), the spontaneous rate of death, d(x), the rate of drug-induced death, c(x), and the initial condition, IC= n(x,0). All rates are functions of the resistance level. In addition, there are contributions from all other subpopulations, depending only on a genetic mutations function, M(x, y). θ(x) denotes the fraction of cells with trait x that can carry out new modifications, where 0 ≤ θ(x) ≤ 1. They suggest that the treatment acts as a selection process, while mutations act as a diffusion process.

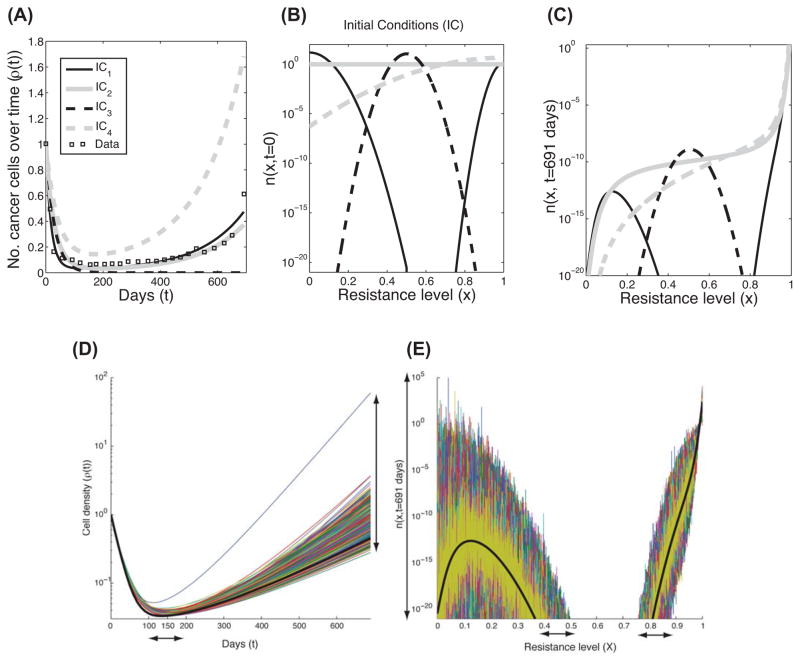
Once resistance level is included in tumor-growth models, we can study how variation in cell division, death, and alteration rates, as a function of the resistance level, can affect the predicted patient’s response. How is such a model different than having a discrete representation of resistance? How can we quantify the dynamic changes in heterogeneity? To address these questions, we analyzed the data points of Stein et al. (squares in Figure 1A), followed by a simplified version of the Lorz model where we assume exponential growth with no mutations (θ= ε =0). We relaxed the assumption that cellular rates are described by step functions, and considered sigmoidal functions instead. The cell division and death rates were estimated using a nonlinear least-squares method (Box 2, Table III and Figure 1B), with an initial condition of 96% of the cancer cell population located below the value of x=0.5 (IC₁ in Figure 1C and Box 2, Table III). Heuristically, we are imagining x=0.5 as the barrier between sensitive and resistant cells. Using the model of Lorz at el., the predicted growth (Figure 1A) gives information about changes in heterogeneity over time (n(x,t)). Figure 1C also gives a more detailed description of the ‘relapse’ case. When starting with approximately 96% ‘sensitive’ cells (described by IC₁), theoretically, after 691 days of treatment, the ‘sensitive’ cells have not totally been eliminated by the drug (dashed curve) and could affect the net-growth over time, after treatment ceases.

We next demonstrate how the net growth (Figure 2A) and the heterogeneity (Figure 2C) of four different non-zero initial conditions (IC₁-IC₄, Figure 2B), would appear at the end of a treatment (on day 691), using the same rates as in Figure 1. It is interesting that the growths of both IC₁ and IC₂ are not significantly different, yet their heterogeneous compositions include different levels of resistance, even if the number of cells of certain types are very few. IC₃ and IC₄ resulted in expected curves. IC₄ assumes that initially the majority of cells have higher cell division rates than death rates, therefore, the tumors grow more than with all the other ICs. IC₃ also resulted in an intuitive curve representing successful treatment. Although the average ‘resistance level’ seems to be high (x=0.5) compared to all possible values of this variable (x∈[0,1]), the important aspect is the relative size of the net death rate (i.e., c(x)+d(x)), the cell division rate (r(x)) over the x-space, and in particular the trait values where the net-growth rate changes its sign, from negative to positive. A negative net growth would result in decreasing tumor size. In this case, almost all the initial cells lie in this region.

Figure 2.

The Lorz model of exponential growth with four different initial trait distributions. (A) Four mathematical predictions of the total number of cancer cells over time, (ρ(t) where t≤691 days), based on four different initial conditions (IC₁-IC₄, given in panel B and Box 2, Table III). These curves are the solutions of Equation 2 in Box 1, Table I, where θ=0, ε=0 along with the rates in Fig. 1B and Box 2, Table III. The patient response data set from Figure 1A is also shown for comparison (boxes). (B) The four different initial conditions (labeled as IC₁-IC₄) that are given in Box 2, Table III. (C) The trait distributions at the end of the treatment, n(x, t=691 day), using the same conditions as in panel A. (D–E) These two panels describe the effect of variations in the net-growth rates on the Lorz model. Using the same conditions as in Figure 1 (continuous-resistance model), we illustrate the outcome of the perturbed net-growth rates of Equation 2 using 1000 simulations. The additional perturbation distribution assumes a normal distribution with mean=0, std=25% of the net-growth rate in Figure 1A applied uniformly over all traits. (D) shows the variation in the growth of cancer cells over time, while (E) shows the variation in the trait profile at the final time (691 days). The different colors are the result of different perturbations corresponding to the aforementioned normal distribution, while the black line corresponds to the simulation in Figure 1 (that is, no perturbation). The arrows stress the size of variations.

Variation in cellular rates

One should keep in mind that the lower the number of sensitive cells, the smaller their contribution within a short time period. Thus, in the short time period after a treatment is stopped (t>691 days), the results derived from the Lorz model do not necessarily contradict the qualitative conclusions of the discrete model. On the other hand, both models are based on a deterministic description, with fixed parameters, and no stochasticity. A noisy environment could result in a more complex resistance distribution, mainly where the cell division and death rates would be closer in value. In this case, a clear separation between the two sub-populations would no longer be seen and the conclusions of the two models would be totally different, even for a short period of time.

Variations in cell division and death rates are very common, especially when administering a drug. Using the exponential model (Equation 2, Figure 1A, solid line), we show in Figures 2D–2E the outcome in terms of cancer growth over time and in its heterogeneity on the last day of treatment (t=691 days), when fixed perturbations of the net-growth rate as a function of the trait were included as initial conditions. The net-growth rates are sampled from a normal distribution where the mean is the initial ‘deterministic-growth rate’ (which can be estimated from Figure 1B), and the standard deviation is 25% of that mean. In that specific example, the maximum growth rate among all traits is 0.0721 (absolute value), and the corresponding maximum standard deviation is 0.018. Given the exponential growth (Equation 2), small perturbations of those rates can result in large differences in cell density (3–4 orders of magnitude, see vertical arrow in Figure 2D), and in the time to reach the minimum-tumor reduction (a delay of up to 50 days, horizontal arrow in Figure 2D). In addition, the heterogeneity at the end of the treatment dramatically varied from the original estimation in the expected traits (x-axis) and in the number of cells with those traits (y-axis) (colored lines versus black line, Figure 2E).

Growth with cell-density dependence

Both models, Stein et al. [9] and Lorz et al. [10] described the total number of metastatic cells, and made an assumption concerning the exponential growth of cancer. However, the total number of cancer cells at any given time can be thought of as an integral of all individual tumors, with different sizes and cell densities: ${\rho }_{\mathit{Total}\mathit{caner}\mathit{cells}}(t)=\underset{\mathit{All}\mathit{tumors}}{\int }{\rho }_{\mathit{Tumor}}(t)$. These two aforementioned models are thus describing the left-hand side of this equation (i.e., ρ_{Total caner cells}(t)). We can however, consider the more fundamental problem of modeling each tumor individually, and describe the right-hand side of this equation (i.e., $\underset{\mathit{All}\mathit{tumors}}{\int }{\rho }_{\mathit{Tumor}}(t)$). Each tumor has its own growth rate, which depends on its heterogeneity and environment. Also, at some point in time, cells may migrate and initiate new tumors with a certain probability, depending on the type of tumor, the mutations, and the tumor size. Mathematically, this can be modeled, assuming a net-growth rate that depends on the intratumoral cell density in addition to the resistance level. The mathematical formula that best describes the ‘growth law’ of cancer cells has long been debated, though there are three commonly used deterministic functions: exponential, logistic, and Gompertzian [23–29]. In most computational studies, the exponential growth describe only the early stages of tumors or the metastasis, but as the tumor size increases, a slower rate of growth provides a better description. Logistic and Gompertzian laws have been mainly considered for this slower type of growth.

Focusing in from a global to a more local-tumor level, the rates of cell division and spontaneous death are known to depend on numerous biological parameters, including the local cell density and the resistance level. Cell density relates to various factors that determine tumor growth, such as cell-cell interactions, cell-matrix interactions, the distribution of nutrients, survival signals, the penetration of anticancer drugs, and the pressure within a tumor. In general, many studies have measured the relationship between the cellular rates as functions of cell density in different environmental conditions [1–6,10–12]. In some studies, the cell division rate was found to be a decreasing function of cell density [10,11], while the death rate was described by an increasing function of cell density [1,2,3].

We have extended the approach of Lorz et al. using the same framework to focus on the single tumor level [11]. The cell division and the spontaneous death rates of the cancer cells we assume to depend on the cell density (see functions: f(ρ), g(ρ) in Equation 3). Using the same rates of cell division and death as described above (Box 2, Table III), we examine the heterogeneity and density over time with the administration of a treatment (t≤691 days), for the four initial conditions (IC₁-IC₄). In all of these cases, the net-growth rates decrease to different degrees and the densities are limited (Figure 3A). The model is flexible enough to include more information on factors that could limit the tumor size/net-growth rate by changing the functions of f(ρ) and g(ρ). Accordingly, the n(x,t) for each IC is different than for exponential growth, even though the same cell division and death rates were assumed (Figure 3B versus Figure 2C). For instance, after t=691 days with treatment, cells with x-trait<0.1 are still present in this example.

Figure 3.

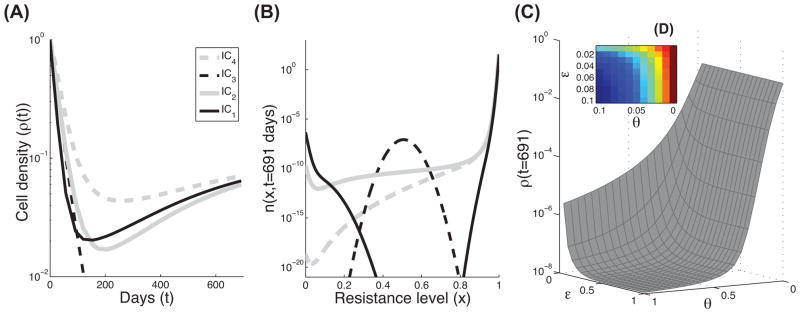
Modeling cell growth with density dependence. As in Figure 2, the effects of four initial conditions on the density and final trait distribution of the third model are shown. (A) Four mathematical predictions of the total number of cancer cells over time, based on IC₁-IC₄. These curves are the solutions of Equation 3 in Box 1, Table I, where θ=0 and ε=0 and the rates in Figure 1B and Box 2, Table III. (B) The trait distributions at the end of the treatment (t=691), using the same conditions as in panel A. (C) Lower plot: numerical predictions of the final cell density, ρ(t=691), using Equation 3, where ε and θ vary over a range of parameters ([0,1]). All other parameters and functions are the same as in panels A and B. (D) Upper plot: as in panel C, ε and θ vary over a limited range of parameters ([0,0.1]).

Furthermore, this model accounts for the occurrence of genetic as well as non-genetic changes, which occur at higher rates than the genetic mutations. A small mutation rate was already shown to function as a diffusion process, for x, since cells with a given trait may spread to a neighboring interval of x-values via mutations [10]. While the effect of such a low rate has a very limited impact on the total cell density, higher rates are expected to increase the spread of x with different cell division and death rates. Therefore, these cells could die or survive depending on their altered traits. We demonstrate the effect of the alteration rate on the tumor density over different scales (Figures 3C–3D). There are two parameters that relate to the alteration process, ε and θ. The alteration kernel, M(y, x), is considered here to be a Gaussian distribution con ned to [0, 1] with mean y and variance ε²/2. In general, the variance, ε, is a function of the external stress and time, ε(stress, t) (see [11]). Here, we present a simple case in which these parameters are constant over time. In Figure 3C, we plot the cell densities at the end of the treatment (ρ(t=691 days)), while varying the ε and θ between [0,1]. The upper plot in Figure 3D focuses on lower values of ε and θ as in [0,0.1]. Both plots clearly demonstrate a decrease in cell density as the alteration rate increases.

Concluding Remarks and Future Perspectives

With the advantages of high-throughput data and new automated techniques comes the obvious problem of how to analyze and understand the high-dimensional complexity of a patient’s information. Researchers can create complex datasets, but a more challenging task is to develop models that are able to simplify and explain complex data. The ideal mathematical approach would simplify, but not over-simplify, complex datasets into meaningful and manageable estimators that predict a patient’s response to specific treatments. Furthermore, there is an urgent need to develop effective methodologies to analyze data from complex diseases such as metastatic cancer, in which tumors are quite heterogeneous, containing cells with different degrees of drug sensitivity, the source of cancer relapses.

In this paper, we have addressed some of the main aspects relating to the mathematical modeling of drug resistance in metastatic cancer. First, we demonstrated the value of having a model based on a continuous representation of the resistance level. Many primary human tumors have been found to contain genetically distinct cellular sub-populations [1]. Even in a system with a single genetic clone, functional variability has been observed among the tumor cells, with distinct cellular sub-populations and different growth rates [3]. Thus, the definition of ‘resistance’ should incorporate all possible cases in which tumor cells survive. In addition to the fact that cells could survive the administered treatment, their survival rate should be included in the model. From that perspective, a tumor contains several sub-populations of cancer cells with different net-growth rates. The net-growth (or survival) rate is a combination of cell division, spontaneous death, and drug-induced death rates. In most, if not all, cases there is an additional rate of alteration (e.g., modification, mutation). The better the treatment, the higher the selection, which minimizes heterogeneity due to convergence of the sub-populations with the highest survival rates. However, as was demonstrated here, there may be non-detectable sub-populations that manage to grow at very low survival rates. After a long period of treatment, the global rate of cancer net growth is mainly influenced by the largest sub-populations with the highest survival rates. This is in accord with the discrete-resistance model. However, when a second drug is administered to target the selected ‘resistant’ sub-populations, the undetected cells with different resistance levels appear. Having a method that can predict the underlying dynamic of the heterogeneity might improve the design of treatment protocols for patients that relapse.

The second topic we addressed is the modeling of metastatic cancer cells using a deterministic approach. Metastases are known to spread rapidly, and therefore exponential growth is the commonly used approach in modeling. We demonstrate how small, yet likely, variations in the net-growth rates, may result in a large variation in the predicted tumor size and its heterogeneity over time. Thus, it is difficult to target using specific treatments. This prediction is the outcome of assuming exponential growth.

Our view of metastatic cancer is to some extent different. We suggest modeling metastatic cancer cells as a collection of individual tumors with different growth rates, in which a single cell can be considered as a tumor of minimal size. When tumor size increases, a slower growth rate is observed [30]. We show here how cell-density dependence can change the dynamic of the heterogeneity, mainly by scaling the time to reach the heterogeneity of the exponential model. Thus, the heterogeneity of the exponential model is not necessarily identical to the average of all tumors with density dependence, which highlights the advantage of using such a model with density dependence. A full model that includes the probability of initiating new tumors and determines tumor size based on the environment and intratumoral alterations will be the subject of future work.

We would like to emphasize the importance of collecting accurate data for estimating tumor size and its heterogeneity during treatment. This description of tumor heterogeneity should include information on the sub-populations within a tumor, which should give us a way to quantify rates of cell division, death, alteration, migration, etc. Having such data would dramatically accelerate the development of computational models, and increase their ability to assist in the design of optimal treatment protocols.

Highlights.

• Drug resistance can be modeled as either a discrete or continuous phenomenon.

• The integration of heterogeneity, cellular rates and density impacts cancer growth.

• Density dependence vs. exponential growth results in different degrees of heterogeneity.