Abstract
Recent advances in population genomics have made it possible to detect previously unidentified structure, obtain more accurate estimates of demographic parameters, and explore adaptive divergence, potentially revolutionizing the way genetic data are used to manage wild populations. Here, we identified 10 944 single-nucleotide polymorphisms using restriction-site-associated DNA (RAD) sequencing to explore population structure, demography, and adaptive divergence in five populations of Chinook salmon (Oncorhynchus tshawytscha) from western Alaska. Patterns of population structure were similar to those of past studies, but our ability to assign individuals back to their region of origin was greatly improved (>90% accuracy for all populations). We also calculated effective size with and without removing physically linked loci identified from a linkage map, a novel method for nonmodel organisms. Estimates of effective size were generally above 1000 and were biased downward when physically linked loci were not removed. Outlier tests based on genetic differentiation identified 733 loci and three genomic regions under putative selection. These markers and genomic regions are excellent candidates for future research and can be used to create high-resolution panels for genetic monitoring and population assignment. This work demonstrates the utility of genomic data to inform conservation in highly exploited species with shallow population structure.
Keywords: Chinook salmon, effective population size, genetic stock identification, population genomics, RAD sequencing, SNPs, western Alaska
Introduction
Discrete management of genetically distinct populations can increase species-wide resilience and stabilize the productivity of ecosystems as a whole (Hilborn et al. 2003; Schindler et al. 2010). For over three decades, genetic data from 10 to 100 putatively neutral markers have been used to identify discrete populations, define conservation units, and estimate demographic parameters (Utter et al. 1974; Wirgin and Waldman 1994; Waples et al. 2008). The use of genetic data for management has been especially successful in Pacific salmon (Oncorhynchus spp.) which exhibit extensive population structure (Utter and Ryman 1993; Shaklee et al. 1999). However, applications have been limited for recently isolated populations of salmonids (Taylor et al. 1997) or marine species with little neutral structure (Waples 1998). In these circumstances, data from thousands of markers (genomic data) may be necessary to resolve population structure and aid management.
Genomic data can provide accurate estimates of neutral population structure (Avise 2010; Funk et al. 2012; Narum et al. 2013), identify genomic regions that display adaptive divergence (Allendorf et al. 2010; Angeloni et al. 2012), and provide increased accuracy when estimating demographic parameters (Allendorf et al. 2010). Genotypes from thousands of loci have been used to elucidate neutral structure in populations of Pacific lamprey (Entosphenus tridentatus, Hess et al. 2013) and to improve resolution of fine-scale structure in Atlantic salmon (Salmo salar, Bourret et al. 2013). Additionally, genome scans have revealed adaptively important markers and genomic regions in sockeye salmon (Oncorhynchus nerka, Russello et al. 2012), Atlantic cod (Gadus morhua, Bradbury et al. 2013; Hemmer-Hansen et al. 2013), and lake whitefish (Coregonus clupeaformis, Renaut et al. 2012). Although many studies have used genomic data to elucidate structure in nonmodel organisms, demographic parameters such as effective size are rarely estimated with these types of data.
Effective population size (Ne) is an important parameter in conservation biology (Frankham 2005), but methods to calculate Ne with genomic data are lacking (Waples and Do 2010). Specifically, many calculations of Ne require knowledge of linkage relationships, which are often unknown for nonmodel organisms. A possible solution to this problem is the use of high-density linkage maps that can now be created rapidly for many species with genotyping by sequencing (e.g., Baxter et al. 2011; Miller et al. 2012; Gagnaire et al. 2013). Using data from these maps, it is possible to obtain estimates of Ne that are not biased by physical linkage. To the best of our knowledge, this method has only been implemented in populations of model organisms (Park 2011; Sved et al. 2013), but the increasing availability of linkage maps will facilitate Ne estimation in many species of conservation concern.
Chinook salmon (Oncorhynchus tshawytscha) from western Alaska represent an excellent system to explore the utility of genomics in a management context. Chinook salmon inhabit four major regions in western Alaska: Norton Sound, the Yukon River, the Kuskokwim River, and Bristol Bay, all of which vary significantly in size, hydrology, and climate (Fig. 1, Olsen et al. 2011). The Kuskokwim and Yukon regions are composed of a mainstem river with many tributaries, whereas Norton Sound is composed of many unconnected and short rivers (mean length ∼110 km; Olsen et al. 2011). The Bristol Bay region is composed of several river systems each with smaller tributaries (i.e., Nushagak, Togiak, Naknek rivers). Past studies using allozymes and single-nucleotide polymorphisms (SNPs) found evidence of structure in western Alaska, but concluded that differences among populations in Norton Sound, the lower portions of the Yukon and Kuskokwim rivers, and Bristol Bay, were insufficient to allocate mixture samples back to their region of origin (Gharrett et al. 1987; Templin et al. 2011). Returns of Chinook salmon to western Alaska over the past decade have been approximately 20% lower than their long-term average, renewing interest in the migration patterns and vulnerability of stocks to fisheries in this region (ADF&G 2013). Improved resolution of population structure would allow managers to investigate these questions using genetic tools. Additionally, estimates of Ne and other demographic parameters could help to inform conservation and management efforts across the region.
Figure 1.
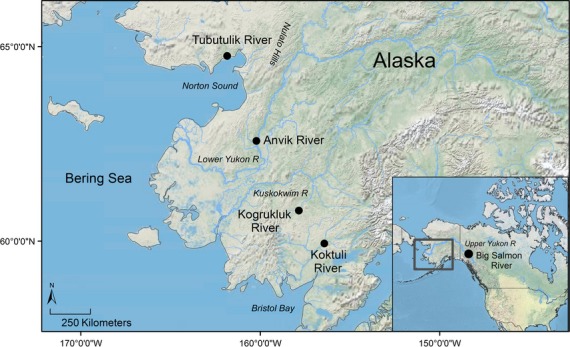
Map of sampling locations. See Table 1 for additional details about each sampling site.
We used restriction-site-associated DNA (RAD) sequencing to investigate the population structure and demography of Chinook salmon from western Alaska. We identified over 10 000 SNPs in 270 individuals from five populations across western Alaska. Patterns of genetic variation were assessed using both population-and individual-based methods and validated with assignment tests. We then aligned our RAD markers to a linkage map to calculate Ne with and without removing physical linkage. We also conducted outlier tests and used the linkage map to detect loci and genomic regions under putative selection. This approach defines an important way that genomics can be used to inform management of nonmodel species with high gene flow.
Materials and methods
Tissue sampling
Tissue samples from spawning Chinook salmon were available from four regions in coastal western Alaska and one in the upper Yukon River (Fig. 1, Table 1). We selected populations that did not have unusually small census sizes and that were genetically similar to proximate populations identified from previous studies (Olsen et al. 2011; Templin et al. 2011); this approach ensured that our conclusions were based on populations that were representative of each region. Chinook salmon from the upper Yukon River are highly differentiated from those of western Alaska (Smith et al. 2005; Templin et al. 2011) and were included to anchor inferences of population structure.
Table 1.
Populations analyzed in this study with year sampled, sample size (N), observed heterozygosity (HO), and expected heterozygosity (HE).
| Sampling location | Region | Year | GPS coordinates | N | HO | HE |
|---|---|---|---|---|---|---|
| Tubutulik River | Norton Sound | 2009 | 64.740, −161.888 | 56 | 0.248 | 0.252 |
| Anvik River | Lower Yukon R | 2007 | 62.681, −160.214 | 54 | 0.260 | 0.261 |
| Kogrukluk River | Kuskokwim R | 2007 | 60.841, −157.846 | 57 | 0.251 | 0.258 |
| Koktuli River | Bristol Bay | 2010 | 59.935, −156.427 | 56 | 0.256 | 0.259 |
| Big Salmon River | Upper Yukon R | 2007 | 61.867, −134.917 | 47 | 0.232 | 0.232 |
RAD sequencing, SNP discovery and genotyping
Restriction-site-associated DNA libraries were prepared with the restriction enzyme SbfI following the methods of Baird et al. (2008) and Everett et al. (2012) and sequenced on an Illumina HiSeq2000 at the University of Oregon Genomics Core Facility. We constructed 18 libraries for single-end sequencing (100 bp target length) containing 12–24 individuals per library and one library for paired-end sequencing (100 × 2 bp target) containing eight individuals to assemble longer sequence contigs for annotation. Pooled individuals were identified with unique 6-bp barcodes.
We used the Stacks software package, version 0.9999 (Catchen et al. 2011) and methods similar to Hohenlohe et al. (2013) to discover and genotype SNPs from the sequenced RAD tags. Quality filtering of raw reads and demultiplexing based on barcode was conducted using process_radtags. Stacks of similar sequences were then assembled in each individual with ustacks, and a catalog of loci was created with cstacks. We included only the two individuals from each population with the greatest amount of sequence data when creating our catalog to reduce the detection of false polymorphisms. Including more individuals per population would have facilitated the detection of low-frequency SNPs, but would not have added additional SNPs to the final data set because these low-frequency SNPs were filtered out in downstream analyses. Finally, we used sstacks and populations to combine the genotypes from each individual into a single Genepop formatted file.
SNP validation
Putative SNPs discovered using Stacks were filtered to remove possible sequencing errors, paralogous sequence variants (PSVs), and uninformative polymorphisms. First, we removed any putative SNP that failed to genotype in >80% of individuals. We then removed those with a minor allele frequency <0.05 in all populations. These polymorphisms are likely to be uninformative, are difficult to distinguish from sequencing errors, can distort signals of selection and drift in natural populations, and may bias tests for selection (Roesti et al. 2012). We also discarded putative SNPs that were found at RAD tag positions >87 bp because these positions contained more polymorphisms on average than the rest of the sequence (138 per bp for bp 1–87, 223 per bp for bp 88–93). This increase in putative SNPs per base pair is likely a result of sequencing errors as Illumina sequencing is more error prone toward the terminal positions of reads (Minoche et al. 2011). We kept only the putative SNP with the highest FST from each RAD tag to reduce linkage in our data set. We also used the program PLINK version 1.07 (Purcell et al. 2007) to test for linkage disequilibrium between each pair of loci. If a locus pair had an r2 value >0.8 in three of five populations, we removed the locus that was genotyped in the fewest individuals.
Paralogous sequence variants, which are abundant in salmonids as a result of an ancient whole-genome duplication event (Allendorf and Thorgaard 1984; Seeb et al. 2011), were removed from the data set when possible. PSVs are closely related sequences from different genomic locations that do not segregate as single loci and are therefore difficult to genotype accurately (Gidskehaug et al. 2011). Haploid individuals can be used to identify PSVs because PSVs will appear heterozygous when all correctly segregating loci are homozygous (Hecht et al. 2013). To screen for PSVs in our data, we genotyped 50 haploid Chinook salmon from Washington, USA, at all putative SNPs discovered above, and loci with >10% heterozygosity were removed.
We also conducted exact tests of Hardy–Weinberg equilibrium in Genepop version 4 (Rousset 2008) and removed loci that were out of equilibrium in three or more populations (P < 0.05). We then removed individuals that were missing genotypes at > 15% of the SNPs. As a final filtration step, we used ML-Relate (Kalinowski et al. 2006) to look for duplicated individuals in our data.
Paired-end assembly and BLAST annotation
We conducted a paired-end assembly with the P1 and P2 reads from each locus using Velvet (v.1.1.06, Zerbino and Birney 2008) and the methods of Etter et al. (2011) and Everett et al. (2012) to increase query lengths for BLAST annotation. Consensus sequences were then aligned to the Swiss-Prot database using the BLASTX search algorithm. Alignments with E-values of ≤10−4 were retained. If multiple alignments had E-values of ≤10−4 for the same locus, the alignment with the lowest E-value was retained.
Population structure and assignment tests
Initial analysis of population structure was conducted with an individual-based principal component analysis (PCA) implemented in the R package adegenet (Jombart 2008). The significance of each principal component was assessed by randomly permuting the data 1000 times and comparing the observed eigenvalues to values generated by conducting PCA on the permuted data. PCA revealed five nonconforming individuals in the Anvik River collection that grouped between the Big Salmon River and Anvik River clusters (Fig. 2). These five individuals were removed from further analyses as they likely represent transient fish from middle or upper Yukon River populations. After removing these individuals, we calculated pairwise FST values (Weir and Cockerham 1984) for each population and performed significance tests for genetic differentiation in Arlequin 3.5 (Excoffier and Lischer 2010) using an exact test with 10 000 permutations.
Figure 2.
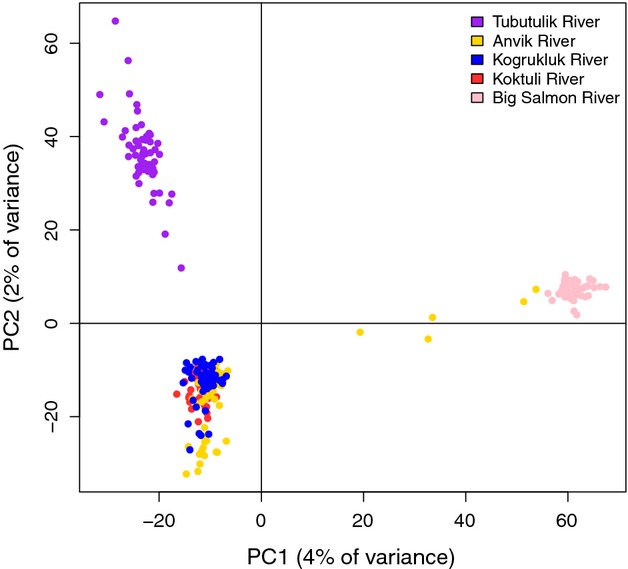
Individual-based principal component analysis for all populations and 10 944 SNPs. The five intermediate individuals from the Anvik River were removed from further analyses (see).
We conducted an analysis of molecular variance (amova) in Arlequin 3.5 to examine the variation within and among groups of genetically similar populations. The hierarchy for this analysis was chosen based on the clustering from the PCA: (i) Koktuli River, Kogrukluk River, and Anvik River, (ii) Tubutulik River, and (iii) Big Salmon River. Separate amovas were conducted for (i) the entire data set and (ii) all populations except the Big Salmon River. Finally, we calculated global and per-locus observed and expected heterozygosities for each population in GenAlEx 6.5 (Peakall and Smouse 2012).
We examined fine-scale structure in the closely related Anvik River, Kogrukluk River, and Koktuli River populations with an individual PCA including only these three populations (see above for PCA methods). This analysis was conducted separately for the 10 944 RAD SNPs and 39 of the 43 SNPs from Templin et al. (2011) that were developed for Chinook salmon from expressed sequence tags. Of the four SNPs from Templin et al. (2011) that were not genotyped, two were removed because they were essentially monomorphic in other populations from western Alaska and two were removed because they were in linkage disequilibrium with another locus (Templin et al. 2011).
Assignment power of four panels was evaluated with leave-one-out tests in GeneClass2.0 (Piry et al. 2004) to compare the influence of number of SNPs and relative divergence of SNPs on assignment accuracies. The four panels were (i) 39 SNPs from Templin et al. (2011), (ii) 39 randomly chosen SNPs from the complete data set of 10 944 RAD SNPs, (iii) the complete data set of 10 944 RAD SNPs, and (iv) the full set of RAD SNPs with the 733 outlier SNPs that were found to be under putative selection removed. We did not construct a panel with only the most divergent RAD SNPs because this approach would have led to an upward bias in the predicated accuracy of assignment for that panel (Anderson 2010). Leave-one-out tests were conducted by removing an individual from the baseline without replacement then assigning that individual back to a reference population using a Bayesian approach described in Rannala and Mountain (1997). Individuals were considered to be assigned to a population if the assignment probability to that population was higher than to any other population.
Alignment to linkage map
We aligned our filtered loci to a linkage map for Chinook salmon consisting of 3534 RAD-derived SNPs distributed across 34 linkage groups ranging in size from 27.75 to 160.23 cM (Table S1, Everett and Seeb 2014). To conduct the alignments, we used BLASTN (Altschul et al. 1990) with the following parameters: minimum alignment length of 90 bp, 95% identity, and no more than two mismatching bases. If a single locus aligned to multiple map loci, we discarded all alignments for that locus. We used relatively strict alignment parameters for this analysis because sequence alignment in tetraploid-origin salmonids can provide ambiguous results when alignment parameters are not sufficiently strict (Everett et al. 2011; Seeb et al. 2011).
Calculating Ne and Ne/N
Estimates of Ne were performed with the linkage disequilibrium method (Hill 1981; Waples 2006) updated for missing data following Peel et al. (2013). This method assumes all loci in the analysis are physically unlinked then utilizes the observed linkage disequilibrium to estimate Ne. We removed comparisons between loci on the same linkage groups to obtain estimates that were unbiased by physical linkage (Park 2011; Sved et al. 2013). Additionally, we removed all loci that were putatively under selection as suggested by Waples (2006) (see below for description of tests for loci under selection). Calculations of Ne were conducted using NeEstimator (Do et al. 2014) and R (R core development team 2011). NeEstimator was used to calculate r2 values for each locus pair with the following parameters: a minimum allele frequency cutoff of 0.02 and a random mating model. We then implemented the methods described in Waples (2006) and Peel et al. (2013) in R to obtain Ne estimates and parametric 95% confidence intervals for each population (scripts available from W. Larson upon request). We calculated Ne for three data sets: (i) all RAD SNPs that aligned to the linkage map, (ii) all RAD SNPs that aligned to the map with pairwise comparisons between markers on the same linkage group removed, and (iii) the 39 SNPs from Templin et al. (2011) that were in linkage equilibrium.
We calculated the ratio of effective size to census size (Ne/N) using Ne calculated with RAD-derived SNPs after removing physical linkage and estimates of total escapement obtained from aerial surveys (Koktuli River, Anvik River, Tubutulik River) and weir counts (Kogrukluk River, Big Salmon River). Multiple aerial surveys were used to estimate total run size for the Anvik River and Koktuli River populations, but only single aerial counts were available for the Tubutulik River population. Single aerial counts from a river near the Tubutulik River collection were approximately four times smaller than those taken from a counting tower; therefore, we multiplied the aerial count from our collection by four. We averaged the last ten years of data to obtain an approximate value of census size for each population (only last 3 years used for Koktuli River due to data availability).
Estimates of Ne for Chinook salmon populations are complicated by the fact that multiple cohorts are represented in each spawning group (Waples 1990). Single-sample estimates of Ne therefore do not precisely reflect the effective number of breeders per year or the effective number of breeders per generation, but instead represent some intermediate value. We calculated two Ne/N ratios to bracket these possible scenarios: Ne divided by the average census size (escapement) per year (Ne/N) and Ne divided by the total census size per generation (Ne/NG). Values of G for each population were obtained from the sources in Table 5 by averaging age compositions across one to 38 years of data depending on availability.
Table 5.
Estimates of effective population size (Ne) for five populations calculated with 1118 RAD-derived SNPs that were placed on the linkage map and 39 of the 43 SNPs that were in linkage equilibrium from Templin et al. (2011). Estimates with RAD SNPs are calculated using only comparisons between loci on different linkage groups (Ne linkage removed) and all comparisons (Ne all data). The ratio of effective population size to census size (Ne/N) and effective population size to census size multiplied by generation length (Ne/NG) for each population is also reported (G is generation length and N is an approximate value of yearly escapement for each population, see methods). The Ne used for these calculations is Ne linkage removed (column 2). We did not calculate Ne/N or Ne/NG for the Bristol Bay and upper Yukon populations because confidence intervals included infinity, suggesting our point estimates may not be completely representative.
| Population | Ne linkage removed | Ne all data | Ne 39 SNPs | G | N | Ne/N | Ne/NG | Source of N | Source of G |
|---|---|---|---|---|---|---|---|---|---|
| Tubutulik River | 1909 (1295–3602) | 808 (674–1009) | Inf (174–Inf) | 5.43 | 3100 | 0.62 | 0.11 | Banducci et al. (2007) | Lingnau (1996) |
| Anvik River | 516 (451–604) | 505 (443–586) | 209 (65-Inf) | 5.48 | 1700 | 0.30 | 0.06 | Howard et al. (2009) | Sandone (1995) |
| Kogrukluk River | 2026 (1375–3825) | 1723 (1233–2842) | Inf (134–Inf) | 5.20 | 12 000 | 0.17 | 0.03 | Williams and Shelden (2011) | Howard et al. (2009) |
| Koktuli River | Inf (6055-Inf) | 26 071 (3733-Inf) | Inf (Inf-Inf) | 5.13 | 6000 | N/A | N/A | Woody (2012) | Howard et al. (2009) |
| Big Salmon River | 13 101 (1505-Inf) | 4243 (1806-Inf) | 520 (70-Inf) | 5.65 | 5000 | N/A | N/A | Mercer and Wilson (2011) | Howard et al. (2009) |
Detection of loci under putative selection
We identified putative loci under selection with Arlequin 3.5. This program uses coalescent simulations to create a null distribution of F-statistics then generates P-values for each locus based on this distribution and observed heterozygosities across loci (Excoffier et al. 2009). A hierarchical island model was selected to reduce false positives introduced due to underlying population structure (Excoffier et al. 2009). The population hierarchy was the same as in the amova. Settings for the analysis were 20 000 simulations, 10 simulated groups, and 100 demes per group. Loci that fell above the 95% quantile of the FST distribution were considered candidates for directional selection.
Detection of candidate genomic regions under selection
We used a linkage map in conjunction with a sliding window analysis to identify highly divergent regions of the genome that may be under selection (c.f., Bourret et al. 2013). This analysis was conducted with a sliding window approach that compares the mean pairwise FST of a small (5 cM) genomic region to a null distribution created by bootstrapping over the complete data set (Hohenlohe et al. 2010; Bourret et al. 2013). For each window, we sampled N FST values with replacement from the entire data set where N was the number of SNPs in the window. This resampling routine was repeated 1000 times to generate a null distribution. Windows with mean FST values above the 95% quantile of the null distribution were candidates for directional selection. If a window mean was above 90% after 1000 replicates, we increased the number of replicates to 5000 to improve accuracy in the tails of the null distribution. We chose a sliding window size of 5 cM and frame shift value of 1 cM. We also required at least two SNPs to be present in a window to conduct the above test. After testing multiple window sizes, we found that a 5-cM window provided sufficient resolution for detecting divergent regions without introducing excessive variance. This value was also used by Bourret et al. (2013) for linkage groups with similar numbers of markers to ours. We conducted this analysis for all pairwise population comparisons.
Results
Sequencing, SNP discovery and filtration
We obtained RAD data from 289 individuals, and the number of sequences obtained for each individual ranged from 1 622 400 to 8 707 337 with an average of 3 796 368 (excluding low-quality individuals, see below). Alignments using Stacks revealed 42 351 putative SNPs. Removing putative SNPs that were genotyped in <80% of individuals eliminated more than half of these, leaving 20 296. After removing polymorphisms in bp 87–94 of each RAD tag, removing all but one putative SNP from each tag, and removing SNPs with minor allele frequency <0.05, 12 585 SNPs remained. Screens for paralogous sequence variants revealed 845 loci that were potentially duplicated; these loci were eliminated. Significant deviations from Hardy–Weinberg equilibrium were observed in 397 SNPs, and these loci were also removed. Significant linkage disequilibrium in three or more populations was found for 399 SNPs, and one SNP from each pair was removed. The final filtered data set consisted of 10 944 SNPs. We removed 17 individuals that were genotyped in <85% of SNPs, seven from the Kogrukluk River, four from the Anvik River, and six from the Big Salmon River (adjusted sample sizes in Table 1). Relatedness analysis revealed two pairs of duplicated individuals (R > 0.9) from the Anvik River population, and one individual from each pair was removed. The final filtered data set consisted of 270 individuals genotyped at 10 944 SNPs. Summary statistics for each locus are available in Table S1, and histograms of overall and pairwise FST for each locus are in Fig. S1.
Paired-end assembly and BLAST annotation
Paired-end assemblies produced 11 666 contigs with an average length of 268 bp (minimum 150 bp, maximum 565 bp). BLAST annotation of these contigs yielded significant hits for 1576 (14%) of 10 944 SNPs (Table S2). Of these hits, over one-third aligned to transposable elements. Other common functional groups included DNA polymerases and transmembrane proteins.
Population structure
Principal component analysis revealed that the Big Salmon River and Tubutulik River populations formed completely separate clusters, while the Koktuli River, Kogrukluk River, and Anvik River populations essentially formed a single cluster (Fig. 2). The overall FST of the full data set was 0.041, and pairwise FST values ranged from 0.003 for the Koktuli River–Kogrukluk River comparison to 0.098 for the Big Salmon River–Tubutulik River comparison (Table 2). Genetic differentiation between all population comparisons was highly significant (P < 0.001). The results of these significance tests should, however, be interpreted with extreme caution due to the large number of loci, which may overestimate precision.
Table 2.
Pairwise FST values calculated using 10 944 SNPs and number of genomic regions that were under putative selection (in parentheses). All pairwise comparisons are significantly differentiated (P < 0.01).
| Tubutulik River | Anvik River | Kogrukluk River | Koktuli River | |
|---|---|---|---|---|
| Anvik River | 0.030 (20) | |||
| Kogrukluk River | 0.027 (20) | 0.005 (20) | ||
| Koktuli River | 0.028 (20) | 0.006 (23) | 0.003 (20) | |
| Big Salmon River | 0.098 (24) | 0.075 (25) | 0.075 (21) | 0.077 (25) |
We conducted hierarchical amova for the entire data set and for a data set without the Big Salmon River population (Table 3). Both analyses displayed much larger variation among groups than within groups. Levels of observed heterozygosity across populations ranged from 0.232 for the Big Salmon River to 0.260 for the Anvik River (Table 1).
Table 3.
Results from two amovas with 10 944 SNPs.
| Source of variation | d.f. | Percentage of variation |
|---|---|---|
| All populations | ||
| Among groups | 2 | 5.26 |
| Among populations within groups | 2 | 0.45 |
| Within populations | 529 | 94.32 |
| Big Salmon River excluded | ||
| Among groups | 1 | 2.41 |
| Among populations within groups | 2 | 0.43 |
| Within populations | 436 | 97.18 |
When the Koktuli River, Kogrukluk River, and Anvik River populations were analyzed separately with 10 944 SNPs, all populations generally formed discrete clusters, but some overlap was present between the Koktuli River and Kogrukluk River populations (Fig. 3A). Additionally, populations from the Anvik River and Kogrukluk River each contained a subset of 10–20 individuals that fell outside the main cluster. When PCA was conducted with the 41 SNPs from Templin et al. (2011), no clustering pattern was apparent (Fig. 3B).
Figure 3.
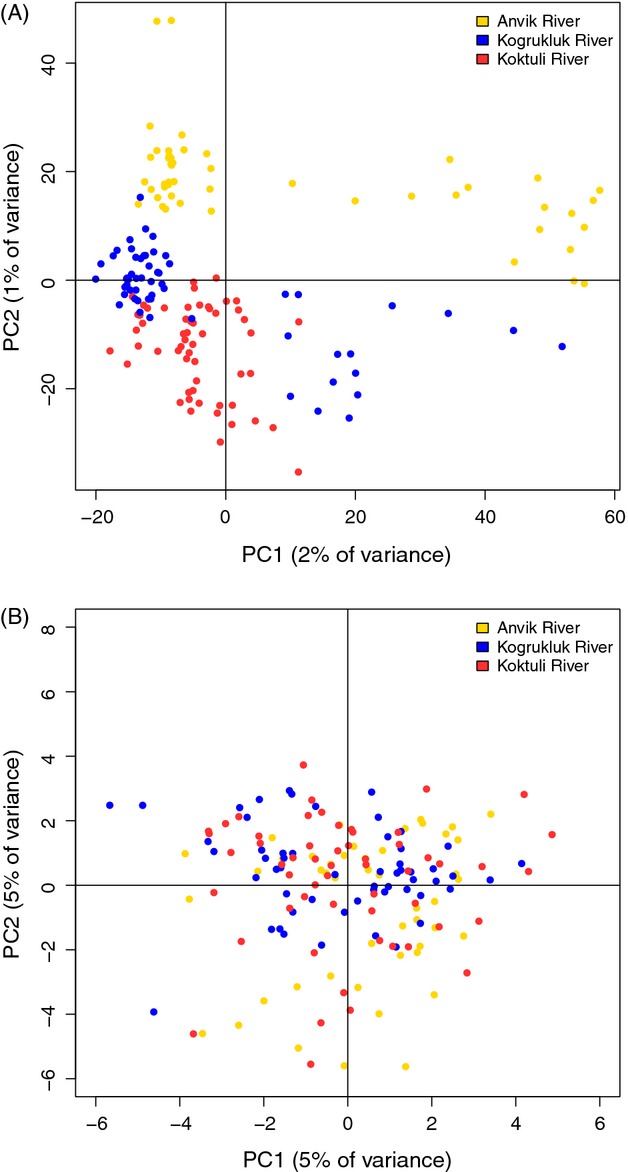
Individual-based principal component analysis for the Anvik River, Kogrukluk River, and Koktuli River populations using (A) 10 944 RAD SNPs and (B) 39 SNPs from Templin et al. (2011).
The relatively small amount of variation (1–5%) explained by the first and second principal components (PCs) in our PCAs (Figs 2 and 3) can be attributed to the large number of axes used. Each PCA contained as many axes as individuals plotted, so PCA using all populations contained 270 axes, and the PCA with three populations contained 163. PCs one and two in both PCAs each explained more than three times the variation of the average axis and explained significantly more variation than would be expected if no real correlation existed (P < 0.001), but because of the large number of axes, the actual proportion of variation explained was small.
Assignment accuracy was much higher using >10 000 SNPs (≥ 89% assignment to correct population) compared to 39 SNPs (∼50% assignment to correct population, Table 4). Panels containing close to the same number of SNPs generally performed similarly, but the 39 SNPs from Templin et al. (2011) did perform slightly better than the 39 randomly chosen RAD SNPs, and the panel containing all 10 944 RAD SNPs performed slightly better than the panel with the 733 outlier SNPs removed (Table 4).
Table 4.
Results of leave-one-out tests for individual assignment with four SNP panels. Panels are: (1) 39 EST: 39 SNPs previously developed for Chinook salmon from expressed sequence tags (ESTs, Templin et al. 2011), (2) 39 RAD: 39 randomly chosen SNPs from the complete data set of 10 944 RAD SNPs, (3) 10 944 RAD: the complete data set of RAD SNPs, and (4) 10 211 RAD no outliers: the full set of RAD SNPs with the 733 outlier SNPs that were found to be under putative selection removed. Individuals were considered to be correctly assigned if the assignment probability to population of origin was higher than to any other population. See Table S3 for assignment probabilities for each individual.
| Regions | % Correct assignment |
|||
|---|---|---|---|---|
| 39 EST | 39 RAD | 10 944 RAD | 10 211 RAD no outliers | |
| Tubutulik River | 67 | 65 | 100 | 100 |
| Anvik River | 46 | 30 | 91 | 89 |
| Kogrukluk River | 34 | 30 | 93 | 93 |
| Koktuli River | 29 | 30 | 98 | 95 |
| Big Salmon River | 96 | 87 | 100 | 100 |
Alignment to linkage map
Of the 10 944 filtered loci, 1156 were successfully placed on the linkage map (33% of loci on the map successfully aligned to one of the 10 944 loci discovered in populations from western Alaska, see Table S1 for map location of successful alignments). This proportion may seem small, but it is important to note that the map was constructed using a single Chinook salmon from Washington State. Chinook salmon from Washington State are substantially diverged from populations in western Alaska (Templin et al. 2011), therefore, it is likely that many RAD tags did not contain loci that were polymorphic in both the mapping cross and our study populations and were not useful for our analyses. Additionally, because only one individual was used for the mapping cross, our alignments were limited to the RAD tags containing SNPs that segregated in the mapped individual.
Demographic estimates
Estimates of Ne with the RAD-derived SNPs were highly variable across populations, ranging from close to 500 in the Anvik River to infinity for the Koktuli River (Table 5). These estimates were calculated using SNPs that were successfully aligned to the linkage map, providing over 500 000 pairwise comparisons between loci. Pairwise comparisons between SNPs located on the same linkage group represented about 20 000 of the 500 000 comparisons (6%). These 20 000 comparisons were removed to estimate Ne between physically unlinked loci. Estimates of Ne were consistently smaller for the data set that included all comparisons (Table 5). This downward bias was not uniform, however, as estimates from Norton Sound appeared to be more affected by linkage than estimates for the other populations.
Estimates of Ne with the 39 SNPs from Templin et al. (2011) ranged from 209 for the Anvik River to infinity for the Koktuli River, Kogrukluk River, and Tubutulik River populations. Confidence intervals for each estimate using 39 SNPs included infinity and were larger than confidence intervals around estimates from the RAD-derived SNPs.
Estimates of Ne/N and Ne/NG were extremely variable, ranging from 0.17 and 0.03 for the Kogrukluk River population to 0.59 and 0.11 for the Tubutulik River population (Table 5). We did not calculate Ne/N or Ne/NG for the Koktuli River or Big Salmon River populations because the confidence intervals around Ne included infinity, suggesting our point estimates of Ne may not be completely representative.
Loci and genomic regions under putative selection
Outlier tests in Arlequin revealed 733 loci (6.7%) that were significant outliers at the 5% level and 178 (1.6%) that were significant at the 1% level. BLAST annotation of the outliers at the 5% level revealed 96 significant hits (13% success rate). Transposable elements represented over one-third of the significant hits which is consistent with the pattern from the complete data set.
The number of genomic regions under putative selection for each population pair ranged from 20 to 25 and generally increased when the Big Salmon River population was included (Fig. 4, Table 2). Overall, these regions appeared to be scattered randomly throughout the genome and were often significant in only one or two population comparisons. Despite this pattern, three genomic regions on separate linkage groups (LG) were candidates for selection in more than half of the population comparisons (Fig. 4). These regions are LG2 at 70–78 cM, LG4 at 2–8 cM, and LG21 at 7–12 cM.
Figure 4.
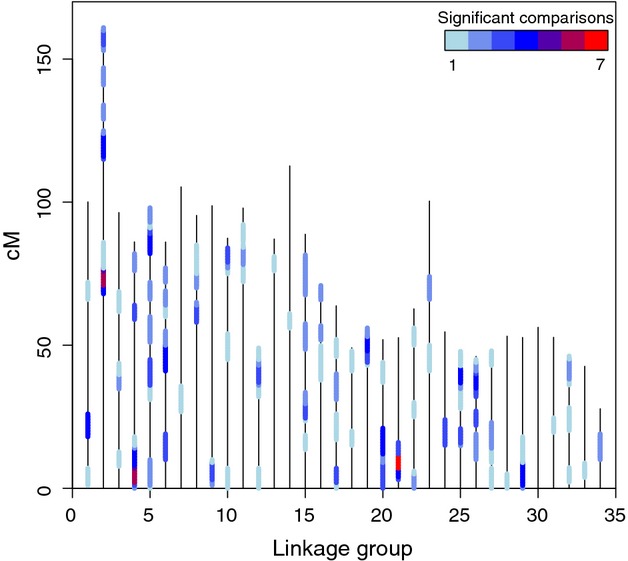
Regions of the genome under putative selection as inferred by pairwise FST across all population pairs. Each vertical line represents a linkage group, and the length of the line is proportional to the size of the linkage group in cM. Shaded areas indicate regions which are significantly diverged in at least one population pair indicating putative selection. The color of the shading corresponds to the number of significant pairwise population comparisons with red and purple indicating over half of the population pairs are divergent in the given region.
Discussion
We used RAD sequencing to characterize the genetic structure, genomic divergence, and demography of five populations of Chinook salmon from western Alaska. Patterns of genetic differentiation were similar to but more identifiable than in past studies (Gharrett et al. 1987; Templin et al. 2011). Estimates of population Ne ranged from 516 to infinity and appeared to be biased downward when loci that were physically linked were not removed. Regions of putative adaptive divergence appeared to be randomly distributed across the genome with few shared areas of high divergence across populations, but we did find three genomic regions that displayed high divergence in multiple populations. Using genomic data, we were able to conduct individual assignment in populations where it was previously unfeasible, discover genomic regions under putative selection, and estimate Ne in populations with >1000 individuals. Our approach therefore represents a significant improvement over previous studies employing fewer markers and no linkage map.
Population structure
The largest genetic differentiation between populations in our data set existed between the Big Salmon River from the upper Yukon River and all other coastal populations. Chinook salmon from the upper Yukon River are thought to have genetically diverged from coastal populations after being isolated during the last glacial maximum (Olsen et al. 2011). Our results support this hypothesis and are consistent with those based on allozymes, microsatellites, and SNPs (Gharrett et al. 1987; Olsen et al. 2010; Templin et al. 2011).
We also found high levels of divergence between the Tubutulik River in Norton Sound and all other populations. This divergence was likely facilitated by the Nulato Hills, a small mountain range that separates the tributaries of Norton Sound from those of the Yukon River (Fig. 1), but could have also been influenced by environmental characteristics such as precipitation (Olsen et al. 2011).
Populations from the lower Yukon, Kuskokwim, and Bristol Bay regions (Anvik River, Kogrukluk River, and Koktuli River) were least divergent, displaying pairwise FST values < 0.01 for all population comparisons. The relatively small divergence we observed is consistent with other salmonids in the region (Olsen et al. 2011; Garvin et al. 2013) and is somewhat expected given the surrounding environment. Western Alaska is characterized by moisture-laden tundra and dynamic rivers that frequently change paths. When such stream captures occur, gene flow is facilitated between populations that were previously isolated. It is therefore likely that substantial historic and possibly continuing low-level gene flow has largely restricted genetic differentiation in this region (Seeb and Crane 1999).
Nevertheless, we found genetic structure among the Anvik River, Kogrukluk River, and Koktuli River populations using both individual-based clustering methods and assignment tests. The Anvik River population displayed the highest levels of divergence, forming a completely isolated cluster. This population may have diverged more quickly as a reflection of its relatively small estimated census and effective sizes (N = 1700, Ne=516). The Kogrukluk River and Koktuli River populations, on the other hand, are at least four times larger than the Anvik River population and may not have been affected as substantially by genetic drift. Individuals that did not fall within major clusters were found in the Kogrukluk River and Anvik River populations. These individuals may represent evidence of gene flow from genetically diverged upriver populations, but could have also resulted from within population variation. Individual-based PCA using 39 SNPs from Templin et al. (2011) did not resolve the population structure that was observed with the RAD data and displayed no apparent clustering pattern. These results emphasize the utility of genome-wide data when attempting to elucidate patterns of population differentiation.
Assignment accuracies with both panels containing over 10 000 SNPs were ≥89% for all populations, while assignment accuracies with the panels containing 39 SNPs were close to 50% on average per population. Additionally, the inclusion of outlier loci only slightly improved assignment accuracy. These results indicate that a large number of neutral SNPs were sufficient to achieve precise assignment and that, for our analysis, the number of SNPs used seemed to have more influence on assignment accuracies than the resolution of those SNPs. Unfortunately, we were unable to evaluate the effectiveness of small panels of high-resolution SNPs compared to large panels of neutral SNPs because this type of analysis requires the use of a training and holdout data set (Anderson 2010), which was not feasible with the sample sizes in our study.
The patterns of population divergence observed here are consistent with previous studies, suggesting structuring of Chinook salmon populations on regional scales (Templin et al. 2011). Despite this pattern, sampling additional populations from each region would likely improve estimates of population divergence and assignment accuracy.
Demography
Estimating and interpreting Ne in salmon populations using single samples can be difficult because multiple cohorts are often present (Waples 1990). Ne estimates therefore reflect a value somewhere between the effective number of breeders in a given year and the effective number of breeders per generation. We divided Ne by the census size (escapement) per year (N) and the census size per generation (NG) to account for both of these possibilities when comparing Ne to census size. The Ne/N and Ne/NG ratios were highly variable across our populations, indicating that effective and census size are not well correlated in our study system.
A meta-analysis of 251 estimates of Ne/N found a median value of 0.14 and also showed that Ne/N ratios are generally larger in smaller populations (Palstra and Ruzzante 2008). Larger Ne/N ratios in smaller populations were also observed in our data. For example, the Anvik River had a census size of 1700 and Ne/N of 0.30, while the Kogrukluk River had a census size of 12 000 and an Ne/N of 0.17. This trend, however, was not consistent in the Tubutulik River population which had a census size of 3100 and Ne/N ratio of 0.62.
The large Ne/N ratio in the Tubutulik River population may have been due to gene flow from proximate populations which can introduce additional genetic diversity and inflate estimates of Ne (Palstra and Ruzzante 2011). The Tubutulik River is a small river in Norton Bay, which contains at least five additional salmon-producing rivers. Gene flow among subpopulations in this region may be quite common and could therefore have resulted in the larger than expected Ne/N estimates that we observed. Gene flow from proximate populations may also be inflating Ne estimates from the Koktuli River and the Big Salmon River as both of these collections have census sizes close to 5000, but Ne estimates with confidence intervals including infinity. It is important to note that estimates of census size are approximate and may not be completely representative. Nevertheless, our results suggest that census size is not an adequate predictor of effective size, especially in populations that may belong to a larger metapopulation.
Removing comparisons between loci on the same linkage group appeared to have a nonuniform effect on estimates of Ne with larger estimates being more affected by removing linkage. For example, the estimate of Ne for the Anvik River population, the smallest population in the study, only changed by 10 when linked comparisons were removed, whereas the estimate for the Big Salmon River changed by almost 9000. This relatively small bias for small populations was also found by Sved et al. (2013) and is expected given that in small populations, the signal of linkage disequilibrium due to genetic drift should be large compared to the signal due to physical linkage.
It also appears that Ne estimates for populations of similar size can be affected nonuniformly by physically linked loci. Specifically, estimates of Ne for the Tubutulik River displayed a larger downward bias when physically linked loci were included than estimates for the Kogrukluk River, even though the effective sizes for these populations were similar with unlinked loci. The nonuniform effects we observed when removing physically linked loci may be due to historic signals of Ne that have been preserved due to linkage (Hill 1981; Tenesa et al. 2007).
Estimating Ne in large populations (Ne > 1000) with 10–100 genetic markers is extremely challenging due to the small amount of linkage disequilibrium caused by drift (Waples and Do 2010), but, with thousands of markers, accurately characterizing the signal of drift and estimating Ne may be feasible (Allendorf et al. 2010). Estimates of Ne from our study were infinite for three of five populations with 39 SNPs, but only infinite for one population with 1118 SNPs. Additionally, all estimates with 39 SNPs, but only two estimates with 1118 SNPs, displayed confidence intervals including infinity, and confidence intervals were consistently smaller with 1118 SNPs. Our results indicate that genomic data can improve the accuracy of Ne estimates in large populations, aiding management in many species.
Putative adaptive divergence
We identified 6.7% of SNPs in our data set as outliers, consistent with past studies identifying 5–10% of markers as candidates for directional selection (Nosil et al. 2009). In general, patterns of divergence observed from our outliers were similar to patterns obtained using neutral markers. BLAST annotation of outlier loci revealed a high frequency of transposable elements, similar to the overall data set. These transposable elements are quite common in teleost fish and are generally assumed to behave as neutral markers (Radice et al. 1994) although some evidence suggests that they can be adaptively important (Casacuberta and González 2013).
Tests for genomic regions under putative selection revealed that these regions appeared to be spread randomly across the genome with few common ‘hot spots’ among populations. This pattern is consistent with Bourret et al. (2013), who found a similar distribution across the Atlantic salmon genome. Despite the apparent randomness, three regions were differentiated in more than five of ten population comparisons. These highly divergent regions may represent adaptively significant areas of the Chinook salmon genome and should be targets of future research. Population comparisons that included the Big Salmon River generally displayed the largest number of divergent regions. Although these regions likely represent adaptively significant areas of the genome, it is possible that at least a portion of them resulted from genetic drift as a result of isolation during the last glacial maximum (Olsen et al. 2011). Research aimed at disentangling signatures of drift from those of natural selection should therefore focus on systems with low neutral divergence across heterogeneous environments (Nielsen et al. 2009).
Management and conservation implications for western Alaska
Returns of Chinook salmon to western Alaska have fallen dramatically over the last decade compared to their long-term average (ADF&G 2013). This precipitous decline has prompted multiple fisheries closures causing extensive economic hardship and threatening subsistence catches for natives of the western Alaska region. Some of these closures stem from the inability of fisheries managers to differentiate a late run that is of normal size from a small run that is returning at a normal date. One way that managers can differentiate these two scenarios is with stock composition estimates facilitated by panels of high-throughput SNPs. Specifically, stock composition estimates from mixed-stock fisheries and test fisheries on the high seas can be used to monitor the contribution of each stock in real time, helping to inform the need for fisheries closures and generally improving fisheries management (Seeb et al. 2000; Smith et al. 2005; Dann et al. 2013). Despite this potential utility, tools for genetic stock identification in marine waters of western Alaska have been severely hampered by lack of genetic divergence among regions (Templin et al. 2011). Our data provide the first evidence that assignment to region of origin is feasible in western Alaska despite low levels of divergence. Although it is not currently possible to screen 10 000 loci on thousands of individuals, a subset of our RAD loci that show high levels of divergence can be used to construct a high-throughput SNP panel to differentiate stocks in this region (c.f., Ackerman et al. 2011).
This high-throughput SNP panel could also be used to investigate the migration and distribution patterns of Chinook salmon on the high seas (e.g., Murphy et al. 2009; Larson et al. 2013). Patterns of productivity in the marine environment are thought to be a major cause of the fluctuations in abundance observed in Chinook salmon from western Alaska (Farley et al. 2005). Despite this variability, most stock assessment models assume a constant marine mortality rate across all stocks. The ability to monitor stock-specific abundance on the high seas could provide important information for stock assessment models which is currently unavailable. Additionally, stock composition estimates could be used to monitor the impact of Chinook salmon interception in the Bering Sea pollock fishery; this fishery has captured as many as 100 000 Chinook salmon in a single year (Gisclair 2009). In summary, our results represent the first step toward a panel of high-throughput SNPs that can be used to conduct genetic stock identification and improve stock-specific management in the western Alaska region.
Applicability to other study systems
Our study demonstrates the utility of genomic data when attempting to differentiate closely related populations and estimate demographic parameters. The methods we employed will be especially applicable in marine species, which are often characterized by low genetic differentiation and large population sizes (Waples 1998; Nielsen and Kenchington 2001). For example, individual-based analyses with thousands of markers can provide extremely accurate estimates of individual genetic variation. Additionally, this method can shed light on patterns of connectivity by identifying migrants and admixture within populations.
Estimates of Ne in large marine populations can also be improved using approaches similar to ours (e.g., Gruenthal et al. 2014). Dense linkage maps have already been developed for many marine species including cod (Hubert et al. 2010), flounder (Castano-Sanchez et al. 2010), and shrimp (Du et al. 2010). By combining these linkage maps with genomic data, it may be possible to accurately estimate Ne and Ne/N in many economically important marine species. These estimates can provide important insights into the adaptive potential of marine populations and can be used to inform management (Hare et al. 2011).
Summary
Our results demonstrated fine-scale structure between regions in western Alaska. This structure allowed us to assign fish back to their region of origin with greater than 90% accuracy, representing a significant improvement over past studies. We also estimated Ne for each population using a novel method for nonmodel organisms. Estimates were generally large and provided some evidence that metapopulation dynamics influence demography in this region. Investigation of loci and genomic regions under putative selection found three potential regions of adaptive divergence. The methods described in our study will be particularly applicable to marine species or any species where large population size and shallow structure are common.
Acknowledgments
We thank the Alaska Department of Fish and Game (ADFG), especially Nick DeCovich and Andrew Barclay, for providing the samples for this project. We also thank Carita Pascal for her excellent laboratory assistance. Additionally, we thank Fred Allendorf, Fred Utter, Kristen Gruenthal, Morten Limborg, and Marissa Jones for their editorial comments. Robin Waples was instrumental in developing the method to estimate effective size. This research was partially funded by the Alaska Sustainable Salmon Fund under Study # 44515 from NOAA, US Department of Commerce, administered by the ADFG. The statements, findings, conclusions, and recommendations are those of the authors and do not necessarily reflect the views of the NOAA, the U.S. Department of Commerce, or the ADFG. Funding was also provided by a grant from the Gordon and Betty Moore Foundation and the H. Mason Keeler Endowment for Excellence. WAL was supported by a National Science Foundation Graduate Research Fellowship (Grant # DGE-0718124).
Data archiving statement
Data for this study are available from the Dryad Digital Repository: http://dx.doi.org/10.5061/dryad.rs4v1. Illumina RAD-tag sequences have been submitted to the NCBI SRA database (accession numbers available upon request).
Supporting Information
Additional Supporting Information may be found in the online version of this article:
Histograms of locus-specific overall FST and pairwise FST for each population comparison.
Summary statistics for all 10 944 loci.
BLAST results for all 10 944 loci.
Assignment probabilites to the three most likely populations for each individual and each SNP panel tested.
Literature cited
- Ackerman MW, Habicht C, Seeb LW. Single-nucleotide polymorphisms (SNPs) under diversifying selection provide increased accuracy and precision in mixed-stock analyses of sockeye salmon from the Copper River, Alaska. Transactions of the American Fisheries Society. 2011;140:865–881. [Google Scholar]
- ADF&G. 2013. Chinook salmon stock assessment and research plan [online]. Alaska Department of Fish and Game, Special Publication No. 13-01. Available from http://www.adfg.alaska.gov/static/home/news/hottopics/pdfs/chinook_research_plan.pdf(accessed on 7 March 2013)
- Allendorf F, Thorgaard GH. Polyploidy and the evolution of salmonid fishes. In: Turner BJ, editor. The Evolutionary Genetics of Fishes. New York: Plenum Press; 1984. pp. 1–53. [Google Scholar]
- Allendorf FW, Hohenlohe PA, Luikart G. Genomics and the future of conservation genetics. Nature Reviews Genetics. 2010;11:697–709. doi: 10.1038/nrg2844. [DOI] [PubMed] [Google Scholar]
- Altschul SF, Gish W, Miller W, Myers EW, Lipman DJ. Basic local alignment search tool. Journal of Molecular Biology. 1990;215:403–410. doi: 10.1016/S0022-2836(05)80360-2. [DOI] [PubMed] [Google Scholar]
- Anderson EC. Assessing the power of informative subsets of loci for population assignment: standard methods are upwardly biased. Molecular Ecology Resources. 2010;10:701–710. doi: 10.1111/j.1755-0998.2010.02846.x. [DOI] [PubMed] [Google Scholar]
- Angeloni F, Wagemaker N, Vergeer P, Ouborg J. Genomic toolboxes for conservation biologists. Evolutionary Applications. 2012;5:130–143. doi: 10.1111/j.1752-4571.2011.00217.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Avise JC. Perspective: conservation genetics enters the genomics era. Conservation Genetics. 2010;11:665–669. [Google Scholar]
- Baird NA, Etter PD, Atwood TS, Currey MC, Shiver AL, Lewis ZA, Selker EU, et al. Rapid SNP discovery and genetic mapping using sequenced RAD markers. PLoS ONE. 2008;3:e3376. doi: 10.1371/journal.pone.0003376. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Banducci A, Kohler T, Soong J, Menard J. 2007. 2005 Annual management report for Norton Sound, Port Clarence, and Kotzebue [online]. Alaska Department of Fish and Game, Fishery Management Report No. 07-32. http://www.adfg.alaska.gov/FedAidPDFs/fmr07-32.pdf(accessed on 30 January 2013)
- Baxter SW, Davey JW, Johnston JS, Shelton AM, Heckel DG, Jiggins CD, Blaxter ML. Linkage mapping and comparative genomics using next-generation RAD sequencing of a non-model organism. PLoS ONE. 2011;6:e19315. doi: 10.1371/journal.pone.0019315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bourret V, Kent MP, Primmer CR, Vasemägi A, Karlsson S, Hindar K, McGinnity P, et al. SNP-array reveals genome-wide patterns of geographical and potential adaptive divergence across the natural range of Atlantic salmon (Salmo salar. Molecular Ecology. 2013;22:532–551. doi: 10.1111/mec.12003. [DOI] [PubMed] [Google Scholar]
- Bradbury IR, Hubert S, Higgins B, Bowman S, Borza T, Paterson IG, Snelgrove PVR, et al. Genomic islands of divergence and their consequences for the resolution of spatial structure in an exploited marine fish. Evolutionary Applications. 2013;6:450–461. doi: 10.1111/eva.12026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Casacuberta E, González J. The impact of transposable elements in environmental adaptation. Molecular Ecology. 2013;22:1503–1517. doi: 10.1111/mec.12170. [DOI] [PubMed] [Google Scholar]
- Castano-Sanchez C, Fuji K, Ozaki A, Hasegawa O, Sakamoto T, Morishima K, Nakayama I, et al. A second generation genetic linkage map of Japanese flounder (Paralichthys olivaceus. BMC Genomics. 2010;11:554. doi: 10.1186/1471-2164-11-554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Catchen JM, Amores AH, Cresko PW, Postlethwait JH. Stacks: building and genotyping loci de novo from short-read sequences. G3 Genes Genomes Genetics. 2011;1:171–182. doi: 10.1534/g3.111.000240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dann TH, Habicht C, Baker TT, Seeb JE. Exploiting genetic diversity to balance conservation and harvest of migratory salmon. Canadian Journal of Fisheries and Aquatic Sciences. 2013;70:785–793. [Google Scholar]
- Do C, Waples RS, Peel D, Macbeth GM, Tillett BJ, Ovenden JR. NeEstimator v2.0: re-implementation of software for the estimation of contemporary effective population size (Ne) from genetic data. Molecular Ecology Resources. 2014;41:209–214. doi: 10.1111/1755-0998.12157. [DOI] [PubMed] [Google Scholar]
- Du ZQ, Ciobanu DC, Onteru SK, Gorbach D, Mileham AJ, Jaramillo G, Rothschild MF. A gene-based SNP linkage map for Pacific white shrimp, Litopenaeus vannamei. Animal Genetics. 2010;41:286–294. doi: 10.1111/j.1365-2052.2009.02002.x. [DOI] [PubMed] [Google Scholar]
- Etter PD, Preston JL, Bassham S, Cresko WA, Johnson EA. Local de novo assembly of RAD paired-end contigs using short sequencing reads. PLoS ONE. 2011;6:e18561. doi: 10.1371/journal.pone.0018561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Everett MV, Grau ED, Seeb JE. Short reads and nonmodel species: exploring the complexities of next-generation sequence assembly and SNP discovery in the absence of a reference genome. Molecular Ecology Resources. 2011;11:93–108. doi: 10.1111/j.1755-0998.2010.02969.x. [DOI] [PubMed] [Google Scholar]
- Everett MV, Miller MR, Seeb JE. Meiotic maps of sockeye salmon derived from massively parallel DNA sequencing. BMC Genomics. 2012;13:521. doi: 10.1186/1471-2164-13-521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Everett MV, Seeb JE. Detection and mapping of QTL for temperature tolerance and body size in Chinook salmon (Oncorhynchus tshawytscha) using genotyping by sequencing. Evolutionary Applications. 2014 doi: 10.1111/eva.12147. DOI: 10.1111/eva.12147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Excoffier L, Lischer HEL. Arlequin suite ver 3.5: a new series of programs to perform population genetics analyses under Linux and Windows. Molecular Ecology Resources. 2010;10:564–567. doi: 10.1111/j.1755-0998.2010.02847.x. [DOI] [PubMed] [Google Scholar]
- Excoffier L, Hofer T, Foll M. Detecting loci under selection in a hierarchically structured population. Heredity. 2009;103:285–298. doi: 10.1038/hdy.2009.74. [DOI] [PubMed] [Google Scholar]
- Farley EV, Murphy JM, Wing BW, Moss JH, Middleton A. Distribution, migration pathways, and size of western Alaska juvenile salmon along the eastern Bering Sea Shelf. Alaska Fishery Research Bulletin. 2005;11:15–26. [Google Scholar]
- Frankham R. Genetics and extinction. Biological Conservation. 2005;126:131–140. [Google Scholar]
- Funk WC, McKay JK, Hohenlohe PA, Allendorf FW. Harnessing genomics for delineating conservation units. Trends in Ecology & Evolution. 2012;27:489–496. doi: 10.1016/j.tree.2012.05.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gagnaire P-A, Normandeau E, Pavey SA, Bernatchez L. Mapping phenotypic, expression and transmission ratio distortion QTL using RAD markers in the Lake Whitefish (Coregonus clupeaformis. Molecular Ecology. 2013;22:3036–3048. doi: 10.1111/mec.12127. [DOI] [PubMed] [Google Scholar]
- Garvin MR, Kondzela CM, Martin P, Finney B, Guyon JR, Templin WD, Gilk-Baumer S, et al. Recent physical connections may explain weak genetic structure in western Alaskan chum salmon (Oncorhynchus keta) populations. Ecology and Evolution. 2013;3:2362–2377. doi: 10.1002/ece3.628. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gharrett AJ, Shirley SM, Tromble GR. Genetic-relationships among populations of Alaskan Chinook salmon (Oncorhynchus tshawytscha. Canadian Journal of Fisheries and Aquatic Sciences. 1987;44:765–774. [Google Scholar]
- Gidskehaug L, Kent M, Hayes BJ, Lien S. Genotype calling and mapping of multisite variants using an Atlantic salmon iSelect SNP array. Bioinformatics. 2011;27:303–310. doi: 10.1093/bioinformatics/btq673. [DOI] [PubMed] [Google Scholar]
- Gisclair BR. Salmon bycatch management in the Bering Sea walleye pollock fishery: threats and opportunities for western Alaska. American Fisheries Society Symposium. 2009;70:799–816. [Google Scholar]
- Gruenthal KM, Witting DA, Ford T, Neuman MJ, Williams JP, Pondella DJ, Bird A, et al. Development and application of genomic tools to the restoration of green abalone in southern California. Conservation Genetics. 2014;15:109–121. [Google Scholar]
- Hare MP, Nunney L, Schwartz MK, Ruzzante DE, Burford M, Waples RS, Ruegg K, et al. Understanding and estimating effective population size for practical application in marine species management. Conservation Biology. 2011;25:438–449. doi: 10.1111/j.1523-1739.2010.01637.x. [DOI] [PubMed] [Google Scholar]
- Hecht BC, Campbell NR, Holecek DE, Narum SR. Genome-wide association reveals genetic basis for the propensity to migrate in wild populations of rainbow and steelhead trout. Molecular Ecology. 2013;22:3061–3076. doi: 10.1111/mec.12082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hemmer-Hansen J, Nielsen EE, Therkildsen NO, Taylor MI, Ogden R, Geffen AJ, Bekkevold D, et al. A genomic island linked to ecotype divergence in Atlantic cod. Molecular Ecology. 2013;22:2653–2667. doi: 10.1111/mec.12284. [DOI] [PubMed] [Google Scholar]
- Hess JE, Campbell NR, Close DA, Docker MF, Narum SR. Population genomics of Pacific lamprey: adaptive variation in a highly dispersive species. Molecular Ecology. 2013;22:2898–2916. doi: 10.1111/mec.12150. [DOI] [PubMed] [Google Scholar]
- Hilborn R, Quinn TP, Schindler DE, Rogers DE. Biocomplexity and fisheries sustainability. Proceedings of the National Academy of Sciences of the United States of America. 2003;100:6564–6568. doi: 10.1073/pnas.1037274100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hill WG. Estimation of effective population-size from data on linkage disequilibrium. Genetical Research. 1981;38:209–216. [Google Scholar]
- Hohenlohe PA, Bassham S, Etter PD, Stiffler N, Johnson EA, Cresko WA. Population genomics of parallel adaptation in threespine stickleback using sequenced RAD tags. PLoS Genetics. 2010;6:e1000862. doi: 10.1371/journal.pgen.1000862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hohenlohe PA, Day MD, Amish SJ, Miller MR, Kamps-Hughes N, Boyer MC, Muhlfeld CC, et al. Genomic patterns of introgression in rainbow and westslope cutthroat trout illuminated by overlapping paired-end RAD sequencing. Molecular Ecology. 2013;22:3002–3013. doi: 10.1111/mec.12239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Howard KG, Hayes SJ, Evenson DF. 2009. Yukon River Chinook salmon stock status and action plan 2010; a report to the Alaska Board of Fisheries. Alaska Department of Fish and Game, Special Publication No. 09-26. Available from http://www.sf.adfg.state.ak.us/FedAidpdfs/Sp09-26.pdf(accessed on 6 May 2012)
- Hubert S, Higgins B, Borza T, Bowman S. Development of a SNP resource and a genetic linkage map for Atlantic cod (Gadus morhua. BMC Genomics. 2010;11:191. doi: 10.1186/1471-2164-11-191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jombart T. adegenet: a R package for the multivariate analysis of genetic markers. Bioinformatics. 2008;24:1403–1405. doi: 10.1093/bioinformatics/btn129. [DOI] [PubMed] [Google Scholar]
- Kalinowski ST, Wagner AP, Taper ML. ML-RELATE: a computer program for maximum likelihood estimation of relatedness and relationship. Molecular Ecology Notes. 2006;6:576–579. [Google Scholar]
- Larson WA, Utter FM, Myers KW, Templin WD, Seeb JE, Guthrie CM, Bugaev AV, et al. Single-nucleotide polymorphisms reveal distribution and migration of Chinook salmon (Oncorhynchus tshawytscha) in the Bering Sea and North Pacific Ocean. Canadian Journal of Fisheries and Aquatic Sciences. 2013;70:128–141. [Google Scholar]
- Lingnau T. 1996. Norton Sound and Kotzebue Sound management area salmon catch and escapement report, 1995 [online]. Alaska Department of Fish and Game, Regional Information Report No. 3A96-23. Available from http://www.adfg.alaska.gov/FedAidpdfs/RIR.3A.1996.23.pdf(accessed on 30 January 2013)
- Mercer B, Wilson JK. 2011. 2010 Chinook salmon sonar enumeration on the Big Salmon River [online]. Prepared for the Yukon River Panel Restoration and Enhancement Fund, CRE-41-10. http://yukonriverpanel.com/salmon/wp-content/uploads/2011/04/cre-41-10-big-salmon-sonar-final-report.pdf(accessed on 30 January 2012)
- Miller MR, Brunelli JP, Wheeler PA, Liu S, Palti CE, III Rexroad Y, Doe CQ, et al. A conserved haplotype controls parallel adaptation in geographically distant salmonid populations. Molecular Ecology. 2012;21:237–249. doi: 10.1111/j.1365-294X.2011.05305.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Minoche AE, Dohm JC, Himmelbauer H. Evaluation of genomic high-throughput sequencing data generated on Illumina HiSeq and Genome Analyzer systems. Genome Biology. 2011;12:R112. doi: 10.1186/gb-2011-12-11-r112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murphy JM, Templin WD, Farley EVJ, Seeb JE. Stock-structured distribution of western Alaska and Yukon juvenile Chinook salmon (Oncorhynchus tshawytscha) from United States BASIS surveys, 2002–2007. North Pacific Anadromous Fish Commission Bulletin. 2009;5:51–59. [Google Scholar]
- Narum SR, Buerkle CA, Davey JW, Miller MR, Hohenlohe PA. Genotyping-by-sequencing in ecological and conservation genomics. Molecular Ecology. 2013;22:2841–2847. doi: 10.1111/mec.12350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nielsen EE, Kenchington E. A new approach to prioritizing marine fish and shellfish populations for conservation. Fish and Fisheries (Oxford) 2001;2:328–343. [Google Scholar]
- Nielsen EE, Hemmer-Hansen J, Larsen PF, Bekkevold D. Population genomics of marine fishes: identifying adaptive variation in space and time. Molecular Ecology. 2009;18:3128–3150. doi: 10.1111/j.1365-294X.2009.04272.x. [DOI] [PubMed] [Google Scholar]
- Nosil P, Funk DJ, Ortiz-Barrientos D. Divergent selection and heterogeneous genomic divergence. Molecular Ecology. 2009;18:375–402. doi: 10.1111/j.1365-294X.2008.03946.x. [DOI] [PubMed] [Google Scholar]
- Olsen JB, Beacham TD, Wetklo M, Seeb LW, Smith CT, Flannery BG, Wenburg JK. The influence of hydrology and waterway distance on population structure of Chinook salmon Oncorhynchus tshawytscha in a large river. Journal of Fish Biology. 2010;76:1128–1148. doi: 10.1111/j.1095-8649.2010.02554.x. [DOI] [PubMed] [Google Scholar]
- Olsen JB, Crane PA, Flannery BG, Dunmall K, Templin WD, Wenburg JK. Comparative landscape genetic analysis of three Pacific salmon species from subarctic North America. Conservation Genetics. 2011;12:223–241. [Google Scholar]
- Palstra FP, Ruzzante DE. Genetic estimates of contemporary effective population size: what can they tell us about the importance of genetic stochasticity for wild population persistence? Molecular Ecology. 2008;17:3428–3447. doi: 10.1111/j.1365-294x.2008.03842.x. [DOI] [PubMed] [Google Scholar]
- Palstra FP, Ruzzante DE. Demographic and genetic factors shaping contemporary metapopulation effective size and its empirical estimation in salmonid fish. Heredity. 2011;107:444–455. doi: 10.1038/hdy.2011.31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park L. Effective population size of current human population. Genetics Research. 2011;93:105–114. doi: 10.1017/S0016672310000558. [DOI] [PubMed] [Google Scholar]
- Peakall R, Smouse PE. GenAlEx 6.5: genetic analysis in Excel. Population genetic software for teaching and research-an update. Bioinformatics. 2012;28:2537–2539. doi: 10.1093/bioinformatics/bts460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peel D, Waples RS, Macbeth GM, Do C, Ovenden JR. Accounting for missing data in the estimation of contemporary genetic effective population size (Ne) Molecular Ecology Resources. 2013;13:243–253. doi: 10.1111/1755-0998.12049. [DOI] [PubMed] [Google Scholar]
- Piry S, Alapetite A, Cornuet JM, Paetkau D, Baudouin L, Estoup A. GENECLASS2: A software for genetic assignment and first-generation migrant detection. Journal of Heredity. 2004;95:536–539. doi: 10.1093/jhered/esh074. [DOI] [PubMed] [Google Scholar]
- Purcell S, Neale B, Todd-Brown K, Thomas L, Ferreira MAR, Bender D, Maller J, et al. PLINK: a tool set for whole-genome association and population-based linkage analyses. American Journal of Human Genetics. 2007;81:559–575. doi: 10.1086/519795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Radice AD, Bugaj B, Fitch DHA, Emmons SW. Widespread occurrence of the TC1 transposon family-TC1-like transposons from teleost fish. Molecular & General Genetics. 1994;244:606–612. doi: 10.1007/BF00282750. [DOI] [PubMed] [Google Scholar]
- Rannala B, Mountain JL. Detecting immigration by using multilocus genotypes. Proceedings of the National Academy of Sciences of the United States of America. 1997;94:9197–9201. doi: 10.1073/pnas.94.17.9197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Renaut S, Maillet N, Normandeau E, Sauvage C, Derome N, Rogers SM, Bernatchez L. Genome-wide patterns of divergence during speciation: the lake whitefish case study. Philosophical Transactions of the Royal Society B-Biological Sciences. 2012;367:354–363. doi: 10.1098/rstb.2011.0197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roesti M, Salzburger W, Berner D. Uninformative polymorphisms bias genome scans for signatures of selection. BMC Evolutionary Biology. 2012;12:94. doi: 10.1186/1471-2148-12-94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rousset F. GENEPOP ' 007: a complete re-implementation of the GENEPOP software for Windows and Linux. Molecular Ecology Resources. 2008;8:103–106. doi: 10.1111/j.1471-8286.2007.01931.x. [DOI] [PubMed] [Google Scholar]
- Russello MA, Kirk SL, Frazer KK, Askey PJ. Detection of outlier loci and their utility for fisheries management. Evolutionary Applications. 2012;5:39–52. doi: 10.1111/j.1752-4571.2011.00206.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sandone G. 1995. Anvik River salmon escapement study, 1994 [online]. Alaska Department of Fish and Game, Regional Information Report No. 3A95-08. Available from http://www.sf.adfg.state.ak.us/FedAidPDFs/RIR.3A.1995.08.pdf(accessed on 30 January 2013)
- Schindler DE, Hilborn R, Chasco B, Boatright CP, Quinn TP, Rogers LA, Webster MS. Population diversity and the portfolio effect in an exploited species. Nature. 2010;465:609–612. doi: 10.1038/nature09060. [DOI] [PubMed] [Google Scholar]
- Seeb LW, Crane PA. High genetic heterogeneity in chum salmon in western Alaska, the contact zone between northern and southern lineages. Transactions of the American Fisheries Society. 1999;128:58–87. [Google Scholar]
- Seeb LW, Habicht C, Templin WD, Tarbox KE, Davis RZ, Brannian LK, Seeb JE. Genetic diversity of sockeye salmon of Cook Inlet, Alaska, and its application to management of populations affected by the Exxon Valdez oil spill. Transactions of the American Fisheries Society. 2000;129:1223–1249. [Google Scholar]
- Seeb JE, Pascal CE, Grau ED, Seeb LW, Templin WD, Harkins T, Roberts SB. Transcriptome sequencing and high-resolution melt analysis advance single nucleotide polymorphism discovery in duplicated salmonids. Molecular Ecology Resources. 2011;11:335–348. doi: 10.1111/j.1755-0998.2010.02936.x. [DOI] [PubMed] [Google Scholar]
- Shaklee JB, Beacham TD, Seeb L, White BA. Managing fisheries using genetic data: case studies from four species of Pacific salmon. Fisheries Research. 1999;43:45–78. [Google Scholar]
- Smith CT, Templin WD, Seeb JE, Seeb LW. Single nucleotide polymorphisms provide rapid and accurate estimates of the proportions of US and Canadian Chinook salmon caught in Yukon River fisheries. North American Journal of Fisheries Management. 2005;25:944–953. [Google Scholar]
- Sved JA, Cameron EC, Gilchrist AS. Estimating effective population size from linkage disequilibrium between unlinked loci: theory and application to fruit fly outbreak populations. PLoS ONE. 2013;8:e69078. doi: 10.1371/journal.pone.0069078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor EB, Harvey S, Pollard S, Volpe J. Postglacial genetic differentiation of reproductive ecotypes of kokanee Oncorhynchus nerka in Okanagan Lake. British Columbia. Molecular Ecology. 1997;6:503–517. doi: 10.1046/j.1365-294x.1997.00213.x. [DOI] [PubMed] [Google Scholar]
- Templin WD, Seeb JE, Jasper JR, Barclay AW, Seeb LW. Genetic differentiation of Alaska Chinook salmon: the missing link for migratory studies. Molecular Ecology Resources. 2011;11:226–246. doi: 10.1111/j.1755-0998.2010.02968.x. [DOI] [PubMed] [Google Scholar]
- Tenesa A, Navarro P, Hayes BJ, Duffy DL, Clarke GM, Goddard ME, Visscher PM. Recent human effective population size estimated from linkage disequilibrium. Genome Research. 2007;17:520–526. doi: 10.1101/gr.6023607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Utter F, Ryman N. Genetic markers and mixed stock fisheries. Fisheries. 1993;18:11–21. [Google Scholar]
- Utter F, Hodgins H, Allendorf F. Biochemical genetic studies of fishes: potentialities and limitations. In: Malins DC, Sargents JR, editors. Biochemical and biophysical perspectives in marine biology. Vol. 1. San Francisco, CA: Academic Press; 1974. pp. 213–238. [Google Scholar]
- Waples RS. Conservation genetics of Pacific salmon. 3. Estimating effective population-size. Journal of Heredity. 1990;81:277–289. [Google Scholar]
- Waples RS. Separating the wheat from the chaff: patterns of genetic differentiation in high gene flow species. Journal of Heredity. 1998;89:438–450. [Google Scholar]
- Waples RS. A bias correction for estimates of effective population size based on linkage disequilibrium at unlinked gene loci. Conservation Genetics. 2006;7:167–184. [Google Scholar]
- Waples RS, Do C. Linkage disequilibrium estimates of contemporary Ne using highly variable genetic markers: a largely untapped resource for applied conservation and evolution. Evolutionary Applications. 2010;3:244–262. doi: 10.1111/j.1752-4571.2009.00104.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Waples RS, Dickhoff WW, Hauser L, Ryman N. Six decades of fishery genetics: taking stock. Fisheries. 2008;33:76–79. [Google Scholar]
- Weir BS, Cockerham CC. Estimating F-statistics for the analysis of population-structure. Evolution. 1984;38:1358–1370. doi: 10.1111/j.1558-5646.1984.tb05657.x. [DOI] [PubMed] [Google Scholar]
- Williams D, Shelden C. 2011. Kogrukluk River salmon studies, 2010 [online]. Alaska Department of Fish and Game, Fishery Data Series No. 11-49. http://www.adfg.alaska.gov/FedAidpdfs/FDS11-49.pdf(accessed on 30 January 2012)
- Wirgin II, Waldman JR. What DNA can do for you. Fisheries. 1994;19:16–27. [Google Scholar]
- Woody CA. 2012. Assessing reliability of Pebble Limited Partnership's salmon escapement studies [online]. Fisheries research and consulting, Anchorage, Alaska. http://www.pebblescience.org/pdfs/Woody_EBD_EscapementFINAL27June2012.pdf(accessed on 30 January 2012)
- Zerbino DR, Birney E. Velvet: algorithms for de novo short read assembly using de Bruijn graphs. Genome Research. 2008;18:821–829. doi: 10.1101/gr.074492.107. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Histograms of locus-specific overall FST and pairwise FST for each population comparison.
Summary statistics for all 10 944 loci.
BLAST results for all 10 944 loci.
Assignment probabilites to the three most likely populations for each individual and each SNP panel tested.


