Parallel Continuous Flow: A Parallel Suffix Tree Construction Tool for Whole Genomes

Abstract

The construction of suffix trees for very long sequences is essential for many applications, and it plays a central role in the bioinformatic domain. With the advent of modern sequencing technologies, biological sequence databases have grown dramatically. Also the methodologies required to analyze these data have become more complex everyday, requiring fast queries to multiple genomes. In this article, we present parallel continuous flow (PCF), a parallel suffix tree construction method that is suitable for very long genomes. We tested our method for the suffix tree construction of the entire human genome, about 3GB. We showed that PCF can scale gracefully as the size of the input genome grows. Our method can work with an efficiency of 90% with 36 processors and 55% with 172 processors. We can index the human genome in 7 minutes using 172 processes.

1. Introduction

The number of completely sequenced genomes stored in the Genome Online Database has already reached the impressive number of 2968. Currently, there are about 99 million DNA sequences in Genbank and 8.6 million proteins in the UniProtKB/TrEMBL database. The GenBank database contains more than 100 Gbp, and it is generally believed that its size will double every 6 months (GeneBank, 2005). The size of the entire human genome is in the order of 3 billion DNA base pairs, whereas other genomes can be as long as 16 Gbp.

In this scenario one of the most important needs is the design of efficient techniques to store and query biological data. The most common full-text indexes are suffix trees (McCreight, 1976), suffix arrays (Manber and Myers, 1993), and string B-trees (Ferragina and Grossi, 1999).

The suffix tree is one of the most studied data structures, and it is fundamental for string processing (Gusfield, 1997). It stores strings in such a way that it enables the implementation of efficient searches. It has been shown that the suffix tree has a myriad of virtues (Apostolico, 1985). Once a suffix tree is built, a variety of operations can be implemented in optimal time, for example, to find the longest common substring across different strings, to compute the matching statistics, to find all locations of a pattern, to extract palindromes, and many others (Gusfield, 1997).

Traditionally the suffix tree has been used in very different fields, spanning from data compression (Ziv and Lempel, 1997; Apostolico et al., 2006) to clustering (Zamir and Etzioni, 1998; Comin and Verzotto, 2011). The use of suffix trees has become very popular in the field of bioinformatics, allowing a number of string operations, like detection of repeats (Kurtz et al., 2001), local alignment (Meek et al., 2003), the analysis of regulatory elements (Comin and Parida, 2008), and the discovery of extensible patterns (Apostolico et al., 2010).

Suffix arrays have been introduced recently as a successful variant of suffix trees (Manber and Myers, 1993). In bioinformatics the use of suffix arrays has become immediately of great help as a valid substitute of suffix trees (Abouelhoda et al., 2002). Several compressed variants have been proposed, also in the specific context of genome indexing (Lippert et al., 2005). In terms of performance, expressiveness is traded for lower memory footprint and improved locality. In general, suffix arrays are superior to suffix trees on exact string matching and memory requirement; however, suffix trees are still widely used as they allow operations otherwise burdensome with suffix arrays. Suffix arrays are not suitable for inexact searches, and they do not allow inference of motifs as suffix trees do (i.e., Federico and Pisanti, 2009), even in the exact case. Moreover, in bioinformatics, applications finding regularities, like transcription factor–binding sites, and inexact searches are of great interest, for these reasons indexing genomic data on suffix trees is still fundamental. For a comprehensive review on prospects and limitations of full text indexes in genome analysis we refer the reader to Vyverman et al. (2012).

The optimal construction of suffix tree has already been addressed by Ukkonen (1995) and McCreight (1976), which provided algorithms in linear time and space. The main issue is that the suffix tree can easily exceed the memory available as the input sequence grows. Moreover these algorithms exhibit poor locality of reference. Thus every time the suffix tree cannot be stored into the main memory these methods become immediately unpractical because the I/O disk cost may dominate the construction time. These algorithms cannot scale when the input is very large like, for example, the human genome (3 GB).

In recent years researchers have tried to remove this bottleneck by proposing disk-based suffix tree construction algorithms (Hunt et al., 2002), TDD (Tata et al., 2004), ST-Merge (Tian et al., 2005), and Trellis (Phoophakdee and Zaki, 2007). In general, the basic idea is to reduce the number of random access to the tree, but these methods can work only if the size of the input string fits the main memory. The complexity of these methods is no longer optimal, but the locality of reference improves over the classical optimal construction algorithms. However, constructing the human genome suffix tree can still take several hours in a workstation with 2 GB of main memory (Tian et al., 2005).

With the advent of modern sequencing technologies, biological sequence databases have grown dramatically. Also the methodologies required to analyze these data have become more complex everyday. The availability of different genomes has enabled a number of studies based on genome comparison. In this context researchers may need to compare different genomes from the same or different species in order to search for similarities or subtle differences. Thus, the ability to efficiently store and query these sequences can be of great help. This can be achieved only if we are able to construct suffix trees for large sequences in a short time.

The current massively parallel systems have a small amount of memory per processing element, and in the future, with clusters of GPUs, the available main memory per processing element will become even smaller. Our algorithm is conceived such that every method can process more data than its available memory.

Another issue of modern parallel systems is that they do not offer high disk I/O bandwidth, whereas they do offer efficient network communication bandwidth among processing elements. Also the amount of total main memory can be very high and coupled with the network performance this can be a great advantage for the development of parallel applications.

We propose a parallel algorithm for the construction of suffix trees with the following properties:

• • All previous algorithms need to preprocess the input data in order to find the best way to partition the workload. This step is inherently sequential and for long sequences can take several minutes (Mansour et al., 2011). We are the first able to parallelize this step so that all processes will start working immediately without any preprocessing of the data.

• • In the context of parallel algorithms all methods internally construct sub-suffix trees. We are the first to use suffix arrays instead. Suffix arrays are always smaller than suffix trees. This will reduce the amount of data being exchanged among the processes.

• • In all previous algorithms the final merge phase can start only when all previous steps have computed all subtrees. In our algorithm all phases can start as soon as some data is produced by the previous steps. This can be achieved because all steps process the data on-line, reading it sequentially, in a predetermined ordered sequence with no back-tracks or random accesses. For this reason, every computing element can process more data than the available memory, without resorting to costly I/O disk operations. Thus for every step of our algorithm we do not require the data to fit into main memory because processes can start working just with a little portion of the data.

The rest of the article is organized as follows. In the next section we review the other suffix tree construction methods, we discuss our parallel method in section 3, and we conclude with an experimental evaluation of the proposed algorithm in Section 4.

2. Preliminaries on Suffix Trees

Let Σ denote a set of characters. Let 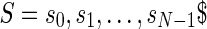, with 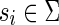, denote an input string of length N, where 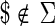. The suffix tree for S is a data structure organized as a tree that stores all the suffixes of S. In a suffix tree all paths going from the root node to the leaf nodes spell a suffix of S. The terminal character $ is unique and ensures that no suffix is a proper prefix of any other suffix. Therefore, the number of leaves is exactly the number of suffixes.

The optimal construction of suffix trees has been addressed by Ukkonen (1995) and McCreight (1976). These methods perform very well as long as the input string and the resulting suffix tree fit in main memory. For a string S of size N, the time and space complexity are O(N), which are optimal. However, these optimal algorithms suffer from poor locality of reference. Once the suffix tree cannot fit in main memory, these algorithms require expensive random disk I/Os. If we consider that the suffix tree is an order of magnitude larger than the input string, these methods become immediately unpractical.

2.1. Construction in external memory

To address this issue several methods have been proposed over the years. In general they all solve this problem by decomposing the suffix tree into smaller subtrees stored on the disk. Among the most important work we can cite (Hunt et al., 2002), TDD (Tata et al., 2004), ST-Merge (Tian et al., 2005) and Trellis (Phoophakdee and Zaki, 2007). TDD and ST-merge partition the input string into blocks of size N/K. For all partitions a subtree is built. A final stage merges the subtrees into a suffix tree. This phase needs to access the input string in a nearly random fashion. ST-merge improved the merge phase of TDD by computing the LCP (longest common prefix) between two consecutive suffixes. However the overall performance improvement was weak. In Trellis, the authors proposed an alternative way to merge the data. Subtrees that share a common prefix are merged together. However this requires the input string to fit in main memory otherwise the performance drops dramatically.

Only recently two methods solved this issue, Wavefront (Ghoting and Makarychev, 2009) and B²ST (Barsky et al., 2011). The first will be reviewed in the next subsection. The latter is the first to use internal suffix arrays instead of suffix trees, and it is also one of the best performing methods. In Section 3 we will describe in more details how we rearchitected this method to scale on a large computing facility.

2.2. Parallel methods

The parallel construction of suffix trees on various abstract machines is a well-studied topic (Apostolico et al., 1998; Hariharan, 1994). Similarly to the optimal serial algorithm, these methods exhibit poor locality of reference. As a consequence they are inefficient when the input string does not fit in main memory. This problem has been addressed by Farach-Colton et al. (2000) that provide a theoretically optimal algorithm. However, due to the intricacy of the method, a practical implementation does not exist.

The only practical parallel implementations of suffix tree construction are Wavefront (Ghoting and Makarychev, 2009) and ERa (Mansour et al., 2011). Wavefront splits the sequence S into independent partitions of the resulting tree. The partition phase is done using variable length prefixes, so that every partition starts with the same prefix. This ensures the independence of the subtrees that can be easily merged. To reduce the cost of expensive I/O, Wavefront reads the string sequentially. However, the cost of partitioning the string into optimal subtrees can be very high. The authors implement two versions of Wavefront, serial and parallel. The parallel version runs on IBM BlueGene/L supercomputer, and it can index the entire human genome in 15 minutes using 1024 processes. So far this is the best time for a large parallel system.

Similarly to Wavefront, ERa (Mansour et al., 2011) divides the string first into independent subtrees. Subtrees are then further divided into partitions, such that each partition can be processed in memory. This method is very similar to Wavefront, but the performance of its parallel implementation is poor. In fact with 16 processes this method operates with an efficiency of 53%. We argue this is a very small number considering that it was obtained with just 16 processes.

3. Parallel Continuous Flow: Parallel Suffix Tree Construction

In this section we present our parallel suffix tree construction algorithm called parallel continuous flow (PCF). We describe how we redesigned the best method to construct suffix trees for very large input in external memory B²ST (Barsky et al., 2011) to achieve better performance on a massively parallel system like MareNostrum (Marenostrum, 2012). We begin with a brief description of this method. The basic idea is that the suffix tree of S can be constructed from the suffix array of S and an additional structure that stores the LCP. It has been shown by Farach-Colton et al., (2000) that the conversion from suffix array to suffix tree can be performed in linear time. This translation can be implemented efficiently also for large strings because it exhibits good locality of reference. In particular the output suffix tree can be computed sequentially while reading the input suffix array, in a streaming fashion, thus avoiding random access to both data structures. The main problem of this approach is to compute the suffix array of the whole input string. Similarly to the other disk-based methods, B²ST divides this problem into smaller ones. At first the input string is divided into k partitions of equal size N/k. The size of the partitions depends on the memory available and for whole genomes in a serial environment the number of partitions is typically in the range [3, 6]. At the end of each partition, except the last one, a tail is attached, which is the prefix of the next partition. This tail must never occur within the partition and it is required to compute the order of the suffixes within a partition. For example, in Table 1 the string S=ababaaabbabbbab is divided into three partitions of size five. The first partition is composed of the string ababa followed by the tail aa. The substring aa is the shortest prefix of the second partition that does not occur in the first one. This will allow us to order each suffix for each partition. The suffix arrays, SA_i, of each partition i are shown in the last row of Table 1.

Table 1.

An Example of Partitions

	Partition A					Partition B					Partition C
S	a	b	a	b	a	a	a	b	b	a	b	b	b	a	b
pos	1	2	3	4	5	1	2	3	4	5	1	2	3	4	5
SA	5	3	1	4	2	1	2	5	4	3	4	5	3	2	1

An example of partitions of size 5 for the input string S=ababaaabbabbbab. The first partition is ababa, followed by the tail aa, which does not occur within the partition. In the last row are the suffix arrays, SA, for each partition.

Once we have built all suffix arrays, one per partition, we need to combine them. This is necessary to establish the relative order of all suffixes. Thus in this second step we generate the suffix arrays SA_ij for each pair of partitions. We use as input the suffix arrays SA_i and SA_j to build the partitions pair suffix array SA_ij, along with the LCP length for each suffix. The LCP is the length of the longest common prefix of each suffix in SA_ij with its predecessor. This will be used in the final merge phase to order all suffixes. In Table 2 the first two partitions, A and B, from the previous example are combined. This generates the suffix array SA_AB of size |SA_A| + |SA_B| = 10, and two other data structures: the LCP array and the partition array. We can observe that by using the latter two data structures and the suffix arrays SA_A and SA_B we can construct the partition pair suffix array SA_AB. Thus the output of this step is the order array OA_AB that is composed by the arrays LCP and partition. We don't need to store explicitly SA_AB since it can be obtained from the output of this step.

Table 2.

An Example of Suffix Arrays of a Pair of Partitions

Suffix start	5	1	3	1	2	5	4	2	4	3
Partition	A	B	A	A	B	B	A	A	B	B
LCP	0	2	1	3	2	3	0	2	3	1

An example of suffix arrays of the pair of partitions A and B. The first two rows represent the suffix array SA_AB, where the first row is the position of the suffix within the partition and the second row identifies the partition. The last row is the length of the LCP between two consecutive suffixes. The last two rows, Partition and LCP, will form the ordered array OA_AB. LCP, longest common prefix.

After the second step we have produced k suffix arrays SA_i, one per partition, of total size N and k(k−1)/2 order arrays OA_ij of total size kN. It is important to notice that all arrays, since they are already ordered, will be scanned sequentially and thus the final suffix tree will be produced in a similar manner. This property ensures good locality of reference since no random access on the data will be performed. This is crucial for the design of our parallel algorithm.

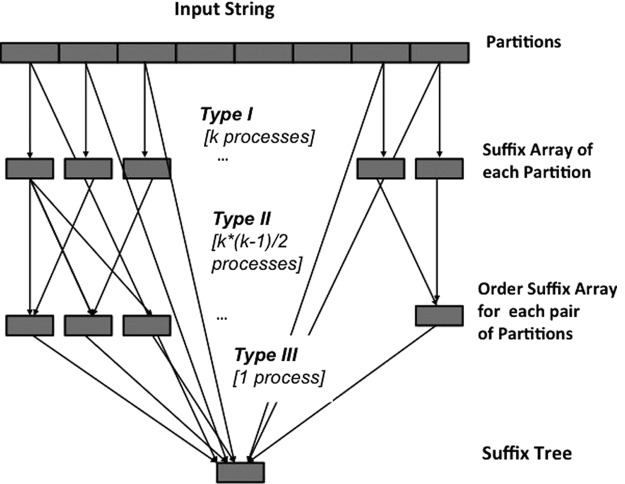
In order to parallelize the above procedure we need to carefully analyze the data dependencies. A summary of the data flow can be found in Figure 1. As already observed, the number of partition pairs grows like k(k−1)/2, whereas the overall data grows like kN. If we analyze the performance reported in Barsky et al. (2011), we can observe that the suffix tree construction for the human genome requires about 3 hours on a modern workstation. Moreover, from the data in Barsky et al. (2011), the most demanding task is the construction of the ordered arrays OA_ij, which account for 95% of the time.

FIG. 1.

A workflow of the data dependencies of B²ST.

Another aspect that we need to take into consideration is the order by which the data is needed at each phase. As already discussed, some steps will process the data sequentially. For example, the construction of the ordered array OA_1,2 will need the suffix arrays SA₁ and SA₂, but to compute the smallest suffix in OA_1,2 we need only the smallest suffixes of SA₁ and SA₂. Thus the construction of OA_1,2 can start as soon as the smallest suffixes of SA₁ and SA₂ are received. Similarly, in the final merge the global smallest suffix can be discovered as soon as the smallest suffixes for all ordered arrays are computed.

To map tasks to processes we take into account the most demanding task, the computation of the order arrays. We choose to allocate k(k−1)/2 processes to construct the order array OA_ij. Thus each of these processes will compute one order array. In principle we can reuse k of these processes to compute also the suffix arrays, SA_i, but this solution has the drawback that all of these k processes have to finish computing the suffix arrays before they can construct also the ordered array, thus the distribution of workload can be highly unbalanced. Moreover, with this configuration we could not exploit the property of sequential data accessing already described. For this reason we decide to allocate additional k processes that are dedicated to the construction of suffix arrays SA_i. Similarly one more process will collect the ordered array and merge the partial results into the final suffix tree. To summarize if k is the number of partitions, our algorithm will use k(k−1)/2+k+1 processes. We will call the processes that compute the suffix arrays SA_i, type I; those that construct the ordered arrays OA_ij, type II; and the process that merges the partial results into the suffix tree, type III.

To achieve better scalability we need to make sure that every process receives a continuous flow of data. This flow should be adequate to maintain active computation of all processes at all times. Moreover, we implement all communications with asynchronous nonblocking primitives, like MPI_Isend, to achieve overlap between communication and computation, so that every process can continue the computation while the network is taking care of the data transfer. For that purpose we need to allocate a series of buffers to keep the in-flight data (data already sent but not yet received at destination) and manage them wisely to orchestrate the continuous flow and maximize parallelism. Next we describe in more detail the main algorithm and the different types of processes.

Main algorithm: The main algorithm divides the processes into different types and calls the appropriate procedures. It also prepares the partitions of S for type I and type II processes. The string S is read collectively by all processes. The use of MPI's collective I/O primitives allows better performance, especially when the input string is large. These collective I/O operations ensure that the same copy of the string is not read multiple times.

Type I process: These processes construct the suffix array SA_i for the partition i. The output SA_i is computed in whole using one of the best performing tools by Larsson and Sadakane (2007). The SA_i is then divided into the subsuffix arrays SubSA_i. The subsuffix array SubSA_i will contain a portion of SA_i of fixed size BuffSize. The data contained in SubSA_i is then sent to type II and III processes.

This procedure uses nonblocking MPI_Isend to send SubSA_i to the other processes. In order to implement this paradigm we need to store the inflight data (not yet received at destination) in a temporary buffer. The number of messages stored in this buffer may affect the overall performance, because the other types of processes that require this data will have different computing loads, thus we need to be able to provide the data as soon as it is needed. For this reason we allocate MemForComm bytes for the communication buffer. This temporary buffer tmpBuff contains up to numBuff messages of size BuffSize. The buffer tmpBuff is implemented as a circular pool of buffers where we can keep the inflight messages and control its correct arrival at the destination through the variables first, last and the vector of message status handle. This pool of buffers allows us to wait for message completion (using the handle) only when strictly necessary, that is, when we are running out of buffers, reducing unnecessary synchronization to keep the continuous flow of data and exploit parallelism as much as possible. However, memory is a limitation and some experiments have been performed to find out the right amount of temporary space and buffer size to maximize performance.

Type II process: The type II processes will take as input the subsuffix arrays SubSA_i and SubSA_j and build the ordered array OA_ij. The procedure ComputeSubOA constructs the ordered array until BuffSize bytes are produced.

The ordered array OA_ij is the suffix array of the pairs of partitions i and j. Since SA_j has already been computed by some process, the construction of OA_ij is equivalent to the extension of SA_j by adding the partition i to the left of the already indexed partition j. The dynamic extension of suffix arrays has already been addressed in Salson et al. (2010). Moreover, in Urbanovich and Ajtkulov (2011) the authors propose a simplified version where a string is appended to the left. They provide an implementation that is based on the results of Salson et al. (2010). We use the basic operation of this method to compare two suffixes using the two input partitions and a data structure called an inverted suffix array. The comparison of two suffixes and the corresponding update of the suffix array require in total O(log²n) time (Urbanovich and Ajtkulov, 2011). The suffixes of SubSA_j are inserted incrementally into SubSA_i. Note that the relative order of all suffixes in SubSA_i and SubSA_j will be preserved in OA_ij.

Similarly with the type I processes the data is kept into a temporary buffer called tmpOA_ij and sent to type III using nonblocking MPI_Isend primitives. In this case, we don't need to store several messages because the only process that will need this data is the type III. It is enough to allocate two buffers so that when the data is stored for communication in the first buffer the process can continue working on the second one. While constructing the ordered arrays ComputeSubOA also consumes the input sub-suffix arrays. Every time one of the two arrays is empty we will require more data from the corresponding type I process.

Type III process: The type III process will merge the data and produce the suffix tree. The main task is to order all suffixes so that we can incrementally construct the suffix tree from the ordered list of suffixes. To do that, we need to compare the suffixes in all arrays SA_i. Since these arrays are already ordered this process can start as soon as the first subSA_i are produced by all type I processes and the correspondent pairs of subordered arrays subOA_ij from type II processes. For this reason, we allocate the space to receive k subSA_i of dimension BuffSize and k(k−1) subordered arrays subOA_ij. Now given all these data we can efficiently search for the smallest suffix among the top elements in subSA_i. Every time we compare two suffixes, if they are within the same partition they are already ordered. Thus we can output the relative order. On the other hand, say one is from SubSA_i and the other from SubSA_j, it is enough to check the top element in the order array subOA_ij and output the suffix encoded in the partition vector. Every time a new smallest suffix, newSuff, is discovered it is inserted into the final output buffer subST. This buffer of size OutputBuffSize contains the partial suffix tree constructed so far; when it is full it is written to the disk. Once a new suffix, from partition partId, is discovered we need to advance a pointer in the corresponding subSA_partId. Similarly also for all k−1 subOA_j,partId that involve the partition partId. If one of these pointers reaches the end of the corresponding array we refill it with a new MPI_Recv until no more data is available.

3.1. Workflow analysis and complexity

To better highlight the properties of our parallel algorithm, Figure 2 presents a workflow. In this diagram we can see the different types of processes along with the data they produce. For type I and II processes, every chunk of data represents BuffSize bytes, whereas the data chunks of type III process are of size OutputBuffSize. In this figure we can appreciate how the different processes cooperate in the suffix tree construction.

FIG. 2.

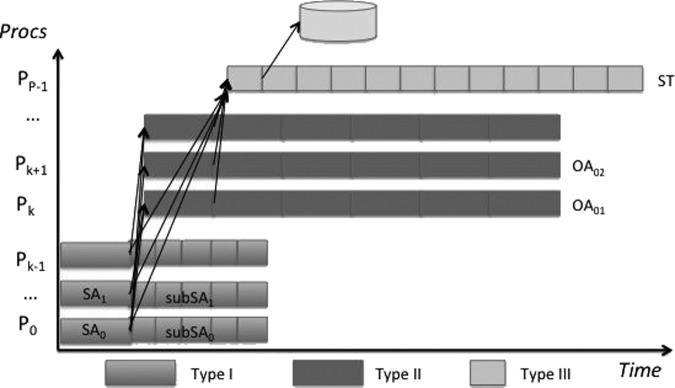
The dataflow of our parallel algorithm, Parallel continuous flow (PCF).

Main(Input: S, MemForComm, BuffSize, OutputBuffSize)
1: i = MPI_Rank();
2: P = MPI_Size();
3: ifi >= 0 and i<kthen
4:  Read the ith partition of string S
5:  ProcTypeI(MemForComm,BuffSize,P)
6: end if
7: ifi >= k and i < P−1 then
8:  Read the ith partition of string S
9:  ProcTypeII(BuffSize)
10: end if
11: ifi == P−1 then
12:  ProcTypeIII(BuffSize,OutputBuffSize)
13: end if

Pseudocode 1: Main Algorithm

ProcTypeI(Input: MemForComm, BuffSize, P; Output: SAi)
1: ptrToSA = 0;
2: SAi ← alloc(Size);
3: numBuff = MemForComm/BuffSize;
4: tmpBuff ← alloc(BuffSize * numBuff);
5: handle ← alloc(MPI_RequestSize * P * numBuff);
6: first = last = 0; Pointers to the pool of bufferstmpBuff
7: Compute(SAi);
8: while partition i is not finished do
9:  ptrToSA ++;
10:  ifptrToSA%BuffSize == 0 then
11:   tmpBuff [last] ← SAi[ptrToSA];
12:   for each process p in P that needs SAido
13:    handle[last][p] = MPI_Isend(p,tmpBuff [last],BuffSize);
14:   end for
15:   last = (last+1)%numBuff ;
16:   iffirst == lastthen
17:    MPI_WaitAll(handle[first]);
18:    first = (first+1)%numBuff ;
19:   end if
20:  end if
21: end while

Pseudocode 2: process TypeI

ProcTypeII(Input: BuffSize; Output: OAij)
1: subSAi ← alloc(BuffSize);
2: subSAj ← alloc(BuffSize);
3: tmpOAij ← alloc(BuffSize * 2);
4: first = last = 0; Pointers to the of buffertmpOAij
5: MPI_Recv(i, subSAi, BuffSize);
6: MPI_Recv(j, subSAj, BuffSize);
7: whileSAi and SAj are not finished do
8:  tmpOSAij[last] ← ComputeSubOA(subSAi,subSAj);
9:  ifsubSAi is empty then
10:    MPI_Recv(i, subSAi, BuffSize);
11: end if
12: ifsubSAj is empty then
13:   MPI_Recv(j, subSAj, BuffSize);
14: end if
15: handle[last] = MPI_Isend(P−1, tmpOAij[last], BuffSize);
16: last = (last+1)%2;
17: iffirst = = lastthen
18:   MPI_Wait(handle[first]);
19:   first = (first+1)%2;
20:  end if
21: end while

Pseudocode 3: process TypeII

ProcTypeIII(Input: BuffSize, OutputBuffSize; Output: SuffixTree)
1: subST ← malloc(OutputBuffSize);
2: SAptr ← alloc(k * integer);
3: OAptr ← alloc(k * (k - 1)/2 * integer);
4: for eachi from 1 to kdo
5:   subSAi ← alloc(BuffSize);
6:   MPI_Recv(pi, subSAi, BuffSize);
7:   S Aptr[i] = 0;
8: end for
9: for eachi from 1 to kdo
10:  for eachj from i+1 to kdo
11:   subOAij ← alloc(BuffSize);
12:   MPI_Recv(pij, subOAij, BuffSize);
13:   OAptr[i,j] = 0
14:  end for
15: end for
16: while String S is not processed do
17:   newSuf ← FindSmallestSuffix(all subSAi, all subOAij)
18:   partId ← ParitionOf (newSuff )
19:   SAptr[partId] ++
20:   ifSAptr[partId] == BuffSizethen
21:    MPI_Recv(pi,subSAi, BuffSize);
22:    S Aptr[partId] = 0;
23:   end if
24:   for each partition i < partIddo
25:    OAptr[i, partId] ++;
26:    ifOAptr[i, partId] == BuffSizethen
27:     MPI_Recv(pi,partId, subOAi,partId, BuffSize);
28:     OAptr[i, partId] = 0;
29:    end if
30:   end for
31:   for each partition i > partId and i < kdo
32:    OAptr[partId, i] ++;
33:    ifOAptr[partId, i] == BuffSizethen
34:     MPI_Recv(ppartId,i, subOApartId,i, BuffSize);
35:     OAptr[partId,i] = 0;
36:    end if
37:   end for
38:   subST ← Insert(newSuf)
39:   ifsizeOf (subST) == OutputBuffSizethen
40:    Write(subST) → Disk
41:    empty(subST)
42:   end if
43: end while

Pseudocode 4: process TypeIII

The construction of a suffix array takes O(NlogN) time in total for the k partitions. In our parallel algorithm this phase is computed by k type I processes, thus the complexity is O((N/k) log(N/k)). The k(k−1)/2 order array can be built in total time of O((kN) log²(kN)). The k(k−1)/2 type II processes in O((N/k) log²(N/k)) time construct all order arrays. Thus the worst case complexity of these two phases is O((N/k) log²(N/k)), but the number of processes P = k(k−1)/2 + k+1 scale like O(k²), thus overall the complexity is 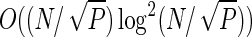. This worst case complexity is 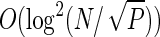, worse than that of other algorithms like Ghoting and Makarychev (2009) and Mansour et al. (2011). However, it is worth noting that although the worst case complexity does not scale linearly with P, in real applications the construction time scales almost linearly with the number of processes. This relates to the fact that the depth of a suffix tree is in the worst case O(N), whereas, for real data like genomes it can be as small as O(log N).

4. Experimental Evaluation

This section presents the results of our performance evaluation. All the experiments were conducted in the MareNostrum supercomputer (Marenostrum, 2012). MareNostrum is a cluster of 2560 JS21 blades, each of them equipped with two dual-core IBM PPC 970-MP processes at 2.3GHz, which share 8 GBytes of main memory. Each core has a 64 KByte instruction/32 KByte data L1 cache and 1024 KBytes of L2 cache. The blades run the SLES10 (Linux) operating system. The interconnection network is Myrinet. Myrinet cards have 2 Gbits/s of interconnection speed. Our implementation uses MPI as message passing. The MPI implementation running on MareNostrum is MPICH (Gropp et al., 1994), configured for running on top of the MX (Myrinet Express) driver. Our method, parallel continuous flow (PCF), is implemented in C++ using MPI primitives for communication.

4.1. Fine tuning/memory

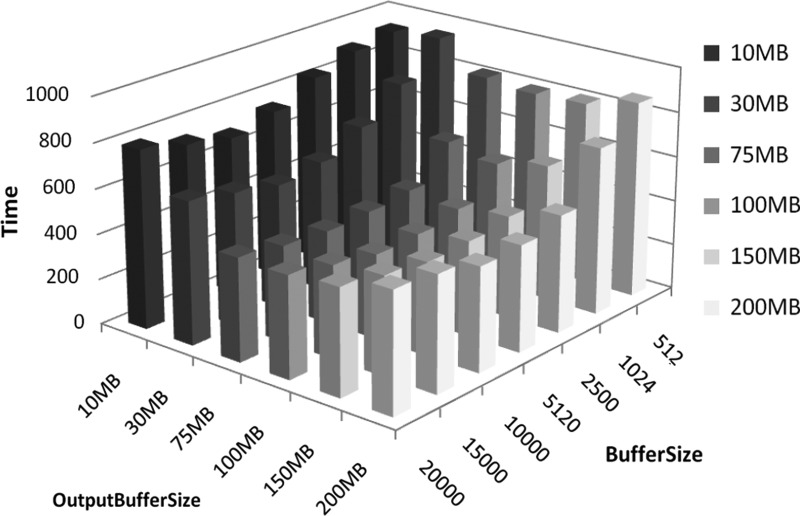
As detailed in the previous section, our parallel algorithm includes as parameters the sizes of two buffers. The first one, BuffSize, controls the size of messages that are being exchanged; the second, OutputBufferSize, determines the output file size. We analyzed the best configuration while varying these parameters. In Figure 3, we report the times to construct the suffix tree of a string of 500 Mb, drawn from the human genome, using 37 processes (8 partitions). In general, if the size of messages is small the communication overhead degradates the performance. Similarly, if the output buffer is too small it increases the frequency of disk writings and reduces the efficiency. However, bigger buffer sizes result in less frequent communication, which may limit the continuous flow of data and hinder load balancing, therefore reducing the overall parallelism of the application. We tested several configurations of these parameters, and after an extensive comparison, we found that messages of size 5 to 10 MB and an output buffer of size 75 to 100 MB are in general the best choice. These settings are also the best performing for longer inputs (data not shown). Based on these observations we set BuffSize to 10 MB and OutputBufferSize to 100 MB.

FIG. 3.

Construction times for the 500 MB genome with 37 processes (eight partitons) while varying the parameters BuffSize and OutputBuffSize.

4.2. Results

We measure execution times for three different data sets of different sizes; all data sets are drawn from the human genome. We used 43 nodes (172 processes) for our experiments. Each experiment was run six times, and the average value was taken. Unfortunately, the code of Wavefront was not available because of IBM policy, the method ERa was only recently published, and MareNostrum has been recently disassembled and is no longer available. To this end, we compare our methods using only the information available from other articles.

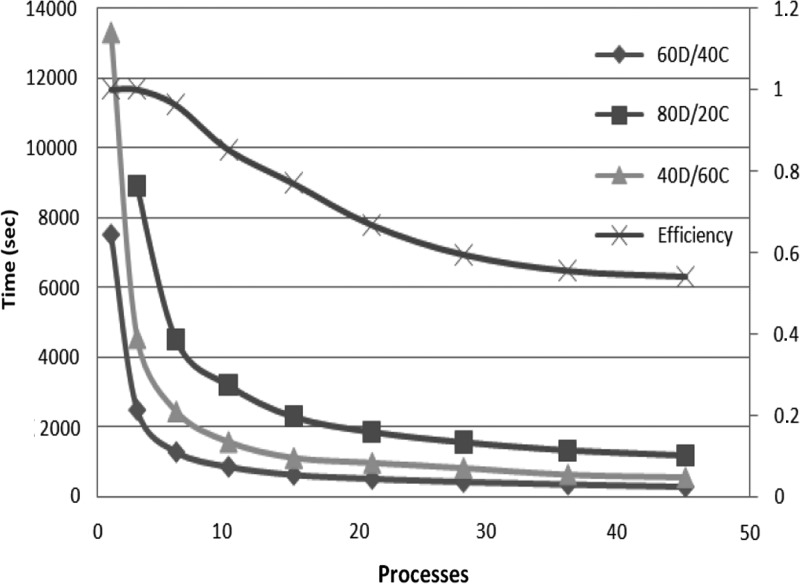
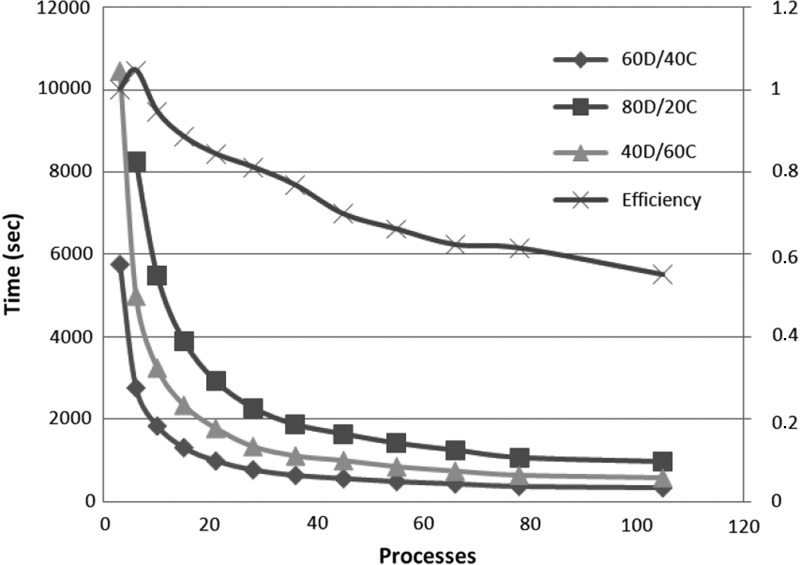
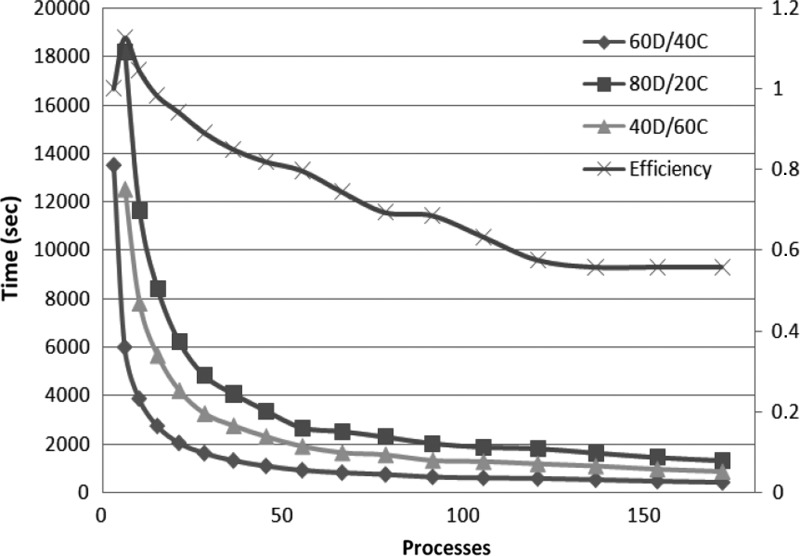
For each different data set, we study different allocations for the memory budget—60D/40C indicates that 60% of the memory budget is reserved for the application data, while the remaining 40% is used for internal communication buffers. Our algorithm works in-memory, and hence the memory is a limitation. To be able to execute the algorithm in-memory, each process needs to maintain in main memory different data structures: (i) the application data, which includes the input string blocks of one partition S_i; part of the suffix arrays, SubSA_i; part of the ordered arrays, SubOA_ij; and part of the suffix tree, SubST; and (ii) the communication buffers. In order to exploit parallelism we need to manage the communication asynchronously, and for that purpose, we need to choose an appropriate value for MemForComm. The application data that needs to be stored in each process is fixed by the input data set and the number of processes, but we can control how much of these data we keep in memory at a time. Working with data chunks that are too small will result in less memory locality, while if the granularity is too big the amount of parallelism will be reduced. At the same time the amount of memory devoted to data will condition how much communication buffers we can allocate; increasing the communication buffers will avoid unnecessary synchronization and thus increase parallelism up to a certain limit, where more buffers will not benefit anymore because no more parallelism can be achieved. Figures 4, 5, and 6 illustrate that the optimal combination is 60D/40C. Less memory used in communication buffers means less exploitation of the application parallelism, and the application becomes communication bounded; however, if more memory is used in communication buffers, the application becomes computation bounded. The measurements show that our algorithm scales up to a certain threshold for every size of the data set. The small size data set (500 Mb) scales up to 46 processes (Fig. 4), up to 106 processes for medium size (1000 Mb) (Fig. 5), and up to 172 for the whole human genome (3000 Mb) (Fig. 6). We attribute this scalability threshold to the inherent parallelism limit of the application.

FIG. 4.

Execution times for different memory allocations and efficiency for the best memory allocation (60D/40C) as we increase the number of processes—dataset human genome of size 500 MB.

FIG. 5.

Execution times for different memory allocations and efficiency for the best memory allocation (60D/40C) as we increase the number of processes—dataset human genome of size 1000 MB.

FIG. 6.

Execution times for different memory allocations and efficiency for the best memory allocation (60D/40C) as we increase the number of processes—dataset whole human genome 3 GB.

We compute the relative efficiency as 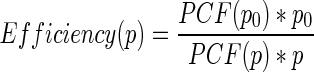, where p is the number of processes and PCF(p) is the construction time with p processes. Ideally, p₀ should be one and PCF(p₀) should be the runtime for the serial algorithm. However, big data sets do not run on a single process due to memory limitations; therefore, we take into account the smallest configuration that is possible to run, which is p₀, being PCF(p₀) the runtime with this configuration. For the whole human genome, the smallest configuration is the run with three processes. Thus, in this case the relative efficiency with p processes is .

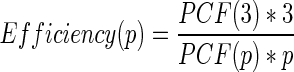The efficiency is close to 90% for small configurations (up to 36 processes for the whole human genome), and it is slightly decreasing as we scale up, due to the parallelization overhead, until it reaches the point where it starts degrading because of the inherent limit of parallelization in the application. For 172 processes we get 55% efficiency (Fig. 6). Similar results are also obtained for the other datasets (Figs. 4 and 5). We argue that the efficiency is relatively good, given the I/O intensive nature of the suffix tree construction. For example, the efficiency of ERa (Mansour et al. 2011) drops very quickly, and the best performance reported an efficiency of 53%, but with just 16 processes.

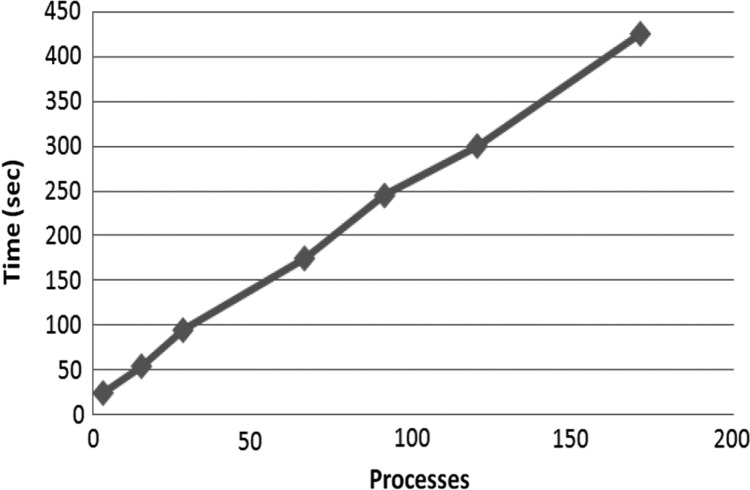
In the last experiment we test the weak scalability, where the ratio between the size of the input and the number of processes is constant. We vary the input from 50 MB for 3 processes to 3 GB for 172 processes. In the ideal case, the construction time should remain constant; this can only happen with embarrassingly parallel problems with no data dependencies where no communication overhead or serial computation parts are present. Figure 7 shows that the construction time of PCF increases linearly with the number of processes. In the same test, the performance of WaveFront grows more than linearly. Only ERa has a similar behavior but with a steeper inclination (see Figure 13 of Mansour et al. 2011). This is very important for real applications, when the input strings can be very long.

FIG. 7.

Weak scalability as we increase the input size from 50 MB for 3 processes to 3 GB for 172 processes.

PCF constructs the whole human genome suffix tree in 425 seconds, about 7 minutes, and uses 172 processes in our testing platform. We argue that this is a very good performance compared with the bibliography. In Ghoting and Makarychev (2009), a time of 880 seconds, 15 minutes, is reported but it requires Blue Gene/L and 1024 processes, similarly in Mansour et al. (2011), a time of 11.3 minutes is reported with 16 machines, each with one dual-core Intel CPU at 3.33GHz and 8 GB RAM. However, these are absolute times on different platforms and thus cannot be directly compared.

5. Conclusions

The construction of suffix trees for very long sequences is essential for many applications, and it plays a central role in the bioinformatic domain. With the advances in sequencing technologies, the amount of biological sequences available in genome and proteome databases has grown dramatically. Therefore, it is essential to have fast methods to build suffix trees. In this article, we presented parallel continuous flow (PCF), a parallel suffix tree construction method that is suitable for very long strings. We tested our method for the suffix tree construction of the entire human genome, about 3 GB. We showed that PCF can scale gracefully as the size of the input string grows. Our method can work with an efficiency of 90% with 36 processes and 55% with 172 processes. We can index the entire human genome in 7 minutes using 172 processes. To the best of our knowledge this is the fastest existing method in terms of absolute time.

Acknowledgments

The authors would like to thank the Barcelona Supercomputing Center for the generous availability of MareNostrum. The work done by M.C. is thanks to the HPC-Europa program. M.C. was partially supported by the Ateneo Project CPDA110239 and by the P.R.I.N. Project 20122F87B2. The researchers at BSC-UPC are supported by the Spanish Ministry of Science and Innovation (contract no. TIN2007-60625 and CSD2007-00050). We also thank Gabor Dozsa for helpful discussions.

Author Disclosure Statement

The authors declare that no competing financial interests exist.