Abstract
Background
Lopinavir (LPV)/ritonavir (RTV) co-formulation (LPV/RTV) is a widely used protease inhibitor (PI) based regimen to treat HIV-infection. As with all PIs, the trough concentration (Ctrough) is a primary determinant of response, but the optimum exposure remains poorly defined. The primary objective was to develop an integrated LPV population pharmacokinetic model to investigate the influence of α-1-acid glycoprotein (AAG) and link total and free LPV exposure to pharmacodynamic changes in HIV-1 RNA and assess viral dynamic and drug efficacy parameters.
Methods
Data from 35 treatment-naïve HIV-infected patients initiating therapy with LPV/RTV 400/100 mg orally twice daily across two studies were used for model development and simulations using ADAPT. Total LPV (LPVt) and RTV concentrations were measured by high-performance liquid chromatography (HPLC) with ultraviolet (UV) detection. Free LPV (LPVf) concentrations were measured using equilibrium dialysis and mass spectrometry.
Results
LPVt typical value of clearance (CLLPVt/F) was 4.73 L/h and distribution volume (VLPVt/F) was 55.7 L. Clearance (CLLPVf/F) and distibution volume (Vf/F) for LPVf were 596 L/h and 6370 L, respectively. Virion clearance rate was 0.0350 h-1. Simulated LPVLPVt Ctrough at 90% (EC90) and 95% (EC95) maximum response were 316 and 726 ng/mL, respectively.
Conclusion
The pharmacokinetic/pharmacodynamic model provides a useful tool to quantitatively describe the relationship between LPV/RTV exposure and viral response. This comprehensive modeling and simulation approach could be used as a surrogate assessment of ARV where adequate early phase dose-ranging studies are lacking in order to define target trough concentrations and possibly refine dosing recommendations.
1. Introduction
Over the past several years, it has become evident that achieving and maintaining adequate antiretroviral (ARV) concentrations is required to produce a sustained virologic response. It is also well recognized that the durability of an ARV regimen is limited not only by inadequate drug exposure and subsequent development of viral resistance, but also by the occurrence of toxicities often related to long-term exposure to higher plasma and tissue drug concentrations [1].
Protease inhibitors (PIs) are bound with high affinity primarily to α-1-acid glycoprotein (AAG), thus free plasma concentrations are inversely related to AAG concentrations. As an acute phase protein, AAG synthesis rises significantly in response to acute and chronic inflammation such as encountered with infections and injuries [2], a factor that may account for the observed variability in plasma AAG concentrations with chronic HIV-infection. Given the PIs high binding affinity for AAG, their high plasma concentrations in the presence of ritonavir (RTV), and the low saturation capacity of AAG, it has been speculated that variations in AAG levels could result in clinically important changes in PI pharmacokinetics and pharmacodynamics. Since a free drug's concentration more accurately reflect its availability to target cells, changes in AAG concentrations could have important clinical implications. However, the inverse relationship between free drug and binding protein concentrations is likely an over simplification of their dynamics. Under normal physiologic conditions, plasma protein binding has little or no effect on the free concentrations for many drugs. This is because at steady state, equilibrium is maintained between free drug concentrations and plasma drug clearance such that the elimination rate is increased as free concentrations increase, and vice versa[3]. For certain drugs, alterations in protein binding can lead to clinically significant changes in pharmacokinetics and pharmacodynamics [4].
Lopinavir (LPV) is an inhibitor of the HIV-1 protease. LPV, co-formulated with low dose ritonavir (RTV) [Kaletra (LPV/RTV, 400/100 mg)], is a frequently used PI regimen for the treatment of HIV infection because of its high effectiveness and reasonable tolerability. LPV is primarily metabolized by cytochrome P450 3A4 (CYP3A4), but co-administration with low dose RTV, a potent inhibitor of CYP3A4, significantly increases LPV plasma concentrations [5]. The in vitro half maximal inhibitory concentration (IC50) of LPV is approximately 10-fold lower than that of RTV, and RTV systemic exposure is low following a 100 mg dose [6]. Thus the antiviral activity of LPV/RTV is due primarily to LPV [6, 7]. A mechanistic understanding of the complex interplay between free concentrations, CYP3A4 inhibition, plasma protein binding, antiviral efficacy and development of viral resistance will lead to more informed dosing strategies with currently approved ARVs and those in development.
Establishing ARV concentrations that exceed the susceptibility of the virus is required for robust suppression of viral replication. PI trough concentrations (Ctrough) are correlated with response, but determination of target Ctrough values are hindered by a dearth of in vivo concentration-response data typically determined during early phase drug development. Without in vivo concentration-response data, protein binding adjusted in vitro susceptibility measurements may provide surrogate estimates for the optimal in vivo Ctrough. To date, population models directly linking free PI concentrations to drug response in vivo are lacking. To address this limitation, we developed an integrated population model to describe the influence of AAG on the equilibrum of total and free plasma LPV concentrations, including the effect of RTV exposure and other relevant covariates. The integrated model also links free LPV concentrations to HIV-1 viral dyamics, which allows an assesment of the role of clinically relevant changes in LPV binding on changes in plasma viral load in treatment naïve HIV-infected individuals with predominantly wild-type virus.
2. Subjects and Methods
2.1 Subjects and Study Design
Data from two studies in treatment-naïve HIV-infected patients initiating ARV therapy were used for these analyses. Both studies were conducted at a single center, and were prospective, multiple dose intensive single and/or steady state pharmacokinetic studies in which subjects were recruited from the Grady Infectious Diseases program (IDP) out-patient clinic in Atlanta, Georgia, USA. Eligibility included male and female subjects age ≥ 18 years and HIV-1 RNA PCR ≥ 50,000 copies/mL. Subjects were not enrolled if they were on medications that could interact with the PIs, on investigational ARV agents, had active opportunistic infection, had renal/hepatic impairment, or were pregnant. At enrollment, demographic information and clinical laboratory data were collected, and ARV adherence counseling was provided to all subjects. Subjects initiated therapy with LPV/RTV 400/100 mg orally twice daily plus standard dosing of 2 nucleoside reverse transcriptase inhibitors. All subjects provided written informed consent before undergoing any study procedures. These trials were designed according to the ethical guidelines for human studies and approved by the Emory University Institutional Review Board.
Plasma AAG concentrations were quantified using an enzyme-linked immunosorbent assay (ELISA). Total LPV (LPVt) and RTV were measured by high-performance liquid chromatography (HPLC) with ultraviolet (UV) detection [8]. Free LPV (LPVf) was quantitated using equilibrium dialysis followed by mass spectrometry. A reversed-phase high performance liquid chromatographic (HPLC) assay, coupled to a triple quadrupole mass spectrometer (MS/MS) for detection, was developed and validated for the determination of free LPV in human plasma (range of 0.25 to 80 ng/mL). Sample preparation involved equilibrium dialysis, the addition of a labeled isotope internal standard (Lopinavir d-8, IS), and a simple protein precipitation method using acetonitrile. The sample was dried down and reconstituted in 100 μL of 50/50 acetonitrile/water to concentrate the sample. Reversed phase chromatographic separation of LPV and IS was performed on an Atlantis® dC18 2.1 × 100 mm column under isocratic conditions. A binary mobile phase was used consisting of 20% 0.1% formic acid in water and 80% 0.1% formic acid in acetonitrile. The detection and quantitation was achieved for LPV and IS by multiple reaction monitoring (MRM). The de-protonated molecular ions [M-H]- were monitored at m/z 629.5 → 447.1 for LPV, and 637.5 → 447.2 for IS. These provided adequate sensitivity with minimal interference from endogenous matrix components.
In study 1 (S1), 16 patients underwent intensive plasma sampling (1, 2, 3, 4, 6, 8, 10 and 12 hr post dose) at 2 and 16 weeks post treatment initiation. The study population, design and enrollment criteria have been previously reported [9]. In study 2 (S2), 20 patients underwent plasma sampling (-2, 0, 1, 2, 3, 4 hr) on day 1 (second dose) and at weeks 2 and 24. In S2, intensive HIV-1 RNA sampling was also performed. Pre-dose (time 0) AAG and HIV-1 RNA samples were obtained and the first dose of a LPV/RTV-based ARV regimen was administered during a 48-hour clinic visit. All S2 participants also received tenofovir disoproxil fumarate and emtricitabine. Intensive HIV-1 RNA samples were collected at hours 2, 4, 6, 12, 18, 24, 30, 36, 42, and 48, and days 3, 4, and 7. Additional HIV-1 RNA samples were collected at weeks 2, 3, 4, 8, 12, 16, 20, and 24. CD4 T-cell counts were obtained at baseline and weeks 8, 16, and 24 as per standard of care. Follow-up AAG and pharmacokinetic samples were collected at weeks 2 and 24.
Thirty six subjects from both studies were available for population pharmacokinetic analysis, and 20 of the S2 subjects had intensive HIV-1 RNA sampling. Thirty five subjects were used for pharmacokinetic analysis: one subject with very low LPV concentrations (suggesting poor adherence) was excluded. Nineteen subjects from S2 were used for pharmacokinetic/pharmacodynamic analyses. One subject with 10 viral load measurements above the limit of quantitation was removed. Five viral load measurements from three different subjects were excluded due to likely problems with adherence.
2.2 Mathematical Modeling
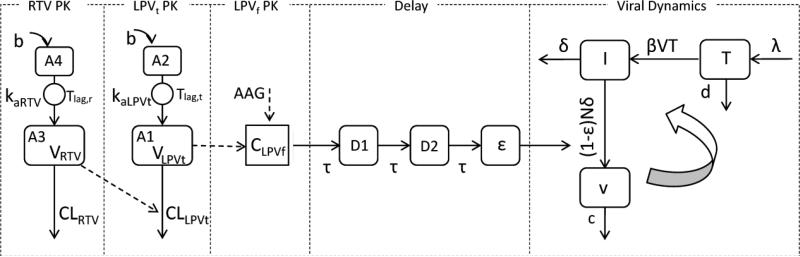
The population model was developed sequentially by first creating a joint model for LPVt and RTV, followed by an independent model relating AAG and LPVt with LPVf. A viral dynamic model was then developed simultaneously with CD4 cell count results and integrated with the submodels to construct the composite final Pharmacokinetic/Pharmacodynamic model depicted in Figure 1. As indicated in Figure 1, LPVt CLLPVt/F depends on the concentration of ritonavir (CRTV), where LPVf concentration (CLPVf) is a function of both LPVt (CLPVt) and AAG. The LPV effect on viral dynamics was modeled by linking CLPVf through transit delay compartments.
Figure 1.
Structure of the final integrated pharmacokinetic-pharmacodynamic model defined by Eqs. (1-11). (RTV: ritonavir; LPVt: total lopinavir; LPVf: free lopinavir; b: bolus input; A1: central compartment of LPVt; A2 depot compartment of LPVt; A3: central compartment of RTV; A4: depot compartment of ; CLLPVt: Clearance of LPVt with ritonavir effect; RTV; CLRTV: clearance of RTV; VRTV: volume distribution of RTV central compartment; VLPVt: volume distribution of LPVt central compartment; CLPVf: concentration of LPVf; kaLPVt: absorption rate constant of LPVt; kaRTV: absorption rate constant of RTV; Tlag,t: absorption lag time of LPVt; Tlag,r: RTV absorption lag time; AAG: α-1-acid glycoprotein; CLPVf: free lopinavir concentration; D1 and D2: delay compartments. mean transit time; T: CD4+ T-cells; I: infected CD4+ T-cells; v free virions; λ the rate of new T cells are generated in the body; d the death rate of T cells; β the infection rate; δ the death rate of infected CD4+ T-cells; c: the clearance rate of free virions; N: the number of new virions produced by each infected CD4+ T-cell during its lifetime; ε the drug inhibit efficacy.
Population analysis was used to develop each of the four components of the overall pharmacokinetic/pharmacodynamic model. Maximum likelihood estimates for model parameters were obtained through the application of the expectation maximization algorithm to the parametric, nonlinear mixed-effects maximum likelihood model, as proposed and developed by Schumitzky [10] and Walker [11] and implemented in ADAPT (version 5, MLEM module) [12]. Model parameters were assumed to follow a multivariate log-normal distribution, with stage 1 random error taken to be normally distributed with a proportional plus additive error variance.
The following covariates collected at baseline were evaluated for their ability to explain the interindividual variability (IIV) in base model parameters: sex, age, race, weight, height, BMI (body mass index), serum creatinine, creatinine clearance, and hepatic enzymes aspartate aminotransferase (AST) and alanine aminotransferase (ALT). The criterion for a covariate to be added to the final model was a decrease of more than 3.84 in minus two loglikelihood value (-2LL), which corresponds to a P value of 0.05 (log likelihood ratio test). Finally, a stepwise backward elimination was carried out. The criteria for a covariate to remain in the final model was P<0.01, corresponding to a decrease of 6.63 in the -2LL.
Model evaluation was assessed using prediction corrected visual predictive check (pcVPC) [13] with NONMEM (version VII) , Perl speaks NONMEM (PsN, version 3.4.2) [14], and Xpose (version 4.4.0) [15] (1000 data sets were simulated). The 95% confidence interval of the median, 5th and 95th percentile of the simulated concentrations at different times were calculated and compared with the prediction corrected observations.
2.2.1 Pharmacokinetic Models
Data from S1 and S2 were used for population modeling of LPVt and RTV. Initially, separate models for LPVt and RTV were established by considering one and two compartment models with and without an absorption lag phase (model selection based on the likelihood ratio test). Next, a joint model of LPVt and RTV (LPVt/RTV) was developed using LPVt and RTV measurements simultaneously by examining various models to represent the relationship between RTV concentrations and LPVt clearance [16]. The following equations (1-4) represent the joint model for both drugs, including an exponential term for the effect of RTV concentration on LPVt clearance:
| (1) |
| (2) |
| (3) |
| (4) |
In the above equations, A1 and A2 are the amount of LPVt in the measured (central) and absorption compartments, respectively, while A3 and A4 represent the amounts of RTV in the measured and absorption compartments, respectively (all amounts in mg). In Eq. (1), CLLPVt0 (L/h) is the typical LPVt clearance and is used to explain the effect of RTV (CRTV, which equals A3/VRTV in mg/L) on LPVt clearance.
The value 299 in Eq. 1 is the median RTV concentration and C1 is the RTV effect coefficient. CLRTV (L/h) is the clearance of RTV, while VLPVt (L) and VRTV (L) are the distribution volumes of LPVt and RTV, and kaLPVt (h-1) and kaRTV (h-1) are the LPVt and RTV absorption rate constants. Throughout the model, CL and V terms represent apparent clearance and volume (CL/F and V/F) for LPVt and RTV as well as LPVf.
2.2.2 AAG - Dependent LPVf Model
The model relating both LPVf and LPVt to AAG assumes that LPVf is in rapid equilibrium with LPVt. A separate population analysis relating measured LPVt and AAG concentrations (model inputs) to LPVf concentrations (observations) was conducted using the pooled data from S1 and S2, and the following model was selected based on previously reported data[17]:
| (5) |
where fu0 is the fraction of unbound LPV at the median AAG (91.8 mg/dL) and p1 is the slope for AAG.
2.2.3 HIV-1 Viral Dynamic Model
To describe the measured plasma HIV-1 RNA concentrations and the CD4+ T-cell counts obtained in S2, we adopted, with slight modification, the following previously reported model [18, 19], representing HIV and immune system dynamics during antiviral treatment.
| (6) |
| (7) |
| (8) |
These three differential equations represent target CD4+ T-cells (T, cells/μL), infected CD4+ T-cells (I, cells/μL) and free virions (v, copies/mL). The measured CD4 count data is the combined total of states T and I. The parameter λ (mL/h) is the rate of formation new CD4+ T-cells, d (h-1) is the death rate of CD4+ T-cells, β (mL/h/virion) is the infection rate, δ (h-1) is the death rate of infected CD4+ T-cells, c (h-1) is the clearance rate of free virions, N (particles/h) is the number of new virions produced by each infected CD4+ T-cell during its lifetime, and ε represents the concentration of free drug required to inhibit viral replication (efficacy). To account for the delay between the initiation of therapy and the observed decrease in viral load, mainly attributed to the time required for the completion of the viral replication cycle in productively infected cells [20], several transit delay compartments where used to link CLPVf to the efficacy term ε. The transduction delay model is as follows:
| (9) |
| (10) |
| (11) |
where D1 and D2 are the signals in the delay compartments, Imax is the maximum inhibition effect of LPVf (fixed at 1 assuming no escaping virus routes ), IC50 is the concentration at half Imax, γ is the hill coefficient, (h) is the mean transit time for each compartment, and CLPVf is the predicted LPVf concentration. The latter was determined for each patient via a separate population analysis (one compartment model with lag time) using measured LPVf concentrations. For model building, 2, 3 and 4 transit delay compartments were evaluated. It was assumed that only LPV, not RTV, acts on the virus since the in vitro antiviral IC50 of LPV is approximately 10-fold lower than that of ritonavir [6]. It was further assumed that the viral dynamics are at steady state prior to the initiation of therapy, at least relative to the time course of drug action, and therefore the following relationships can be derived from Eqs. (6-8)
| (12) |
where T0, I0 and v0 are the initial value of target CD4+ T-cells, infected CD4+ T-cells, and viral load, respectively.
2.3 Exposure-Response Simulations
Simulation studies were conducted to explore exposure-response relationships using the LPVf, the AAG-dependent LPVf, and the viral dynamic models. Simulated LPV doses ranged from 5 mg to 700 mg twice daily (18 different doses). The pharmacodynamic determinant of response was the decrease in log10 time averaged area under the viral load-time curve from 0 to 7 days (AUC0-7days) minus baseline (AAUCMB) [21, 22] of HIV-1 RNA. The AAUCMB was determined for each patient using their estimated population mean values of viral dynamic model and AAUCMB was used to determine the average viral load decrease over the first 7 days of treatment. The goal of these simulations was to link the LPVf 12 hour steady-state concentrations (Cf12h) to changes in AAUCMB and determine the corresponding LPVt 12 hour steady state concentration (Ct12h) required to produce 50% (EC50), 90% (EC90), and 95% (EC95) of the maximum drug effect (Emax). The exposure-response relationship of Cf12h and decrease in AAUCMB was fitted using the following Emax model:
| (13) |
where Emax is the maximum response, EC50 is Cf12h that corresponds to 50% of Emax, and hill describes the shape of the sigmoid curve. The Cf12h EC90 and EC95 values were calculated from Eq. (13) using the estimated values of EC50 and hill. The corresponding EC95 for Ct12h was calculated using the AAG-dependent LPVf model (eq. (5)), for the median and range of Cf12h and AAG measurements in this study.
3. Results
3.1 Demographic and Baseline Data
Of the 35 subjects included in the pharmacokinetic modeling analysis, 25 were male and 10 were female, 31 were African American and 4 were Caucasian. Table 1 lists baseline values for several clinical variables. A total of 1218, 1236, 575 and 165 samples of RTV, LPVt, LPVf and AAG respectively, were collected and used for the pharmacokinetic analysis. In S2, a total of 412 measurements of HIV-1 RNA and 63 measurements of CD4 T-cell counts from 19 subjects were used for modeling. Changes in plasma HIV-1 RNA over time are shown in Supplementary Fig. 1.
Table 1.
Baseline Demographics and Clinical Characteristics
| Characteristics | Median (interquartile range) |
|---|---|
| Age (yr) | 38.5 (33.8-47.3) |
| Weight (kg) | 64.5 (59.6-74.3) |
| Body mass index (kg/m2) | 22.5 (21.4-24.9) |
| Log10 HIV-1 RNA PCRa (copies/mL) | 5.18 (4.73-5.61) |
| Plasma α-1-acid glycoprotein (AAG) (mg/dL) | 91.8 (67.4-134.) |
| Baseline CD4 + T-cell counts (cells/μl) | 69.0 (20.5-153.) |
| Creatinine clearanceb (mL/min) | 99.3 (73.0-124.) |
| Aspartate amino transferase (mg/dL) | 29.5 (24.0-52.6) |
| Alanine amino transferase (mg/dL) | 30.5 (21.0-53.8) |
| Fraction of unbound lopinavir (%) | 0.730 (0.540-0.953) |
PCR: polymerase chain reaction
Creatinine clearance calculated by the Cockroft-Gault equation.
3.2 Mathematic Models
3.2.1 Pharmacokinetic Models
LPVt and RTV plasma concentrations were each well described by a one-compartment model with an absorption lag. A proportional model was used to describe the residual error variance. For the LPVt base model the population mean (IIV CV%) of clearance (CLLPVt/F), volume (VLPVt/F), absorption rate constant (kaLPVt) and lag time (Tlag,t) were 4.45 (34.6) L/h, 52.2 (54.9) L, 0.358 (77.7) h-1 and 0.826 (59.8) h, respectively.
The combined LPVt/RTV model was constructed sequentially (the RTV model was established and its parameters fixed at their conditional mean estimates for each subject to develop the combined model) and includes BMI as a significant covariate (reduction of 9.81 in -2LL) explaining some of the variability in CLLPVt0 as follows:
| (14) |
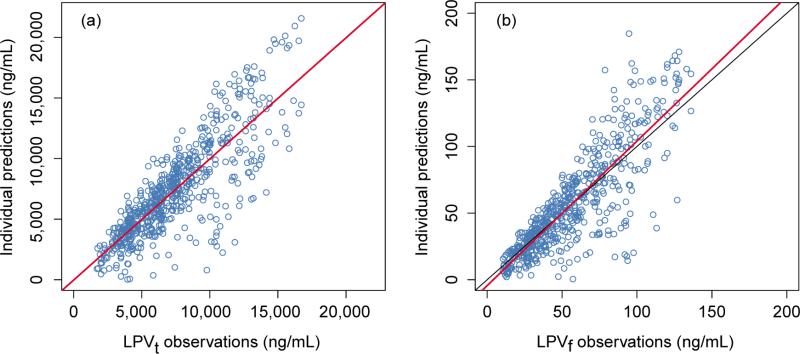
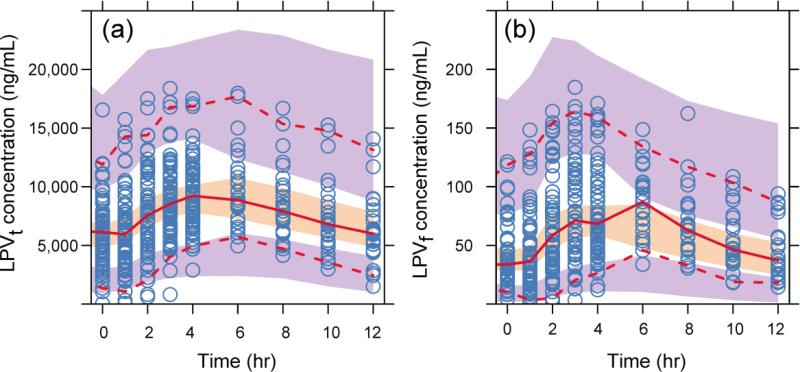
where CLLPVt1 is typical clearance at median BMI (22.5 kg/m2) and CLLPVt2 is the coefficient of BMI effect. The population parameter estimates of the combined LPVt/RTV model are shown in Table 2 (BMI was not a significant covariate in the RTV analysis). The absorption rate constant (kaLPVt) and lag time (Tlag,t) for LPVt were both fixed to their individual conditional mean values from the separate LPVt modeling in developing the integrated LPVt/RTV model. An exponential term was used to incorporate the effect of RTV concentration on the clearance of LPVt (see Eq. (1)). At the median values of BMI (22.5 kg/m2) and plasma RTV concentration (299 ng/mL), the model predicts LPVt CL to be 4.73 (L/h). Figure 2 displays the individual prediction goodness of fit plots of LPVt and LPVf concentrations for the combined LPVt/RTV model. The population prediction goodness of fit plots are presented in Supplementary Fig. 2. The prediction corrected visual predictive check (pcVPC) for LPVt and LPVf are shown in Figure 3, which represent the combination of week 2 and week 16 for S1, and week 2 and week 24 for S2.
Table 2.
Population Estimation Results for the Final Combined Pharmacokinetic-Pharmacodynamic Model.
| Parametera | Mean (%RSE)e | IIV CV%(%RSE)e | Literature values | Reference |
|---|---|---|---|---|
| CLLPVt0 (L/h) | -- | 24.0 (61.8) | ||
| CLLPVt1 | 4.73 (14.6) | -- | 3.2-5.22 | [25-29] |
| CLLPVt2 | 0.055 (34.5) | -- | NA | |
| C1 | 6.24E-04 (47.5) | 28.3 (259.) | NA | |
| VLPVt (L) | 55.7 (15.2) | 55.2 (30.7) | 42.6-61.6 | [5, 16, 25, 27] |
| KaLPVt (1/h)c | 0.325 | -- | 0.267-0.564 | [5, 26, 27] |
| Tlag,t (h)c | 0.875 (32.7) | 60.5 (63.2) | NA | |
| CLRTV (L/h) | 22.0 (11.9) | 50.5(18.3) | 8.00-24.3 | [16, 29, 33, 34] |
| Vrtv (L) | 177. (29.3) | 61.7 (41.5) | 81-275 | [33, 34] |
| KaRTV (1/h) | 0.740 (47.0) | 107. (56.6) | 0.898-1.57 | [33, 34] |
| Tlag,r (h) | 1.10d (52.3) | 69.8(64.6) | 1.05-1.96 | [33, 34] |
| fu0 | 0.00930 (4.48) | 23.4 (18.3) | NA | |
| p1 | 1.13E-05 (25.7) | 103. (31.4) | NA | |
| c (1/h) | 0.0350 | 39.3 | 0.0138 - 1.67 | [24, 35] |
| IC50 (ng/mL) | 5.84 | 53.1 | 3-7 | [6] |
| τ (h) | 3.22 | 41.6 | NA | |
| d (1/h) | 2.5E-04b | -- | 4.17E-05 - 4.17E-04 | [24, 36] |
| Δ (1/h) | 0.00288 | 61.6 | 0.00416 - 0.029 | [24, 35, 37, 38] |
| γ | 1.88 | 19.2 | NA | |
| β (mL/h/virion) | 4.79E-09 | 217. | 8.3E-10 - 1.25E-8 | [24] |
| γ (mL/h) | 75.0 | 75.3 | 5.83 - 129 | [24] |
| N (particles/h) | 19.2 | 183. | 4.17 - 292 | [39, 40] |
LPVt: total lopinavir; RTV: ritonavir; CLLPVt0: LPVt clearance; CLLPVt1: typical clearance of LPVt with median BMI (body mass index); CLLPVt2: coefficient of BMI effect.; c1: the coefficient of RTV effect; VLPVt : distribution volume of LPVt; kaLPVt: absorption rate constant of LPVt ; Tlag,t: absorption lag time of LPVt; CLRTV: clearance of RTV ;VRTV : RTV distribution volume; kaRTV: RTV absorption rate constant; Tlag,r: RTV absorption lag time; fu0: fraction of unbound drug with median α-1-acid glycoprotein [AAG (91.8 mg/dL)] , and p1 is slope for AAG; c: the clearance rate of free virions; Imax: the maximum inhibition effect of free lopinavir (LPVf); IC50: LPVf concentration at half Imax; τ mean transit time; d: the death rate of T cells; Δ death rate of infected CD4 cells; γ : hill coefficient; β infection rate; Λ: rate of new T cells are generated in the body; N: number of new virions produced by each infected CD4 cell during its lifetime.
Fixed from reference [24].
kaLPVt at and Tlag,t obtained from LPVt model with BMI as a covariate.
The maximum of Tlag,r was limited to 1.5 hours.
IIV: Inter-individual variability; CV: coefficient of variation; RSE: relative standard error.
NA. Not avaliable.
Figure 2.
The goodness of fit of individual predictions plots for the combined total lopinavir/ritonavir (LPVt/RTV) model (a) and the free lopinavir (LPVf) model (b). Symbols are the observed data; the red lines are the linear regression fit; the black lines are the lines of unity.
Figure 3.
Prediction corrected visual predictive check of the combined total lopinavir/ritonavir (LPVt/RTV) model (a) and free lopinavir (LPVf) (b). The middle solid line is the median. The dash lines are the 5th and 95th percentiles of observed data. The shaded areas are the corresponding 95% confidence intervals of the simulated data.
3.2.2 AAG-Dependent LPVf Model
The LPVt and LPVf plasma concentration data from S1 and S2 were pooled, along with the associated AAG measurements, and a separate population analysis using Eq. (5) resulted in model parameter estimates shown in Table 2 (goodness of fit plots presented in Supplementary Fig. 3). Simulated fu as a function of AAG for each individual were also performed. The individual predictions over the AAG range measured in each subject are shown in Supplementary Fig. 4. The AAG-dependent LPVf model found that over the range of AAG values in the two studies (23.6 to 479 mg/dL) there is a significant effect of AAG on binding with fu values ranging from 0.00903 to 0.00389, which is consistent with prior protein-free LPV studies [23].
3.2.3 HIV-1 Dynamic Model
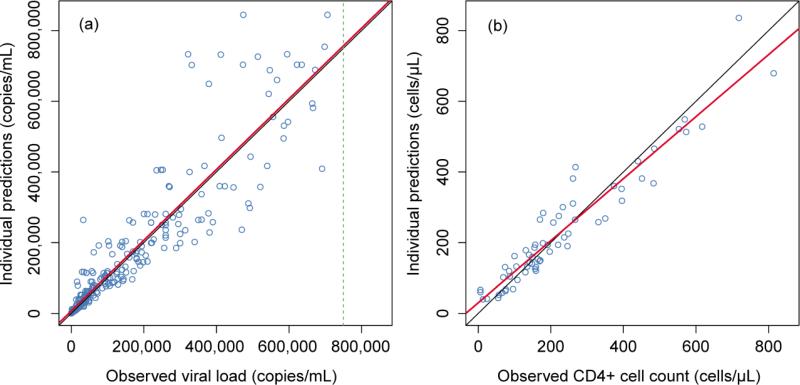
Table 2 lists the viral dynamic parameters derived using individual conditional mean values obtained from the LPVf and viral dynamic models from Eqs. (6-11). In this analysis, d and delta could not be simultaneously estimated because CD4 cell count data was modeled using the combined total of states T and I. As a result, death rate of T cells (d) was fixed at reference value [24]. The resulting individual prediction goodness of fit plots for viral load and CD4 cell count are shown in Figure 4. Relative standard errors could not be calculated for the limited CD4+ cell results due to high variability. Despite this limitation, the viral load dynamic model described the time course of measured HIV-1 RNA data with reasonable fidelity, as indicated by the individual prediction plot (see Supplementary fig. 5). Moreover, estimated parameter values are generally comparable to those reported in several other studies as shown in Table 2. Results of the independent compartment model describing LPVf pharmacokinetics were used as parameter input for developing the HIV viral dynamic model presented in Table 3.
Figure 4.
Goodness of fit of individual predictions plots for viral load (a) and CD4 cell count (b). The symbols are the observed data; the red lines are the linear regression; the black lines are the line of unity; dashed line is the upper limit of HIV-1 RNA quantitation.
Table 3.
Population Estimation Results for LPVf Model
| Parametera | Mean (%RSE)b | IIV CV% (%RSE)b |
|---|---|---|
| CLLPVf (L/h) | 596. (9.61) | 41.0 (17.2) |
| VLPVf (L) | 6370 (15.9) | 52.6 (26.3) |
| kaLPVf (1/h) | 0.884 (47.5) | 120. (95.6) |
| Tlag,f (h) | 1.05 (15.0) | 45.1 (48.8) |
IIV: Inter-individual variability; CV: coefficient of variation; RSE: relative standard error.
CLLPVf: free LPV (LPVf) clearance; VLPVf : LPVf distribution volume; kaLPVf: absorption rate constant; Tlag,f: absorption lag time.
3.2.4 Simulated Exposure-Response Model
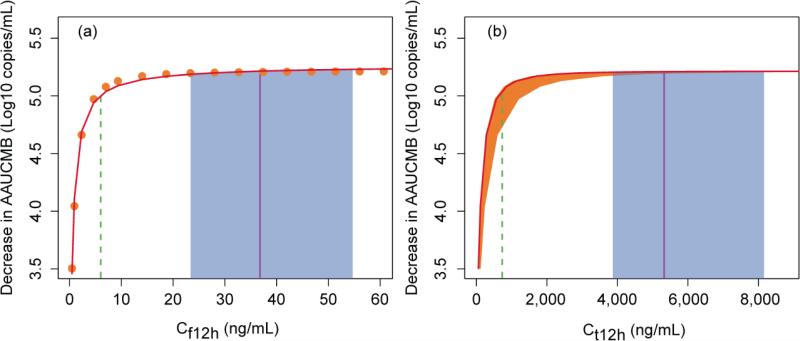
Based on the viral dynamic model simulation, the AAUCMB and Cf12h with LPV dose ranging from 5 mg to 700 mg twice daily were obtained. The plot of decrease in AAUCMB vs. Cf12h is shown in Figure 5 (a). A sigmoid Emax model successfully described the decrease in AAUCMB relative to Cf12h (exposure-response). The estimated Emax was a decrease in the AAUCMB of 5.28 log10 copies/mL, hill was 0.899, and the EC50 for Cf12h was 0.227 ng/mL. The calculated EC90 and EC95 for Cf12h were 2.61 and 6.00 ng/mL, respectively. Figure 5 (b) depicts the decrease in AAUCMB vs. Ct12h. The estimated EC50, EC90, and EC95 for Ct12h at the median (range) AAG concentration were 27.5 (25.1-58.3), 316 (289-672), and 726 (664-1542) ng/mL, respectively. The median LPVf and LPVt concentrations (interquartile range) at 12 hours post-dose at steady state were 368 (23.4-547) and 5327 (3870-8157) ng/mL, respectively.
Figure 5.
Relationship between 12 hour steady-state concentrations of free lopinavir (Cf12h) (a), total lopinavir (Ct12h) (b) and exposure [expressed as decrease in area under the viral load-time curve minus baseline (AAUCMB)] at day 7. The symbols and the solid red curve in (a) are the predicted Cf12h and sigmoid Emax fitted line, respectively. The Ct12h was calculated by eq. (5) with Cf12h and α-1-acid glycoprotein (AAG). The solid red curve and shaded orange area around the curve corresponds to the median (range) AAG of 91.8 (23.6-479) mg/dL in (b). The vertical dash green, solid purple line and shaded blue areas are the estimated EC95, observed median and interquartile range of Cf12h and Ct12h at lopinavir/ritonavir 400/100 mg, respectively.
4. Discussion
4.1 Pharmacokinetic Models
The population pharmacokinetic model parameter estimates for LPVt and RTV compared well with previously reported literature values. The estimated clearance of LPVt from the final model in this work is 4.73 L/h, compared to prior CL/F values ranging from 3.2 to 5.22 L/h [25-29]. Distribution volume for LPVt has been reported ranging from 42.6 to 61.6 L, [5, 25, 27] which is similar to our result of 55.7 L. The LPVt absorption rate (KaLPVt) shown in Table 2 is 0.325 h-1, which is also within the previously reported range of 0.267 to 0.564 h-1 [5, 26]. While there have been no previously reported compartmental models for LPVf pharmacokinetic on which to base a comparison of the results of our model presented in Table 2, several published studies have reported AUC values for LPVf following therapy with LPV/RTV. The estimated AUC0-12h obtained via simulation from our model is 414 ng·h/mL, while Boffito et al [30] reported an AUC0-12h result of 890.14 ng·h/mL, considerably higher than our result. However, this difference could be attributable to the different unbound fractions between the two studies: 0.92% vs. 0.73% (current studies). The differences in fraction unbound may itself be due to the differences in AAG ranges observed across patients in the two studies: 58–116 mg/dL vs. 23.6-479 mg/dL in the current studies. Of note, our studies enrolled treatment-naïve patients with advanced disease as evidenced by a baseline median CD4+ T-cell counts of 69 cells/μL. HIV-1 induced immune activation up-regulates AAG synthesis. Conversely, down regulation in immune activation following ARV therapy decreases AAG synthesis [2, 31]. Thus participants in our studies likely had higher baseline AAG concentrations due to their advanced disease and treatment-naïve status. Methodological differences may have also played a role in the different free AUC0-12h results, as our studies employed equilibrium dialysis compared with ultrafiltration.
4.2 AAG-Dependent LPVf Model
An independent population analysis was performed to develop a model relating measured LPVt and AAG concentrations to LPVf concentrations (see Table 2 and Figure 4). A linear model (see Eq. (5)) best described the individual data over the AAG range of our studies. The data and modeling results presented herein suggest that variations in AAG concentrations could result in clinically significant changes in LPV pharmacokinetics. The model predicts that over the range of AAG values across the two studies there is a significant effect of AAG on LPV binding, with fu ranging from 0.00903 to 0.00389 (a 2.3 fold difference). Using the AAG-dependent LPVf model, the LPVf exposure changes can be predicted from AAG and CLPVt measurements.
4.3 HIV-1 Dynamic Model
In this work, we established a viral dynamic model to describe the viral load trajectory based on LPVf plasma concentration. This is the first analysis utilizing LPVf concentrations as the drug exposure metric linked to a HIV-1 viral dynamic model. The estimated drug efficiency and other viral dynamic parameters obtained in this study are in general agreement with other values reported in the literature as indicated in Table 2, with the exception of the death rate of infected CD4+ T-cells, which is smaller than the lowest value previously reported. The model estimated LPVf EC50 is 5.84 ng/mL, which is consistent with the prescribing information for Kaletra from the US Food and Drug Administration[6] that indicates a range of LPVf concentrations of 3-7 ng/mL against several HIV-1 subtype B clinical isolates. In the presence of 50% human serum, the mean EC50 of LPV against five laboratory strains ranged from 40-180 ng/mL.
4.4 Simulated Exposure-Response Model
The median (interquartile range) of observed LPV Ct12h at 400 mg (with 100 mg RTV) is 5327 (3870-8157) ng/mL. In contrast, the estimated Ct12h required to achieve the EC95 was 726 (664-1542) ng/mL at the median (range) AAG concentration in these two studies of 91.8 (23.6-479) mg/dL. Figure 5 depicts the simulated exposure-response relationship for LPVf (a) and LPVt (b). Despite the wide range of AAG results, the 25th percentile of observed Ct12h (3870 ng/mL) was considerably greater than the modeled EC95 of LPVt; even the 5th percentile of observed Ct12h (1909 ng/mL) was 2.6 times greater than the EC95 of LPVt. The simulated LPVt EC50 was 27.5 ng/mL, which is lower than but relatively close to the range stated against different laboratory strains with 50% human serum and nearly identical to the protein binding corrected EC50 (31 ng/mL) derived from a separate in vitro susceptibility study [32].
5. Conclusions and Clinical Implications
Collectively, these modeling and simulation results demonstrate in part why LPV/RTV is a highly effective PI treatment regimen. As seen in Figure 5, observed trough concentrations consistently exceed, by a large margin, the concentrations required to durably suppress HIV-1 replication in vivo. This creates some flexibility for patients receiving the drug, as deviations from a strict every 12 hour dosing schedule are unlikely to significantly affect clinically outcomes. Importantly, this modeling and simulation approach could serve as a surrogate for determining clinically significant target drug exposures that must be achieved and maintained for durable therapeutic success and to prevent drug resistant viral strains. Concentration-response relationships for many ARVs are scarce or non-existent. Our approach demonstrates that even for an ARV drug (particularly PIs) already approved for use at a fixed dose, it is possible to model and simulate minimum effective trough concentrations using data collected from well-designed clinical trials in a relatively small number of participants.
Supplementary Material
Acknowledgments
Supported by National Institutes of Health grants 1K23 A1073119 (IO), 5K12 RR017643 (IO), 1U01AI103408-01 (IO), P41-EB001978 (DZD), KL2TR000455 (ANS), UL1TR000454(ANS), Emory University CFAR (NIH P30 A1050409), and the Atlanta Clinical and Translational Science Institute (NIH MO1 RR00039). We would like to acknowledge the individuals that participated in these studies. Without their dedication this work could not have been accomplished.
Footnotes
Conflicts of Interest:
All authors declare no conflicts or interest
References
- 1.AIDSinfo . Guidelines for the use of antiretroviral agents in HIV-1-infected adults and adolescents. Department of Health and Human Services; 2013. [6th July 2013]. Available at http//aidsinfo.nih.gov/ContentFiiles/AdultandAdolescentGL.pdf. [Google Scholar]
- 2.Kushner I. The phenomenon of the acute phase response. Annals of the New York Academy of Sciences. 1982;389:3–9-48. doi: 10.1111/j.1749-6632.1982.tb22124.x. [DOI] [PubMed] [Google Scholar]
- 3.Benet LZ, Hoener BA. Changes in plasma protein binding have little clinical relevance. Clinical pharmacology and therapeutics. 2002 Mar;71(3):1–15-21. doi: 10.1067/mcp.2002.121829. [DOI] [PubMed] [Google Scholar]
- 4.Belpaire FM, Bogaert MG. Pharmacokinetic and pharmacodynamic consequences of altered binding of drugs to alpha 1-acid glycoprotein. Progress in clinical and biological research. 1989;300:3–37-50. [PubMed] [Google Scholar]
- 5.Crommentuyn KM, Kappelhoff BS, Mulder JW, et al. Population pharmacokinetics of lopinavir in combination with ritonavir in HIV-1-infected patients. British journal of clinical pharmacology. 2005 Oct;60(4):3–78-89. doi: 10.1111/j.1365-2125.2005.02455.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.FDA [26th March 2013]; prescribing information for KALETRA. Reference ID: 2909830. [cited; Available from: www.accessdata.fda.gov/drugsatfda_docs/label/2011/021251s039,021906s032lbl.pdf]
- 7.Sham HL, Kempf DJ, Molla A, et al. ABT-378, a highly potent inhibitor of the human immunodeficiency virus protease. Antimicrobial agents and chemotherapy. 1998 Dec;42(12):3–218-24. doi: 10.1128/aac.42.12.3218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ofotokun I, Chuck SK, Binongo JN, et al. Lopinavir/Ritonavir pharmacokinetic profile: impact of sex and other covariates following a change from twice-daily to once-daily therapy. Journal of clinical pharmacology. 2007 Aug;47(8):9–70-7. doi: 10.1177/0091270007302564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Ofotokun I, Lennox JL, Eaton ME, et al. Immune activation mediated change in alpha-1-acid glycoprotein: impact on total and free lopinavir plasma exposure. Journal of clinical pharmacology. 2011 Nov;51(11):1–539-48. doi: 10.1177/0091270010385118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Schumitzky A. EM Algorithms and two stage methods in pharmacokinetic population analysis. In: D'Argenio DZ, editor. Advanced methods of pharmacokinetic and pharmacodynamic systems analysis. Vol. 2. Plenum Press; New York: 1995. pp. 6–0. [Google Scholar]
- 11.Walker S. An EM Algorithm for Nonlinear Random Effects Models. Biometrics. 1996;52(3):9–34-44. [Google Scholar]
- 12.D'Argenio D, Schumitzky A, Wang X. ADAPT 5 user's guide: pharmacokinetic/pharmacodynamic systems analysis software. Biomedical Simulations Resource; Los Angeles: 2009. [Google Scholar]
- 13.Bergstrand M, Hooker AC, Wallin JE, et al. Prediction-corrected visual predictive checks for diagnosing nonlinear mixed-effects models. The AAPS journal. 2011 Jun;13(2):1–43-51. doi: 10.1208/s12248-011-9255-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Lindbom L, Ribbing J, Jonsson EN. Perl-speaks-NONMEM (PsN)--a Perl module for NONMEM related programming. Computer methods and programs in biomedicine. 2004 Aug;75(2):8–5-94. doi: 10.1016/j.cmpb.2003.11.003. [DOI] [PubMed] [Google Scholar]
- 15.Jonsson EN, Karlsson MO. Xpose--an S-PLUS based population pharmacokinetic/pharmacodynamic model building aid for NONMEM. Computer methods and programs in biomedicine. 1999 Jan;58(1):5–1-64. doi: 10.1016/s0169-2607(98)00067-4. [DOI] [PubMed] [Google Scholar]
- 16.Zhang C, Denti P, Decloedt E, et al. Model-based approach to dose optimization of lopinavir/ritonavir when co-administered with rifampicin. British journal of clinical pharmacology. 2012 May;73(5):7–58-67. doi: 10.1111/j.1365-2125.2011.04154.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Baker SD, Li J, ten Tije AJ, et al. Relationship of systemic exposure to unbound docetaxel and neutropenia. Clinical pharmacology and therapeutics. 2005 Jan;77(1):4–3-53. doi: 10.1016/j.clpt.2004.09.005. [DOI] [PubMed] [Google Scholar]
- 18.Wu H, Huang Y, Acosta EP, et al. Modeling long-term HIV dynamics and antiretroviral response: effects of drug potency, pharmacokinetics, adherence, and drug resistance. Journal of acquired immune deficiency syndromes. 2005 Jul 1;39(3):2–72-83. doi: 10.1097/01.qai.0000165907.04710.da. [DOI] [PubMed] [Google Scholar]
- 19.Bonhoeffer S, May RM, Shaw GM, et al. Virus dynamics and drug therapy. Proceedings of the National Academy of Sciences of the United States of America. 1997 Jun 24;94(13):6–971-6. doi: 10.1073/pnas.94.13.6971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Fang J, Jadhav PR. From in vitro EC50 to in vivo dose-response for antiretrovirals using an HIV disease model. Part I: a framework. Journal of pharmacokinetics and pharmacodynamics. 2012 Aug;39(4):3–57-68. doi: 10.1007/s10928-012-9255-3. [DOI] [PubMed] [Google Scholar]
- 21.Weller S, Radomski KM, Lou Y, et al. Population pharmacokinetics and pharmacodynamic modeling of abacavir (1592U89) from a dose-ranging, double-blind, randomized monotherapy trial with human immunodeficiency virus-infected subjects. Antimicrobial agents and chemotherapy. 2000 Aug;44(8):2–052-60. doi: 10.1128/aac.44.8.2052-2060.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Gieschke R, Fotteler B, Buss N, et al. Relationships between exposure to saquinavir monotherapy and antiviral response in HIV-positive patients. Clinical pharmacokinetics. 1999 Jul;37(1):7–5-86. doi: 10.2165/00003088-199937010-00005. [DOI] [PubMed] [Google Scholar]
- 23.Gulati A, Boudinot FD, Gerk PM. Binding of lopinavir to human alpha1-acid glycoprotein and serum albumin. Drug metabolism and disposition: the biological fate of chemicals. 2009 Aug;37(8):1–572-5. doi: 10.1124/dmd.109.026708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Funk GA, Fischer M, Joos B, et al. Quantification of in vivo replicative capacity of HIV-1 in different compartments of infected cells. Journal of acquired immune deficiency syndromes. 2001 Apr 15;26(5):3–97-404. doi: 10.1097/00126334-200104150-00001. [DOI] [PubMed] [Google Scholar]
- 25.Takahashi M, Kudaka Y, Okumura N, et al. Pharmacokinetic parameters of lopinavir determined by moment analysis in Japanese HIV type 1-infected patients. AIDS research and human retroviruses. 2008 Jan;24(1):1–14-5. doi: 10.1089/aid.2007.0176. [DOI] [PubMed] [Google Scholar]
- 26.Dailly E, Reliquet V, Raffi F, et al. A population approach to study the influence of nevirapine administration on lopinavir pharmacokinetics in HIV-1 infected patients. European journal of clinical pharmacology. 2005 Apr;61(2):1–53-6. doi: 10.1007/s00228-005-0900-2. [DOI] [PubMed] [Google Scholar]
- 27.Bouillon-Pichault M, Jullien V, Azria E, et al. Population analysis of the pregnancy-related modifications in lopinavir pharmacokinetics and their possible consequences for dose adjustment. The Journal of antimicrobial chemotherapy. 2009 Jun;63(6):1–223-32. doi: 10.1093/jac/dkp123. [DOI] [PubMed] [Google Scholar]
- 28.Ng J, Chiu YL, Awni W, et al. Pharmacokinetics and safety of the lopinavir/ritonavir tablet 500/125 mg twice daily coadministered with efavirenz in healthy adult participants. Journal of clinical pharmacology. 2012 Aug;52(8):1–248-54. doi: 10.1177/0091270011410568. [DOI] [PubMed] [Google Scholar]
- 29.Overton ET, Tschampa JM, Klebert M, et al. The effect of acid reduction with a proton pump inhibitor on the pharmacokinetics of lopinavir or ritonavir in HIV-infected patients on lopinavir/ritonavir-based therapy. Journal of clinical pharmacology. 2010 Sep;50(9):1–050-5. doi: 10.1177/0091270009357431. [DOI] [PubMed] [Google Scholar]
- 30.Boffito M, Hoggard PG, Lindup WE, et al. Lopinavir protein binding in vivo through the 12-hour dosing interval. Therapeutic drug monitoring. 2004 Feb;26(1):3–5-9. doi: 10.1097/00007691-200402000-00008. [DOI] [PubMed] [Google Scholar]
- 31.Bree F, Houin G, Barre J, et al. Pharmacokinetics of intravenously administered 125I-labelled human alpha 1-acid glycoprotein. Clinical pharmacokinetics. 1986 Jul-Aug;11(4):3–36-42. doi: 10.2165/00003088-198611040-00006. [DOI] [PubMed] [Google Scholar]
- 32.Acosta EP, Limoli KL, Trinh L, et al. Novel method to assess antiretroviral target trough concentrations using in vitro susceptibility data. Antimicrobial agents and chemotherapy. 2012 Nov;56(11):5–938-45. doi: 10.1128/AAC.00691-12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Schipani A, Dickinson L, Boffito M, et al. Simultaneous population pharmacokinetic modelling of atazanavir and ritonavir in HIV-infected adults and assessment of different dose reduction strategies. Journal of acquired immune deficiency syndromes. 2013 Jan 1;62(1):6–0-6. doi: 10.1097/QAI.0b013e3182737231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Lopez Aspiroz E, Santos Buelga D, Cabrera Figueroa S, et al. Population pharmacokinetics of lopinavir/ritonavir (Kaletra) in HIV-infected patients. Therapeutic drug monitoring. 2011 Oct;33(5):5–73-82. doi: 10.1097/FTD.0b013e31822d578b. [DOI] [PubMed] [Google Scholar]
- 35.Ho DD, Neumann AU, Perelson AS, et al. Rapid turnover of plasma virions and CD4 lymphocytes in HIV-1 infection. Nature. 1995 Jan 12;373(6510):1–23-6. doi: 10.1038/373123a0. [DOI] [PubMed] [Google Scholar]
- 36.Mohri H, Bonhoeffer S, Monard S, et al. Rapid turnover of T lymphocytes in SIV-infected rhesus macaques. Science. 1998 Feb 20;279(5354):1–223-7. doi: 10.1126/science.279.5354.1223. [DOI] [PubMed] [Google Scholar]
- 37.Wei X, Ghosh SK, Taylor ME, et al. Viral dynamics in human immunodeficiency virus type 1 infection. Nature. 1995 Jan 12;373(6510):1–17-22. doi: 10.1038/373117a0. [DOI] [PubMed] [Google Scholar]
- 38.Perelson AS, Neumann AU, Markowitz M, et al. HIV-1 dynamics in vivo: virion clearance rate, infected cell life-span, and viral generation time. Science. 1996 Mar 15;271(5255):1–582-6. doi: 10.1126/science.271.5255.1582. [DOI] [PubMed] [Google Scholar]
- 39.Dimitrov DS, Willey RL, Sato H, et al. Quantitation of human immunodeficiency virus type 1 infection kinetics. Journal of virology. 1993 Apr;67(4):2–182-90. doi: 10.1128/jvi.67.4.2182-2190.1993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Stafford MA, Corey L, Cao Y, et al. Modeling plasma virus concentration during primary HIV infection. Journal of theoretical biology. 2000 Apr 7;203(3):2–85-301. doi: 10.1006/jtbi.2000.1076. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.