Automatic Segmentation of Invasive Breast Carcinomas from DCE-MRI using Time Series Analysis

Abstract

Purpose

Quantitative segmentation methods based on black-box modeling and pharmacokinetic modeling are highly dependent on imaging pulse sequence, timing of bolus injection, arterial input function, imaging noise and fitting algorithms. To accurately segment invasive ductal carcinomas (IDCs) from dynamic contrast enhanced MRI (DCE-MRI) using time series analysis based on linear dynamic system (LDS) modeling.

Methods

We modeled the underlying dynamics of the tumor by a LDS and use the system parameters to segment the carcinoma on the DCE-MRI. Twenty-four patients with biopsy-proven IDCs were analyzed. The lesions segmented by the algorithm were compared with an expert radiologist’s segmentation and the output of a commercial software, CADstream. The results are quantified in terms of the accuracy and sensitivity of detecting the lesion and the amount of overlap, measured in terms of the Dice similarity coefficient (DSC).

Results

The segmentation algorithm detected the tumor with 90% accuracy and 100% sensitivity when compared to the radiologist’s segmentation and 82.1% accuracy and 100% sensitivity when compared to the CADstream output. The overlap of the algorithm output with the radiologist’s segmentation and CADstream output, computed in terms of the DSC was 0.77 and 0.72 respectively. The algorithm also shows robust stability to imaging noise. Simulated imaging noise with zero mean and standard deviation equal to 25% of the base signal intensity was added to the DCE-MRI series. The amount of overlap between the tumor maps generated by the LDS-based algorithm from the noisy and original DCE-MRI was DSC=0.95.

Conclusion

The time-series analysis based segmentation algorithm provides high accuracy and sensitivity in delineating the regions of enhanced perfusion corresponding to tumor from DCE-MRI.

1. INTRODUCTION

Dynamic contrast enhanced MRI (DCE-MRI) is a highly sensitive technique to diagnose and stage breast cancer (1). Quantitative methods have been developed to determine the presence and the extent of the lesion. These quantitative methods can be categorized into three classes: 1. Black-box methods, 2. Pharmacokinetic (PK) models, and 3. Clustering based methods. The black-box methods do not explicitly model the underlying physiological process of contrast perfusion. Instead, institution-dependent, heuristic metrics such as maximum enhancement (2), washout slope (3), time to peak (4) etc. are derived from the time-intensity curves at each voxel. Based on these metrics, the voxels are classified into the tumor and healthy classes. Additionally, commercial softwares such as CADstream (Merge Healthcare Inc., Chicago), iCAD (Nashua) and DynaCAD (Invivo, Gainesville) utilize the washout pattern of the contrast agent to categorize the voxels. These patterns are classified as type I, persistently enhancing (progressive), which is suggestive of benignity; type II, plateau type, which has an intermediate probability for malignancy; and type III, washout type, which is indicative of malignancy (5). These methods of qualitatively identifying a lesion on DCE-MRI are highly sensitive to the image acquisition parameters, timing of contrast injection, imaging noise etc.

The second class of lesion quantification from DCE-MRI is based on modeling the underlying physiology of the contrast perfusion from the intravascular space to the extracellular space. Examples of such models include the standard (6) and extended Tofts model (7), shutter-speed model (8), Brix model (9,10) etc. Modeling the diffusion of contrast through the capillaries into extracellular space is complex and most models make assumptions to simplify the computations. Typically, the models assume that the contrast perfuses across two compartments from the intravascular to the extracellular space. Jansen et al. (11) showed that the mechanism of contrast perfusion is still debatable. Using X-ray fluorescence, the contrast was shown to perfuse across three compartments from intravascular space to extracellular space and further to the ducts, implying that the mechanism for contrast perfusion is more likely to involve three or more compartments, making the assumptions of traditional PK models invalid. Sourbron et al. (12) have also shown the narrow range of applicability of the models to weakly vascularized or highly perfused tissue, both of which are not necessarily true for IDCs.

The third class of lesion quantification based on clustering algorithms reduces the dimensionality of the data and automatically cluster the voxels into tumor and healthy voxels (13,14). Further, noise insensitivity can be achieved by modeling and estimating the imaging noise prior to clustering the voxels into healthy and tumor class (15).

Time-series analysis has been utilized in numerous applications such as mobile object tracking (16), video sequencing (17), environmental modeling (18), biomedical signal processing (19) etc. to extract feature vectors from time-series data in the presence of noise and data uncertainty. In this paper, we propose to use the time-series analysis to extract relevant features from the time-intensity curves at each voxel in the DCE-MRI and characterize the dynamic response of the tissue in the presence of noise and other imaging inhomogeneities. The feature vectors are extracted by modeling the underlying tissue as a LDS that characterize the evolving system dynamics. Tumors have a fast dynamic response that is measured by rapid increase of signal intensity in the DCE-MRI and then subsequent decrease in signal intensity over the next few time points while healthy tissue has a dynamic response characterized by a slow increase in signal intensity. The parameters of the LDS estimated at each voxel are then clustered into healthy and tumor class, the result of which is a tumor map that delineates the breast carcinoma. To the best of the authors’ knowledge, this is the first paper that uses the LDS-based time series modeling to identify the system dynamics and further segment the breast tumor on DCE-MRI.

2. MATERIALS AND METHODS

2.1 Linear Dynamics System based Time-series Analysis

Given the observed time-intensity signal from each voxel, we aim to extract the hidden dynamics of the underlying physiology using a LDS formulation (17). The hypothesis is that the hidden states of the LDS will describe the evolving dynamics of the tumor and healthy parenchyma. The hidden states are further linearly transformed to the observed interpolated time-intensity signal output. The LDS model is described by the following equations

$${\overline{x}}_1={\overline{\mu }}_0+{\overline{\xi }}_1$$ [1]

$${\overline{x}}_{n+1}=\mathbf{A}{\overline{x}}_n+{\overline{\xi }}_{n+1}$$ [2]

$${\overline{y}}_n=\mathbf{C}{\overline{x}}_n+{\overline{\nu }}_n$$ [3]

where x̄_n is the hidden state variable which encodes the evolutionary dynamics of the system, ȳ_n is the observed output variable, A is the transition matrix that predicts the state variable at the next time instant n+1 given the present state variable, C is the output matrix which maps the output variable to the hidden state variables, ξ̄_n is the process noise and ν̄_n is the observation noise and μ₀ is the initial system state. The process noise ξ̄ and observation noise ν̄ are assumed to be independent of the system states x̄ and are uncorrelated Gaussian noises with co-variances as Q and R respectively. Only the output of the system is observed, the hidden states and noise are unknown parameters. Further, from [1], [2] and [3] the conditional densities for the state and output are given as

$$\begin{array}{l}P({\overline{y}}_n\mid {\overline{x}}_n)=exp\{-\frac{1}{2}{[{\overline{y}}_n-\mathbf{C}{\overline{x}}_n]}^{\prime }{\mathbf{R}}^{-1}[{\overline{y}}_n-\mathbf{C}{\overline{x}}_n]\}{(2\pi )}^{-p/2}{\mid \mathbf{R}\mid }^{-1/2}\\ P({\overline{x}}_n\mid {\overline{x}}_{n-1})=exp\{-\frac{1}{2}{[{\overline{x}}_n-\mathbf{A}{\overline{x}}_{n-1}]}^{\prime }{\mathbf{Q}}^{-1}[{\overline{x}}_n-\mathbf{C}{\overline{x}}_{n-1}]\}{(2\pi )}^{-k/2}{\mid \mathbf{Q}\mid }^{-1/2}\end{array}$$

Denoting y = {y₁, y₂, … y_T} and x = {x₁, x₂, … x_T}, the joint probability can be written as

$$P(\overline{\mathbf{x}},\overline{\mathbf{y}})=P({\overline{x}}_1){\prod }_{n=2}^{T}P({\overline{x}}_n\mid {\overline{x}}_{n-1}){\prod }_{n=1}^{T}P({\overline{y}}_n\mid {\overline{x}}_n)$$

Given the observed output variable, the goal is to estimate the parameters of the system A, C, R, Q and the initial hidden state x̄₁. The expectation-maximization (EM) algorithm has been widely used to solve such optimization problems, wherein the optimal parameters of the system are obtained by minimizing a cost function, while keeping the hidden states fixed (M-step), and the hidden states are estimated while maintaining fixed system parameters (E-step) (20). The cost function is the expected log-likelihood of the joint probability of the hidden states given the observed sequence, i.e.,

$$\mathcal{Q}=E[logP(\overline{\mathbf{x}},\overline{\mathbf{y}}\mid \overline{\mathbf{y}})]$$ [4]

which involves the computation of x̄_n = E(x_n|ȳ), $P_n=E({\widehat{x}}_n{\widehat{x}}_n^{\prime }\mid \overline{\mathbf{y}})$ and $P_{n,n-1}=E({\widehat{x}}_n{\widehat{x}}_{n-1}^{\prime }\mid \overline{\mathbf{y}})$

M-step

To compute the system parameters, the expected log likelihood, given by [4], is differentiated with respect to the system parameters and set to 0 to solve for the optimal system parameters. In the M-step, the system parameters are updated according to the following equations

$$\begin{array}{l}{\mathbf{C}}^{\mathbf{new}}=\left(\sum _{n=1}^T{\overline{y}}_n{\widehat{x}}_n^{\prime }\right){\left(\sum _{n=1}^T{P}_n\right)}^{-1}\\ {\mathbf{A}}^{\mathbf{new}}=\left(\sum _{n=2}^T{P}_{n,n-1}\right)\left(\sum _{n=2}^T{P}_{n-1}\right)\\ {\mathbf{R}}^{\mathbf{new}}=\frac{1}{T}\sum _{n=1}^T({\overline{y}}_n{\overline{y}}_n^{\prime }-{\mathbf{C}}^{\mathbf{new}}{\widehat{x}}_n{\overline{y}}_n^{\prime })\\ {\mathbf{Q}}^{\mathbf{new}}=\frac{1}{T-1}\left(\sum _{n=2}^T{P}_n-{\mathbf{A}}^{\mathbf{new}}\sum _{n=2}^T{P}_{n-1,n}\right)\end{array}$$

Each of the parameters is then re-estimated after the M-step. This process continues till the process reaches a terminating condition, which could be either reaching the maximum number of iterations or obtaining a negligible change in the estimated parameters.

E-step

Given the system parameters, the hidden states are then estimated using the Kalman filter (21). Using the notation ${\widehat{x}}_n^{\tau }=E(x_n\mid {\overline{\mathit{y}}}_1^{\tau })$ for observed sequence till time τ, the Kalman filter provides the update equations for the hidden states as follows,

$$\begin{array}{l}{\widehat{x}}_n^{n-1}=\mathbf{A}{\widehat{x}}_{n-1}^{n-1}\\ V_n^{n-1}=\mathbf{A}{V}_{n-1}^{n-1}{\mathbf{A}}^{\prime }+\mathbf{Q}\\ {\widehat{x}}_n^n={\widehat{x}}_n^{n-1}+K_n({\overline{y}}_n-\mathbf{C}{\widehat{x}}_n^{n-1})\\ V_n^n=V_n^{n-1}-K_n\mathbf{C}{V}_n^{n-1}\end{array}$$

where $K_n=V_n^{n-1}{\mathbf{C}}^{\prime }{(\mathbf{C}{V}_n^{n-1}{\mathbf{C}}^{\prime }+\mathbf{R})}^{-1}$ is the Kalman gain. Further ${\widehat{x}}_n={\widehat{x}}_n^T,P_n=V_n^T+{\widehat{x}}_n^T{{\widehat{x}}_n^T}^{\prime }$ and $P_{n,n-1}=V_{n,n-1}^T+{\widehat{x}}_n^T{{\widehat{x}}_{n-1}^T}^{\prime }$. Given the updated values of the hidden states, the system parameters are then updated in the E-step. The E and M-step are recursively executed till an optimal value of the system parameters is obtained. Once the system parameters are estimated, the output matrix C is used as the feature vector to further classify the voxel into healthy or tumor class.

Fuzzy c-means clustering (FCM)

The FCM algorithm (22) assigns each voxel to a healthy or tumor class (two-class clustering, K = 2) with a certain probability that is assigned using a membership grade (U_N×K = {u_ij, i = 1…N, j = 1…K}) based on the feature vector obtained from the output matrix C. The cluster centers and membership grade are iteratively computed by minimizing the weighted distance of the feature vector from the center of the cluster. The membership grade represents the segmentation mask corresponding to the healthy and tumor classes.

Further, the first parameter of the C matrix, which corresponds to most dominant dynamics of the system, is overlaid as a color map over the tumor mask generated from the FCM algorithm with red representing high values of the parameter and blue representing the low values of the parameter.

2.2 Patient selection and MRI acquisition

Twenty-four patients (mean age: 55.5 years, range: 25 to 78 years) images with biopsy proven IDCs were analyzed in this Institutional Review Board and Health Insurance Portability and Accountability Act (HIPAA) compliant study. Informed consent was waived since the study was conducted retrospectively and did not affect patient care management. For each patient, diagnostic DCE-MRI, T2 weighted image and sagittal post-contrast images were obtained.

The women were imaged prone in a 3T scanner; matrix size: 512 × 512; slice thickness: 2-mm; TE = 1.76; TR = 4.4; flip angle: 8⁰ with a dedicated breast-surface coil (InVivo 7-Channel Breast Biopsy Array, Invivo Research). Scanning protocols included pre- and post- VIBRANT (Volume Imaging Breast Assessment) or VIBE (Volumetric Interpolated Breath hold Examination) fat saturated sequences in either the sagittal or axial planes. The dynamic contrast sequences were obtained at 90s, 180s, 270s and 360s following intravenous contrast administration. Patients received 0.2ml/kg of gadolinium (Magnevist, Bayer HealthCare) contrast infused at 2ml/s. After the diagnostic MRI exam was obtained, all patients underwent MR-guided biopsies that further confirmed Invasive Ductal Carcinoma.

2.3 Algorithm Evaluation Methodology

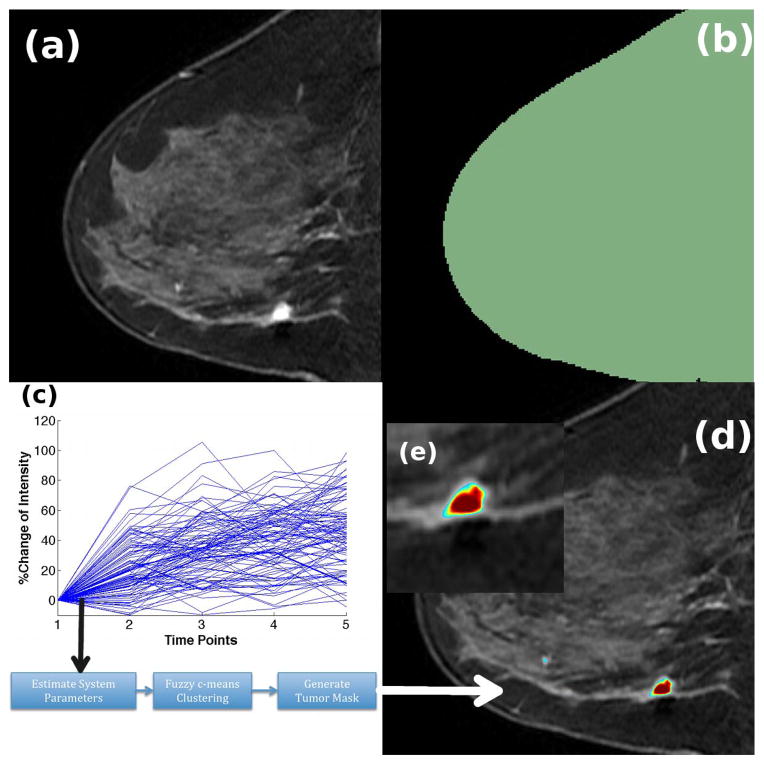
The DCE-MRI was first loaded in 3D Slicer¹, an open-source image processing and navigation software, using the 4D Image module. Thereafter, a region of interest (ROI) was delineated on the images using the Editor module in 3D Slicer, as shown in Figure 1(b). The role of the ROI is to constrain the computation of the algorithm to the voxels underneath this ROI and speed up the computation process. The time-intensity curves of all voxels under the mask are logged and provided to the algorithm, as shown in Figure 1(c) and detailed in the subsection above, which is implemented in MATLAB. Thereafter, the results of the algorithm, which are the tumor and healthy tissue mask, are saved in DICOM format and loaded into 3D Slicer. The “RedtoBlue Rainbow” color map is utilized to highlight the tumor on the algorithm output, as shown in Figures 1(d) and (e). The user then outlined the tumor mask on the algorithm output for further comparison with the commercial tumor map output and radiologist’s segmentation.

Figure 1.

Workflow of the LDS segmentation algorithm. (a) First post-contrast image of the DCE-MRI series (b) ROI delineated on the DCE-MRI using the Editor module in 3D Slicer (c) Time-intensity curves from all voxels under the ROI are logged and provided to the algorithm, which computes the LDS system parameters, clusters the voxels and generates the tumor mask (d) Tumor mask overlaid on the DCE-MRI. Red represents high tumor activity and blue represents low tumor activity

For each of these patients, we also segmented the lesion on the DCE-MRI using a commercial software available at our hospital, CADstream (Merge Healthcare, Chicago). A screenshot of the CADstream output was loaded into 3D Slicer after appropriate scaling. The CADstream output was manually registered to the DCE-MRI. A user then manually outlined the tumor detected by CADstream using the Editor module in 3D Slicer. This tumor mask was compared to the tumor mask generated by the algorithm.

In addition to the CADstream output, an expert breast radiologist outlined the tumor boundaries based on DCE-MRI and subtraction images with the additional knowledge of the biopsy results on 3D Slicer. The pre-contrast and post-contrast images were overlaid over each other and the brightly enhanced region was delineated as the tumor, again using the Editor module in 3D Slicer. Additional information from the biopsy reports was also utilized to precisely localize the IDC on the DCE-MRI.

2.4 Performance Assessment

The performance of the algorithm was assessed with the following measurables: accuracy, sensitivity and Dice similarity coefficient (DSC). Any overlap between the two tumor masks is considered as a true positive finding while no overlap between the two tumor masks is considered as a false positive or negative finding. Although numerous tumor foci may be present, we only considered those that were biopsied and proven to be IDC. In the vicinity of such a foci, the radiologist was asked to delineate the extent of all the tumor foci on 3D Slicer. The accuracy and sensitivity of detecting a tumor focus by the algorithm was calculated, considering the radiologist’s segmentation and the CADstream output as the reference validation independently. Although targeted biopsy or histological analysis is the only gold standard method of validating the tumor map, obtaining a one-to-one relation between the histology findings and tumor map is nontrivial due to the highly deformable nature of breast tissue. The amount of overlap between the algorithm output and the radiologist’s segmentation was quantified in terms of the DSC. DSC is computed as the ratio of twice the number of voxels in the overlapped region to the sum of the voxels in the two tumor masks. A DSC of 0 implies no overlap while a DSC of 1 implies perfect overlap between the two volumes. In addition to evaluating the accuracy, sensitivity and amount of overlap of the tumor mask generated by the algorithm with the radiologist’s segmentation and CADstream output, we also estimated the computation time for generating the tumor mask by the LDS algorithm in MATLAB using the tic and toc functions. The simulation was run on a Macbook Pro laptop with 16GB RAM, Intel Quad Core 2.5GHz processor.

3. RESULTS

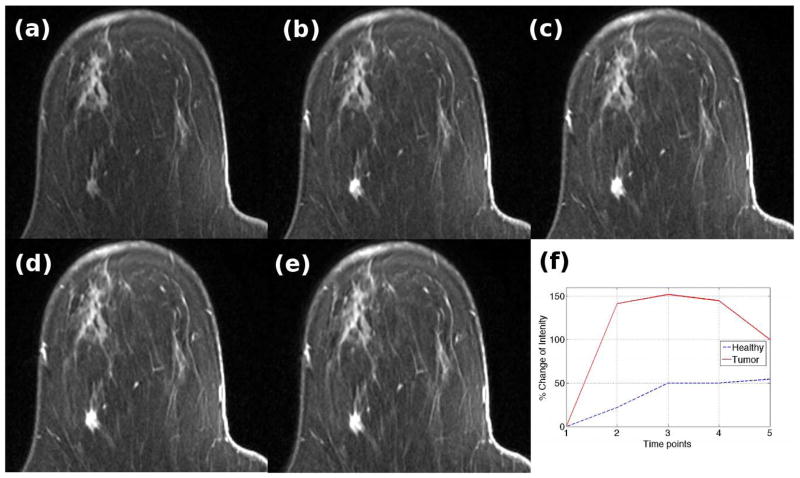
Figure 2 shows the DCE-MRI of a patient with a 10 mm IDC. Figure 2(a) is the pre-contrast image while Figures 2(b) to (e) correspond to images obtained 90s, 180s, 270s and 360s after contrast injection. The tumor focus shows up brighter on the post-contrast images compared to the surrounding healthy parenchyma. Figure 2(f) shows the percentage increase in signal intensity of a voxel within the healthy parenchyma (shown in blue) and tumor (shown in red). Due to angiogenesis, the tumor has a proliferation of blood vessels due to which the contrast rapidly washes into the tumor. However, the tumor vessels are malformed and leaky, resulting in subsequent washout of contrast. On the other hand, the surrounding parenchyma shows a gradual increase in the brightness on T1 images due to a steady increase in contrast medium.

Figure 2.

DCE-MRI series of a patient with a 10mm IDC. (a) Pre-contrast (b) First post-contrast image (c) Second post-contrast image (d) Third post-image (e) Fourth post-contrast image (f) Time-intensity curves of a voxel within the tumor mass (red) and healthy tissue (blue)

Figure 3 shows the time-intensity curves and heat map of the parameters obtained from the LDS for six voxels – three chosen within the tumor foci (T1 to T3) and three within the healthy parenchyma (H1 to H3). Figure 3(a) shows the time-intensity curves while Figure 3(b) shows the heatmap corresponding to each of these time-intensity curves. The y-axis corresponds to the index of the voxel while the x-axis corresponds to the three parameters of the C matrix. The heatmap shows a clear distinction between the tumor (top 3 rows) and healthy (bottom 3 rows) voxels. The first parameter of the C matrix is nearly a factor of 2 higher for the tumor class compared to the healthy class, while the second and third parameters are greater by a factor of 14 and 4 respectively.

Figure 3.

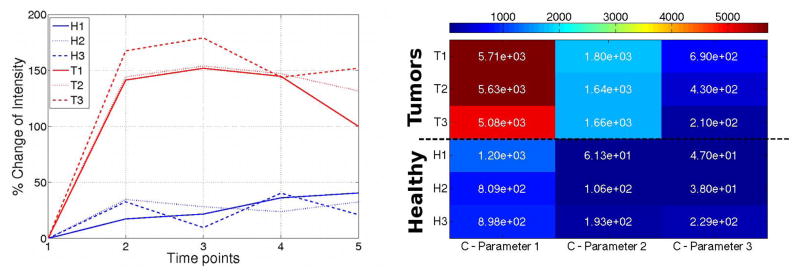
Time-intensity curves of three voxels in each of the healthy and tumor classes. The corresponding heat map of the parameters of the C matrix is shown on the right. X-axis corresponds to each of the parameters of the C matrix and Y-axis corresponds to the voxel index. Scale factor for C-parameter 1=1, C-parameter 2=1e3, C-parameter 3=1e4

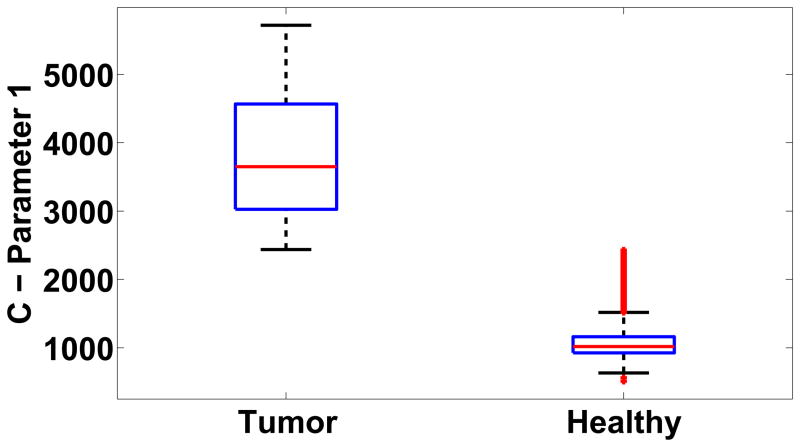
For the case shown in Figure 2, the box plot of the first parameter of the C matrix that defines the dominant dynamics of the system is shown in Figure 4. The mean value of the first parameter was 3.77e3 and 1.07e3 for the tumor and healthy class respectively. The difference between the parameters of the LDS for the tumor and healthy class was statistically significant (p < 0.05, Mann-Whitney-Wilcoxon test), thereby showing that the segmentation algorithm was capable of differentiating between voxels based on the parameters of the LDS. The result of the example case is shown in Figure 5(a). The FCM algorithm further clustered the voxels into two classes corresponding to the healthy and tumor class. A color map proportional to the magnitude the first parameter of the C matrix was overlaid on the tumor mask generated from the algorithm with red representing high tumor activity and blue representing low tumor activity. Figure 5(b) shows the output of the commercial software, CADstream for the same case. The output closely corresponds to the tumor map generated by the LDS algorithm. Further, an expert radiologist outlined the carcinomas on the DCE-MRI using information from the biopsy reports, pre- and post-contrast images. The radiologist’s segmentation is overlaid on the tumor boundaries generated by the LDS algorithm and the CADstream output, as shown in Figure 5(c). The figure shows significant overlap between the tumor map generated by the LDS algorithm and the radiologist’s segmentation. The amount of overlap, measured in terms of the DSC, between the algorithm output and the radiologist’s segmentation and CADstream output was 0.8 and 0.75 respectively. The total processing time for segmenting a sub-volume of size 55×31×7 voxels was 27.06 minutes.

Figure 4.

Box-plot of the first parameter of the C matrix of the tumor and healthy classes

Figure 5.

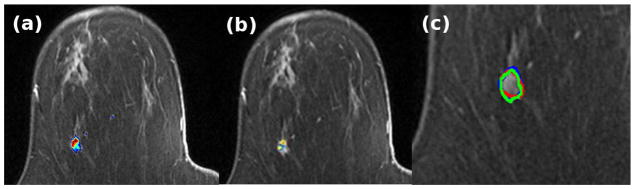
(a) Output of the LDS segmentation algorithm (b) CADstream output (c) Overlay of the outlines of the result of the LDS segmentation algorithm (green), CADstream output (blue) and Radiologist’s segmentation (red)

Figure 6 shows the result of the segmentation algorithm for four cases. The top row corresponds to the output of the LDS algorithm while the bottom row compares the output of the LDS algorithm with the radiologist’s segmentation and the CADstream output. Considering the radiologist’s segmentation as the gold standard segmentation, the results of the LDS algorithm for the 24 cases is shown in Table 1. The accuracy of detecting a tumor mass by the LDS algorithm was 90%. The LDS algorithm also has a high sensitivity of 100% in detecting the tumor mass delineated by the radiologist. The mean overlap between the LDS generated tumor map and the radiologist’s segmentation, quantified in terms of the DSC, was 0.77. The results suggest that the algorithm can automatically segment the tumors with high accuracy and sensitivity, and with significant overlap with the radiologist’s segmentation.

Figure 6.

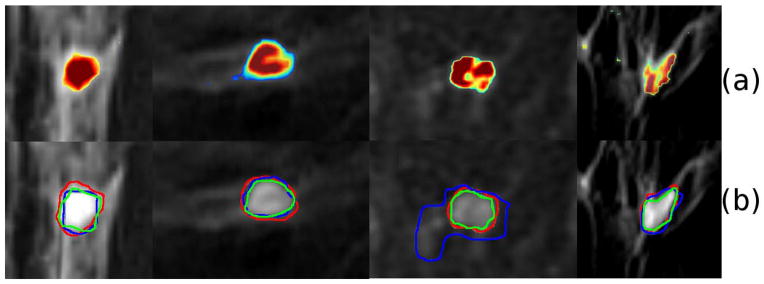
Results of the LDSTS algorithm for four cases, each column is a case. (a) Output of LDS algorithm (b) Magnified view of the smoothened tumor outlines defined by LDS (green), Radiologist (red) and Commercial tumor map (blue).

Table 1.

Comparison of the results of the LDS algorithm and radiologist’s segmentation, LDS algorithm and CADstream output, CADstream output and radiologist’s segmentation.

	LDS and Rad. Seg.	LDS and CADstream	CADstream and Rad. Seg.
Accuracy	90%	82.1%	79.3%
Sensitivity	100%	100%	85.1%
DSC	0.77	0.72	0.66

The result of the LDS segmentation was also compared to the CADstream output. In 8.3% (2/24) of the cases CADstream did not detect the biopsy proven IDC. For these cases, the LDS algorithm detected the tumor with an overlap of 0.71 with the radiologist’s segmentation. For the remaining 22 cases, the results of the LDS algorithm compared to the CADstream output are summarized in Table 1. The LDS algorithm detected every tumor mass detected by CADstream, resulting in a sensitivity of 100%. However, the LDS algorithm detected additional masses, resulting in an accuracy of 82.1%. The mean DSC for overlap between the tumor mass and the CADstream output was 0.72. We also compared the output of CADstream with the radiologist’s segmentation, which has been summarized in Table 1. Comparatively, CADstream demonstrated lower accuracy (79.3%) and sensitivity (85.1%) in detecting IDC compared to the LDS algorithm and with lower mean DSC (0.66).

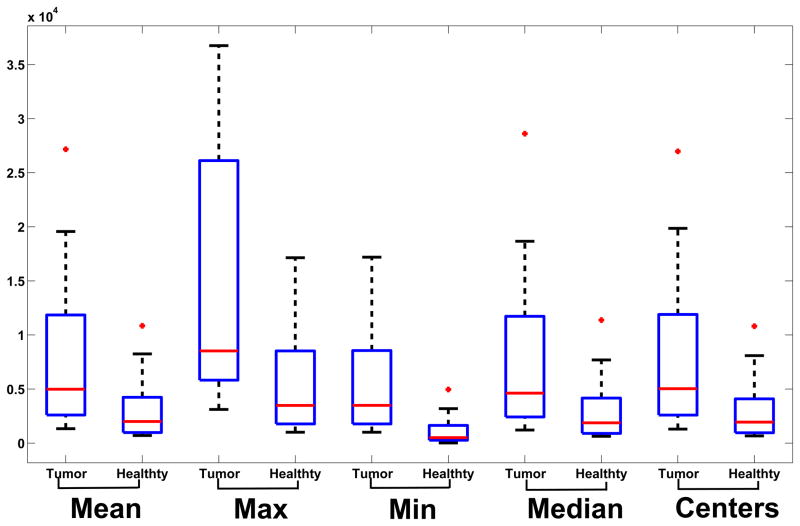
For the 24 cases analyzed in this paper, the mean, maximum, minimum, median of the first parameter of the C matrix and the cluster centers for the tumor and healthy classes were computed, plotted in Figure 5 and summarized in Table 2. For each computed value, the difference in the parameter for the tumor and healthy class was statistically significant (p<0.05, Mann-Whitney-Wilcoxon test). The median value of the first parameter of the C matrix for the tumor class was 4.98e3 and for the healthy class was 2.0e3. The higher value of the parameter indicates a faster dynamics for the tumor mass compared to surrounding healthy tissue. To test the stability of the algorithm, Gaussian noise with 0 mean and standard deviation equal to 25% of the base intensity of each voxel in the DCE-MRI was added. The tumor map was then computed on the noisy DCE-MRI and compared with the tumor map generated from the original DCE-MRI series. The addition of the noise resulted in 2.37% change in the mean value of parameter 1 for the C matrix for the tumor class. The amount of overlap between the tumor maps generated from the two series was quantified to be 0.95. The results demonstrate excellent noise rejection capabilities and robustness to imaging noise.

Table 2.

Mean, Maximum, Minimum, Median values of the first parameter of the C matrix and cluster centers for the tumor and healthy classes.

	Tumor	Healthy	p
Mean	2374	805	2.40e-03*
Maximum	4453	1585	8.39e-04*
Minimum	1585	286	1.11e-05*
Median	2085	742	3.20e-03*
Cluster Centers	2384	786	2.30e-03*

^*represents significant difference between tumor and healthy class (p<0.05).

4. DISCUSSION

In this paper, we have developed a novel tumor segmentation algorithm based on the time series analysis. This method of analysis has been utilized in numerous fields, such as financial markets (23), air pollution level monitoring (24), dynamic motion analysis (16), biomedical signal analysis (19) etc. At each voxel, the time-intensity curves are utilized as the observation vector of an LDS, based on which the parameters of the LDS are estimated. The output matrix C is then utilized as a feature vector and input to the FCM clustering algorithm to automatically cluster the voxels into the tumor and healthy class.

The LDS based segmentation algorithm showed high accuracy and sensitivity in detecting the biopsy-proven IDC compared to the radiologist’s segmentation. The amount of overlap with the radiologist’s segmentation was also significant, implying that the algorithm has the capability of automatically segmenting the extent of the lesion. Such an algorithm would be useful to detect carcinomas and staging therapies. For the cases analyzed in this paper, the CADstream software was unable to detect biopsy-proven IDCs in 8.3% of the cases. This demonstrates the shortcoming of the black-box method of detecting the tumors. The commercial software only highlights voxels above a minimum signal intensity threshold. In these cases, the voxels within the tumor mass had a signal intensity wash-in less than the threshold. CADstream also had lower accuracy and sensitivity in detecting the tumor masses compared to the LDS algorithm, considering the radiologist’s segmentation as the gold standard. The LDS-based segmentation algorithm also showed excellent noise rejection capabilities. The Kalman filter has been utilized to estimate the statistically optimal system states of the LDS in the presence of noise. Significant simulated imaging noise was added to the DCE-MRI. The tumor mask generated from the algorithm has an overlap of DSC=0.95 with the original tumor map, with minimal variation in the system parameters (2.37%), thereby demonstrating robust performance in presence of imaging noise.

Although numerous studies have applied the black-box methods and the pharmacokinetic models to detect tumors from DCE-MRI, only a few studies have investigated the validity of such models (25). Most models make assumptions on differences in the time-intensity curves obtained from tumor and healthy voxels, the arterial input function, number of compartments for pharmacokinetic analysis, sampling time, contrast-to-noise ratio etc. Jansen et al. (11) showed using X-ray fluorescence microscopy that the contrast perfuses from the intravascular compartment to the extracellular space and further into the intraductal space for the invasive component of Ductal Carcinoma In Situ, thereby demonstrating that the perfusion phenomenon involves three or more compartments. Since DCIS is a precursor for IDC, the perfusion mechanism for IDC would also likely involve the three compartments. Therefore, the basic assumption of the pharmacokinetic models such as the Tofts model (6), Brix model (9) etc. is no longer valid. In addition, due to the perfusion through multiple compartments, the time-intensity curves could be slow and persistent. Therefore, metrics such as maximum slope, time to peak, area under the curve etc. may not be sufficient to distinguish between tumor and healthy tissue.

Further, even if we assume that the contrast perfuses across two compartments from the intravascular space to the extracellular space, the parameters estimated using the Tofts model such as K^trans and v_e are highly dependent on the temporal sampling step, acquisition window and contrast-to-noise ratio (26). It was shown that even for the ideal measurement conditions, the parameters could deviate from ideal values by over 200%. Therefore, extreme caution must be used to utilize the Tofts model to segment the tumor from DCE-MRI or deriving hemodynamic parameters from the time-intensity time courses. Further in (25), the authors have shown that the results of the Tofts model and extended Tofts model are accurate if and only if the tissue is weakly vascularised or highly perfused, neither of which may be true for breast carcinomas. Studies correlating the parameters obtained from the pharmacokinetic models with non-functional vascular parameters obtained by immunostaining blood vessels and measuring microvascular density were inconclusive (27). This lays the basis of the modeling in the paper, which does not make any assumptions on the pharmacokinetic modeling of the underlying tissue and only assumes that a dynamic system is responsible for the observation of the time-intensity curves, based on which the tumor is segmented from the DCE-MRI. The EM algorithm combined with the Kalman filter allows for the robust estimation of the system parameters and further segmentation of the carcinoma on DCE-MRI.

The LDS based algorithm could also be potentially utilized to quantify the response of breast tumors to neoadjuvant chemotherapy. The parameters of the model could quantify the “aggressiveness” of the tumor segmented from DCE-MRI pre- and post-chemotherapy. Further, the heterogeneity of the tumor could also be quantified in terms of fractal dimensions, such as the Rényi Entropy (28), computed from the parameter maps obtained from the LDS-based segmentation algorithm.

In this study, all patients were imaged with a dedicated breast-surface coil (InVivo 7-Channel Breast Biopsy Array, Invivo Research). The coil provides a stable support for the breast during imaging. For this case, we have not utilized any registration algorithm to register the 4 time series volumes to the pre-contrast volumes. In case significant motion is noticed between the four time series volumes, a non-rigid registration algorithm based on B-spline formulation (29) can be adopted to compensate for any motion-induced artifacts.

There are several limitations of the study. First, the deformation of the breast during the imaging is not accounted for. This could lead to errors in estimating the extent of the tumor. As part of our future work, we are working on integrating the registration step as part of the algorithm to simultaneously register and segment the tumors. The number of cases analyzed in this paper is also limited. We are also working on improving the specificity of the algorithm to differentiate between the different types of tumors (IDC, Ductal Carcinoma In Situ, Invasive Lobular Carcinoma etc.) by analyzing the heterogeneity of the tumor map. Another limitation is the absence of targeted biopsy results to validate the accuracy of the algorithm. We will validate the extent of the tumor margin delineated by the algorithm in the state-of-the-art Advanced Multimodality Image Guided Operating (AMIGO) suite at the Brigham and Women’s Hospital. Further improvement in the computation speed can be achieved by utilizing a dedicated Graphics Processing Unit (GPU), which is part of our future work.

In conclusion, we have developed a novel segmentation algorithm based on time series analysis using an LDS to segment IDC from DCE-MRI. The algorithm shows high sensitivity and accuracy in detecting the biopsy-proven carcinomas. The algorithm also demonstrates excellent noise rejection capability, showing minimal change in the model parameters on addition of simulated imaging noise. The parameters of the LDS have been utilized to differentiate between voxels belonging to the tumor and healthy class. Potentially, the parameters of the dynamic model could also be utilized to analyze the response of tumors to chemotherapy drugs or help preoperatively plan the extent of surgical resection.

Figure 7.

Box-plot of the mean, maximum, minimum and median of the first parameter of the C matrix for the healthy and tumor classes. The difference in each parameter between the tumor and healthy class is statistically significant (p<0.05).