Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 Mar 24;4:4448. doi: 10.1038/srep04448

A multimode electromechanical parametric resonator array

I Mahboob 1,a, M Mounaix 1, K Nishiguchi 1, A Fujiwara 1, H Yamaguchi 1
PMCID: PMC3963032  PMID: 24658349

Abstract

Electromechanical resonators have emerged as a versatile platform in which detectors with unprecedented sensitivities and quantum mechanics in a macroscopic context can be developed. These schemes invariably utilise a single resonator but increasingly the concept of an array of electromechanical resonators is promising a wealth of new possibilities. In spite of this, experimental realisations of such arrays have remained scarce due to the formidable challenges involved in their fabrication. In a variation to this approach, we identify 75 harmonic vibration modes in a single electromechanical resonator of which 7 can also be parametrically excited. The parametrically resonating modes exhibit vibrations with only 2 oscillation phases which are used to build a binary information array. We exploit this array to execute a mechanical byte memory, a shift-register and a controlled-NOT gate thus vividly illustrating the availability and functionality of an electromechanical resonator array by simply utilising higher order vibration modes.

Inspired by the unprecedented control over the vibration dynamics of a mechanical resonator by a parametrically coupled electromagnetic resonator1 has led to the re-emergence of the concept of coupled mechanical resonators. The most extreme example of this approach is the idea of an array of mechanical resonators which offers the prospect of fundamental science that is beyond a single mechanical resonator for example modelling neural networks and studying phase transitions2,3,4,5,6,7,8,9,10,11,12,13,14,15. In spite of this promise, electromechanical resonator arrays have remained scarce mainly due to the formidable challenges involved in their fabrication and the technical difficulties involved in addressing and controllably intercoupling the individual mechanical elements of the array2. This has also lead to more practical applications for such arrays for example in sensors16,17,18 or signal processors19,20 remaining largely unexplored.

One alternative to fabricating an array of mechanical resonators is instead to utilise the multitude of higher order vibration modes available to mechanical resonators21,22,23,24. Indeed the ability to couple pairs of modes in the same mechanical resonator has recently been the subject of intense interest8,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39. However, extending this concept to create an array of modes has proved to be prohibitive due to the weaker transduction efficiencies associated with the higher order vibration modes primarily as a consequence of their low quality factors.

On the other hand, parametric resonators are not only ubiquitous in nature40 but they have also found widespread use in electromagnetic platforms for a range of applications including computers41,42,43,44,45. These concepts have increasingly gained traction in the electromechanical resonator community20,29,46,47,48, where a parametric resonance can be activated by modulating the parameters of the underlying oscillator (i.e. its spring or damping constant) at twice its natural frequency40. Although parametric resonances in higher order electromagnetic modes are a necessary precursor to extracting their technological functionality, such multimode operation in the electromechanical resonator domain has remained elusive as invariably, a parametric resonance can only be implemented in the fundamental mode due to its usually high quality factor making the temporal modulation of its intrinsic parameters more accessible20,30,47,49,50,51.

Motivated by this dual objective of a mechanical resonator array with practical functionality, we have developed an electromechanical resonator which sustains a spectrum of high quality factor harmonic modes, a number of which also exhibit parametric resonances. We exploit the unique vibration characteristics of this parametric resonator array to build the essential components of computer20,45 namely a byte memory, a shift-register and logic elements thus not only demonstrating the emergence of new functions by utilising an array of mechanical vibration modes but also further crystallising the possibility of an electromechanical computer52,53.

Results

Electromechanical resonator

The experiments were executed in a GaAs based electromechanical resonator incorporating piezoelectric displacement transducers, shown in Fig. 1a, and detailed elsewhere20,24,29,31,39. The electromechanical resonator exhibits a harmonic fundamental flexural mode at 181147.5 Hz with a quality factor of 2 × 105 as shown in Fig. 2a as well as a further 74 harmonic modes up to a frequency of 1.6 MHz as shown in Fig. 1b24.

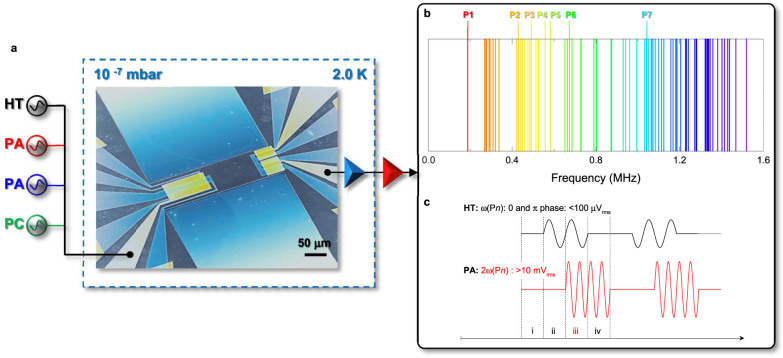
Figure 1. The multimode electromechanical parametric resonator array.

Figure 1

Open in a new tab

(a), An electron micrograph of the mechanical resonator integrated with piezoelectric transducers at both clamping points via the 2 dimensional electron gas (blue) and Schottky gate electrodes (yellow). The electromechanical resonator, when activated with the appropriate combination of inputs (HT: harmonic trigger PA: parametric actuation PC: parametric coupling) can act as a byte memory, a shift-register or an inverter logic gate. The resultant nanometre scale mechanical vibrations generate a piezovoltage which is amplified by an on-chip silicon nano-transistor, a room temperature transimpedance amplifier and is measured in a lock-in detector (b), Harmonically activating the electromechanical resonator in a homodyne measurement configuration reveals 75 resonances as indicated by each line up to 1.6 MHz. Periodically modulating the spring constant of the 75 harmonic modes at twice their frequency in a subharmonic detection configuration reveals 7 parametric resonances up to a frequency of 1.05 MHz and these elements of the array are sequentially labelled P1–P7 from low to high frequency. (c), A pulse sequence which can write binary information into the 7 parametrically resonating modes as detailed in Figs. 2j–2l and Figs. S1m–S1p enables the realisation of a binary phase information array.

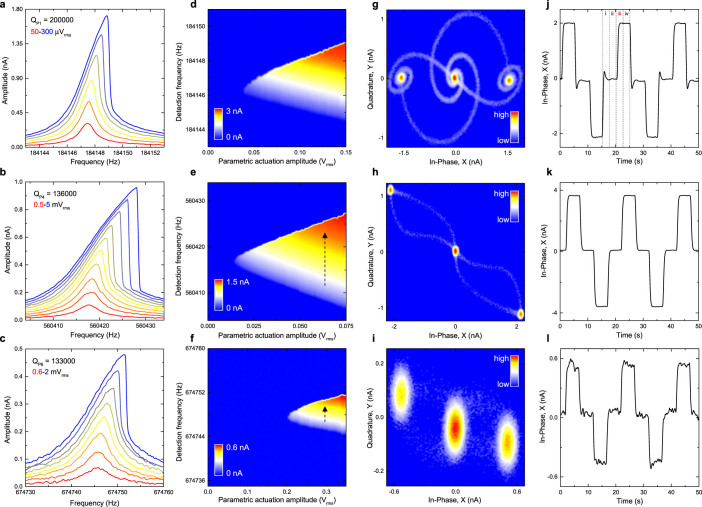
Figure 2. The harmonic and parametric resonance dynamics of modes P1, P4 and P6.

Figure 2

Open in a new tab

(a–c), The harmonic response of modes P1, P4 and P6 as a function of actuation amplitude. (d–f), The parametric response of the same modes as a function of the actuation amplitude measured in a subharmonic detection configuration. (g–i), The stability diagrams indicate the occupation probabilities of the parametric resonances in phase space and are measured with parametric actuation amplitudes and frequencies of 0.1 Vrms and 368294 Hz, 0.05 Vrms and 1120834 Hz, 0.3 Vrms and 1349496 Hz for modes P1, P4 and P6 respectively. The resultant phase portraits indicate that when the parametric actuation is activated, each mode evolves from its stationary state which is indicated by the high probability lobe at the origin, to one of the two available oscillating states, that again can be identified by the high probability lobes at finite amplitudes, where the 2 oscillating states always exhibit a π radians phase separation. In addition the stability diagrams also reveal that only a single trajectory from the stationary state to each oscillating state is possible which is different to the single trajectory from each oscillating state to the stationary state54. (j–l), Using the pulse sequence outlined in Fig. 1c, binary information can be written, stored and erased in the bi-stable oscillation states of the parametric modes20,45. The resultant periodic switching corresponds to sequentially moving between the lobes of the oscillating states via the stationary state in the phase portraits detailed in Figs. 2g–2i.

The piezoelectric transducer can also modulate the spring constant of the electromechanical resonator enabling the frequency of the mechanical vibration modes to be tuned20,24 thus providing a natural means to activate a parametric resonance20,30,40,47,49,50,51. Consequently, by modulating the spring constant of the mechanical resonator at twice the frequency of the 75 harmonic modes, we find that only 7 modes can sustain a parametric resonance as shown in Fig. 1b. The inability of all 75 harmonic modes to exhibit parametric resonances is a consequence of the insufficient variation of their eigenfrequencies via the piezoelectric spring constant modulation (possibly due to the mismatch in the position of the driving electrode with respect to their mode shapes) and/or their low quality factors. Indeed the 7 modes that can sustain parametric resonances are unified by their consistently high quality factors of > 105 as shown in Figs. 2a–2c and supplementary Figs. S1a–S1d.

Instability tongue

The first available parametric resonance corresponds to the fundamental mode of the electromechanical resonator (P1) and its frequency response as a function of parametric actuation amplitude, shown in Fig. 2d, exhibits an instability tongue which is a signature feature of parametric resonators20,30,47,49,50,51. The spectral response of the parametric resonance is underpinned by Mathieu's equation: 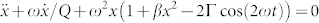Inline graphic where ω, Q and β are the natural frequency, quality factor and the Duffing nonlinearity respectively of the Pnth parametric mode while Γ is proportional to the parametric excitation amplitude that modulates the spring constant in the third term, which in turn generates the mechanical displacement x20. This equation can be numerically solved in the rotating frame of the mode in question, by writing x(t) = X cos(ωt) + Y sin(ωt) where X and Y are the slowly varying in-phase and quadrature components of the position, as detailed in ref. 20. This formalism can readily reproduce the experimental response as outlined in supplementary Fig. S2a and it provides a benchmark with which to evaluate the other parametric modes.

Extending this measurement to the remaining higher order modes i.e. P2 to P7 confirms that all 6 exhibit the characteristic instability tongue of a parametric resonator as shown in Figs. 2e, 2f and Figs. S1e–S1h thus confirming the realisation of an array of parametrically resonating modes.

Binary oscillation phases

A unique feature of the vibration generated from parametric excitation is that it can only oscillate with one of two phases separated by π radians20,45,49. In order to confirm this, all the parametrically active modes, in turn, are repeatedly switched on and off (where the switching period is much longer than the ring up/down time of the mode in question) and the corresponding in-phase and quadrature components of the position are recorded as it repeatedly evolves from its stationary state to its vibrating state and back during a period of 5 hours. This measurement enables stability diagrams to be compiled, shown in Figs. 2g–2i and Figs. S1i–S1l, which indicate the most probable vibration phase of the parametrically resonating modes54. All 7 modes exhibit parametric resonances that can only oscillate with 2 phases separated by π radians (except P7 where the phase separation is π/2 and is detailed in Fig. S1l) thus confirming the presence of oscillation phase bi-stability in higher order parametric modes for the first time. Again solving Mathieu's equation in this configuration can reproduce the experimentally observed responses, as detailed in Fig. S2b, and it confirms that all the available higher order modes exhibit almost perfect parametric resonance dynamics.

Phase memory

The availability of only 2 oscillation phases to the parametrically resonating mechanical modes provides a natural platform within which binary information protocols can be developed and indeed this property in inductor-capacitor based parametric resonators was utilised in primitive electrical computers20,45. At the heart of all computers is the presence of a memory in which binary information can be written, stored and erased. To that end, the availability of this function in the higher order parametric modes is investigated using the protocol depicted in Fig. 1c which has previously been implemented via the parametric resonance of the fundamental mode in an electromechanical resonator.

In summary a parametrically active mode is first weakly harmonically triggered with a particular phase. Next, while the trigger switch is still active, the parametric resonance of the mode in question is excited at twice its frequency followed by the trigger switch being deactivated. The resultant parametric resonance has its phase determined by the trigger and this then represents writing and storage of the 0 logical in the 0 phase of the mechanical oscillator. The 0 phase logical information can be erased by simply deactivating the parametric driving. Similarly by implementing the above sequence but now with the trigger incorporating a π phase shift enables the 1 logical to be written and stored in the π phase of the mechanical resonator. By convention the 0 (1) logical is assigned the label 0 (π) phase which is set to correspond to the positive (negative) in-phase component of the parametric resonance (see the phase portraits in Figs. 2g–2i and Figs. S1i–S1l). Consequently by measuring the in-phase components of the parametrically resonating modes when subjected to the above pulse sequence, binary information can successfully be written, stored and erased in the bi-stable oscillation phase of all the higher order parametric modes for the first time as shown in Figs. 2j–2l and Figs. S1m–S1p. This result demonstrates that a binary information array can be realised in the electromechanical resonator where the parametric resonance modes play the role of binary elements in the array.

Electromechanical byte

Although bit memories20,55 have previously been demonstrated in electromechanical resonators, the realisation of an electromechanical byte has remained elusive56. However, the electromechanical parametric resonator array naturally provides a venue within which a byte memory can be created.

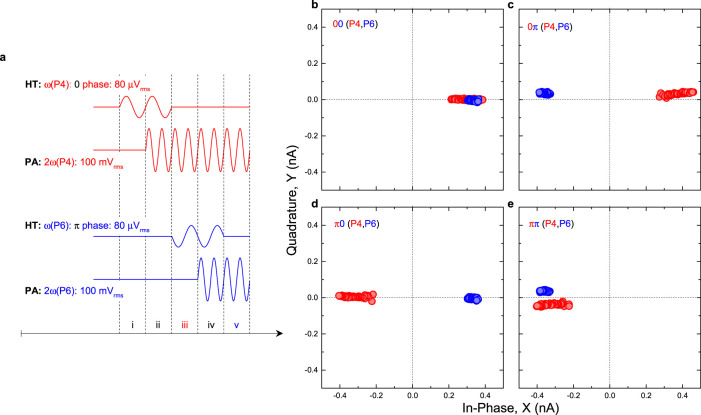
To that end, the pulse sequence shown in Fig. 3a is developed to implement a 2-bit byte via parametric modes P4 and P6 as shown in Figs. 2h and 2i respectively. Briefly, a 0 or π logical is first written (via the harmonic trigger) and then stored (via the parametric resonance) in mode P4 (steps ii and iii in Fig. 3a) followed by same process in mode P6 (steps iv and v in Fig. 3a) thus enabling multiple elements of the array to be utilised in parallel. To confirm the viability of this protocol, all 4 possible combinations of a 2-bit byte are measured, namely 00, 0π, π0 and ππ where the first (second) binary logical corresponds to mode P4 (P6). The results of this measurement, plotted in phase space as shown in Figs. 3b–3e, confirm that a 2-bit byte can indeed be implemented in the electromechanical parametric resonator array via the higher order modes for the first time. Moreover, this protocol can readily be extended to include more bits i.e. more elements of the array and 3-bit byte via modes P4, P6 and P5 has also been executed and is detailed in Fig. S3.

Figure 3. An electromechanical byte memory.

Figure 3

Open in a new tab

(a), The pulse sequence used to execute a 2-bit byte in the electromechanical parametric resonator array where the steps to write the string 0π are shown. Note that the parametric actuation amplitudes of modes P4 and P6 need to be modified when compared to the instability tongues in Figs. 2e and 2f to enable both modes to be activated in unison. (b–e), The response of modes P4 and P6, when subjected to the above sequence with the measured outputs projected in phase space confirm the successful execution of a 2-bit byte. The responses of modes P4 and P6 are smeared out by different amounts due to their parametric actuation frequencies being increased across their respective instability tongues (along the schematic black arrows in Figs. 2e and 2f) enabling the electromechanical byte memory to be more easily readout.

Electromechanical shift register

Another key component in digital computing is the shift register which is usually realised in an array of transistors where the output of one transistor is the input of the next transistor and so. Again the multimode parametric resonator array entertains the prospect of an electromechanical shift register where the key to realising this in practice is the ability to couple the elements of the array to one another.

This requirement can be readily satisfied via the piezoelectric transducer which can modulate the eigenfrequencies of the mechanical modes. Specifically implementing this modulation at the sum frequency for a pair of modes results in the emergence of sidebands which overlap with the constituent modes and it naturally leads them to couple and even hybridise as described in refs. 29, 31, 39. To confirm if coupling between the elements of the array is possible, mode P6 is harmonically probed whilst the coupling pump at the difference frequency to mode P4 is activated as shown in Fig. 4a. The response of mode P6, shown in the inset of Fig. 4a (see also Fig. S4), reveals that activating the coupling pump results in mode P6 undergoing parametric normal mode splitting thus confirming that it can couple to mode P431.

Figure 4. Phase information transfer in the electromechanical parametric resonator array.

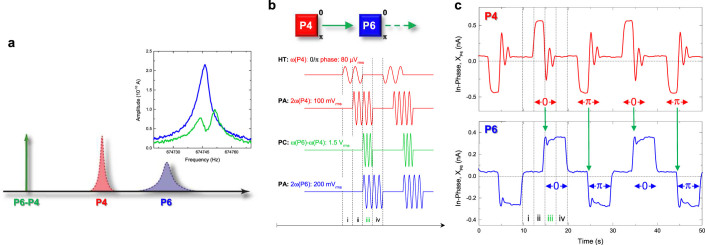
Figure 4

Open in a new tab

(a), The elements of the parametric resonator array can be controllably coupled by modulating the tension in the electromechanical resonator at their frequency difference via the parametric coupling pump. This is experimentally confirmed in the inset by first harmonically probing mode P6 with an amplitude of 1 mVrms in the absence of the pump which results in a typical Lorentzian spectral response (blue line). Repeating this measurement in the presence of the pump with an amplitude of 1.5 Vrms results in the spectral response of mode P6 undergoing parametric normal mode splitting indicating that it is coupled to mode P4 at a rate of ~8 Hz (green line)31,39. (b), The block diagram summarising the corresponding pulse sequence used to implement phase information transfer between elements of the parametric resonator array. (c), Implementation of the pulse sequence described in Fig. 4b where the positive/negative polarity of the in-phase component of the parametric resonances corresponding to logical 0/π is conserved during transmission between the modes. Note also that when the parametric coupling pump is activated in step iii, the parametric resonance of mode P4 fluctuates during the information transfer.

Consequently the pulse sequence shown in Fig. 4b is developed which should enable the realisation of a shift register in the electromechanical parametric resonator array. Briefly, the 0 phase logical is first written and stored into mode P4 via the harmonic trigger and the parametric actuation respectively (steps ii and iii in Fig. 4b). Next the parametric coupling pump is activated at the frequency difference between modes P6 and P4 and in parallel mode P6 is also parametrically activated (step iii in Fig. 4b). Here the parametric coupling pump shifts or transfers the 0 phase logical by triggering or writing this information into mode P6. Finally the coupling pump and mode P4 are deactivated and the 0 phase logical is stored in mode P6 (step iv in Fig. 4b). This sequence is then repeated but now with the π phase logical being written and then shifted from modes P4 to P6. Consequently, implementation of this protocol is expected to result in the sequential shifting of 0 and π logicals from modes P4 to P6 as summarised by the block diagram in Fig. 4b. The results of this measurement shown in Fig. 4c confirm that phase information can successfully be transmitted between parametrically resonating modes for the first time8,37,39. Indeed this process can even be implemented in reverse where information is first written and stored in mode P6 and then shifted to mode P4 as shown in Fig. S5. Consequently, binary phase information can be readily shifted in both directions between the elements of the electromechanical parametric resonator array without the need for hardware rewiring as is the case for transistor based shift registers.

The fidelity and temporal flexibility of the electromechanical shift register as a function of the harmonic trigger amplitude, parametric coupling pump amplitude and information storage time respectively are further detailed in supplementary Figs. S6–S8.

In a realistic shift register information is not externally written each time, namely step i in Figs. 4b, but rather is simply transferred between the elements of the array. To that end the sequence shown in Fig. 5a is implemented where a 0 or π logical is first written into mode P4 via the harmonic trigger which is then permanently deactivated and the binary information is then simply cycled between modes P4 and P6 via the parametric coupling pump.

Figure 5. The electromechanical shift register.

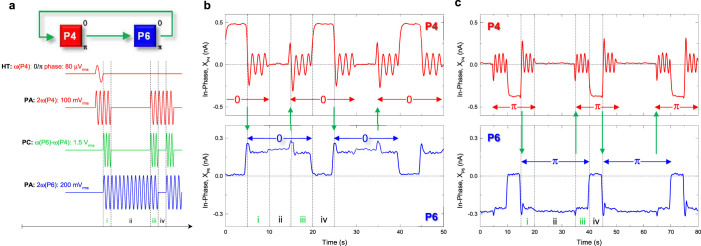
Figure 5

Open in a new tab

(a), The block diagram summarising the corresponding pulse sequence used to implement a shift register in the electromechanical parametric resonator array where logical 0 or π is first written via the harmonic trigger and stored in mode P4 via its parametric resonance. This information is then shifted via the parametric coupling pump and stored in mode P6 (steps i and ii). The same information is then shifted back to P4 for storage (steps iii and iv) following which it is repeatedly cycled between the 2 modes where this process preserves phase information and the storage time in steps ii and iv can be varied as desired. (b) (c), Implementation of the pulse sequence described in Fig. 5a where logical 0 (π) is first prepared by the harmonic trigger resulting in positive (negative) in-phase components for the parametric modes P4 and P6 where this information can be stored for (un)equal durations in steps ii and iv and be repeatedly cycled between them. Note also that when the parametric coupling pump is activated in steps i and iii, it causes the parametric resonance of mode P4 to fluctuate during the information transfer.

This pulse sequence is implemented with 0 (π) phase logical which yields positive (negative) in-phase components in modes P4 and P6 with the information storage time in steps ii and iv being (un)equal and is shown in Fig. 5b (5c). The resultant outputs confirm that the electromechanical shift register has successfully been implemented for the first time where the parametric resonance phase information is not destroyed when being shifted or cycled between the elements of the parametric resonator array. Although in this case the binary phase information is shifted from modes P4 to P6 and is then simply shifted back to mode P4, the information in P6 could easily be shifted to the next element in the parametric resonator array via a suitable parametric coupling pump and so on.

Electromechanical CNOT gate

Although electromechanical logic gates and even circuits have previously been reported19,57,58, an electromechanical resonator based invertor or NOT gate has proved more demanding until only recently59. However, the parametric coupling pump utilised in shifting information between the elements of the electromechanical parametric resonator array offers the possibility of manipulating the binary oscillation phase information. It is anticipated that by tuning the phase of the parametric coupling pump, a phase fluctuation will be induced on the 0/π logical being shifted between the parametrically resonating elements of the array resulting in a phase slip from 0 to π or vice versa where this inversion of binary logicals corresponds to a NOT gate.

In order to evaluate the viability of this proposition, the pulse sequence shown in Fig. 6a and summarised in the block diagram in Fig. 6c is developed. Here the logical 0 is first encoded and stored in mode P4 as described earlier in Figs. 2j–2l. Next this information is shifted to mode P6 via the parametric coupling pump with phase ϕ = 0, which is set when all the input excitations are initialised, and this process conserves phase information resulting in a 0 logical in mode P6 as demonstrated in Figs. 4 and 5. This information is stored in mode P6 for a short time and is then shifted back via the parametric coupling pump, again with ϕ = 0, resulting in the 0 logical in mode P4. Next this process is repeated but now the parametric coupling pump has ϕ = π as depicted in step v in Fig. 6a. It is anticipated that in this configuration the logical phase information will be flipped during transmission resulting in a π logical in mode P6. The π logical is then shifted to mode P4 and back to P6 but crucially the parametric coupling pump has ϕ = 0 during these shifts and as result the π logical is conserved as shown in steps vii to ix in Fig. 6a. Finally after 2 logical conserving shifts, the next shift is executed with ϕ = π for the parametric coupling pump which again is expected to result in the π logical being inverted to a 0 logical as it shifts from mode P6 to mode P4 as shown in step xi in Fig. 6a. This asymmetric pulse sequence is expected to result in a train of logical outputs in modes P4 and P6 that also exhibit this asymmetry namely mode P4 is expected to yield an output sequence 0 0 π 0 0 π 0 0 π and so on whereas mode P6 is expected to yield the sequence 0 π π 0 π π 0 π π and so on enabling the successful implementation of the invertor gate to be more easily identified.

Figure 6. The electromechanical CNOT gate.

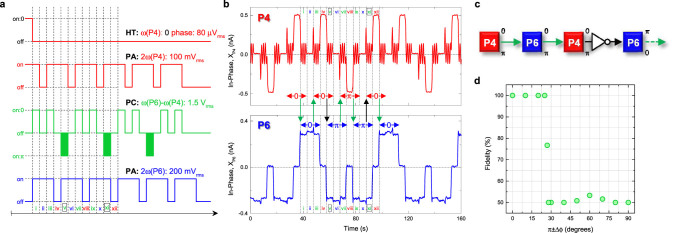
Figure 6

Open in a new tab

(a) and (c), The pulse sequence used to implement an inverter logic gate and the corresponding block diagram respectively. The phase information being shifted between parametric modes P4 and P6 is expected to undergo inversion by introducing a π phase shift in the parametric coupling pump as depicted in steps v and steps xi. (b), The experimental implementation of the pulse sequence described in Fig. 6a clearly confirms that the 0 (π) logical is inverted to π (0) when it is shifted from mode P4 (P6) to P6 (P4) in step v (xi) only by introducing the controlled π phase shift into the parametric coupling pump. Note also that the parametric resonance of mode P4 fluctuates when the parametric coupling pump is activated. (d), The fidelity of the invertor shift between elements of the electromechanical parametric resonator array when subjected to the pulse sequence described in Fig. 6a as a function of the phase difference around the parametric coupling pump with ϕ = π. The invertor logic gate can be executed with 100% fidelity when the parametric coupling pump operates with phase differences close to its node namely at ϕ = π.

The results of implementing this sequence are shown in Fig. 6b where the above described asymmetry in the logical output trains from modes P4 and P6 is clearly observed thus confirming successful execution of the invertor gate. To emphasise, by simply operating the parametric coupling pump with ϕ = π (as in steps v and xi) the input binary logical can be inverted as in a NOT gate. More fundamentally the operation of the NOT gate is actually controlled by the phase information in the pump signal, namely 0 or π for example in steps iii and v in Fig. 6a, thus the above results also demonstrate the realisation of an electromechanical controlled-NOT i.e. CNOT gate for the first time.

The inversion fidelity, when the phase of the pump is varied by Δϕ around ϕ = π is also investigated and is plotted in Fig. 6d. This measurement indicates that for Δϕ ± 22.5° the invertor gate can be executed with 100% fidelity but this abruptly falls for Δϕ values outside this range. This suggests that the pump phase is most explicit close to its nodes thus enabling the binary phase information in the parametric resonator array to be deftly manipulated.

Discussion

The concept of an electromechanical computer has proved inspirational in recent years52,53 especially as it harks back to Babbage's pioneering difference engines60. Indeed some of the requisite components in modern computing architectures have already been developed in electromechanical resonators in various guises including bit memories, 2-bit logic gates and even logic circuits19,20,55,56,58,59 but other core components such as byte memories and shift registers have remained elusive. More fundamentally, the ability to unify all these primary functions within a single conceptual framework has proved to be a formidable challenge in realising practical electromechanical computing.

Consequently, the above results represent a landmark in that all the major functions of a computer namely a byte memory, a shift register and logic gates can be executed in the electromechanical parametric resonator array where crucially all these functions are underpinned by the same physical principle i.e. the parametric resonance of the elements in the array. Consequently, this unifying nature enables these core computational functions to be more naturally combined to build an electromechanical computer as previously pioneered in inductor-capacitor multi-resonator systems45 and as result it brings the promise of ultra-low power computing with mechanically compliant elements a step closer to reality52.

Equally as important, this study demonstrates that electromechanical resonator arrays can be successfully realised by utilising the multitude of higher order vibration modes available to mechanical resonators. Indeed this report vividly illustrates that the higher order vibration modes have been sorely underutilised to date but can be readily exploited and it is anticipated that this in turn will motivate a whole host of new applications to developed in this multimode architecture.

Methods

The sample was mounted in a high vacuum insert (10−7 mbar), which was then placed in a4He cryostat at 2 K. The oscillating signals for the harmonic trigger, parametric actuation and parametric coupling were generated by up to 6 signal generators (NF Wavefactory 1974), which were coupled and synchronized via their internal 10 MHz reference clock. The electromechanical oscillator's response was amplified by an on-chip Si nano-transistor with a 30 dB gain, followed by a transimpedance amplifier (Femto DHPCA-100) with a gain of 106 VA−1 and measured in up to 3 lock-in amplifiers (SRS SR844) in parallel.

Author Contributions

I.M. conceived the experiment, designed and fabricated the electromechanical resonator. M.M. and I.M. performed the measurements and analysed the data. K.N. and A.F. designed and fabricated the Si-nanoFET amplifiers. I.M. wrote the paper based on discussions with all the authors and H.Y. planned the project.

Supplementary Material

Supplementary Information

Supplementary Information

srep04448-s1.pdf (4.7MB, pdf)

Acknowledgments

The authors are grateful to S. Miyashita for growing the heterostructure and D. Hatanaka for support. This work was partly supported by JSPS KAKENHI (23241046).

References

  1. Kippenberg T. J. & Vahala K. J. Cavity optomechanics: Back-action at the mesoscale. Science 321, 1172–1176 (2008). [DOI] [PubMed] [Google Scholar]
  2. Truitt P., Hertzberg J., Huang C., Ekinci K. & Schwab K. Efficient and sensitive capacitive readout of nanomechanical resonator arrays. Nano Lett. 7, 120–126 (2007). [DOI] [PubMed] [Google Scholar]
  3. Shim S. B., Imboden M. & Mohanty P. Synchronised oscillation in coupled nanomechanical oscillators. Science 316, 95 (2007). [DOI] [PubMed] [Google Scholar]
  4. Karabalin R. B. et al. Signal amplification by sensitive control of bifurcation topology. Phys. Rev. Lett. 106, 094102 (2011). [DOI] [PubMed] [Google Scholar]
  5. Massel F. et al. Multimode phonon cooling via three-wave parametric interactions with optical fields. Nature Commun. 3, 987 (2012).22871806 [Google Scholar]
  6. Zhang M. et al. Synchronization of micromechanical oscillators using light. Phys. Rev. Lett. 109, 233906 (2012). [DOI] [PubMed] [Google Scholar]
  7. D. Hatanaka K. O., Mahboob I. & Yamaguchia H. A phonon transistor in an electromechanical resonator array. Appl. Phys. Lett. 102, 213102 (2013). [Google Scholar]
  8. Okamoto H. et al. Coherent phonon manipulation in coupled mechanical resonators. Nature Phys. 9, 480484 (2013). [Google Scholar]
  9. Bagheri M., Poot M., Fan L., Marquardt F. & Tang H. X. Photonic cavity synchronization of nanomechanical oscillators. Phys. Rev. Lett. 111, 213902 (2013). [DOI] [PubMed] [Google Scholar]
  10. Matheny M. H. et al. Phase synchronization of two anharmonic nanomechanical oscillators. Phys. Rev. Lett. 112, 014101 (2014). [DOI] [PubMed] [Google Scholar]
  11. Bhattacharya M. & Meystre P. Multiple membrane cavity optomechanics. Phys. Rev. A 78, 041801(R) (2013). [Google Scholar]
  12. Heinrich G., Ludwig M., Qian J., Kubala B. & Marquardt F. Collective dynamics in optomechanical arrays. Phys. Rev. Lett. 107, 043603 (2011). [DOI] [PubMed] [Google Scholar]
  13. Holmes C. A., Meaney C. P. & Milburn G. J. Synchronization of many nanomechanical resonators coupled via a common cavity field. Phys. Rev. E 85, 066203 (2012). [DOI] [PubMed] [Google Scholar]
  14. Ludwig M. & Marquardt F. Quantum many-body dynamics in optomechanical arrays. Phys. Rev. Lett. 111, 073603 (2013). [DOI] [PubMed] [Google Scholar]
  15. Xuereb A., Genes C., Pupillo G., Paternostro M. & Dantan A. Reconfigurable long-range phonon dynamics in optomechanical arrays. arXiv:1312.5303 (2013). [DOI] [PubMed]
  16. Cleland A. N. & Roukes M. L. A nanometre-scale mechanical electrometer. Nature 392, 160 (1998). [Google Scholar]
  17. Rugar D., Budakian R., Mamin H. J. & Chui B. W. Single spin detection by magnetic resonance force microscopy. Nature 430, 329 (2004). [DOI] [PubMed] [Google Scholar]
  18. Chaste J. et al. A nanomechanical mass sensor with yoctogram resolution. Nature Nanotech. 7, 301–304 (2012). [DOI] [PubMed] [Google Scholar]
  19. Masmanidis S. C. et al. Multifunctional nanomechanical systems via tunably coupled piezoelectric actuation. Science 317, 780–783 (2007). [DOI] [PubMed] [Google Scholar]
  20. Mahboob I. & Yamaguchi H. Bit storage and bit flip operations in an electromechanical oscillator. Nature Nanotech. 3, 275–279 (2008). [DOI] [PubMed] [Google Scholar]
  21. Schliesser A., Anetsberger G. Riviére R. Arcizet O. & Kippenberg T. J. High-sensitivity monitoring of micromechanical vibration using optical whispering gallery mode resonators. New J. Phys. 10, 095015 (2008). [Google Scholar]
  22. Eichenfield M., Chan J., Camacho R. M., Vahala K. J. & Painter O. Optomechanical crystals. Nature 462, 78–82 (2009). [DOI] [PubMed] [Google Scholar]
  23. Adiga V. P. et al. Modal dependence of dissipation in silicon nitride drum resonators. Appl. Phys. Lett. 99, 253103 (2011). [Google Scholar]
  24. Mahboob I., Nishiguchi K., Fujiwara A. & Yamaguchi H. Phonon lasing in an electromechanical resonator. Phys. Rev. Lett 110, 127202 (2013). [DOI] [PubMed] [Google Scholar]
  25. Lin Q. et al. Coherent mixing of mechanical excitations in nano-optomechanical structures. Nature Photon. 4, 236–242 (2010). [Google Scholar]
  26. Westra H. J. R., Poot M., van der Zant H. S. J. & Venstra W. J. Nonlinear modal interactions in clamped-clamped mechanical resonators. Phys. Rev. Lett. 105, 117205 (2010). [DOI] [PubMed] [Google Scholar]
  27. Venstra W., Westra H. & van der Zant H. Q-factor control of a microcantilever by mechanical sideband excitation. Appl. Phys. Lett. 99, 151904 (2011). [Google Scholar]
  28. Gaidarzhy A., Dorignac J., Zolfagharkhani G., Imboden M. & Mohanty P. Energy measurement in nonlinearly coupled nanomechanical modes. Appl. Phys. Lett. 98, 264106 (2011). [Google Scholar]
  29. Mahboob I., Wilmart Q., Nishiguchi K., Fujiwara A. & Yamaguchi H. Wide-band idler generation in a gaas electromechanical resonator. Phys. Rev. B 84, 113411 (2011). [Google Scholar]
  30. Westra H. J. R. et al. Interactions between directly- and parametrically-driven vibration modes in a micromechanical resonator. Phys. Rev. B 84, 134305 (2011). [Google Scholar]
  31. Mahboob I., Nishiguchi K., Okamoto H. & Yamaguchi H. Phonon-cavity electromechanics. Nature Phys. 8, 387–392 (2012). [Google Scholar]
  32. Faust T. et al. Non-adiabatic dynamics of two strongly coupled nanomechanical resonator modes. Phys. Rev. Lett 109, 037205 (2012). [DOI] [PubMed] [Google Scholar]
  33. Castellanos-Gomez A., Meerwaldt H. B., Venstra W. J., van der Zant H. S. J. & Steele G. A. Strong and tunable mode coupling in carbon nanotube resonators. Phys. Rev. B 86, 041402 (2012). [Google Scholar]
  34. Eichler A., del Álamo Ruiz M., Plaza J. A. & Bachtold A. Strong coupling between mechanical modes in a nanotube resonator. Phys. Rev. Lett. 109, 025503 (2012). [DOI] [PubMed] [Google Scholar]
  35. Lulla K. J. et al. Nonlinear modal coupling in a high-stress doubly-clamped nanomechanical resonator. New J. Phys. 14, 113040 (2012). [Google Scholar]
  36. Matheny M. H., Villanueva L. G., Karabalin R. B., Sader J. E. & Roukes M. L. Nonlinear mode-coupling in nanomechanical systems. Nano Lett. 13, 1622–1626 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Faust T., Rieger J., Seitner M. J., Kotthaus J. P. & Weig E. M. Coherent control of a nanomechanical two-level system. Nature Phys. 9, 485488 (2013). [Google Scholar]
  38. Huang P. et al. Demonstration of motion transduction based on parametrically coupled mechanical resonators. Phys. Rev. Lett. 110, 227202 (2013). [DOI] [PubMed] [Google Scholar]
  39. Mahboob I., Nier V., Nishiguchi K., Fujiwara A. & Yamaguchi H. Multi-mode parametric coupling in an electromechanical resonator. Appl. Phys. Lett 103, 153105 (2013). [DOI] [PubMed] [Google Scholar]
  40. Nayfeh A. H. & Mook D. T. Nonlinear Oscillations (Wiley, 1995). [Google Scholar]
  41. Yurke B. et al. Observation of parametric amplification and deamplification in a josephson parametric amplifier. Phys. Rev. A 39, 2519–2533 (1989). [DOI] [PubMed] [Google Scholar]
  42. Movshovich R. et al. Observation of zero-point noise squeezing via a josephson-parametric amplifier. Phys. Rev. Lett. 65, 1419–1422 (1990). [DOI] [PubMed] [Google Scholar]
  43. Giordmaine J. A. & Miller R. C. Tunable coherent parametric oscillation in linbo3 at optical frequencies. Phys. Rev. Lett 14, 973–976 (1965). [Google Scholar]
  44. Burnham D. C. & Weinberg D. L. Observation of simultaneity in parametric production of optical photon pairs. Phys. Rev. Lett 25, 84–87 (1970). [Google Scholar]
  45. Goto E. The parametron, a digital computing element which utilises parametric oscillation. Proc. IRE 47, 1304 (1959). [Google Scholar]
  46. Rugar D. & Grütter P. Mechanical parametric amplification and thermomechanical noise squeezing. Phys. Rev. Lett. 67, 699–702 (1991). [DOI] [PubMed] [Google Scholar]
  47. Turner K. L. et al. Five parametric resonances in a microelectromechanical system. Nature 396, 149 (1998). [Google Scholar]
  48. Karabalin R. B., Masmanidis S. C. & Roukes M. L. Efficient parametric amplification in high and very high frequency piezoelectric nanoelectromechanical systems. Appl. Phys. Lett. 97, 183101 (2010). [Google Scholar]
  49. Chan H. B. & Stambaugh C. Activation barrier scaling and crossover for noise-induced switching in micromechanical parametric oscillators. Phys. Rev. Lett. 99, 060601 (2007). [DOI] [PubMed] [Google Scholar]
  50. Unterreithmeier Q. P., Weig E. M. & Kotthaus J. P. Universal transduction scheme for nanomechanical systems based on dielectric forces. Nature 458, 1001–1004 (2009). [DOI] [PubMed] [Google Scholar]
  51. Eichler A., Chaste J., Moser J. & Bachtold A. Parametric amplification and self-oscillation in a nanotube mechanical resonator. Nano Lett. 11, 2699–2703 (2011). [DOI] [PubMed] [Google Scholar]
  52. Roukes M. L. Mechanical computation, redux? IEEE IEDM Technical Digest 539–542 (January2004). [Google Scholar]
  53. Freeman M. & Hiebert W. Nems: Taking another swing at computing. Nature Nanotech. 3, 251–252 (2008). [DOI] [PubMed] [Google Scholar]
  54. Chan H. B., Dykman M. I. & Stambaugh C. Switching-path distribution in multidimensional systems. Phys. Rev. E 78, 051109 (2008). [DOI] [PubMed] [Google Scholar]
  55. Badzey R. L., Zolfagharkhani G., Gaidarzhy A. & Mohanty P. A controllable nanomechanical memory element. Appl. Phys. Lett. 85, 3587–3589 (2004). [Google Scholar]
  56. Blick R. H., Qin H., Kim H.-S. & Marsland R. A nanomechanical computer-exploring new avenues of computing. New J. Phys. 9, 241 (2007). [Google Scholar]
  57. Guerra D. N. et al. A noise-assisted reprogrammable nanomechanical logic gate. Nano Lett. 10, 1168–1171 (2010). [DOI] [PubMed] [Google Scholar]
  58. Mahboob I., Flurin E., Nishiguchi K., Fujiwara A. & Yamaguchi H. Interconnect-free parallel logic circuits in a single mechanical resonator. Nature Commun. 2, 198 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Wenzler J. S., Dunn T., Toffoli T. & Mohanty P. A nanomechanical fredkin gate. Nano Lett. 14, 89–93 (2014). [DOI] [PubMed] [Google Scholar]
  60. Swade D. The Difference Engine: Charles Babbage and the Quest to Build the First Computer (Viking, New York, 2001). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Information

srep04448-s1.pdf (4.7MB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES