Global architecture of F-actin cytoskeleton regulates cell shape-dependent endothelial mechanotransduction

Abstract

Uniaxial stretch is an important biophysical regulator of cell morphology (or shape) and functions of vascular endothelial cells (ECs). However, it is unclear whether and how cell shape can independently regulate EC mechanotransductive properties under uniaxial stretch. Herein, utilizing a novel uniaxial cell-stretching device integrated with micropost force sensors, we reported the first experimental evidence showing cell shape-dependent EC mechanotransduction via cytoskeleton (CSK) contractile forces in response to uniaxial stretch. Combining experiments and theoretical modeling from first principles, we showed that it was the global architecture of the F-actin CSK that instructed the cell shape-dependent EC mechanotransductive process. Furthermore, a cell shape-dependent nature was relayed in EC mechanotransduction via dynamic focal adhesion (FA) assembly. Our results suggested a novel mechanotransductive process in ECs wherein the global architecture of the F-actin CSK, governed by cell shape, controls mechanotransduction via CSK contractile forces and force-dependent FA assembly under uniaxial stretch.

Introduction

Mammalian cells utilize their intrinsic mechano-sensing and -transductive molecular machineries to probe and respond to the extracellular biophysical cues such as the mechanical and topographical properties of extracellular matrix (ECM), adhesive constraints and external mechanical forces.^1–6 In recent years, there is mounting evidence suggesting that the filamentous actin cytoskeleton (F-actin CSK), CSK contractile force, and focal adhesion (FA) constitute an interconnected feedback control and mechanotransductive network responsible for cellular mechanosensory properties under many different contexts.^7–19 Thus, elucidating how the F-actin CSK structure, CSK contractile force and FA interact and regulate each other under external biophysical stimuli can provide important fundamental insights for intracellular mechanotransductive processes that induce long-term cellular mechanoresponsive behaviors such as gene expression, proliferation and differentiation.

In the vascular system, endothelial cells (ECs) lining the lumen of blood vessels are subject to mechanical stimuli such as fluid shear stress and circumferential stretching.^20–22 Previous studies have demonstrated that external cell stretch plays an important regulatory role in determining EC morphology and functions.^23–29 Notably, under cyclic uniaxial stretches, ECs actively remodel cell morphology and the F-actin CSK structure to make them aligned in perpendicular to the direction of uniaxial stretch.^23–25 It has been hypothesized that the F-actin CSK aligned perpendicular to stretch can minimize changes of intracellular CSK contractility, which may be critical for minimizing intracellular pro-inflammatory signaling activities (such as the NF-κB, ROS, and JNK pathways) and thus promoting maintenance of EC functional homeostasis.^20,26 However, till now, there is limited experimental evidence directly supporting this hypothesis, largely due to a lack of biomechanical tools to precisely modulate uniaxial cell stretch while simultaneously quantifying live-cell CSK contractile responses and mechanosensitive molecular dynamics.

Although correlations between EC morphology and functional phenotypes have often been observed²⁰, there so far have been limited experimental studies to investigate whether cell morphology or shape can independently regulate the mechanotransductive processes in ECs when responding to uniaxial stretch. Furthermore, although the F-actin CSK, FA and CSK contractile force are all important for EC morphological remodeling,^20,30,31 it is unclear how these mechanosensory components interact with each other and how their interdependent regulations play a role in determining cell shape-mediated endothelial mechanotransduction. Understanding both questions can help advance our mechanistic understanding regarding cell shape as a functional regulator for mechanotransduction in vascular physiology and pathology such as atherogenesis.

Here we report a novel uniaxial cell stretching device (CSD) integrated with subcellular force sensors for simultaneous applications of uniaxial stretch and quantitative measurements of reactive cellular CSK contractile forces. Using this uniaxial CSD, we presented the first experimental evidence that cell shape determined endothelial mechano-transductive and -responsive behaviors in response to uniaxial stretch via reactive CSK contractile forces. Combining experimental investigation with theoretical modeling from first principles, we demonstrated that it was the global architecture of the F-actin CSK, rather than local cellular properties, that instructed cell shape-dependent endothelial mechano-transductive and -responsive properties. Using live-cell imaging with fluorescence FA proteins, we further explored how cell shape-dependent mechanotransduction via CSK contractile forces might relay extracellular cell stretching signal to FA dynamics and morphogenesis. Together, our results revealed a novel functional role of the F-actin CSK architecture in instructing cell shape-dependent endothelial mechanotransduction under uniaxial stretch via governing reactive CSK contractile forces and force-dependent FA assembly.

Results

Uniaxial stretching of endothelial cells on integrated micropost force sensors

In this study, we applied in-plane uniaxial stretching to an elastomeric membrane on which live single ECs were cultured to mimic circumferential uniaxial stretch experienced by ECs in vivo. Since external mechanical stretch of a substrate on which mechanosensitive adherent cells are cultured can immediately affect CSK contractile forces exerted by the cells at the cell-substrate interface,^32–36 we reckoned that CSK contractile forces against the substrate, which are originated from the contractile F-actin CSK and transmitted through FAs to the substrate, were a primary mechanosensing component that responded to cell stretch. Thus, it is critical to develop a CSD that can precisely modulate global homogenous uniaxial stretch while simultaneously measuring live-cell dynamic response of CSK contractile forces (Fig. 1).

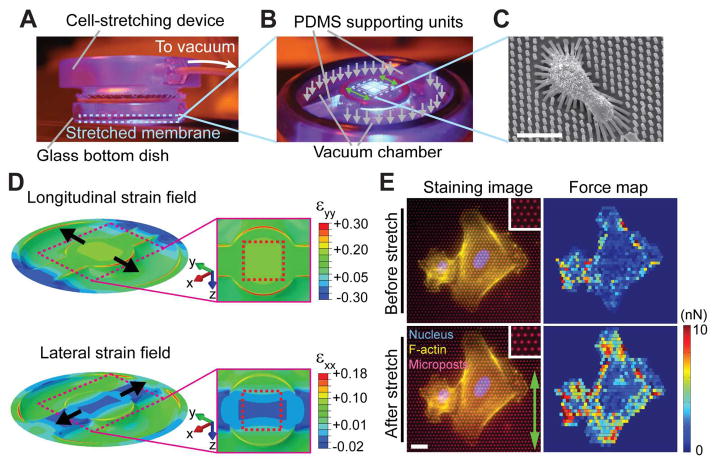
Fig. 1.

Uniaxial cell stretching device (CSD) integrated with PDMS micropost force sensors for quantitative control and measurement of mechanical stimuli and cellular contractile responses. (A) Experimental setup of the CSD with a circular viewing aperture surrounded by a vacuum chamber. A PDMS basal membrane mounted on the CSD was stretched under a vacuum when placed in a glass bottom dish for high-resolution live-cell imaging. (B) Operational mechanism of the CSD for uniaxial stretch. Two identical PDMS supporting units inserted symmetrically in the vacuum chamber divided the chamber into two same compartments. A bipolar suction (grey arrows) generated by the vacuum created a uniaxial stretching field (green arrows) in the central region of the PDMS basal membrane, on which PDMS micropost force sensors were integrated for in situ cellular contractile force measurements. (C) Scanning electron microscopy (SEM) image showing an adherent cell seeded on PDMS microposts and bending of microposts underneath the cell due to cellular contractile forces. (D) Finite element (FE) simulations showing longitudinal (ε_yy; top) and lateral (ε_xx; bottom) strain fields of the PDMS basal membrane when uniaxially stretched on the CSD. The central region of the PDMS basal membrane integrated with PDMS microposts was marked by dashed red rectangles. (E) Immunofluorescence images (left) showing HUVECs on PDMS microposts before (top) and after (bottom) the onset of uniaxial stretch (green arrow). Fluorescently labeled PDMS microposts were used as force sensors to quantify cellular contractile forces (right). As fiducial markers, undeflected PDMS microposts (in insets) were continuously monitored during stretch to assess the stretch ratio, directionality and spatial uniformity. Scale bars, 20 μm.

Herein, we developed a novel uniaxial CSD integrated with subcellular force sensors for simultaneous applications of uniaxial stretch and quantitative measurements of reactive CSK contractile forces. The CSD was adapted from an equibiaxial cell stretching apparatus developed previously from our laboratory,^37,38 of which cell stretching was achieved based on vacuum driven stretching of a basal elastomeric membrane made of polydimethylsiloxane (PDMS) (Fig. 1A). To generate uniaxial stretch in the PDMS basal membrane, we modified the internal topology of the annular vacuum chamber of the CSD by placing two identical PDMS supporting units at two opposite locations in the chamber to divide the chamber into two exact vacuum compartments (Fig. 1B). When vacuum was applied, the PDMS basal membrane resting on the top of both vacuum compartments was sucked into the vacuum chamber, while the supporting units prohibited the rest of the PDMS basal membrane from any out-of-plane movement, leading to uniform in-plane uniaxial stretch in the central area of the PDMS basal membrane, with the uniaxial stretch direction perpendicular to the orientation crossing the two PDMS supporting units (Fig. 1B).

For quantitative measurements of reactive CSK contractile forces, elastomeric PDMS micropost force sensors (with a post diameter of 1.83 μm) were integrated onto the central region of the PDMS basal membrane (Fig. 1C; for details, see SI Text and Supplementary Fig. S1).^39–42 Significant advantages of integrating the PDMS micropost force sensors with the uniaxial CSD included their uniform surface geometry and different post heights to modulate substrate rigidity independent of effects on adhesion and other material surface properties,^40,41 their capability for real-time sensitive monitoring of live-cell subcellular contractile forces without a need for cell lysis or re-suspension,^39,42 and their additional benefit as convenient fiducial markers for assessments of directionality and uniformity of uniaxial stretching by the CSD.^37,38

To characterize performance of the uniaxial CSD, we conducted finite element (FE) simulations to examine the effects of the size and geometry of the PDMS supporting unit on directionality and uniformity of uniaxial stretching within the central region of the PDMS basal membrane (Fig. 1D and Supplementary Fig. S2A&B). Our simulations supported that the final design of our device used in this study successfully generated uniform uniaxial stretching within the central region of the PDMS basal membrane on which the PDMS micropost force sensors were integrated (Fig. 1D and Supplementary Fig. S2C&D). Experimental calibrations of uniformity and directionality of uniaxial stretching of the PDMS basal membrane using fluorescently labeled PDMS microposts as fiducial markers confirmed our simulation results (Fig. 1E and Supplementary Fig. S3).

We further conducted FE simulations to assess the effect of uniaxial stretching of the PDMS basal membrane on the deflection and nominal spring constant of the PDMS micropost when responding to a horizontal force acting on the top surface of the PDMS micropost along different directions. Our FE simulations proved that although the basal end of the PDMS micropost was stretched along with the basal PDMS membrane underneath, the effect of such post geometrical variation on the micropost spring constant was negligible, especially for the PDMS micropost with a post height greater than 7 μm, which was used exclusively in the current study (Supplementary Fig. S4).

Cell shape-dependent sensitivity of cytoskeleton contractile forces to uniaxial stretching

To study how cell shape dictates endothelial mechanosensitivity to uniaxial stretching, we used primary ECs (human umbilical vein ECs, or HUVECs) in the current study and defined morphology of single HUVECs as circle, square and rectangle using microcontact printing (Supplementary Fig. S1) while keeping the total cell spread area a constant of 2,500 μm², close to the cell area of single HUVECs when spreading freely on an unconstrained adhesive surface.

From immunofluorescence of FAs (Fig. 2A) and live-cell contractile force measurements (Fig. 2B) for single HUVECs, it was noticeable that orientations of both FAs and CSK contractile forces were centripetal and aligned with each other, consistent with previous observations about the interdependence between CSK contractile forces and FAs.^7,9,10,43,44 To exclude the possibility that the discontinuous adhesive surface of the PDMS micropost array might have undesired effects on subcellular organizations and distributions of the F-actin CSK and FAs, we performed comparative studies and confirmed that subcellular organizations and distributions of F-actin CSK and FAs visualized using immunofluorescence were comparable on the PDMS micropost array integrated onto the PDMS basal membrane and a flat featureless PDMS membrane (Supplementary Fig. S5).

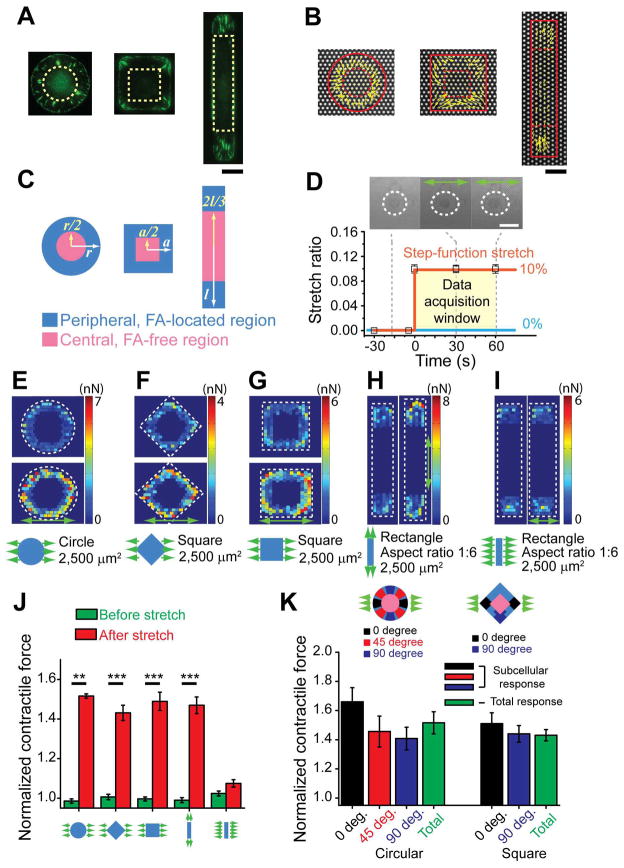
Fig. 2.

Cell shape-dependent sensitivity of cellular contractile forces to uniaxial stretch. (A) Representative immunofluorescence images showing subcellular distributions of FAs in single HUVECs conformed to circular (left), square (middle) and rectangular (right) adhesive islands of an equal area (2,500 μm²). Noticeably, FAs were largely absent from the central region of cells marked by dashed yellow patterns. Scale bar, 20 μm. (B) Vector force maps showing live-cell subcellular contractile forces of single HUVECs conformed to circular (left), square (middle) and rectangular (right) adhesive islands (highlighted by solid red lines) of an equal area (2,500 μm²) patterned on PDMS microposts. Noticeably, cellular contractile forces were mostly concentrated on cell peripheries marked between dashed and solid red lines. Scale bar, 20 μm. (C) Schematic of dividing the whole cell area into peripheral (blue) and central (pink) cell areas, for single HUVECs conformed to different shaped adhesive islands. (D) Step function of static uniaxial stretch. Shown on the top were phase contrast images of a circular-shaped HUVEC recorded before (left) and after (middle and right) the onset of 10% stretch along the horizontal direction (green arrows). Cells were continuously monitored 30 sec before and 1 min after the onset of stretch. Scale bar, 50 μm. (E–I) Representative colorimetric maps showing subcellular contractile forces before and 1 min after the onset of 10% static uniaxial stretch (green arrows) applied to single HUVECs conformed to different shaped adhesive islands of an equal area (2,500 μm²): circular (E), square (F: along the diagonal direction; G: along the side direction), rectangular (H: along the long axis; I: along the short axis). (J) Normalized whole-cell contractile forces before and 1 min after 10% static uniaxial stretch as a function of cell shape and stretch direction. (K) Normalized contractile forces as a function of subcellular location. Peripheral regions of circular- and square-shaped HUVECs were divided into subcellular areas according to their angular positions relative to stretch direction as indicated, with each subcellular area covering an angular range of 30°. Whole-cell contractile forces were included for comparisons. Data in J & K were calculated by normalizing the CSK contractile force 1 min after stretch against the value before stretch. For circular-shaped cells, n = 15; for each of other groups, n = 11. Data represents the mean ± s.e.m. P-values were calculated using two-side unpaired student t-tests. *: p < 1×10⁻⁴; **: p < 1×10⁻⁵; ***: p < 1×10⁻⁶.

Examinations of subcellular distributions of FAs and CSK contractile forces revealed that both were concentrated at cell peripheries, regardless of cell morphology (Fig. 2A&B), and the level of CSK contractile force in the cell central region was comparable to background noise (0.5 – 0.8 nN per micropost) (Supplementary Fig. S6), rendering the cell peripheral region “the region of interest (ROI)” for the remainder of this study (Fig. 2C).

Since CSK contractile forces against a substrate is a primary mechanosensory component responding to cell stretch, here we chose to first examine the immediate CSK contractile response to uniaxial stretch, to assess cell shape-dependent endothelial mechanosensitivity while avoiding complicating long-term effects such as mechanotransductive crosstalk between CSK contractile forces, FAs and other intracellular signaling events. In accordance with this methodology, we utilized the CSD to apply a step-function uniaxial stretch of 10% to single live HUVECs while simultaneously mapping subcellular CSK contractile responses using the PDMS micropost force sensors (Fig. 2D). Prior to stretch, each single live HUVEC was monitored for 30 sec – 1 min to obtain their baseline contractility. At the onset of stretch, a rapid step increase of static uniaxial stretch (10%) was applied to HUVECs and was held constant for an additional 1 min, with the temporal evolution of the HUVEC contractile response continuously monitored.

Figure 2E–I plotted colorimetric maps showing the magnitude and subcellular distribution of CSK contractile forces of single live HUVECs before and after the onset of 10% uniaxial stretch. Notably, single HUVECs of circular and square shapes demonstrated an acute increase of CSK contractility at cell peripheries in response to the single rapid step change of uniaxial stretch. Such acute contractile response was comparable among single HUVECs of circular and square shapes and undergoing stretching of different directions, e.g., along the diagonal and side directions for square-shaped HUVECs (Fig. 2E–G&J). In distinct contrast, single HUVECs of rectangular shape with the ratio between short and long axes of 1:6 demonstrated a differential contractile response to uniaxial stretching depending on the relative orientation of uniaxial stretch with the long axis of the rectangular cell shape (Fig. 2H&I). Specifically, single HUVECs of rectangular shape showed an acute increase of CSK contractility when responding to uniaxial stretch in parallel with the long axis of the rectangular cell shape but exhibited minimal contractile response to uniaxial stretching in parallel with the short axis of the rectangular cell shape (Fig. 2H–J).

Local cellular properties were not sufficient to dictate cell shape-dependent contractile response

The cellular mechanism underlying cell shape-dependent mechanosensitivity of CSK contractile force could be governed by either local or global cellular properties. Local cellular properties such as orientations of contractile forces and force-dependent FAs have recently been proposed as regulators or indicators of cellular mechano-sensitive and -transductive properties.^7,8,18 Indeed, there was a clear difference between single HUVECs of rectangular shape undergoing uniaxial stretching along the long vs. short axis of the rectangular cell shape, in terms of the relative orientation of local contractile forces with respect to the direction of uniaxial stretch. For HUVECs undergoing uniaxial stretching in parallel with the long axis of their rectangular cell shape, local contractile forces mostly aligned with stretch, whereas for uniaxial stretching parallel to the short axis of the rectangular cell shape, local contractile forces mostly lined perpendicular to stretch (Supplementary Fig. S7A).

To further examine the possible connection between local CSK contractile forces and cell shape-dependent contractile response, we performed subcellular analysis for single HUVECs of circular and square shapes by dividing cell peripheral regions into different subcellular areas of varying angular positions with respect to the direction of uniaxial stretch (Fig. 2K). Single HUVECs of circular and square shapes exhibited spatially varying orientations of local contractile forces that were centripetal in nature (Supplementary Fig. S7B&C). However, a rather homogeneous subcellular contractile force response to uniaxial stretching were observed for single HUVECs of both circular and square shapes (Fig. 2K), suggesting that local cellular properties such as subcellular contractile forces were not sufficient to dictate cell shape-dependent mechanosensitivity of CSK contractile force in response to uniaxial stretch.

Global architecture of F-actin CSK instructed cell shape-dependent contractile force response

As one of the most prominent intracellular structures, the F-actin CSK plays an essential role in mechano-sensing and -transduction owing to its capability of rapid polymerization/depolymerization, its intrinsic contractile property exerting forces on the surrounding ECM, and its mechanical connection to other mechanosensory machineries such as cell-ECM and cell-cell adhesions and membrane ion channels.^5,45–48 The concept of “cellular tensegrity” introduced in 1990’s also has centralized the functional role of the contractile F-actin CSK, in addition to microtubules, in regulating mechanotransductive biomechanical and biochemical events inside the cell in different physiological and pathological contexts.^46,49–51

However, since the conceptualization of cellular tensegrity, few experimental investigations have achieved quantitative recapitulation of how the F-actin CSK may govern the spatial and temporal coordination of biomechanical and biochemical events in the cell in response to external biomechanical stimuli.^5,52 Here, we sought to bring a novel quantitative perspective into such a paradigm by addressing specifically questions of whether and how the F-actin CSK might instruct the cell shape-dependent endothelial mechanosensing of uniaxial stretch via CSK contractile forces.

We first noticed that the F-actin CSK in single HUVECs of different shapes exhibited drastically different architectural features (Fig. 3A). Specifically, in HUVECs of circular and square shapes, there were not only radial F-actin stress fibers but also circumferential ones forming a ring-like structure and interconnecting radial stress fibers; whereas in HUVECs of rectangular shape, only highly aligned stress fibers with minimal interconnections between them were visible (Fig. 3A). Based on the global architecture of the F-actin CSK and its biomechanical connection to FAs at cell peripheries (Supplementary Fig. S8A), we constructed a theoretical model that described cell shape-dependent CSK contractile forces and further predicted how they responded to uniaxial stretch (Fig. 3B).

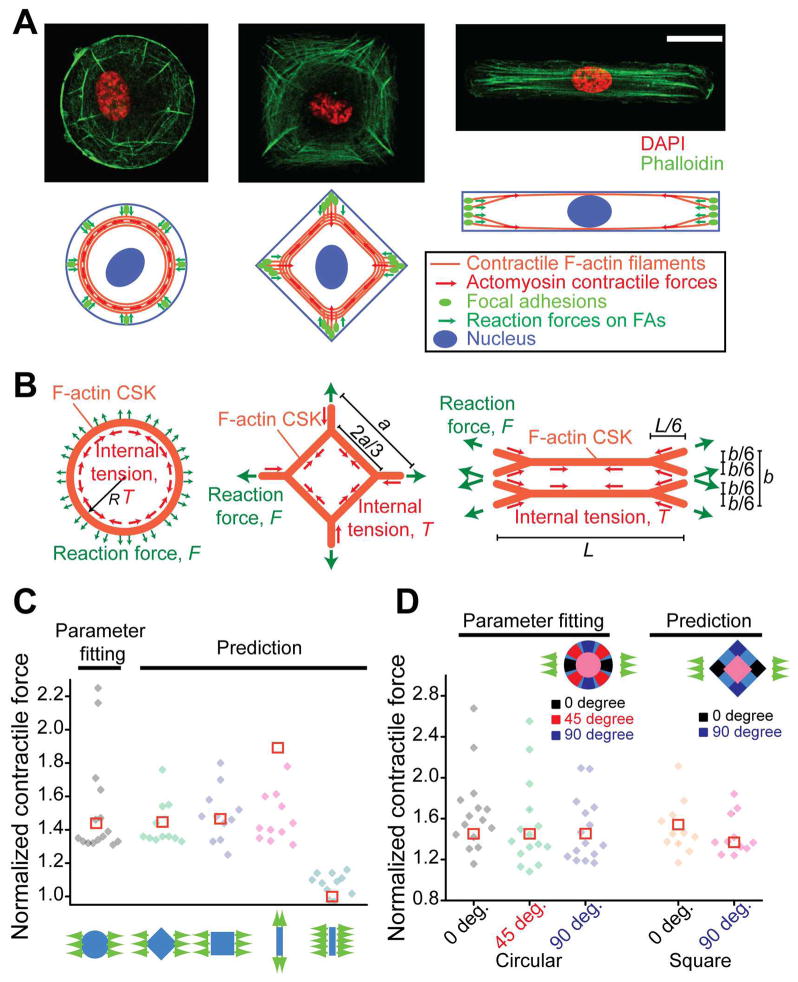
Fig. 3.

Global architecture of the F-actin cytoskeleton (CSK) regulates cell shape-dependent contractile force response. (A) Confocal immunofluorescence micrographs (top) showing the F-actin CSK structure in single HUVECs conformed to circular (left), square (middle) and rectangular (right) adhesive islands of an equal area (2,500 μm²). Cartoon representations (bottom) of global architectures of the F-actin CSK and their mechanical linkages to focal adhesions (FAs) were included, with force balance achieved between intracellular CSK tension and contractile forces transmitted through FAs against substrates. Scale bar, 20 μm. (B) Schematics of theoretical models of the F-actin CSK for single HUVECs conformed to circular (left), square (middle) and rectangular (right) adhesive islands. The dimensions shown were for the F-actin CSK at rest, i.e., when neither intracellular tension nor external stretch was applied. For contractile cells, force equilibrium between intracellular CSK tension T and reactive contractile force F can be established in pre-stressed and stretched configurations, respectively. See SI Text for description of theoretical modeling. (C&D) Comparisons between theoretical results (□) and experimental data (◆) for both total cellular (C) and subcellular (D) contractile forces from single HUVECs of different shapes under uniaxial stretch, as indicated. Parameter fitting was performed using experimental data from circular-shaped cells to determine the pre-strain, ε_pre, which was then used for calculations for cells with other shapes. For circular-shaped cells, n = 15; for each of other groups, n = 11.

Specifically, in our model, the F-actin CSK was represented by a network of nonlinearly elastic strings, whose global architecture recapitulated the F-actin CSK structure in single HUVECs of different shapes. The constitutive equation for each string (or, “F-actin fiber”) was assumed to follow a parabolic relation⁵³

$$T=K{({\mathrm{\epsilon }}_{\text{pre}}+{\mathrm{\epsilon }}_{\text{deform}})}^2$$ (1)

, where T was the internal tension within F-actin fibers, K was the spring constant of F-actin fibers, ε_pre was the tensile pre-strain within F-actin fibers before stretch, and ε_deform was the added mechanical strain within F-actin fibers resulted from stretch. All material parameters were assumed constant across the whole F-actin CSK structure. It should be noted that the viscoelastic properties of the F-actin CSK⁵⁴ was not considered in our model because of the short time scale of our observations (~ 30 sec). Given fixed boundary conditions due to confined cell shapes, we applied mechanical equilibrium to calculate the total CSK contractile force F transmitted through anchorages (or, “FAs”) located at cell peripheries to the substrate (Fig. 3B). F was measured in our experiments using the PDMS microposts as force sensors.

We noticed that in theory the total CSK contractile force F should observe the following general implicit function (for detailed mathematical description, see SI Text and Supplementary Fig. S8B–F)

$$F=f(c_1,c_2,\cdots ,c_{\mathrm{n}},K,{\epsilon }_{\text{pre}},\lambda )$$ (2)

, where c₁, c₂, …, c_n symbolized each known length of the F-actin CSK structure for each cell shape (i.e., R for circular shape, a for square shape, L and b for long and short axes of rectangular shape), and λ was the stretch ratio (λ = 0 before stretch; λ = 0.1 after the onset of stretch). Using dimensional analysis, equation (2) was rewritten as a dimensionless function

$$\frac{F}{{Kc}_1^2}=f^{\ast }(\frac{c_2}{c_1},\cdots ,\frac{c_{\mathrm{n}}}{c_1},{\epsilon }_{\text{pre}},\lambda )$$ (3)

Thus, given that all lengths and the stretch ratio λ were known a priori from our experiments, the normalized total CSK contractile force after the onset of stretch was given by

$$\frac{F^{\prime }}{F}=\frac{f^{\ast }({\epsilon }_{\text{pre}},\lambda =0.1)}{f^{\ast }({\epsilon }_{\text{pre}},\lambda =0)}=\mathrm{\Theta }({\epsilon }_{\text{pre}})$$ (4)

, where F and F′ were the total CSK contractile force before and after stretch, respectively.

Our dimensional analysis suggested that the total CSK contractile response to uniaxial stretch depended solely on the pre-strain within F-actin stress fibers, ε_pre. Given that the cellular contractile force per micropost had a similar magnitude among cells of different shapes (Supplementary Fig. S5), in this work ε_pre was assumed a constant for single HUVECs of different shapes and was determined through data fitting using experimental results obtained from HUVECs of circular shapes.

Specifically, for a circular cell (Fig. 3B and Supplementary Fig. S8B) under pre-stress, given that the outer cell boundary was considered as fixed, the reaction force, F, with a dimension of force per length, was related to internal tension T as

$$F=\frac{T}{\pi R}$$ (5)

, where R was the cell radius and T was given by

$$T=K{\epsilon }_{\text{pre}}^2$$ (6)

For a circular cell under stretch (Supplementary Fig. S8B), the outer cell boundary was uniaxially stretched by 10% and became elliptically shaped. As an approximation, the same scaling relation n Eq. (6) was used for estimating the reaction force F′ and thus the normalized response of reaction force as

$$\frac{F^{\prime }}{F}=\frac{T^{\prime }}{T}=\frac{K{\left({\epsilon }_{\text{pre}}+\frac{P_{\text{ellip}}-P_{\text{circ}}}{P_{\text{circ}}}\right)}^2}{K{\epsilon }_{\text{pre}}^2}$$ (7)

, where P_circ = 2πR and P_ellip were the circumferences for the cell before and after stretch, respectively, and P_ellip was approximated from the elliptical integral as

$$P_{\text{ellip}}=2\pi \sqrt{\frac{{(1.1R)}^2+R^2}{2}}$$ (8)

Thus, the normalized reaction force response was calculated as

$$\frac{F^{\prime }}{F}=\frac{{\left({\epsilon }_{\text{pre}}+0.0512\right)}^2}{{\epsilon }_{\text{pre}}^2}$$ (9)

, which depended only on the pre-strain ε_pre. In order to compare theoretical results with experimental data, ε_pre was first determined by fitting normalized reaction force data obtained from circular cells, and ε_pre = 0.25 (Fig. 4C&D). This fitted parameter ε_pre was then utilized for theoretical predictions of normalized CSK contractile responses in single HUVECs of other shapes (see SI Text for the complete mathematical description).

Fig. 4.

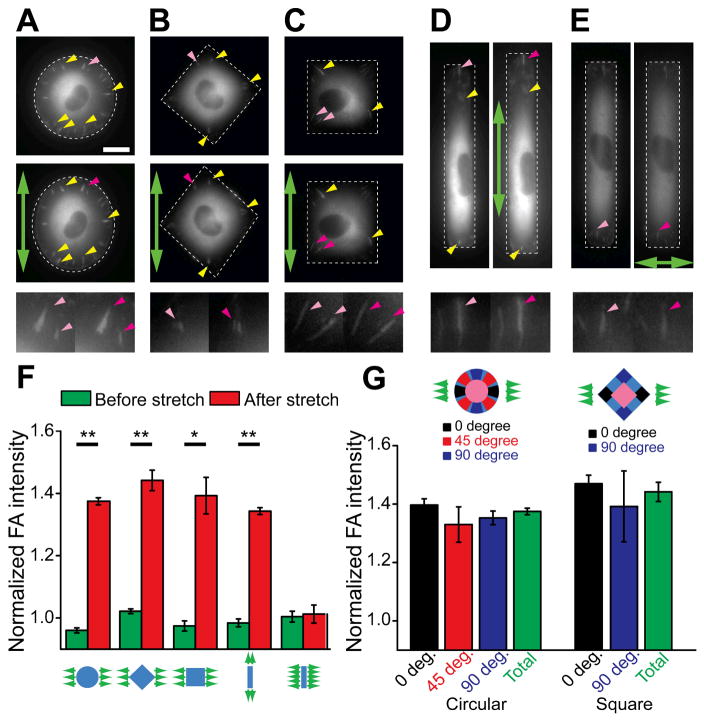
Dynamics of focal adhesions (FAs) during cell shape-dependent endothelial mechanotransduction. (A–E) Live-cell fluorescent images showing FAs in single GFP-paxillin expressing HUVECs before (top or left) and 1 min after (middle or right) the onset of uniaxial stretch (green arrows). Representative single FAs whose total fluorescent intensities increased after stretch were highlighted by yellow arrow heads. (bottom) Magnified images of individual FAs (highlighted by magenta arrow heads) before (light magenta) and after (dark magenta) stretch. (F&G) Normalized total (F) and subcellular (G) FA intensity as a function of cell shape, stretch direction and subcellular location. Whole-cell FA intensity was included in the latter for comparisons. For rectangular-shaped cells under stretch along the long axis of the rectangular cell shape, n = 4; for each of other groups, n = 3. Data represents the mean ± s.e.m. P-values were calculated using two-side unpaired student t-tests. Scale bar: 20 μm. *: p < 0.05; **: p < 0.01.

As shown in Fig. 3C&D (see additional discussion in SI Text), our theoretical predictions agreed well with experimental results, except a slight overestimation for HUVECs of rectangular shapes under uniaxial stretch along the direction of the long axis of the rectangular cell shape, possible due to a slightly different pre-strain value for cells of the rectangular cell shape. Together, our theoretical model clearly suggested that even simple mechanical models constructed from first principles could greatly provide insights for understanding quantitatively how biomechanical responses of ECs were regulated by the F-actin CSK structure. Our experimental and theoretical results strongly suggested that the global architecture of the F-actin CSK could instruct the cell shape-dependent endothelial mechanotransduction via CSK contractile forces.

Dynamics of FAs during cell shape-dependent endothelial mechanotransduction

FAs, the integrin-mediated protein complex that anchors intracellular CSK structure to the ECM while simultaneously transmitting CSK contractile forces, are often found responsive in parallel with CSK contractile forces during mechano-sensing and -transduction, through its dynamic morphogenesis and compositional remodeling as well as a feedback control between FAs and CSK contractile forces.^4,6,18,55 To assess the involvement of FAs in cell-shape dependent endothelial mechanotransduction, live single GFP-paxillin expressing HUVECs were patterned into circular, square and rectangle shapes on flat featureless PDMS membranes before stretched uniaxially. Paxillin-containing FAs were continuously monitored before and after the onset of uniaxial stretching.

Paralleling cell shape-dependent CSK contractile response to uniaxial stretch, the size and fluorescence intensity of individual FAs in HUVECs of circular and square shapes showed acute increases after stretch, suggesting force-dependent reinforcement of FAs (Fig. 4). Importantly, such dynamic strengthening of FAs was distributed across the whole circular and square-shaped HUVECs and not restricted to specific subcellular regions (Fig. 4A–C&F–G). In distinct contrast, in HUVECs with rectangular shape, although fluorescence intensity of FAs increased in response to stretch along the long axis of the rectangular cell shape (Fig. 4D&F), it showed undetectable changes under stretch along the short axis of the rectangular cell shape (Fig. 4E&F). In the latter case, even though some FAs became slightly larger under stretch, the FA intensity decreased slightly and thus the overall total FA intensity was not significantly changed (Fig. 4E&F).

DISCUSSION

Endothelial mechanobiology is of great importance for understanding the molecular and cellular mechanisms underlying vascular physiology and pathology. Previous studies have provided mounting evidence supporting the notion that circumferential stretch and fluid shear stress from blood flow are two critical biophysical factors that regulate endothelial morphogenesis and functions. Specifically, polarized and elongated EC morphology correlated with normal endothelial phenotypes is observed under physiological conditions where laminar shear flow and circumferential stretch are exerted in parallel and perpendicular to the major axis of EC morphology, respectively; whereas non-polarized, low-aspect-ratio EC morphology correlated with dysregulated EC phenotypes is a signature of endothelial dysfunction in human vascular diseases.^20,21 It is still unclear, however, whether cell morphology or shape of ECs plays an independent regulatory role in providing a feedback control to determine the extent of EC responses to external biophysical stimuli, or is merely a downstream phenotypic response closely correlated with their physiological and pathological functions.

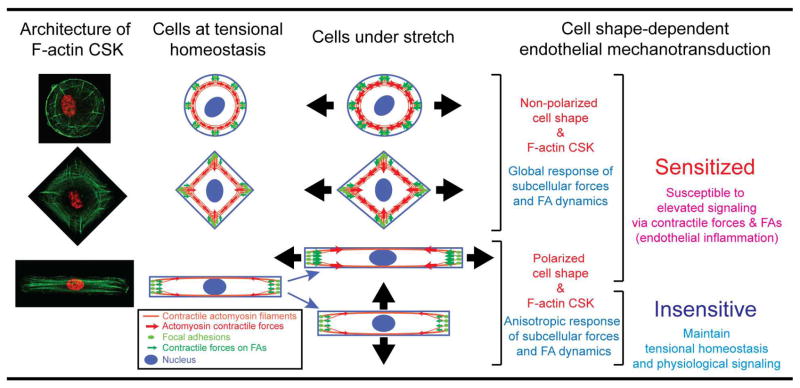
In this study, we presented the first experimental evidence supporting that cell shape could directly regulate endothelial mechano-sensitivity and -transduction in response to uniaxial stretching via cellular CSK contractile forces and FAs. In particular, the cell-shape dependent global architecture of F-actin CSK of ECs not only determined subcellular distributions of both cellular CSK contractile forces and FAs, but also dictated their immediate responses to uniaxial stretching. Importantly, our results proved that ECs with non-polarized shapes were sensitized for cell stretching with acute reinforcements of both CSK contractile forces and FA assembly in response to cell stretching, whereas ECs of polarized shape were only sensitive to stretch along the major axis of EC morphology, but could maintain functional homeostasis in terms of CSK contractility and FA dynamics under stretch perpendicular to the major axis of EC morphology (Fig. 5).

Fig. 5.

Effect of the global architecture of the F-actin cytoskeleton (CSK) on cell shape-dependent endothelial mechanotransduction. Our experimental results and theoretical modeling suggested that cell shape, by modulating the global architecture of the F-actin CSK, could independently dictate the extent of EC mechanosensitive contractile and adhesion responses to uniaxial stretch, which might further determine downstream pro- or anti-inflammatory signaling activities in ECs. Our results suggested a direct feedback between EC morphology and cellular mechanoresponsiveness to external stretch, with non-polarized cell morphology primed for elevated EC responses leading to EC inflammation and polarized cell morphology with the major axis of cell morphology perpendicular to stretch insensitive to stretch and promoting maintenance of EC homeostasis.

The global coordination between cellular contractile force, F-actin CSK and FAs found in this study has been implicated in previous studies as an important mechanism for large-scale cellular sensing of substrate rigidity⁵⁶ and muscle-like cellular responses to environmental rigidity⁵⁷. In complementary to the short-term cellular responses observed in this study, the long-term dynamic interplay between cellular force and F-actin CSK has also been identified in previous studies as a key regulator for cellular adaptations such as cytoskeletal fluidization and reinforcement under transient uniaxial stretches.^58,59

All together, our data provided indisputable evidence supporting that non-polarized or misaligned EC morphology correlated with dysregulated EC phenotypes could render ECs hypersensitive to biophysical stimuli from the local cellular microenvironment and thus amplify downstream pro-inflammatory signaling activities, whereas ECs with elongated morphology lined in perpendicular to directional circumferential stretch could minimize changes of intracellular CSK contractility, critical for minimizing pro-inflammatory signaling activities and thus promoting maintenance of EC homeostasis. Our study could open the opportunity to mechanistically investigate cellular responses to other external mechanical stimuli by exploring and theorizing the structural and functional coordination and integration of F-actin CSK, cellular contractile forces and FA dynamics.

MATERIALS and METHODS

Fabrication and functionalization of PDMS microposts on the basal PDMS membrane

The PDMS membrane integrated with PDMS microposts was generated using a protocol modified from our previous publications (for details, see SI Text and Supplementary Fig. S1).^37,38,42 In brief, PDMS prepolymer (Sylgard-184, Dow Corning) was prepared with the base/curing agent ratio of 10:1 (w/w). A coverslip was silanized before spin-coated with a thin PDMS prepolymer and baked at 70°C for 24 hr. The PDMS micropost array was generated as described previously using the coverslip as a substrate.⁴² In parallel, PDMS stamps with patterned relief structures generated using photolithography and replica molding were inked with a fibronectin solution (50 μg ml⁻¹; Sigma-Aldrich) for 1 hr, blown dry under nitrogen gas, and put into conformal contact with UV-ozone (Jelight) activated PDMS microposts for 30 sec. After functionalization, the PDMS thin film holding the PDMS micropost array was released from the coverslip.

To generate the basal PDMS membrane, PDMS prepolymer (with the base/curing agent ratio of 10:1) was spin-coated on 100-mm petri dish covers at 500 rpm for 30 sec before baked at 70°C for > 48 hr, which resulted in a fully cured PDMS membrane with a thickness of 200 – 300 μm. The backside of the PDMS thin film and the top surface of the PDMS basal membrane were both treated with oxygen plasma (Harrick Plasma) for 50 sec before permanently bonded together via plasma-assisted PDMS-PDMS bonding. The PDMS microposts were further incubated with a solution of Δ⁹-DiI (5 μg ml⁻¹; Life Technologies) for 1 hr. After rinsing with PBS, surface passivation was achieved by incubating the PDMS microposts in 0.2% Pluronic F-127 (Sigma-Aldrich) for 30 min. Before use, the PDMS micropost array was rinsed thoroughly with PBS, submerged in culture media, and pre-equilibrated at 37°C in 5% CO₂.

Vacuum-driven uniaxial cell-stretching device (CSD)

The uniaxial CSD was adapted from our previously reported equibiaxial cell-stretching apparatus.^37,38 Briefly, two PDMS supporting units were inserted at opposite positions in the annular vacuum chamber of the CSD and divided the chamber into two symmetrical compartments. A small amount of vacuum grease (Dow Corning) was applied to the contact interface between the PDMS basal membrane and the CSD, ensuring air tightness and a low friction during stretch. The vacuum, provided by a portable vacuum generator (Vacu-Cell Vacuum System, C&L Instruments), was regulated using a vacuum regulator (Airtrol Inc.). It should be noted that it is unavoidable that stretching of the PDMS basal membrane will induce some out-of-focus effects. This effect was corrected by manually re-adjusting the focal plane within 30 sec after the onset of cell stretch.

Finite element (FE) simulations

FE simulations were performed using software Abaqus 6.9.1 (SIMULIA, Dassault Systèmes). The base structure of the CSD was modeled by a 3D discrete rigid body, and the PDMS basal membrane was modeled by a 3D shell with a thickness of 200 μm. Simpson integration with 5 integration points was assigned across the membrane thickness. Quadrangle linear shell elements with reduced integration were used to partition the membrane. The CSD device was fixed in space, and the outer rim of the PDMS basal membrane was affixed to the CSD underneath. The contact between the PDMS membrane and any other part of the CSD device was modeled by hard frictionless contact. The vacuum was mimicked by applying negative pressure onto the part of the PDMS membrane resting on the top of the two vacuum compartments. Non-linear geometry was used in all simulations. To stabilize the initial contact between the PDMS membrane and the CSD in simulations, a large dissipation factor was used at first, which was later switched back to a very small value for more accurate simulations.

To characterize the spring constant of the PDMS micropost, individual microposts and the stretchable PDMS basal membrane were modeled by cylindrical and orthorhombic geometries, respectively. The post diameter was 1.83 μm, and microposts of three different heights (2.3 μm, 7.1 μm and 12.9 μm) were characterized. Since the center-center distance between microposts was 4 μm, the in-plane dimension of the basal PDMS membrane was chosen as 4 μm × 4 μm, representing a periodic unit of the micropost array. The thickness of the PDMS membrane was chosen as 15 μm in FE simulations to reduce simulation loads. Although a thickness of 15 μm was much thinner than the actual thickness of the PDMS basal membrane (ca. 200 μm), our simulations gave convergent results when compared with models of thicker membranes.

Linear hexagonal 3D stress elements were used for partitioning the PDMS micropost and underlying membrane. Uniaxial stretches of 0%, 10% and 20% were simulated by applying boundary displacements of 0, 0.4 and 0.8 μm along the x-axis, respectively, to the PDMS membrane. Z-symmetrical conditions were applied to the membrane cross-sections with z-axis as the normal. To simulate bending of the micropost under a lateral force f, an in-plane force (within x-z plane) of 15 nN was applied across the top surface of the micropost. The nominal spring constant of the micropost was calculated by dividing the lateral force, f, over the bending displacement of the micropost top. An oblique angle, β, between force f and the uniaxial stretch was applied to describe the anisotropy of the spring constant of the micropost under uniaxial stretching of the basal membrane.

In all FE models, PDMS was simulated as an isotropic neo-Hookean hyperelastic material with parameters C₁₀ = 4.40 × 10⁵ KPa and D₁ = 3.84 × 10⁻⁷ KPa⁻¹, equivalent to a Young’s modulus of 2.5 MPa and Poisson’s ratio of 0.42.

Cell culture

Human umbilical vein endothelial cells (HUVECs; Lonza) were cultured in the endothelial basal medium (EBM-2, Lonza) supplemented with fetal bovine serum (FBS) and soluble factors (EGM-2 SingleQuot Kit, Lonza) including hEGF, VEGF, hFGF-B, R3-IGF-1, heparin, ascorbic acid, hydrocortisone, gentamicin, and amphotericin. Cells were maintained on tissue culture plates pre-coated with 0.1% gelatin (w/v; Sigma-Aldrich). After reaching 70% – 90% confluence, HUVECs were trypsinized (0.025% trypsin/EDTA, Lonza) and passaged with a seeding density of 5 × 10³ cells cm⁻². Before cell stretching assays, single HUVECs were plated at a density of 3 × 10³ cells cm⁻² on the PDMS basal membrane. Cells were cultured at 37°C and 5% CO₂ and allowed to attach to the PDMS membrane overnight before downstream assays. Only early passages of HUVECs (passage 3 – 6) were used in this study.

Immunocytochemistry

A CSK extraction buffer (10 mM PIPES, 150 mM sucrose, 50 mM NaCl, 3 mM MgCl₂, pH ~ 6.8) was used to remove cytoplasmic proteins before cell fixation. In brief, cells were rinsed briefly with the CSK extraction buffer supplemented with 20 μg ml⁻¹ Aprotinin (Sigma Aldrich), 5 μg ml⁻¹ Pepstatin (Sigma Aldrich), and 5 μg ml⁻¹ Leupeptin (Sigma Aldrich), on ice before incubated in chilled CSK extraction buffer supplemented with 0.5% Trition X-100 (Sigma-Aldrich) for 1 – 2 min. Cell fixation was performed thereafter using 4% paraformaldehyde (PFA; Electron Microscopy Sciences) in PBS at room temperature for 20 min. Non-specific binding was blocked by incubating with 10% goat serum (Life Technologies) supplemented with 0.1% Triton X-100 for 1 hr. For immunofluorescence of FAs, anti-vinculin primary antibody (1:200 dilution in 10% goat serum; Sigma-Aldrich) was applied for 1 hr and followed by rinsing 3 times with PBS, before incubation with the secondary antibody (1:100 dilution in 10% goat serum; Alexa-Fluor 488 goat anti-mouse IgG (H+L) antibody, Life Technologies) for an additional 1 hr. F-actin staining by phalloidin (Alexa-Fluor 555 or 647 Phalloidin; Life Technologies) was performed simultaneously with incubation with the secondary antibody. After rinsing briefly, counterstaining of nuclei was performed using DAPI (Life Technologies) for 10 min. The sample was rinsed and then mounted onto glass slides using either ProLong Gold antifade reagents (for long-term storage and confocal microscopy) or SlowFade Gold antifade reagents (for immediate imaging with epifluorescence) (Life Technologies).

Lentiviral transduction

LentiBrite paxillin-GFP biosensors were purchased from Millipore. Aliquots were stored at −80 °C and thawed on ice right before use. Before lentiviral transduction, low-passage HUVECs were cultured in 12-well tissue culture plates for 36 – 48 hr till reaching 50% confluence. Cell media were replaced with pre-equilibrated EGM-2 media containing lentiviral particles at MOI (multiplicity of infection) of 50 – 70. Cell culture was maintained under lentiviral infection for an additional 24 – 36 hr, before the media was replaced with fresh pre-equilibrated EGM-2 medium. HUVECs were cultured for another 12 – 24 hr before re-suspended and seeded for downstream assays.

Microscopy

Live-cell imaging and epifluorescence were performed using a monochrome charge-coupled device (CCD) camera (AxioCam, Carl Zeiss MicroImaging) attached to an inverted microscope (Zeiss Axio Observer Z1, Carl Zeiss Microimaging) with a 40× EC Plan-Neofluar objective (NA 0.75, Ph2, Carl Zeiss MicroImaging). For live-cell imaging, the microscope was enclosed in an environmental incubator (XL S1 incubator, Carl Zeiss MicroImaging) to maintain a cell culture condition at 37°C and 5% CO₂. Laser scanning confocal microscopy was performed using a Nikon A-1 confocal microscope (Nikon Instruments) with diode based lasers and a Plan APO VC 60× oil immersion objective (NA 1.4, Nikon Instruments).

Quantification of cellular contractile forces

Fluorescent microscopic images of the top surfaces of the PDMS microposts were recorded for quantifying bending of microposts under cellular CSK contractile forces. Images were analyzed using a customized MATLAB program (Mathworks) to compute the bending displacement, δ, of each micropost top. Contractile force applied by the cell on the micropost was then calculated as f = kδ, where k was the nominal spring constant of the micropost obtained from FE simulations. PDMS microposts with a post diameter and height of 1.83 μm and 7.1 μm, respectively, and an effective spring constant of 10.2 nN μm⁻¹ were used in all experiments.

Quantification of FA intensity

Fluorescence microscopic images of FAs before and after uniaxial stretch were recorded and analyzed using ImageJ (NIH). Specifically, fluorescence background was first subtracted and the image was displayed in a thresholded fashion to sharpen the FA boundary. An ellipse was then fitted to each individual FA, and the total fluorescence intensity within the ellipse was quantified as the total intensity of individual FAs, which was then summed up across the whole cell for the total FA intensity of individual cells.

Insight Statement.

Vascular endothelial cells (ECs) probe and respond to extracellular mechanical signals such as uniaxial stretch via intracellular machineries constituted by filamentous actin cytoskeleton (F-actin CSK), actomyosin contractile forces and focal adhesions (FAs). Herein, we addressed the mechanistic question regarding whether and how EC morphology could be an independent regulator of EC mechanotransduction under uniaxial stretch. By developing and implementing a uniaxial cell-stretching device with integrated microscale force sensors, we reported the first experimental evidence showing cell shape could independently regulate EC mechanotransduction via subcellular contractile forces and FA assembly. Theorization of our experimental observations was achieved using a biomechanical cell model considering the global architecture of the F-actin CSK and its mechanistic role in governing cellular contractile responses.