Computationally Efficient Steady-State Solution of the Bloch Equations for Rapid Sinusoidal Scans Based on Fourier Expansion in Harmonics of the Scan Frequency

Abstract

Rapid-scan EPR has been shown to improve the signal-to-noise ratio relative to conventional continuous wave spectroscopy. Equations are derived for the steady-state solution to the Bloch equations as a Fourier expansion in the harmonics of the scan frequency. This simulation method is about two orders of magnitude faster than time-domain numerical integration.

1. Introduction

Rapid-scan EPR provides enhanced signal-to-noise relative to conventional continuous wave (CW) for samples ranging from nitroxides [1] and spin-trapped radicals [2] in fluid solution to paramagnetic centers in materials [3]. When the magnetic field is scanned through resonance in a time that is short relative to relaxation times, passage effects may result in oscillations on the trailing edge of the signal. Initially linear scans were employed because of the availability of a deconvolution procedure [4] to recover the slow-scan absorption and dispersion signals. Sinusoidal scans with resonated coils permit faster and wider scans within the constraints of the power available from the coil driver [5]. Development of sinusoidal deconvolution and background subtraction procedures made it practical to employ rapid sinusoidal scans of the external magnetic field [6,7]. The rapid-scan signals can be simulated using numerical integration of the Bloch equations [8]. However, numerical integration is computationally intensive. For a spectrum with many hyperfine lines, it may take from minutes to hours to compute the fitting function.

Robinson and co-workers described a method to simulate continuous wave (CW) EPR spectra including the effects of power saturation, magnetic field modulation, and modulation frequency [9]. Since the spin excitation is periodic, the steady-state signal can be expressed as a Fourier expansion in the harmonics of the modulation frequency [9]. We now show that an analogous approach starting from the Bloch equations can be used to efficiently compute rapid-scan spectra. Since the method does not require the B₁ excitation magnetic field to be in the linear response regime, it can be used to simulate spectra at a range of microwave powers, as in a power saturation curve. The Fourier expansion method reduces computation time by two to three orders of magnitude relative to time-domain integration of the Bloch equations. Explicit equations are provided that can be easily implemented in software.

2. Periodic solution of Bloch Equations

The Bloch equations for a sinusoidal magnetic field scan [8] are:

$$\{\begin{array}{lll}\frac{{\mathit{\text{dm}}}_x}{\mathit{\text{dt}}}\hfill & =\hfill & -\frac{m_x}{T_2}-(\mathrm{\Delta }\omega +{\mathrm{\Omega }}_{cos}{\omega }_s\mathrm{t})m_y\hfill \\ \frac{{\mathit{\text{dm}}}_y}{\mathit{\text{dt}}}\hfill & =\hfill & -\frac{m_y}{T_2}+(\mathrm{\Delta }\omega +{\mathrm{\Omega }}_{cos}{\omega }_s\mathrm{t})m_x-{\omega }_1{m}_z,\hfill \\ \frac{{\mathit{\text{dm}}}_z}{\mathit{\text{dt}}}\hfill & =\hfill & \frac{M_0}{T_1}-\frac{m_z}{T_1}+{\omega }_1{m}_y\hfill \end{array}$$ (1)

$$\text{with}\mathrm{\Delta }\mathrm{\omega }=\mathrm{\gamma }\mathrm{\Delta }\mathrm{B},\mathrm{\Omega }=\frac{1}{2}\mathrm{\gamma }{\mathrm{B}}_{\text{pp}},{\mathrm{\omega }}_1=\mathrm{\gamma }{\mathrm{B}}_1,{\mathrm{\omega }}_{\mathrm{s}}=2\mathrm{\pi }{\mathrm{f}}_{\mathrm{s}},$$ (2)

where B is the offset in gauss of the center field from the resonance field for the spin packet, B_pp is the scan width, B₁ is the amplitude of the excitation field, and f_s is the scan frequency. The variables in Eq. (1) are expressed in angular frequency units.

T₁ and T₂ are the longitudinal and transverse relaxation times, m_x, m_y and m_z are the projections of the magnetization vector on the Cartesian axes. The time evolution of the spin system starts at time t = 0 with m_x = m_y = 0 and m_z = M₀. In about 5T₁ the spin system comes to dynamic equilibrium, and the EPR signal becomes periodic with period P = 2 /_s. Since data acquisition normally starts more than 5T₁ after the initialization of the field scans, one can neglect the transition of the spin system to the steady state when simulating experimental data. This allows us to seek periodic solutions of the Bloch equations in a form:

$$\{\begin{array}{lll}{m}_x\hfill & =\hfill & {\displaystyle \sum _{k=-N}^N}{X}_k{e}^{\mathit{\text{jk}}{\omega }_{\mathrm{s}}\mathrm{t}}\hfill \\ m_y\hfill & =\hfill & {\displaystyle \sum _{k=-N}^N}{Y}_k{e}^{\mathit{\text{jk}}{\omega }_{\mathrm{s}}\mathrm{t}}\hfill \\ m_z\hfill & =\hfill & {\displaystyle \sum _{k=-N}^N}{Z}_k{e}^{\mathit{\text{jk}}{\omega }_{\mathrm{s}}\mathrm{t}}\hfill \end{array},$$ (3)

where X_k, Y_k, and Z_k are the complex Fourier amplitudes for the k^th harmonic of _s, and j is the imaginary unit. The number of included harmonics, N, should be large enough that X_N, Y_N, and Z_N are negligibly small. The maximum frequency in the rapid-scan signal would occur if the spins were excited at an extreme of the scan and T₂ was long enough that the rapid-scan oscillations continued until the other extreme of the scan. This frequency would be about B_pp, so N could be as large as the closest integer above (B_pp)/ _s.

Substitution of Eq.(3) into Eq.(1) and collection of the coefficients of e^jkω_st, produces a system of algebraic equations:

$$\mathit{\text{jk}}{\omega }_{\mathrm{s}}{X}_k=-\frac{1}{T_2}{X}_k-(\mathrm{\Delta }\omega Y_k+\frac{1}{2}\mathrm{\Omega }[Y_{k-1}+Y_{k+1}]),$$ (4.1)

$$\mathit{\text{jk}}{\omega }_{\mathrm{s}}{Y}_k=-\frac{1}{T_2}{Y}_k+(\mathrm{\Delta }\omega X_k+\frac{1}{2}\mathrm{\Omega }[X_{k-1}+X_{k+1}])-{\omega }_1{Z}_k$$ (4.2)

$$\mathit{\text{jk}}{\omega }_{\mathrm{s}}{Z}_k=\frac{{\delta }_{0k}}{T_1}-\frac{Z_k}{T_1}+{\omega }_1{Y}_k,k=-N,\dots ,N.$$ (4.3)

Since the solution is proportional to M₀, M₀ is set equal to 1 in Eq. (4.3). In the derivation of Eq.(4), the term cos _st was substituted by $\frac{1}{2}({\mathrm{e}}^{-\mathrm{j}{\mathrm{\omega }}_{\mathrm{s}}\mathrm{t}}+{\mathrm{e}}^{\mathrm{j}{\mathrm{\omega }}_{\mathrm{s}}\mathrm{t}})$. _0k is the Kronecker delta function that is equal to 1 if k=0 and equal to zero otherwise. By expressing X_k and Z_k in Eqs. (4.1) and (4.3) in terms of Y_k, and substitution into Eq.(4.2) one can obtain an equation for the Y_k unknowns:

$${\mathrm{A}}^{\mathrm{k}}{\mathrm{Y}}_{\mathrm{k}-2}+{\mathrm{B}}^{\mathrm{k}}{\mathrm{Y}}_{\mathrm{k}-1}+{\mathrm{C}}^{\mathrm{k}}{\mathrm{Y}}_{\mathrm{k}}+{\mathrm{D}}^{\mathrm{k}}{\mathrm{Y}}_{\mathrm{k}+1}+{\mathrm{F}}^{\mathrm{k}}{\mathrm{Y}}_{\mathrm{k}+2}={\mathrm{G}}^{\mathrm{k}},\mathrm{k}=-\mathrm{N},\dots ,\mathrm{N}.$$ (5)

Here A^k, B^k, C^k, D^k, F^k and G^k are parameters that can be computed using the following relations:

$$\begin{array}{lll}{A}^k\hfill & =\hfill & \frac{j{T}_2{\mathrm{\Omega }}^2}{-4j+4(k-1)T_2{\omega }_s}\hfill \\ B^k\hfill & =\hfill & \frac{1}{2}j{T}_2\mathrm{\Delta }\omega \mathrm{\Omega }\left[\frac{1}{-j+(k-1)T_2{\omega }_s}+\frac{1}{-j+k{T}_2{\omega }_s}\right]\hfill \\ C^k\hfill & =\hfill & -\frac{1}{T_2}-\mathit{\text{jk}}{\omega }_s-\frac{T_1{\omega }_1^2}{1+\mathit{\text{jk}}{T}_1{\omega }_s}+\frac{j{T}_2\mathrm{\Delta }{\omega }^2}{-j+k{T}_2{\omega }_s}+\frac{j{T}_2{\mathrm{\Omega }}^2}{-4j+4(k-1)T_2{\omega }_s}+\frac{j{T}_2{\mathrm{\Omega }}^2}{-4j+4(k+1)T_2{\omega }_s}\hfill \\ D^k\hfill & =\hfill & \frac{1}{2}j{T}_2\mathrm{\Delta }\omega \mathrm{\Omega }\left[\frac{1}{-j+(k+1)T_2{\omega }_s}+\frac{1}{-j+k{T}_2{\omega }_s}\right]\hfill \\ F^k\hfill & =\hfill & \frac{j{T}_2{\mathrm{\Omega }}^2}{-4j+4(k+1)T_2{\omega }_s}\hfill \\ G^k\hfill & =\hfill & {\omega }_1{\delta }_{0k}\hfill \end{array}$$ (6)

Eq.(6) represents a linear system of 2N +1 algebraic equations, that constitute a pentadiagonal matrix Eq. (7).

$$\left[\begin{array}{lllllll}{C}^{-N}\hfill & D^{-N}\hfill & F^{-N}\hfill & \hfill & \hfill & \hfill & \hfill \\ B^{-N+1}\hfill & C^{-N+1}\hfill & D^{-N+1}\hfill & F^{-N+1}\hfill & \hfill & \hfill & \hfill \\ A^{-N+2}\hfill & B^{-N+2}\hfill & C^{-N+2}\hfill & D^{-N+2}\hfill & F^{-N+2}\hfill & \hfill & \hfill \\ \hfill & \hfill & \hfill & \dots \hfill & \hfill & \hfill & \hfill \\ \hfill & \hfill & A^{N-2}\hfill & B^{N-2}\hfill & C^{N-2}\hfill & D^{N-2}\hfill & F^{N-2}\hfill \\ \hfill & \hfill & \hfill & A^{N-1}\hfill & B^{N-1}\hfill & C^{N-1}\hfill & D^{N-1}\hfill \\ \hfill & \hfill & \hfill & \hfill & A^N\hfill & B^N\hfill & C^N\hfill \end{array}\right]\ast \left[\begin{array}{l}{Y}_{-N}\hfill \\ Y_{-N+1}\hfill \\ Y_{-N+2}\hfill \\ \dots \hfill \\ Y_{N-2}\hfill \\ Y_{N-1}\hfill \\ Y_N\hfill \end{array}\right]=\left[\begin{array}{l}0\hfill \\ 0\hfill \\ \hfill \\ {\omega }_1\hfill \\ \hfill \\ 0\hfill \\ 0\hfill \end{array}\right]$$ (7)

The system can be solved for vector Y by inversion of the matrix. Since the matrix is pentadiagonal, a computationally-efficient method is available to find Y [10]. This approach is very efficient in term of both computational time and memory allocation. After array Y is obtained, X and Z can be found using Eqs.(4.1) and (4.3). Time-domain solutions m_x, m_y, and m_z can be computed by Fourier transformation of X, Y and Z.

To verify performance of the Fourier expansion approach to solution of the Bloch equations, a Matlab program was written that uses the pentsolve routine downloaded from the Matlab Central File Exchange to solve Eq.(7). The program performs computations two to three orders of magnitude faster than an analogous program that used the ode45 Matlab routine to numerically integrate the Bloch equations. For both methods the spectra were constructed by summing contributions from multiple spin packets with different field offsets. Three comparisons are shown.

3. Examples

The time-domain (numerical integration) and frequency-domain (solution of Eq. (7)) methods produce identical results. The latter method is substantially faster for two major reasons. The first reason is that it seeks the periodic solution, while the time-domain method requires integration of a number of scan cycles for the spin system to come to a dynamic equilibrium. Secondly, a system of three differential equations is transformed to a matrix-vector form Eq. (7), which can be solved using an efficient algorithm.

In Figure 1 four cycles of a calculated rapid-scan signal obtained by the two methods for a single spin packet are compared. The scan frequency was selected to be 50 kHz. This corresponds to a time per cycle of 10 s, which is short relative to the T₁ of 50 s. In the time-domain integration method the signal must be calculated for multiple cycles before the steady-state signal amplitude is obtained. By contrast, the Fourier expansion method gives the steady-state solution in the first cycle (dashed green). For comparison three additional cycles are shown for the steady-state solution (Fig.1), which shows that the time-domain solution (blue) converges into the steady-state solution. Transient oscillations at the beginning of the time-domain integration are the result of the sudden jump of excitation from zero to ₁, which produces broad band excitation. The decrease of the signal amplitude calculated by time-domain integration over the first three cycles is due to saturation of the spin system. The steady-state lineshapes and oscillations calculated by the two methods are indistinguishable.

Fig. 1.

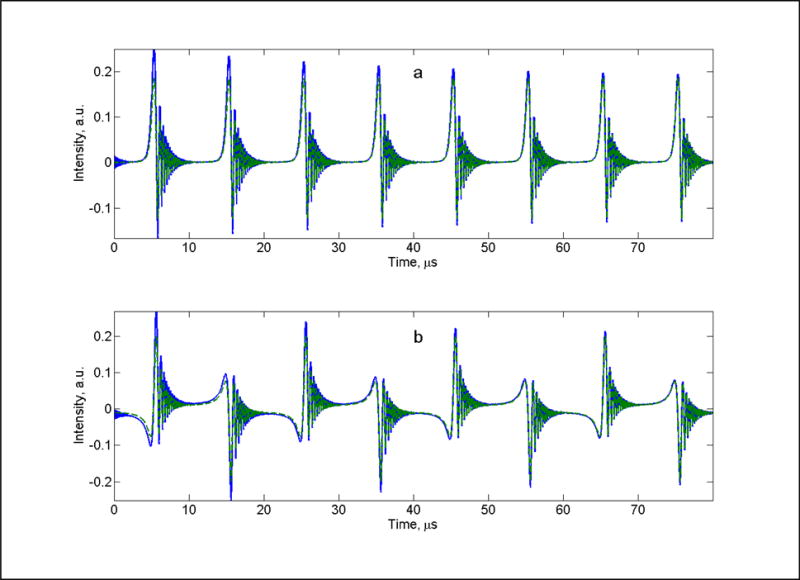
Comparison of four cycles of the absorption (a) and dispersion (b) rapid-scan signals calculated by the Fourier expansion and time-domain numerical integration methods for B_pp = 4.0 G, B = 0.0 G, T₁ = 50 s, T₂ = 1 s, f_m = 50 kHz, B₁ = 0.03 G.

When contributions from multiple spin packets need to be summed in a simulation to account for unresolved hyperfine structure, time-domain integration becomes extremely time consuming. If in addition, the computations have to be repeated for a series of B₁ values to simulate a power saturation curve, the task may take days to accomplish. For example, X-band rapid-scan experimental data for the nitroxide ¹⁵N-mHCTPO (4-protio-3-carbamoyl-2,2,5,5-tetraperdeuteromethyl-3-pyrrolin-1-yloxy) in aqueous solution were reported previously [1]. Figure 2 shows the rapid-scan signal of the nitroxide and its simulation using the Fourier expansion method, which is in excellent agreement with both the absorption and dispersion components of the experimental spectrum. The EPR signals for 38 spin packets were calculated and summed with corresponding weighting factors to account for the resolved and unresolved hyperfine structure [1]. The simulation required only a fraction of a second, so that it was done in essentially real time. A similar calculation using time-domain integration took a few minutes.

Fig. 2.

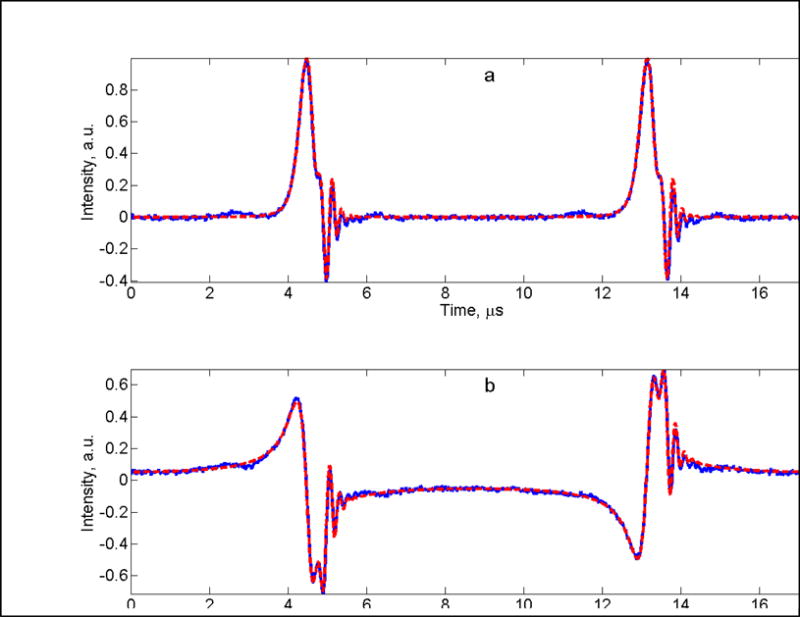
Simulation of experimental X-band rapid-scan spectrum of the low-field nitrogen hyperfine line for the nitroxide ¹⁵N-mHCTPO in water obtained with B_pp = 10.43 G, f_m = 57.454 kHz, and incident power = 21 mW (B₁ = 0.06 G) (a) absorption and (b) dispersion. The scan rate in the center of the sinusoidal scan is 1.9 MG/s.

The power saturation curves for rapid scans of ¹⁵N-mHCTPO were reported previously in Fig. 3 of Ref. [1]. Simulations of the power saturation curve in the published paper were obtained by time-domain numerical integration, which required about 4.2 hr. The simulations of the same data with the Fourier expansion method were indistinguishable from the published simulations, but required only about 29 s, which is an approximately factor of 500 decrease in calculation time.