Abstract
Thioredoxins are enzymes that catalyse disulphide bond reduction in all living organisms1. Although catalysis is thought to proceed through a substitution nucleophilic bimolecular (SN2) reaction1,2, the role of the enzyme in modulating this chemical reaction is unknown. Here, using single-molecule force-clamp spectroscopy3,4, we investigate the catalytic mechanism of Escherichia coli thioredoxin (Trx). We applied mechanical force in the range of 25–600 pN to a disulphide bond substrate and monitored the reduction of these bonds by individual enzymes. We detected two alternative forms of the catalytic reaction, the first requiring a reorientation of the substrate disulphide bond, causing a shortening of the substrate polypeptide by 0.79 ± 0.09 Å (± s.e.m.), and the second elongating the substrate disulphide bond by 0.17 ± 0.02 Å (±s.e.m.). These results support the view that the Trx active site regulates the geometry of the participating sulphur atoms with sub-ångström precision to achieve efficient catalysis. Our results indicate that substrate conformational changes may be important in the regulation of Trx activity under conditions of oxidative stress and mechanical injury, such as those experienced in cardiovascular disease5,6. Furthermore, single-molecule atomic force microscopy techniques, as shown here, can probe dynamic rearrangements within an enzyme’s active site during catalysis that cannot be resolved with any other current structural biological technique.
One of the principal challenges of understanding enzyme catalysis, a central problem in biology, is resolving the dynamics of enzyme–substrate interactions with sub-ångström resolution—the length scale at which chemistry occurs7. Although nuclear magnetic resonance (NMR) and X-ray crystallography determinations of protein structures can reach down to the sub-ångström level, they cannot yet provide dynamic information about enzyme catalysis at this length scale8. Here we demonstrate the ability of single-molecule techniques in probing the dynamics of enzyme catalysis at the sub-ångström scale.
We used a polyprotein made of eight repeats of the I27 domain of human cardiac titin9 with engineered cysteines, (I27SS)8, as a sub-strate protein to monitor the Trx-catalysed reduction of individual disulphide bonds (SS) placed under a stretching force. In our experiments, we used atomic force microscopy in force-clamp mode3 to extend single (I27SS)8 polyproteins (Fig. 1a, far left). The constant applied force caused individual domains to unfold, resulting in a stepwise increase in the length of the molecule after each unfolding event. This is illustrated in Fig. 1b, in which a single (I27SS)8 polyprotein was first mechanically unfolded at 165 pN for 400 ms. A series of 10.8-nm steps was rapidly observed (Fig. 1b, inset); each step corresponds to the partial unfolding of a single I27SS domain up to the disulphide bond (red, Fig. 1a). The disulphide bond is buried in the folded protein4 and is exposed to the bathing solution only after partial unfolding. The unfolding force pulse was followed by a test pulse (100 pN in this case). No further steps were observed during the test pulse because the disulphide bond could not be broken by the applied force alone10 in the absence of Trx. After unfolding, the stretching force was applied directly to the disulphide bond and, if Trx is present in solution, the bond can be chemically reduced by the enzyme. Such a result is shown in Fig. 1c, with a similar experiment in the presence of 8 μM Trx. Now, during the test pulse, seven steps of ~13.2 nm were observed as individual disulphide bonds were reduced by single Trx enzymes, allowing for the immediate extension of the residues previously trapped behind the disulphide bond (blue, Fig. 1a). The size of the increases in step length observed during these force-clamp experiments corresponds to the number of amino acids released, serving as a precise fingerprint to identify the reduction events4,11.
Figure 1. Identification of single Trx catalytic events.
a, Single (I27SS)8 molecules were stretched using an atomic force microscope in force-clamp mode (left). After unfolding of the red residues, the disulphide bond is exposed to the solution. On disulphide reduction by Trx, the blue residues previously trapped behind the disulphide bond are immediately extended. b, A single (I27SS)8 molecule is stretched in the absence of Trx. At least six individual domains are unfolded up to the disulphide bond during the unfolding pulse to 165 pN (inset). No further steps are noted during the test pulse to 100 pN. c, In the presence of 8 μM Trx, seven steps of ~13.2 nm are observed during the test pulse, corresponding to the extension of the trapped residues in each module after the reduction of individual disulphide bonds by single Trx enzymes.
We used an ensemble of single-molecule recordings to measure the kinetics of disulphide bond reduction by Trx. At each force and Trx concentration, we averaged (Supplementary Fig. 1) 10–30 test-pulse recordings of the type shown in Fig. 1c. Averaged traces at various forces are shown in Fig. 2a. The averaged traces were fitted by a single exponential with a time constant τ (see Supplementary Figs 2 and 3). We define the observed rate constant of disulphide reduction as r =1/τ.
Figure 2. Force-dependent Trx catalysis.
a, Multiple single-molecule recordings of the test pulse only (n = 10–30) were averaged to monitor the kinetics of disulphide bond reduction under force F. A single exponential is fitted to each averaged trace (smooth line), and the rate constant of reduction r = 1/τ. b, r as a function of force at [Trx] = 8 μM. c, r as a function of [Trx] at various forces. Error bars in b and c represent the s.e.m. obtained from bootstrapping (see Methods). Solid lines in b and c are fits using the kinetic model shown in d. This model describes two modes of Trx catalysis (path I in red, path II in blue), where the catalytic rate constants are exponentially dependent on the applied force. The dashed green line in b represents model fits in the absence of path II, with k02 = 0.
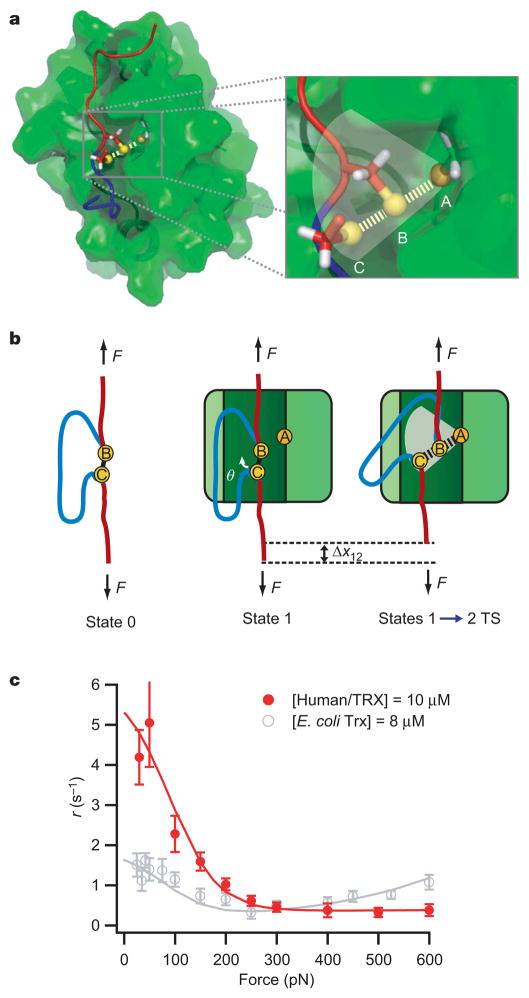
Figure 2b shows a plot of r as a function of the applied (test pulse) force. The figure shows that the rate of reduction decreases fourfold between 25 and 250 pN, and then increases approximately threefold when the force is increased up to 600 pN, demonstrating a biphasic force dependency. This result is in contrast with the uniform acceleration of dithiothreitol (DTT) reduction rate with increasing force4, underlining a much more complex chemical reaction catalysed by Trx. Furthermore, the rate of reduction becomes saturated as the concentration of Trx is increased (Fig. 2c).
To explain our data, we tested different kinetic models of force-dependent Trx catalysis (Supplementary Figs 4–6, and Supplementary Tables 2 and 3). We found that the model that could best describe our data incorporates an intermediate state as well as two different force-dependent rate constants (Fig. 2d). Path I (red, Fig. 2d) is similar to a Michaelis–Menten mechanism, with a catalytic step inhibited by force. Path II (blue, Fig. 2d) is governed solely by the rate constant k02 (where subscripts refer to steps in Fig. 2d), which is accelerated by force. Our model can be globally fitted to the data of Fig. 2b and c (solid lines), obtaining values for the model parameters (Supplementary Table 1). The goodness of fit for this model was measured using statistical methods12 (see Methods and Supplementary Table 3; χ2ν = 0.835, and ν = 26, six free parameters; P(χ2ν) = 0.705). An extrapolation to zero force predicts a second-order rate constant for Trx reduction of 2.2 × 105 M−1 s−1. This is ~30,000 times faster than that found for I27SS disulphide reduction by DTT (6.5 M−1 s−1, ref. 4). This result is consistent with bulk biochemical experiments, in which Trx has been found to reduce insulin disulphide bonds ~20,000 times faster than DTT (1 × 105 M−1 s−1 for Trx versus 5 M−1 s−1 for DTT at pH 7 (ref. 13)).
The experimental data shown in Fig. 2b suggest that there are two separate pathways for disulphide bond reduction by Trx. Further support for this hypothesis was gained by probing the force-dependent reduction kinetics of an active site mutant, Trx(P34H) (Fig. 3). In our single-molecule experiments, the extrapolated zero-force rate of reduction for Trx(P34H) is less than one-half of that for the wild-type enzyme (8.8 × 104 M−1 s−1 versus 2.2 × 105 M−1 s−1), showing a similar relationship to bulk biochemical experiments (3 × 103 M−1 s−1 for Trx(P34H) versus 2 × 104 M−1 s−1 for wild-type Trx at pH 8 and 15 °C (ref. 14)). In Trx(P34H), the rate of Trx binding to the substrate (k01) decreased significantly, whereas the other kinetic parameters remain mostly unchanged (Supplementary Table 1). By fitting this data with two alternate kinetic models, we found that the Trx(P34H) mutant supports the view that Trx has two distinct forms of catalysis, without a common intermediate (see Supplementary Figs 5–7 and Supplementary Table 3).
Figure 3. Trx(P34H).
Plot of r as a function of force at [Trx(P34H)] = 8 μM. Error bars represent the s.e.m. obtained from bootstrapping (see Methods). The solid line is the best fit obtained with the three-state model of Fig. 2d. This point mutation significantly decreases parameter k01—the rate of enzyme binding to the substrate—whereas other parameters in the kinetic model remain similar to wild-type Trx (see Supplementary Table 1).
In the kinetic model shown in Fig. 2d, the catalytic rate constants are described by a straightforward Arrhenius term. For example, k12 = β0exp(FΔx12/kBT), where β0 is the rate constant at zero force, kB is Boltzmann’s constant, T is the temperature and Δx12 is the distance to the transition state along the length coordinate15. Fits of the kinetic model (Fig. 2d) to the data of Fig. 2b and c gave values of Δx12 = −0.79 ± 0.09 Å for the catalytic step of path I and Δx02 = 0.17 ± 0.02 Å for the catalytic step of path II (±s.e.m. obtained by downhill simplex procedure for model fitting, see Methods). Similar parameters were also found for the Trx(P34H) mutant (Supplementary Table 1). Thus, the two catalytic pathways are very different: the transition state of reduction by way of path I requires a shortening of the substrate polypeptide by ~0.8 Å, whereas path II requires an elongation by ~0.2 Å.
Our experiments show that sub-ångström-level distortions of the substrate disulphide bond take place dynamically during Trx catalysis. A glimpse of the transition state for Trx catalysis can be obtained from the NMR structure of human TRX (also known as TXN) a homologue of the E. coli enzyme16,17, in a complex with a substrate peptide from the signalling protein NF-κB (Fig. 4a, PDB accession number 1MDI). In this structure (ref. 18), as well as in the structure of human TRX bound to REF-1 (also known as APEX1) (ref. 19), a peptide-binding groove is identified on the surface of TRX in the vicinity of the catalytic Cys 32. The sulphur atom in Cys 32 (sulphur atom A) of the active site of TRX forms a disulphide bond with the sulphur atom of the NF-κB peptide (sulphur atom B).
Figure 4. Structural model for force-dependent Trx catalysis.
a, TRX (peptide-binding groove in dark green) bound to an NF-κB peptide. The inset (yellow spheres are sulphur atoms A, B and C) shows the relative position of the disulphide bond between TRX Cys 32 (sulphur atom A) and the NF-κB cysteine (sulphur atom B). The third sulphur atom (sulphur atom C) belonging to the leaving cysteine was placed 180° from the disulphide bond, as required by the SN2 chemical reaction. b, Cartoon representation of the reduction by Trx of a disulphide bond in a stretched polypeptide. On binding, the substrate disulphide bond (between sulphur atoms B and C) has to rotate by an angle θ to acquire the correct SN2 geometry at the transition state (TS) of the reaction, causing a contraction of the substrate polypeptide by an amount Δx12. This rotation is opposed by the pulling force. c, Force-dependent reduction by human TRX compared to E. coli Trx. Error bars represent the s.e.m. obtained from bootstrapping (see Methods).
We used the orientation of the disulphide bond within the Trx active site in an attempt to predict the structure of the catalytic transition state in our experiments. It is known that disulphide bond reduction proceeds by means of an SN2 mechanism. This reaction is highly directional, proceeding via a transition state in which the three involved sulphur atoms form an ~180° angle20–22. Thus, the relative positions of these sulphur atoms must be important for efficient Trx catalysis. We found that the disulphide bond in 1MDI forms an angle of ~70° with respect to the axis of the peptide-binding groove. Assuming that this orientation applies to the SN2 reaction that reduces the I27SS bond of our experiments, and that the stretched polypeptide is bound to the groove, it is apparent that the target disulphide bond must rotate with respect to the pulling axis to acquire the correct SN2 geometry (Fig. 4b). Given that the disulphide bond in the stretched polypeptide is aligned within ~20° of the pulling force (Supplementary Fig. 8), a further rotation by an angle θ = 50° would be required for catalysis (Fig. 4b), causing a contraction of the target polypeptide by ~1.2 Å, close to the measured value of Δx12 ≈ −0.8 Å. However, molecular dynamics simulations have previously identified multiple conformations of the catalytic thiol in glutaredoxin, a member of the thioredoxin superfamily23.
Similarly, we have performed molecular dynamics simulations of the 1MDI structure to examine the conformational diversity of the NF-κB to Cys 32 disulphide bond. Our simulations show that the disulphide bond samples a range of conformations with θ = 50° –80° in either the clockwise or the counterclockwise direction (shaded area in the inset of Fig. 4a, and Supplementary Figs 9 and 10). We then combined the results of these molecular dynamics simulations with a theoretical model that treats the substrate backbone as a freely jointed chain24. This model predicts the likelihood of the substrate disulphide achieving the correct geometry for the reaction transition state under a pulling force (see Supplementary Information and Supplementary Fig. 10). We found that, in the cases of NF-κB, REF-1 and the apo TRX, an average bond rotation on the sub-ångström scale (resulting in Δx12 values of −0.77, −0.45 and −0.19 Å, respectively) must take place to allow SN2 chemistry in the TRX active site (Supplementary Table 4).
To probe this model of catalysis, which is based on the structure of human TRX complexes, we also tested the force-dependent mechanism of disulphide bond reduction by human TRX (Fig. 4c). At low forces, it is clear that human TRX catalyses disulphide bond reduction in I27SS much more rapidly than Trx from E. coli. However, at high forces it appears that path II is quite diminished in the human TRX variant. Thus, the data for human TRX resemble a simple Michaelis–Menten model (dashed green line in Fig. 2b), indicating that the two thioredoxin variants differ in their catalytic mechanisms at high force. Our three-state kinetic model also describes the human TRX data well with a fixed Δx12 = −0.79 Å (Fig. 4c and Supplementary Tables 1 and 3). Thus, it is clear that the mechanism that governs the force-dependence of path I is conserved between these homologues, and the results for human TRX at low forces can also be explained by our structural model.
The origin of the Δx02 ~0.2 Å elongation at the transition state of catalysis for E. coli Trx, measured from the force-dependency of path II, is less clear. However, as demonstrated in the theoretical calculations of thiol/disulphide exchange in ref. 22, other reaction geometries are possible, even if they are typically unfavourable energetically. Thus, Δx02 may correspond to the lengthening of the I27SS disulphide bond at a transition state4 other than the standard SN2 form.
Our results show that a mechanical force can alter the chemistry of the catalytic site in thioredoxin significantly. This is a novel concept in biology, that mechanical stresses applied to tissues may completely change the enzymatic chemistry from that observed in solution biochemistry. These effects may be particularly significant in tissues exposed to pathological force levels such as those that occur during mechanical injury. For example, it is well known that the increased mechanical stress during hypertension triggers an oxidative stress response in vascular endothelium and smooth muscle5 that is compensated by an increase in the activity of thioredoxin6,25. In this context, we predict that the increased mechanical forces applied to target disulphide bonds would inhibit the activity of thioredoxin, diminishing the effectiveness of the antioxidant properties of the enzyme. The capability of single-molecule atomic force microscopy techniques directly to probe the dynamic sub-ångström molecular rearrangements during catalysis may prove to be an important tool in understanding the fundamental mechanisms underlying enzymatic chemistry.
METHODS
Protein engineering, expression and purification
The expression and purification of (I27SS)8 has been described previously4. In brief, we used the QuikChange site-directed mutagenesis method (Stratagene) to introduce Gly 32 Cys and Ala 75 Cys mutations into the I27 module from human cardiac titin. We used multiple rounds of successive cloning9 to create an aminocarboxy linked, eight-domain polyprotein gene, (I27G32C–A75C)8. In this work, we call this construct (I27SS)8. This gene was encoded in vector pQE30 and expressed in E. coli strain BL21(DE3). Pelleted cells were lysed by sonication, and the His 6-tagged protein was first purified using an immobilized Talon-Co2+ column (Clontech) and then further purified by gel filtration on a Superdex 200 column (GE Healthcare). The purified protein was verified by SDS–PAGE and stored at 4 °C in a buffer of 10 mM HEPES, 150 mM NaCl, 1 mM EDTA and 0.02% NaN3 (w/v), pH 7.2.
Both wild-type Trx and Trx(P34H) were expressed and purified by the same method described previously26. Briefly, the E. coli Trx gene encoded in plasmid pTK100, was expressed in E. coli strain JF521. Cell pellets were lysed using a French press and stirred with streptomycin sulphate (10% w/v) at 4 °C for 16 h. The filtered supernatant was then loaded onto a 2-l Sephacryl S-100 High Resolution (GE Healthcare) gel filtration column. Trx fractions were pooled and applied to a 250-ml Fractogel EMD DEAE(M) (Merck) ion exchange column equilibrated in a buffer containing 1 mM EDTA and 30 mM TRIZMA, pH 8.3. The protein was eluted by a linear gradient between 0 and 0.5 M NaCl. The proteins were pure, as measured by SDS–PAGE gel densitometry. The molecular weight of pure proteins was confirmed by mass spectrometry. Trx fractions were dialysed into a buffer of 10 mM HEPES, 150 mM NaCl and 1 mM EDTA, pH 7.2. Trx concentration was determined spectrophotometrically at 280 nm using a molar absorption coefficient ε280 of 13,700 M−1 cm−1 (ref. 27). The bulk activity of Trx and Trx(P34H) was confirmed by monitoring spectrophotometrically at 412 nm the reduction of 5,5′-dithiobis(2-nitrobenzoic acid) (DTNB, Sigma) as described28.
TRX was purified as previously described29. Briefly, the pACA/TRX plasmid was expressed in BL21(DE3) cells. Cell pellets were lysed using a French press and stirred with 7% w/v streptomycin sulphate. Protein was then precipitated by adding ammonium sulphate to 85% saturation. The crude extracts were applied to a DEAE 52 column equilibrated with 50 mM Tris-HCl, pH 7.5, 1 mM EDTA and 0.1 mM DTT. Protein was eluted with an NaCl gradient, pooled and concentrated, and then applied to a Sephadex G-50 column equilibrated with 50 mM Tris-HCl, pH 7.5, 1 mM EDTA and 0.1 mM DTT. Fractions were pooled, concentrated and further purified using E. coli Trx antibody affinity chromatography. Protein concentration was determined spectrophotometrically at 280 nm using an ε280 of 8,050 M−1 cm−1.
Single-molecule force-clamp spectroscopy
Our custom-built atomic force microscope has been described previously30. Typical resolution in extension was ~0.5 nm and typical analogue feedback lag in the force-clamp following unfolding was ~5 ms. The spring constant of silicon nitride cantilevers (Veeco), typically ~20 pN nm−1, was calibrated as described previously31. The buffer used for all experiments contained 10 mM HEPES, 150 mM NaCl, 1 mM EDTA and 2 mM NADPH, and was controlled to pH 7.2. Before beginning the experiment, thioredoxin reductase (Sigma; from E. coli for E. coli Trx experiments, or from rat liver for human TRX experiments) was added to the experimental buffer to a final concentration of 50 nM. Thioredoxin was then added to the experimental buffer to the indicated concentration. An excess of NADPH and a catalytic amount of thioredoxin reductase are both necessary to maintain ~98% of Trx in the active, reduced form during the experiment1. In the Trx system, reducing equivalents are donated from NADPH to the FAD domain of thioredoxin reductase, and these electrons subsequently reduce a catalytic disulphide bond in thioredoxin reductase. Reduced E. coli thioredoxin reductase is very specific for reducing the disulphide bond in oxidized Trx1 and does not non-specifically reduce other disulphides. This is demonstrated by recordings shown in Fig. 1b and Supplementary Fig. 1b; when Trx was not included in the solution, no disulphide reduction in I27SS was observed even in the presence of thioredoxin reductase and NADPH.
In the experiment, ~5 μl (I27SS)8 solution was added to a ~100 μl droplet of Trx-containing experimental buffer deposited on a substrate coverslide. Single (I27SS)8 protein molecules were stretched by first pressing the cantilever on the coverslide at a constant force of 800 pN for 3 s, then retracting to a constant force of 165 pN for 400 ms during the unfolding pulse. The indicated test-pulse force was applied for ~5 s. In our experiments we did not control the precise point of attachment between the (I27SS)8 molecule and the cantilever; thus, varying numbers of disulphide reduction events may be observed in a given single-molecule recording.
Data analysis
All data were recorded and analysed using custom software written in Igor Pro 5.0 (Wavemetrics). We analysed only recordings that exhibited disulphide reduction events of the expected step size in the test pulse. (For a discussion of expected disulphide reduction step size as a function of force, see the Supporting Online Material of ref. 4.) We summated and normalized the test-pulse portions of numerous (n = 10–30) recordings that contained only disulphide reduction events and no unsequestered unfolding events. We fitted these averaged traces with a single exponential to obtain the observed rate constant of reduction, r. This type of summation procedure is standard in the ion channel literature and has been used in many contexts to obtain macroscopic kinetics from single-molecule recordings32,33. We assume that disulphide reduction in (I27SS)8 is markovian (that is, that each reduction event is independent of all others); thus, averaging traces with different numbers of reduction steps will result in invariant exponential kinetics4. To estimate the error on our experimentally obtained rate constant, we carried out the nonparametric bootstrap method34. At a given value of force and [Trx], n staircases were randomly drawn with replacement from our original data set. These were summed and fitted to obtain a rate constant. This procedure was repeated 1,000 times for each data set, resulting in a distribution that provided the standard error of the mean for the reduction rate constant, shown as the error bars in Figs 2b and c, 3 and 4c.
Kinetic model
In the kinetic model shown in Fig. 2d (and Supplementary Fig. 4a), three states are used to describe our experimental system. The rate equations for the concentrations of states 0, 1 and 2 as a function of time t are:
| (1) |
| (2) |
| (3) |
Where each rate constant is defined by the following parameters (α0, β0, γ0 and δ0 are coefficients used to calculate each rate constant as a function of force and [Trx]):
| (4) |
| (5) |
| (6) |
| (7) |
As shown in the kinetic model scheme in Supplementary Fig. 4a (also shown in Fig. 2d), rate constants k01 and k02 are linearly dependent on the concentration of Trx and have units of μM−1 s−1. k10 is a constant with units of s−1. k12 is in units of s−1 and is modelled to be exponentially dependent on the applied force, following the Bell equation15. k02 also demonstrates an exponential dependence on the applied force. There are no reverse rate constants for the 0→2 and 1→2 transitions (that is, k20 = 0 and k21 = 0). Immediately after disulphide bond reduction in an I27SS module by Trx, the two thiol groups in I27SS are pulled more than 10 nm apart by the applied force. This prevents any reoxidation of the disulphide bond in I27SS, so the formation of state 2 is irreversible in our experiment. We assume that the concentration of Trx remains constant throughout the experiment because the rare oxidation of single enzymes will not significantly affect the overall solution concentration of active Trx. The [Trx] term is input as a constant from the experimental conditions. The I27SS concentration is not a factor in the rate equations because only single molecules are monitored at any given time and all results are unaffected by the bulk concentration of I27SS.
To describe the obtained experimental data, we solved this kinetic model using matrix analysis. By determining the eigenvalues and eigenvectors of the kinetic matrix (see equation (8)) it is possible to calculate the probability of a single I27SS module being in a given state as a function of time.
| (8) |
If we input values for the parameters α0, β0, γ0, δ0, Δx12 and Δx02 as well as the experimental [Trx], we can solve the matrix for a discrete set of forces in the range of 0–600 pN. The output of the analysis shows the probability of a single disulphide bond existing in state 0 (Supplementary Fig. 4b), state 1 (Supplementary Fig. 4c) or state 2 (Supplementary Fig. 4d) as a function of time. We note that the model is solved with the initial condition of P(0) = 1 at time = 0. State 2, where disulphide reduction by Trx has occurred, is the only state that we can directly monitor using our experimental technique. Thus, the calculated probability of being in state 2 as a function of time directly corresponds to the observed single-molecule recordings shown in Fig. 2a. By fitting these calculated probabilities with a single exponential (Supplementary Fig. 4d), we can obtain the observed rate constant of reduction (r = 1/τ from the exponential fit to the model plot) in the same manner that we determined r for the experimental data.
To find the optimal kinetic parameters to describe the experimental data, we first solved the kinetic model for several, widely ranging values for each parameter (typically over three orders of magnitude). We then compared the model r values to those obtained experimentally (see Fig. 2c, d for wild-type Trx, and Fig. 3b for Trx(P34H)) and calculated the goodness of the fit χ2, where ; here, N is the number of data points, yi is the experimentally observed rate, f (xi) is the calculated rate from the kinetic model, and σ is the magnitude of the error of the observed rate35. The combination of parameter values with the lowest χ2 then served as the starting point for the downhill simplex method36 to optimize further the global fit of the model to the data.
Errors for each parameter were again obtained with the bootstrap method in combination with the downhill simplex method. At each given value of force and [Trx], a value for the rate constant from the distribution obtained with the bootstrap method (see the ‘Data Analysis’ section above) was picked at random. By using different values for the rate at each force, extracted from the bootstrap analysis, the experimental error in each rate constant is accounted for when performing fits to the model. The downhill simplex method was then applied to these rate constants, giving the best fitting values for each parameter for that particular combination of rates. The downhill simplex simultaneously varied all six fitting parameters to globally fit the 32 data points for wild-type Trx (14 at 8 μM Trx; 18 at other concentrations). This procedure was repeated 200 times, resulting in distributions, and thereby standard errors, for each model parameter. The values that provided the best fit to the data as well as their standard errors for wild-type Trx, Trx(P34H) and TRX are shown in Supplementary Table 1.
To determine the goodness of fit of the various kinetic models shown in Supplementary Fig. 5, we first used the above methods to globally fit each model to the force-dependent and concentration-dependent data for wild-type Trx (Supplementary Fig. 6). We measured an overall χ2 value for the best fit to each model (best-fitting parameters shown in Supplementary Table 2). We then obtained a reduced chi-squared value, χ2ν = χ2/ν, where ν is the number of degrees of freedom in the fit (ν = N – c, where N is the number of data points and c is the number of free fitting parameters). To determine the statistical goodness of fit, we calculated P(χ2ν), the likelihood of obtaining the observed χ2ν if the experimental data are truly represented by the proposed kinetic model35. This method has been used previously to determine the goodness of fits of various kinetic models to single-molecule data12. P(χ2ν) was calculated using the web-based program available at http://www.fourmilab.ch/rpkp/experiments/analysis/chiCalc.html. Parameters relating to the analysis of various kinetic models are shown in Supplementary Table 3.
Force-probe molecular dynamics and structural modelling
Simulations were carried out with the Gromacs 3.3.1 simulation suite (http://www.gromacs.org)37. The simulations were started from the NMR structure of human TRX in an intermediate complex with a disulphide bond to a substrate, the NF-κB peptide (PDB accession number 1MDI, ref. 18). Protonation states of the standard amino acids were adopted from the solution structure.
The OPLS (optimized potentials in liquid simulations) force field38 was applied. The protein was solvated in a 7.3 ×7.3 ×7.4 nm3 box of TIP4P water molecules. Twenty-two sodium and 18 chloride ions were added to the simulation system to compensate for the overall positive charge of the protein and to mimic physiological conditions. This yielded a total system size of 49,220 atoms. Simulations were carried out with periodic boundary conditions. Application of the Lincs39 and Settle40 methods allowed for an integration time step of 2 fs. Electrostatic and Lennard–Jones interactions were calculated within a cut-off of 1 nm, and the neighbour list was updated every ten steps. For the long-range electrostatic interactions, the Particle-Mesh-Ewald (PME) method41 with a grid spacing of 0.12 nm was used. An N, p, T ensemble, where N is the number of atoms, p is the pressure and T is the temperature, was simulated, with separate coupling of the protein, solvent and ions to a 300 K heat bath (τ = 0.1, ref. 42). The system was isotropically coupled to a 1 bar pressure bath (τ = 1.0, ref. 42). Initially, the system was energy-minimized (steepest descent, 1,000 steps), before equilibrating the solvent for 700 ps with positional restraints on protein heavy atoms. Then, the whole system was equilibrated (300 K). Input coordinate files and system parameters are also included in the Supplementary Information. (Owing to the large size of the output file it is not practical to include it in the Supplementary Information. Therefore, we will send the output file of our simulations to any researcher, on request.)
To model an approximate transition state geometry for the SN2 reaction in the active site of Trx, in a subsequent simulation the Trx–NF-κB disulphide bond was elongated from 2.05 Å to 2.60 Å (the length of the extended bond found for the transition state in an SN2 reaction22) within 160 ps using the free-energy perturbation code in Gromacs and starting from the equilibrated system. Next, the third sulphur atom taking part in the SN2 reaction was placed along the resulting vector of the extended disulphide bond between Trx and the NF-κB peptide in a distance of 2.40 Å, as found for the SN2 transition state22. The cysteine residue to which the third sulphur atom is bound was placed into the location defined by the sulphur atom, and was oriented such that it did not clash with Trx or peptide residues. Using 20 different starting structures of equilibrated Trx for the modelling of the reduction transition state resulted in somewhat different active-site geometries. The angle between the peptide-binding groove and the axis of the sulphur atoms varies and exists in the range between 50° and 130°. The average conformation of the disulphide bond was observed to fall into two populations (Supplementary Fig. 10). The resulting structures were plotted with Pymol43.
In another set of simulations, titin I27 with residues 32 and 75 mutated to cysteines was unfolded to monitor the disulphide bond orientation in the unfolded state with respect to the pulling direction. The OPLS force field was applied for I27. The wild-type protein (PDB accession number 1TIT, ref. 44) was solvated in TIP4P water in a 6.8 ×5.7 ×5.0 nm3 box. Sixteen sodium and ten chloride atoms were added to neutralize the protein charges and to give physiological ion strength. The resulting system size was 23,524 atoms. I27 was minimized, the solvent initially equilibrated with restraints on the protein heavy atoms (500 ps), and then the entire system subsequently equilibrated for a further 8 ns. The simulation software and parameters as described above were applied. Residues 32 and 75 of the equilibrated structure were mutated to cysteine residues using the program WHATIF (ref. 45). The mutant I27SS was re-solvated in a larger box (19.2 ×5.5 ×5.0 nm3), allowing sufficient space to completely unfold the protein, yielding a system size of 112,156 atoms. The system was minimized, resulting in a shortening of the S–S bond to the value typical for an S–S bond (2.05 Å). The solvent was equilibrated with restraints on the protein heavy atoms (2 ns), followed by the equilibration of side chains with restraints on the protein backbone atoms (2 ns), and finally by the equilibration of the whole system (11 ns). No distortion of the structure adjacent to the point mutations was observed. Force-probe molecular dynamics simulations46 of the equilibrated I27SS mutant were performed. The Cα-atoms of the terminal residues were subjected to harmonic pulling potentials with a spring constant of 500 kJ mol−1 nm−2, and were moved away from each other with a constant velocity of 0.4 nm ns−1. As expected, the unfolded structure (Supplementary Fig. 8), obtained after ~14 ns of the force-probe molecular dynamics simulation time, showed alignment of the disulphide bond within ~20° of the pulling direction, with a projection of the S–S bond length on the pulling axis of ~1.9 Å.
For comparison of the active-site geometry, additional standard equilibrium molecular dynamics simulations have been performed for the reduced state of Trx in the absence of a peptide, and for the other available Trx intermediate, the Trx–Ref-1 complex. For the simulation of the reduced state, the NF-κB peptide in the 1MDI structure was deleted. The apo structure with an unprotonated Cys 32 was solvated in water. After addition of ions to yield physiological ion strength, the system comprised 33,606 atoms. The Trx–Ref-1 complex (PDB accession number 1CQH, ref. 19) was solvated in water with physiological ion strength, resulting in a system size of 38,760 atoms. Both systems were minimized and equilibrated as described above and results are shown in Supplementary Fig. 10.
Supplementary Material
Acknowledgments
We thank D. Rodriguez-Larrea for thioredoxin purification and S. Posy for assistance with structural modelling. This work was supported by NIH grants to J.M.F., an NIH grant to B.J.B., a grant from the Swedish Society for Medical Research to A.H., and a grant from the Spanish Ministry of Science and Education to J.M.S.-R. F.G. is supported by an ISE Columbia University grant to J.M.F. and B.J.B. A.P.W. is supported by an NIH Medical Scientist Training Program grant to Columbia University.
Footnotes
Supplementary Information is linked to the online version of the paper at www.nature.com/nature.
Author Contributions A.P.W., R.P.-J. and J.M.F. designed the experiments. A.P.W. and R.P.-J. performed the experiments and analysed the data. K.A.W. designed the kinetic model and performed error analysis. F.G. and B.J.B. performed molecular dynamics simulations. A.H. provided TRX. J.M.S.-R. provided Trx and Trx(P34H). A.P.W., F.G., K.A.W., R.P.-J. and J.M.F. wrote the paper.
Reprints and permissions information is available at www.nature.com/reprints.
References
- 1.Holmgren A. Thioredoxin. Annu Rev Biochem. 1985;54:237–271. doi: 10.1146/annurev.bi.54.070185.001321. [DOI] [PubMed] [Google Scholar]
- 2.Holmgren A. Thioredoxin structure and mechanism: conformational changes on oxidation of the active-site sulfhydryls to a disulfide. Structure. 1995;3:239–243. doi: 10.1016/s0969-2126(01)00153-8. [DOI] [PubMed] [Google Scholar]
- 3.Schlierf M, Li H, Fernandez JM. The unfolding kinetics of ubiquitin captured with single-molecule force-clamp techniques. Proc Natl Acad Sci USA. 2004;101:7299–7304. doi: 10.1073/pnas.0400033101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Wiita AP, Ainavarapu SRK, Huang HH, Fernandez JM. Force-dependent chemical kinetics of disulfide bond reduction observed with single-molecule techniques. Proc Natl Acad Sci USA. 2006;103:7222–7227. doi: 10.1073/pnas.0511035103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Paravicini TM, Touyz RM. Redox signaling in hypertension. Cardiovasc Res. 2006;71:247–258. doi: 10.1016/j.cardiores.2006.05.001. [DOI] [PubMed] [Google Scholar]
- 6.World CJ, Yamawaki H, Berk BC. Thioredoxin in the cardiovascular system. J Mol Med. 2006;84:997–1003. doi: 10.1007/s00109-006-0109-6. [DOI] [PubMed] [Google Scholar]
- 7.Kraut DA, Carroll KS, Herschlag D. Challenges in enzyme mechanism and energetics. Annu Rev Biochem. 2003;72:517–571. doi: 10.1146/annurev.biochem.72.121801.161617. [DOI] [PubMed] [Google Scholar]
- 8.Hammes-Schiffer S, Benkovic SJ. Relating protein motion to catalysis. Annu Rev Biochem. 2006;75:519–541. doi: 10.1146/annurev.biochem.75.103004.142800. [DOI] [PubMed] [Google Scholar]
- 9.Carrion-Vazquez M, et al. Mechanical and chemical unfolding of a single protein: a comparison. Proc Natl Acad Sci USA. 1999;96:3694–3699. doi: 10.1073/pnas.96.7.3694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Grandbois M, Beyer M, Rief M, Clausen-Schaumann H, Gaub HE. How strong is a covalent bond? Science. 1999;283:1727–1730. doi: 10.1126/science.283.5408.1727. [DOI] [PubMed] [Google Scholar]
- 11.Ainavarapu SR, et al. Contour length and refolding rate of a small protein controlled by engineered disulfide bonds. Biophys J. 2007;92:225–233. doi: 10.1529/biophysj.106.091561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Abbondanzieri EA, Greenleaf WJ, Shaevitz JW, Landick R, Block SM. Direct observation of base-pair stepping by RNA polymerase. Nature. 2005;438:460–465. doi: 10.1038/nature04268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Holmgren A. Reduction of disulfides by thioredoxin. Exceptional reactivity of insulin and suggested functions of thioredoxin in mechanism of hormone action. J Biol Chem. 1979;254:9113–9119. [PubMed] [Google Scholar]
- 14.Krause G, Lundstrom J, Barea JL, Pueyo de la Cuesta C, Holmgren A. Mimicking the active site of protein disulfide-isomerase by substitution of proline 34 in Escherichia coli thioredoxin. J Biol Chem. 1991;266:9494–9500. [PubMed] [Google Scholar]
- 15.Bell GI. Models for the specific adhesion of cells to cells. Science. 1978;200:618–627. doi: 10.1126/science.347575. [DOI] [PubMed] [Google Scholar]
- 16.Qin J, Clore GM, Gronenborn AM. The high-resolution three-dimensional solution structures of the oxidized and reduced states of human thioredoxin. Structure. 1994;2:503–522. doi: 10.1016/s0969-2126(00)00051-4. [DOI] [PubMed] [Google Scholar]
- 17.Eklund H, Gleason FK, Holmgren A. Structural and functional relations among thioredoxins of different species. Proteins. 1991;11:13–28. doi: 10.1002/prot.340110103. [DOI] [PubMed] [Google Scholar]
- 18.Qin J, Clore GM, Kennedy WP, Huth JR, Gronenborn AM. Solution structure of human thioredoxin in a mixed disulfide intermediate complex with its target peptide from the transcription factor NFκB. Structure. 1995;3:289–297. doi: 10.1016/s0969-2126(01)00159-9. [DOI] [PubMed] [Google Scholar]
- 19.Qin J, Clore GM, Kennedy WP, Kuszewski J, Gronenborn AM. The solution structure of human thioredoxin complexed with its target from Ref-1 reveals peptide chain reversal. Structure. 1996;4:613–620. doi: 10.1016/s0969-2126(96)00065-2. [DOI] [PubMed] [Google Scholar]
- 20.Rosenfield RE, Parthasarathy R, Dunitz JD. Directional preferences of nonbonded atomic contacts with divalent sulfur. 1. Electrophiles and nucleophiles. J Am Chem Soc. 1977;99:4860–4862. [Google Scholar]
- 21.Pappas JA. Theoretical studies of reactions of sulfur–sulfur bond. 1 General heterolytic mechanisms. J Am Chem Soc. 1977;99:2926–2930. [Google Scholar]
- 22.Fernandes PA, Ramos MJ. Theoretical insights into the mechanism for thiol/ disulfide exchange. Chem Eur J. 2004;10:257–266. doi: 10.1002/chem.200305343. [DOI] [PubMed] [Google Scholar]
- 23.Foloppe N, Nilsson L. The glutaredoxin -C-P-Y-C- motif: influence of peripheral residues. Structure. 2004;12:289–300. doi: 10.1016/j.str.2004.01.009. [DOI] [PubMed] [Google Scholar]
- 24.Grosberg AY, Khokhlov AR. Statistical Physics of Macromolecules. AIP; New York: 1994. [Google Scholar]
- 25.Tao L, et al. Cardioprotective effects of thioredoxin in myocardial ischemia and reperfusion: role of S-nitrosation. Proc Natl Acad Sci USA. 2004;101:11471–11476. doi: 10.1073/pnas.0402941101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Perez-Jimenez R, Godoy-Ruiz R, Ibarra-Molero B, Sanchez-Ruiz JM. The effect of charge-introduction mutations on E. coli thioredoxin stability. Biophys Chem. 2005;115:105–107. doi: 10.1016/j.bpc.2004.12.012. [DOI] [PubMed] [Google Scholar]
- 27.Holmgren A, Reichard P. Thioredoxin 2: cleavage with cyanogen bromide. Eur J Biochem. 1967;2:187–196. doi: 10.1111/j.1432-1033.1967.tb00125.x. [DOI] [PubMed] [Google Scholar]
- 28.Holmgren A, Slaby I. Thioredoxin-C’: mechanism of noncovalent complementation and reactions of the refolded complex and the active site containing fragment with thioredoxin reductase. Biochemistry. 1979;18:5591–5599. doi: 10.1021/bi00592a011. [DOI] [PubMed] [Google Scholar]
- 29.Ren X, Bjornstedt M, Shen B, Ericson ML, Holmgren A. Mutagenesis of structural half-cystine residues in human thioredoxin and effects on the regulation of activity by selenodiglutathione. Biochemistry. 1993;32:9701–9708. doi: 10.1021/bi00088a023. [DOI] [PubMed] [Google Scholar]
- 30.Fernandez JM, Li H. Force-clamp spectroscopy monitors the folding trajectory of a single protein. Science. 2004;303:1674–1678. doi: 10.1126/science.1092497. [DOI] [PubMed] [Google Scholar]
- 31.Oberhauser AF, Hansma PK, Carrion-Vazquez M, Fernandez JM. Stepwise unfolding of titin under force-clamp atomic force microscopy. Proc Natl Acad Sci USA. 2001;98:468–472. doi: 10.1073/pnas.021321798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Sigworth FJ, Neher E. Single Na+ channel currents observed in cultured rat muscle cells. Nature. 1980;287:447–449. doi: 10.1038/287447a0. [DOI] [PubMed] [Google Scholar]
- 33.Aldrich RW, Corey DP, Stevens CF. A reinterpretation of mammalian sodium channel gating based on single channel recording. Nature. 1983;306:436–441. doi: 10.1038/306436a0. [DOI] [PubMed] [Google Scholar]
- 34.Efron B. The Jackknife, the Bootstrap, and Other Resampling Plans. SIAM; Philadelphia: 1982. [Google Scholar]
- 35.Taylor JR. An Introduction to Error Analysis. 2. Univ. Science Books; Sausalito: 1997. pp. 261–293. [Google Scholar]
- 36.Press WH, Teukolsky SA, Vetterling WT, Flannery BP. Numerical Recipes in C. Cambridge Univ. Press; Cambridge, UK: 1992. [Google Scholar]
- 37.Lindahl E, Hess B, van der Spoel D. GROMACS 3.0: a package for molecular simulation and trajectory analysis. J Mol Model. 2001;7:306–317. [Google Scholar]
- 38.Jorgensen WL, Swenson CJ. Optimized intermolecular potential functions for amides and peptides. Structure and properties of liquid amides. J Am Chem Soc. 1985;107:569–578. [Google Scholar]
- 39.Hess B, Bekker H, Berendsen HJC, Fraaije JGEM. LINCS: a linear constraint solver for molecular simulations. J Comput Chem. 1997;18:1463–1472. [Google Scholar]
- 40.Miyamoto S, Kollman PA. Settle—an analytical version of the shake and rattle algorithm for rigid water models. J Comput Chem. 1992;13:952–962. [Google Scholar]
- 41.Darden T, York D, Pedersen L. Particle mesh Ewald—an Nlog(N) method for Ewald sums in large systems. J Chem Phys. 1993;98:10089–10092. [Google Scholar]
- 42.Berendsen HJC, Postma JPM, Vangunsteren WF, Dinola A, Haak JR. Molecular dynamics with coupling to an external bath. J Chem Phys. 1984;81:3684–3690. [Google Scholar]
- 43.Delano WL. Pymol Manual 〈. 2001 http://www.delanoscientific.com〉.
- 44.Improta S, Politou AS, Pastore A. Immunoglobulin-like modules from titin I-band: extensible components of muscle elasticity. Structure. 1996;4:323–337. doi: 10.1016/s0969-2126(96)00036-6. [DOI] [PubMed] [Google Scholar]
- 45.Vriend G. WHAT IF: a molecular modeling and drug design program. J Mol Graph. 1990;8:52–58. doi: 10.1016/0263-7855(90)80070-v. [DOI] [PubMed] [Google Scholar]
- 46.Grubmüller H, Heymann B, Tavan P. Ligand binding: molecular mechanics calculation of the streptavidin biotin rupture force. Science. 1996;271:997–999. doi: 10.1126/science.271.5251.997. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.