Using Joint Utilities of the Times to Response and Toxicity to Adaptively Optimize Schedule-Dose Regimes

Abstract

A Bayesian two-stage phase I-II design is proposed for optimizing administration schedule and dose of an experimental agent based on the times to response and toxicity in the case where schedules are non-nested and qualitatively different. Sequentially adaptive decisions are based on the joint utility of the two event times. A utility function is constructed by partitioning the two-dimensional positive real quadrant of possible event time pairs into rectangles, eliciting a numerical utility for each rectangle, and fitting a smooth parametric function to the elicited values. We assume that each event time follows a gamma distribution with shape and scale parameters both modeled as functions of schedule and dose. A copula is assumed to obtain a bivariate distribution. To ensure an ethical trial, adaptive safety and efficacy acceptability conditions are imposed on the (schedule, dose) regimes. In stage 1 of the design, patients are randomized fairly among schedules and, within each schedule, a dose is chosen using a hybrid algorithm that either maximizes posterior mean utility or randomizes among acceptable doses. In stage 2, fair randomization among schedules is replaced by the hybrid algorithm. A modified version of this algorithm is used for nested schedules. Extensions of the model and utility function to accommodate death discontinuation of follow up are described. The method is illustrated by an autologous stem cell transplantation trial in multiple myeloma, including a simulation study.

1 Introduction

In clinical trials involving cytotoxic or other potentially harmful agents, adverse events (toxicities) generally occur at random times after the start of treatment. Most phase I clinical trial designs determine an optimal dose, or a maximum tolerable dose (MTD), using a binary indicator of toxicity occurring by a predetermined time from the start of therapy. These designs include the continual reassessment method (CRM, O’Quigley, et al., 1990) and many others. To use more available information, improve logistics, and protect patients from late onset toxicities, phase I designs based on Y_T = time to toxicity have been proposed, including the time-to-event (TiTE) CRM (Cheung and Chappell, 2000), and the designs of Braun (2006) and Bekele, et al. (2008). Many phase I/II designs based on binary or categorical response and toxicity have been proposed (Thall and Russell, 1998; Braun, 2002; Thall and Cook, 2004; Zhang, et al., 2006). Phase I/II designs also may be based on Y_T and Y_R = time to response. Denoting $Y_m^o=\text{time}\text{to}\text{the}\text{event}\text{or}\text{right}-\text{censoring}$ and ${\delta }_m=I(Y_m=Y_m^o)$ for m = R, T, with Y = (Y_R, Y_T), ${\mathit{Y}}^o=(Y_R^o,Y_T^o)$, and δ = (δ_R, δ_T), dose-finding may be based on (Y^∘, δ) (cf. Yuan and Yin, 2009).

Most phase I and phase I/II designs focus on dose, but many agents have schedule-dependent effects. An example in oncology is a nucleoside analog for which the MTD of a 30-minute infusion is (i) 2100 mg/m² if given once, (ii) 1000 mg/m² if given weekly for three weeks with total dose 3000 mg/m² over 21 days, and (iii) 300 mg/m² if given twice in each of weeks 1, 3, and 5 for total dose 1800 mg/m² over 35 days. An example of an unexpected increase in toxicity after changing the schedule of a preparative agent in stem cell transplantation (SCT) from (d/2, d/2) on days (−8, −3) to (d/3, d/3, d/3) on days (−8, −6, −3) is described by Thall (2010, Section 1.1). Braun, et al. (2005) proposed a Bayesian design to optimize the schedule of administration times, s = (s₁, …, s_k), based on ( $Y_T^o$, δ_T), with fixed per-administration dose (PAD), assuming nested schedules with each s corresponding to a number of cycles of therapy. Braun, et al. (2007) extended this to allow PAD to vary, and jointly optimized (s, PAD) by minimizing the absolute difference between a fixed target probability and the posterior mean probability of toxicity by a specified time, $t_T^{\mathit{ref}}$, similar to the TiTE CRM. Li, et al. (2008) proposed an approach to optimizing dose and schedule for the case of two nested schedules and bivariate binary outcomes. However, no designs currently exist that optimize either schedule or (schedule, dose) in the case of non-nested, qualitatively different schedules, or where the outcomes are bivariate event times.

We address the problem of sequential adaptive optimization of treatment regime τ = (s, d) in a phase I/II clinical trial where schedules may differ qualitatively or quantitatively, and the outcomes are possibly right-censored event times (Y^∘, δ). The total dose is d, with fractions given at the successive administration times. No solution to this design problem currently exists. We propose an adaptive Bayesian method using a utility function, U(y), defined on the positive real quadrant [0, ∞)² of possible Y values. We construct U(y) by partitioning a compact subset of [0, ∞)² where Y pairs are likely to occur into rectangles, eliciting a numerical utility on each rectangle from the physicians planning the trial, and fitting a parametric function to the elicited values. For each Y_m, m = R, T, we specify a gamma marginal with shape and scale parameters each modeled as functions of (s, d), and use a copula to obtain association.

The design has two stages, and only allows τ with both acceptable safety and efficacy to be assigned. In stage 1, patients are randomized fairly among schedules in blocks. Within each schedule, the acceptable dose with maximum posterior mean utility is chosen, unless the current sample size for the optimal dose is larger than all current sample sizes for the other doses. In that case, patients are randomized among the assigned schedule’s acceptable doses with probabilities proportional to their posterior mean utilities. In stage 2, the block randomization among schedules is unbalanced using similar criteria, with each schedule’s assignment probability proportional to the posterior mean utility of its optimal dose. We include randomization to reduce the chance of getting stuck at suboptimal τ, which may occur with a “greedy” algorithm that only maximizes posterior mean utility.

Our design differs from those of Braun et al. (2007) and Li et al. (2008) in that we (1) use both time-to-response and time-to-toxicity, (2) use utilities as decision criteria, (3) use unbalanced randomization to choose regimes, (4) assume a bivariate gamma regression model, and (5) allow non-nested schedules. We also consider the case where Y_R is evaluated at a sequence of times rather than continuously, hence is interval censored. We describe extensions of the model and utility to accommodate death or discontinuation of follow up at toxicity. Our methodology synthesizes the above and several other existing ideas, including use of a copula to obtain association, randomizing to avoid getting stuck at a suboptimal regime, and regression modeling of both first and second order parameters.

To provide a concrete frame of reference, we describe the illustrative SCT trial in Section 2. Section 3 describes a method for constructing a utility function from elicited values. Gamma regression models for [Y_R|s, d] and [Y_T|s, d], and likelihoods for both continuous and interval censored Y_R are given in Section 4. The design is presented in Section 5. Section 6 illustrates the method by application to the SCT trial, which has two schedules and three doses (six regimes), including a simulation study with comparison to two alternative designs, and evaluation of robustness and of sensitivity to the prior, cohort size, and sample size. We close with a discussion in Section 7.

2 Motivating Application

Melphalan is an alkalating agent commonly used as part of the preparative regimen for autologous SCT to treat multiple myeloma (MM), but there is no consensus for what (schedule, dose) combination is best in older patients. To address this, we designed a phase I/II trial to evaluate total doses d = 140, 180, or 200 mg/m² of melphalan given either as a single 30-minute bolus infused on day −2 before SCT, or with the dose split into two equal boluses infused on days −3 and −2. Toxicity is defined as severe (grade 3 or 4) gastrointestinal toxicity or diarrhea, graft failure, or regimen-related death. Response is evaluated at 1, 3, 6, 9, and 12 months post transplant, so Y_R is interval censored while Y_T is observed continuously, which is common in early phase oncology trials. Response has three requirements, (i) normal bone marrow (< 5% myeloma cells), (ii) no new lytic lesions on bone X-ray, and (iii) absence of β₂ microglobulin, a monoclonal protein characterizing MM in two consecutive tests.

Transforming pre-transplant administration days (−3, −2) to (0, 1), so transplant is on day 3 after the first administration, the six regimes in the MM trial are τ₁ = {1, 140}, τ₂ = {1, 180}, τ₃ = {1, 200}, τ₄ = {(0, 1), 140}, τ₅ = {(0, 1), 180}, τ₆ = {(0, 1), 200}. The subsets 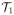= {τ₁, τ₂, τ₃} of one-day schedules and 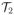= {τ₄, τ₅, τ₆} of two-day schedules have natural orderings, since the probabilities of toxicity and response each increase with d within each schedule. In contrast, for either response or toxicity, there is no obvious ordering among all six regimes in 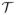= 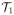∪ 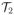. For example, although τ₁ and τ₄ deliver the same total dose, a 1-day or 2-day schedule may either be more toxic or have higher response rate. The terms “escalate” or “de-escalate” thus are meaningful when assigning doses within 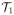or 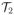. but not for assigning regimes within 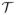. The additive hazard model of Braun et al. (2007) does not accommodate qualitatively different schedules with all administrations given early, or bivariate event time outcomes. We address this by treating schedule as qualitative and dose as quantitative, and defining a joint utility function for the two event times.

3 Utility Functions

We obtain a utility function, U(y), that represents the clinical desirability of each possible outcome pair. This utility may be used for decision-making with any sort of regime, and is not limited to dose-schedule optimization. Given follow up time T_max, the physician is asked to partition the domains of Y_R and Y_T into subintervals that determine a grid of rectangular subsets partitioning [0, T_max]². A numerical utility is elicited for each rectangular subset, and nonlinear regression is used to fit a smooth surface by treating the midpoints of the rectangles in the Y domain as predictors and the corresponding elicited utilities as outcomes. The partition should be sufficiently refined to provide a discretization of Y in terms of the anticipated joint probability distribution that is realistic based on clinical experience, but sufficiently coarse that the elicitation is feasible. To facilitate refinement of the elicited numerical utilities or the grid, it is useful to show the physician a plot of the fitted surface, and iterate this process until an acceptable utility surface is obtained.

Since smaller y_R and larger y_T are more desirable, U(y) must decrease in y_R and increase in y_T, formally, ∂U(y_R, y_T)/∂y_R < 0 < ∂U(y_R, y_T)/∂y_T. We used the parametric function

$$U(y_R,y_T)=100\frac{b_1{e}^{-c_1{y}_R}+b_2{e}^{-c_2{y}_T}+b_3{e}^{-c_1{y}_R-c_2{y}_T}-U_{\mathit{min}}}{U_{\mathit{max}}-U_{\mathit{min}}}\text{for}{y}_R,y_T>0.$$ (1)

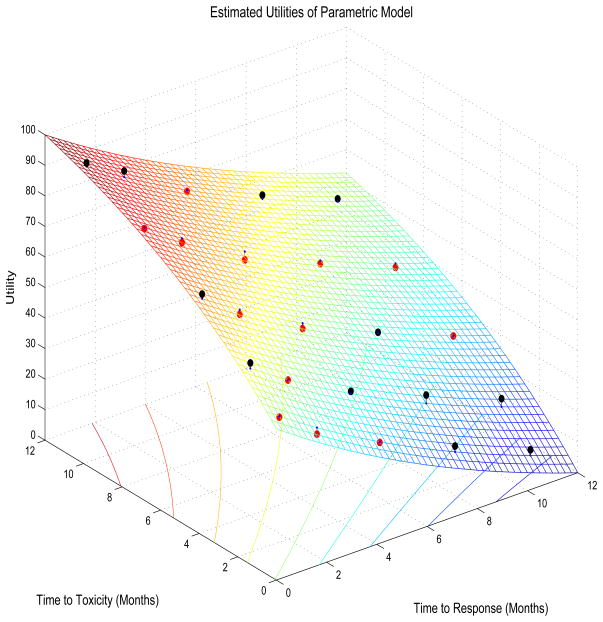
To obtain 0 ≤ U(y_R, y_T) ≤ 100 with 0 corresponding to the worst and 100 to the best possible outcomes, we used the norming constants U_max = U^∘(y_R,min, y_T,max) and U_min = U^∘(y_R,max, y_T,min), denoting U^∘(y_R, y_T) = b₁ e^−c₁y_R+ b₂ e^−c₂y_T+ b₃ e^{−c₁y_R−c₂y_T}. Any compact domain for U may be used, however. The inequalities c₁, c₂ > 0, b₂ < 0 < b₁, and b₂ < −b₃ < b₁ are sufficient to ensure monotonicity of U(y_R, y_T) in each argument. Subject to these constraints, we solved for (c₁, c₂, b₁, b₂, b₃) using nonlinear least squares with the midpoint of each rectangle as the X-variable and the elicited utilities U^(e) on the rectangle as the Y-variable. For the autologous SCT trial design (Table 1) this gave estimates (ĉ₁, ĉ₂, b̂₁, b̂₂, b̂₃) = (0.0631, 0.1088, 9.3557, −7.8677, 0.5301). Table 1 also gives the fitted utilities Û(y), and the surface obtained by plotting Û(y) on y is illustrated by Figure 1, where T_max = 12 months for the SCT trial. For example, the rectangle defined by 1 < y_R < 3 and 3 < y_T < 6 has midpoint y^mid = (2, 4.5) and elicited utility U^(e) = 64.

Table 1.

Utilities for rectangles of Y_R = time to response and Y_T = time to toxicity in the multiple myeloma autologous stem cell transplantation trial. For each (Y_R, Y_T) rectangle, the two tabled values are U^(e) = the elicited utility and Û = the fitted parametric function evaluated at the rectangle’s midpoint.

YT = Months to Toxicity	YR = Months to Response
	[0, 1)	[1, 3)	[3, 6)	[6, 9)	[9, 12)
[9, 12)	95, 93.9	88, 86.0	74, 74.5	64, 62.8	54, 53.1
[6, 9)	85, 85.3	76, 77.4	63, 65.8	53, 54.0	43, 44.3
[3, 6)	75, 73.5	64, 65.5	52, 53.8	42, 41.9	32, 32.1
[1, 3)	62, 60.2	52, 52.1	41, 40.3	31, 28.3	21, 18.4
[0, 1)	50, 50.3	40, 42.2	30, 30.2	20, 18.1	10, 8.1

Figure 1.

Fitted utility surface for the times to response and toxicity in the multiple myeloma stem cell transplantation trial. Black and red dots show elicited values above and below the fitted surface, respectively.

Our criterion for choosing each cohort’s treatment regime is the posterior mean utility,

$$u(\tau ,\mathit{data})=E_{\mathit{\theta }}[E_{\mathit{Y}\mid \mathit{\theta }}\{U(\mathit{Y})\mid \tau ,\mathit{\theta }\}\mid \mathit{data}]=E_{\mathit{\theta }}[\overline{U}(\tau ,\mathit{\theta })\mid \mathit{data}],$$ (2)

where we denote Ū(τ, θ) = E_Y|θ{U(Y) | τ, θ}, the mean over Y of the utility U(Y) of using regime τ for given θ. Another way to view u(τ, data) is obtained by applying the Fubini-Tonelli Theorem to switch the order of expectations in (2). Denoting the joint pdf of [Y | τ] by f_R,T(y | τ, θ), this gives

$$u(\tau ,\mathit{data})={\int }_{\mathit{y}}U(\mathit{y})E_{\mathit{\theta }\mid \mathit{Y}=\mathit{y}}\left\{f_{R,T}(\mathit{y}\mid \tau ,\mathit{\theta })\mid \mathit{data}\right\}d\mathit{y}={\int }_{\mathit{y}}U(\mathit{y})f_{R,T}(\mathit{y}\mid \tau ,\mathit{data})d\mathit{y}.$$

The posterior expectation f_R,T(y | τ, data) is the predictive distribution of Y, given the current data, for a patient treated with regime τ. Thus, u(τ, data) is the expected utility of τ for a newly enrolled patient. The design makes adaptive decisions based on the values of {u(τ, data), τ ∈ 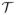}, subject to safety and efficacy acceptability requirements.

4 Probability Model

4.1 Marginal Model

Our modeling strategy is to construct marginals for Y_R and Y_T that are functions of s and d, and use a bivariate copula (Nelsen, 1999) to obtain a joint distribution. For each outcome m = R, T and regime τ = (s, d), denote the pdf, cdf, and survivor function of Y_m at time y > 0 by f_m(y | τ, θ_m), F_m(y | τ, θ_m) = Pr(Y_m ≤ y | τ, θ_m) and F̄_m(y | τ, θ_m) = 1 − F_m(y | τ, θ_m), where θ_m is the marginal model parameter vector. The joint model parameter vector is θ = (θ_R, θ_T, ζ), where ζ is the copula’s association parameter.

We assume that, given s, larger d is associated with stochastically smaller Y_R and smaller Y_T. This says that, at any follow up time y, the probability of response, F_R(y | (s, d), θ_R), and the probability of toxicity, F_T (y | (s, d), θ_T), both increase in d for any s. The marginals are formulated so that these probabilities may either vary qualitatively with schedule or have monotone schedule effects. The utility function addresses the conflict between the goals to choose τ to make F_R(y_R|τ, θ_R) large while not allowing F_T (y_T |τ, θ_T) to become unacceptably large by quantifying the desirability of each possible (y_R, y_T) pair.

Let d₁ < d₂ < ··· < d_J denote the doses being considered. A practical difficulty when using u{(s, d), data} for decision making based on bivariate outcomes is that simply assuming F_R(t | (s, d), θ_R) and F_T (t | (s, d), θ_T) both are monotone in d may not distinguish adequately between different values of u{(s, d_j), data} for doses d_j near the optimum, in the case d₁ < d_j < d_J. A given change in an intermediate d_j may produce changes of very different magnitudes in F_R(t | (s, d_j), θ_R) and F_T (t | (s, d_j), θ_T), which in turn may make it difficult to identify a middle dose for which (s, d_j) has true maximum utility. To address this problem, for each outcome we define outcome-specific standardized doses,

$$x_{m,j}=\frac{d_1}{\overline{d}}+{\left(\frac{d_j-d_1}{d_J-d_1}\right)}^{{\lambda }_m}\left(\frac{d_J-d_1}{\overline{d}}\right),m=R,T,j=1,\dots ,J,$$

denoting d̄ = (d₁ + ··· + d_J)/J. The parameter λ_m controls the relative effects of doses that are not close to either d₁ or d_J. Note that x_R,1 = x_T,1 = d₁/d̄ and x_R,J = x_T,J = d_J /d̄, while all intermediate standardized doses for f_m are parameterized by λ_m.

For brevity, hereafter we will index schedules by k = 1, ···, K and denote τ = (k, j) for the k^th schedule and dose d_j. To formulate flexible but reasonably parsimonious marginals for [Y_m | τ], m = R, T, in preliminary simulations we explored the lognormal, Weibull, and gamma distributions across a diverse set of regime-outcome scenarios and true event time distributions. We chose the gamma, since it had the best overall performance and robustness of the three distributions. We used gamma marginals having the parametric form

$$f_m(t\mid \tau ,{\mathit{\theta }}_m)=\frac{t^{{\varphi }_{m,1}-1}{e}^{-t/{\varphi }_{m,2}}}{\mathrm{\Gamma }({\varphi }_{m,1}){\varphi }_{m,2}^{{\varphi }_{m,1}}},$$

where Γ(·) denotes the gamma function. The shape parameter ϕ_m,1 and scale parameter ϕ_m,2 both depend on dose and schedule as follows:

$${\varphi }_{m,1}\{(k,j),{\mathit{\theta }}_m\}={\beta }_{m,1}{({\gamma }_{m,k}{x}_{m,j})}^{-{\alpha }_{m,1}}$$ (3)

and

$$log\{{\varphi }_{m,2}\{(k,j),{\mathit{\theta }}_m\}+1\}={\beta }_{m,2}{({\gamma }_{m,k}{x}_{m,j})}^{-{\alpha }_{m,2}},m=R,T.$$ (4)

We require α_m,1, α_m,2, β_m,1, β_m,2 > 0, and assume the schedule effects, γ_m,1, ···, γ_m,K, have support [0, 2]. Different transformations are used for ϕ_m,1(k, j) and ϕ_m,2(k, j) because the shape and scale parameters play very different roles in determining the form of the gamma distribution, and we found that using a log transformation for ϕ_m,2{(k, j), θ_m} provided a well behaved dose-outcome model. For each outcome m = R, T and gamma shape (r = 1) or scale (r = 2) parameter, if dose is fixed and only schedule is varied, the right-hand sides of (3) and (4) reduce to β_m,rγ_m,k, so there are K + 1 parameters for K effects. We thus define ${\gamma }_{m,1}=2-{\{{\prod }_{k=2}^K{\gamma }_{m,k}\}}^{1/(K-1)}$.

The utility U(Y) reduces the two-dimensional outcome Y to a one-dimensional value, which in turn yields the posterior mean utility, u{(k, j), data}, that is used for decision making. In the models (3) for shape and (4) for scale, the relative magnitudes of the parametric contributions of k and x_m,j must reflect their actual effects on u{(k, j), data}. In these models, β_m,r may be thought of as the gamma’s usual shape (r = 1) or scale (r = 2) parameter, modified by the effects of dose and schedule. For each m = R, T, the same λ_m is used to define each standardized dose x_m,j and, for each schedule k, the same parameter γ_m,k is used as a multiplicative effect on x_m,j, for both ϕ_m,1 and ϕ_m,2.

4.2 Likelihood for Continuously Observed Response Times

Let t^* denote study time, defined as the time from the start of the trial to the current time when a new patient is enrolled and an interim decision must be made. Let n^* denote the number of patients accrued by t^*. For the i^th patient, i = 1, ···, n^*, denote the treatment regime by τ_i and the outcome vectors evaluated at t^* by ${\mathit{Y}}_{i,t^{\ast }}^o=(Y_{i,R,t^{\ast }}^o,Y_{i,T,t^{\ast }}^o)$ and δ_i,t* = (δ_i,R,t*, δ_i,T,t*). For a patient with entry time e_i < t^*, the patient time at trial time t^* is t_i = t^* − e_i. Each patient’s outcome data change over time, starting at ${\mathit{Y}}_{i,t^{\ast }}={\mathit{Y}}_{i,t^{\ast }}^o=(0,0)$ and δ_i,t* = (0,0) at accrual when t_i = 0. Thereafter, each $Y_{i,m,t^{\ast }}^o=t_i$ as long as δ_i,m,t* = 0, and $Y_{i,m,t^{\ast }}^o$ achieves the final value Y_i,m if and when the patient experiences event m, when δ_i,m,t* jumps from 0 to 1. That is, each ( ${\mathit{Y}}_{i,t^{\ast }}^o$, δ_i,t*) is a bivariate sample path of two step functions, jumping from 0 to 1 at their respective event times, with administrative right-censoring, from the time from that patient’s accrual to the most recent follow up time. Consequently, before computing posterior quantities used for making outcome-adaptive interim decisions at any study time t^*, it is essential to update the trial data. We denote the interim data at trial time t^* by ${\mathit{data}}^{\ast }=\{(e_i,{\tau }_i,{\mathit{Y}}_{i,t^{\ast }}^o,{\mathit{\delta }}_{i,t^{\ast }}):i=1,\dots ,n^{\ast }\}$.

Denote the joint cdf and survivor function of [Y | τ] by F_R,T (y | τ, θ) and F̄_R,T (y | τ_i, θ) = Pr(Y_R > y_R, Y_T > y_T | τ_i, θ). When both Y_R and Y_T are observed continuously, the likelihood for patient i at study time t^* is

$$\begin{array}{l}\mathcal{L}({\mathit{Y}}_{i,t^{\ast }}^o,{\mathit{\delta }}_{i,t^{\ast }}\mid {\tau }_i,\mathit{\theta })={\left\{f_{R,T}(Y_{i,R,t^{\ast }}^o,Y_{i,T,t^{\ast }}^o\mid {\tau }_i,\mathit{\theta })\right\}}^{{\delta }_{i,R,t^{\ast }}{\delta }_{i,T,t^{\ast }}}\\ \times {\left\{{\int }_{v=Y_{i,T,t^{\ast }}^o}^{\infty }{f}_{R,T}(Y_{i,R,t^{\ast }}^o,v\mid {\tau }_i,\mathit{\theta })dv\right\}}^{{\delta }_{i,R,t^{\ast }}(1-{\delta }_{i,T,t^{\ast }})}\\ \times {\left\{{\int }_{u=Y_{i,R,t^{\ast }}^o}^{\infty }{f}_{R,T}(u,Y_{i,T,t^{\ast }}^o\mid {\tau }_i,\mathit{\theta })du\right\}}^{(1-{\delta }_{i,R,t^{\ast }}){\delta }_{i,T,t^{\ast }}}\\ \times {\left\{{\overline{F}}_{R,T}(Y_{i,R,t^{\ast }}^o,Y_{i,T,t^{\ast }}^o\mid {\tau }_i,\mathit{\theta })\right\}}^{(1-{\delta }_{i,R,t^{\ast }})(1-{\delta }_{i,T,t^{\ast }})}.\end{array}$$ (5)

Once the marginals have been specified, a joint distribution of Y_R and Y_T may be defined in numerous ways. To obtain a parsimonious and tractable model, we use the bivariate Farlie-Gumbel-Morgenstern (FGM) copula (Nelsen, 1999). Hereafter, we will suppress t^*, i, τ_i, and θ for brevity when no meaning is lost. The FGM copula is given in terms of the marginals and one association parameter ζ ∈ [−1, 1] by

$$F_{R,T}(y_R,y_T\mid \zeta )=F_R(y_R)F_T(y_T)\{1+\zeta {\overline{F}}_R(y_R){\overline{F}}_T(y_T)\}.$$ (6)

To obtain the terms in (5) under the FGM copula, for (δ_R, δ_T) = (1,1) the joint pdf is

$$f_{R,T}(y_R,y_T\mid \zeta )=f_R(y_R)f_T(y_T)\left[1+\zeta \{1-2F_R(y_R)\}\{1-2F_T(y_T)\}\right],$$

and F̄_R,T (y_R, y_T) = F_R,T (y_R, y_T) + F̄_R(y_R) + F̄_T (y_T) − 1. For (δ_R, δ_T) = (0,1) and a > 0,

$${\int }_a^{\infty }{f}_{R,T}(y,y_T)dy={\overline{F}}_R(a)f_T(y_T)\left[1-\zeta F_R(a)\{1-2F_T(y_T)\}\right],$$

and the term for (δ_R, δ_T) = (1,0) is obtained by symmetry. All likelihood contributions thus are determined by ζ and the marginal pdfs, with F_R and F_T and terms corresponding to administratively censored event times computed by numerical integration.

4.3 Likelihood for Interval Censored Response Times

To account for interval censoring when response is evaluated at successive times 0 = a₀ < a₁ < ··· < a_L−1 < a_L = ∞, rather than continuously, let A_l = (a_l−1, a_l] denote the l^th subinterval. If a response did not occur by a_l−1 but did occur by a_l, then Y_R ∈ A_l. Let δ_1,l denote this event. Given the partition {A₁, ···, A_L} of [0, ∞), the pair ( $Y_{i,R}^o$, δ_i,R) for continuously observed Y_i,R are replaced by the vector of indicators δ_i,R = (δ_i,R,1, ···, δ_i,R,L), having one entry 1 and all other entries 0. At study time t^*, the observed data of the i^th patient are {δ_i,R(t^*), $Y_{i,T,t^{\ast }}^o$, δ_i,T,t*}. When $Y_{i,T}^o=Y_{i,T}$ has been observed by study time t^*, so that δ_i,T,t* = 1, the i^th patient’s likelihood contribution is

$$\begin{array}{l}\mathcal{L}({\mathit{\delta }}_{i,R}(t^{\ast }),Y_{i,T,t^{\ast }}^o,1\mid {\tau }_i,\mathit{\theta })=\prod _{l=1}^L{\left\{{\int }_{a_{l-1}}^{a_l}{f}_{R,T}(y,Y_{i,T,t^{\ast }}^o\mid {\tau }_i,\mathit{\theta })dy\right\}}^{{\delta }_{i,R,l}(t^{\ast })}\\ =\prod _{l=1}^L{\left\{P_{R,T}^{(1)}(A_l,Y_{i,T,t^{\ast }}^o\mid {\tau }_i,\mathit{\theta })\right\}}^{{\delta }_{i,R,l}(t^{\ast })},\end{array}$$ (7)

denoting $P_{R,T}^{(1)}(A_l,Y_T^o)={\int }_{A_l}{f}_{R,T}(y,Y_T^o)dy$. Under the copula (6), this takes the form $P_{R,T}^{(1)}(A_l,Y_T^o)=f_T(Y_T^o)\{F_R(a_l)-F_R(a_{l-1})\}[1+\zeta \{2F_T(Y_T^o)-1\}\{F_R(a_l)+F_R(a_{l-1})-1\}]$. Similarly, when patient i has not yet experienced toxicity, so δ_i,T,t* = 0 and Y_i,T is censored at study time t^*, the likelihood contribution is

$$\begin{array}{l}\mathcal{L}({\mathit{\delta }}_{i,R}(t^{\ast }),Y_{i,T,t^{\ast }}^o,0\mid {\tau }_i,\mathit{\theta })=\prod _{l=1}^L{\left\{{\int }_{Y_{i,T,t^{\ast }}^o}^{\infty }{\int }_{a_{l-1}}^{a_l}{f}_{R,T}(y,w\mid {\tau }_i,\mathit{\theta })\mathit{dydw}\right\}}^{{\delta }_{i,l}(t^{\ast })}\\ =\prod _{l=1}^L{\left\{P_{R,T}^{(2)}(A_l,Y_{i,T}^0(t^{\ast })\mid {\tau }_i,\mathit{\theta })\right\}}^{{\delta }_{i,l}(t^{\ast })},\end{array}$$ (8)

denoting $P_{R,T}^{(2)}(A_l,Y_T^o)={\int }_{Y_T^o}^{\infty }{\int }_{A_l}{f}_{R,T}(y,w)\mathit{dydw}$. Under the copula (6), this takes the form $P_{R,T}^{(2)}(A_l,Y_T^o)={\overline{F}}_T(Y_T^o)\{F_R(a_l)-F_R(a_{l-1})\}[1+\zeta F_T(Y_T^o)\{F_R(a_l)+F_R(a_{l-1})-1\}]$. Combining terms (7) and (8), if Y_R is interval censored the likelihood at trial time t^* is

$$\mathcal{L}(Y_{i,T,t^{\ast }}^o,{\mathit{\delta }}_i(t^{\ast })\mid {\tau }_i,\mathit{\theta })=\prod _{l=1}^L{\left[P_{R,T}^{(1)}{(A_l,Y_{i,T}^o(t^{\ast })\mid {\tau }_i,\mathit{\theta })}^{{\delta }_{i,T,t^{\ast }}}{P}_{R,T}^{(2)}{(A_l,Y_{i,T}^0(t^{\ast })\mid {\tau }_i,\mathit{\theta })}^{1-{\delta }_{i,T,t^{\ast }}}\right]}^{{\delta }_{i,l}(t^{\ast })}.$$

5 Trial Design

5.1 Treatment Regime Acceptability

While using utilities is a sensible way to combine efficacy and toxicity for optimizing treatment regimes, in practice some regimes may be excessively toxic or inefficacious. Such regimes should not be used to treat patients, and in the extreme case where all regimes are found to be either too toxic or inefficacious the trial should be terminated. We thus employ the following acceptability criteria, similar to those used by Thall and Cook (2004) and others for phase I/II trials. For m = R, T, let $t_m^{\mathit{ref}}$ be a reference time from the start of therapy used to specify a limit on $F_m(t_m^{\mathit{ref}}\mid \tau ,\mathit{\theta })$. Let π̄_T be a fixed upper limit on $F_R(t_R^{\mathit{ref}}\mid \tau ,\mathit{\theta })$ and π_R be a fixed lower limit on $F_T(t_T^{\mathit{ref}}\mid \tau ,\mathit{\theta })$, both specified by the physician. Given upper probability cut-offs p_T and p_R, a regime τ is unacceptable if

$$Pr\{F_T(t_T^{\mathit{ref}}\mid \tau ,\mathit{\theta })>{\overline{\pi }}_T\mid {\mathit{data}}^{\ast }\}>p_T\text{or}Pr\{F_R(t_R^{\mathit{ref}}\mid \tau ,\mathit{\theta })<{\underset{\_}{\pi }}_R\mid {\mathit{data}}^{\ast }\}>p_R.$$ (9)

and we denote the set of acceptable strategies by .

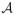5.2 A Design for Non-Nested Schedules

The problem that a “greedy” sequential search algorithm, that always chooses the optimal action, may get stuck as a suboptimal action is well-known in optimization, but only recently has been addressed in dose-finding trials (Azriel, Mandel and Rinott, 2011; Thall and Nguyen, 2012). Our proposed design is a hybrid of a greedy design that always chooses τ = (k, j) to maximize posterior mean utility, and a nonadaptive, hence unethical design that simply randomizes patients fairly among regimes. The idea is avoid getting stuck at a suboptimal regime, but still conduct the trial ethically by using adaptive rules.

For each successive cohort of c patients, τ is chosen adaptively, as follows. Denote the regime maximizing u(τ, data^*) among all τ ∈ 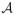by τ^opt. Denote the index of the optimal dose among acceptable regimes having schedule k by

$$j^{\mathit{opt}}(k)=\underset{1\le j\le J,(k,j)\in A}{\text{argmax}}u\{(k,j),{\mathit{data}}^{\ast }\}.$$

Because the posterior mean utility u(τ, data^*) is highly variable throughout much of the trial, randomizing among regimes with u{(k, j), data^*} close to τ^opt is ethical, and reduces the risk of getting stuck at a suboptimal regime. The proposed hybrid design, Design 1, has two stages. Let n^*(k, j) denote the number of patients up to trial time t^* treated with τ = (k, j). Since only τ ∈ may be chosen, if is empty then the trial is stopped and no τ is selected. If is not empty, then for qualitatively different, non-nested schedules Design 1 proceeds as follows. Let N be the maximum overall sample size, and N₁ the maximum stage 1 sample size, with N₁ chosen to be a multiple of Kc reasonably close to N/2.

Stage 1

Randomize K cohorts of size c fairly among the schedules, restricted so that each schedule is assigned to exactly c patients. Repeat this until N₁ patients have been treated. Within schedule k, starting at the lowest dose and not skipping an untried dose when escalating, treat the next patient at dose j^opt(k), unless

$$n\{k,j^{\mathit{opt}}(k)\}\ge \underset{j}{\mathit{max}}\{n(k,j):j\ne j^{\mathit{opt}}(k),(k,j)\in \mathcal{A}\}+{\mathrm{\Delta }}_{1}c,$$ (10)

where Δ₁ is a small positive integer. If the inequality (10) holds, then within schedule k choose an acceptable dose randomly with probability proportional to u{(k, j), data^*}.

Stage 2

For patients i = N₁ + 1, ···, N, choose the schedule k^opt with largest u{k, j^opt(k)}, unless

$$n\{k^{\mathit{opt}},j^{\mathit{opt}}(k^{\mathit{opt}})\}\ge \underset{k}{\mathit{max}}[n\{k,j^{\mathit{opt}}(k)\}:k\ne k^{\mathit{opt}},\{k,j^{\mathit{opt}}(k)\}\in \mathcal{A}]+{\mathrm{\Delta }}_{2}c,$$ (11)

where Δ₂ is a small positive integer. If (11) holds, choose a schedule with probability proportional to u{(k, j^opt(k)), data^*}. Choose doses within schedules as in Stage 1.

The inequality (10) in Stage 1 says that the current sample size at the best acceptable dose within schedule k is at least Δ₁ c larger than the current sample size at any other acceptable dose with that schedule. One may use Δ₁ = Δ₂ = 1, or slightly larger values, depending on c and possibly N, to control the amount of sample size imbalance between regimes. The randomization probabilities among doses within schedule k in Stage 1 at t^* are

$$r_1(k,j)=\frac{u\{(k,j),{\mathit{data}}^{\ast }\}I\{(k,j)\in \mathcal{A}\}}{{\sum }_{j^{\prime }=1}^{J}u\{(k,j^{\prime }),{\mathit{data}}^{\ast }\}I\{(j^{\prime },k)\in \mathcal{A}\}}j=1,\cdots ,J.$$

Similarly, the inequality (11) says that the current sample size at the best acceptable regime is at least Δ₂ c larger than the current sample size at any other acceptable regime. The randomization probabilities among schedules in Stage 2 at t^* are

$$r_2(k)=\frac{u\{(k,j^{\mathit{opt}}(k)),{\mathit{data}}^{\ast }\}I\{(k,j^{\mathit{opt}}(k))\in \mathcal{A}\}}{{\sum }_{k^{\prime }=1}^{K}u\{(k^{\prime },j^{\mathit{opt}}(k^{\prime })),{\mathit{data}}^{\ast }\}I\{(k^{\prime },j^{\mathit{opt}}(k^{\prime }))\in \mathcal{A}\}},k=1,\cdots ,K.$$

Design 2, the “greedy” design, is a much simpler version Design 1 that chooses τ ∈ by simply maximizing u{(k, j), data^*}, subject to the constraint that an untried dose may not be skipped when escalating within any schedule. With Design 2, schedules are chosen by fair randomization without replacement, as in the hybrid Design 1, but this is done throughout the trial, and within schedule k the current dose j^opt(k) is chosen.

If schedules are nested, then γ_m,1 < γ_m,2 < ··· < γ_m,K for m = R, T, and consequently Y_R and Y_T are stochastically increasing in k as well as j, so the regime-finding algorithm must reflect this. Since in this case the word “escalate” pertains to both schedule and dose, i.e. to both k and j, the trial could be conducted by choosing (k, j) to maximize u{(k, j), data^*} subject to a two-dimensional “do-not-skip” rule similar to that used by Braun et al. (2007), with escalation from (k, j) to optimize u{τ, data^*} restricted to the three adjacent untried combinations (k +1, j), (k, j + 1), or (k + 1, j + 1). This could be elaborated, as in Design 1, to include randomization among regimes based on u{(k, j), data^*}.

5.3 Accommodating Death During Follow Up

The model and utility may be modified to account for death during follow up, or discontinuation of follow up due to toxicity, possibly because the regime was changed at Y_T. This may be done parsimoniously using a semi-competing risks model, wherein we call either death or discontinuation of follow up at Y_T “fatal” toxicity, indicated by δ_TD, with δ_TA indicating “non-fatal” toxicity that allows follow up to continue for Y_R. Thus, δ_TD + δ_TA = δ_T, and (δ_TD, δ_TA) has possible values (1,0) or (0,1) if δ_T = 1 and (0,0) if δ_T = 0. If δ_TD = 1 and Y_T < Y_R then response will not occur. In this case, we define Y_R = +∞ and δ_R = 1, and extend the domain of (Y_R, Y_T) from E₂ = [0, ∞)² to $E_2^{+}=E_2\cup [\{+\infty \}\times [0,\infty )]$. We do not assume that Y_R censors Y_T, however. Suppressing τ and θ, we define an extended distribution $f_{R,T,D}^{+}(Y_R,Y_T,{\delta }_{TD})$ in terms of π_TD = Pr(δ_TD = 1) and the conditional probabilities $f_{R,T\mid D}^{+}(y_R,y_T\mid {\delta }_{TD}=0)=f_{R,T}(y_R,y_T)$ and $f_{R,T\mid D}^{+}(y_R,y_T\mid {\delta }_{TD}=1)=f_{R,T}(y_R,y_T)I(y_R<y_T)+f_T(y_T){\pi }_{NR}I(y_R>y_T)$, where π_NR = Pr(Y_R > Y_T) is the probability of death before response if δ_TD = 1. It follows that $f_{R,T,D}^{+}$ is a probability distribution on $E_2^{+}$, since ${\int }_{E_2^{+}}{\sum }_{a=0}^1{f}_{R,T\mid D}^{+}(y_R,y_T\mid {\delta }_{TD}=a)Pr({\delta }_{TD}=a){dy}_R{dy}_T=1$.

To extend the likelihood (5) to this case, we first note that lines 2 and 4 of (5) are unchanged since in these cases Y_T is right-censored. The first line of (5) becomes

$${\left\{f_{R,T}{(Y_R^o,Y_T^o)}^{I(Y_R^o<+\infty )}{\{f_T(Y_T^o){\pi }_{NR}\}}^{I(Y_R^o=+\infty )}{{\pi }_{TD}}^{{\delta }_{TD}}{(1-{\pi }_{TD})}^{{\delta }_{TA}}\right\}}^{{\delta }_R{\delta }_T}.$$

For line 3 of (5), if Y_R is censored and fatal toxicity occurs, then δ_TD = 1 and Y_R = +∞, a case already accounted for by line 1. If Y_R is censored and non-fatal toxicity occurs, this is accounted for by simply replacing δ_T with δ_TA.

The utility may be modified to accommodate death by considering the scaled original utility, U(y_R, y_T)/100, as a multiplicative discount factor for survival time on the follow-up interval [0, T_max]. A utility function that does this is U ⁺(y_R, y_T) = T_max U (y_R, y_T)/100 if y_T is the time of non-fatal toxicity and U ⁺(y_R, y_T) = y_T if y_T is the time of death. Thus, 0 ≤ U⁺(y_R, y_T) ≤ T_max, and the trial is conducted as described above. The model may be extended similarly if follow up is stopped at Y_R, although this is not commonly done if toxicity occurring over a prespecified follow up period of T_max is considered important. One also might model π_TD as a function of (s, d), if the death rate is sufficiently high to estimate the additional parameters, although this may be unlikely in practice.

6 Application to the SCT Trial

6.1 Prior and Design Parameters

We assumed that the positive real valued parameters α_R,1, α_R,2, β_R,1, β_R,2, λ_R, α_T,1, α_T,2, β_T,1, β_T,2, λ_T followed lognormal priors. The means were determined from the elicited values in Table 2 using a pseudo-sample based method similar to that described in Section 4.2 of Thall et al. (2011). Prior variances were calibrated to obtain a design with good performance across a broad range of scenarios. We assumed that ζ followed a beta distribution with parameters (1.1, 1.1), rescaled to have support on (−1, +1). Numerical values of the prior hyperparameters are given in Supplementary Table 1.

Table 2.

Elicited prior means of F_R(t | τ) and F_T (t | τ) for the autologous stem cell transplantation trial to optimize (schedule, dose) of melphalan. For each total dose d, the prior means for the regimes τ = (−2, d) and τ = ((−3, −2), d) were identical.

Days of Follow up	Prior Means of FR(t | τ)			Prior Means of FT (t | τ)
	Total dose of Melphalan (mg/m2)			Total dose of Melphalan (mg/m2)
	d = 140	d = 180	d = 200	d = 140	d = 180	d = 200
t = 1	–	–	–	.01	.02	.03
t = 3	–	–	–	.05	.07	.09
t = 6	–	–	–	.15	.18	.20
t = 10	–	–	–	.25	.30	.32
t = 14	–	–	–	.30	.35	.40
t = 28	–	–	–	.33	.38	.43
t = 30	.05	.08	.10	–	–	–
t = 90	.09	.11	.15	–	–	–
t = 180	.13	.16	.19	.34	.39	.44
t = 270	.16	.19	.24	–	–	–
t = 360	.20	.25	.30	.35	.40	.45

Since each schedule effect acts multiplicatively on the outcome-specific standardized doses, we found that γ_m,j ≤ 0.80 or ≥ 1.20 may have a large effect on x_m,j. For example, γ_m,j = .80 would reduce some x_m,j values by more than one full dose level. A more disperse prior on the γ_m,j’s also may cause the method to misinterpret a dose effect for a schedule effect in certain cases, especially those where a middle dose has highest utility. Consequently, we specified the priors of the γ_m,j’s to be highly concentrated beta distributions with domain [0, 2] and parameters (47.3, 47.3), which gives Pr[0.80 < γ_m,j < 1.20] = 0.95. Although these priors may appear to be overly informative, in fact small changes within the subdomain [0.80, 1.20] of [0, 2] allow the posterior mean utility to change substantively, so that one may detect true differences between schedules. In this case, the observed data easily have the necessary effect on the posterior distributions of the γ_m,j’s.

6.2 Simulation Study

We simulated the SCT trial with N₁ = 36, N = 72, and c = 3, with Y_T monitored continuously and Y_R interval censored per the actual evaluation schedule at 1, 3, 6, 9, 12 months. We studied three competing designs: the hybrid design (Design 1), the greedy design (Design 2), and a randomized design with no interim decisions, restricting the randomization to treat exactly 12 patients at each of the six τ pairs, with the regime maximizing u(τ, data) selected at the end. We considered eight simulation scenarios (Supplementary Table 2). In Scenario 1, there is no schedule effect, toxicity is acceptable, and efficacy increases with dose. Scenario 2 also has no schedule effect, but toxicity is much higher, so the lowest dose has the highest utility. In Scenario 3, the 2-day schedule is superior due to higher efficacy. In Scenario 4, the 1-day schedule is superior. Scenario 5 has no schedule effect, but the middle dose is best. In Scenario 6, for both schedules, the utility is “V” shaped, lowest for the middle dose with the highest dose optimal. All regimes are unacceptably toxic in Scenario 7, and unacceptably inefficacious in Scenario 8. Each case was simulated 3000 times.

We use the statistic R_select = {u^true(τ_select) − u_min}/(u_max − u_min), (cf. Thall and Nguyen, 2012) to quantify reliability of regime selection. This is the proportion of the difference between the utilities of the best and worst possible regimes achieved by τ_select. A statistic quantifying the ethics of how well the method assigns regimes to patients in the trial is $R_{\mathit{treat}}=\{N^{-1}{\sum }_{i=1}^N{u}^{\mathit{true}}({\tau }_{[i]})-u_{\mathit{min}}\}/(u_{\mathit{max}}-u_{\mathit{min}})$, where u^true(τ_[i]) is the true utility of the regime given to patient i, and N is the final sample size.

The main simulation results are summarized in Table 3. In each of Scenarios 1 – 6, the hybrid design does a good job of selecting regimes with high true utilities, and is very likely to correctly stop early in both Scenarios 7 and 8. Table 4 compares the hybrid, greedy, and balanced designs in terms of R_treat and R_select. More detailed summaries of the simulations of the greedy and balanced non-adaptive designs are given in Supplementary Tables 3a and 3b, respectively. The main messages from Scenarios 1 – 6 in Table 3 are that (i) compared to the greedy design, the hybrid design has the same or higher R_select while neither design is uniformly superior in terms of R_treat; (ii) compared to the balanced design, the hybrid design has nearly identical R_select but much higher values of R_treat, so is much more ethical; and (iii) in Scenarios 7 and 8, both the hybrid and greedy designs correctly stop early with high probability, and both have much higher R_select and R_treat than the balanced design. In summary, the hybrid design has the best overall performance of the three designs and, as may be expected, the balanced design is ethically unacceptable.

Table 3.

The main simulation results using the hybrid algorithm with sample size 72 and cohort 3. The true time distribution is assumed to be lognormal.

Scenario		1-Day Schedule			2-Day Schedule			None	Rselect Rtreat
		Dose 1	Dose 2	Dose 3	Dose 1	Dose 2	Dose 3
1	ūtrue(s, d)	52.2	57.5	62.9	52.2	57.5	62.9
	% Sel	5	8	38	5	8	35	1	0.82
	# Pats	11.6	9.8	14.5	11.6	9.5	14.4		0.54
2	ūtrue(s, d)	59.0	53.7	48.1	59.0	53.7	48.1
	% Sel	39	7	4	39	6	5	1	0.85
	# Pats	22.6	8.2	5.0	22.7	8.2	4.9		0.75
3	ūtrue(s, d)	53.1	58.4	63.8	56.8	62.1	67.6
	% Sel	3	5	16	6	12	58	1	0.81
	# Pats	11.1	9.1	12.9	11.6	10.5	16.5		0.54
4	ūtrue(s, d)	58.6	54.6	49.7	55.4	51.4	46.5
	% Sel	54	12	5	18	5	5	1	0.80
	# Pats	23.1	9.0	5.1	21.0	8.3	5.1		0.69
5	ūtrue(s, d)	52.9	63.6	50.2	52.9	63.6	50.2
	% Sel	8	34	6	9	36	6	1	0.74
	# Pats	13.0	16.7	0.5	12.8	16.7	6.2		0.54
6	ūtrue(s, d)	53.5	48.1	56.5	53.5	48.1	56.5
	% Sel	21	4	23	21	4	25	2	0.76
	# Pats	17.2	7.3	11.0	17.2	7.2	11.2		0.62
7	ūtrue(s, d)	35.3	34.2	33.0	35.3	34.2	33.0
	% Sel	0	0	0	0	0	0	100	0.87
	# Pats	5.0	1.6	0.5	5.0	1.6	0.5		0.81
8	ūtrue(s, d)	39.9	37.8	35.6	39.9	37.8	35.6
	% Sel	1	0	1	1	0	1	96	0.54
	# Pats	5.8	4.0	4.5	5.8	4.0	4.5		0.54

Table 4.

Summary statistics for the hybrid design, greedy design, and non-adaptive balanced allocation, for the (3-dose, 2-schedule) trial. The “balanced” method assigns 12 patients to each (schedule, dose) pair and does only one posterior computation, at the end of the trial. The number in parentheses after each R_select is the percentage of times the trial is stopped with no (schedule, dose) selected. Because scenarios 7 (too toxic) and 8 (too inefficacious) have no acceptable treatments, the R_select values are less relevant and thus are shown with a gray background.

Scenario	Hybrid		Greedy		Balanced
	Rselect	Rtreat	Rselect	Rtreat	Rselect	Rtreat
1	0.82 (1)	0.54	0.78 (1)	0.45	0.85 (0)	0.50
2	0.85 (1)	0.75	0.85 (1)	0.84	0.85 (0)	0.51
3	0.81 (1)	0.54	0.78 (1)	0.48	0.83 (0)	0.50
4	0.80 (1)	0.69	0.80 (0)	0.77	0.80 (0)	0.51
5	0.74 (1)	0.54	0.65 (1)	0.48	0.77 (0)	0.40
6	0.76 (2)	0.62	0.75 (3)	0.62	0.77 (0)	0.55
7	0.87 (100)	0.81	1.00 (100)	0.83	0.94 (98)	0.50
8	0.54 (96)	0.54	0.54 (96)	0.59	0.35 (72)	0.50

In supplementary Table 4, we evaluate robustness of the hybrid design to the true event time distribution (lognormal, gamma, Weibull, or uniform). It shows that that (i) R_treat is insensitive to the distributions studied, (ii) R_select is insensitive to whether the true distribution is lognormal, gamma, or Weibull, but (iii) for a uniform distribution R_select may be lower (Scenarios 1 and 3) or higher (Scenarios 2 and 4) than for the other distributions. Supplementary Table 5a shows that the hybrid design is insensitive to changes in prior hyperparameter σ̃ = 8 to 14, the assumed common prior sd of log(α_m,l), log(β_m,l), and log(λ_m) for all m = R, T and l = 1, 2. Supplementary Table 5b shows that the hybrid design is insensitive to changes in the 95% prior interval for the γ_m,j’s varying from (0.9, 1.1) to (0.6, 1.4), although R_select and R_treat both decrease slightly with the width of this interval in Scenario 5. This motivated our use of the 95% prior interval (0.8, 1.2). Supplementary Table 6 shows that R_select is insensitive to c = 1, 2, or 3, and that R_treat may increase or decrease slightly with c depending on the scenario. Supplementary Table 7 shows that, as N is increased from 48 to 360, both R_select and R_treat increase substantially.

We also evaluated the hybrid design for an extended version of the SCT trial, with 4 doses and 3 schedules (12 regimes), obtained by interpolating the elicited priors and scenarios of the original 6-regime design. The three doses of the original trial are mapped into the first, third and fourth doses of the extended trial, with a new, second lowest dose corresponding to d = 160 mg/m² added. Elicited prior and scenario probabilities of the original first two doses were interpolated to obtain values for the new dose. A new third schedule was obtained by averaging the prior and scenario probabilities of the two original schedules. Results for this 12-regime setting are given in Supplementary Tables 8 – 12.

Supplementary Table 8a gives a hypothetical utility that places greater weight on quick responses. Either for the 6 regime case (Supplementary Table 8b) or 12 regime case (Supplementary Table 15), the hybrid design’s behavior for this different utility, compared to the actual utility, has an equally high probability of correctly stopping the trial early in Scenarios 7 and 8, and in Scenarios 1 – 6 is better in three cases and worse in three cases. This is desirable, since otherwise there would be little point in using an elicited, subjective utility as an objective function.

7 Discussion

We have proposed an adaptive Bayesian method for jointly optimizing schedule of administration and dose in phase I-II trials based on event times for efficacy and toxicity. We modeled schedules qualitatively because either of the two outcome events may occur long after administration. This is very different from the additive hazard model, with a component for each administration, used by Braun et al. (2007), who dealt with time to toxicity occurring over a much shorter time frame. For regimes administered over a period longer than a few days, our methodology could be extended to allow each patient’s initial dose to be changed adaptively based on interim events or new data from other patients.

Our design uses a regime assignment algorithm that is a hybrid of a greedy algorithm and adaptive randomization. Extensive simulations show that, for a maximum sample size of 72, the proposed model and method provide a design that is reliable, safe, and robust, and that it works well in the cases of either six or 12 regimes.