Three-dimensional Neumann-series approach to model light transport in nonuniform media

Abstract

We present the implementation, validation, and performance of a three-dimensional (3D) Neumann-series approach to model photon propagation in nonuniform media using the radiative transport equation (RTE). The RTE is implemented for nonuniform scattering media in a spherical harmonic basis for a diffuse-optical-imaging setup. The method is parallelizable and implemented on a computing system consisting of NVIDIA Tesla C2050 graphics processing units (GPUs). The GPU implementation provides a speedup of up to two orders of magnitude over non-GPU implementation, which leads to good computational efficiency for the Neumann-series method. The results using the method are compared with the results obtained using the Monte Carlo simulations for various small-geometry phantoms, and good agreement is observed. We observe that the Neumann-series approach gives accurate results in many cases where the diffusion approximation is not accurate.

1. INTRODUCTION

Diffuse optical tomography (DOT) is an emerging noninvasive biomedical imaging technique in which images of optical properties of the object are derived based on the measurements of near-infrared (NIR) light on the surface of the object [1–4]. The modality has received significant attention in the past decade due to its capability to provide functional images of the tissue under investigation using nonionizing radiation. DOT has been applied in breast-cancer detection and characterization [5,6], in functional brain imaging [7,8], in imaging of small joints for early diagnosis of rheumatoid arthritis [9], and in small-animal imaging for studying physiological processes and pathologies [10]. However, the task of image reconstruction in DOT is a nonlinear ill-posed inverse problem [4,11]. Small errors in measurements or inaccuracies in modeling the DOT system can cause significant errors in the reconstruction task. Therefore, it is essential that the modeling of the DOT system be very accurate. An important component of modeling the DOT system is to simulate the propagation of light through biological tissue. Models that accurately describe light propagation within biological tissues are therefore required.

A major difficulty in simulating light transport in biological tissue at NIR wavelengths is the phenomenon of scattering that occurs at these wavelengths in the tissue. We can use the radiative transport equation (RTE) to account for the scattering effects, but the RTE is a computationally intensive integro-differential equation. To reduce the computational complexity, a simplified approximation of the RTE, termed the diffusion approximation, is widely used [2,12,13]. The diffusion approximation has been implemented with finite element methods [14–17] and boundary element methods [18,19]. The approximation assumes that light propagates diffusely in tissues, an assumption that breaks down near tissue surfaces, in anisotropic tissues, and in high-absorption or low-scatter regions [1,3,20,21]. As a result, the diffusion approximation cannot model light propagation accurately in highly absorbing regions such as haematoma, and voidlike spaces such as ventricles and the subarachnoid space [21–25]. Moreover, when imaging small-tissue geometries, e.g., whole-body imaging of small animals, the diffusion model is not very accurate [20].

Higher-order approximations to the RTE such as the discrete-ordinates method (S_N) [26] and spherical harmonic equations (P_N) [27,28] have been developed to overcome these issues. The S_N method has been implemented with finite difference [21,24,29] and boundary element [30] methods, and the P_N method has been used along with finite element methods [31,32]. Although the approximations lead to exact solutions as N → ∞, they require solutions to many coupled differential equations, so these methods are still computationally very expensive. To illustrate their computational requirement, a full three-dimensional (3D) reconstruction of the mouse model to recover the fluorescent-probe distribution can take up to several hours or days of computation time using these methods [20]. To improve the computational efficiency, a simplified spherical harmonics (SP_N) approximation has been validated [20,25]. The method is asymptotic, but it can model light propagation with small error in some circumstances, and is computationally faster.

There has thus been significant research in using the RTE to model light propagation for optical imaging. However, most of these studies have focused on using differential methods to solve the RTE. In nuclear imaging, integral approximations to the RTE are often used to model photon propagation [33–35]. The advantage with the integral methods is that, unlike the differential methods, they do not require solutions to a large number of coupled equations. However, in nuclear imaging, photon propagation mostly occurs in the forward direction, and scattering effects are minimal. While the same is not true with optical imaging, the scattering phenomenon is strongly forward biased even in optical imaging [20,36–38]. Therefore, it is of interest for us to study the validity and performance of the integral form of the RTE, using a Neumann-series formulation, in diffuse optical imaging.

The Neumann-series formulation of the RTE has been explored for various tasks, such as modeling scattering effects in nuclear imaging [33,39,40], neutron-transport modeling [41], retrieving atmospheric properties from remotely sensed microwave observations [42], and modeling the scatter of sunlight in the atmosphere [43]. However, in optical imaging, the scattering phase function, imaging-system geometry, light emission source, and some other factors are quite different from the above-mentioned cases. Our study focuses on developing the mathematical methods and the software to implement the Neumann-series method specifically for optical imaging. As part of this study, we have developed a software to solve the Neumann-series RTE, specifically for uniform media [44]. The experiments with the uniform-medium software provide us with numerous insights into the feasibility, convergence characteristics, and computational requirements of the Neumann-series approach. We have presented these insights, along with a detailed treatment of the theory of the Neumann-series approach to model light propagation in uniform medium, in another paper [44]. In optical imaging, the problem of simulating light propagation in nonuniform tissue is also very important. The software we developed cannot be used for nonuniform media. Thus, in parallel, we attempted to solve the more general problem of light propagation in heterogeneous media. In a preliminary study, we have shown that the RTE in integral form can model photon propagation in simple heterogeneous media [45]. In the presented work, we extend the approach to completely nonuniform 3D media. We express the RTE as a Neumann series and solve it in the spherical harmonic basis. Implementation of this method on computing systems with only sequential processing units takes considerable execution time. However, the method is parallelizable, and to reduce the computational time, we implement it on parallel processing architectures, more specifically the NVIDIA graphics processing units (GPUs).

In this paper, our main objectives are the following: to present the theory and implementation details of the Neumann-series approach specific to a nonuniform medium, to describe the implementation of the algorithm for NVIDIA GPUs, to demonstrate that the method computes accurate results with small-phantom geometry for nonuniform medium, and to show the speedup obtained with our GPU implementation. Since we have presented detailed theory of the Neumann-series approach for optical imaging in uniform media [44], the mathematical treatment that is similar for uniform and nonuniform media will be just summarized in this paper.

2. THEORY

A. Radiative Transport Equation

The RTE takes into account all the physical processes of absorption, scattering, emission, and propagation of radiation through a medium. The fundamental radiometric quantity that we describe using the RTE is the distribution function w(r, ŝ, ε, t). In terms of photons, w(r, ŝ, ε, t)ΔVΔΩΔε can be interpreted as the number of photons contained in volume ΔV centered on the 3D position vector r = (x, y, z), traveling in a solid angle ΔΩ about direction ŝ = (θ, ϕ), and having energies between ε and ε + Δε at time t. The emission source is described using the function Ξ(r, ŝ, ε, t). In the DOT implementation, we assume a monoenergetic time-independent emission source, so that the emission function can be written as Ξ(r, ŝ). Moreover, in optical imaging, elastic scattering is the dominant scattering mechanism, and thus the scattered photon does not lose any energy. Since there are no other energy-loss mechanisms for the photon, the dependence of the distribution function on energy is dropped completely.

Let 𝒦 and 𝒳 denote the scattering and attenuation operators in integral form, which represent the effect of scattering, and the effect of attenuation and propagation of photons, respectively. Let the absorption and scattering coefficients at location r be denoted by μ_a(r) and μ_s(r), respectively, and let μ_tot(r) = μ_a(r) + μ_s(r). The effect of the scattering operator 𝒦 on the distribution function is given by [46]

$$[𝒦w](\mathit{r},\mathit{ŝ},t)={\int }_{4\pi }\mathrm{d}\mathrm{\Omega }\prime K(\mathit{ŝ},\mathit{ŝ}\prime |\mathit{r})w(\mathit{r},\mathit{ŝ}\prime ,t),$$ (1)

where ŝ and ŝ′ denote the direction of the outgoing and incoming photons, respectively, and K(ŝ, ŝ′|r) is the scattering kernel. Since the scattering phase function in biological tissue is typically given by the Henyey–Greenstein function [25,47], the scattering kernel is [44]

$$K(\mathit{ŝ},\mathit{ŝ}\prime |\mathit{r})=\frac{{\mu }_{\mathrm{s}}(\mathit{r})c_{\mathrm{m}}}{4\pi }\{\frac{1-g^2}{{[1+g^2-2g\text{cos}(\mathit{ŝ}·\mathit{ŝ}\prime )]}^{3/2}}\},$$ (2)

where c_m denotes the speed of light in the medium. The anisotropy factor g characterizes the angular distribution of scattering in the tissue.

The attenuation operator 𝒳 is the standard attenuated x-ray transform, and its effect on the distribution function is given by [46]

$$[𝒳w](\mathit{r},\mathit{ŝ},t)=\frac{1}{c_{\mathrm{m}}}{\int }_{\lambda =0}^{\infty }\mathrm{d}\lambda w(\mathit{r}-\mathit{ŝ}\lambda ,\mathit{ŝ},t)\times \text{exp}[-{\int }_0^{\lambda }\mathrm{d}\lambda \prime {\mu }_{\text{tot}}(\mathit{r}-\mathit{ŝ}\lambda \prime )].$$ (3)

This transform denotes that the radiance at location r in direction ŝ can be found by integrating the source distribution along a line parallel to ŝ and passing through the point r, where the more distant points along the line contribute less due to the exponential attenuation factor.

In terms of the defined attenuation and scattering operators, for the monoenergetic time-independent source Ξ(r, ŝ), the RTE can be written as a Neumann series [44,46]

$$w(\mathit{r},\mathit{ŝ})=𝒳\mathrm{\Xi }+𝒳𝒦𝒳\mathrm{\Xi }+𝒳𝒦𝒳𝒦𝒳\mathrm{\Xi }+\dots ,$$ (4)

where we note that the distribution function is also no more a function of time. An intuitive way to interpret this Neumann-series solution is that successive terms in the series represent successive scattering events; in fact photons that have scattered n times contribute to the term 𝒳(𝒦𝒳)ⁿΞ in this series [46]. Figure 1 schematically illustrates the effect of the initial terms of the Neumann series.

Fig. 1.

(Color online) DOT setup: a 3D cuboidal phantom with a laser source along the optical axis. The figure also roughly shows the effect of different terms of the Neumann series.

This section has summarized the general theory behind the Neumann-series RTE, which has been presented in more detail by Jha et al. [44]. We will now discuss the implementation details, where the framework and mathematical treatment we suggest will be general enough to model light propagation through nonuniform media. Therefore, the sections that follow are the specific contribution of this paper.

B. Discretization: Spherical Harmonics and Voxel Basis

Implementation of the RTE on a computing system requires discretization of the distribution function along the angular and spatial coordinates. To discretize the distribution function along the angular coordinates, we realize that the scattering kernel is only a function of the dot product between the entrance and exit direction of the photons, i.e., ŝ · ŝ′ [Eq. (2)]. In the language of group theory, the symmetry group of the 𝒦 operator is SO(3), and the spherical harmonics are basis functions for irreducible representations of SO(3) [46]. Since 𝒦 is invariant to this group, the scatter kernel takes a simple diagonal form in the spherical harmonic basis [46]. To use this simplification, we solve the RTE in a spherical harmonic basis. The distribution function is expressed in the spherical harmonic basis as

$$w(\mathit{r},\mathit{ŝ})=\sum _{l=0}^{\infty }\sum _{m=-1}^l{W}_{lm}(\mathit{r})Y_{lm}(\mathit{ŝ}),$$ (5)

where the spherical harmonic basis functions are denoted by Y_lm(ŝ), and the distribution function in spherical harmonics is denoted by W_lm(r). For ease of notation, we denote all the spherical harmonic coefficients W_lm(r) by W.

To discretize the spatial variable r, we use a voxel basis. We consider the domain over which we model photon propagation to be divided into voxels of length Δx, Δy, and Δz along the x, y, and z axis, respectively. The number of voxels along the x, y, and z axis are denoted by I, J, and K, respectively. We define the voxel basis function ψ_ijk(r) to be 0 outside the (i, j, k)th voxel and 1 inside that voxel, where (i, j, k) denote the 3D index of the voxel along the x, y, and z axis, respectively. The center of the (i, j, k)th voxel is denoted by r_ijk = (x_i, y_j, z_k). For brevity of notation, we will often denote the 3D index (i, j, k) by the 3D vector v. The voxel basis is an orthogonal basis, so the coefficients in this basis are obtained by a simple integration of the distribution function inside the volume. For the (i, j, k)th voxel, let us denote the (l, m)th spherical harmonic coefficient of the distribution function by W_lm(i, j, k). Then, we can obtain W_lm(i, j, k) from W_lm(r) as

$$W_{lm}(i,j,k)=\frac{1}{\mathrm{\Delta }V}{\int }_{S_{ijk}}{\mathrm{d}}^{3}r{W}_{lm}(\mathit{r}),$$ (6)

where S_ijk denotes the support of the voxel function ψ_ijk(r), and ΔV = ΔxΔyΔz is the volume of the voxel. The distribution function is then represented in the spherical harmonic and voxel basis as

$$w(\mathit{r},\mathit{ŝ})=\sum _{i,j,k=1}^{I,J,K}\sum _{l=0}^L\sum _{m=-l}^l{W}_{lm}(i,j,k){\psi }_{ijk}(\mathit{r})Y_{lm}(\mathit{ŝ}),$$ (7)

where we truncate the spherical harmonic expansion at l = L. For ease of notation, we denote the distribution function represented in the spherical harmonic and voxel basis by W_d. The absorption and scattering coefficients are also discretized in the voxel basis. For the (i, j, k)th voxel, the absorption and scattering coefficients are denoted by μ_a(i, j, k) and μ_s(i, j, k), respectively.

Let us denote the scattering operator in the spherical harmonics and voxel basis by the discrete-discrete operator D. The effect of this operator on the distribution function in a spherical harmonic and voxel basis is given by

$${[\mathit{D}{\mathit{W}}_{\mathbf{d}}]}_{lm}(i,j,k)=\sum _{l\prime m\prime }{W}_{l\prime m\prime }(i,j,k)D_{lm,l\prime m\prime }(i,j,k),$$ (8)

where D_lm,l′m′ (i, j, k) denotes the kernel of the scattering operator in the spherical harmonic and voxel basis. As we mentioned earlier, since the scattering operator 𝒦 depends only on the cosine of the angle between the entrance and exit direction of the photons, using Eqs. (1), (2), and (5), we can derive that the operator D is just a diagonal matrix with elements given by [44]

$$D_{lm,l\prime m\prime }(i,j,k)=c_{\mathrm{m}}{\mu }_{\mathrm{s}}(\mathit{r})g^l{\delta }_{ll\prime }{\delta }_{mm\prime },$$ (9)

where δ_ll′ is the Kronecker delta. As we observe, this matrix exists only for l = l′ and m = m′, since the scattering operator is diagonalized in the spherical harmonic basis.

Let us denote the attenuation operators in the spherical harmonic basis, and the spherical harmonic and voxel basis, by 𝒜 and A, respectively. The effect of the attenuation operator 𝒜 on the distribution function in spherical harmonic basis is given by

$${[𝒜\mathit{W}]}_{lm}(\mathit{r})=\sum _{l\prime =0}^{\infty }\sum _{m\prime =-l}^l{\int }_{\infty }{\mathrm{d}}^3\mathit{r}\prime W_{l\prime m\prime }(\mathit{r}\prime )A_{lm,l\prime m\prime }(\mathit{r},\mathit{r}\prime ),$$ (10)

where the elements of the attenuation kernel are given by

$$A_{lm,l\prime m\prime }(\mathit{r},\mathit{r}\prime )=\frac{1}{c_{\mathrm{m}}{|\mathit{r}-\mathit{r}\prime |}^2}{Y}_{lm}^{*}\left(\frac{\mathit{r}-\mathit{r}\prime }{|\mathit{r}-\mathit{r}\prime |}\right)Y_{l\prime m\prime }\left(\frac{\mathit{r}-\mathit{r}\prime }{|\mathit{r}-\mathit{r}\prime |}\right)\times \text{exp}[-{\int }_{\lambda \prime =0}^{|\mathit{r}-\mathit{r}\prime |}\mathrm{d}\lambda \prime {\mu }_{\text{tot}}(\mathit{r}-\lambda \prime \frac{\mathit{r}-\mathit{r}\prime }{|\mathit{r}-\mathit{r}\prime |}\left)\right].$$ (11)

The effect of the attenuation operator on the distribution function in the spherical harmonic and voxel basis is given by

$${[\mathit{A}{\mathit{W}}_{\mathbf{d}}]}_{lm}(i,j,k)=\sum _{i\prime ,j\prime ,k\prime =1}^{I,J,K}\sum _{l\prime =0}^L\sum _{m\prime =-l\prime }^{l\prime }{A}_{lm,l\prime ,m\prime }(i,j,k,i\prime ,j\prime ,k\prime )\times W_{l\prime m\prime }(i\prime ,j\prime ,k\prime ).$$ (12)

Thus the attenuation operator A accounts for the effect of the distribution function at the (i′, j′, k′), or the v′th voxel, on the distribution function at the (i, j, k), or the vth voxel. This effect depends on the location of both the voxels and the path between them. Let us denote the vector that joins the center of these two voxels by R_vv′ û_vv′. While R_vv′ denotes the magnitude of the vector, and, therefore, is the distance between the two voxel midpoints, û_vv′ denotes the unit vector joining the two voxel midpoints. Let û_vv′ = u_xx̂ + u_yŷ + u_zẑ, where x̂, ŷ, and ẑ denote the unit vectors along the x, y, and z axis, respectively. Then, using Eqs. (6), (10), (11), and (12), we get the elements of the attenuation operator in matrix form as

$$A_{lm,l\prime m\prime }(i,j,k,i\prime ,j\prime ,k\prime )=\frac{\mathrm{\Delta }V}{c_{\mathrm{m}}{R}_{\mathit{v}\mathit{v}\prime }^2}{Y}_{lm}^{*}({\mathit{û}}_{\mathit{v}\mathit{v}\prime })Y_{l\prime m\prime }({\mathit{û}}_{\mathit{v}\mathit{v}\prime })\times \text{exp}[-\sum _{q=0}^{R_{\mathit{v}\mathit{v}\prime }/\mathrm{\Delta }\lambda \prime }\mathrm{\Delta }\lambda \prime {\mu }_{\text{tot}}(i-\frac{q{u}_x\mathrm{\Delta }\lambda \prime }{\mathrm{\Delta }x},j-\frac{q{u}_y\mathrm{\Delta }\lambda \prime }{\mathrm{\Delta }y},k-\frac{q{u}_z\mathrm{\Delta }\lambda \prime }{\mathrm{\Delta }z}\left)\right].$$ (13)

Using this expression, we can evaluate the effect due to the attenuation operation between photons present in two different voxels. The photons in the same voxel also have an effect on each other due to the attenuation operation. This effect cannot be computed using the above expression, due to the $1/R_{\mathit{v}\mathit{v}\prime }^2$ term, which is zero when v = v′. Therefore, we consider a different approach in this case.

Let us consider that we wish to evaluate the effect that the photons in the (i, j, k)th voxel have on each other. We then require a method to determine the attenuation-kernel element A_lm,l′m′ (i, j, k, i, j, k), which we henceforth denote by A_lm,l′m′ (i, j, k) for ease of notation. We could consider determining this quantity by performing a numerical integration of the expression for A_lm,l′m′ (r, r′), given by Eq. (11), over the space of the (i, j, k)th voxel in Cartesian coordinates. However, this is difficult due to the 1/|r − r′|² term in this expression, which becomes very high for locations r and r′ within the same voxel. To solve this issue, we evaluate the attenuation operation [Eq. (10)] for this case in spherical coordinates instead. Let us denote the vector r − r′ by Rû, so that we can replace d³r′ by R²dRdΩ_u in Eq. (10), where dΩ_u corresponds to the infinitesimally small solid angle around the unit vector û. Further, substituting the expression for A_lm,l′m′(r, r′) from Eq. (11) into Eq. (10), we get

$${[𝒜\mathit{W}]}_{lm}(\mathit{r})=\frac{1}{c_{\mathrm{m}}}\sum _{l\prime m\prime }{\int }_{4\pi }\mathrm{d}{\mathrm{\Omega }}_u{Y}_{lm}^{*}(\mathit{û})Y_{l\prime m\prime }(\mathit{û}){\int }_0^{\infty }\mathrm{d}R{W}_{l\prime m\prime }(\mathit{r}\prime )\times \text{exp}[-{\int }_{\lambda \prime =0}^R\mathrm{d}\lambda \prime {\mu }_{\text{tot}}(\mathit{r}-\mathit{û}\lambda \prime )],$$ (14)

so that the 1/|r − r′|² term cancels out. We next use Eq. (6) in the above expression to evaluate the effect of the photons over the (i, j, k)th voxel. We find that since we are integrating only over the volume of the (i, j, k)th voxel, μ_tot(r − ûλ′) and W_l′m′ (r′) are constant over this volume in the voxel basis and equal to μ_tot(i, j, k) and W_l′m′ (i, j, k), respectively. Therefore, these terms come out of the integral over λ′ and R, respectively. The exponential integral is then simply equal to exp[−μ_tot(i, j, k)R]. Also, for a particular direction û = (θ_u, ϕ_u), the integral over R varies only from 0 to β(θ_u, ϕ_u), where β(θ_u, ϕ_u) is the distance from the center of the voxel to the face of the voxel for a particular direction. Thus, using Eq. (6) in Eq. (14) yields

$${[{\mathit{A}}_{\mathit{D}}{\mathit{W}}_{\mathbf{d}}]}_{lm}(i,j,k)=\frac{1}{c_{\mathrm{m}}}\sum _{l\prime m\prime }{W}_{l\prime m\prime }(i,j,k){\int }_{\theta =0}^{\pi }\mathrm{d}\theta \text{sin}\theta \times {\int }_{\varphi =0}^{2\pi }\mathrm{d}\varphi Y_{lm}^{*}(û)Y_{l\prime m\prime }(û)\times \left\{\frac{1-\text{exp}[-{\mu }_{\text{tot}}(i,j,k)\beta ({\theta }_u,{\varphi }_u)]}{{\mu }_{\text{tot}}(i,j,k)}\right\},$$ (15)

where A_D is a diagonal matrix in the voxel basis that describes the effect that photons in a voxel have on each other. We evaluate the integral over (θ_u, ϕ_u) numerically by sampling the angular coordinates at discrete values, and determining β(θ_u, ϕ_u) for each value. To determine β(θ_u, ϕ_u), we inscribe the voxel with a sphere. We find the coordinates at which the ray from the center of the voxel at an angle (θ_u, ϕ_u) intersects the sphere. From these coordinates, we determine the coordinate of intersection of the ray with the planes corresponding to the voxel faces that lie in the path of the ray. The distance of the closest intersection gives β(θ_u, ϕ_u). Therefore, the effect that photons in the same voxel have on each other is evaluated. Equation (15) is written in short-hand notation as

$${[{\mathit{A}}_{\mathit{D}}{\mathit{W}}_{\mathbf{d}}]}_{lm}(i,j,k)=\sum _{l\prime m\prime }{W}_{l\prime m\prime }(i,j,k)A_{lm,l\prime m\prime }(i,j,k).$$ (16)

Finally, the RTE in the spherical harmonic and voxel basis is given by [44]

$${\mathit{W}}_{\mathbf{d}}=\mathit{A}{\mathit{\xi }}_{\mathbf{d}}+\mathit{A}\mathit{D}\mathit{A}{\mathit{\xi }}_{\mathbf{d}}+\mathit{A}\mathit{D}\mathit{A}\mathit{D}\mathit{A}{\mathit{\xi }}_{\mathbf{d}}+\dots ,$$ (17)

where ξ_d denotes the source function in the spherical harmonic and voxel basis.

C. Procedure

In our DOT set up, shown in Fig. 1, the source outputs a unidirectional beam along the optical axis, which we refer to as the z axis. We denote the two-dimensional (2D) profile of this beam by the function h(x, y). Let the radiant exitance of the source across the circular region be α. The source can then be represented as

$$\mathrm{\Xi }(\mathit{r},\mathit{ŝ})=\alpha \delta (\mathit{ŝ}-\mathit{ẑ})h(x,y)\delta (z),$$ (18)

where δ(z) indicates that the photons are being emitted from only the z = 0 plane, and δ(ŝ − ẑ) indicates that the source is a unidirectional beam along the z axis. To solve the RTE in spherical harmonic basis, we will have to represent this source term in the spherical harmonic basis. It is practically impossible to do so for a beamlike source function, since that requires an infinite number of spherical harmonic coefficients. However, in many DOT setups, the emission source is a pencil beam or a combination of pencil-beam-like sources. We apply some mathematical procedures to solve this issue. We first realize that the 𝒳Ξ term is just an attenuation transform applied on a unidirectional-beam source. Thus, it can be easily computed in the normal (r, ŝ) basis. Substituting Eq. (18) into Eq. (3), we can derive that in our experimental setup, the distribution function due to the 𝒳Ξ term is given by

$$[𝒳\mathrm{\Xi }](\mathit{r},\mathit{ŝ})=\frac{\alpha }{c_{\mathrm{m}}}{\int }_0^{\infty }\mathrm{d}\lambda \delta (\mathit{ŝ}-\mathit{ẑ})h(x,y)\delta (z-\mathit{ẑ}\lambda )\times \text{exp}[-{\int }_0^{\lambda }\mathrm{d}\lambda \prime {\mu }_{\text{tot}}(\mathit{r}-\mathit{ŝ}\lambda \prime )]=\frac{\alpha }{c_{\mathrm{m}}}\delta (\mathit{ŝ}-\mathit{ẑ})h(x,y)\text{exp}[-{\int }_0^z\mathrm{d}\lambda \prime {\mu }_{\text{tot}}(\mathit{r}-\mathit{ẑ}\lambda \prime )],$$ (19)

where we have used the sifting property of the delta function. Also, in the Neumann series in spherical harmonic basis [Eq. (17)], except for the first term, ξ_d is always preceded by DA. In fact, an alternative way to rewrite the RTE is

$${\mathit{W}}_{\mathbf{d}}=\mathit{A}{\mathit{\xi }}_{\mathbf{d}}+\mathit{A}\left[\sum _{n=0}^{\infty }{(\mathit{D}\mathit{A})}^n\right](\mathit{D}\mathit{A}{\mathit{\xi }}_{\mathbf{d}}).$$ (20)

The representation of DAξ_d is feasible in the spherical harmonic basis since the scattering operator causes the pencil beam to spread out. Therefore, we compute the spherical harmonic coefficients for DAξ_d. Using Eqs. (1), (2), and (19), the term [𝒦𝒳Ξ](r, ŝ) is derived to be

$$[𝒦𝒳\mathrm{\Xi }](\mathit{r},\mathit{ŝ})=\frac{\alpha {\mu }_{\mathrm{s}}(\mathit{r})}{4\pi }h(x,y)\left\{\frac{1-g^2}{{[1+g^2-2g\text{cos}(\mathit{ŝ}·\mathit{ẑ})]}^{3/2}}\right\}\times \text{exp}[-{\int }_0^z\mathrm{d}\lambda \prime {\mu }_{\text{tot}}(\mathit{r}\mathit{-}\mathit{ẑ}\lambda \prime )].$$ (21)

To represent this distribution function in the spherical harmonic basis, we follow a similar treatment as in Jha et al. [44], which leads the spherical harmonic coefficients due to the 𝒦𝒳Ξ term to be

$${[W]}_{lm}(\mathit{r})=\alpha {\mu }_{\mathrm{s}}(\mathit{r})h(x,y)g^l\sqrt{\frac{2l+1}{4\pi }}\text{exp}[-{\int }_0^z\mathrm{d}\lambda \prime {\mu }_{\text{tot}}(\mathit{r}-\mathit{ẑ}\lambda \prime )].$$ (22)

Using Eq. (6) to represent the above distribution function in the voxel basis, we obtain the (l, m)th spherical harmonic coefficient of the distribution function due to the DAξ_d term in the (i, j, k)th voxel to be

$$W_{lm}(i,j,k)=h(x_i,y_i)\frac{g^l}{\mathrm{\Delta }V}\sqrt{\frac{2l+1}{4\pi }}\sum _{k\prime =1}^K\frac{{\mu }_{\mathrm{s}}(i,j,k\prime )}{{\mu }_{\text{tot}}(i,j,k\prime )}\times \text{exp}[-{\mu }_{\text{tot}}(i,j,k\prime )z_{k\prime }]\{1-\text{exp}[-{\mu }_{\text{tot}}(i,j,k\prime )\mathrm{\Delta }z)]\},$$ (23)

where (x_i, y_j) denote the x and y coordinates of the center of the (i, j, k)th voxel. After evaluating the DAξ_d term in the spherical harmonic basis, we solve the RTE using an iterative approach based on Eq. (20). In each iteration, we apply the attenuation operator, and then the scattering operator, on an effective source term. We then add the resulting distribution function to the Neumann series, and also use it as the source for the next iteration. To illustrate our procedure, we first apply the attenuation and scattering operators on DAξ_d. We thus obtain DADAξ_d, which is added to the Neumann series, and also used as the source term in the next iteration. We run the iterations until convergence is achieved, evaluating convergence using a criterion that we have developed [44]. After that, we apply the attenuation operator on all the computed Neumann-series terms. To compute the flux at the transmitted face of the medium due to all the terms except the 𝒳Ξ term, we then integrate the computed distribution function in spherical harmonic and voxel basis over space and angles. In this study, we consider a pixilated contact detector with the detector plane parallel to the transmitted face of the medium. Assuming that the detector has uniform sensitivity over a given pixel, the flux measured by the (i, j)th pixel of the detector is then computed in units of Watts as [44]

$${\mathrm{\Phi }}_{ij}=c_{\mathrm{m}}{A}_{\mathrm{p}}{\int }_{2\pi }\mathrm{d}\mathrm{\Omega }\mathit{ẑ}·\mathit{ŝ}w(x_i,y_i,H,\mathit{ŝ}),$$ (24)

where (x_i, y_j) denote the x and y coordinates of the center of the (i, j)th detector pixel, H is the size of the medium along the z axis so that z = H corresponds to the detector plane, and A_p is the area of a pixel. This flux can be directly obtained from the distribution function represented in the spherical harmonic and voxel basis [44]. Finally, the flux due to the 𝒳Ξ term at the transmitted face in the (i, j)th voxel, which we denote by Φ_ij,𝒳Ξ, is derived by substituting the expression for [𝒳Ξ](r, ŝ) from Eq. (19) in Eq. (24). This yields

$${\mathrm{\Phi }}_{ij,𝒳\mathrm{\Xi }}=\alpha A_{\mathrm{p}}h(x_i,y_i)\text{exp}[-\sum _{k\prime =1}^K\mathrm{\Delta }z{\mu }_{\text{tot}}(i,j,k\prime )].$$ (25)

This flux is added to the flux computed from the rest of the terms to obtain the total flux at the transmitted face. We implement this algorithm, first without using any GPU hardware, which we refer to as the central processing unit (CPU) implementation, and then on a system consisting of multiple GPU cards, which we refer to as the GPU implementation.

3. IMPLEMENTATION

A. CPU Implementation

The software to solve the Neumann-series form of the RTE in nonuniform media is developed using the C programming language on a computing system with a 2.27 GHz Intel Xeon quad core E5520 processor as the CPU running a 64 bit Linux operating system. The software reads the input-phantom specifications and follows the procedure described in Subsection 2.C to evaluate the Neumann series. However, performing the attenuation operation in this procedure is a computationally challenging and memory-intensive task. As is evident from Eq. (12), to evaluate the distribution function in a voxel after the attenuation operation, we need the contribution from all the other voxels in the medium. We also require the corresponding terms of the A matrix given by Eq. (13). Since we need the terms of the matrix A in every iteration of the Neumann series, if the size of A is not very large, we can precompute and store these elements. For a homogeneous medium, we can exploit the shift-invariant nature of the attenuation operator, which reduces the size of the A matrix and therefore allows its storage [44,45]. However, in a heterogeneous medium, this operator is no longer shift-invariant, and storing the elements of the A matrix requires more memory than is typically available. To get around this issue, in a previous work [45], we devised a pattern-based scheme for simple heterogeneous phantoms. However, for more complicated heterogeneous phantoms, the pattern-based method is very difficult to implement. Because of the large memory requirements, it is instead more pragmatic to compute the elements of A in each iteration of the Neumann series. This implies that in a medium consisting of N voxels, since for each voxel, we have to compute the effect due to all the other voxels, even when L = 0, we need to perform N operations for each voxel. Thus, to compute the distribution function for all the N voxels, we must perform N² operations. In each of these operations, we have to compute an element of the matrix A using Eq. (13). When the number of the spherical harmonic coefficient is higher, such as when L = L₀, then we need to perform N²(L₀ + 1)⁴ operations. Furthermore, we have to perform these many operations in every iteration of the Neumann series.

To add to the computational requirement, computing every element of the matrix A requires determining the exponential attenuation factor present in Eq. (13). We refer to the negative of the exponent of this exponential as the radiological path between the voxels. To compute the radiological path, we use an improved version of the Siddon’s algorithm [48]. We implement this algorithm for a 3D medium. We further modify this improved algorithm for rays completely enclosed inside the medium. This modification is required since the original Siddon’s algorithm [48,49] is designed for computed-tomography applications. Thus, in the original algorithm, all the rays start from and end outside the medium. In contrast, in our algorithm, the rays start and end at the midpoints of the different voxels of the medium, and are thus completely enclosed within the medium. To briefly summarize the scheme, we first define a grid consisting of multiple planes along the x, y, and z axis, based on the voxel basis representation. To determine the voxels that a ray starting from a certain voxel passes through until it reaches the destination voxel, we trace a line between the midpoint of these voxels. Considering a parameterized form for this line, we determine the locations at which the line intersects the different planes in the grid, using which, on the fly, we determine the voxels that the ray passes through and the distance that it covers in those voxels. This is a computationally intensive set of operations.

To reduce the computational requirements of the attenuation operation, we implement a numerical approximation in our code. From the expression of the attenuation operation [Eq. (14)], it is evident that due to the exponential term in the attenuation kernel, voxels that are far away from a given voxel have very little effect on the distribution function of that voxel. Thus, the effect of the voxels that are beyond a certain threshold distance can be approximately neglected. This threshold is determined by computing the average value of the attenuation coefficient in the medium, and using this value to determine the distance |r − r′| = R_thresh at which the exponential attenuation term becomes almost negligible in Eq. (11). Also, when g = 0, we use a simplification described in Jha et al. [44] that helps simplify the computational requirements considerably. To further increase the computational efficiency, we parallelize the execution of the attenuation kernel on the Intel E5520 CPU, a processor that consists of four cores and eight threads, using the open multiprocessing (OpenMP) application programming interface (API). In spite of these procedures, the execution of the Neumann-series RTE still takes considerable time, to the order of hours. We profile this code using the GNU profiler, and find that the attenuation operation takes more than 95% of the execution time for almost all phantom configurations.

Because of the excessive time taken by the attenuation operation, and the fact that the implementation of this operation can be parallelized, we studied the use of GPUs for this task.

B. GPU Implementation

In each term of the Neumann series, the scattering and attenuation operations are executed for every voxel. Therefore, for every voxel, the same code is executed, albeit on different data. Assigning the code that is executed for different voxels to different parallel processing elements can therefore increase the speed of the code significantly. This parallelization scheme, also known as data-level parallelism, can be implemented on the GPUs.

GPUs are rapidly emerging as an excellent platform to provide parallel computing solutions, due to their efficient design features, such as deeply optimized processing pipelines, hierarchical thread structures, and high memory bandwidth. With the advent of compute unified device architecture (CUDA) as an extension of the C language for general purpose GPU (GPGPU) computing, GPUs are being extensively used for scientific computing. Even in the field of simulating photon propagation in tissue, significant speedups have been achieved using GPUs. Alerstam et al. [50] have shown that using GPUs to perform Monte Carlo (MC) simulation of photon migration in a homogeneous medium can increase the speed by a factor of 1000. Similarly, for heterogeneous media, Fang and Boas [51] have shown that the speed of MC simulations can be increased by about 300 times by using GPUs. Huang et al. [52] have developed a radiative transfer model on GPUs for satellite-observed radiance. Gong et al. [53] and Szirmay-Kalos et al. [54] have also implemented the RTE on GPUs using a discrete-ordinates approach.

While GPUs are suitable for parallelizing our code, a constraint with the GPU is the limited global and on-chip memory available on these devices. The Neumann-series algorithm implementation requires significant memory. In particular, applying the attenuation operator is both computationally and memorywise intensive. As is evident from Eqs. (12) and (13), for a single computation using the attenuation operator, the code should have access to the distribution function values of all the voxels in the phantom, the attenuation coefficients of all the voxels, and finally the spherical harmonic values for all the angles and (l,m) values. This can translate to megabytes of memory requirement even in simple cases. Therefore, our code design should be optimized memorywise to exploit the benefits of parallelization. Another issue is that for an efficient GPU implementation, the code that runs on different parallel processing units should ideally require little storage memory for its local variables. This is because the number of registers, which are shared by the different parallel processing units on the GPU, is limited, and if each thread’s memory requirements are high, this would lead to a small number of threads running in parallel. Moreover, if each kernel’s local memory requirements are high, then the code will be inefficient. However, the attenuation operation code requires many local variables. In the next few subsections, we describe how we handle these issues.

1. Device and Programming Tools

We implement the Neumann-series algorithm on a 2.26 GHz Intel quad core system running 64 bit Linux and consisting of four NVIDIA Tesla C2050 GPUs. These GPUs are based on the Fermi architecture, which apart from its other advantages is very efficient for double-precision computations. The Tesla C2050 is a device of compute capability 2.0. Each C2050 card consists of 14 multiprocessors, 448 CUDA cores, dedicated global memory of 3 GB, and single- and double-precision floating point performances of 1.03 Tflops and 515 Gflops, respectively [55].

To implement the RTE on our GPU system, we use POSIX thread (pthread) libraries [56] and NVIDIA CUDA [57]. While pthread libraries are used to split the programming task onto the multiple GPUs, CUDA is used to implement our algorithm on the individual GPUs. Pthread libraries are a computationally efficient, standards-based thread API for C/C++ that allows the programmer to spawn a new concurrent process flow. CUDA is a general purpose parallel computing architecture, with a parallel programming model and instruction set architecture to harness the computing power of NVIDIA GPUs for general purpose programming [57,58]. A CUDA application consists of two parts: a serial program that runs on the CPU and a parallel program, referred to as the kernel, that runs on the GPU [59]. The kernel executes in parallel as a set of threads. The threads are grouped into blocks, where the threads within a block can concurrently execute and cooperate among themselves through barrier synchronization and shared memory access to a memory space that is private to that block. A grid is one level higher in the hierarchy and is a set of blocks that can be executed independently and in parallel. When invoking a thread using CUDA, we can specify the number of threads per block and the number of blocks. The memory requirements of the kernel often restrict the number of threads that are executed together.

CUDA-enabled devices also adhere to a common memory management scheme. Each GPU device possesses a global random access memory (RAM), called the global memory, which can be accessed by all the multiprocessors on the GPU. In addition, each multiprocessor has its own on-chip memory that is accessible only to the cores on that multiprocessor. The on-chip memory of the GPU consists of registers, shared memory, and the L1 cache [60]. The shared memory is shared among the threads in a block. There are also two additional read-only memory spaces accessible by all threads: the constant and texture memory spaces [55], which are cached onto the on-chip memory of the GPU. The constant memory is efficient to use if different threads in a multiprocessor access the same memory location. As for texture memory, for applications that do not benefit from using texture memory, its usage can be counterproductive on devices with compute capability 2.x, since global memory loads are cached in the L1 cache, and the L1 cache has higher bandwidth than texture cache [61].

2. Parallelization Scheme and Software Design

The flowchart of the software implementation is shown in Fig. 2. The basic procedure is similar to the procedure outlined in Subsection 2.C, but we incorporate many computational and memory optimizations. The distribution function due to DAξ_d terms is computed on the CPU using Eq. (23). Similarly, the spherical harmonic coefficient values Y_l,m(ŝ) for different angles are computed on the CPU. The distribution function due to the DAξ_d term and the spherical harmonic coefficient values, due to their large memory requirement, are transferred to the global memory of the GPU using CUDA memory allocation techniques. Since the constant memory on the GPU is very efficient for storing data that all the threads access simultaneously, we store such data in our software, such as the geometric configuration and the properties of the phantom that are the same for all the voxels, in the constant memory. Storing the scattering and absorption coefficients for each voxel requires considerable memory. To reduce this memory requirement, we use the fact that although the number of voxels in the phantom is high, the number of tissue types, i.e., tissues with different absorption or scattering coefficients, is quite lower in most cases. For more efficient memory use, we instead store a tissue map, which is a data structure that stores the tissue type of the different voxels. In this scheme, only 1 byte storage space is required for each voxel. The absorption and scattering coefficients of the different tissue types are stored in the constant memory, while the tissue map is stored in the global memory. Also the terms of matrix A_D, i.e., A_lm,l′m′ (i, j, k) are the same for voxels with the same tissue type, as is evident from Eqs. (15) and (16). Therefore instead of evaluating and storing these terms for each voxel, we instead just compute it for the different tissue types. We store these terms in the constant memory of the GPU since often, many threads in a block will access the same terms. This is because voxels with similar tissue type are generally close to each other, and in our parallelization scheme, voxels in the same block are close to each other. The Neumann-series iteration procedure is then executed, which begins with applying the attenuation operator to the distribution function.

Fig. 2.

(Color online) Flowchart of our algorithm implementation on the GPU. Blue boxes (filled with dotted pattern) denote the code running on the CPU, orange boxes (filled with solid pattern) denote code running on the GPU, and green boxes (filled with vertical-line pattern) are the interface routines between CPU and GPU.

As mentioned in Subsection 3.A, the attenuation operation, given by Eq. (13), takes the most computation time. Therefore our main objective is to parallelize the attenuation-kernel execution. To achieve this objective, we divide the voxelized phantom into four layers along the z dimension, and each layer is allotted to one of the four GPUs using pthreads. On the GPU, the allotted layer is further split along the z dimension into sublayers. Each sublayer is assigned to one grid, and the grid is further divided into blocks. The number of threads in a block is user-configurable. The basic idea can be to assign the attenuation operation code for one voxel to one thread. However, the attenuation operation code performs a number of computations including computing the radiological path. Thus, this code requires many local variables, which can lead to inefficient implementation, as described earlier. To solve this issue, the attenuation operation code for each voxel is split into two separate kernels that execute one after the other. Splitting the attenuation operation code into two kernels results in each thread having a smaller number of register requirements. The first kernel evaluates the effect that the voxel has on itself using Eq. (16). The second kernel evaluates the effect that the other voxels have on the distribution function in a given voxel by computing the elements of the attenuation kernel A_lm(i, j, k, i′, j′, k′) using Eq. (13), followed by evaluating the attenuation operation using Eq. (12). In this kernel, the radiological path between two voxels is also computed using the Siddons algorithm. The parallelization scheme is illustrated in Fig. 3.

Fig. 3.

(Color online) Summary of the parallelization scheme to implement the RTE.

The attenuation kernel is evaluated on the GPUs with the parallelization scheme mentioned above. The scattering operation, given by Eq. (23), is then performed on the GPU by allotting one thread to each voxel. The computed distribution function as a result of the attenuation and the scattering operation is then transferred to the host memory from the global memories of the four GPUs. This distribution function is added to the Neumann series on the host memory and is also used as the source for the next iteration. The Neumann-series iterations are performed until convergence is achieved, following which, the attenuation operation is applied for one last time. Using the computed distribution function in spherical harmonics, the transmitted flux at the exit face is computed. The flux due to the 𝒳Ξ term, given by Eq. (25), is added to the computed transmitted flux at the exit face. Finally, the computed output image is displayed.

We experiment with various mechanisms such as coalesced global memory access, on-chip shared memory use, thread block synchronization, constant memory use, and minimum-memory assignment for the different local variables to achieve efficient GPU implementation of the algorithm. The various local variables that are required in the kernel code are stored in as little memory as possible, which helps minimize GPU register usage. We try to perform less global memory access, but once the data from global memory is accessed, it is stored in the L1 cache for a small duration. We make use of this caching mechanism also while implementing the kernel. Also, threads that are part of the same block correspond to voxels that are near each other in a 3D sense. Therefore, the data required by the threads along one of these dimensions lie in memory locations that are close to each other, so we can take advantage of coalesced global memory access to a certain extent. We were very keen to use the on-chip shared memory and experimented various configurations for its usage. However, the use of shared memory results in computationally inefficient code, due to the limited amount of shared memory and the high memory requirements of the Neumann-series algorithm. Although threads in a block share data such as the source distribution function, in most of the computations, the memory required by such data exceeds the available shared memory. Therefore, we instead configure the GPU before each kernel call so that most of the on-chip memory is allotted to the L1 cache instead of the shared memory. Also, since we did not find any specific advantage in using the texture memory, we prefer the global memory to texture memory for our application. Because of the multiple kinds of optimization mechanisms [60], each with its own tradeoffs, we perform a number of experiments with different mechanisms to achieve a computationally efficient code. To help with the optimization of the code, we use various methods such as inspecting the assembly level file, using the CUDA Occupancy Calculator, and compiling with specific flags to study the usage of different memories [60]. We also develop a complex-arithmetic library of functions for the GPU that performs some specific complex number computations that our code requires.

4. EXPERIMENTS AND RESULTS

In this section, we compare results obtained using our Neumann-series approach with the results obtained using an MC approach to model photon propagation [62]. It has been shown that the diffusion approximation is valid in optically thick media and in cases where scattering dominates absorption [15]. In our experiments, we study different cases where the standard diffusion approximation breaks down, such as media illuminated by collimated light sources [63,64], optically thin media [65], media with low-scattering voidlike regions [32], and media where the absorption coefficient is similar to the scattering coefficient [20,24].

The simulation setup is shown in Fig. 1, where the scattering medium is a 3D slab, characterized by a reduced-scattering coefficient ${\mu }_{\mathrm{s}}^{\prime }={\mu }_{\mathrm{s}}(1-g)$. The collimated source emits NIR light with a transverse circular profile. The beam is incident on the center of the entrance face of the scattering medium. The boundary-transmittance measurements are made at the exit face of the scattering medium. All the experiments are carried out for nonreentry boundary conditions, so that the refractive index of the medium is equal to 1. In the Neumann-series method, for all the experiments, we choose the number of spherical harmonic coefficients to be such that L = 3. In the GPU simulation, the number of threads per block is kept as 10 × 10 × 5 along the x, y, and z axis, respectively. The MC simulations are performed using the tMCimg software [62]. The number of simulated photons in each MC simulation is 1 × 10⁷. The simulation results shown in all the cases denote the linear profile of the transmitted image. The linear profile is taken along the line passing through the center of the transmitted image.

A. Homogeneous Medium

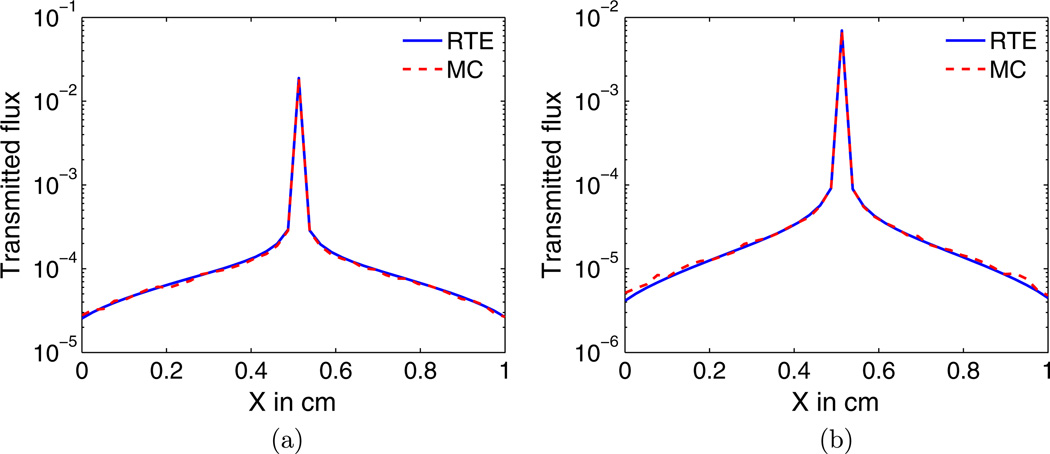
We first validate our code on homogeneous scattering media. In our first experiment, the homogeneous medium has optical properties μ_a = 0.01 cm⁻¹, ${\mu }_{\mathrm{s}}^{\prime }=1{\text{cm}}^{-1}$, and g = 0. The medium has a size of 2 × 2 × 2 cm³ and is discretized into 20 × 20 × 20 voxels. We know that the standard diffusion approximation does not yield good results when the medium is optically thin [65], although it can be used with several modifications [66]. The Neumann-series method accurately models this situation, as shown in Fig. 4(a).

Fig. 4.

(Color online) Neumann-series and MC transmittance outputs in a homogeneous low-scattering medium ${\mu }_{\mathrm{s}}^{\prime }=1{\text{cm}}^{-1}$ with (a) low-absorption coefficient (μ_a = 0.01 cm⁻¹) and (b) high-absorption coefficient (μ_a = 1 cm⁻¹).

Another issue with the diffusion approximation is that it breaks down when ${\mu }_{\mathrm{a}}~{\mu }_{\mathrm{s}}^{\prime }$ [24]. To verify the performance of the Neumann-series method in this regime, we perform another experiment in which the absorption and scattering coefficients in an isotropic medium are both equal to 1 cm⁻¹. As the results in Fig. 4(b) show, using the Neumann-series approach, we can model light propagation accurately in this scenario.

We next consider a midscattering medium with ${\mu }_{\mathrm{s}}^{\prime }=4{\text{cm}}^{-1}$, of size 1 × 1 × 1 cm³ with μ_a = 0.01 cm⁻¹ and g = 0. Since this medium has a higher scattering coefficient and thus a smaller mean free path for the photon, for accurate spatial discretization of the distribution function, we need to have smaller-sized voxels. From the analysis performed in our uniform-media paper [44], we know that the voxel size should be 0.1 times the mean free path of the photon to obtain an accurate output using the Neumann-series approach. The medium is thus divided into 40 × 40 × 40 voxels. The results comparing the MC and the Neumann-series outputs are shown in Fig. 5(a), and we see a very good match between the two. In another experiment, we increase the absorption coefficient of this medium by 100 times, so that μ_a = 1 cm⁻¹, which leads to μ_a being close to ${\mu }_{\mathrm{s}}^{\prime }$. The Neumann-series approach is accurate in this scenario, as confirmed by the result shown in Fig. 5(b).

Fig. 5.

(Color online) Neumann-series and MC transmittance outputs in a midscattering medium ${\mu }_{\mathrm{s}}^{\prime }=4{\text{cm}}^{-1}$ with (a) low-absorption coefficient (μ_a = 0.01 cm−1) and (b) high-absorption coefficient (μ_a = 1 cm⁻¹).

B. Heterogeneous Medium

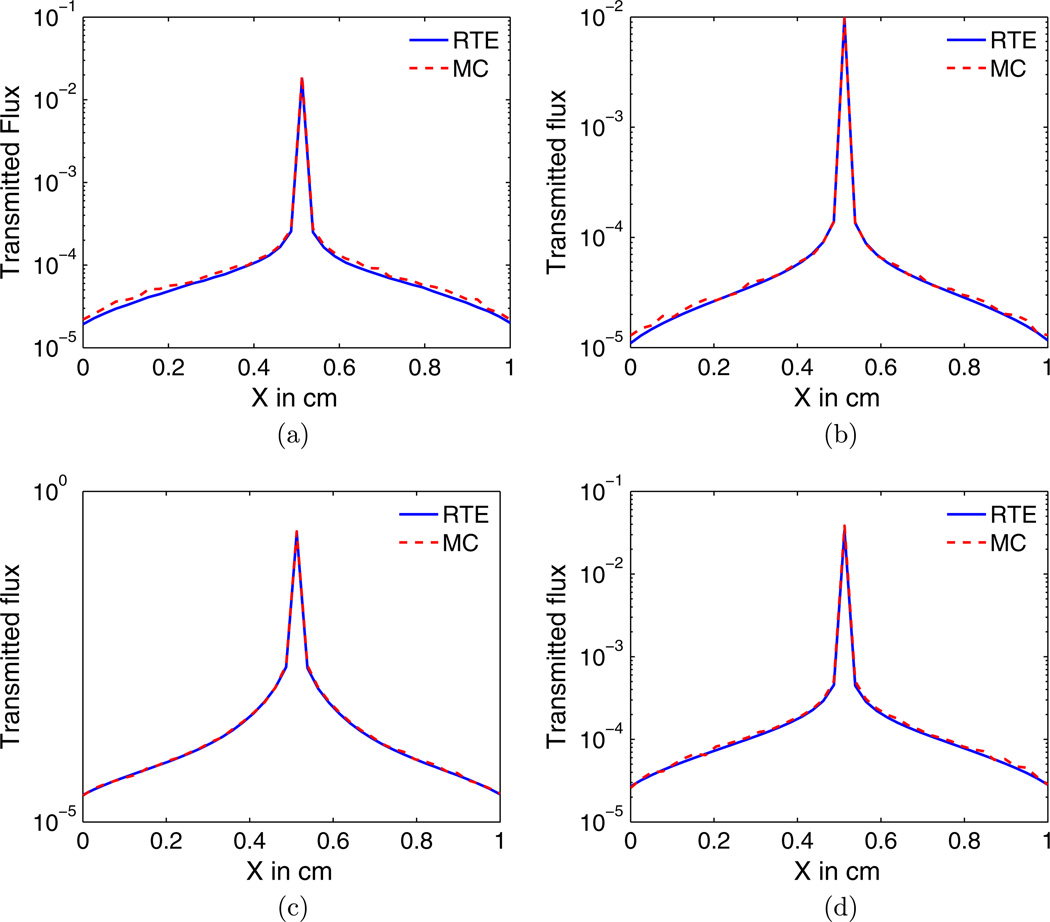
To validate the performance of the Neumann-series approach for a nonuniform midscattering medium, we consider a 1 × 1 × 1 cm³ sized phantom with different kinds of heterogeneity models as shown in Fig. 6. The first experiment is with a phantom that has three different tissue types scattered randomly, as shown in Fig. 6(a). The three tissue types have their reduced-scattering and absorption coefficients, (${\mu }_{\mathrm{s}}^{\prime }$, μ_a), equal to (4 cm⁻¹, 0.01 cm⁻¹), (4 cm⁻¹, 1 cm⁻¹), and (2 cm⁻¹, 0.01 cm⁻¹), respectively. The anisotropy factor g is 0 for all the tissue types. As shown in Fig. 7(a), for this particular case, the Neumann-series results are in agreement with the MC results.

Fig. 6.

(Color online) Different heterogeneous tissue geometries: (a) three different tissue types scattered randomly, (b) spherical inclusion in the center of the medium, and (c) medium consisting of three layers.

Fig. 7.

(Color online) Neumann-series and MC transmittance outputs in a midscattering heterogeneous medium with (a) three different tissue types scattered randomly, (b) a high-absorption spherical inclusion at the center of the medium, (c) a very-low-scattering inclusion at the center of the medium, and (d) layered medium.

In the next experiment, we place a high-absorption spherical inclusion (${\mu }_s^{\prime }=4{\text{cm}}^{-1}$, μ_a = 1 cm⁻¹) of diameter 0.67 cm at the center of an otherwise homogeneous isotropic medium with ${\mu }_{\mathrm{s}}^{\prime }=4{\text{cm}}^{-1}$ and μ_a = 0.01 cm⁻¹, as shown in Fig. 6(b). As we observe from the output shown in Fig. 7(b), the Neumann-series output matches well with the MC output. To study the performance of the Neumann-series approach when a very-low-scattering inclusion is present in the medium, we consider a low-scattering spherical inclusion with diameter 0.67 cm and optical properties of ${\mu }_{\mathrm{s}}^{\prime }=0.1{\text{cm}}^{-1}$, μ_a = 0.001 cm⁻¹, and g = 0, placed in an isotropic medium with ${\mu }_{\mathrm{s}}^{\prime }=4{\text{cm}}^{-1}$ and μ_a = 0.01 cm⁻¹. The geometry of the scattering medium is shown in Fig. 6(b). The reduced-scattering and absorption coefficients of the low-scattering region mimic the cerebro-spinal-fluid [24]. We find that the Neumann-series results match with the MC results, as shown in Fig. 7(c).

Finally, we consider a layered phantom model as shown in Fig. 6(c), where each of the layers has different optical properties. The three layers have thicknesses of 2.5, 2.5, and 5 mm, respectively. The reduced-scattering and absorption coefficients, (${\mu }_{\mathrm{s}}^{\prime }$, μ_a), of the media in the three layers from top to bottom are (2 cm⁻¹, 0.001 cm⁻¹), (3 cm⁻¹, 0.001 cm⁻¹), and (4 cm⁻¹, 0.01 cm⁻¹), respectively. The Neumann-series and MC results match well for this layered phantom, as shown in Fig. 7(d).

A similar set of experiments is repeated with a low-scattering heterogeneous medium of size 2 × 2 × 2 cm³. The first experiment has three different isotropic tissue types scattered randomly [Fig. 6(a)], with reduced-scattering and absorption coefficients (${\mu }_{\mathrm{s}}^{\prime }$, μ_a) equal to (1 cm⁻¹, 0.01 cm⁻¹), (1 cm⁻¹, 1 cm⁻¹), and (0.5 cm⁻¹, 0.01 cm⁻¹), respectively. The second experiment is with a phantom consisting of a high-absorption spherical inclusion (${\mu }_{\mathrm{s}}^{\prime }=1{\text{cm}}^{-1}$, μ_a = 1 cm⁻¹, g = 0) of diameter 0.67 cm placed at the center of a homogeneous isotropic medium with ${\mu }_{\mathrm{s}}^{\prime }=1{\text{cm}}^{-1}$ and μ_a = 0.01 cm⁻¹ (Fig. 6(b)]. In the third experiment, we have a isotropic medium with ${\mu }_{\mathrm{s}}^{\prime }=1{\text{cm}}^{-1}$, μ_a = 0.01 cm⁻¹, that has a 0.67 cm diameter low-scattering spherical inclusion at the center, as shown in Fig. 6(b). The optical properties of the low-scattering inclusion are ${\mu }_{\mathrm{s}}^{\prime }=0.1{\text{cm}}^{-1}$, μ_a = 0.001 cm⁻¹, and g = 0. The fourth experiment is with an isotropic medium consisting of three layers [Fig. 6(c)] of thickness 5, 5, and 10 mm, respectively, and the reduced-scattering and absorption coefficients (${\mu }_{\mathrm{s}}^{\prime }$, μ_a) equal to (1 cm⁻¹, 0.01 cm⁻¹), (0.5 cm⁻¹, 0.1 cm⁻¹), and (0.5cm⁻¹, 0.01cm⁻¹), respectively. The results for these four types of low-scattering heterogeneous media are shown in Figs. 8(a)–8(d). We see that in all the cases, the Neumann-series output is in agreement with the MC output.

Fig. 8.

(Color online) The Neumann-series and MC transmittance outputs in a low-scattering heterogeneous medium with (a) three different tissue types scattered randomly, (b) a high-absorption spherical inclusion at the center of the medium, (c) a very-low-scattering inclusion at the center of the medium, and (d) layered medium.

C. Computational Requirements

In this subsection, we first show the speedup obtained with the GPU-based implementation of the code. As mentioned earlier, the CPU-version of the code is executed on an Intel quad core E5520 2.65 GHz processor, which has four cores and eight threads, so the execution on this system is not really single-threaded. To evaluate the timing improvements, we perform multiple experiments, in which we vary the number of voxels in the medium, the scattering and absorption coefficients, and the number of spherical harmonics. The results are shown in Table 1; in the second and third columns, we show the time required by the CPU and GPU implementations for a single execution of the attenuation kernel. The final column shows the corresponding speedup obtained with the GPU implementation. In the table, nVox denotes the number of voxels in the phantom. We find that even in simple cases, there is up to two orders of speed improvement when using the GPU as compared to a state-of-the-art but non-GPU hardware.

Table 1.

Speedup with GPU Implementation

Configuration	CPU (in sec)	GPU (in sec)	Speedup
nVox = 203, L = 0	50	1.3	45X
nVox = 203, L = 1	237	3.3	72X
nVox = 203, L = 2	674	7.2	94X
nVox = 203, L = 3	1578	14.2	111X
nVox = 403, L = 0	5614	35.4	159X
nVox = 403, L = 1	22764	134.2	170X

The GPU implementation leads to good computational efficiency for the code. For example, all the simulations executed for the low-scattering isotropic medium in Subsections 4.A and 4.B require less than a minute. However, the computation time increases significantly for medium and high-scattering media, since such media require a higher number of voxels for accurate discretization, and the execution of a larger number of Neumann-series terms. Also, the computation time increases significantly as the number of spherical harmonic coefficients required to represent the distribution function increases. Theoretically, the timing requirements increase almost linearly with the value of (L + 1)². For anisotropic-scattering media (g ≠ 0), the number of spherical harmonics required to represent the distribution function accurately is high. Therefore, for such media, the computational time required will be considerably higher.

5. DISCUSSION AND CONCLUSIONS

In this paper, we have presented the mathematical methods and the software to implement the integral form of the RTE for modeling light propagation in nonuniform media for a diffuse-optical-imaging setup. Using the Neumann-series approach, the RTE is solved for a completely heterogeneous 3D media. The method is parallelizable and, with the implementation on the GPU, the computational efficiency of the method is also very good, and up to 2 orders of magnitude higher than a non-GPU implementation. As part of this software, we have also implemented the Siddon’s algorithm on the GPU. We demonstrate the accuracy of the Neumann-series method in simulating light propagation in small-geometry heterogeneous phantoms with different kinds of models.

We observe that the Neumann-series RTE algorithm simulates photon propagation accurately in scenarios where the diffusion approximation is inaccurate. For example, it can handle pencil-beam-like sources as the emission source, unlike the diffusion approximation [63,64]. Also, the Neumann-series approach can simulate photon propagation accurately when the absorption coefficient is close to the scattering coefficient. The Neumann-series method works well in these scenarios since it handles the effect due to the absorption event accurately. This is possible due to the mathematical formalism of the Neumann series, and our implementation procedure, where we evaluate the effect of the 𝒳Ξ term separately and in the normal (r, ŝ) basis instead of the spherical harmonic basis. We also see that the Neumann-series method can simulate photon propagation even when the scattering and absorption coefficients are extremely small, which is true in voidlike spaces such as ventricles and the subarachnoid space. Our method can also simulate light propagation through optically thin regions, which can be useful in many studies [65,67]. We also show that the Neumann-series approach can simulate light propagation in thin layered media, where the diffusion approximation is not applicable [68]. Therefore, there are many advantages to the Neumann-series implementation as compared to the diffusion approximation.

While the Neumann-series method is completely general and can be used to model light propagation in any media, it is computationally very intensive for optically thick media. We have observed that the Neumann-series approach is practical to use for media that have the product of their scattering coefficient and length, i.e., μ_sH less than 4. However, for media with greater optical thickness, increase in computational capacity will lead to the method being more practical. In contrast, the diffusion-approximation is very effective for optically thick media. Thus, the Neumann-series method can be used to complement the diffusion-approximation-based methods in many cases. The usage of the Neumann-series method for modeling light propagation through optically thin media such as skin, and in imaging techniques like window chamber imaging [69], can also be explored. Also, with the increase in computing technology, the Neumann-series approach can be implemented in lesser time in future. NVIDIA plans to release the Maxwell generation of GPU architecture in 2013, which is predicted to perform about 16 times faster than the current GPU architectures [70]. Similarly, there are significant advances occurring in the fields of multiprocessor, multicore, and cluster computing [71,72], all of which will lead to higher computational capacity. A single-equation framework to simulate light propagation can be advantageous when the computational power increases.

In the proposed Neumann-series implementation, we have two variable simulation parameters, namely the number of spherical harmonic coefficients, and the number of voxels used to discretize the medium. To determine an appropriate value for these parameters, we execute the Neumann-series algorithm with increasing values for these parameters. We have verified the convergence of the Neumann-series approach to the correct solution as the value of these parameters is increased, in our uniform-media paper [44]. Therefore, the value at which the output of the Neumann-series approach converges approximately gives us a good value for these simulation parameters. We have also added another feature in our software that can help determine suitable values for these parameters. This feature computes the number of photons that are output from all the faces of the medium. For a non-absorbing medium, by the principle of photon conversation, the number of photons that enter and exit the medium should be equal. Let us consider a medium that has its scattering coefficient much greater than the absorption coefficient. For this medium, we execute the Neumann-series simulations with the absorption coefficient set to zero and find out those values of spherical harmonic coefficients and the number of voxels at which the number of output photons is approximately equal to the number of input photons. The values thus determined give us an approximate number for the two simulation parameters for this media. Since scattering is often the dominant photon-interaction mechanism at optical wavelengths, this feature can be used in many scenarios.

We would also like to discuss the performance of the Neumann-series method with MC-based methods for simulating photon propagation. We find that for low-scattering media, the times required by the GPU implementation of the Neumann-series method and CPU-based MC simulation are similar. However, for high-scattering media, the time required by the CPU-based MC method is smaller. Based on these comparisons, we believe that the GPU-based MC method would outperform the Neumann-series method in terms of computational time requirements. However, the MC method is a stochastic approach to model photon simulation, which can lead to uncertainty in the computed output. The Neumann-series method is an analytic deterministic approach, and thus the output computed using this method is exact and does not suffer from issues due to randomness. The Neumann-series method can have errors due to finite discretization, but these errors can be reduced by increasing the number of voxels or the number of spherical harmonics.

Another advantage of the Neumann-series method compared to the MC method is with regard to the reconstruction task in DOT. As we mentioned earlier, the forward modeling of photon propagation in DOT is mainly required to perform the reconstruction task, i.e., to determine the optical properties of the tissue. The image reconstruction approaches are often based on some kind of gradient-descent mechanism, where the gradient of some distance measure between the experimentally determined output image and the simulated output with respect to the optical properties of the medium are evaluated [4]. The value of this gradient is then used to update the optical properties of the medium. Therefore, it is essential in these gradient-descent schemes that the gradient be computed accurately. In a MC-based scheme, this gradient can be computed only as a numerical approximation; i.e., we evaluate the output image at two nearby values of the optical properties of the tissue, compute the distance between these output images, and divide it by the difference between the optical properties of the tissue. The computed gradient can also be erroneous due to the uncertainty in the output obtained using MC-based schemes. In contrast, the Neumann-series approach, due to its analytic nature, provides us with an avenue to evaluate the gradient analytically. We are currently investigating in this direction and plan to discuss such an approach in a future publication. Thus, there are some advantages of the Neumann-series method as compared to the MC-based method, in spite of the high computational requirements of the former.

We would like to highlight that in the Neumann-series RTE formulation, the number of terms in the series is equal to the number of scattering events. Therefore, our method can be used to separate the measured output light in an experiment into components with a different number of scattering events, as has previously been attempted [73,74]. Also, using the Neumann-series method, we can separate the scattered light from the measured light distribution in a DOT imaging system. This information can be used to design reconstruction algorithms to obtain optical properties of the media. Another important application for the Neumann-series method is in the field of computer graphics, where the suggested software can be used either for rendering or to estimate the scattering properties of the media [67].

A limitation of the suggested method is the zero-reflection boundary conditions. While this condition can be partially met in some experimental setups with highly absorptive boundaries, in a tissue, it is unlikely that no reflection will occur at the surfaces. Based on our initial studies, incorporating the boundary conditions will require a fundamental change in the Neumann-series form of the RTE and we are currently investigating this. Another improvement in the suggested approach is to use block structured grids that are adaptively discretized, similar to the approach suggested by Montejo et al. [29]. This can also improve the computational efficiency of the method.

To summarize, we have developed a software to propagate light propagation through completely nonuniform 3D media using the Neumann-series form of the RTE. The method is completely general and gives very accurate results in cases where the diffusion approximation breaks down, but is computationally intensive for optically thick media. With further mathematical and algorithmic research in optimizing the Neumann-series algorithm and with the advances in parallel computing hardware, we believe that the Neumann-series approach can produce accurate results for many types of media in reasonable times. With the advances in technology, an interdisciplinary research in this field by scientists in the fields of physics, mathematics, computer science, and medicine can lead to important advances and has exciting prospects.