Mathematical Models Light Up Plant Signaling

Abstract

Plants respond to changes in the environment by triggering a suite of regulatory networks that control and synchronize molecular signaling in different tissues, organs, and the whole plant. Molecular studies through genetic and environmental perturbations, particularly in the model plant Arabidopsis thaliana, have revealed many of the mechanisms by which these responses are actuated. In recent years, mathematical modeling has become a complementary tool to the experimental approach that has furthered our understanding of biological mechanisms. In this review, we present modeling examples encompassing a range of different biological processes, in particular those regulated by light. Current issues and future directions in the modeling of plant systems are discussed.

INTRODUCTION

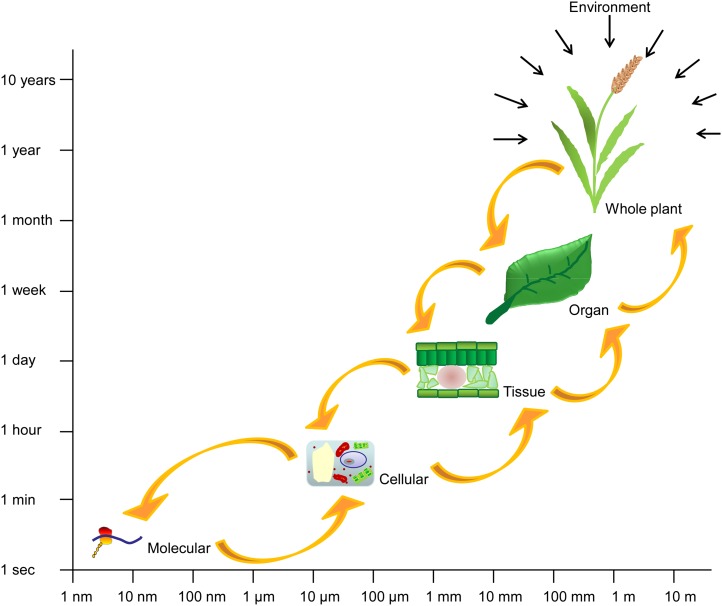
In the last decade, our understanding of plant systems from the molecular level to the whole-plant level has increased significantly with the development of new analytical tools in conjunction with advanced high-throughput experimental techniques. To facilitate predictive biology and crop improvement, there is not just a need to fully understand physiology at the molecular, cellular, tissue, and whole-plant levels, but also the cross-level interactions (Figure 1). This can be achieved using systems biology approaches that attempt to understand the behavior and functional relationships between multiple elements in the whole system or organism (Baldazzi et al., 2012; Band et al., 2012; Mitra et al., 2013). The emergence of bioinformatics has facilitated the analysis of complicated networks, helping to identify novel components and biological pathways, especially as the vast quantity of experimental data being generated is difficult or impossible to handle manually. Mathematical modeling of these pathways in turn drives new hypotheses and experimental designs, thus improving our understanding of biochemical processes in planta (Kitano, 2002b; Di Ventura et al., 2006). In the context of computational systems biology, modeling can be used to identify connections between elements in a network and to predict the spatio-temporal dynamics of a system through simulations of model variables (Kitano, 2002a). In this review, we discuss how mathematical modeling of plant systems, particularly those regulated by external cues such as light, has helped further our understanding of the molecular network structure and their functional mechanisms.

Figure 1.

Plant Systems Span a Wide Range of Spatio-Temporal Scales.

To cope with a constantly changing environment, plants respond to external factors by triggering and synchronizing a series of activities at different levels of organization that interact with one another.

We focus mainly on simulation-based modeling of dynamical systems that are fundamentally time dependent. Simulation-based models have been developed to represent events occurring at a wide range of biological levels, from molecular regulation up to cell growth, tissue patterning, and plant development. The mathematics employed in these models is very diverse; ordinary differential equations (ODEs) are commonly used to represent changes with regards to time, but other variants or a combination of methodologies is sometimes necessary when considering compartmentalization, pattern of distribution, and organ shapes (Coen et al., 2004). As a result, most models do not strictly fall into a particular category. However, models are usually constructed with the aim of answering specific biological questions, and the models in this review are grouped accordingly. Using specific case studies, we highlight how modeling has facilitated the investigation of several phenomena in plant systems, with an emphasis on light signaling and responses to the environment. The models reviewed here can be classified in three groups, depending on the nature of the biological question, including (1) models probing molecular mechanisms. In this section, we further divide the case studies into two subcategories: (a) oscillating systems in which the relevant variables continuously change with time in repeated cycles. Examples used here include the circadian clock system that oscillates in a daily cycle of 24 h and the clock-regulated photoperiod pathway; and (b) nonoscillating systems wherein variables eventually settle into time-independent constant values (steady state). In this case, it may be of interest simply to obtain steady state values or to determine the full-time evolution of the variables to the steady state, depending on the application at hand. Here, a mathematical model of phytochrome signaling is presented. (2) Models investigating cellular growth, tissue patterning, and organ development include examples examining the orientation of dividing cells within a growing tissue or organ, which is fundamental to developmental biology. (3) Models focusing on growth and developmental events at the organismal level form the third category, where we present a phenology model that studies the effects of photoperiod and temperature on flowering time.

In this review, we also highlight various aspects that are essential for model construction, including current modeling trends and limitations. Finally, we offer some perspectives on future developments in the modeling of plant systems.

MODELS PROBING MOLECULAR MECHANISMS

Oscillating Systems

The Circadian Clock: A Sensor of Time

The circadian clock is an oscillating system that consists of interlinked feedback loops (Rand et al., 2004; Akman et al., 2010; Pokhilko et al., 2012) and feed-forward network motifs (Mangan and Alon, 2003). Due to its complexity, mathematical modeling has been a convenient way of elucidating the key structures or network motifs that give rise to observed clock-regulated phenomena. Here, we discuss how mathematical modeling of the plant circadian clock has helped to further our understanding of the underlying molecular mechanisms through which plant development is regulated by the external environment.

Circadian clocks are biological timing mechanisms that entrain internal biochemical processes to daily cycles (reviewed in Dunlap, 1999). An entrained circadian clock controls plant responses, for example, leaf movement, such that they maintain 24-h rhythms in the absence of external cues like dawn and dusk (Millar et al., 1995). The duration of a cycle in constant conditions is referred to as the free-running period (i.e., wild-type circadian rhythms have a period of ∼24 h). It has been shown that the circadian clock maintains a 24-h period over a range of light qualities, light intensities, and temperatures (Somers et al., 1998; Devlin and Kay, 2000; Gould et al., 2006; Gould et al., 2013). Hence, the clock correctly times plant functions despite fluctuations in the external environment.

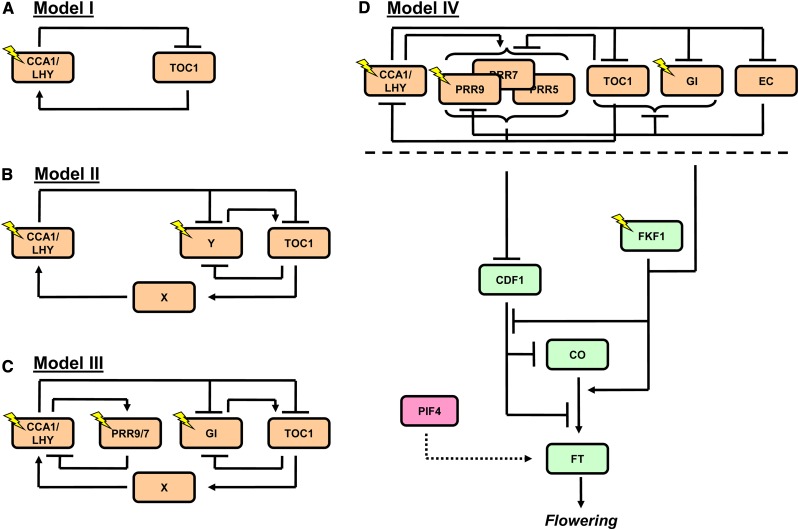
To elucidate the circadian clock mechanism, initial studies identified genetic mutations that alter the free-running period of the clock. These screens found that TIMING OF CAB EXPRESSION1/PSEUDO-RESPONSE REGULATOR1 (TOC1/PRR1) and CIRCADIAN CLOCK ASSOCIATED1 (CCA1) are key components of the circadian clock (Millar et al., 1995; Wang and Tobin, 1998). In a first approximation of the plant clock system, CCA1, with its homolog LATE ELONGATED HYPOCOTYL (LHY), was postulated to repress transcription of TOC1, with TOC1 in turn activating CCA1/LHY transcription (see Model I, Figure 2A; Alabadí et al., 2001; Locke et al., 2005). Using transcript profiles of the clock components and period phenotypes obtained from wild-type and transgenic plants grown in different light:dark (diurnal) cycles, Locke et al. (2005) constructed a deterministic ODE model of the simple CCA1/LHY-TOC1 feedback loop and tested whether this minimal circuit could accurately reproduce observed clock behaviors. While this simple CCA1/LHY-TOC1 system was an effective oscillator, it was unable to describe how transcriptional rhythms alter in different photoperiods. Model analysis predicted that two further components were required to deliver the requisite behavior: “X,” postulated to mediate TOC1 (PRR1) activation of CCA1/LHY transcription; and “Y,” to allow the clock to respond to light in the absence of CCA1/LHY (see Model II, Figure 2B; Locke et al., 2005). Indeed, with the inclusion of these components, the model was then able to describe mRNA rhythms across a range of photoperiods. The similarity between simulated expression rhythms and data identified GIGANTEA (GI) as a candidate for Y (Locke et al., 2005), a prediction that was later validated experimentally (Locke et al., 2005, 2006). Further model developments included the incorporation of other members of the PRR family (in addition to TOC1). These PRRs were shown to negatively regulate CCA1/LHY transcription, forming a feedback loop as PRR9 and PRR7 mRNA are activated by CCA1/LHY (see Model III, Figure 2C; Farré et al., 2005; Locke et al., 2006; Nakamichi et al., 2012). By including this new feedback loop, the model was able to describe the short period rhythms of CCA1 and LHY transcription caused by TOC1 and GI mutations and the long period phenotypes in prr9;7 loss-of-function mutants (Locke et al., 2006; Zeilinger et al., 2006).

Figure 2.

Mathematical Models Describing the Circadian Clock and the Photoperiod Pathway in Arabidopsis.

The CCA1/LHY-TOC1 feedback loop (Model I) was extended to include a delay between TOC1 and CCA1/LHY mRNA (X) and a light input independent of CCA1/LHY (Y) (Model II). Y was identified to be GI (Model III) and X as the EC (Model IV). The circadian clock model has also been extended to include the photoperiod pathway, which described the dual roles of CDF1 and FKF1 in regulating CO and FT mRNA (Model IV). PIF4 regulates FT mRNA in a temperature-dependent manner (red); this is not considered in the mathematical model (dotted lines). Orange, circadian clock; green, photoperiod pathway.

Recent studies have elucidated the role of EARLY FLOWERING3 (ELF3), ELF4, and LUX ARRHYTHMO (LUX) in the circadian clock (Nusinow et al., 2011). ELF3 localization to nuclear bodies is enhanced through interactions with ELF4, where it interacts with the DNA binding protein LUX (Nusinow et al., 2011; Herrero et al., 2012). The ELF4-ELF3-LUX complex (hereafter referred to as the evening complex [EC]) represses transcription of target genes, such as PRR9 (Dixon et al., 2011; Helfer et al., 2011; Nusinow et al., 2011). Conversely, transcriptional rhythms of the EC are altered in cca1 lhy loss-of-function double mutants (Dixon et al., 2011). Thus, the EC forms part of the clock mechanism. An extended clock model included the role of the EC in place of X, producing the correct delay between TOC1 and CCA1/LHY transcription in different diurnal cycles (see Model IV, Figure 2D; Pokhilko et al., 2012).

Analysis of the Pokhilko 2012 model led to a new understanding of clock circuitry. While this model was able to describe a wide range of clock properties, it could not explain why rhythms of CCA1 and LHY transcription are dampened in both toc1 loss-of-function and TOC1 overexpressing (TOC1-ox) mutants (Alabadí et al., 2001; Gendron et al., 2012). In clock Models I to III (Figure 2), TOC1 acts solely as a repressor of CCA1/LHY transcription; however, evaluation of the Pokhilko 2012 model suggested that TOC1 acts as both an activator and an inhibitor of CCA1/LHY transcription. This proposal was supported by the observation that TOC1 was shown to inhibit the transcription of other PRR genes, which in turn repress CCA1/LHY expression (Huang et al., 2012). Including the TOC1 inhibition of multiple clock components enabled the next iteration of the clock model to generate similar CCA1/LHY rhythms in both toc1 and TOC1-ox simulations (see Model IV, Figure 2D; Pokhilko et al., 2013). Hence, CCA1/LHY regulation is balanced by TOC1 repression and indirect activation resulting from the repression of PRR genes by TOC1 (Pokhilko et al., 2013).

The examples above have shown how mathematical modeling has been a useful tool in elucidating the complex network of the plant circadian clock. The most recent model illustrates that, at its heart, the clock comprises a three-component repressilator system (Pokhilko et al., 2012). In this simplified network architecture, CCA1/LHY inhibits the accumulation of the EC that prevents transcription of the PRR components, which in turn inhibit transcription of CCA1/LHY throughout the day. Thus, by defining molecular pathways mathematically, complex biological systems can be simplified into their key components or network motifs. As more becomes known about new and existing core clock components (reviewed in Nagel and Kay, 2012), it will be important to determine the role of these components in the circadian system. New questions will also arise aimed at understanding the molecular mechanisms that mediate external signals to the clock. For example, removing light-signaling pathways by perturbing phytochrome B (phyB) leads to long period phenotypes (Devlin and Kay, 2000; Somers et al., 1998). Recently, Gould et al. (2013) analyzed mathematical models of the circadian clock to determine how temperature and blue light regulate the clock mechanism. The results showed that both temperature and blue light alter the levels of LHY protein, and this hypothesis was validated experimentally. The challenge of future circadian clock models is to understand how other signals from the external environment interact with the endogenous clock system and whether this requires the addition of new components, such as TIME FOR COFFEE, TOPLESS, REVEILLEs, and/or NIGHT LIGHT-INDUCIBLE AND CLOCK-REGULATEDs that have been found experimentally to form part of the circadian clock (Hall et al., 2003; Hsu et al., 2013; Rugnone et al., 2013; Wang et al., 2013).

The Photoperiod Pathway

The circadian clock regulates many genes that play important roles in plant growth and development (Harmer et al., 2000). Examples of circadian-regulated processes that affect plant growth include hypocotyl elongation, opening of stomata, cold acclimation, photosynthetic rate, hormone signaling, and starch turnover (Dodd et al., 2005; Harmer et al., 2000; Nozue et al., 2007; Legnaioli et al., 2009; Graf et al., 2010; Dong et al., 2011; Nomoto et al., 2012; Keily et al., 2013). Here, we look at how the circadian clock enables plants to perceive daylength, such that they flower and reproduce in favorable seasonal conditions.

In many species, flowering is strongly influenced by the duration of light (photoperiod) in a diurnal cycle. For example, the model plant Arabidopsis thaliana is a long-day (LD) plant as it flowers earlier when grown in longer photoperiods (Corbesier et al., 1996). The acceleration of flowering in long photoperiods correlates with elevated expression of FLOWERING LOCUS T (FT) mRNA (Corbesier et al., 2007). Under these conditions, the increase in FT mRNA correlates with the abundance of CONSTANS (CO) protein since it activates FT transcription (Suárez-López et al., 2001; Imaizumi et al., 2003). Transcription of CO is under the control of the circadian oscillator (Suárez-López et al., 2001; Yanovsky and Kay, 2002). Our existing knowledge of the clock, combined with the availability of highly reproducible quantitative data, allowed the development of mathematical models that aided our understanding of photoperiodic flowering (Salazar et al., 2009; Song et al., 2012).

In LDs, the rhythm of CO mRNA peaks at the end of the photoperiod, leading to a correlating accumulation of FT mRNA that is not seen in short days (SDs) (Imaizumi et al., 2003). The circadian clock regulates this peak in CO transcription indirectly through GI-dependent degradation of CYCLING DOF FACTOR (CDF) proteins that suppress CO expression (Imaizumi et al., 2005; Sawa et al., 2007; Fornara et al., 2009). GI forms a blue light–dependent protein complex with FLAVIN BINDING, KELCH REPEAT, F-BOX1 (FKF1) that colocalizes with CDF1 on the CO promoter, leading to CDF1 degradation (Imaizumi et al., 2005; Sawa et al., 2007). Hence, in fkf1 mutants, the first peak of CO mRNA is diminished due to increased levels of CDF1 (Imaizumi et al., 2005). Using a similar methodology to that used in representing the circadian clock system, a deterministic ODE model of the photoperiod pathway has supported biological observations that CO protein is not the only regulator of FT transcription (Sawa et al., 2007; Salazar et al., 2009; Song et al., 2012). An initial model of the photoperiod pathway accurately described rhythms of CO mRNA in fkf1 mutants (Salazar et al., 2009). However, the simulations produced too much FT mRNA compared with experimental data. This suggested that FKF1 plays two roles in the system (i.e., besides regulating CO mRNA, it also regulates FT mRNA in a feed-forward loop) (Salazar et al., 2009). This hypothesis was later validated experimentally, showing FKF1 also stabilizes CO protein that in turn activates FT mRNA (Song et al., 2012). However, FKF1 is not the only component to have two roles in the system; both CDF1 and GI also regulate FT transcription (Sawa et al., 2007; Song et al., 2012). By updating the Salazar 2009 model to include the feed-forward network, a range of CDF1-, FKF1-, and CO-related genetic mutations could then be described (Figure 2D; Song et al., 2012). In addition, simulations using the updated model showed that FKF1-regulated stability of CO protein has a larger effect on FT mRNA levels than FKF1-mediated degradation of CDF1 (Song et al., 2012). There is also a direct regulation by the clock of CDF1 and FKF1 transcription (Nakamichi et al., 2007; Niwa et al., 2007). Current evidence suggests that the transcription of CDF1 is controlled by the PRR proteins, while FKF1 mRNA rhythms closely match those of GI (Nakamichi et al., 2007, 2012; Niwa et al., 2007); these are not included in the Song 2012 model. Future models must be extended to include CDF1 and FKF1 regulation to provide a fuller understanding of how the circadian clock regulates photoperiodic flowering.

Besides photoperiod, temperature is another environmental factor that regulates flowering in A. thaliana. Recently, Kumar et al. (2012) investigated temperature regulation of flowering through transcriptional activation of FT. In this study, PHYTOCHROME INTERACTING FACTOR4 (PIF4) was found to activate transcription of FT across the warm temperature range due to altered chromatin dynamics (Figure 2D). At 22°C, H2A.Z nucleosomes prevent the binding of PIF4 to the FT promoter preventing transcriptional activation. However, at 27°C, H2A.Z is absent from the FT promoter, allowing PIF4 to bind and activate transcription, accelerating flowering in warm temperatures (Kumar et al., 2012). Interestingly, this phenomenon has been proposed to occur independently of CO activation of FT since these results were obtained from experiments conducted in SDs (Balasubramanian et al., 2006; Kumar et al., 2012). This observation provides a useful hypothesis that can be further explored both in silico and experimentally. By analyzing how temperature regulates flowering in LD conditions, it may be possible to determine how the temperature and photoperiodic regulation of FT transcription, and flowering, are integrated. This would result in a model that can explain thermo-photoperiodic flowering across a wide range of environmental conditions.

In general, mathematical models that describe dynamic molecular processes can be used to help understand what is observed experimentally (e.g., by correlating gene expression with observable phenotypes) and to further enhance our understanding of the molecular mechanisms in many biological systems. Here, in the example of the photoperiodic response, we used the circadian clock model as a module in a larger system of the flowering pathway. A recent study has linked simulated FT expression level to flowering time in Arabidopsis halleri, a perennial relative of A. thaliana (Satake et al., 2013). Thus, there is potential in connecting molecular models to phenology or flowering models, which are presented in a later section.

A Nonoscillating System: Phytochrome Activation by Red Light

In this section, we consider a case study that examines the molecular processes involved in red light activation of the phytochrome photoreceptor (Rausenberger et al., 2010). A novel aspect of this study was the multiscale approach that linked photoreceptor protein dynamics (a molecular level description) to hypocotyl length (a common macroscopic physiological measurement in light-signaling studies). In general, given the large range of spatio-temporal scales in plant systems (Figure 1), it is common to partition them into fast (lower level of organization) and slow (higher level) subsystems. The fast subsystem is characterized by timescales that are much shorter than the slow subsystem; hence, the former is approximately in steady state. In this case, the concentration of each component in the fast subsystem can be modeled as constant over time (i.e., the change in amount is assumed negligible). On the other hand, the slower subsystem continues to change with time. In this case study, the red light–signaling pathway is modeled as a fast subsystem, and hypocotyl elongation is considered to occur at a slower timescale (Rausenberger et al., 2010).

Plants can sense and react to both the quality (emitted colors) and intensity of light. The shade avoidance syndrome is a notable example of the response to light quality. Here, a group of specialized phytochrome photoreceptors detect alterations in the ratio of far-red to red light in vegetation-rich habitats (Keller et al., 2011). In A. thaliana, there are five red and far-red light-sensing phytochrome A (phyA) to phyE (Mathews and Sharrock, 1997). Phytochromes photoconvert between an inactive red light–absorbing state, Pr, and an active far-red-light–absorbing state, Pfr (Chen et al., 2004). The relative amount of active P_fr is therefore directly influenced by the proportion of red:far-red light, which in turn reflects the proximity of neighboring plants (Li et al., 2011). In A. thaliana, phyB is a principal regulator of light-induced hypocotyl inhibition, a well-studied response that is fluence rate dependent. When grown in the dark A. thaliana seedlings have very long hypocotyls, as under these conditions phyB is usually inactive. The introduction of light at increasing intensities leads to elevated levels of active phyB and an incremental inhibition of hypocotyl elongation. A review of phytochrome behavior can be found in Franklin and Quail (2010).

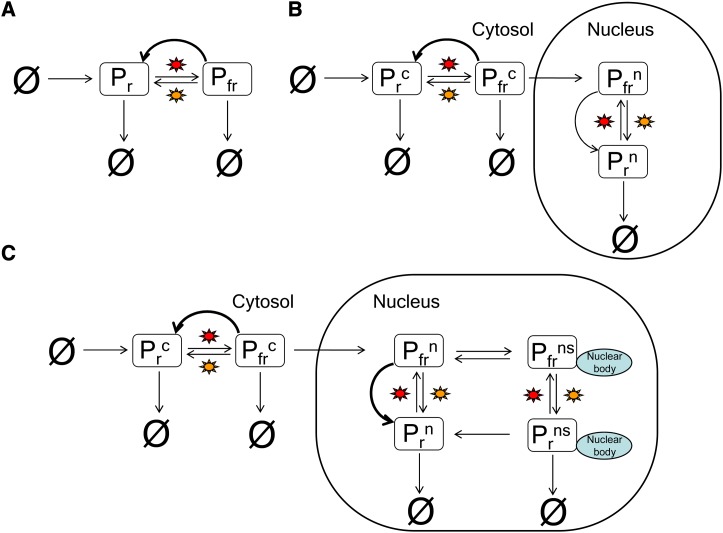
The idea of a reversible photoreaction was first postulated by Borthwick et al. (1952), and since then there have been numerous attempts to understand the phytochrome signaling mechanism. In the simplest realistic representation of the red light–signaling pathway, phyB is formed in the cytosol in its inactive Pr state, and upon activation by red light, it is photoconverted into the active Pfr state; far-red light photoconverts Pfr back into Pr (Figure 3A). The conversion from active to inactive phyB can also occur through a light-independent process known as dark reversion (thick black arrow in Figure 3A) (Linschitz and Kasche, 1966).

Figure 3.

Models Describing the phyB Signaling Mechanism.

(A) and (B) The basic model for the photoconversion of phyB (A), which was extended to a compartmental model (B).

(C) The model was later extended to include the formation and degradation of nuclear bodies. Red and far-red-light–dependent reactions are indicated by a red star and an orange star, respectively. Thick black arrows represent dark reversion.

A further evolution of the basic postulation was the separation of phyB into cytosolic and nuclear pools (i.e., P_fr^c and P_frⁿ where the superscripts “c” and “n” refer to the cytosol and nuclear, respectively); this is because phyB is formed in the cytosol, and once in its active form, it is translocated into the nucleus (Figure 3B; Yamaguchi et al., 1999). Within the nucleus, phyB forms two types of phytochrome nuclear bodies: transient phytochrome nuclear bodies, which occur within minutes of changes in light quality, and longer lasting photostable phyB-containing nuclear bodies (Chen, 2008). A compartmental model is therefore required to more accurately represent signaling from phyB. Based on these observations, a multiscale compartmental mathematical model of the phyB pathway was constructed, linking molecular events to hypocotyl elongation (Figure 3C; Rausenberger et al., 2010). This model was written as a system of deterministic ODEs, with each equation representing the change in concentration of one molecular player in the model (e.g., nuclear Pfr) over time. It also included one additional equation linking the amount of active phytochrome to the hypocotyl growth rate. An implicit assumption in the use of such models is that each of the molecular players is distributed uniformly within the compartments modeled (i.e., the cytosol and the nucleus) (Grima and Schnell, 2008). The model was solved in steady state conditions since the measurements of hypocotyl length were obtained when the phyB system had attained a steady state level (Rausenberger et al., 2010). Solution of the model then explicitly reveals how the levels of all the components are related to one another and allows one to deduce precisely how hypocotyl elongation is related to light intensity.

The kinetic parameters in the Rausenberger 2010 model were estimated by fitting it to multiple data sets of phyB levels and hypocotyl length. This method proved effective as the model provides a quantitatively accurate prediction of how the hypocotyl length depends on the total amount of phyB and, thus, on the red light intensity. Although this is a basic photobiological observation, nevertheless the power of the modeling approach is that (1) it can recapitulate this from a molecular level model and (2) it allows easy manipulation of individual parameters to investigate the sensitivity of the hypocotyl growth rate to the various biochemical processes orchestrating the fluence response. In particular, Rausenberger et al. (2010) found that changing the rates of formation and degradation of Pfr nuclear bodies have a significant effect on the growth rate, indicating the importance these entities have on phyB signaling. The simulation-based analysis also showed that, in order to recreate the classic fluence response curve, an additional inactivation of active phyB is needed, either through dark reversion and/or the formation of nuclear bodies. These results are difficult to infer from a purely experimental approach, which indeed points to the importance and need of systems-based approaches to further biological discovery.

One simplifying assumption of the Rausenberger 2010 model is that phyB can be directly linked to hypocotyl elongation; however, it is known that phyB does not work in isolation. To further our understanding of how suppression of hypocotyl elongation occurs in red light, it will be necessary to extend the Rausenberger 2010 model to incorporate downstream components. The transcription factor family PIFs are key regulators of phyB signaling that promote hypocotyl elongation (reviewed in Leivar and Monte, 2014). When phyB is active, an interaction with PIF proteins rapidly induces their phosphorylation and triggers their degradation; conversely, PIF induces proteolytic degradation of phyB over longer timescales (Al-Sady et al., 2008; Jang et al., 2010). The effect of this on phyB signaling, and therefore the overall hypocotyl elongation, is difficult to predict; however, we anticipate that mathematical modeling will constitute a useful tool to examine the nonintuitive effects of this mutual degradation.

Another example of a nonoscillating model is that by Rausenberger et al. (2011), which showed that the shifting of peak in the phyA action spectrum from red to far red is due to photocycling of the phyA receptor between its Pr and Pfr forms. The significance of mathematical modeling is apparent when one considers that this shifting phenomenon has been known for over half a century (Mohr, 1957), but experimental studies failed to link it to known molecular components or events.

Here, we have shown how modeling provides insights into the molecular network structures of both oscillating and nonoscillating systems. As illustrated in our case studies, these molecular pathways regulate events at higher levels, such as flowering time and hypocotyl elongation. In the next section, we look at models designed for studying tissue patterns and organ shapes.

Models Investigating Cell Growth, Tissue Patterning, and Organ Development

Plants have distinctive macroscopic features, such as leaf shape and shoot orientation. Light affects plant architecture in a number of ways. Examples include the orientation of organ growth toward or away from light in a behavior known as phototropism and the shade avoidance response to encroaching neighbor plants (see previous section on phytochrome signaling and a review by Casal, 2013). Organ development is a complex process, involving the coordination of gene expression, cell growth, and cell division across both time and space. This coordination originates at the microscopic level, within and between individual cells, and results in features such as the budding of a leaf or formation of a root tip. There has been much work in recent years in establishing the mechanistic bases of plant development at the cellular level, and the complex interactions involved in these systems have necessitated substantial use of mathematical modeling techniques. Furthermore, the modeling frameworks developed in the process are expected to be invaluable in investigating more complicated signaling, such as the direct and indirect effects of light on plant development. In this section, we discuss models of cellular and tissue development that span a range of complexity levels, from biomechanical models that do not involve molecular components, to models that incorporate complex gene regulatory networks.

Plant Development under Physical Constraints

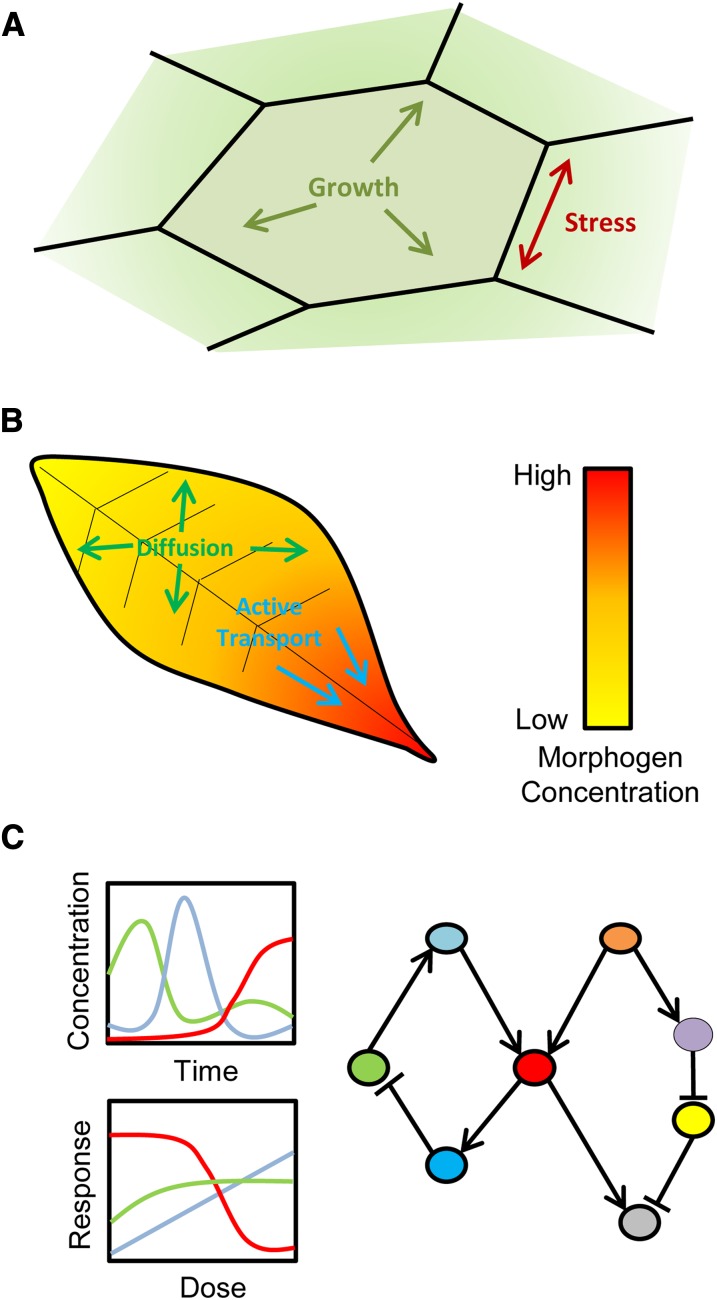
Cells in multicellular organisms are subject to a variety of physical and geometrical constraints, which have important consequences for development (Figure 4A) (Mirabet et al., 2011). Mathematical modeling of cell growth under these constraints provides a minimal framework within which hypotheses can be tested and refined. The fact that all cells are subject to the same physical laws has allowed generic modeling frameworks to be developed in this context and general theories for cell growth and division to be suggested (Besson and Dumais, 2011). This has been invaluable, as biomechanical modeling methodologies originally developed and applied to one system have been reapplied to many others. These methodologies differ widely, but a common starting point is the assumption that cell walls can be modeled as elastic membranes. Here, we present some salient examples of modeling studies in this area, and the interested reader is referred to comprehensive reviews of the field (Chickarmane et al., 2010; Mirabet et al., 2011).

Figure 4.

Modeling Plant Development and Morphology.

(A) Cell geometry, growth, expansion, and division place physical constraints on any model of plant organ morphogenesis. Models that consider only the implications of these constraints on plant growth have in some cases been able to suggest simple physical mechanisms for complex organ morphologies.

(B) Spatial distributions of morphogens (such as auxin) underlie many developmental processes. Models of active transport and diffusion of these factors allow the mechanisms of pattern formation to be investigated.

(C) Analysis of dose–response curves generated from both quantitation and model simulation are often useful in revealing the regulatory network of a system. Spatial models of gene and signaling networks allow hypotheses concerning the molecular mechanisms of morphogenesis to be investigated and potentially linked to models of other scales.

One recent modeling study of cell growth and division considered how the distribution of cell sizes in the sepal epidermis of A. thaliana is regulated by patterns of endoreduplication (Roeder et al., 2010). The sepal epidermis was chosen in this case because of its accessibility to live imaging and because the rectangular geometry of the cells makes them amenable to automated image processing. A model of cell growth and division in the epidermis was developed, under simple assumptions about the orientation of division planes and the stochasticity of cell division. This model was then integrated with a stochastic model of cell cycle switching between mitotic and endoreduplicating states, in which, at the end of each cycle, cells were assumed either to divide mitotically or to enter an endoreduplicating state. The probability of transitioning to an endoreduplicating state was determined by fitting the model to the measured distributions of cell ploidy. The resulting model was able to generate a complete sepal epidermis with the appropriate distribution of cell sizes and thus link the observed patterns of endoreduplication with the size of individual cells in this tissue, providing a simple mechanistic explanation for the complex phenotype observed. Similar techniques have been used to study the coupling of growth and division of cells in Coleocheate scutata, a freshwater green alga (Dupuy et al., 2010). This model highlighted an important role for the plane orientation of cell division in determining cell shape. In addition, biomechanical modeling has also been applied to more complex tissues, such as the shoot apical meristem. In this case, mathematical modeling of the tissue mechanics demonstrated how cell growth is modulated by mechanical forces (Hamant et al., 2008; Kierzkowski et al., 2012).

The above examples show how models that apply simple physical and geometrical rules to a growing tissue can be used to understand morphogenesis in a wide variety of cases. In cases where these factors are not the primary driving force for development, models of this type still provide a framework within which additional forms of regulation, such as gene regulatory networks, may be included. In the context of developing tissues, the molecular components responsible for growth may have distinct spatial distributions, both between different cells and within single cells. These spatial distributions may respond to physical stresses resulting from growth and, in turn, may control the direction and rate of growth. The two most commonly applied modeling methodologies in this context are compartmentalized ODEs and reaction-diffusion models. In compartmentalized ODE models, the molecular dynamics of individual cells are coupled to one another by intercellular transport. By contrast, in reaction-diffusion models, individual cells are not represented, and the tissue is treated as a single continuum in which species are free to diffuse. In this case, partial differential equations can be used to represent changes with regards to both time and space.

A framework for understanding the link between growth and tissue polarization was originally presented by Coen et al. (2004) and has been developed considerably since (Green et al., 2010; Kennaway et al., 2011). In this framework, both the orientations and rates of cell growth are regulated by spatial distributions of hypothetical factors, in what may be considered a minimalistic representation of the molecular mechanisms underlying polarized tissue growth. One example where this methodology has been applied is in determining leaf morphology of A. thaliana (Kuchen et al., 2012). Here, iteration between imaging experiments and modeling led to a model in which the direction of growth was directed by local growth orientations. This model reproduced both the overall morphology of a growing leaf and the growth orientation of individual cells. The model also correctly predicted the dynamics of recovering growth in a leaf excised of its distal tip. This demonstrated that the apparent regeneration of the distal tip is not a consequence of a growth response to the cut but is rather a consequence of continued growth in the leaf primordium.

This study was recently complemented by modeling of petal morphology in A. thaliana (Schiessl et al., 2012; Sauret-Güeto et al., 2013). Similar rules were expected to apply to petal and leaf development. Indeed, an initial model found that the basic shape of petals, with their broad distal tip, could be described by a similar mechanism to the leaf model. However, clonal analysis demonstrated that the local orientations of growth could not be described by this model. An additional polarizing component was introduced to the model that stimulated divergent orientations of growth in distal cells. Comparison of phenotypes produced by transgenic plants to simulations with reduced expression of hypothetical model components suggested that the transcription factor JAGGED (JAG) might regulate divergent growth at the distal tip. Further experiments showed that the pattern of JAG expression in the petal at different stages of growth is consistent with it playing this role in development.

Connecting Tissue/Organ Level Phenomena to Molecular Mechanisms

The above examples show how mathematical modeling has been used to understand development in cases where the molecular and genetic mechanisms are not well understood. In some cases, however, parts of the mechanism are understood, and quantitative experimental measurements are available at the molecular level, as was the case for the construction of phyB and clock models presented in earlier sections. A widely studied system in this context is auxin transport and polarity, which has been suggested to direct development in a variety of ways, including root initiation and leaf vasculature development. Auxin has been shown to move through plant tissue under directed active transport (Figure 4B). This flux is under the control of the polar distribution of auxin import and export proteins on cell membranes. For example, PIN proteins are responsible for directed auxin efflux from cells, and the pattern of PIN polarity orientation in a tissue directs the distribution of auxin in the tissue (Wisniewska et al., 2006). PIN proteins are, in turn, regulated by auxin at several levels (Geldner et al., 2001; Vieten et al., 2005). Mathematical modeling has been applied to understand the resulting feedback regulation between auxin transport and PINs across tissues, as has been well reviewed elsewhere (Garnett et al., 2010; Band et al., 2012).

Modeling of gene regulatory networks in this context can also be found in studies of tissue patterning, in which the distribution of differentiated cells in a tissue is studied (Torii, 2012). One such example is found in the leaf epidermis, where pavement cells are interspersed by distinctive organization of trichomes. The regulatory mechanisms underlying this pattern of cell differentiation have been widely studied, and mathematical modeling approaches have been used to explain the spatial arrangements of cells observed in the epidermis of wild-type plants and various mutants. For example, a basic framework has been developed considering the role of freely diffusing inhibitors of differentiation in tandem with nondiffusing activators (Digiuni et al., 2008). Similar approaches may be taken to further understand other tissue patterning processes for which some molecular mechanisms are understood, such as stomatal formation and patterning (Torii, 2012).

A number of the examples presented here have employed minimalistic models in which no explicit representation of molecular regulators was included. The success of such models in describing phenomena and guiding experiments demonstrates the utility of modeling in cases where detailed understanding of regulation is not available, but for which high-quality quantitative measurements of phenomena can still be made. Indeed, recent developments in this area have been strongly driven by improvements in imaging technology (Fernandez et al., 2010; Federici et al., 2012). Further technological improvements will bring improved quantitation and opportunities for further modeling of molecular systems underpinning spatial development of A. thaliana (Figure 4C). In particular, approaches that integrate modeling of tissue mechanics, growth, and molecular regulation promise to aid further study of these systems (Barrio et al., 2013) and contribute toward the development of whole-plant models, as discussed in the next section.

Models Focusing on Growth and Developmental Events at the Organismal Level

The models presented in the previous sections focus on events at the molecular, cellular, and tissue levels and were facilitated by the advancement in molecular and systems biology. In this section, we look at mathematical models that simulate the growth and/or developmental processes at the organismal level. This group of models has a long history and has practical applications, such as the prediction of crop growth and development. Some contemporary crop models now incorporate genetic information that improves predictive power, though no molecular mechanisms are represented explicitly. This modeling approach has also been applied to noncrop model species such as A. thaliana. Therefore, in this section, we give a brief background review of early crop models and then discuss the application of contemporary crop modeling approaches in A. thaliana studies, which have increased our understanding of plant growth and development.

Early Crop Models

The concept used in crop models dates back to the 18th century, when René Réaumur observed that developmental events such as flowering occurred once plants had experienced a cumulative daily temperature that exceeded a critical threshold (Robertson, 1968). This suggested that the speed of plant development is positively correlated with temperature, though later studies showed that above a critical temperature plant responses are impaired (Haniu et al., 1983; Summerfield et al., 1992; Dingkuhn et al., 1995). Following the discovery of photoperiodism, the effect of temperature on plant development was found to depend on daylength (Robertson, 1968). These observations led to the creation of (photo) thermal-time (also commonly known as degree-day) phenology models that are widely used in crop modeling (Weir et al., 1984; Brisson et al., 2003; Stockle et al., 2003; Dingkuhn et al., 2008). More recent thermal-time models incorporate additional factors, such as the effect of winter chilling (vernalization) (Wang and Engel, 1998; Chuine, 2000; Harrington et al., 2010).

Growth processes can also be considered in crop models, by simulating net photosynthetic production and the allocation of assimilated carbon to different organs. One of the breakthroughs that facilitated growth modeling was the Farquhar model that simulates photosynthesis in C3 plants (Farquhar et al., 1980). This model contains kinetic details of both the light-dependent electron transport and carboxylation processes, which are two rate-limiting factors determining carbon assimilation in plants. Functional-structural plant models, which stem from early plant architectural models, have more recently emerged to incorporate the effects of shoot structure on light interception and, consequently, biomass available for the growth of individual organ and the whole plant (Lindenmayer, 1968a, 1968b; Honda, 1971; Jaeger and De Reffye, 1992; Yan et al., 2004; Godin and Sinoquet, 2005; Vos et al., 2007).

Applying Contemporary Crop Modeling Approaches to A. thaliana

Advances in molecular biology have helped shape approaches to contemporary crop modeling. Information on the genetic control of plant traits is increasingly being considered in crop models. One of the earliest efforts was a gene-based crop simulation model of the dry bean Phaseolus vulgaris, which used genotype-specific parameter values to represent different cultivars (White and Hoogenboom, 1996). Some studies have also attempted to link information from quantitative trait loci analyses to model parameters to incorporate genotype-phenotype relationships into crop models (Yin et al., 2000a; Letort et al., 2008; Xu et al., 2011). By incorporating such links, statistics from the quantitative trait loci analysis can partly remove the random errors associated with model parameters, thus improving model prediction of yield differences among different inbred lines (Yin et al., 2000b, 2003). These exemplar studies demonstrated how physiological modeling and genetic mapping can be combined to resolve the genotype × environment interactions, which may aid future plant breeding efforts.

The crop models discussed above have been used mainly in either agricultural or ecosystem research. However, many knowledge-swapping efforts have recently been initiated between the applied and fundamental plant research communities. For example, several growth, architectural, and functional-structural models for A. thaliana have been developed using crop modeling techniques (Mündermann et al., 2005; Rasse and Tocquin, 2006; Christophe et al., 2008). These studies have the shared advantage of being constructed using the high amounts of data produced by studies of A. thaliana and the well-established concepts of crop modeling. This was demonstrated recently by a gene-based thermal-time model that predicted flowering time in A. thaliana (Wilczek et al., 2009). This model was able to reproduce the observed flowering phenotypes of different A. thaliana genotypes grown in various seasons and latitudes (Wilczek et al., 2009). As an LD plant, high temperatures coupled with the long photoperiod during the summer promotes early flowering in A. thaliana. As summer turns into autumn, daylength decreases and temperature lowers. Therefore, the later in the year plants germinate, the longer they take to flower. Interestingly, the model predicted the existence of a narrow window in which the timing of germination acutely affects the plant life cycle. Plants that germinate slightly later within this sensitive window may switch abruptly from the summer-annual (early flowering) to the winter-annual (late flowering) life cycle; this behavior was predicted for all the genotypes used in the study, though the window size varied with genotypes (Wilczek et al., 2009). These effects of germination timing on plant development were later confirmed with experimental data from a series of repeated field plantings. This is a good example of how experimental data are required to construct a model, and model prediction can in turn drive new hypotheses for testing in the lab and the field.

Modeling studies do not necessarily end at the model-development stage. We can also learn new information from analyzing the performance and behavior of the model itself. When the A. thaliana flowering model was first developed, it was found that model accuracy was higher when only day temperatures were considered in the thermal-time accumulation (Wilczek et al., 2009). In a more recent study, model accuracy was further analyzed by considering the different seasons and plantings separately, along with the associated meteorological data (Chew et al., 2012). It was subsequently found that the effect of night temperatures on flowering time depends on the season. During summer months, temperature peaks at daytime and drops at night. In agreement with the previous study, analysis for summer plantings showed good model accuracy even though night temperatures were discounted in the accumulation of thermal-time. This suggested that night temperature in this period has very little effect on flowering time. However, the diurnal variation in temperature becomes less predictable in the autumn and winter. When night temperatures were included in the new study, albeit with a lower effectiveness relative to daytime temperatures, model performance was improved across seasons and plantings (Chew et al., 2012). These results reflected the switch from a photoperiod-dependent pathway to the gibberellin pathway, which is known to promote flowering in SDs and display different sensitivity to day and night temperatures (Wilson et al., 1992; Moon et al., 2003; Stavang et al., 2007, 2009). The different day/night temperature sensitivities also mirror the observed circadian gating of temperature response in plants (Rikin et al., 1993; Fowler et al., 2005; Espinoza et al., 2010).

In an attempt to extend the flowering model to include the role of photoreceptors, Chew et al. (2012) also observed an involvement of phyB in the gating of temperature response. phyB is known to delay flowering time by regulating degradation of CO protein in the photoperiod pathway (see earlier section), and a phyB lack-of-function mutant displays a temperature-dependent early-flowering phenotype (Halliday et al., 2003; Halliday and Whitelam, 2003). Interestingly, the model fit the field data of the phyB photoreceptor mutant only when the effectiveness of temperature was similar both during the day and the night, in addition to changing the model parameters for photoperiod response. The result therefore suggested a possible gating mechanism by which phyB mediates the temperature signal to control flowering. This hypothesis was made possible by a combination of experimental and modeling efforts and good physiological understanding of the photoreceptors in A. thaliana.

The few examples presented above demonstrate how mathematical modeling can facilitate the discovery of emergent properties. Some simulated-driven hypotheses have been confirmed experimentally, some are awaiting further tests, while others may be difficult to validate at present due to technical limitations. In addition, some models require various types of high-throughput data. In this respect, the rapid development of large-scale phenotyping technologies may provide part of the solution (Granier et al., 2006; Reuzeau et al., 2006; Tisné et al., 2013).

SUMMARY AND FUTURE PROSPECTS

We looked at different examples of mathematical models that cover various levels of biological organization, systems, and scales. As demonstrated in our examples, simulation-based models are useful in identifying new network components and interactions that are not always intuitive from experimental data. The model of phyB signaling pathway has identified reactions that are important for the regulation of physiological response (Rausenberger et al., 2010); a model of petal morphology suggested the involvement of a transcription factor (later identified as JAG) in regulating petal tip growth (Sauret-Güeto et al., 2013); the gene dynamic model of the circadian clock proposed two hypothetical components whose identities were later confirmed experimentally as GI and the EC (Dixon et al., 2011; Locke et al., 2005, 2006); and when this circadian clock model was linked to the flowering pathway, model simulation suggested additional roles for FKF1, CDF1, and ELF3 (Salazar et al., 2009; Song et al., 2012). Associating gene functions to phenology models, which are generally used to predict crop development, can also be useful. This was shown in the thermal-time flowering model, which identified a possible gating mechanism of temperature by phyB (Chew et al., 2012). Future models that link, for example, the flowering model (Chew et al., 2012) to the models of phyB signaling (Rausenberger et al., 2010) and clock-regulated photoperiod pathway (Salazar et al., 2009; Song et al., 2012) may reveal more information regarding plant behavior under varying conditions and the underlying mechanisms.

The examples discussed above are all very different, leading to the question of whether they show any similarities or specific properties that made them amenable to mathematical analysis. Preliminary understanding of a system is very helpful in forming the basic structure of a model. The existence of an active and inactive form of phyB, for example, was important in conceiving the Rausenberger 2010 model of phytochrome action (Rausenberger et al., 2010). Knowing the key components of a system also plays a vital role, as in the case of the earliest plant clock model, but it is not always a necessity (Alabadí et al., 2001; Locke et al., 2005). One may develop a minimal model consisting only of hypothetical components, as illustrated in the leaf tissue growth model (Green et al., 2010; Kennaway et al., 2011). It is also possible to model a mechanism by applying similar rules that describe a related system. An example of this is a petal development model, which adopted the same principles used in leaf development (Kuchen et al., 2012; Sauret-Güeto et al., 2013). Some general rules are available, such as the notable L-system, which is useful in describing systems consisting of a repetitive growth unit like a cell or a branch segment (Lindenmayer, 1968a, 1968b). General structures also exist for different classes of oscillating systems (Purcell et al., 2010). A simple repressilator structure, which is a ring made up of three inhibitors, is embedded within the complex circuit of the plant clock model (Model IV, Figure 2D; Pokhilko et al., 2012). This class of repressilator ring system was first synthetically constructed in Escherichia coli but has also been found in mammalian circadian clocks (Elowitz and Leibler, 2000; Hogenesch and Ueda, 2011; Ukai-Tadenuma et al., 2011). The implication here is that while different techniques and certain assumptions may be required, modeling can be applied to a wide range of biological systems. This is encouraging, especially in systems for which models do not yet exist but would benefit from a theoretical understanding of the mechanism involved.

The Data Gap

A central requirement in developing a useful mathematical model is data availability. Experimental data are essential for both model training and validation. One big limitation in molecular network modeling is the lack of quantified protein data, particularly time-resolved data. As a consequence, some dynamic models like the circadian clock adopt an arbitrary unit for the expression of specific components (i.e., the simulated concentration levels are only relative values and do not directly relate to the actual concentrations or copy numbers of different components seen in planta) (Locke et al., 2005, 2006; Pokhilko et al., 2012). For models investigating cellular and tissue development, obtaining high-quality images can be a big challenge. Image analysis presents another technical difficulty, as analysis tools to acquire the desired information do not always exist. Physiological data such as hypocotyl length and cotyledon area are relatively abundant, especially in A. thaliana. However, there is a lack of data from older plants which is necessary for a comprehensive understanding of plant growth and development, but collecting these data on a large scale can be laborious and time-consuming.

Realizing the need for high-throughput data collection, many new and improved phenotyping tools have been developed recently. Novel automated systems are now able to capture the image of dark-grown or light-grown seedlings within a short timescale in parallel with molecular events (Miller et al., 2007; Wang et al., 2009; Cole et al., 2011). These nondestructive systems are equipped with computer algorithms to analyze the images and calculate hypocotyl length, apical hook opening, and phototropic bending. For older plants, some automated platforms can capture the image and weigh each plant (Granier et al., 2006; Reuzeau et al., 2006; Tisné et al., 2013). Besides the whole-plant monitoring systems described above, high-resolution imaging technologies at the organ and cellular level are also under rapid development. Cell-segmented 3D images of the whole organ can be acquired by reconstructing confocal microscopic images taken at multiple angles (Fernandez et al., 2010). An automated in planta cytometric method has also been developed, where gene activity and cellular geometry such as cell topology, size, and shape can be simultaneously monitored and analyzed quantitatively (Federici et al., 2012). Together, these phenotyping platforms can increase the quality and quantity of data generated at multiple levels of cellular organization. A comprehensive review of these systems is provided by Dhondt et al. (2013).

Experimental design is another important aspect to be considered. Experimental conditions, sampling frequency, and the choice of control(s) depend on the objective(s) of studies, driven by hypotheses supported by preliminary or previous results. As illustrated in our examples, modeling can generate nonintuitive hypotheses, but the design of experiments and the quality of data play a big role in determining the success of hypothesis testing. Communication between modelers and experimentalists is therefore important to ensure data efficacy. Experimentalists should understand the modeling results that lead to the hypotheses, including any model assumptions and limitations. In this regard, sensitivity and uncertainty analyses have been valuable for understanding model robustness and to identify the boundaries beyond which predictions should be treated with caution (Dietze et al., 2013). Modelers, on the other hand, need to understand the technologies behind the measurement techniques and their limitations to avoid overinterpretation of data. In addition, exchanging experimental and simulated observations, including those not directly related to the hypothesis being tested, may trigger new ideas and improve understanding between the two communities.

The Future in Plant Systems Modeling

Global concerns regarding the impact of climate change have generated various research activities to identify alternatives for improving plant yield and productivity. With overall crop yields predicted to decline with climate change, renewed efforts are needed that bring together studies addressing the interaction between plants and the environment at all levels of organization (Tao et al., 2006; Estrella et al., 2007; Luterbacher et al., 2007).

Modeling of molecular networks in the context of systems biology will continue with the development of more advanced experimental and analytical tools. In recent years, it has become possible to obtain data with near or single cell resolution for various types of cells (Elowitz et al., 2002; Suter et al., 2011; Wenden et al., 2012), facilitating the study of the intricate details of intracellular biochemical processes, in particular the relationship between cellular-level and population-level phenomena and the role played by intercellular heterogeneity. The modeling of processes at the cellular or subcellular level presents distinct challenges; the low copy number of many molecular players inside cells (Grima and Schnell, 2008) means that stochasticity must be considered. The models described in this review are mostly deterministic and, hence, ill-suited to tackle such challenges; indeed, it has been shown that some phenomena cannot be captured even qualitatively by deterministic approaches (Ramaswamy et al., 2012). Stochastic modeling frameworks have been developed in the past few decades, notably the stochastic simulation algorithm (Gillespie, 1977) and its various approximations (Thomas et al., 2012), which have led to means to efficiently probe single-cell dynamics. Examples of stochastic modeling in plants are relatively few (compared with deterministic modeling), but there is clearly a growing trend (Kang et al., 2008; Guerriero et al., 2012), which is necessitated by the acquisition of ever more high-resolution data. In addition, advances in plant systems biology are likely to follow the lead of a recently published whole-cell computational model for the bacteria Mycoplasma genitalium that considers the whole genome (Karr et al., 2012). However, two main challenges lie ahead in developing such a model for plant systems. First, even though the genomes of Arabidopsis and various crop species such as rice (Oryza sativa), maize (Zea mays), and soybean (Glycine max) have been fully sequenced, there are still many gene functions yet to be discovered (Goff et al., 2002; Kaul et al., 2000; Matsumoto et al., 2005; Schmutz et al., 2010; Schnable et al., 2009; Yu et al., 2002). Second, plants are complex multicellular organisms with many biological, chemical, and physical processes that overlap and interact with each other over both temporal and spatial scales.

Application of modeling techniques from engineering and physical sciences will help in understanding how a suite of different biological, physical, and chemical signals interact and regulate plant growth and development. Indeed, these techniques are already used in plant modeling, such as to describe water, gas, and nutrient transport in the fruit, root, and stem systems (De Schepper and Steppe, 2010; Ho et al., 2010). The next step is then to combine various different techniques and build a comprehensive model that incorporates all the genetic information. There is also potential in integrating existing models using a modular approach, as practiced in climate modeling (Collins et al., 2006). We have seen from the case studies presented earlier that a number of models have the potential to be linked. In the future, there is likely to be greater coordination between modelers and plant biologists and more knowledge transfer between model species such as Arabidopsis and crops. These developments will expedite the links between molecular-level knowledge and system-level understanding, allowing the simulation of plant phenotypes in a changing environment to aid crop improvement, advances in fundamental plant biology, and the design of genetic circuits to facilitate synthetic biology (Kitano, 2002a; Collins, 2012).