Amphidynamic Crystals of a Steroidal Bicyclo[2.2.2]octane Rotor: A High Symmetry Group that Rotates Faster than Smaller Methyl and Methoxy Groups

Abstract

The synthesis, crystallization, single crystal X-ray structure, and solid state dynamics of molecular rotor 3 provided with a high symmetry order and relatively cylindrical bicyclo[2.2.2]octane (BCO) rotator linked to mestranol fragments were investigated in this work. Using solid state ¹³C NMR, three rotating fragments were identified within the molecule: the BCO, the C19 methoxy and the C18 methyl groups. To determine the dynamics of the BCO group in crystals of 3 by variable temperature ¹H spin-lattice relaxation (VT ¹H–T₁), we determined the ¹H–T₁ contributions from the methoxy group C19 by carrying out measurements with the methoxy-deuterated isotopologue rotor 3-d₆. The contributions from the quaternary methyl group C18 were estimated by considering the differences between the VT ¹H–T₁ of mestranol 8 and methoxy-deuterated mestranol 8-d₃. From these studies it was determined that the BCO rotator in 3 has an activation energy of only 1.15 kcal mol⁻¹, with a barrier for site exchange that is smaller than those of methyl (E_a = 1.35 kcal mol⁻¹) and methoxy groups (E_a = 1.91 kcal mol⁻¹), despite their smaller moments of inertia and surface areas.

Introduction

Amphidynamic crystals are materials designed to display engineered mechanical processes in the solid phase. They are built with a combination of static components that guide crystalline order, which are generally linked to dynamic elements that display conformational motions along well-defined directions.¹ One of the most interesting challenges in molecular structure and crystal design is the preparation of structures with components that rotate close to the limit of their moment of inertia, as the result of barriers that are smaller than thermal energies. While this is an unchartered territory, one may expect their physics to be fascinating and their perspectives in materials science very exciting. Amphidynamic crystals have the potential of exhibiting spontaneous organization guided by internal forces, and externally addressable functions with the use of external fields. These properties may lead to novel devices and to the construction of artificial molecular machines.² Knowing that the physical properties of solids depend on their molecular units, their packing interactions, and the symmetry of the lattice,³ materials scientists and crystal engineers⁴ have sought the development of structure-function relationships leading to specific crystal arrangements and desirable functions.⁵ Based on this, a relatively large number of crystalline structures with internal rotation has been studied in structures that range from close-packed molecular crystals,⁶ to supramolecular complexes⁷ and MOFs.⁸ Particularly, molecular rotors with a central rotator linked by a linear diethynyl axle to bulky triarylmethanes acting as stator have been synthesized and used to analyze the relationship between the size of the stator and the dynamics of the rotator. We have adopted in this paper the nomenclature proposed by Michl, where the word “rotor” is reserved to describe entire molecular assemblies and the terms “rotator” and “stator” to define the to rotary units and the static frames that are used to define the frame of reference.⁹ These studies have revealed that variations in the internal dynamics in crystals depend on the steric shielding provided by the stator¹⁰ and on the symmetry order of the rotator.¹¹ While bulky stators can generate larger cavities, highly symmetric cylindrical rotators require lower activation energies to move within the shape-conforming environments that result from short-range van der Waals packing forces.

Using these design concepts, we recently reported structures based on 1,4-disubstituted phenylenes flanked by two steroid molecules.^12,13 The use of mestranol allows the molecule to adopt an overall “U” conformation (compound 1, Figure 1) that packs in a helical array of nested molecular rotors that at room temperature display ultrafast 180° rotations (k_r >> 10⁷ s⁻¹) and strongly correlated slower motions with angular displacements of ca. 85°.¹³ The use of homochiral steroids is also appealing because their non-centrosymmetric crystals will enable valuable physical properties, such as piezoelectricity, pyroelectricity, and optical activity.¹⁴ We noticed that the dynamically disordered phenylenes in 1 occupy a significantly greater volume than a static ring, suggesting that the formation of isomorphic structures may be possible with a more cylindrical rotator. We hypothesized that the packing properties of chiral mestranol combined with the C₃ rotational symmetry of a 1,4-disubstituted bicyclo[2.2.2]octane (BCO) rotator,¹⁵ may lead to smaller rotational barriers. The efficient rotational properties of the BCO group had been recently demonstrated in other BCO crystals, including compound 2, which was shown to have ambient temperature site exchange rates of 4.3 × 10¹¹ s⁻¹ and 7.7 × 10¹⁰ s⁻¹, with activation energies of 1.48 and 2.75 kcal/mol for two distinct crystallographic sites.^15a

Figure 1.

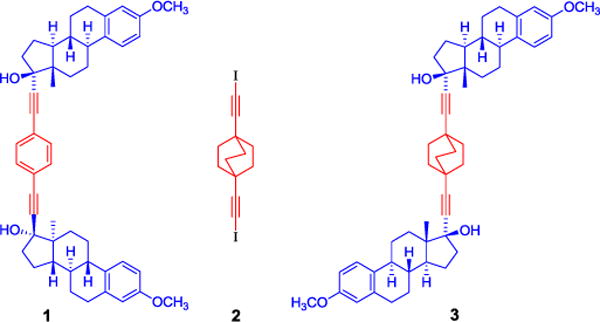
Line diagrams of crystalline compounds with fast rotating portions in red and static fragments in blue. At 25 °C, the phenylene ring in compound 1 with a syn-steroid orientation presents two distinct dynamic processes with site exchange rates of ca. 1.5 × 10⁶ and >10⁶ s⁻¹. Ordered and disorderd sites of the bicyclo[2.2.2]octane in 2 have site exchange rates of ca. and 4.3 × 10¹¹ s⁻¹ and 7.7 × 10¹⁰ s⁻¹, respectively. A combination of components in molecular rotor 3 studied in this paper is expected to facilitate faster rotation.

In this paper we describe the synthesis, molecular and crystal structure, solid state characterization, and rotational dynamics of molecular rotor 3. Although the packing of 3 turned out to be substantially different than that previously documented for 1, it does exhibits exceedingly fast rotation in the solid state, with an activation energy of only E_a = 1.15 kcal/mol, as characterized by variable-temperature ¹H spin-lattice relaxation experiments (T₁). In order to assign the dynamics of the BCO fragment in 3 it was essential to carry out measurements with a methoxy-deuterated isotopologue, 3-d₆, as well as crystals of mestranol 8 and its methoxy-deuterated isotopologue 8-d₃, which allowed us to identify the contributions of the methyl groups of the steroidal backbone to the overall spin-lattice relaxation time.

Results and Discussion

As outlined in Scheme 1, our synthetic strategy relied on the diastereoselective addition of bicyclo[2.2.2]octane-1,4-diethynylmagnesium bromide to two molecules of mestrone 5. The synthesis began with conversion of estrone 4 to mestrone 5 by treatment with sodium hydride and methyl iodide. We planned to access to the bicyclo[2.2.2]octane-1,4-dilithiumdiacetylide by a Corey-Fuchs one-carbon homologation of the corresponding aldehyde. Thus, Swern oxidation of bicyclo[2.2.2]octane-1,4-dimethanol 6¹⁶ afforded the corresponding bicyclo[2.2.2]octane-1,4-dicarbaldehyde which proved to be highly unstable, hence the crude product was immediately reacted with CBr₄/PPh₃ to produce the 1,4-bis(2,2-dibromovinyl)bicyclo[2.2.2]octane 7¹⁶ in 95% yield over two steps.

Scheme 1.

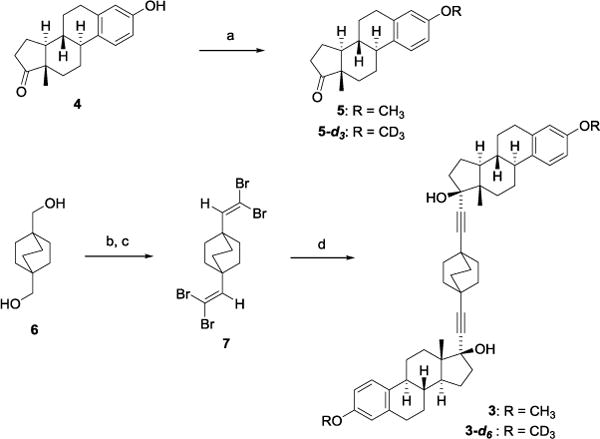
Reagents and conditions: a) MeI or CD₃I, NaH, THF, r.t., 5 (94%), 5-d₃ (90%); b) DMSO, (COCl)₂, Et₃N, CH₂Cl₂, −78 – 0 °C; c) CBr₄, PPh₃, CH₂Cl₂, 0 °C – r.t., 95% over two steps; d) i. n-BuLi, THF, −78 – 0 °C; ii. MgBr₂·OEt₂, Et₂O, −78 °C; iii. 5 or 5-d₆, THF, CH₂Cl₂, −78 °C – r.t., 3 (46%), 3-d₆ (53%).

At this stage we developed a one-pot, three-step process to couple the steroid and 1,4-diethynylbicyclo[2.2.2]octane fragments to reach the desired compound by converting bis-dibromoalkene 7¹⁶ to its Grignard reagent by treatment with n-butyllithium followed by transmetalation with MgBr₂.OEt₂. Subsequent addition of a solution of mestrone 5 delivered molecular rotor 3 in 46% yield as a single diastereomer. Compared to the lithium acetylide intermediate, the derived Grignard reagent provided higher yields. The remarkable diastereoselectivity is a result of the directing effect of the angular methyl group that forces the nucleophile to enter from the opposite alpha face of the ketone. The deuterated analogue 3-d₆ was obtained in a slightly higher yield of 53% following the same synthetic route starting from 5-d₃. Signals belonging to the central rotator in 3 in solution were observed at 1.76 ppm in the ¹H NMR, and at 32.1 ppm in the ¹³C NMR spectra. Both spectra were consistent with a time-averaged C₂-symmetry.

Single crystals of 3 suitable for X-ray diffraction experiments were obtained from slow evaporation of a solution in hexanes/ethyl acetate (8:2) and were analyzed at 100(2) K. The main crystallographic parameters are included in the Supporting Information. The solvent-free structure was solved in the space group P4₃2₁2; a chiral space group (with no center of inversion) in the tetragonal system with four molecules in the unit cell (Z = 4) and only half molecule in the asymmetric unit (Z’ = 0.5). The steroidal fragments do not present geometric deviations when compared to previously reported mestranol structures (Figure 2a)¹⁷ and the dialkynyl molecular axis is slightly deviated from the idealized 180° linearity, as described by the angle C17-C21-BCO_centroid = 172°. Perhaps the most interesting and unmistakable feature from the X-ray crystal studies is the disorder in the bicyclo[2.2.2]octane fragment (Figure 3), which occurs over two positions with a 50:50 occupancy. The disorder of the BCO group originates from the mismatch that exists between the two-fold symmetries of the lattice [C₂(cryst)] and the rotator [C₂(BCO)].

Figure 2.

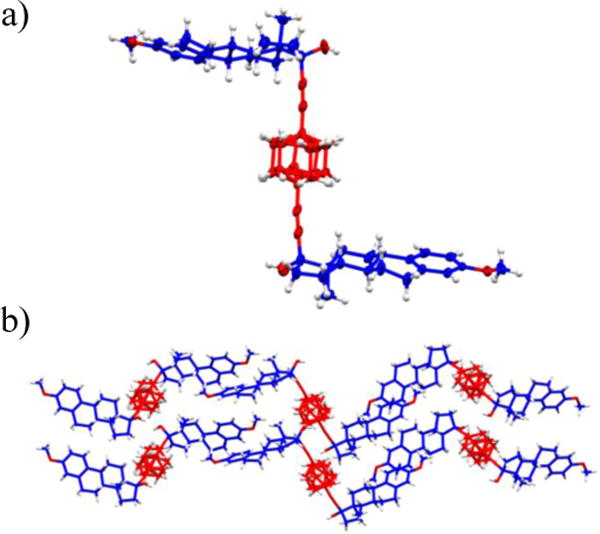
(a) Molecular structure of the molecular rotor 3 showing the disordered bicyclo[2.2.2]octane rotator over two positions. (b) Packing arrangement of compound 3 showing a ribbon-like array found in the P4₃2₁2 space group.

Figure 3.

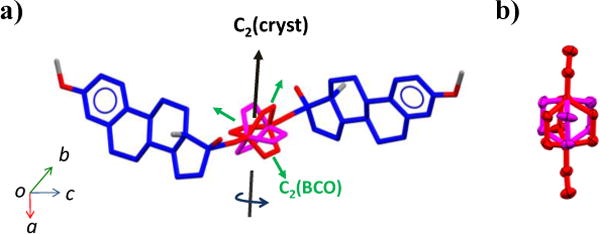
(a) Misalignment between the crystallographic [C₂(cryst)] and bicyclo[2.2.2]octane [C₂(BCO)] two-fold symmetry axes gives rise to the two sites of the BCO fragment in 3 with the two symmetry related positions colored purple (light) and red (dark). (b) Close up of the resulting crystallographic disorder with 50:50 occupancy with the hydrogen atoms removed for clarity.

The lattice two-fold rotational symmetry [C₂(cryst)] relates the two steroids of the structure by rotation along the axis that lays on the diagonal of the ab-plane of the unit cell. Although the BCO group has three 2-fold axes that cut each of the three bridges in the middle (average point group D₃h), none of them is coincident with the two fold axis defined by the crystal (Figure 3a). The superposition of non-coincident two-fold symmetries generates the two sites (Figure 3b), which produces an effective six-fold symmetric potential if rotation about the principal axis of the molecule is considered. The disordered positions of the bicyclo[2.2.2]octane are related by an angular displacement of 48° and 72°, suggesting that any possible rotation in the crystal must occur by two non-equivalent, short and long jumps.¹⁵

The packing of compound 3 presents the rather infrequent OH^…π interaction reported in crystals from similar structures; namely, 2-ethynyladamantan-2-ol, and gem-alkynols.¹⁸ We observed close contacts between the hydroxyl groups at C17 and the triple bonds in neighboring molecules with H^…C≡C_centroid distance of 2.533 Å and O–H^…C≡C_centroid angle of 149.6°. Through these self-complementary interactions involving the two triple bonds, molecular rotors can accommodate in parallel displaced layers in the crystal (Figure 2b). With the relative position of the steroids close to an anti, or “Z-shaped” conformation (torsional angle C3–C17–C17’–C3’ = 153°), layers accommodate such that the empty spaces left by the steroidal portions in a particular layer are filled with molecules from a second layer, giving rise to the ribbon-like arrangement that characterizes the crystal (Figure 2b). Additionally, analysis of the packing array revealed that the surrounding stators display some contacts with the two disordered positions of the rotator.

Considering that the rotation of groups linked to triple bonds is essentially barrierless in solution, we reasoned that a “U” conformation such as that previously observed in compound 1 should be accessible for compound 3. Searching for a similar polymorph we carried out crystallization in a large selection of pure solvents and solvent mixtures that included acetone, benzene, o-xylene, dichloromethane, dimethylformamide, and ethyl acetate, among several others. We used powder X-ray diffraction (PXRD) to characterize the solids resulting from the crystallization experiments and discovered that only the P4₃2₁2 is obtained, judging by the excellent match between the calculated and experimental X-ray powder patterns in the range of 4–50° (2θ degrees) (Please see Supporting Information). Only the fast removal of dichloromethane under vacuum gave an amorphous solid. Furthermore, seeding saturated solutions of compound 3 with small crystallites of compound 1, did not affect the outcome of the crystallization experiments.

Once the identity and crystallinity of compound 3 were established, the thermal stability of the P4₃2₁2 form was determined by differential scanning calorimetry (DSC) in the −50 °C to 350 °C range. A melting transition was observed in the range of 251–253 °C with no indications of phase transitions before melting. Thermogravimetric analysis (TGA) confirmed that the solid contains no solvent and that it decomposes well after the melting point, as shown by an abrupt weight loss at 323 °C.¹⁹ Freshly crystallized samples of compound 3 were analyzed by CPMAS ¹³C NMR. In agreement with the X-ray information, the solid state CPMAS ¹³C NMR spectrum (see Supporting Information) showed a number of signals that correspond to one half of the molecule, confirming that the two halves of the molecular rotor are crystallographically equivalent. Relatively narrow signals with full width at half maximum (FWHM) between 35–45 Hz corroborated the high crystallinity of the sample. The signal corresponding to the methylenes of the bicyclo[2.2.2]octane fragment was readily identified by the use of a dipolar-dephasing, non-quaternary suppression sequence (NQS), which removes all the static protonated signals but retains those that correspond to groups undergoing rapid motion. This and other assignments were consistent with those previously determined in solution NMR based on 2-D techniques. It was determined that the methylene carbon atoms of the bicyclo[2.2.2]octane give rise to a very strong single signal at δ 32.3, which is very close to the value δ 32.1 determined in CDCl₃. That the intensity of this sharp signal is unaffected even by long dephasing (60 μs) times indicates that the bicyclo[2.2.2]octane fragment displays a rotational behavior with a frequency that is greater than that of the heteronuclear ¹H–¹³C dipolar coupling (25–30 kHz), showing that the disorder observed in the X-ray analysis is dynamic. In addition to the BCO signal, those corresponding to the methyl C18 (δ 12.0) and methoxy group C19 (δ 53.8) also remained in the NQS spectrum.

Based on literature precedent²⁰ and the CPMAS ¹³C NMR-NQS results, which suggest that rotation of the BCO rotator occurs beyond the kilohertz regime, we decided to explore the internal dynamics of molecular rotor 3 using ¹H spin lattice relaxation experiments.²¹ It is well-known that molecular rotation in the solid state is an important mechanism for longitudinal spin lattice relaxation (T₁). Fluctuating magnetic fields arising from motion-mediated magnetic modulations of hydrogen nuclei with a strong dipolar coupling can lead to effective spin-lattice relaxation. If a particular motion has a characteristic correlation time τ_c that follows an Arrhenius behavior, the correlation time will vary as a function of temperature and a minimum will be obtained when the τ_c matches the inverse of the Larmor frequency (ω⁻¹) of the nuclei being observed. The activation energy (E_a, eq 1) of the corresponding dynamic process in the solid can then be extracted by fitting the experimental T₁ values to the Kubo-Tomita equation (eq 2).²²

$${\tau }_C={\tau }_{\mathit{0}}\text{exp}(Ea/RT)$$ (Eq. 1)

$${\mathrm{T}}_1^{-1}=C{[{\tau }_C{(1+{\mathrm{\omega }}^2{\tau }_C^2)}^{-1}+4{\tau }_C(1+4{\mathrm{\omega }}^2{\tau }_C^2)]}^{-1}$$ (Eq. 2)

$$C=\mathrm{n}/\mathrm{N}(9/40){[{\mathrm{\mu }}_{\mathrm{o}}/4\mathrm{\pi }]}^2{\mathrm{\gamma }}^4{\mathrm{h}}^{-2}/{\mathrm{r}}^6$$ (Eq. 3)

It should be noted that equation 2 describes the relaxation rate for a given process, which is simply given by the inverse of the relaxation time (i.e., 1/T₁). The constant C in equation 2 characterizes the strength of the various dipole-dipole interactions modulated by the rotation of the molecular fragments, and can its magnitude can be approximated with help of equation 3.²³ The proton-proton separation in the rotating group is r, the permeability of free space is μ_o and the ¹H magnetogyric ratio is γ.²⁴ The value of C is further affected by a reducing factor n/N, where n represents the number of mobile protons that are responsible for the relaxation of the total number of protons N in the corresponding molecule.²⁴

In the case of crystalline molecular rotor 3, experiments between 395 K and 155 K using a saturation-recovery pulse sequence revealed 1/T₁ values that were satisfactorily adjusted to the Kubo-Tomita fit from high temperatures down to 195 K (Figure 4, triangles and Supporting Information). Below 195 K, the 1/T₁ values increase when a monotonic decrease was expected. This deviation suggested that the relaxation recorded may be the result of overlapping dynamics that contribute to the overall relaxation of the sample, suggesting that the rotation of the BCO could be similar to that of the smaller methyl and methoxy groups (Figure 5a).²⁵ The time constant for inertial rotation in the gas phase (τ_IR) at a temperature T can be estimated from the rotator moment of inertia, I, according to: τ_IR = (2π/9) (I/k_BT)^1/2, where k_B is the Boltzmann constant.²⁶ With moments of inertia of ca. 89 and 3.4 g•mol⁻¹A⁻¹ for BCO and methyl groups, respectively, one would expect the gas phase rotation of the larger one to be about one order of magnitude slower at ambient temperature. Furthermore, with a ca. three times greater molecular surface area, it would be reasonable to expect that the larger BCO should have greater barriers to rotation due to more van der Waals interactions and short contacts with the environment. Given this simple analysis, it became of great interest to investigate the potential similarity between the rotational dynamic of the BCO and the methyl and methoxy groups.

Figure 4.

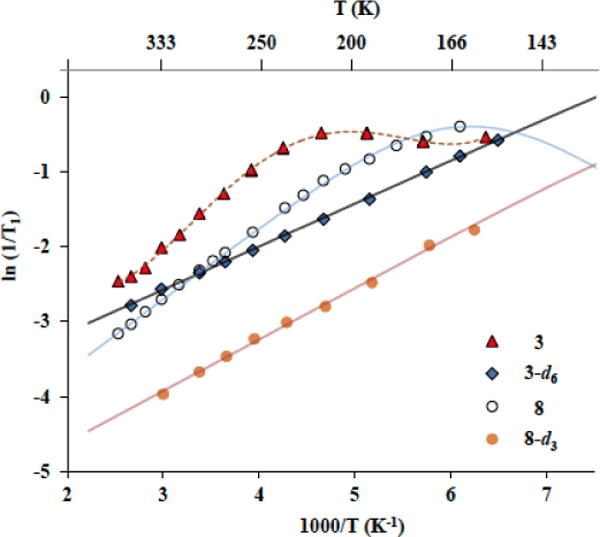
Comparison of the measured spin lattice relaxation rates 1/T₁ of compounds studied in this paper. In compound 3 both the BCO and MeO groups contribute with significance to the relaxation process (triangles). In crystals of methoxy-deuterated 3-d₆ the BCO group is the main responsible of the relaxation (filled squares). Similarly, the MeO group causes the relaxation in mestranol 8 (open circles) whereas the Me group is responsible for the relaxation in methoxy-deuterated mestranol 8-d₃ (solid circles).

Figure 5.

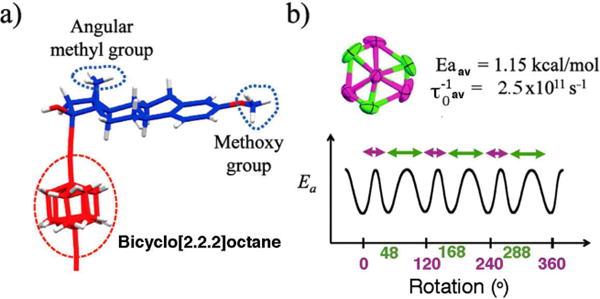
(a) Components of molecular rotor 3 involved in dynamic processes. (b) Qualitative representation of the rotational potential with angular displacements between the sites of the BCO (green and purple). While the two sites are isoenergetic (50% occupancy each), each of the two barriers may have different heights, such that the measured activation energy is an average.

For structures that have two or more fragments that contribute to the magnetic relaxation in a coupled spin system that is at the same spin temperature, the observed relaxation rate (1/T₁)_Total is given by the sum of the relaxation rates from the different contributors. In the case of compound 3, we initially considered that the observed relaxation was realized by all the rotating components in the molecule, (1/T₁)_Total = (1/T₁)_BCO + (1/T₁)_OMe + (1/T₁)_Me, where the subscripts identify each of the three mobile groups. To examine the contributions of the methyl and methoxy groups,, and assuming that differences in crystal structures will not be dominant, we determined the spin-lattice relaxation of mestranol 8, which has only the steroid frame and the triple bond but not the BCO rotator. We considered that the relaxation in compound 8 would be dictated by [(1/T₁)_Mestranol = (1/T₁)_OMe + (1/T₁)_Me]. Similarly, knowing that deuterium does not contribute to the ¹H spin-lattice relaxation, we studied the methoxy-deuterated analog 8-d₃²⁷ to pin-down the contribution of the angular methyl groups to the relaxation of mestranol [(1/T₁)_Mestranol-d3 =(1/T₁)_Me].

As observed in Figure 4 (open circles), a fit of the experimental 1/T₁ values of 8 to Kubo-Tomita expression revealed an activation energy of only 1.92 kcal mol⁻¹, a pre-exponential factor ${\tau }_{\mathit{0}}^{-\mathit{1}}$ = 1.8 x 10¹¹ s⁻¹, and a C value of 1.42 × 10⁸ s⁻². These values are collected in Table 1. Regarding compound 8-d₃ (Figure 4, filled circles), even though we could not reach the maximum in 1/T₁ values a linear regression of the data indicated an activation energy of E_a = 1.35 kcal mol⁻¹. Such low activation energies are consistent with analogous measurements for – CH₃ groups reported in the literature.²⁸ The smaller relaxation rate from the methyl group makes a very small contribution to the relaxation of mestranol 8 in the range of temperatures explored, as indicated by the lower position of the fitted line in Figure 4, indicating that the rotation of the OMe group constitutes the relaxation sink for all the protons in the molecule, thus the expression for mestranol 8 could be reduced to [(1/T₁)_Mestranol ≈ (1/T₁)_OMe]. In the absence of this group, the angular methyl group (Me) is solely responsible of the relaxation in derivative 8-d₃.

Table 1.

Arrhenius Parameters Derived from Fits of the 1/T₁ Data.

Compound	Group causing the relaxation	Ea (kcal/mol)	τ0−1 (s−1)	C (s−2)
3	OMe + BCO	2.5a
	OMeb	3.2	1.0 × 1012*	1.0 × 108*
3-d6	BCO	1.15c	2.5 × 1011*	6.8 × 108*
8	OMe	1.9	1.9 × 1011	1.4 × 108
8-d3	Me	1.35c	3.3 × 1011*	1.7 × 108*

^aApparent activation energy resulting from contributions of two groups.

^bObtained from the difference between compounds 3 and 3-d₆ (SI, Figure S8)

^cObtained from linear regression of the data.

^*Resulting from 1/T₁ data extrapolation using the Kubo-Tomita expression.

Assuming that mestranol is a reasonable model to determine the behavior of the methyl and methoxy groups of molecular rotor 3, we replaced the hydrogens of the methoxy group in 3 by deuterons and studied the resulting analog, 3-d₆ to determine (1/T₁)_Total ≈ (1/T₁)_BCO. Interestingly, even though no maximum in the 1/T₁ values (Figure 4, filled squares) was observed due to low temperature limitation of our spectrometer, a linear regression fit obtained from 3-d₆ reveals a very low activation energy of only 1.15 kcal mol⁻¹. The activation energy for the rotation of the BCO portion obtained in this manner should be considered an average that reflects two distinct site exchange processes with angular displacements of 48° and 72° (Figure 5), which are isoenergetic, but may have different magnitude barriers. An average E_a value of 1.15 kcal/mol deduced in this manner is smaller than those of the methyl and methoxy groups in the same structure, suggesting that small jumps in a six-fold potential are advantageous when compared to the larger 120° jumps required for rotation of the smaller methyl groups. The barrier in crystals of 3 is also smaller than the one reported for the reorientation of pure BCO over its 1,4 axis in its plastic crystalline state (1.84 kcal mol⁻¹),²⁹ and the structurally related and also positionally disordered one in 1,4-bis(iodoethynyl)bicyclo[2.2.2]octane (1.48 kcal mol⁻¹).¹⁵

Based on the results obtained, we have attempted to develop a model that can predict the dynamic behavior of the Me, OMe and BCO groups adapting the 1/T₁ data and fitting the values to the Kubo-Tomita expression. The parameters obtained using these models are compiled in Table 1. In order to reduce the number of possible results, we used the activation energies described above as constraints. From our simplified model, we noticed that regardless of the residual dipolar interactions that originate the C values, their relative magnitude agrees reasonably well when considering the reducing factor (n_mobile/N_total): when the two OMe groups (n/N = 6/62) are responsible of the relaxation, the C value should be smaller than that obtained from compound 3-d₆ (C = 6.8 × 10⁸) where the BCO acts as the relaxation sink and the protons from the OMe groups were removed (n/N = 12/56). Similarly, in compound 8 (C = 1.42 × 10⁸) one OMe relaxes the molecule (n/N = 3/26), and its C value is smaller than that found for compound 8-d₃ (C = 1.65 × 10⁸) with no protons in the OMe group (n/N = 3/23).

This data analysis allowed us to use the temperature variation in the spin lattice relaxation rate of natural abundance 3, (1/T₁)_total, and in the BCO molecular rotor deduced from 3-d₆, (1/T₁)_BCO to qualitatively obtain the relaxation rates of the methoxy group in the stator, (1/T₁)_MeO. That is to say, the trend in the line describing the relaxation of molecular rotor 3, represented by the filled triangles in Figure 4, results from the addition of the lines that correspond to the behavior of the BCO (filled squares) and the MeO groups, as shown in Figure S8 in the SI section. We noticed that there is a shift in the incipient maximum of the Kubo-Tomita fit of the model steroid MeO (open circles) as compared to that of the molecular rotor (filled triangles), which indicates that the MeO group in 3 has different activation parameters as compared to the one in 8. Using the simulated curve, one can estimate a barrier of ca. 3.2 kcal/mol (Table 1) indicating that there is more hindrance to the MeO group in crystals of rotor 3 than in crystals of the steroid 8.³⁰ Based on this analysis, we reformulate our expression for the relaxation of compound 3 to be (1/T₁)_Total = (1/T₁)_BCO + (1/T₁)_OMe.

The low activation energy determined in compound 3-d₆ implies that the BCO rotator has a site exchange rate of 1.4 × 10¹⁰ s⁻¹ at ambient temperature. It is worth noting that the pre-exponential factor simulated for the site exchange of the BCO group in 3 ( ${\tau }_{\mathit{0}}^{-\mathit{1}}$ = 2.22 x 10¹¹) is about an order of magnitude smaller than those of the same group in crystals of 2 ( ${\tau }_{\mathit{0}}^{-\mathit{1}}$ = 5.21 x 10¹² and 8.0 × 10¹²). Similarly, the rotational dynamics of the BCO group in two crystallographic sites of a tetrabutylammonium salt of an analogous 1,4-bis(carboxyethynyl)bicyclo[2.2.2]octane were reported have barriers of 2.03 and 2.72 kcal mol⁻¹ with pre-exponential factors, ${\mathit{t}}_{\mathit{0}}^{-\mathit{1}}$ = 3.6x10¹² and ${\mathit{t}}_{\mathit{0}}^{-\mathit{1}}$ = 3.1x10¹² s⁻¹.^15b It is interesting that those compounds do not have the BCO linked to a large rigid stator, and may be considered to have plastic crystal character. By contrast, the rotation of a BCO group linked by triple bonds to bulky triphenylsilyl groups in a previously reported molecular gyroscope displayed a barrier of 3.5 kcal/mol and a smaller pre-exponential factor of ${\mathit{t}}_{\mathit{0}}^{-\mathit{1}}$ = 3.6 x 10¹⁰ s⁻¹.¹¹ Taking all of these results together, it is remarkable that BCO rotators present such a low, and relatively similar activation energies, despite occurring in widely different molecular structures and crystalline environments. In one exceptional case involving an organic conductor, a dialkynyl BCO rotator was shown to have a barrier of ca. 7.3 kcal/mol, which was speculated to arise from local interactions in the lattice of perhaps a quantum dissipation phenomenon.^15b Although the amount of data is rather limited, they suggest that structures with rotators covalently linked to larger, rigid stators are likely to reduce the magnitude of the pre-exponential factor, a hypothesis that will be worth testing with molecular dynamics calculations.

Conclusions

We have combined the rigidity of the steroid mestranol with the three-fold symmetric and relatively cylindrical bicyclo[2.2.2]octane (BCO) fragment in the crystalline molecular rotor 3 to explore its crystallization and solid state dynamics. Compound 3 and its isotopologue 3-d₆ were synthesized by a one-pot, three-step coupling reaction between mestrone and 1,4-diethynylbicyclo[2.2.2]octane with perfect diastereoselectivity and good overall yields. It was discovered that compound 3 does not form crystals isomorphous to those of compound 1 with a central phenylene instead of a BCO rotator. Single crystal X-ray diffraction analysis of 3 showed that substitution of the 1,4-phenylene rotator with a bicyclo[2.2.2]octane originates a ribbon-like packing of the molecular rotors with a disordered BCO rotator. Notably, the disorder results in two distinct sites related by angular displacements of 48° and 72°, which are equally occupied. Analysis of solid state CPMAS ¹³C NMR data indicated that the BCO group undergoes rapid rotary motion with exchange rates well beyond the tens of 10³ s⁻¹ regime, as indicated by ¹H dipolar dephasing experiments. For that reason, the exchange dynamics of the BCO rotator were explored by variable temperature ¹H spin-lattice relaxation experiments. By comparing ¹H T₁ values of molecular rotors 3 and methoxy-deuterated 3-d₆ along with those of mestranol 8 and methoxy-deuterated 8-d₃, it was possible to assign the relative relaxation contributions of the BCO, methyl and methoxy groups. These results indicate that the BCO rotator has an effective average barrier of E_a = 1.15 kcal mol⁻¹, which allows it reach an average site exchange rate of 1.4 × 10¹⁰ s⁻¹ at ambient temperature, which is rather remarkable considering that the BCO group is relatively large. These results demonstrate that the relatively cylindrical BCO and suitable analogs and derivatives will be promising building blocks for the design of ultrafast responsive materials and molecular machines based on amphidynamic crystals with inertial rotors.

Experimental section

General Information

All reactions were carried out under an inert atmosphere of argon in oven or flame-dried glassware. All chemicals were purchased from commercial suppliers and used as received. Mestrone (4) and Ethynylestradiol (9) are commercially available and bicyclo[2.2.2]octane-1,4-dimethanol (6) was prepared following literature procedures.¹⁶ Solvents were dried and purified following standard literature procedures. Analytical thin-layer chromatography (TLC) was performed using pre-coated TLC plates with silica gel and visualized using combinations of UV, potassium permanganate (KMnO₄), and cerium molybdate (CAM) staining. Flash column chromatography was performed using silica gel as the stationary phase. Proton magnetic resonance spectra were recorded at 500 MHz, and carbon-13 magnetic resonance spectra were recorded at 125 MHz, respectively. All chemical shifts are reported in ppm on the δ-scale relative to TMS (δ 0.0) using residual solvent as reference (CDCl₃ δ 7.26 and δ 77.16 for proton and carbon, respectively). Coupling constants J are reported in Hz. Multiplicities are reported as broad (br), singlet (s), doublet (d), triplet (t), quartet (q), quintet (qnt), sextet (sxt), septuplet (spt) and multiplet (m). Uncorrected melting points were recorded on a melting point apparatus using open glass capillaries. IR spectral data were obtained using an Attenuated Total Reflectance (ATR) spectrometer as the neat compound and the units are stated in cm⁻¹. Optical Rotations were measured on a polarimeter with a sodium lamp and a light wavelength of 589 nm (the sodium D line). High resolution mass spectrometric data were collected using Electrospray Ionization technique with a Time-of-Flight detector (ESI-TOF) mass spectrometer and a Liquid Introduction Field Desorption Ionization mass spectrometer with a Time-of-Flight detector (LIFDI-TOF).

Synthesis of molecular rotor 3

Step 1

Preparation of MgBr₂OEt₂. Some drops of 1,2-dibromoethane were added to a mixture of Magnesium turnings (50 mg, 2.05 mmol, 4.0 equiv) and dry diethyl ether (3.0 mL). The mixture was heated until reflux started, then the remaining 1,2-dibromoethane (0.18 mL (total), 386 mg, 2.05 mmol, 4.0 equiv) was added dropwise. The mixture was allowed to stir at room temperature for 1 h after completion of the addition.

Step 2

n-BuLi (1.6M in hexanes, 1.76 mL, 2.82 mmol, 5.5 equiv) was added dropwise to a solution of bis-dibromoalkene 7 (245 mg, 0.51 mmol, 1.0 equiv) in dry THF (3.6 mL) at −78 °C, the reaction mixture was stirred at this temperature under argon atmosphere for 1.5 h and 30 min at 0 °C. The resulting mixture was cooled again to −78 °C and the previously prepared MgBr₂OEt₂ mixture was added by syringe. Afterwards, mestrone 5 (292 mg, 1.03 mmol, 2.0 equiv) was added dissolved in dry diethyl ether (2.7 mL) and dry CH₂Cl₂ (2.7 mL). Then the dry ice bath was replaced by a 0 °C ice bath and the reaction mixture was stirred 15 h, allowing the mixture reach room temperature slowly. Then, the mixture was cooled to −78 °C, and aqueous saturated solution of NH₄Cl (6.0 mL) was added, the mixture was stirred at room temperature and after separation of the layers, brine was added (6 mL). The organic phase was separated and the aqueous phase was extracted with ethyl acetate (3 × 20 mL). The combined organic phases were dried over Na₂SO₄, filtered and the solvent was evaporated in vacuo. The crude product was purified by flash column chromatography (20% ethyl acetate-hexanes) to afford compound 3 (170 mg, 46%) as a white solid.

Spin lattice relaxation experiments (T₁, NMR)

¹H T₁, NMR relaxation was measured on polycrystalline samples of compound 3 and 3-d₃ recrystallized from hexanes/ethyl acetate and polycrystalline samples of commercial mestranol 8 and mestranol-d₃ (8-d₃) recrystallized from ethanol. The experiments were carried out with a static wideline probe using solid-state spectrometer operating at a ¹H Larmor frequency of 300 MHz. The saturation recovery sequence used contains a saturation pulse comb followed by a time τ’ (τ’ values taken from the variable delay list) with a π/2 pulse p1. For each measurement, an acquisition time of 2.0985 ms was used. The ¹H spin-lattice relaxation experiments were determined for T=165 – 395 K. For compounds 3, 3-d₆, 8 and 8-d₃ the T₁ experiments were analyzed using the TopSpin software from Bruker and were suitably fit to a monoexponential behavior.