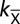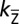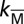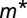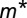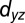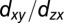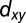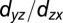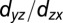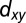Anisotropic two-dimensional electron gas at SrTiO₃(110)

Significance

Although still in its infancy, electronics based on all-oxide materials is a rapidly developing field, and strontium titanate is its key player. For this area to thrive, an atomic-scale control and understanding of the materials’ surfaces and interfaces needs to be achieved. A SrTiO₃ crystal with (110) orientation automatically forms an overlayer that is more insulating than the bulk and chemically less reactive, akin to the native SiO₂ on conventional wafer. With appropriate doping a two-dimensional electron gas (2DEG) forms underneath the SrTiO₃(110) surface. This (110) 2DEG is very different from (001): The effective mass here depends on the quantum number, and a completely flat band can be realized. Such a flat band bears good prospects for, among others, magnetism and thermoelectricity.

Abstract

Two-dimensional electron gases (2DEGs) at oxide heterostructures are attracting considerable attention, as these might one day substitute conventional semiconductors at least for some functionalities. Here we present a minimal setup for such a 2DEG––the SrTiO₃(110)-(4 × 1) surface, natively terminated with one monolayer of tetrahedrally coordinated titania. Oxygen vacancies induced by synchrotron radiation migrate underneath this overlayer; this leads to a confining potential and electron doping such that a 2DEG develops. Our angle-resolved photoemission spectroscopy and theoretical results show that confinement along (110) is strikingly different from the (001) crystal orientation. In particular, the quantized subbands show a surprising “semiheavy” band, in contrast with the analog in the bulk, and a high electronic anisotropy. This anisotropy and even the effective mass of the (110) 2DEG is tunable by doping, offering a high flexibility to engineer the properties of this system.

The 2D electron gas (2DEG) observed in oxide heterostructures such as LaAlO₃/SrTiO₃ (1, 2) offers a possible alternative to conventional semiconductors, not only for electronics at the nanoscale (3) but also because of the possibility of spin-polarized (4) and superconducting (5, 6) currents. An even simpler setup is to create a 2DEG directly at SrTiO₃. Recently this was achieved by irradiating a (001) surface (7, 8) with synchrotron radiation, albeit the origin of the resulting 2DEG is still under debate (7–9). This system has two major drawbacks: (i) surface oxygen vacancies are very reactive and (ii) the (001) surface has no unique surface termination, as TiO₂ and SrO terraces may develop, and the surface structure strongly depends on sample treatment and history (10).

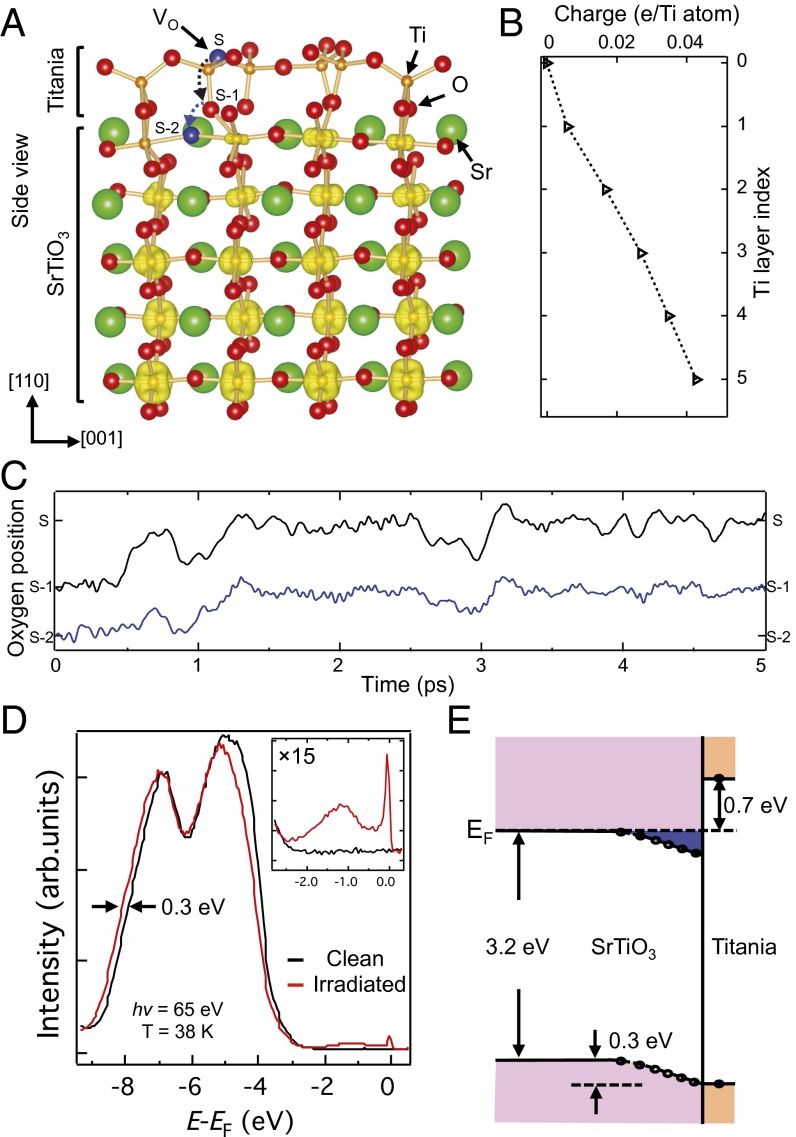
Here, we show that a 2DEG can also be induced at SrTiO₃(110), which is stabilized and covered by a reconstructed overlayer. This overlayer automatically forms to compensate the intrinsic polarity of the system. A SrTiO₃ crystal can be viewed as a stack of alternating (SrTiO)⁴⁺ and (O₂)⁴⁻ planes along the [110] orientation, resulting in a dipole moment that diverges with increasing crystal thickness (11). As is often true for polar surfaces, this is prevented by one of several compensation mechanisms (11). Specifically, the SrTiO₃(110) surface spontaneously forms a (4 × 1) reconstruction upon various different sample treatments, including annealing in a tube furnace with flowing high-purity oxygen (12) and standard ultrahigh vacuum preparation procedures (13, 14). The reconstruction consists of a 2D, tetrahedrally coordinated titania overlayer (Fig. 1A), which, with a nominal stoichiometry of (Ti_1.5O₄)²⁻, quenches the overall dipole moment (12, 15). Because the Ti atoms in the tetrahedral titania surface layer of the reconstruction are saturated by strong, directional bonds, the (4 × 1) surface is chemically quite inert (16).

Fig. 1.

SrTiO₃(110)-(4 × 1) surface. (A) Structural model; an oxygen vacancy (V_O) formed at the reconstructed surface spontaneously migrates to the (SrTiO)⁴⁺ plane beneath the top titania layer. The excess electrons from the V_O form a 2DEG confined within a region of about 2 nm thickness. The layer-dependent charge is represented by the yellow lobes and plotted in B. (C) MD simulation of the V_O diffusion from the surface (S) to the subsurface (S-2) sites represented by the accompanying upward oxygen migration from S-2 to S-1 (blue line) and from S-1 to S (black line). (D) Angle-integrated photoemission spectroscopy of the clean surface and after creating V_Os by synchrotron radiation. An in-gap state and a metallic peak near the Fermi level (E_F) develop (Inset). (E) Schematic band structure at a surface with V_Os; the bands bend downward by 0.3 eV as deduced from the spectra in D. The dots denote the surface potential obtained from the shift of Ti 3s states in DFT+U calculations.

Results and Discussion

Exposing the SrTiO₃(110)-(4 × 1) surface to synchrotron radiation creates oxygen vacancies (V_Os) at the surface (16); they spontaneously migrate beneath the titania overlayer; Fig. 1A and SI Appendix. The V_O’s downward diffusion mechanism is well described by ab initio molecular dynamics (MD) in terms of the concomitant upward diffusion of oxygen atoms from the topmost (SrTiO)⁴⁺ plane to the surface (see Fig. 1C and SI Appendix, Figs. S8 and S9 for details). This is a major difference from the SrTiO₃(100) surface, where oxygen vacancies remain at the surface; hence in that case the V_Os are not protected by an overlayer and will be filled when oxygen is present at the ambient. The subsurface V_Os at SrTiO₃(110) lead to electron doping, and the photoemission spectrum in Fig. 1D shows the development of a metallic peak at E_F. Simultaneously, the O 2p valence band in Fig. 1D shifts to higher binding energy, indicating a downward band bending of ∼0.3 eV (relative to E_F) in the vicinity of the surface. This is in agreement with the density functional theory (DFT+U) (17, 18) calculated potential shown as (layer-resolved) dots in Fig. 1E. Note that the topmost titania overlayer has a larger bandgap so that it is not only chemically but also electrically inert.

The pronounced surface potential arising from the downward band banding confines the free charge carriers to a thin layer so that a 2DEG develops beneath the titania overlayer. From our DFT+U calculations we conclude that the charge carriers are localized in the SrTiO₃ layers within about 2 nm thickness (Fig. 1B and SI Appendix, Fig. S12).

We now turn to the unusual properties of the 2DEG at SrTiO₃(110)-(4 × 1). Experimentally we identify these from angle-resolved photoemission spectroscopy (ARPES) experiments (see Figs. 3 and 4 below) but for a better understanding we start with a tight-binding modeling of this 2DEG; the details of the calculations are presented in SI Appendix, Sec. S12. In the bulk, SrTiO₃ has a gap of 3.2 eV and the three lowest conduction bands are Ti t_2g (i.e., 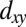, , 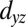and 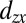; Fig. 2C) orbitals that are degenerate at the Γ-point. As the lobes of the 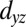orbital point into the y–z plane (see 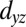in Fig. 2A), the 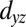band has a small hopping amplitude in the Γ–X direction and is hence weakly dispersive (heavy) along Γ–X. In contrast, 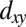and 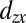have a larger overlap and hopping amplitude 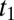in this direction, and are thus strongly dispersive (light), as well as degenerate. Along Γ–M, the 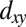band is strongly dispersive (light) with hopping amplitude 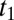, whereas the 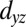and 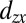bands are “semilight” with an effective hopping amplitude (t₁ + t₂)/2; Fig. 2C.

Fig. 3.

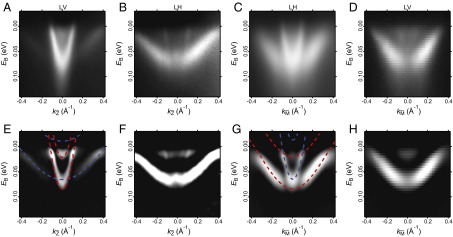
ARPES of the electronic structure at SrTiO₃(110)-(4 × 1). (A–D) Energy-momentum intensity maps (, 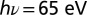) along the (or [001]) direction and the (or 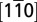) direction, respectively. (E–H) Corresponding second derivatives. In each direction, the spectra were measured with linear vertical (A and D) and linear horizontal (B and C) polarized light. Tight-binding fits are overlaid for both directions. The 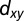-like bands are drawn in blue and the 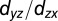-like bands in red. The 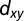-derived bands are weakly dispersive and 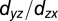-derived bands are strongly dispersive along [001]; the 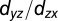-derived bands become weakly dispersive and 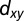-derived band becomes strongly dispersive along 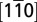. The subbands become more visible in E–H.

Fig. 4.

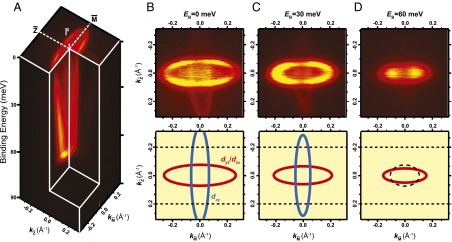
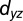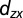Overview of the electronic structure. (A) Full photoemission mapping and (B–D) constant energy cuts at different binding energies (E_B = 0, 30, and 60 meV) and schematic constant-energy surfaces (Lower). Data taken with LV light, which emphasizes and orbitals. These appear bright, whereas 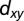-derived states appear faint. In the schematics the reconstructed (4 × 1) Brillouin zone is indicated by dotted lines. Note that the Fermi surface lies in the (1 × 1) Brillouin zone, consistent with the 2DEG being confined at the SrTiO₃ layers beneath the surface reconstruction. At higher binding energy, E_B = 60 meV, only the 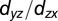-derived ellipsoid is occupied. The resulting constant-energy surface is strongly anisotropic compared with the bulk projected energy surface (black dashed ellipsoid).

Fig. 2.

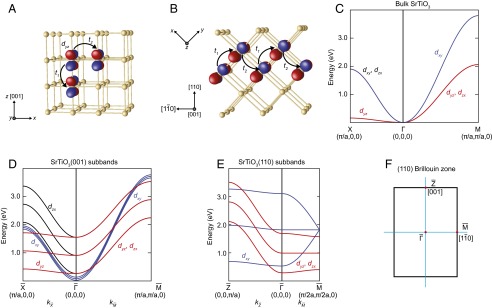
Effect of quantum confinement on the electronic structure of (001)- and (110)-oriented SrTiO₃. (A and B) Schematics of the Ti lattice in SrTiO₃ oriented along the [001] and [110] direction, respectively. Ti 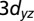orbital lobes expand in the y–z plane. Large 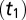and small 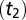hopping amplitudes depend on the overlap of the nearest-neighbor d orbitals. (C) Bulk band structure of SrTiO₃, consisting of a heavy 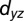band (red) and light 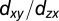bands (blue) along 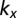, as well as a light 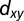band (blue) and semilight bands (red) along . 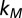(D and E) Quantum well states (or subbands) of SrTiO₃ confined along the [001] and [110] direction, respectively. The band dispersions of all the quantum well states confined in the (001) direction are the same as in the bulk. Confinement along (110) is different: here the 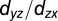band becomes semiheavy along the 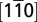direction and the different (110)-quantum-confined states have a different mass. (F) 2D Brillouin zone of the SrTiO₃(110) surface.

When the 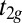electrons are now confined within a few nanometers at the SrTiO₃(001) surface, quantum well states (or subbands) are formed. Due to the anisotropy of the 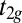orbitals, the level spacing of the quantized subbands strongly depends on the orbital character (7, 19, 20). Notwithstanding, the [001] confinement does not change the carrier properties, i.e., the band dispersion of the subbands stays the same as in the bulk (Fig. 2D). In striking contrast, a confinement along the [110] direction modeled with a wedge-shaped potential well (Fig. 1E) strongly changes the properties of the carriers, i.e., their band dispersion. As we show in SI Appendix, Sec. S12, the effective hopping amplitude of the 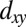orbital along the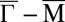 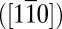direction becomes 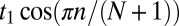, where N is the number of layers and n the quantum number (or subband index). That is, the effective mass of the quantum confined states now depends on the subband index n. For particular values of n, such as 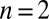in Fig. 2E, the dispersion becomes flat. This is also the case for the 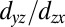orbitals where the quantum confinement leads to an effective hopping amplitude 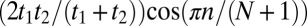along 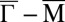. Here, in addition to the quantum number n dependence, the prefactor also changes from its bulk value. As 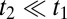, this prefactor is 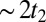so that the 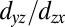bands become semiheavy, whereas they are semilight (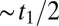; Fig. 2C) in the bulk. A simple picture for this semiheavy behavior is that the 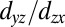electrons are quantum confined along [110] and movement along 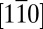requires a zigzag path with hopping amplitude alternating between 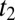and 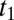; Fig. 2B. Hence only one 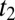hopping is required for moving the electrons by two sites, which explains the effective hopping amplitude .

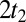Fig. 3 shows ARPES results from the SrTiO₃(110)-(4 × 1) surface. The measurements were taken along the [001] and 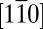directions. The intensity of the observed bands strongly depends on the light polarization (linear vertical, LV, and linear horizontal). These dichroic effects are due to selection rules (21), and allow disentangling the symmetry and orbital character of the various bands (SI Appendix, Figs. S1–S3). 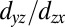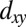This enables us to ascribe the strongly and weakly dispersing bands along the [001] direction to - and -like orbitals, respectively. 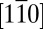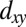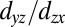Accordingly, the strongly and weakly dispersing bands along the direction correspond to - and -like orbitals.

The strongly (weakly) dispersing 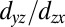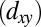-like band along [001] has a bandwidth of ∼72 meV (∼62 meV) and a Fermi momentum of 0.11 Å⁻¹ (0.40 Å⁻¹). A fit to a parabolic dispersion yields an effective mass 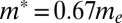(9.7 m_e), with m_e the free electron mass. These [001] effective masses are consistent with those from a 2DEG on the vacuum-fractured SrTiO₃(001) surface (7, 8) and the tight-binding description; Table 1. Around the Γ-point the orbital degeneracy is lifted by a splitting of ∼10 meV between the 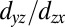- and 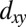-like bands.

Table 1.

Comparisons of experimental and theoretical effective masses of 2DEGs

	SrTiO3(001)		SrTiO3(110)
	Along		Along		Along
Expt.	10∼20†	0.7†	9.7	0.67	6.1	0.74
		0.5∼0.6‡
Theor.	8.2	0.6	8.2	0.6	4.7	0.6
Orbital

The experimental effective masses are slightly larger than those obtained from tight-binding calculations, indicating a minor mass renormalization due to electronic correlations.

^†Ref. 7.

^‡Ref. 8.

From our tight-binding calculations we expect a quite different behavior along the 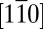direction. The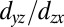 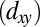-derived ARPES bands have bandwidths of ∼72 meV (62 meV), Fermi momenta of 0.34 Å⁻¹ (0.10 Å⁻¹), and effective masses of 6.1 (0.74); Fig. 3 C and D. The former corresponds to a semiheavy band distinct from its semilight behavior in the bulk. In particular, the semiheavy carriers predicted by the tight-binding calculations agree well with the experimental ones; see Table 1 for a summary of the effective masses.

Fig. 3 E–H shows the second derivatives of the ARPES data along with the corresponding tight-binding subbands dispersion (Fig. 3 E and J). In addition to the bands discussed above, shallower bands become more visible. These are attributed to 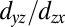-like subbands, indicating that quantum well states of a 2DEG are formed at SrTiO₃(110). The 2D character of the observed bands is further confirmed by the fact that the bands have no dispersion along the [110] direction (surface normal) in photon-energy-dependent measurements (SI Appendix, Fig. S4). From the tight-binding calculations we found both 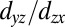- and 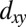-like carriers to be confined within ∼2 nm, in excellent agreement with the DFT+U prediction (SI Appendix, Figs. S12 and S15).

Fig. 4 shows full photoemission mapping and constant-energy cuts obtained with LV light polarization and detection along the 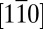direction. The resulting Fermi surface consists of two perpendicular ellipsoids and a small ellipsoid centered at the Γ-point. The bright (faint) ellipsoid is derived from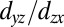 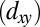-like band and has semiaxes of ∼0.11 Å⁻¹ (0.4 Å⁻¹) and 0.34 Å⁻¹ (0.10 Å⁻¹) along [001] and 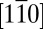, respectively. From the area (A_F) enclosed by each Fermi surface, the corresponding 2D carrier density is 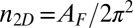. Taking into account the three bands that cross E_F, we find 0.39 electrons per 1 × 1 unit cell of SrTiO₃(110) (or about 1.8 × 10¹⁴ cm⁻²), a value even larger than the sheet carrier density measured at the bare SrTiO₃(100) surface (7, 8).

The Fermi surface measurements further support the conclusion that the 2DEG is not residing at, but underneath, the reconstructed surface layer, as in the former case we would expect a gap opening related to the “4×” periodicity along the [001] direction. Indeed, the Fermi surface lies in the (1 × 1) but not in the reconstructed (4 × 1) Brillouin zone (the latter is indicated by the dashed lines in Fig. 4 B–D).

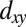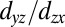Our results explain the dopant-dependent anisotropy at the (110)-oriented LaAlO₃/SrTiO₃ interface that was observed recently (22). Although both - and -derived Fermi surfaces are strongly anisotropic, the difference along the [001] and 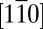directions themselves is not very pronounced at higher carrier density, when both ellipsoids are occupied (Fig. 4). However, at a higher binding energy of 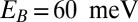, only the 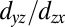-derived ellipsoids appears, with a corresponding carrier density of ∼1.7 × 10¹³ cm⁻². Remarkably, this is the same carrier density where a pronounced anisotropic conductivity was observed in transport measurements (22). At this doping level, the big difference between the semiheavy and light carriers comes to bear. In the bulk, however, the anisotropy is not so pronounced (see the dashed ellipsoid in Fig. 4D).

In conclusion, we have demonstrated that an anisotropic 2DEG can be created on SrTiO₃(110). The chemically inert and electrically insulating titania overlayer is native to this system, as it forms spontaneously to lift the intrinsic polarity of this system. It provides for a 2DEG that should be less vulnerable against atmospheric contamination than a 2DEG at the bare surface, and less dependent on the chemical complexity inherent to interfacial 2DEGs. The (110) 2DEG turns out to be strikingly different from the (001) 2DEG, which has been the subject of previous ARPES studies. The band dispersion is not only distinct from the one of the bulk, it even depends on the quantum number for the (110) confinement. Hence one can engineer a completely flat band along 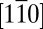, offering good prospects to find exotic properties in the future. For example, as was shown firstly in ref. 23, a flat band naturally leads to so-called “flat-band ferromagnetism,” hence offering a route to spin-polarized currents. The high density of states associated with the flat band is also advantageous for thermoelectric applications (24) and affects superconducting properties (25). To exploit the flat-band physics as well as the anisotropic features of the (110) 2DEG, a tuning of the carrier density is needed. This is possible in principle by the amount of oxygen vacancies, applying an electric field (26), and the deposition of metal adatoms on the titania overlayer (27). An alternative, more robust way of generating this (110) 2DEG might be a (110)-oriented heterostructure consisting of buried δ-doped La:SrTiO₃ layers sandwiched in between undoped SrTiO₃ buffer layers.

Materials and Methods

Experiments.

The Nb-doped (0.5 wt %) SrTiO₃(110) surface was prepared by cycles of Ar⁺ sputtering (1 keV, 5 μA, 10 min) followed by annealing in 3 × 10⁻⁶ mbar oxygen at 900 °C for 1h. The samples were heated by electron bombardment and the temperature was monitored with an infrared pyrometer. The surface reconstruction was checked by low-energy electron diffraction (LEED) and tuned by depositing Sr metal on the surface, followed by annealing until a sharp (4 × 1) LEED patter was observed (14). The ARPES measurements were performed at the ARPES 1² beamline (BESSY II storage ring at the Helmholtz-Zentrum Berlin). All ARPES spectra were recorded using photon energies of 50–70 eV, linearly polarized along the horizontal or vertical direction. A Scienta R8000 analyzer with vertical detection slit geometry was used, with the energy and angular resolution of ∼10 meV and 0.3°, respectively. Sample temperature was at ∼38 K.

Theory.

DFT calculations with the inclusion of an effective on-site Coulomb repulsion 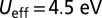for the Ti d states were carried out with the Vienna ab initio simulation package, VASP (17, 18), within the projector augmented-wave method and the Perdew–Burke–Ernzerhof functional (28). The computational cell was modeled with a symmetric slab consisting of 45 atomic layers separated by a 12-Å-thick vacuum region. One oxygen vacancy was created on both sides of the symmetrical slab (SI Appendix). The kinetic-energy cutoff for the plane-wave expansion was set to 600 eV. We adopted a (4 × 1) 2D unit cell, and a (2 × 3 × 1) Monkhorst–Pack k-point mesh. During the structural optimization, atoms in the central nine layers were kept fixed to the corresponding bulk positions, whereas the other atoms were allowed to relax until the forces on each atom were less than 0.02 eV/Å. The V_O diffusion was studied in a seven-layer-thick slab by means of ab initio canonical molecular dynamics at a simulating temperature of 1000 K for 5 ps, with a time step of 1 fs, using the Nosé thermostat (29).

The hopping parameters for the tight-binding calculations have been obtained both by (i) fitting the nearest-neighbor hopping parameters to the DFT bandwidth of bulk SrTiO₃ yielding 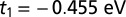and 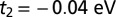, and (ii) more thoroughly through a Wannier function projection (30, 31) of a Wien2K (32) DFT calculation, using the generalized gradient approximation (28) and 10 × 10 × 10 k-point grid. For further tight-binding calculations, up to next-nearest-neighbor hopping has been taken into account; see SI Appendix, Secs. S12 and S13 for details.