Harvesting renewable energy from Earth’s mid-infrared emissions

Significance

Renewable energy can be generated whenever heat flows from a hotter to a colder body. One such flow is from the warm surface of Earth to cold outer space, via infrared thermal radiation. An emissive energy harvester (EEH) is a device that can generate energy from emitting thermal radiation into the clear sky. We calculate how much power is thermodynamically available, using a location in Oklahoma as a case study. We discuss two possible ways to make such a device: A thermal EEH (analogous to solar thermal power generation) and an optoelectronic EEH (analogous to photovoltaic power generation). For the latter, we propose using a rectifying antenna, and we discuss its operating principles, efficiency limits, system design considerations, and possible technological implementations.

Abstract

It is possible to harvest energy from Earth's thermal infrared emission into outer space. We calculate the thermodynamic limit for the amount of power available, and as a case study, we plot how this limit varies daily and seasonally in a location in Oklahoma. We discuss two possible ways to make such an emissive energy harvester (EEH): A thermal EEH (analogous to solar thermal power generation) and an optoelectronic EEH (analogous to photovoltaic power generation). For the latter, we propose using an infrared-frequency rectifying antenna, and we discuss its operating principles, efficiency limits, system design considerations, and possible technological implementations.

Whenever energy flows from hotter to colder, there is an opportunity to harvest renewable energy. For example, solar energy and biofuels rely on the energy flow from the Sun to the Earth, and wind power and hydroelectricity rely on the energy flow from hotter to colder areas on Earth. However, there is one massive energy flow that has been neglected: The roughly 10¹⁷ W of infrared thermal radiation that Earth continuously emits into cold outer space. The technology does not yet exist to siphon renewable energy out of this flow, but we will argue that it is possible to make a device that does exactly that. We call such a device an emissive energy harvester (EEH).

In general terms, we propose a device that has a large emissivity in the long-wave infrared (LWIR) “atmospheric window” at 8–13 µm, where the atmosphere is mostly transparent, and small emissivity at other wavelengths, where the atmosphere is mostly opaque. It would sit outdoors with its emissive surface pointing upward, emitting thermal radiation toward the sky, but receiving far less radiation back (1, 2). This imbalance between incoming and outgoing radiation can be converted into an imbalance in electron motion, i.e., into useful electrical power. With a perfectly transparent atmosphere, an EEH would be a kind of heat engine harnessing the temperature difference between Earth’s surface at ∼275–300 K and outer space at 3 K. However, because the atmosphere is not perfectly transparent, EEH power generation will be affected by weather and atmospheric conditions—and stopped altogether by thick, low clouds. On the other hand, because the Sun emits negligible LWIR compared with the atmosphere, an EEH can operate during both day and night. The effects of sunlight are discussed in more detail below.

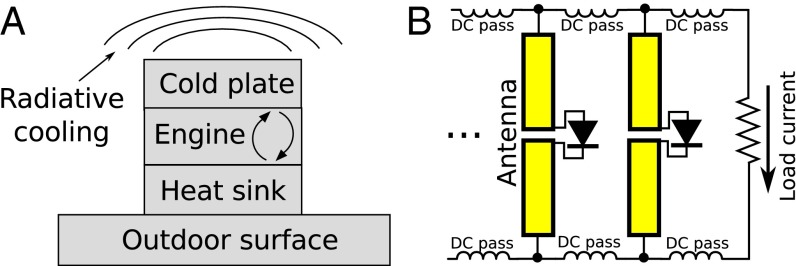
One possible design of an EEH, shown in Fig. 1A, is a heat engine running between the ambient temperature and a cold panel, where the latter maintains its temperature by radiative cooling (1, 2). We will argue below that this is not the most promising EEH design, but it is a simple example that illustrates the principle.

Fig. 1.

Two possible EEH designs. (A) In a thermal EEH, a heat engine operates between the ambient temperature and a radiatively cooled plate. (B) In an infrared rectenna EEH, the whole panel is at ambient temperature, but the circuit’s electrical noise is coupled to the cold radiation field via antennas.

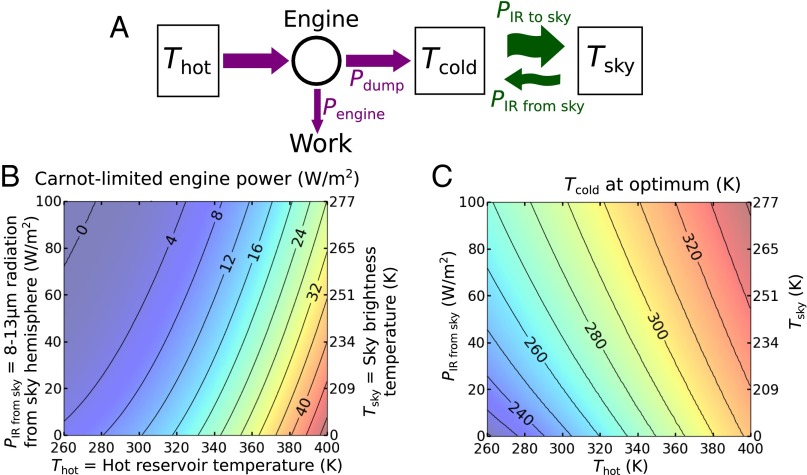
Fig. 2A shows the energy flows involved in EEH operation. There are three relevant temperatures, T_hot > T_cold > T_sky, corresponding to the hot reservoir temperature, the cold panel temperature, and the radiation brightness temperature of the sky, respectively. T_sky is calculated via Planck’s law from P_{IR from sky}, the incident 8–13-µm LWIR radiation power from the sky hemisphere. (T_sky is a weighted average of the air temperature at all levels of the atmosphere, along with the temperature of outer space.) Although T_hot and T_sky are fixed by external constraints, T_cold can be varied, by adjusting engine throughput, to maximize useful power generation. This maximum is calculated by combining Carnot’s law with the assumption of steady-state heat flow:

(see Fig. 2A for definitions). Putting these together, the maximum possible power generation (shown in Fig. 2B) is:

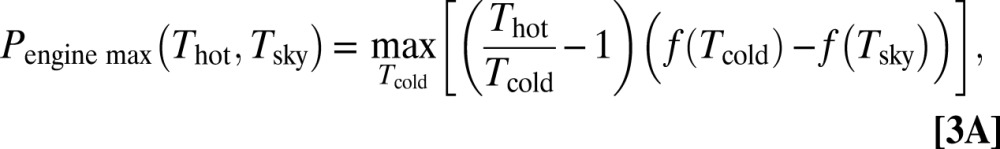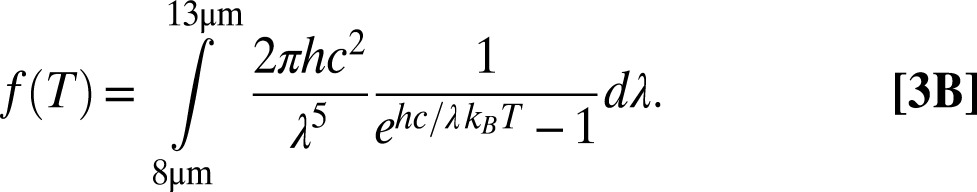Fig. 2.

Energy flows and the Carnot-limited power of an EEH. (A) The cold reservoir accepts heat from the engine, and radiates it into the sky, with T_hot > T_cold > T_sky (T_sky is the sky radiation brightness temperature). Assuming T_hot and T_sky are fixed, the engine throughput can be adjusted to achieve a T_cold that maximizes power generation. The maximal power (B), and corresponding T_cold (C), are calculated assuming the cold reservoir has a hemispherical field of view, a perfect (blackbody) emissivity in 8–13 µm, and zero emissivity at other wavelengths.

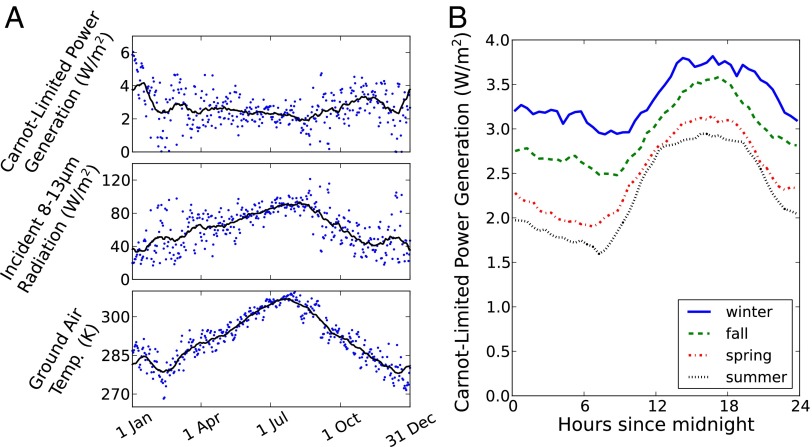
The data in Fig. 2B are not useful without an understanding of what the sky radiation might be in practical situations. Therefore, as a case study, we examine hypothetical ideal EEH performance at Lamont, Oklahoma, where a facility has been measuring downwelling LWIR radiation intensity spectra (3–5). In Fig. 3, we use the 2011–2012 data (3) to calculate the Carnot-limited power generation based on Eq. 3. We have assumed that T_hot equals the ground air temperature, and T_sky is calculated from the incident 8–13µm intensity (Fig. 3A; Supporting Information). An EEH works best when there is little downwelling radiation; i.e., when the air is cold and dry, and also works best when the ground is hot (Fig. 2B). Because these two conditions are anticorrelated, the power does not dramatically vary over the year, although it is somewhat higher during winter. Within each day, the power typically peaks in the afternoon and evening, when the ambient temperature is highest. The year-round, 24-h average power is 2.7 W/m², or 0.06 kWh/m² per d. In principle, Earth has enough EEH power to power all of humanity many times over, but this power density is quite low for large-scale generation applications. At this particular location, even a 1.5%-efficient photovoltaic panel could generate the same total energy (6). However, these calculations all assume that the hot reservoir stays at the ambient air temperature, and is not heated by sunlight. As discussed below, the power generation could be perhaps 5 times higher with solar heating.

Fig. 3.

Theoretical EEH power generation potential at Lamont, OK, 2011–2012, for a Carnot-efficient panel at the ambient air temperature (3) (Supporting Information). (The power could be 5 times higher if the panel heats under sunlight.) (A) EEH power generation, incident radiation, and ground air temperature variation over a year. Each point is a daily average assuming 24-h operation. Solid lines are 1-mo moving averages. (B) Average daily profile of instantaneous power for each of the four seasons.

We may define the EEH percentage efficiency as P_{engine max}/f(T_hot), in which case the Carnot-limited EEH efficiency in the above example is 1–2%. This is far lower than (1 – T_sky/T_ambient) ∼ 15%, because entropy is generated in the light emission process, i.e., because T_cold is not as cold as T_sky. There is an analogous situation in solar power: A calculation similar to Eq. 3 gives a Carnot-limited solar-cell efficiency of ∼87% (under highly concentrated sunlight), which is lower than the “Landsberg limit” of (1 – T_ambient/T_sun) ∼ 93%, because entropy is generated in the light absorption process (7). In this work, we treat the entropy generated during absorption and emission as an unavoidable loss, but in principle, it can be reduced in certain situations by using magnetooptical components that break time-reversal symmetry (7, 8).

Cooling Certain Electronic Degrees of Freedom

The EEH design discussed above and in Fig. 1A is conceptually simple, but challenging in practice. It is usually quite difficult to radiatively cool an object far below ambient (Fig. 2C), because the object cannot be perfectly isolated from the air and ground, nor (during daytime) from sunlight (1, 2, 9, 10). We will focus instead on a quite different, optoelectronic approach, inspired by photovoltaics.

In a photovoltaic cell under sunlight, most degrees of freedom stay near ambient temperature, including atomic motion (phonons) and electron motion (intraband excitations). However, the sunlight creates electron–hole pairs far in excess of their thermal-equilibrium density. For example, a 300-K piece of silicon under sunlight may have as many electron–hole pairs as an 800-K piece of silicon in the dark. The sun is therefore heating the interband excitation degree of freedom (11), and the material itself remains at ambient temperature. In an analogous way, an EEH could work by radiatively cooling one or more electronic degrees of freedom, while the material itself remains at ambient temperature.

Although photovoltaics are a good inspiration, the analogy is limited. A semiconductor p–n junction EEH is possible in principle, but probably not in practice, due to the frequent Auger recombination and generation in room-temperature midinfrared-bandgap semiconductors (see below for details). A much more promising candidate is the rectifying antenna, or rectenna (Fig. 1B). Rectennas are traditionally used to generate power from microwaves (12), but have also been demonstrated for higher-frequency radiation, up to visible (12–18).

We mention for completeness that, in addition to work toward rectennas harvesting visible and near-IR solar light (12, 13, 15, 19), there have also been occasional suggestions in the literature to use rectennas or other devices to harvest energy from LWIR radiation (20–23). However, these analyses have neglected the thermal fluctuations of the diode, as discussed below and in ref. 12, which leads to the absurd conclusion that a room-temperature device can generate useful power from collecting the ambient radiation from room-temperature objects.

Nevertheless, a LWIR rectenna can generate useful power by operating as an EEH. The normal description of what a rectenna does is as follows: A radiation field creates an AC voltage across the antenna, which the diode rectifies to DC. This description, which does not consider the thermal fluctuations of the diode (12), is too simplistic for our purposes. Instead, we will view the rectenna as a variant of the diode-resistor generator circuit (24, 25) in which DC power is generated when a resistor and diode with two different temperatures are connected. Therefore, we aim to answer two questions: First, what is a diode-resistor generator circuit and how does it work? Second, how is this circuit related to a rectenna EEH?

Starting with the first question, Fig. 4 shows the simplest kind of classical diode-resistor generator circuit. This circuit and its variants have been discussed in the literature (24–28), mainly as a toy model to quantitatively explore the thermodynamics of nonlinear systems. We provide here a qualitative overview of how this circuit can generate DC electric power, in an ideal classical circuit theory analysis. We defer to the references for further discussion and quantitative analysis (24–28), as well as experimental verification (25).

Fig. 4.

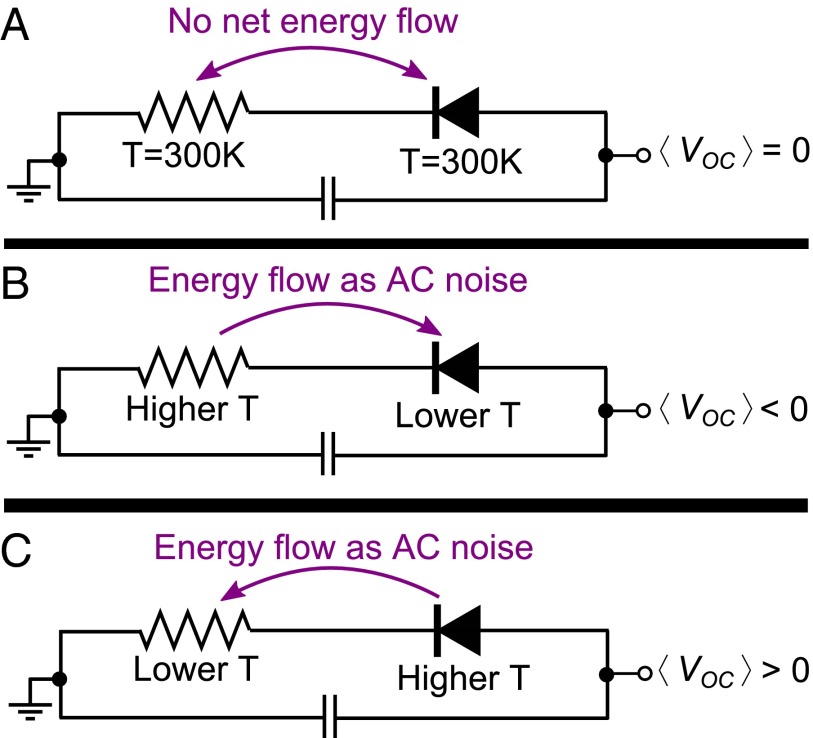
A diode-resistor generator circuit with different temperature inputs; <V_OC> is the time-averaged voltage under open-circuit conditions. (A) In thermal equilibrium, there is no net energy flow, and no open-circuit voltage. (B) This is a conventional rectifier circuit: The diode rectifies the resistor’s AC noise to a DC signal. (C) The behavior of a hot diode/cold resistor circuit can be extrapolated from A and B.

Fig. 4 shows the diode-resistor generator circuit in three configurations: in thermal equilibrium (Fig. 4A), as a conventional rectifier (Fig. 4B), and in the unusual configuration with a hot diode (Fig. 4C). As discussed below, a rectenna EEH operates similarly to Fig. 4C. (In this idealized analysis, the capacitor’s temperature does not matter—lossless components do not generate thermal noise.)

Physically, in Fig. 4B, the temperature difference causes a net diffusion of electrons in the form of a rectified current, which will negatively charge the capacitor. When the sign of the temperature difference is inverted (hot diode), as in Fig. 4C, the electron flow is in the opposite direction leading to a positively charged capacitor. In this regime, the diode’s role is to create thermal voltage fluctuations with asymmetric properties, i.e., favoring a certain direction of current. The diode’s fluctuations are asymmetric because its current-voltage (I-V) curve is asymmetric—Johnson noise is proportional to the diode AC impedance, i.e., its differential resistance at the device bias point.

Next, how does this diode-resistor generator circuit relate to a rectenna? Normally, a lossy electrical component at temperature T generates electrical noise with the same noise temperature T. However, an antenna is different: As long as its radiation efficiency (ratio of radiation resistance to total resistance) is high, its electrical noise temperature equals the brightness temperature of the incoming radiation field (29). In other words, an antenna in a strong radiation field imitates a hot resistor, and an antenna in a weak radiation field imitates a cold resistor, regardless of the temperature of the antenna itself. This is unsurprising in light of the fluctuation–dissipation theorem: A resistor dissipates electrical energy into phonons, and an antenna “dissipates” electrical energy into electromagnetic radiation.

In this way, a rectenna in a strong radiation field imitates a hot resistor/cold diode generator circuit (like Fig. 4B), and a rectenna in an especially weak radiation field imitates a hot diode/cold resistor generator circuit (like Fig. 4C). The former describes the normal use of rectennas, and the latter describes a rectenna EEH. Again, both these circuits are expected to generate DC voltage and current, with opposite polarities in the two cases (24, 25).

Therefore, in principle, a rectenna in a weak radiation field should work as an optoelectronic EEH. However, what operating efficiency could it achieve in practice? Infrared-frequency rectennas are a developing technology, and only proof-of-principle devices have been made to date (16). As described below, the devices made so far would generate negligible EEH power. However, rectenna technology may improve in the future. A different question is whether a rectenna EEH can approach the Carnot limit in principle. A proper theoretical calculation, including quantum effects and frequency-dependent components, has not been done. However, if the rectenna can achieve a voltage |V| ≫ hν/e ∼0.15 V (h is Planck’s constant, ν is frequency, and e is the elementary charge), a classical circuit-theory analysis is appropriate (30). These analyses have concluded that the simplest diode-resistor generator circuit (Fig. 4A) has an efficiency limit lower than Carnot by as much as a factor of 10 (24), but that a more complex circuit with a second diode can approach the Carnot limit (26, 27).

More Power Available Through Heating

A key difference between the two EEH designs in Fig. 1 is the effect of sunlight. If the EEH emissivity in the visible and near-infrared (NIR) were exactly 0, as assumed above, then sunlight would have negligible effect on the EEH. However, consider what happens in the more realistic case, in which some or all of the sunlight is absorbed. In the thermal EEH (Fig. 1A), solar heating of the sky-facing panel is detrimental, and would make daytime operation quite difficult (1, 10). In the rectenna EEH (Fig. 1B), on the other hand, the panel should be as hot as possible (Fig. 2B), so solar heating actually helps. The key is that the antenna, optimized for 8–13 μm, can have very low radiation efficiency in NIR and visible, which isolates the sunlight from the cold electronic degrees of freedom. In other words, the sunlight energy goes into the cold reservoir for the thermal EEH, but into the hot reservoir for the rectenna EEH (cf. Fig. 2A). There is an analogous situation in solar power generation: Auxiliary heat sources are helpful for solar–thermal generators, but harmful for photovoltaics.

Therefore, in applications, a rectenna EEH could absorb sunlight to warm far above ambient temperature during daytime. Black color is enough to make a sunlit object hot, but even higher temperatures (in excess of 100 °C) are possible by using solar-cooker techniques such as reflectors and insulated enclosures (31). An enclosure window could be made of polyethylene, which is transparent in both visible and LWIR (1, 9). Integration with solar water heaters is another promising direction.

A solar-heated rectenna EEH is similar to a small-scale solar–thermal Seebeck generator, in that both use solar heating to generate electricity with no moving parts. However, they work differently on both a system level (e.g., requirements for heat flux and heat sinks) and a device level (e.g., it may turn out that rectennas are more efficient and manufacturable than thermoelectrics).

In the case study of Lamont, Oklahoma, discussed above and in Fig. 3, it was assumed that the hot reservoir stays at the ambient air temperature. The conclusions are quite different if the panel is a solar-heated rectenna EEH. For example, suppose that solar-cooker techniques raised the panel temperature from 20 to 100 °C. Then the Carnot-limit engine power would rise from 1.2 to 20 W/m² (assuming P_{IR from sky} = 80 W/m²; Fig. 2B). The 24-h-average power would increase about fivefold in this example.

Possible Technology Implementations and Challenges

In this final part of the paper, we assess the likeliest paths toward a practical EEH technology. As described above, an EEH could be thermal or optoelectronic. For a thermal EEH, there are two primary technological requirements. The first requirement is a low-temperature-differential heat engine. This challenge is familiar because it arises in the context of waste-heat harvesting and similar applications (32, 33), and we will not discuss it further. The second requirement is a panel with good radiative-cooling properties—blackbody in LWIR, whitebody or transparent in NIR and visible (1, 2, 9, 10). This challenge is familiar because it arises in the context of improving the energy efficiency of buildings in warm climates (1, 2). Nanophotonic technology may enable breakthroughs in this area: According to recent simulations, a nanostructured metal–dielectric panel can achieve net cooling even under direct sunlight (10). If these predictions are borne out, a thermal EEH will be possible, although it will remain challenging to achieve reasonable cost, efficiency, and manufacturability.

For the rest of the section, we will discuss the optoelectronic EEH. We start more specifically with the rectenna EEH. A rectenna, at its simplest, consists of an antenna and a diode. Out of these two components, the antenna is relatively straightforward, in the sense that its challenges are well understood and apparently tractable. Recent work indicates that soft lithography can be used to manufacture infrared antennas over large areas at reasonable cost (21). The diode, however, requires much more work and thought.

We believe that diode asymmetry at low voltage is the central challenge in developing a working rectenna EEH. A diode cannot show very asymmetric conductance if the voltage is too low. Unfortunately, too-low voltage is expected in a rectenna EEH using conventional designs. For example, the infrared rectenna made by Fumeaux et al. (34) used a 70-Ω bowtie antenna matched to a 70-Ω metal-insulator-metal (MIM) diode. If this configuration were used as an EEH, the oscillating thermal-noise voltage across the diode would be a mere ∼1 mV_rms, calculated by integrating the 300-K Johnson noise formula over the 8–13-µm frequency window. At such a low voltage, the MIM diode has negligible asymmetry—it would behave like an ordinary resistor—so the circuit would not generate DC power.

Why, more precisely, does an only slightly asymmetric diode preclude an efficient EEH? A slightly asymmetric diode can be thought of as a very asymmetric diode in parallel with a shunt resistor. The shunt resistor draws current that dissipates the circuit’s power, especially reducing the open-circuit voltage. The importance of strong diode asymmetry is unique to rectenna energy harvesters, and is not such a severe problem for rectenna infrared detectors: these detectors work at zero bias where the shunt resistor will not affect the DC current (the shunt resistor is merely an undesirable generator of noise).

This problem, i.e., insufficient diode asymmetry at low voltage, can be addressed technologically in two ways. First, the voltage could be increased. Second, a diode could be used that is asymmetric at extremely low voltage.

The first approach—a relatively-high-voltage rectenna EEH—requires matching a high-feedpoint-impedance antenna to a high-differential-resistance diode. Such components would generate a larger oscillating voltage and a smaller current. For example, a 70-mV_rms oscillation could be generated by the noise of a 300-K diode, if its impedance is 500 kΩ. If the diode is to efficiently transfer power to the antenna, the antenna’s feedpoint impedance should be equally high, or alternatively an impedance transformer could make up the difference. For example, a 500-kΩ diode could be matched to a 70-Ω bowtie antenna (34) using a broadband impedance transformer with the unusually large step-up ratio of 7,000. Such a ratio could be achieved at a single frequency by using a high-quality-factor electromagnetic resonator. However, it is not clear how to achieve such a large step-up ratio across a reasonable bandwidth. There have been helpful recent developments in this direction (35, 36), including the discovery of terahertz transmission lines with extremely high characteristic impedance (37), and the fabrication of plasmonic waveguides with 3D tapers (38). A suggestive example along these lines is shown in Fig. 5A. In summary, we believe that this approach has not been adequately explored.

Fig. 5.

Illustrations of possible directions toward a practical EEH. (A) An antenna connected to a very-high-impedance infrared transmission line (37), which also functions as a MIM traveling-wave rectifier (16). (B) A rectenna EEH incorporating a backward diode. Tunneling diodes such as this have high on/off ratio at relatively low voltage (39–41)—a key EEH requirement. (C) MIM tunnel diodes can have low-voltage rectification in certain geometries (23); also, the sphere’s local plasmon resonance could help increase voltage. (D) Ballistic diodes are also good at low-voltage rectification, and therefore promising for EEHs. In this figure, electrons travel more easily rightward than leftward through the constriction (42–44). (E) A quantum cascade EEH is an example of an optoelectronic EEH not based on rectennas. See text for description.

For the second approach—a rectenna EEH enabled by an ultralow-voltage diode—the challenge is to make an appropriate diode. Diodes with a high ratio of forward-to-backward conductance at very low voltage (far below k_BT/q) are unusual and challenging, but not impossible. Three prototypical examples are shown in Fig. 5 B–D.

Tunnel diodes (Fig. 5 B–C) are one category of low-voltage diodes. In particular, a material’s density of states (DOS) can have a sharp feature, from which a tunnel diode can inherit an equally sharp voltage dependence. For example, in backward diodes, an applied voltage can create an overlap between a conduction band and a valence band, and the sharpness of the band edge controls the sharpness of the diode turn on. Indeed, backward diodes work at lower voltages than even Schottky diodes (39). Tunnel diodes based on lower-dimensional electronic systems are believed to have even sharper turn on (40), and ongoing research has uncovered promising designs (41). Although MIM diodes are the traditional tunnel diodes for infrared-frequency applications, they are not normally low-voltage diodes, because metals do not have sharp DOS features. However, they can operate at low voltage using a different mechanism: When the electron-tunneling probability is low, it becomes exquisitely sensitive to the shape of the barrier. For example, a recent study has calculated that a sharp metal tip near a metal plane should function as a diode with a 400:1 forward-to-backward conductance ratio at ±100 mV (23) and T = 0 K. This result is encouraging, but more work is needed to clarify whether it can work at even lower voltages, at high temperature, and at an appropriate capacitance and impedance.

A second category of ultralow-voltage diodes are ballistic devices with geometrical asymmetry (Fig. 5D) (42–44). These are said to operate at arbitrarily low voltage, even at room temperature (42–44), and they have low capacitance. For a ballistic diode to work in this application, the electron transit time through the device must be not only much faster than the scattering time, but also much faster than an LWIR optical half-cycle, around 15 fs. This requires a much smaller device than those made to date; for example, an electron traveling at the Fermi velocity in graphene can move just 15 nm in 15 fs. It is not clear how to fabricate such a device, or whether it would still work properly when scaled down, but this is an interesting avenue for future research.

As mentioned earlier, rectennas are not the only possible approach to an optoelectronic EEH, although we believe they are most promising. For completeness, we discuss two nonrectenna possibilities. One possibility is a p–n junction from a small-bandgap (LWIR absorbing) semiconductor. Current would flow in the forward direction despite a small reverse bias, because radiative recombination would occur more frequently than photogeneration, thanks to the lack of incoming radiation. Unfortunately, at room temperature, nonradiative (especially Auger) recombination and generation would occur far more frequently than radiative processes (45), and the result would be a very low efficiency EEH.

Fig. 5E shows another nonrectenna optoelectronic EEH, based on intersubband transitions in a multiple-quantum-well heterostructure (the quantum wells are not shown). The thick arrows depict an electron path: Thermal diffusion to higher energy, followed by photoemission. This process moves electrons rightward despite an opposing voltage. The inverse process—relaxation to lower energy, followed by photon absorption—occurs less often due to a lack of incoming radiation. As with the p–n junction, high efficiency requires the radiative recombination rate to be much higher than the nonradiative recombination rate, and it is unclear whether devices can meet this exacting standard.

In conclusion, the energy flow from Earth to outer space provides a hitherto neglected opportunity to generate a potentially enormous amount of renewable energy. Today’s technology is not sufficient to make an efficient, cost-effective, optoelectronic EEH, but we have described a number of paths that could plausibly lead there over time. We hope that a vigorous research effort will open up this frontier and create a role for EEHs in the renewable energy landscape.